Optimal Battery Dispatch Using Finite-Input Set Non-Linear Model Predictive Control: Algorithm Development and Case Study
Abstract
:1. Introduction
1.1. Motivation
1.2. Related Work
- (1)
- Primary Control: The objective is to regulate the load sharing of distributed energy resources and storage via the local control of output voltage and frequency to attain balanced and autonomous operation of these distributed systems [7,8]. The prototypical strategy is droop control, which dispatches local storage based upon local active and reactive power estimates and frequency voltage/measurements and requires no time-critical communication to a centralised entity [9].
- (2)
- Secondary Control: Secondary control has the responsibility of correcting system-wide voltage and frequency offsets that are achieved by the primary control. Therefore, and an entity to play the role of a system-wide or local system state observer to provide trim commands for the primary control is required. Reactive power-sharing, accurate frequency regulation and PQ compensation are prototypical services provided, using trim commands for frequency and voltage [10,11]. Typically, time-critical communication to a centralised entity playing the role of system-wide observer is required [9]. In a decentralised (or partially decentralised) solution, communications to a central entity are not required (or kept to a minimum) at the expense of added local complexity.
- (3)
- Tertiary Control: This is the highest control level of the control hierarchy. Tertiary Control is typically liable for managing gross active and reactive power entering or leaving the local microgrid, to solve system-wide optimal power flow problems and constraints (OPF) [12]. Again, an entity to play the role of a system-wide state observer is required to solve the OPF and provide local power flow commands. Again time-critical communication to a centralised entity playing the role of system-wide observer is required [9]. In a decentralised (or partially decentralised) solution, communications to a central entity are not required (or kept to a minimum) at the expense of added local complexity.
1.3. Contributions
1.4. Structure
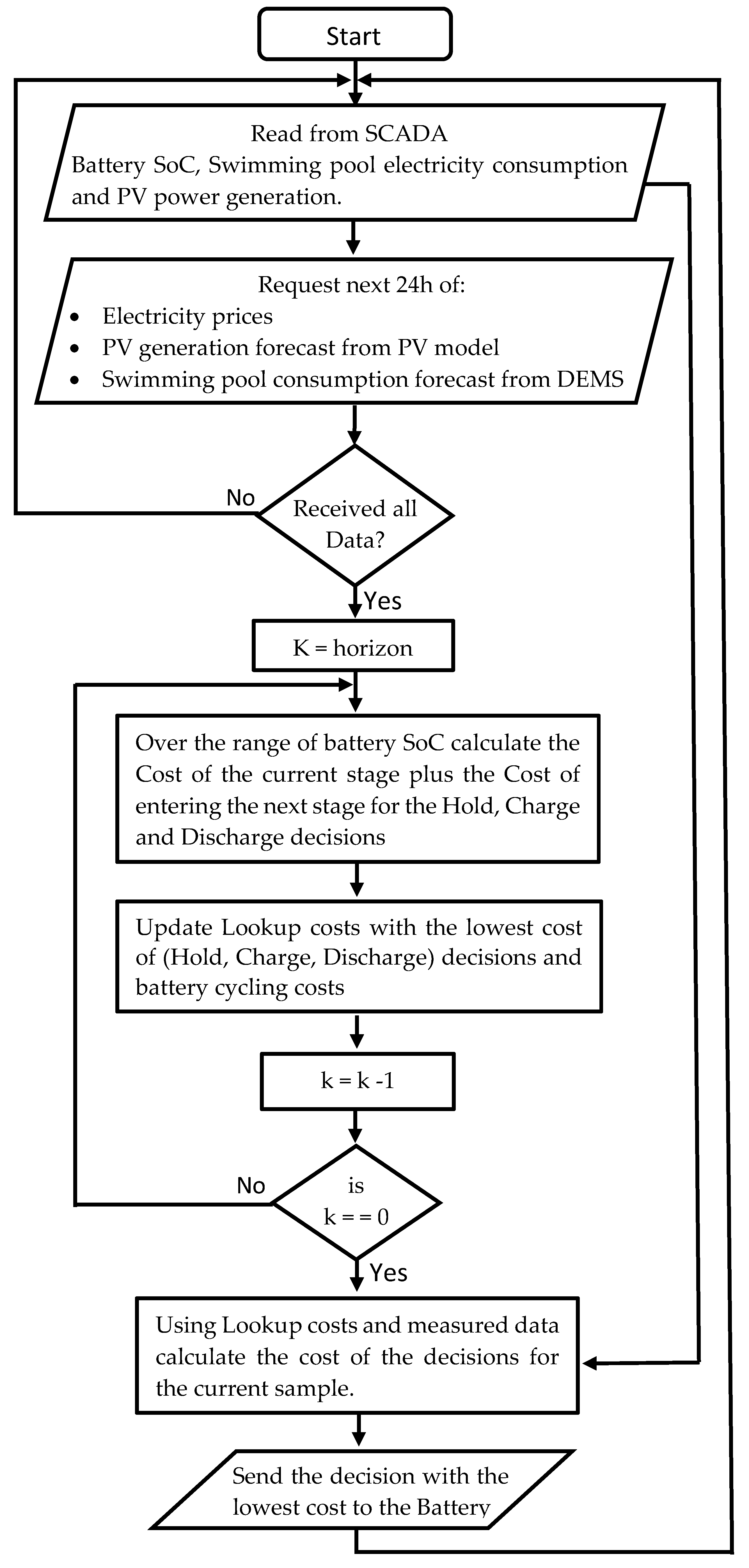
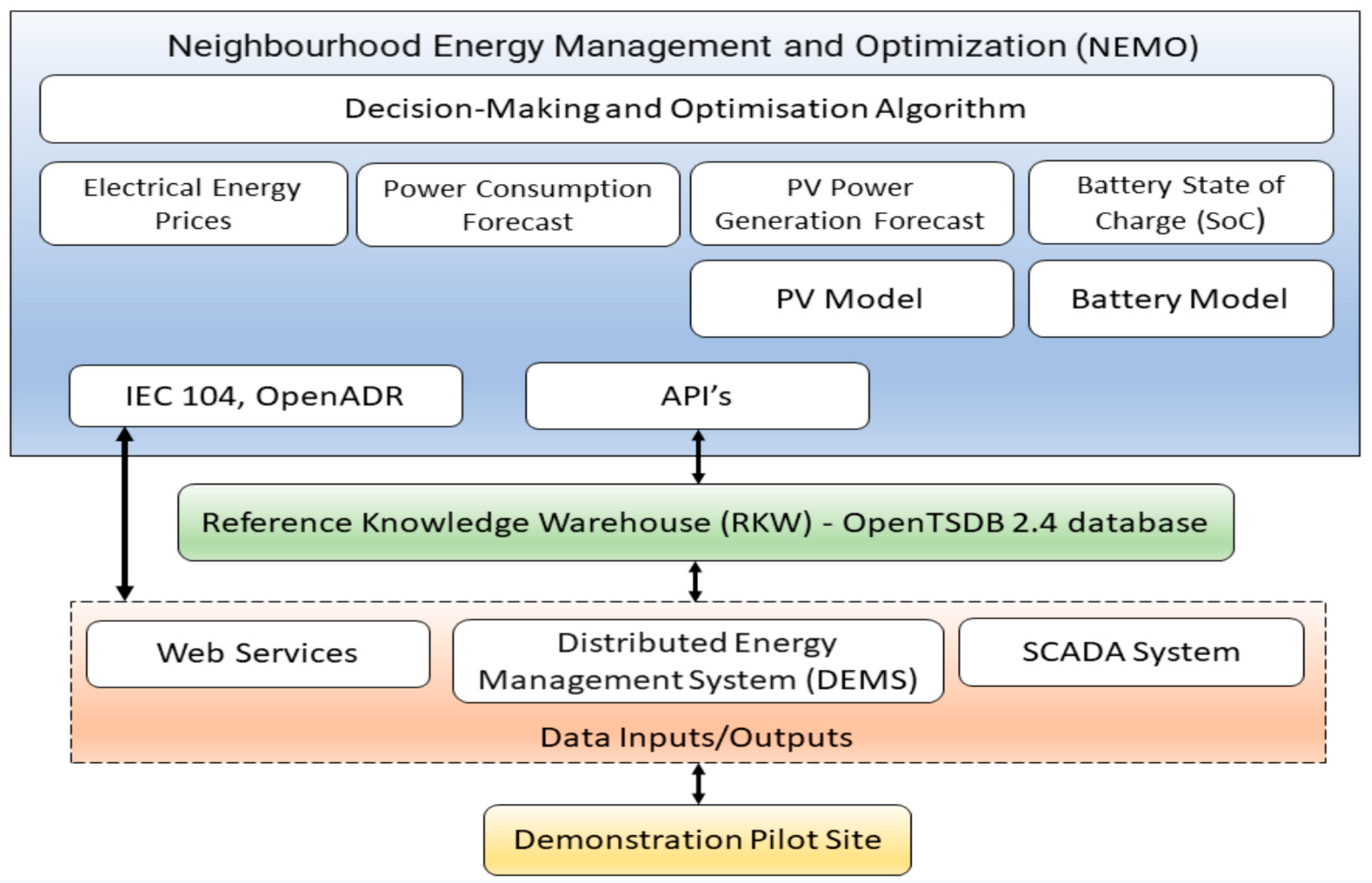
2. Methodology
2.1. Model and Assumptions
2.2. Charge/Discharge Optimization
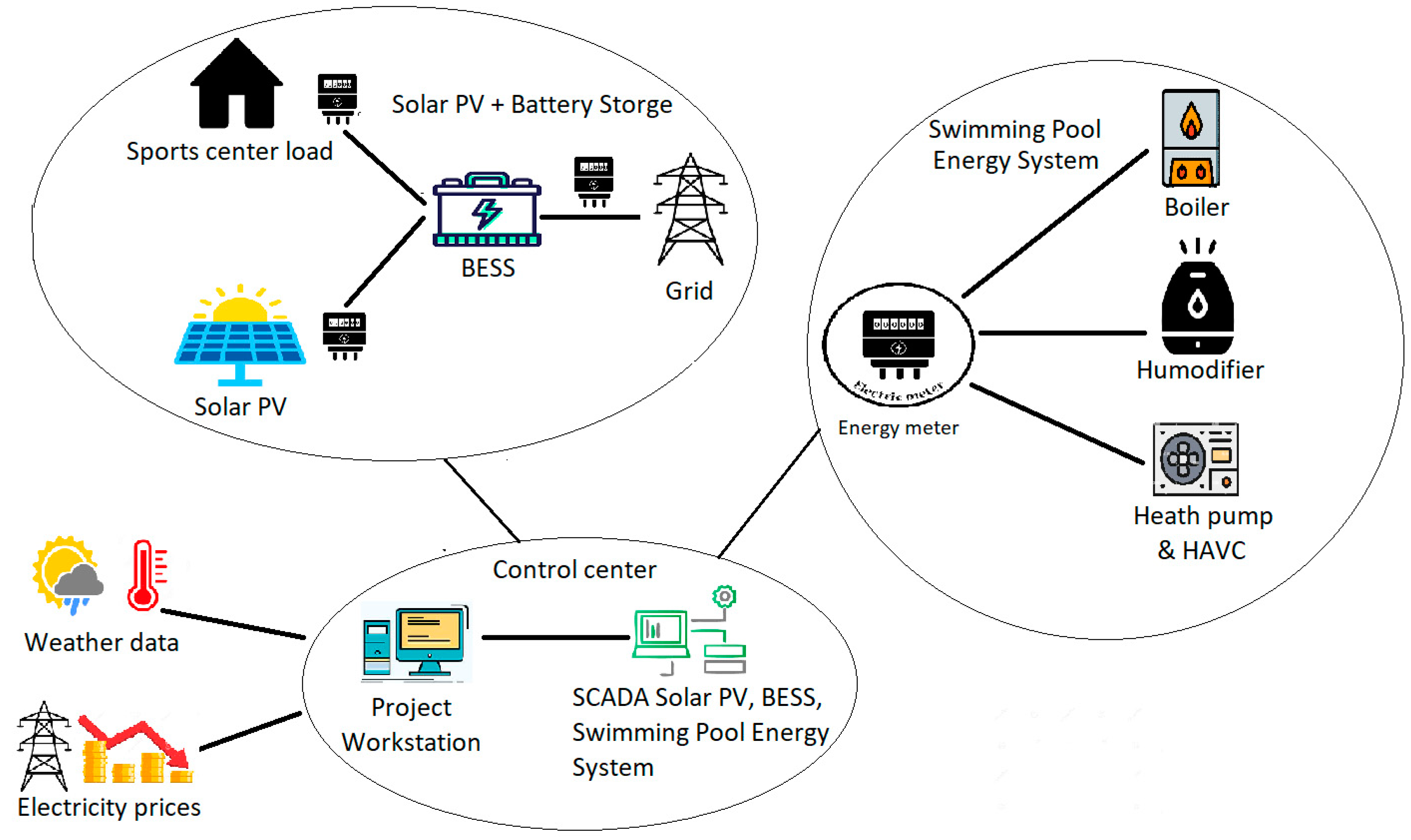
3. Case Study
3.1. Description of the Pilot Site
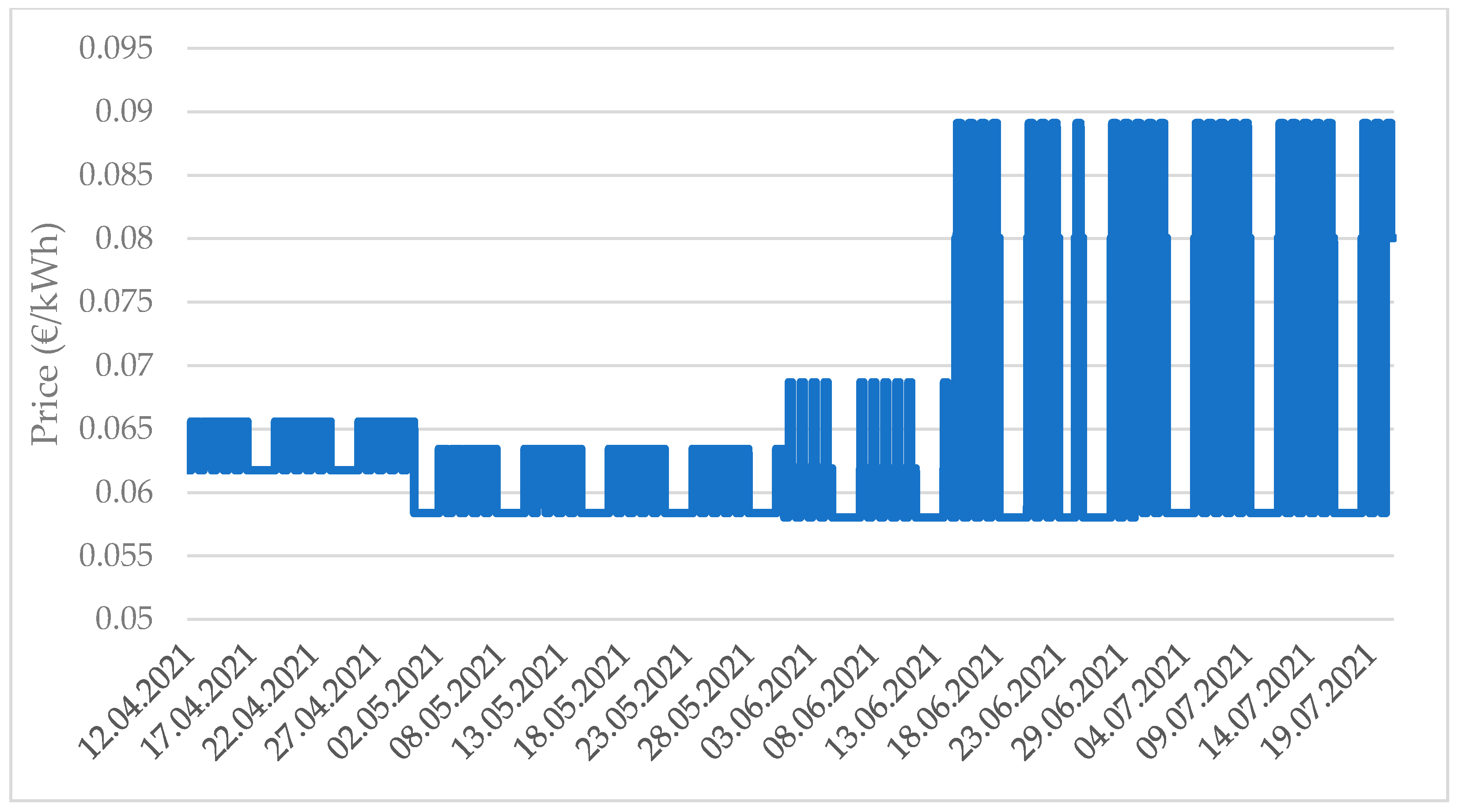
3.2. Use Case Specification
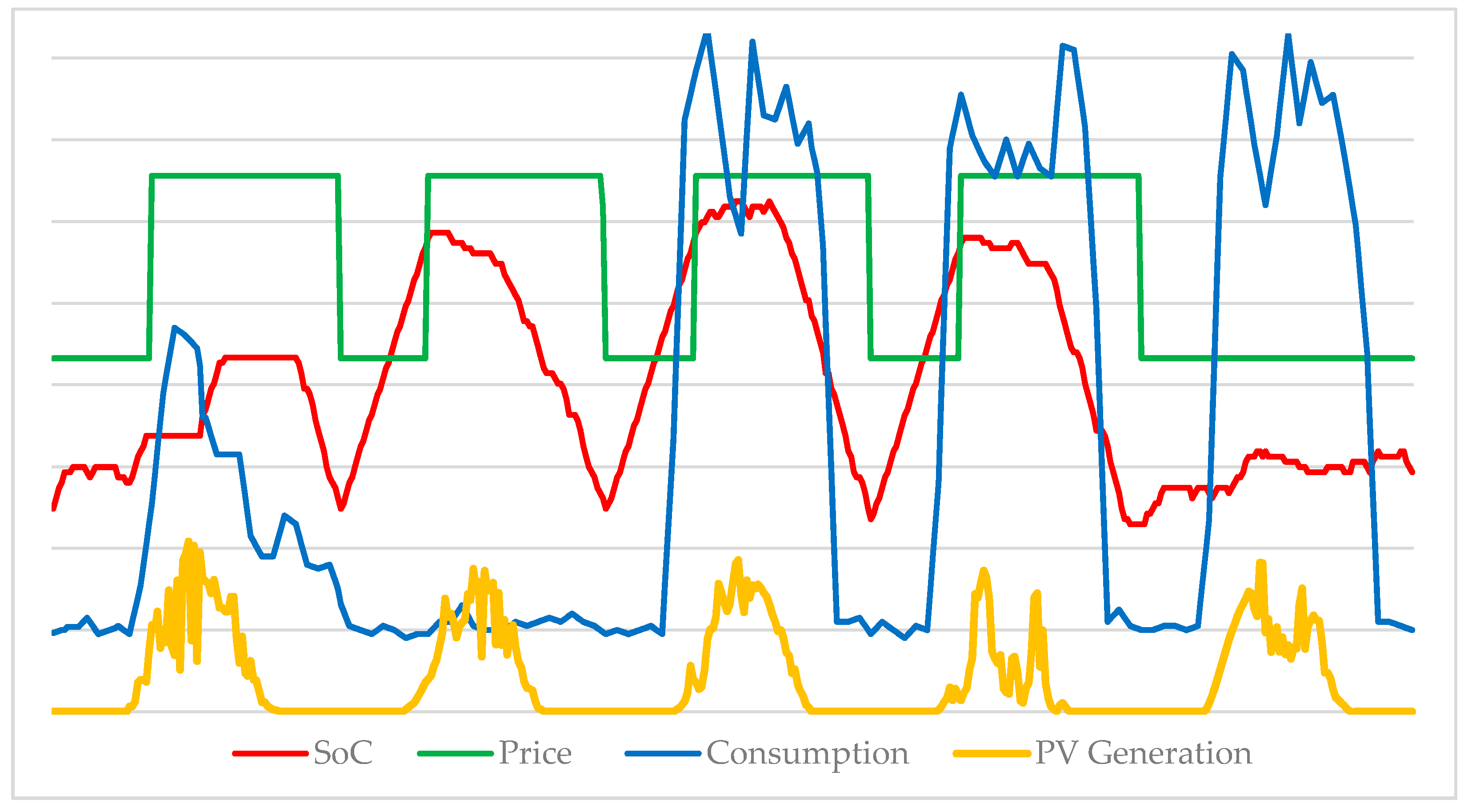
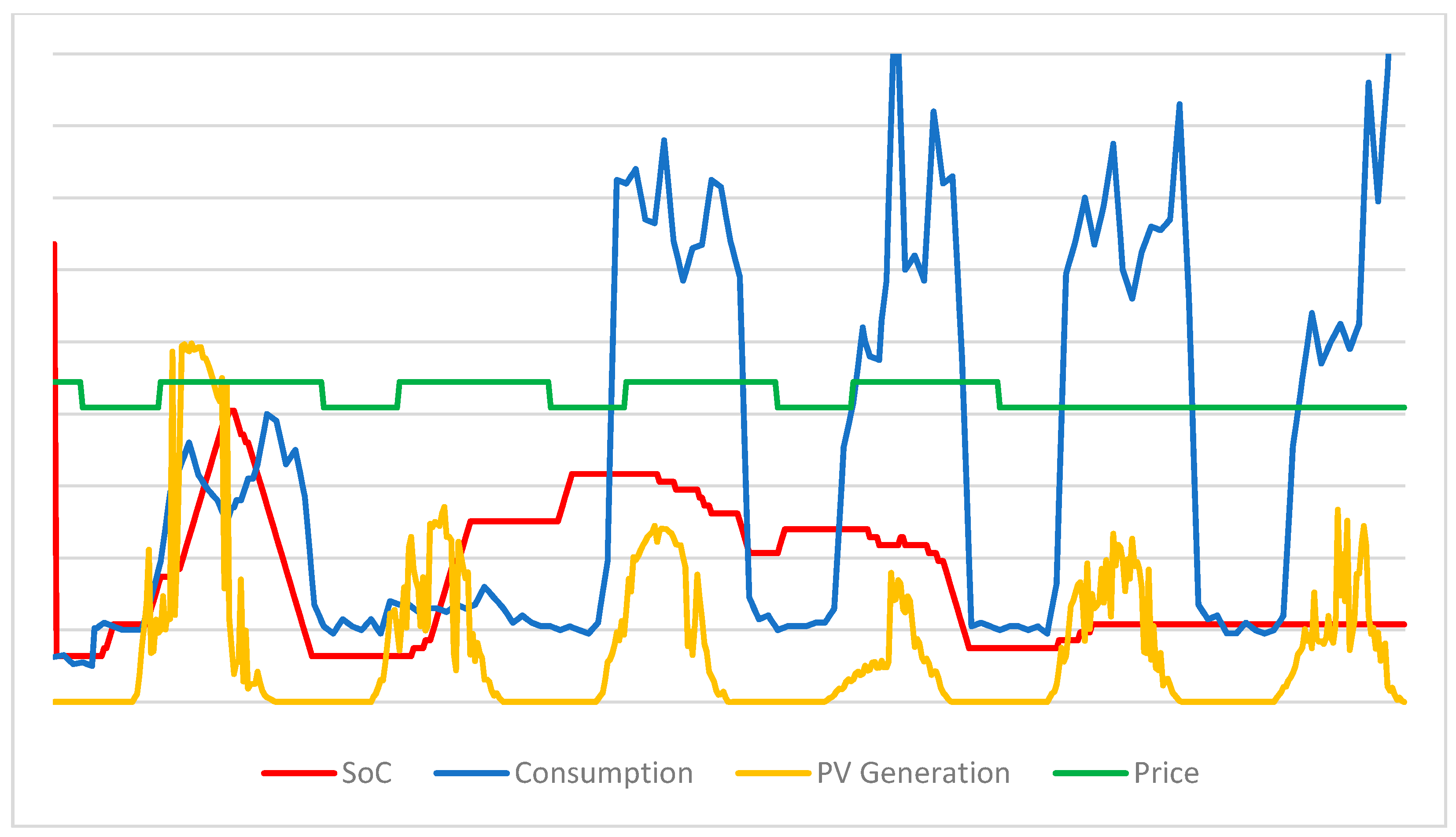
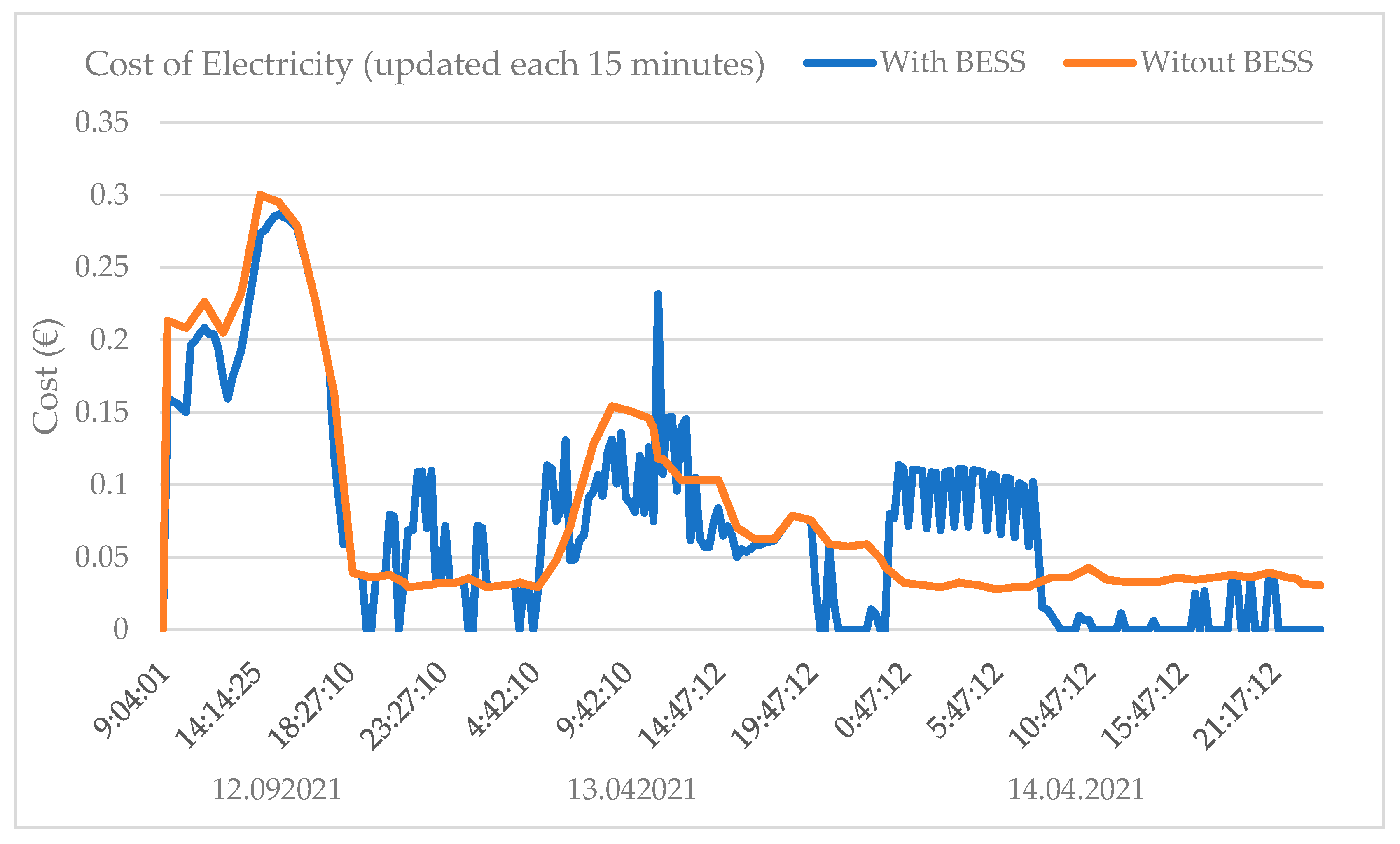
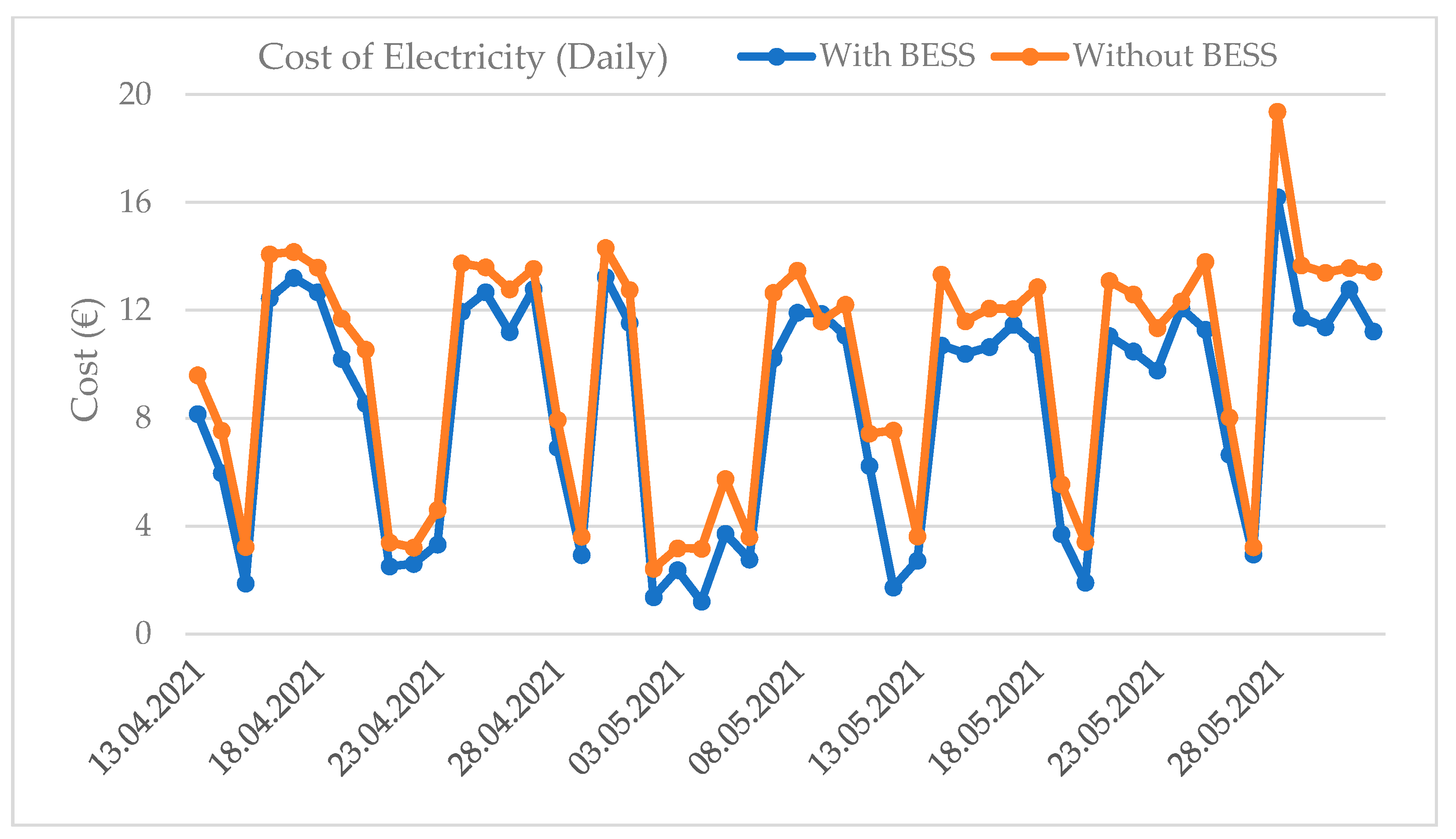
4. Results and Analysis
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviation
| Terms | Description |
| AC | Alternating Current |
| AHU | Air Handling Unit |
| AM | Air Mass |
| API | Application Programming Interface |
| ARM | Advanced RISC Machines |
| BESS | Battery Energy Storage System |
| DC | Direct Current |
| DDP | Discrete Dynamic Programming |
| DEMS | Distributed Energy Management System |
| DC | Direct Current |
| DDP | Discrete Dynamic Programming |
| DEMS | Distributed Energy Management System |
| DG | Distributed Generations |
| DP | Dynamic Programming |
| DR | Demand Response |
| EV | Electric Vehicle |
| FIT | Feed in Tariff |
| GHG | Greenhouse Gas |
| MILP | Mixed Integer Linear Programming |
| MPC | Model Predictive Control |
| NEMO | Neighborhood Energy Management and Optimization |
| OpenADR | Open Automated Demand Response |
| PV | Photovoltaic |
| RES | Renewable Energy Storage |
| RKW | Reference Knowledge Warehouse |
| RTP | Real Time Pricing |
| SCADA | Supervisory Control and Data Acquisition |
| SoC | State of Charge |
| SoH | State of Health |
| STC | Standard Test Conditions |
| TOU | Time of Use |
Nomenclature
| Terms | Description |
| K | Discrete time-step |
| ∆ | Sampling time interval between any discrete steps k and k + 1 |
| C(K) | Battery SoC |
| L(k) | Battery source/sink power level |
| P(k, x) | Economic cost of delivering x kW power demand |
| u(k) | Battery charge/discharge (control) signal |
| Battery maximum SoC | |
| Battery minimum SoC | |
| λ | Battery cycling cost |
| I(k) | Binary indicator variables to signal changes in the battery charging status |
| EI(t) | Electricity imported from the grid |
| PV(t) | Electricity generated by the PV system |
| Change in the battery state of charge |
References
- Short, M.; Rodriguez, S.; Charlesworth, R.; Crosbie, T.; Dawood, N. Optimal Dispatch of Aggregated HVAC Units for Demand Response: An Industry 4.0 Approach. Energies 2019, 12, 4320. [Google Scholar] [CrossRef] [Green Version]
- Al-Saadi, M.; Al-Greer, M.; Short, M. Strategies for Controlling Microgrid Networks with Energy Storage Systems: A Review. Energies 2021, 14, 7234. [Google Scholar] [CrossRef]
- Zhao, J.; Zhu, Z.; Yu, Y.; Lin, C.; Wei, W. Optimal charging/discharging scheme of battery energy storage systems in active distribution network. In Proceedings of the IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–6. [Google Scholar]
- Kapoor, A.; Sharma, A. Optimal Charge/Discharge Scheduling of Battery Storage Interconnected with Residential PV System. IEEE Syst. J. 2019, 14, 3825–3835. [Google Scholar] [CrossRef]
- Cialdea, S.; Orr, J.; Emmanuel, A.; Zhang, T. An optimal battery energy storage charge/discharge method. In Proceedings of the IEEE Electrical Power and Energy Conference, Halifax, NS, Canada, 21–23 August 2013; pp. 1–5. [Google Scholar]
- IRENA. REthinking Energy 2017: Accelerating the Global Energy Transformation; International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2017. [Google Scholar]
- Muhtadi, A.; Pandit, D.; Nguyen, N.; Mitra, J. Distributed energy resources based microgrid: Review of architecture, control, and reliability. IEEE Trans. Ind. Appl. 2021, 57, 2223–2235. [Google Scholar] [CrossRef]
- Legry, M.; Dieulot, J.-Y.; Colas, F.; Saudemont, C.; Ducarme, O. Non-linear primary control mapping for droop-like behavior of microgrid systems. IEEE Trans. Smart Grid 2020, 11, 4604–4613. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Chandorkar, M.; Lee, T.-L.; Loh, P.C. Advanced control architectures for intelligent microgrids—Part I: Decentralized and hierarchical control. IEEE Trans. Ind. Electron. 2012, 60, 1254–1262. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Li, J.; Song, H.; Nawaz, A.; Qu, Y. Nonlinear secondary voltage control of islanded microgrid via distributed consistency. IEEE Trans. Energy Convers. 2020, 35, 1964–1972. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Shafiee, Q.; Dörfler, F.; Vasquez, J.C.; Guerrero, J.M.; Bullo, F. Secondary frequency and voltage control of islanded microgrids via distributed averaging. IEEE Trans. Ind. Electron. 2015, 62, 7025–7038. [Google Scholar] [CrossRef]
- Zhang, R.; Savkin, A.V.; Hredzak, B. Centralized nonlinear switching control strategy for distributed energy storage systems communicating via a network with large time delays. J. Energy Storage 2021, 41, 102834. [Google Scholar] [CrossRef]
- Salinas, S.; Li, M.; Li, P.; Fu, Y. Dynamic energy management for the smart grid with distributed energy resources. IEEE Trans. Smart Grid 2013, 4, 2139–2151. [Google Scholar] [CrossRef]
- Sun, S.; Dong, M.; Liang, B. Real-time power balancing in electric grids with distributed storage. IEEE J. Sel. Top. Signal Process. 2014, 8, 1167–2151. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Mao, S.; Nelms, R. Distributed online algorithm for optimal real-time energy distribution in the smart grid. IEEE Internet Things J. 2014, 1, 70–80. [Google Scholar] [CrossRef]
- Wang, J.; Lu, K.; Ma, L.; Wang, J.; Dooner, M.; Miao, S.; Li, J.; Wang, D. Overview of compressed air energy storage and technology development. Energies 2017, 10, 991. [Google Scholar] [CrossRef] [Green Version]
- Bender, D. Flywheels Energy Storage; Crawley, G.M., Ed.; University of South Carolina: Columbia, SC, USA, 2017; pp. 249–289. [Google Scholar]
- Faraji, F.; Majazi, A.; Al-Haddad, K. A comprehensive review of flywheel energy storage system technology. Renew. Sustain. Energy Rev. 2017, 67, 477–490. [Google Scholar]
- Li, X.; Wang, S. Energy management and operational control methods for grid battery energy storage systems. CSEE J. Power Energy Syst. 2021, 7, 1026–1040. [Google Scholar]
- Li, X.; Yao, L.; Hui, D. Optimal control, and management of a large-scale battery energy storage system to mitigate fluctuation and intermittence of renewable generations. J. Mod. Power Syst. Clean Energy 2016, 4, 593–603. [Google Scholar] [CrossRef] [Green Version]
- Jeong, H.W.; Cha, M.; Oh, U.; Choi, J. Reliability assessment of BESS integrated with PCS by using operation data. IFAC-PapersOnLine 2016, 49, 235–237. [Google Scholar] [CrossRef]
- Byrne, R.H.; Nguyen, T.A.; Copp, D.A.; Chalamala, B.R.; Gyuk, I. Energy management and optimisation methods for grid energy storage systems. IEEE Access 2018, 6, 13231–13260. [Google Scholar] [CrossRef]
- Rizopoulos, D.; Esztergar-Kiss, D. A method for the optimisation of Daily Activity Including Electric Vehicles. Energies 2020, 13, 906. [Google Scholar] [CrossRef] [Green Version]
- Mahmoudi, C.; Flah, A.; Sbita, L. An overview of Electric Vehicle Concept and Power Management Strategies. In Proceedings of the 2014 International Conference on Electrical Sciences and Technologies in Maghreb, Tunis, Tunisia, 3–6 November 2014; pp. 1–8. [Google Scholar]
- Tran, M.-K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Williams, S.; Short, M. Electricity demand forecasting for decentralised energy management. Energy Built Environ. 2020, 1, 178–186. [Google Scholar] [CrossRef]
- Ogwumike, C.; Short, M.; Abugchem, F. Heuristic Optimisation of Consumer Electricity Costs using a Generic Cost Model. Energies 2016, 9, 6. [Google Scholar] [CrossRef] [Green Version]
- Ogwumike, C.; Short, M.; Abugchem, F. Heuristic scheduling of multiple smart home appliances: Utility planning perspective. In Proceedings of the International Conference for Students on Applied Engineering (ICSAE), Newcastle upon Tyne, UK, 20–21 October 2016; pp. 237–241. [Google Scholar]
- Gailani, A.; Al-Greer, M.; Short, M.; Crosbie, T. Degradation Cost Analysis of Li-Ion Batteries in the Capacity Market with Different Degradation Models. Electronics 2020, 9, 90. [Google Scholar] [CrossRef] [Green Version]
- Camacho, E.F.; Bordons, C. Model Predictive Control, 2nd ed.; Springer: London, UK, 2004. [Google Scholar]
- Agnetis, A.; de Pascale, G.; Detti, P.; Vicino, P.A. Load scheduling for household energy consumption optimization. IEEE Trans. Smart Grid 2013, 4, 2364–2373. [Google Scholar] [CrossRef]
- Farrokhifar, N.; Aghdam, F.H.; Alahyari, A.; Monavari, A.; Safari, A. Optimal energy management and sizing of renewable energy and battery systems in residential sectors via a stochastic MILP model. Electr. Power Syst. Res. 2020, 187, 106483. [Google Scholar] [CrossRef]
- Bellman, R.E. Dynamic Programming; 3 Press: Princeton, NJ, USA, 1957. [Google Scholar]
- Bertsekas, D.P. Dynamic Programming and Optimal Control; Athena Scientific: Belmont, MA, USA, 2005. [Google Scholar]
- Short, M. Development Guidelines for Dependable Real-Time Embedded Systems. In Proceedings of the 6th IEEE/ACSInternational Conference on Computer Systems and Applications (AICCSA 2008), Doha, Qatar, 31 March–4 April 2008; pp. 1032–1039. [Google Scholar]



| PV Module Characteristics | |
|---|---|
| Brand and Model | JA Solar—JAM72S10-335/SC |
| Rated Power | 335 Wp |
| Maximum Power Current | 8.95 A |
| Maximum Power Voltage | 37.45 V |
| Short Circuit Current | 9.42 V |
| Open Circuit Voltage | 46.10 V |
| Module Efficiency | 17% |
| Dimesnsions | 1979 × 996 × 35 mm |
| Weight | 22.3 kg |
| On-Grid Inverter Technical Parameters | |
|---|---|
| Brand and Model | SMA Sunny Boy 5.0 TL |
| Rated Output Power (AC) | 5000 W |
| Nominal Output (AC) Voltage | 230 V |
| Maximum Power PV field | 7500 Wp |
| Maximum Input Voltage | 600 V |
| MPP voltage range | 175 V to 500 V |
| Efficiency | 96.6% |
| Number of independent MPP inputs | 2 |
| Strings per MPP input | 2 + 2 |
| Dimensions | 435 × 470 × 176 mm |
| Weight | 16 kg |
| Battery Bank’s Characteristics | |
| Brand and Model | CALB CA180 201412 |
| Storage capacity (Wh) | 63,072 Wh |
| Storage capacity (Ah) | 1080 Ah |
| Rated Voltage | 58.4 V |
| Nominal Voltage | 51.2 V |
| Number of Elements in series | 16 |
| Number of series in parallel | 6 |
| Configuration | 16s6p scheme |
| Battery Unit’s Characteristics | |
| Technology | LiFeO4 |
| Storage Capacity (WhC100) | 657 Wh |
| Storage capacity (AhC100) | 180 Ah |
| Rated Voltage | 3.65 V |
| Nominal Voltage | 3.2 V |
| Number of cycles 60% DOD (Depth of Discharge) | 2000 |
| SoC Usage Window | 10–90% |
| Weight | 5.70 kg |
| KPIs | Values | Units |
|---|---|---|
| Total energy consumption | 13,853.67397 | kWh |
| Energy imported from the grid | 11,518.3434 | kWh |
| Self-consumption | 2335.330568 | kWh |
| Self-consumption rate | 16.88011839 | % |
| CO2 emission reduction | 772.9944181 | kgCO2 |
| Retailer cost of energy | 903.7044321 | € |
| Average cost of energy consumption | 0.045446171 | €/kWh |
| Cost of energy reward | 177.596953 | € |
| Cost of reduction rate | 19.65210597 | % |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abugchem, F.; Short, M.; Ogwumike, C.; Dawood, H. Optimal Battery Dispatch Using Finite-Input Set Non-Linear Model Predictive Control: Algorithm Development and Case Study. Electronics 2022, 11, 101. https://doi.org/10.3390/electronics11010101
Abugchem F, Short M, Ogwumike C, Dawood H. Optimal Battery Dispatch Using Finite-Input Set Non-Linear Model Predictive Control: Algorithm Development and Case Study. Electronics. 2022; 11(1):101. https://doi.org/10.3390/electronics11010101
Chicago/Turabian StyleAbugchem, Fathi, Michael Short, Chris Ogwumike, and Huda Dawood. 2022. "Optimal Battery Dispatch Using Finite-Input Set Non-Linear Model Predictive Control: Algorithm Development and Case Study" Electronics 11, no. 1: 101. https://doi.org/10.3390/electronics11010101
APA StyleAbugchem, F., Short, M., Ogwumike, C., & Dawood, H. (2022). Optimal Battery Dispatch Using Finite-Input Set Non-Linear Model Predictive Control: Algorithm Development and Case Study. Electronics, 11(1), 101. https://doi.org/10.3390/electronics11010101









