A Hierarchical Multicast Key Distribution Protocol
Abstract
1. Introduction
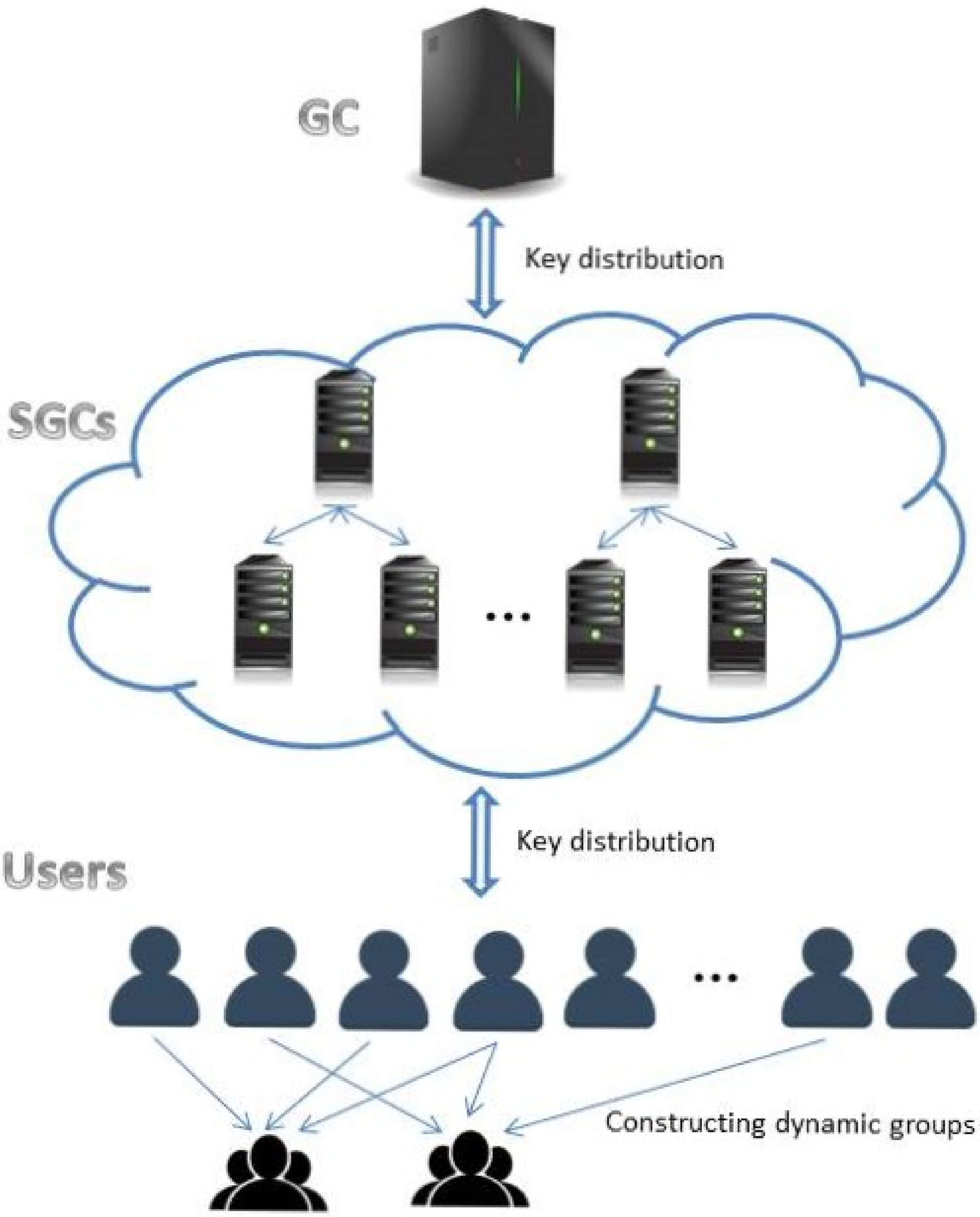
- A balanced GC works on multi-level servers. Each controller manages only the next-level nodes. Thus, no matter the group size, controllers will not be overworked.
- SGC replacement mechanism. The superior controller retains the ability to maintain the subordinate nodes’ keys (not only the next nodes). Hence, if an SGC breaks down, the upper controller can directly and easily take its place.
- Dynamic conference without controllers. Each group member can easily find all sub-trees covering all group members, and use the IDs of their roots to encrypt the CK.
- Customized specific information to limit the group member. We could add the time information into ID and it could be used to force the group member to decrypt the rekeying message at a certain time.
2. Related Work
3. System Model and Security Requirements
3.1. Notation
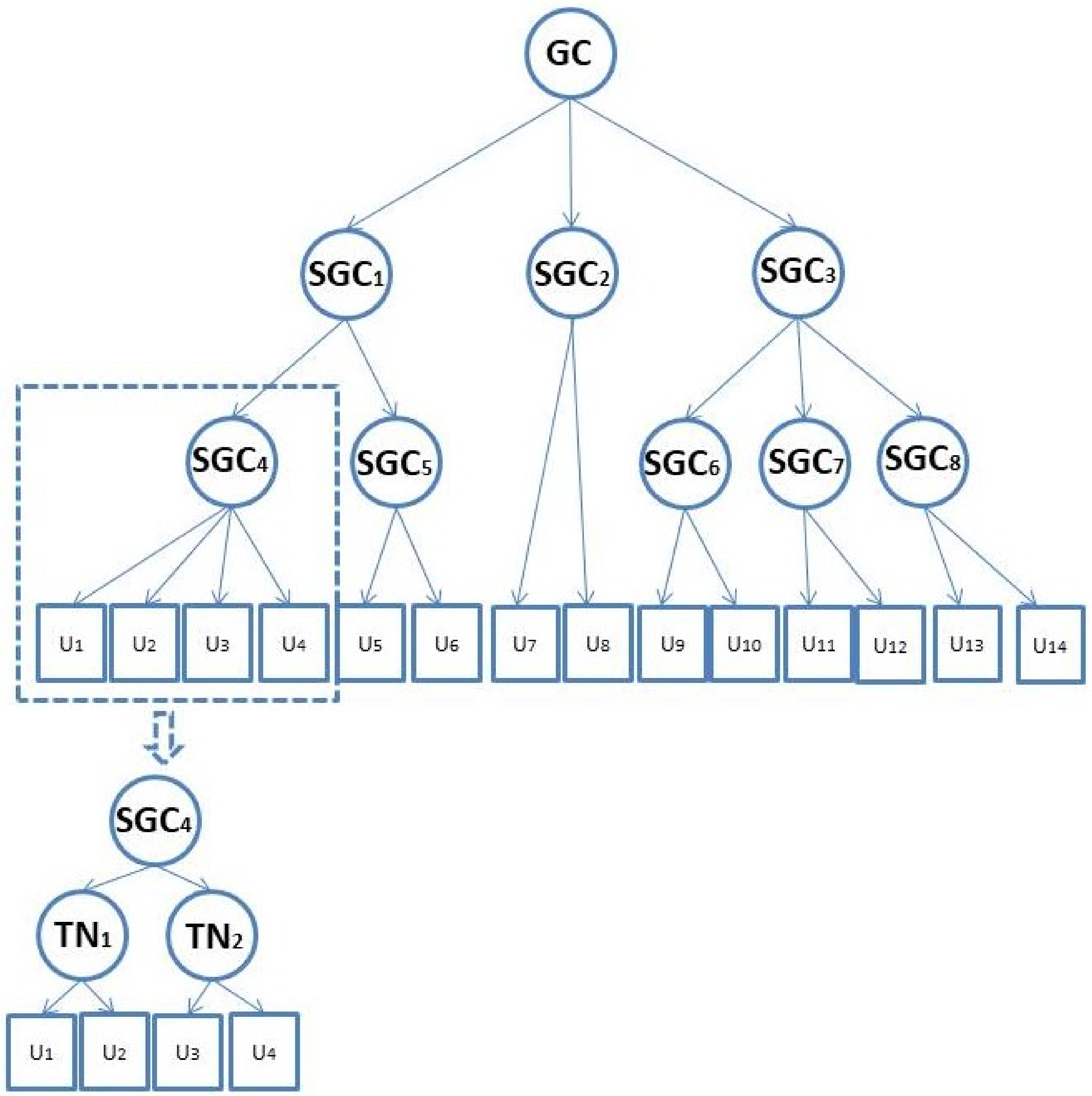
3.2. System Model
3.3. Security Requirements
- Group confidentiality: Anyone not in the group cannot obtain any information about group communication.
- Backward secrecy: A new group member cannot decrypt group communication prior to his/her joining, even with new keys.
- Forward secrecy: An old member cannot decrypt future group communication after leaving, even with the old keys.
- Collusion resistance: Members who are not in the group at time t cannot decrypt group communication of time t.
4. Our Construction
4.1. Hierarchical Identity-Based Encryption
- : This algorithm takes a security parameter as input, and outputs the public parameters and the master key . The description of the message space, ciphertext space, and identity space is given in . Let l denote the maximal level of the HIBE. and l are public, and is secret. This algorithm is run by the PKG.
- : This algorithm generates a private key for an identity . It has two kinds of inputs, which apply to three situations. If the inputs are the identity and master key , this algorithm is run by the PKG. If the inputs are the identity , private key , and number of distinct layers k, this algorithm is run by the SGC.
- : This algorithm takes the public parameters , identity , and message as inputs, and outputs the ciphertext. It can be run by anyone.
- : This takes the private key and ciphertext as the inputs, and generates a plain message. This algorithm is run by member .
4.2. Construction
4.2.1. System-Init
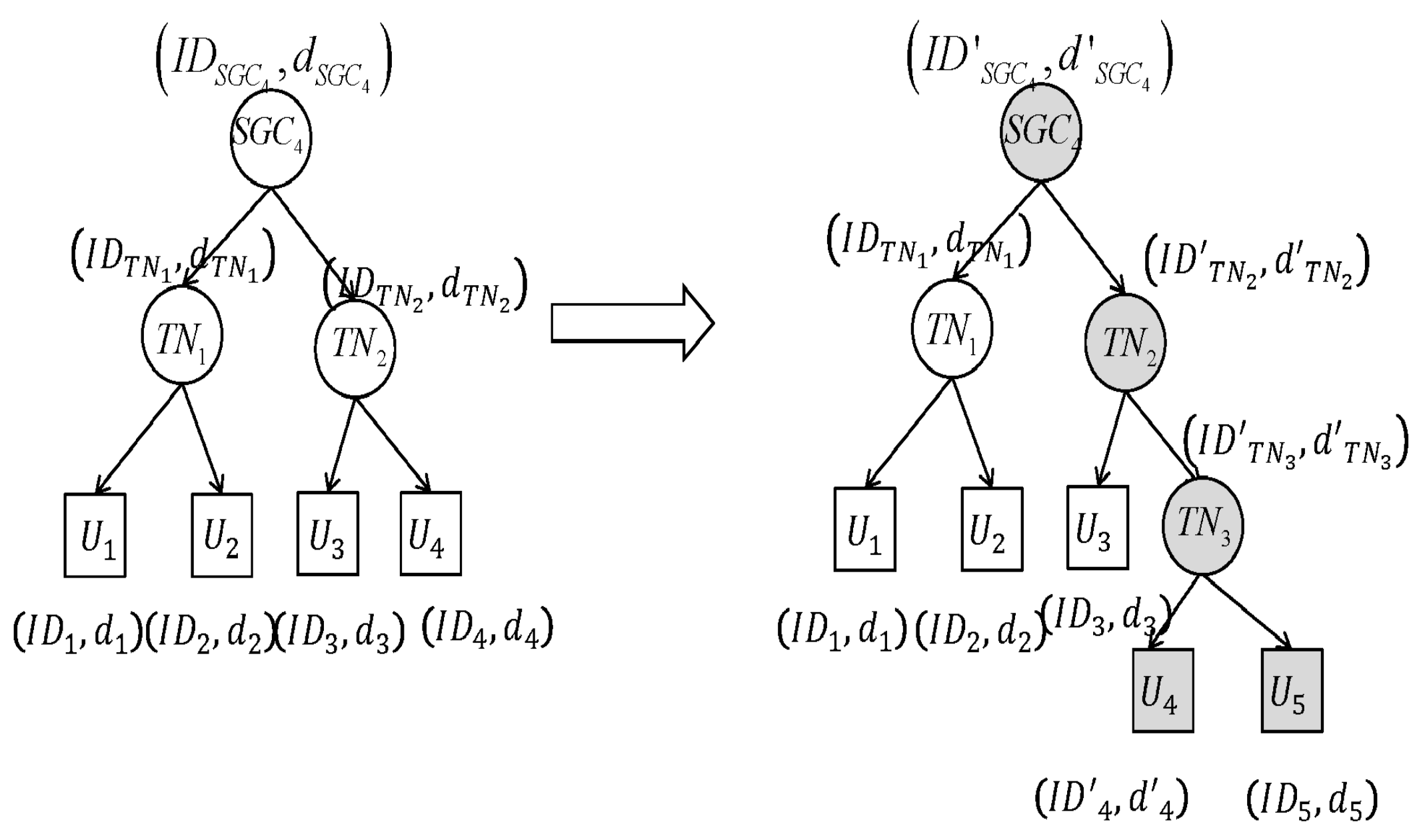
4.2.2. Member-Join
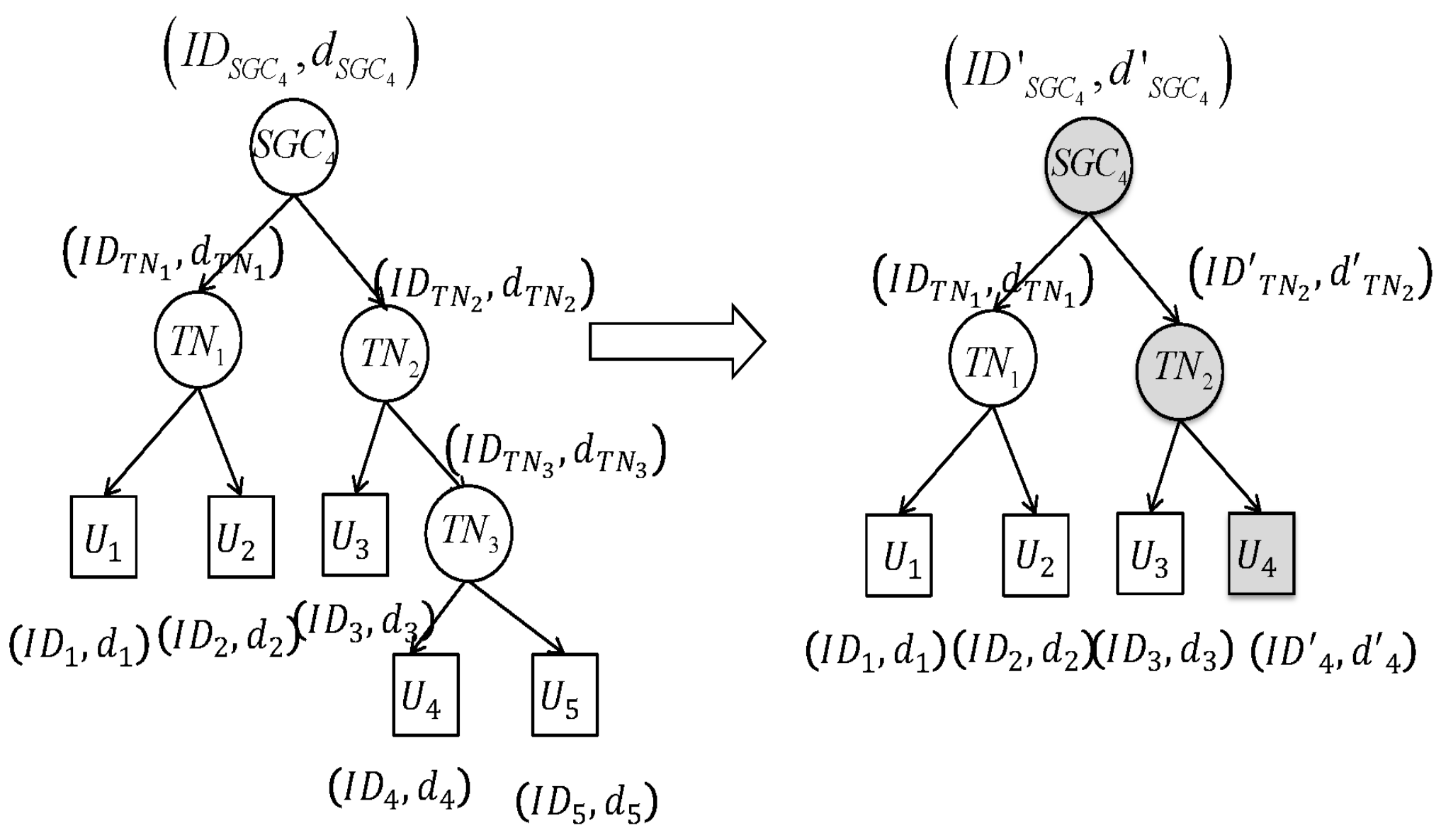
4.2.3. Member-Leave
4.2.4. SGC Replacement Mechanism
4.3. Security Proof
4.4. Extension on Dynamic Conference
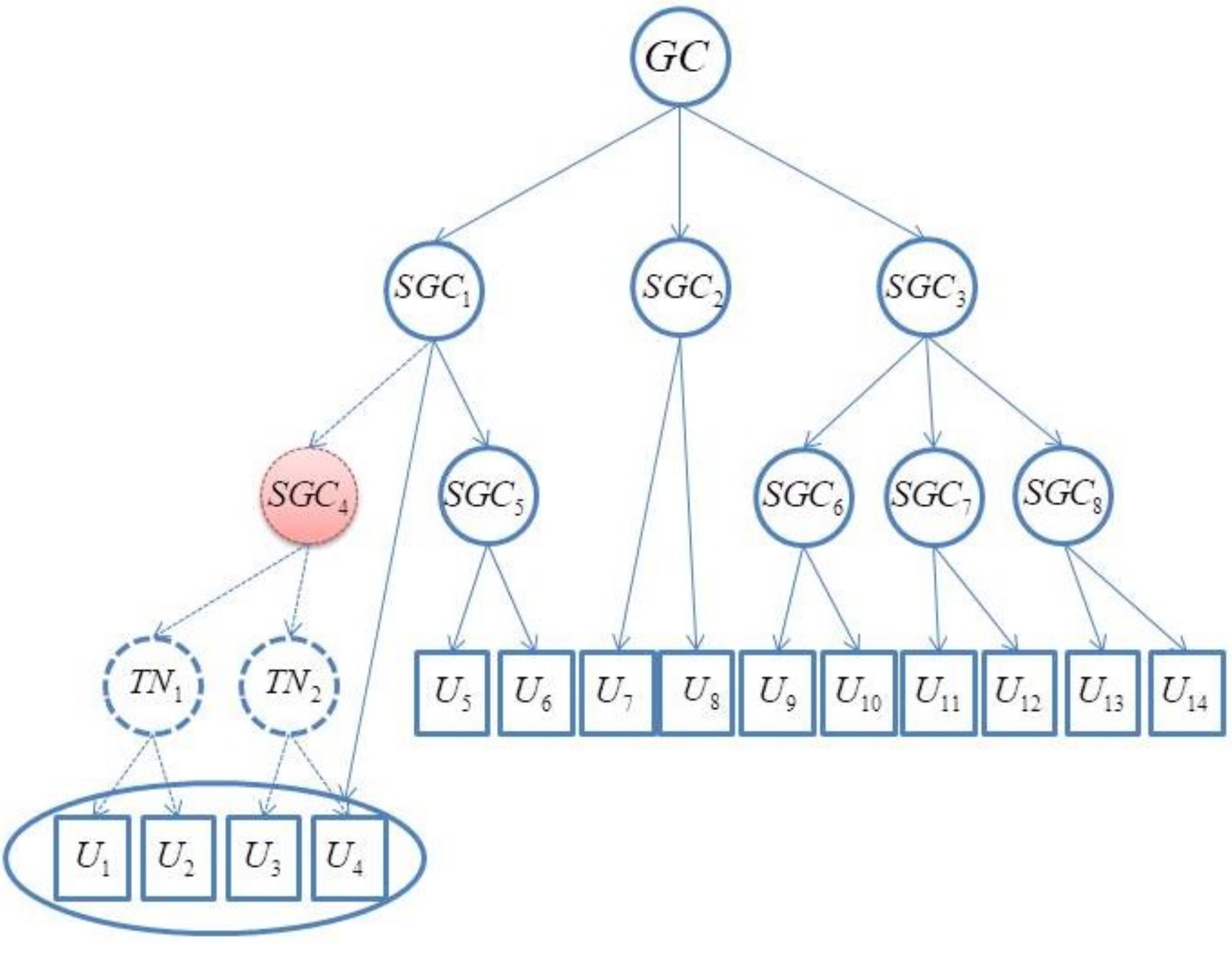
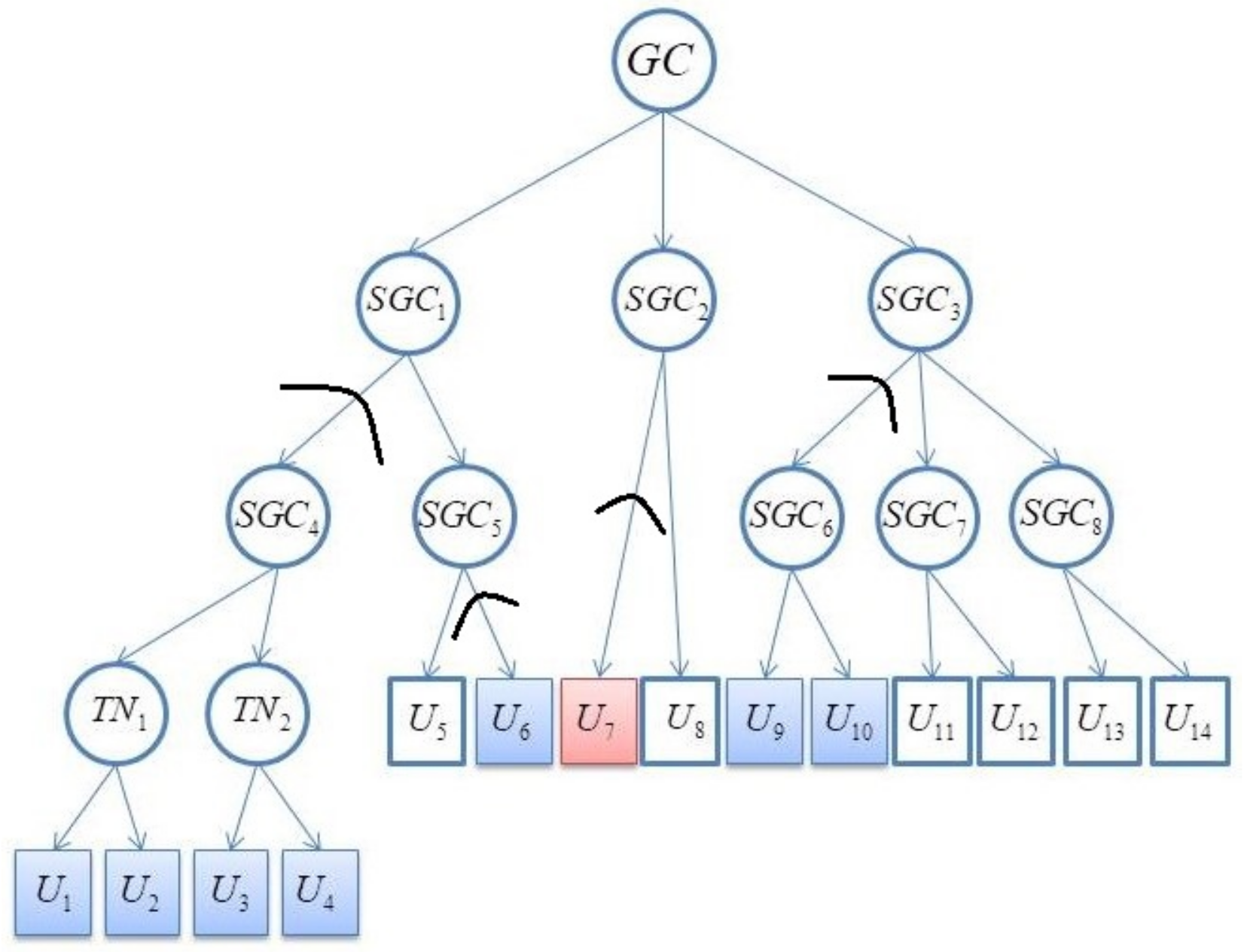
- Building a Steiner tree. Let be a Steiner tree containing all the R nodes and nodes in the path from the leaf node to the root.
- Finding the subtrees. Let T be the whole key tree. The subtrees are . As Figure 6 shows, the subtrees consist of nodes linked by black lines with curves.
- Sending safely. The member who sets up the conference generates a encrypts it with the public keys of the subtrees’ root nodes, and broadcasts it to all the members. Referring to Figure 6, the message of the conference key distribution is .
- Recovering . When the legal members receive the message, they can decrypt it and obtain .
5. Comparison
5.1. Performance
5.1.1. Theoretical Analysis
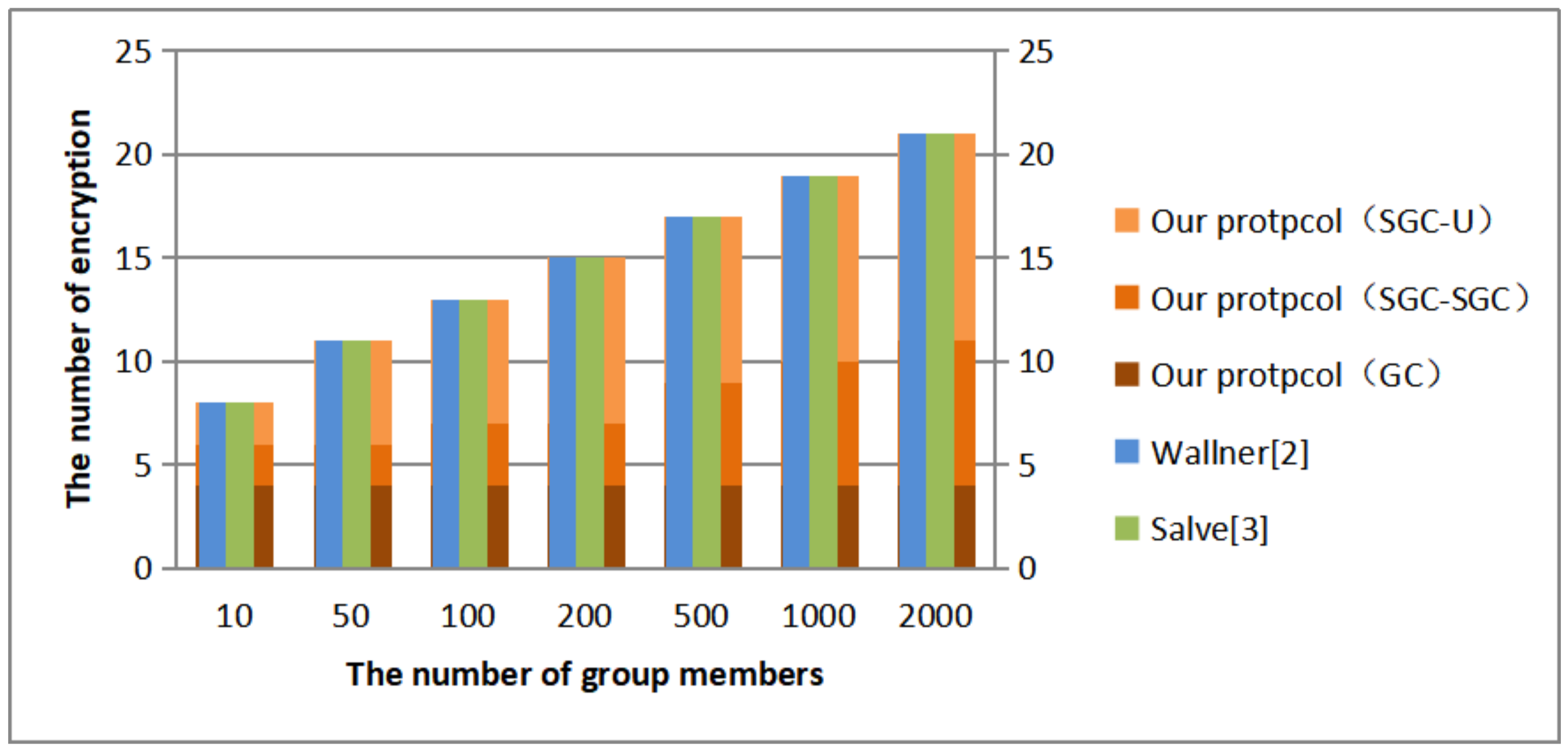
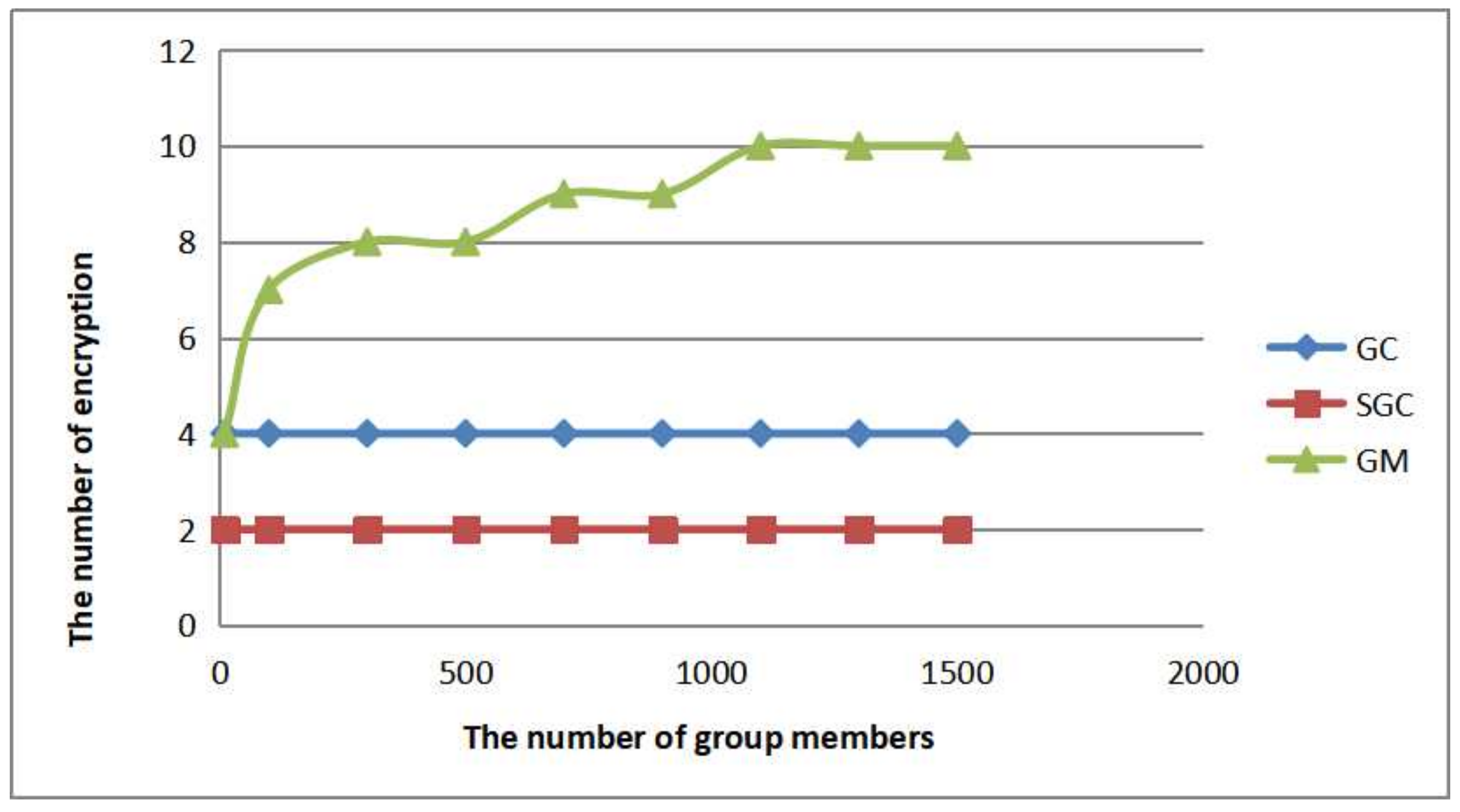
5.1.2. Experimental Analysis
5.2. Functionality and Security
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hardjono, T.; Dondeti, L.R. Multicast and Group Security; Artech House: Boston, MA, USA, 2003. [Google Scholar]
- Wallner, D.; Harder, E.; Agee, R. Key Management for Multicast: Issues and Architectures; RFC 2627; Internet Society: Reston, VA, USA, 1999. [Google Scholar]
- De Salve, A.; Di Pietro, R.; Mori, P.; Ricci, L. A logical key hierarchy based approach to preserve content privacy in decentralized online social networks. IEEE Trans. Dependable Secur. Comput. 2017, 17, 2–21. [Google Scholar] [CrossRef]
- Sun, F.; Zang, W.; Huang, H.; Farkhatdinov, I.; Li, Y. Accelerometer-Based Key Generation and Distribution Method for Wearable IoT Devices. IEEE Internet Things J. 2021, 8, 1636–1650. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Vijayakumar, P.; He, D.; Ma, J. Blockchain Based Mutual-Healing Group Key Distribution Scheme in Unmanned Aerial Vehicles Ad-Hoc Network. IEEE Trans. Veh. Technol. 2019, 68, 11309–11322. [Google Scholar] [CrossRef]
- Lei, A.; Cruickshank, H.; Cao, Y.; Asuquo, P.; Ogah, C.P.A.; Sun, Z. Blockchain-based dynamic key management for heterogeneous intelligent transportation systems. IEEE Internet Things J. 2017, 4, 1832–1843. [Google Scholar] [CrossRef]
- Rao, R.V.; Selvamani, K.; Kanimozhi, S.; Kannan, A. Hierarchical group keymanagement for secure data sharing in a cloud-based environment. Concurr. Comput. Pract. Exp. 2019, 31, 4866. [Google Scholar]
- Pande, A.; Joshi, D.Y.; Joshi, D.; Wadhwa, D. Analysis of Tree structure for Secure Group Communication Using LKH Approach. Int. J. Comput. Sci. Eng. 2019, 7, 1130–1136. [Google Scholar] [CrossRef]
- Anand, A.; Conti, M.; Kaliyar, P.; Lal, C. TARE: Topology Adaptive Re-kEying scheme for secure group communication in IoT networks. Wirel. Netw. 2020, 26, 2449–2463. [Google Scholar] [CrossRef]
- Pandi Vijayakumar, M.A.; Kannan, A.; Deborah, L.J. Dual authentication and key management techniques for secure data transmission in vehicular ad hoc networks. IEEE Trans. Intell. Transp. Syst. 2016, 17, 1015–1028. [Google Scholar] [CrossRef]
- Joshi, M.Y.; Bichkar, R.S. A Centralized Key Table based Communication Efficient Group Key Management Protocol. Int. J. Comput. Netw. Inf. Secur. 2015, 7, 49–55. [Google Scholar] [CrossRef][Green Version]
- Tang, S.; Xu, L.; Liu, N.; Huang, X.; Ding, J.; Yang, Z. Provably secure group key management approach based upon hyper-sphere. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 3253–3263. [Google Scholar] [CrossRef]
- Tsitaitse, T.J.; Cai, Y.; Ditta, A. Secure self-healing group key distribution scheme with constant storage for SCADA systems in smart grid. Wirel. Pers. Commun. 2018, 101, 1749–1763. [Google Scholar] [CrossRef]
- Nabeel, M.; Bertino, E. Poster: Towards attribute based group key management. In Proceedings of the 18th ACM conference on Computer and Communications Security, Chicago, IL, USA, 17–21 October 2011; pp. 821–824. [Google Scholar]
- Rajkumar, N.; Kannan, E. Attribute-Based Collusion Resistance in Group-Based Cloud Data Sharing using LKH Model. J. Circuits Syst. Comput. 2020, 29, 2030001. [Google Scholar] [CrossRef]
- Zhong, H.; Luo, W.; Cui, J. Multiple multicast group key management for the Internet of People. Concurr. Comput. Pract. Exp. 2017, 29, 3817–3831. [Google Scholar] [CrossRef]
- Kung, Y.H.; Hsiao, H.C. GROUPIT: Lightweight Group Key Management for Dynamic IoT Environments. IEEE Internet Things J. 2018, 5, 5155–5165. [Google Scholar] [CrossRef]
- Alphand, O.; Amoretti, M.; Claeys, T.; Dall’Asta, S.; Zanichelli, F. IoTChain: A Blockchain Security Architecture for the Internet of Things. In Proceedings of the 2018 IEEE Wireless Communications and Networking Conference (WCNC), Barcelona, Spain, 15–18 April 2018; pp. 1–6. [Google Scholar]
- Pal, O.; Alam, B. Key management scheme for secure group communication. In Advances in Data and Information Sciences; Springer: Berlin/Heidelberg, Germany, 2020; pp. 171–177. [Google Scholar]
- Boneh, D.; Boyen, X.; Goh, E.J. Hierarchical identity based encryption with constant size ciphertext. In Annual International Conference on the Theory and Applications of Cryptographic Techniques; Springer: Berlin/Heidelberg, Germany, 2005; pp. 440–456. [Google Scholar]
- Aboba, B.; Simon, D. Ppp eap tls Authentication Protocol; RFC 2716; Internet Society: Reston, VA, USA, 1999. [Google Scholar]
- Panjwani, S.K. Private Group Communication: Two Perspectives and A Unifying Solution. Ph.D. Thesis, UC San Diego, San Diego, CA, USA, 2007. [Google Scholar]
| Variables | Description |
|---|---|
| Subgroup controller | |
| Group key generated by GC or SGC whose identity is | |
| Identity of member | |
| Private key of member | |
| Key encryption key | |
| Temporary node | |
| Cipher block | |
| Rekeying message that consists of cipher blocks |
| Protocol | Wallner | Salve | Our Protocol | |
|---|---|---|---|---|
| Storage overload | GC | - | ||
| SGC | - | |||
| GM | h | |||
| Computational overload (Join) | GC | - | ||
| SGC | - | |||
| GM | ||||
| Computational overload (Leave) | GC | - | ||
| SGC | - | |||
| GM | ||||
| Communication overload | Join | |||
| Leave | h | |||
| Protocol | Reliability | Group Type | Security |
|---|---|---|---|
| Nabeel [14] | Strong | Multiple | Unable to resist collusion attacks |
| Rajkumar [15] | Strong | Multiple | Secure against collusion attacks |
| Salve [3] | Weak | Single | Secure against collusion attacks |
| Lei [6] | Strong | Single | Secure against collusion attacks |
| Our protocol | Strong | Multiple | Secure against collusion attacks |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Yao, S.; Liu, J.; Wu, Y. A Hierarchical Multicast Key Distribution Protocol. Electronics 2021, 10, 995. https://doi.org/10.3390/electronics10090995
Li J, Yao S, Liu J, Wu Y. A Hierarchical Multicast Key Distribution Protocol. Electronics. 2021; 10(9):995. https://doi.org/10.3390/electronics10090995
Chicago/Turabian StyleLi, Jie, Shaowen Yao, Jing Liu, and Yunyun Wu. 2021. "A Hierarchical Multicast Key Distribution Protocol" Electronics 10, no. 9: 995. https://doi.org/10.3390/electronics10090995
APA StyleLi, J., Yao, S., Liu, J., & Wu, Y. (2021). A Hierarchical Multicast Key Distribution Protocol. Electronics, 10(9), 995. https://doi.org/10.3390/electronics10090995





