DoA Estimation Using Neural Tangent Kernel under Electromagnetic Mutual Coupling
Abstract
1. Introduction
- We leverage recent progress in modeling and deriving DNNs using kernel regression with a NTK to estimate DoA. In the infinite width limit, instead of training the network, the exact dynamics of its outputs are characterized by a differential equation (through gradient descent training). Numerical experiments show that the developed method has good performance in term of the estimation accuracy and computational time under the effect of electromagnetic mutual coupling.
- We incorporate the PRF feature into NTK to estimate multiple DoAs, which largely enhances the generalization of the proposed method to multiple arriving signals scenarios. This method performs well even though the training dataset represents single incoming waves.
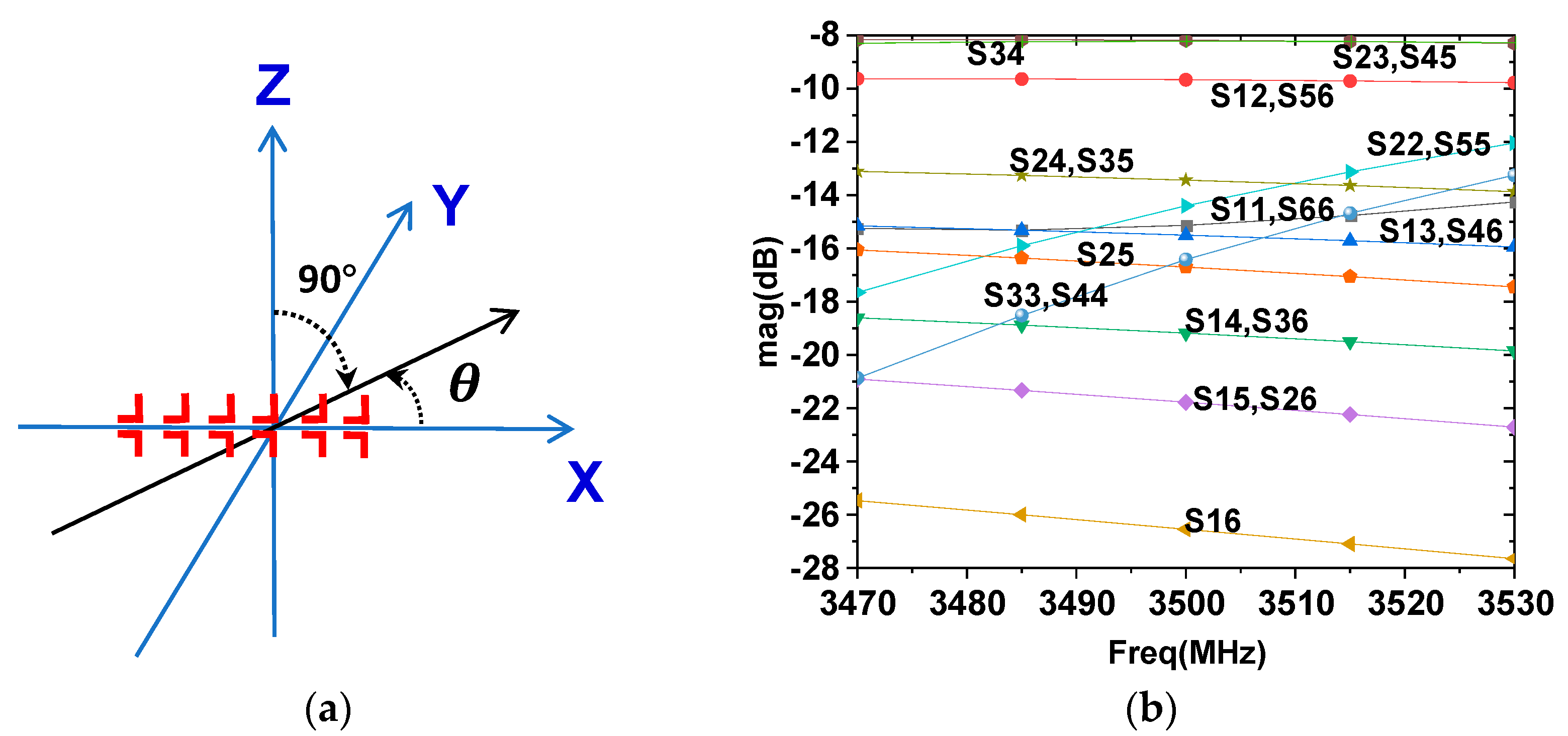
- We use signal models with electromagnetically exact active electric fields of Multi Element Antenna (MEA) systems, including mutual coupling (captured by full S-parameter matrices).
2. System Model and Methodology
2.1. System Model and the Creation of Realistic Sensor Data
2.2. Neural Tangent Kernel Based DoA Estimation
2.3. NTK-Augmented Polynomial Root Finder DoA Estimation
| Algorithm 1: NTK-PRF for multiple DoAs estimation |
| ■Input: Training dataset , where , |
| Test inputs with signals, where , |
| Output: estimated DoAs |
| 1: for do |
| 2: |
| 3: , where |
| 4: end |
| 5: obtain new training data pairs |
| 6: is substituted for and redo 2–3 without iteration. |
| 7: initialize the NTK-parameterized networks |
| 8: compute and using Equations (5) and (8) with and . |
| 9: compute using Equation (4) |
| 10: return |
2.4. Baseline DoA Estimation Methods
- ESPRIT [4]. This is another parameter estimation technique, based on the fact that the signal at one element is a constant phase shift from the earlier element in the steering vector. In the simulation, the signal data is same as the case for Root-MUSIC.
- Auxiliary array [10]. We add 6 auxiliary sensors on each side of the array to form a new ULA with the same element spacing compared to the original. In this way, the effect of mutual coupling between the middle sensors is reduced. Then the Root-MUSIC as mentioned above is used to estimate DoA.
- SVR. The support vector regression is trained using LIBSVM [34] with Gaussian kernel, defined as . A parameter is introduced to control the number of support vectors. The upper diagonal elements of the covariance matrix of the array output are utilized as features since they contain sufficient information about the received signals [24].
- DNN [26]. The framework of DNN consists of two parts, a multitask auto-encoder and a series of parallel multilayer classifiers. The multitask auto-encoder is introduced before the multilayer classifiers to decompose the inputs into 10 spatial subregions. For the training of the auto-encoder, the network is designed to be linear. The covariance matrix of the array outputs is computed and the upper diagonal elements are used as the input. The space is sampled with an interval of to obtain the training data in single-signal scenarios. For the training of classifiers, another data set is collected in the two-signal scenarios with inter-signal angle sampled from the set of . The network of each classifier has hidden layers with ReLU as activation function.
- DNN-PRF. The neural network with ReLU as activation function is designed using TensorFlow [35], and we use the Adam optimizer to train the network with 50,000 iterations [36]. The number of the hidden layers is chosen to be L = 3, i.e., the same as with the NTK-PRF proposed here. The widths (i.e., number of neurons) of the three hidden layers are 64, 32, and 16, respectively. In order to make a more reasonable comparison with NTK-PRF, the polynomial root of the covariance matrix is calculated to train the neural network, which is similar to NTK-PRF.
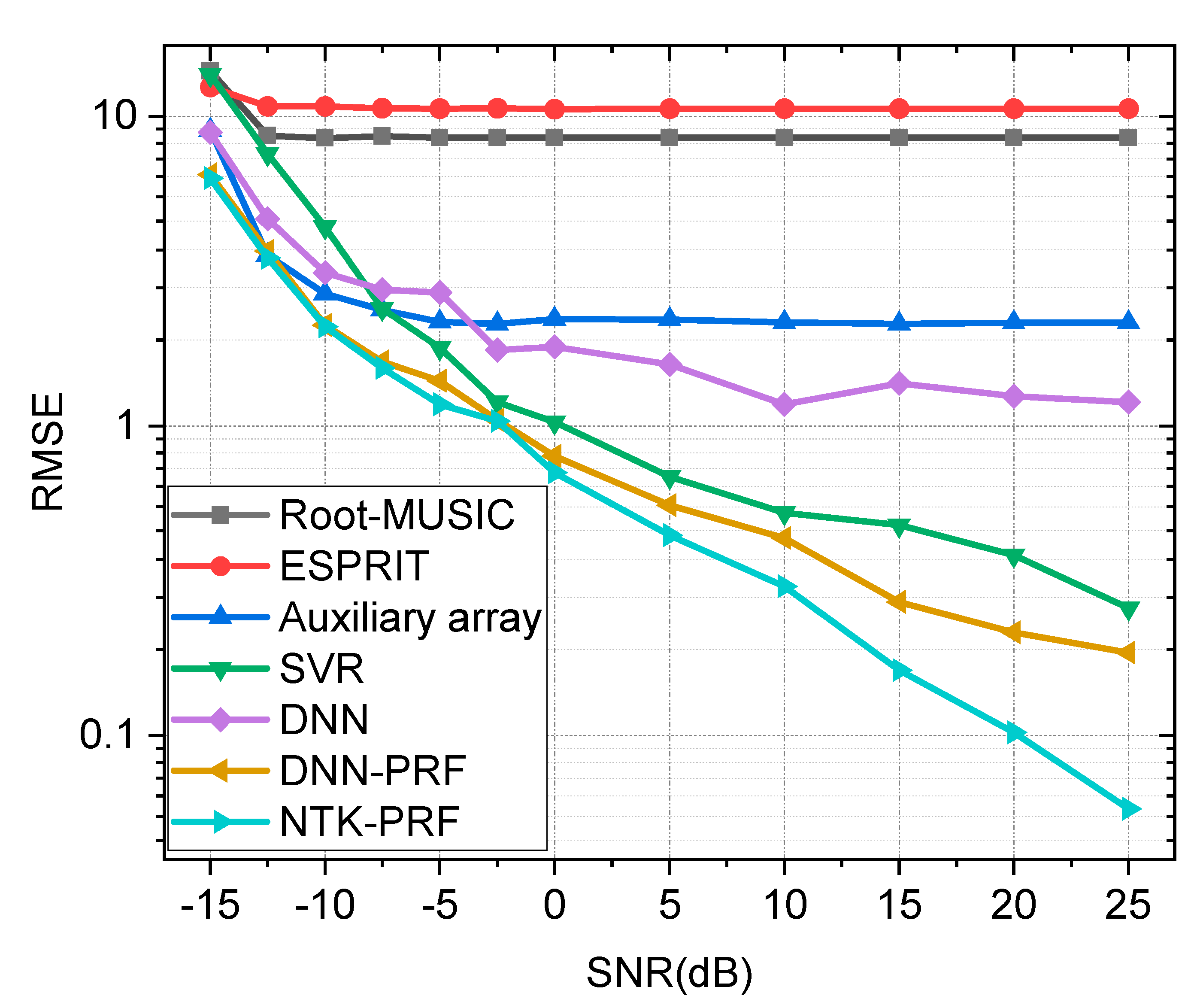
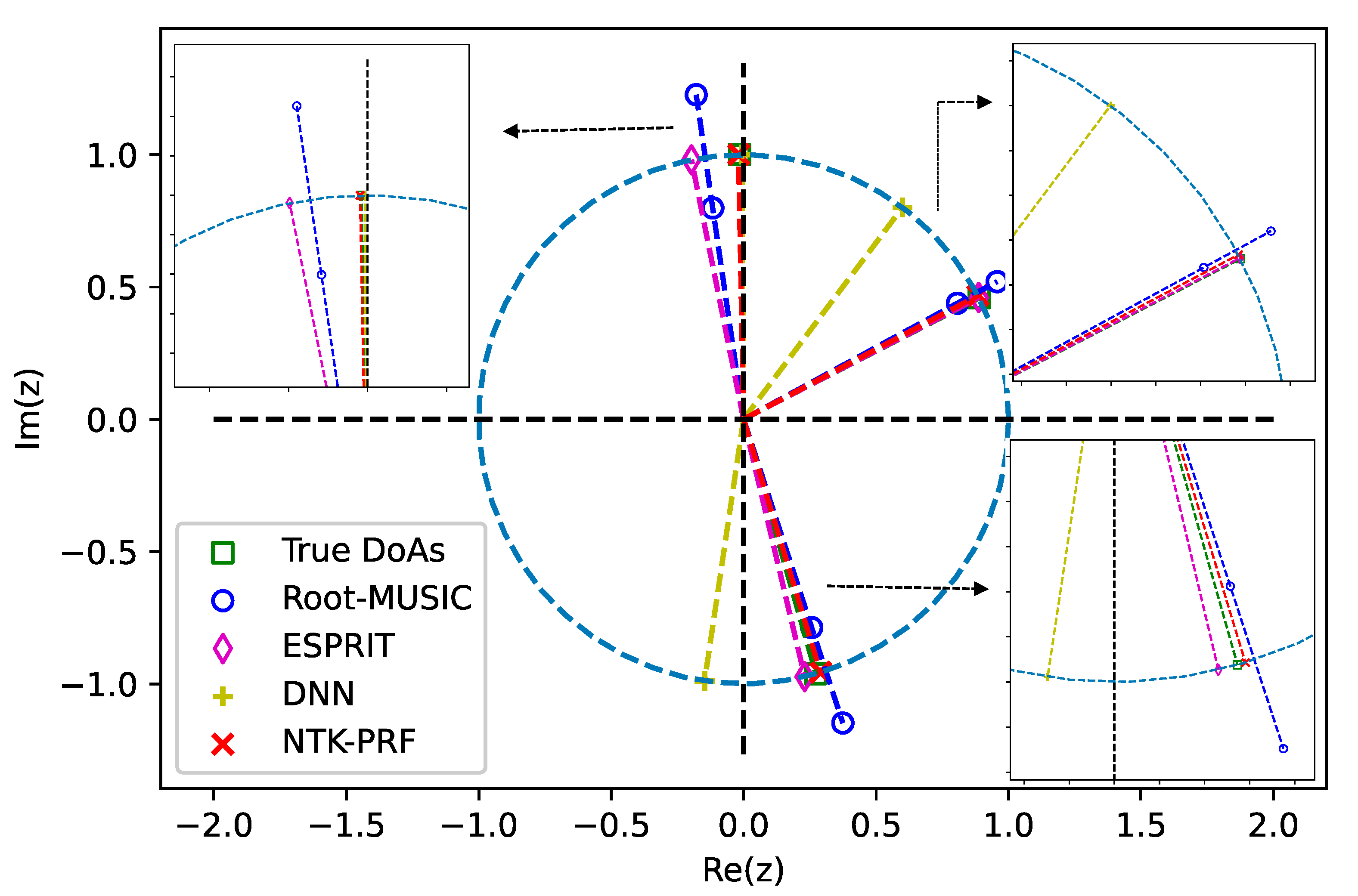
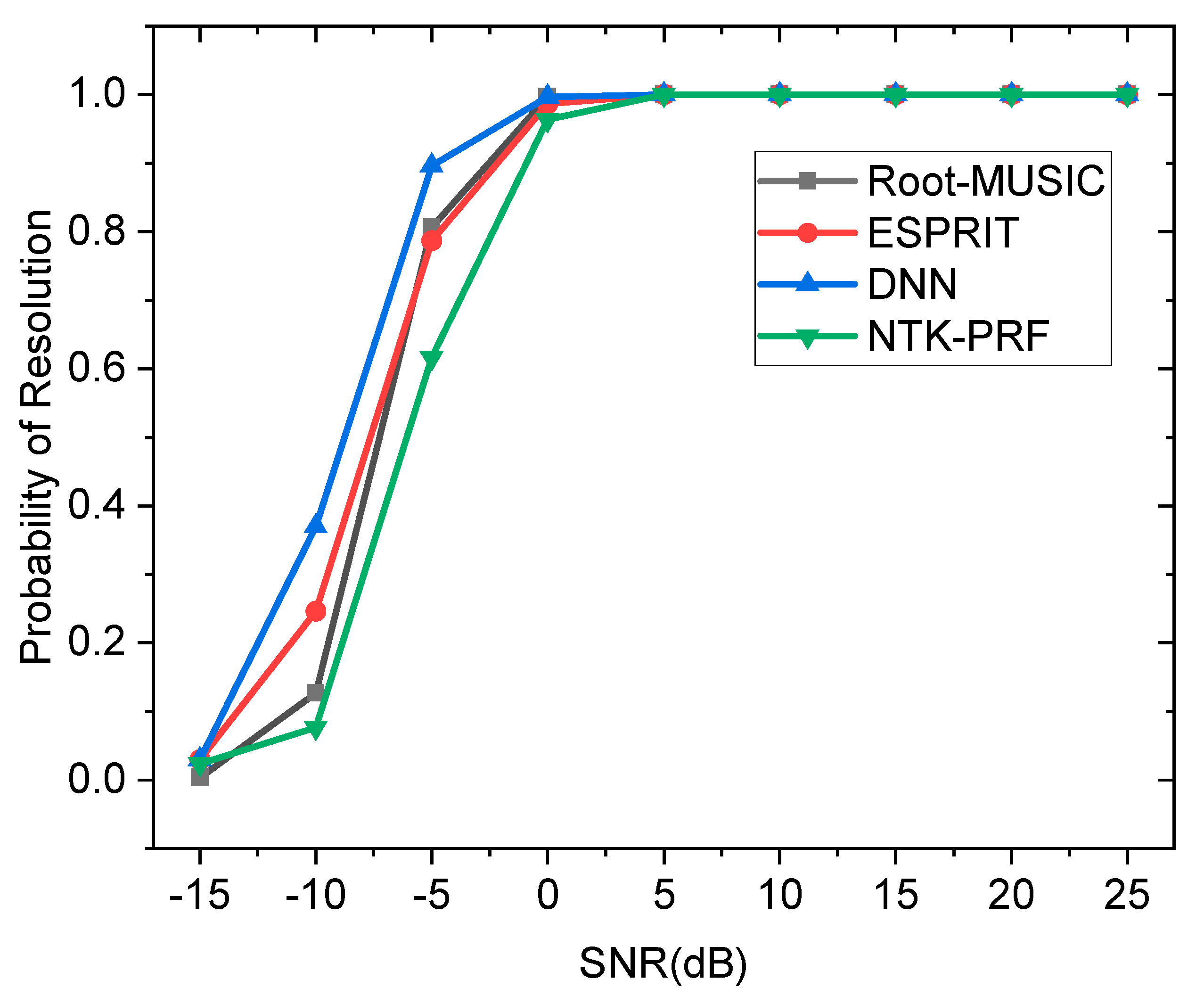
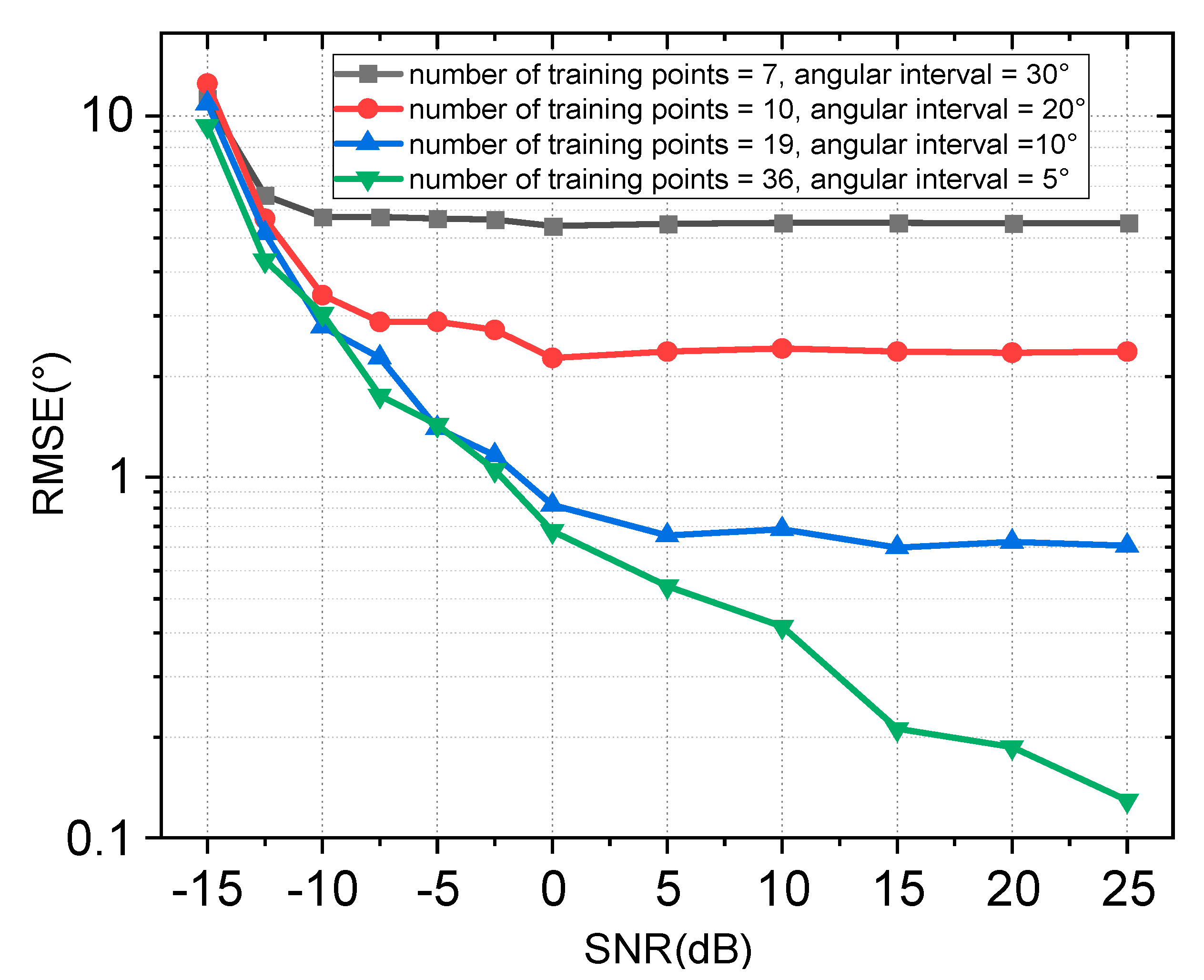
3. Simulation Experiments and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Johnson, D.H.; Dudgeon, D.E. Array Signal Processing: Concepts and Techniques; PTR Prentice Hall: Englewood Cliffs, NJ, USA, 1992. [Google Scholar]
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Stoica, P.; Nehorai, A. MUSIC, maximum likelihood, and Cramer-Rao bound. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 720–741. [Google Scholar] [CrossRef]
- Malioutov, D.; Cetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L.; Zhang, C. Off-grid direction of arrival estimation using sparse Bayesian inference. IEEE Trans. Signal Process. 2012, 61, 38–43. [Google Scholar] [CrossRef]
- Carlin, M.; Rocca, P.; Oliveri, G.; Viani, F.; Massa, A. Directions-of-arrival estimation through Bayesian compressive sensing strategies. IEEE Trans. Antennas Propag. 2013, 61, 3828–3838. [Google Scholar] [CrossRef]
- Friedlander, B.; Weiss, A.J. Direction finding in the presence of mutual coupling. IEEE Trans. Antennas Propag. 1991, 39, 273–284. [Google Scholar] [CrossRef]
- Ye, Z.; Liu, C. On the resiliency of MUSIC direction finding against antenna sensor coupling. IEEE Trans. Antennas Propag. 2008, 56, 371–380. [Google Scholar] [CrossRef]
- Dai, J.; Zhao, D.; Ji, X. A sparse representation method for DOA estimation with unknown mutual coupling. IEEE Antennas Wirel. Propag. Lett. 2012, 11, 1210–1213. [Google Scholar] [CrossRef]
- Wang, Q.; Dou, T.; Chen, H.; Yan, W.; Liu, W. Effective block sparse representation algorithm for DOA estimation with unknown mutual coupling. IEEE Commun. Lett. 2017, 21, 2622–2625. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Xie, J.; Trinkle, M.; Ng, B.W.-H. DOA estimation under mutual coupling of uniform linear arrays using sparse reconstruction. IEEE Wirel. Commun. 2019, 8, 1004–1007. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, X.; Chen, H. DOA estimation algorithm for strictly noncircular sources with unknown mutual coupling. IEEE Commun. Lett. 2019, 23, 2215–2218. [Google Scholar] [CrossRef]
- Wang, B.H.; Hui, H.T.; Leong, M.S. Decoupled 2D direction of arrival estimation using compact uniform circular arrays in the presence of elevation-dependent mutual coupling. IEEE Trans. Antennas Propag. 2009, 58, 747–755. [Google Scholar] [CrossRef]
- Elbir, A.M. Direction finding in the presence of direction-dependent mutual coupling. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 1541–1544. [Google Scholar] [CrossRef]
- Ge, Q.; Zhang, Y.; Wang, Y. A low complexity algorithm for direction of arrival estimation with direction-dependent mutual coupling. IEEE Commun. Lett. 2019, 24, 90–94. [Google Scholar] [CrossRef]
- Zheng, Z.; Yang, C. Direction-of-Arrival Estimation of Coherent Signals under Direction-Dependent Mutual Coupling. IEEE Commun. Lett. 2020, 25, 147–151. [Google Scholar] [CrossRef]
- Ge, X.; Zi, R.; Wang, H.; Zhang, J.; Jo, M. Multi-user massive MIMO communication systems based on irregular antenna arrays. IEEE Trans. Wirel. Commun. 2016, 15, 5287–5301. [Google Scholar] [CrossRef]
- Rocca, P.; Oliveri, G.; Mailloux, R.J.; Massa, A. Unconventional phased array architectures and design methodologies—A review. Proc. IEEE 2016, 104, 544–560. [Google Scholar] [CrossRef]
- Friedlander, B.; Weiss, A.J. Direction finding for wide-band signals using an interpolated array. IEEE Trans. Signal Process. 1993, 41, 1618–1634. [Google Scholar] [CrossRef]
- Belloni, F.; Richter, A.; Koivunen, V. DoA estimation via manifold separation for arbitrary array structures. IEEE Trans. Signal Process. 2007, 55, 4800–4810. [Google Scholar] [CrossRef]
- Pastorino, M.; Randazzo, A. A smart antenna system for direction of arrival estimation based on a support vector regression. IEEE Trans. Antennas Propag. 2005, 53, 2161–2168. [Google Scholar] [CrossRef]
- Wu, L.-L.; Huang, Z.-T. Coherent SVR learning for wideband direction-of-arrival estimation. IEEE Signal Process. Lett. 2019, 26, 642–646. [Google Scholar] [CrossRef]
- Chen, M.; Gong, Y.; Mao, X. Deep Neural Network for Estimation of Direction of Arrival with Antenna Array. IEEE Access 2020, 8, 140688–140698. [Google Scholar] [CrossRef]
- Liu, Z.-M.; Zhang, C.; Philip, S.Y. Direction-of-arrival estimation based on deep neural networks with robustness to array imperfections. IEEE Trans. Antennas Propag. 2018, 66, 7315–7327. [Google Scholar] [CrossRef]
- Lee, J.; Bahri, Y.; Novak, R.; Schoenholz, S.S.; Pennington, J.; Sohl-Dickstein, J. Deep Neural Networks as Gaussian Processes. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Jacot, A.; Gabriel, F.; Hongler, C. Neural tangent kernel: Convergence and generalization in neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 2–8 December 2018; pp. 8571–8580. [Google Scholar]
- MIMObit. Available online: www.nebens.com (accessed on 27 April 2021).
- Buris, N.E. Active E-field gain: Toward a standard description of MEAs. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, California, CA, USA, 9–14 July 2017; pp. 2061–2062. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Lee, J.; Xiao, L.; Schoenholz, S.S.; Bahri, Y.; Novak, R.; Sohl-Dickstein, J.; Pennington, J. Wide neural networks of any depth evolve as linear models under gradient descent. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Rao, B.D.; Hari, K.S. Performance analysis of root-MUSIC. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 1939–1949. [Google Scholar] [CrossRef]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
| Acronyms | Description |
|---|---|
| DoA | Direction of Arrival |
| NTK | Neural Tangent Kernel |
| PRF | Polynomial Root Finding |
| DNN | Deep Neural Network |
| SVR | Support Vector Regression |
| CBF | Conventional Beamforming |
| MUSIC | Multiple Signal Classification |
| ESPRIT | Estimating Signal Parameters via Rotational Invariant Techniques |
| CS | Compressive Sensing |
| ML | Maximum Likelihood |
| MCM | Mutual Coupling Matrix |
| MST | Manifold Separation Technique |
| ULA | Uniform Linear Array |
| MEA | Multi Element Antenna |
| LoS | Line of Sight |
| MIMO | Multi Input Multi Output |
| UAT | Universal Approximation Theorem |
| ReLU | Rectified Linear Unit |
| SNR | Signal-to-Noise Ratio |
| RMSE | Root Mean Squared Error |
| Algorithms | Need Calibration Data | Real Time | Multiple DoAs Estimation | Suitable for Mutual Coupling |
|---|---|---|---|---|
| Root-MUSIC | No | Yes | Yes | No |
| ESPRIT | No | Yes | Yes | No |
| Auxiliary Array | No | Yes | Yes | Yes |
| SVR | Yes | No | No | Yes |
| DNN | Yes | No | Yes | Yes |
| DNN-PRF | Yes | No | Yes | Yes |
| NTK-PRF | Yes | Yes | Yes | Yes |
| - | - | Settings |
|---|---|---|
| Rx | Array | ULA, |
| Antenna | 6-port V-pol half-wavelength dipole | |
| Frequency | 3.5 GHz | |
| Tx | Antenna | 1-port V-pol half-wavelength dipole |
| Geometry | Tx-Rx distance | 400 m |
| Spatial range | ||
| Propagation model | - | LoS |
| - | N = 2 | N = 3 | |||
|---|---|---|---|---|---|
| SNR (dB) | 5 | 5 | |||
| True DoAs (°) | 30.09 | 134.95 | 30.09 | 74.95 | 134.95 |
| Root-MUSIC (°) | 21.27 | 133.64 | 20.16 | 74.59 | 133.32 |
| ESPRIT (°) | 12.90 | 138.18 | 15.10 | 74.88 | 136.92 |
| DNN (°) | 32.14 | 135.87 | 30.57 | 59.56 | 159.72 |
| NTK-PRF (°) | 30.50 | 134.41 | 29.84 | 74.62 | 134.13 |
| - | NTK-PRF | DNN-PRF | DNN | SVR |
|---|---|---|---|---|
| Training time (s) | 0.255 | 152.764 | 2059.968 | 1515.466 |
| Test time (s) | 0.252 | 0.316 | 0.295 | 0.199 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Hu, X.; Deng, X.; Buris, N.E. DoA Estimation Using Neural Tangent Kernel under Electromagnetic Mutual Coupling. Electronics 2021, 10, 1057. https://doi.org/10.3390/electronics10091057
Wang Q, Hu X, Deng X, Buris NE. DoA Estimation Using Neural Tangent Kernel under Electromagnetic Mutual Coupling. Electronics. 2021; 10(9):1057. https://doi.org/10.3390/electronics10091057
Chicago/Turabian StyleWang, Qifeng, Xiaolin Hu, Xiaobao Deng, and Nicholas E. Buris. 2021. "DoA Estimation Using Neural Tangent Kernel under Electromagnetic Mutual Coupling" Electronics 10, no. 9: 1057. https://doi.org/10.3390/electronics10091057
APA StyleWang, Q., Hu, X., Deng, X., & Buris, N. E. (2021). DoA Estimation Using Neural Tangent Kernel under Electromagnetic Mutual Coupling. Electronics, 10(9), 1057. https://doi.org/10.3390/electronics10091057






