LQR-Based Adaptive Virtual Inertia for Grid Integration of Wind Energy Conversion System Based on Synchronverter Model
Abstract
1. Introduction
- ✓
- An AVI model based on linear dynamic systems is proposed. The proposed linear dynamic system’s state variables are the frequency deviation and the rotor angle deviation, and the control inputs are the virtual inertia and frequency droop gain.
- ✓
- The proposed AVI model is computed with an LQR control in order to minimize frequency deviations with minimum effort and, therefore, to manage an optimal balance between fast frequency response and WTGS stress during disturbances.
- ✓
- The performance of the proposed AVI model is evaluated in three different cases of wind speed considering a short-circuit. Furthermore, the proposed AVI model is compared with the conventional synchronverter model (SM), where, in all cases, the proposed AVI model has a better performance.
2. Wind Energy Conversion System
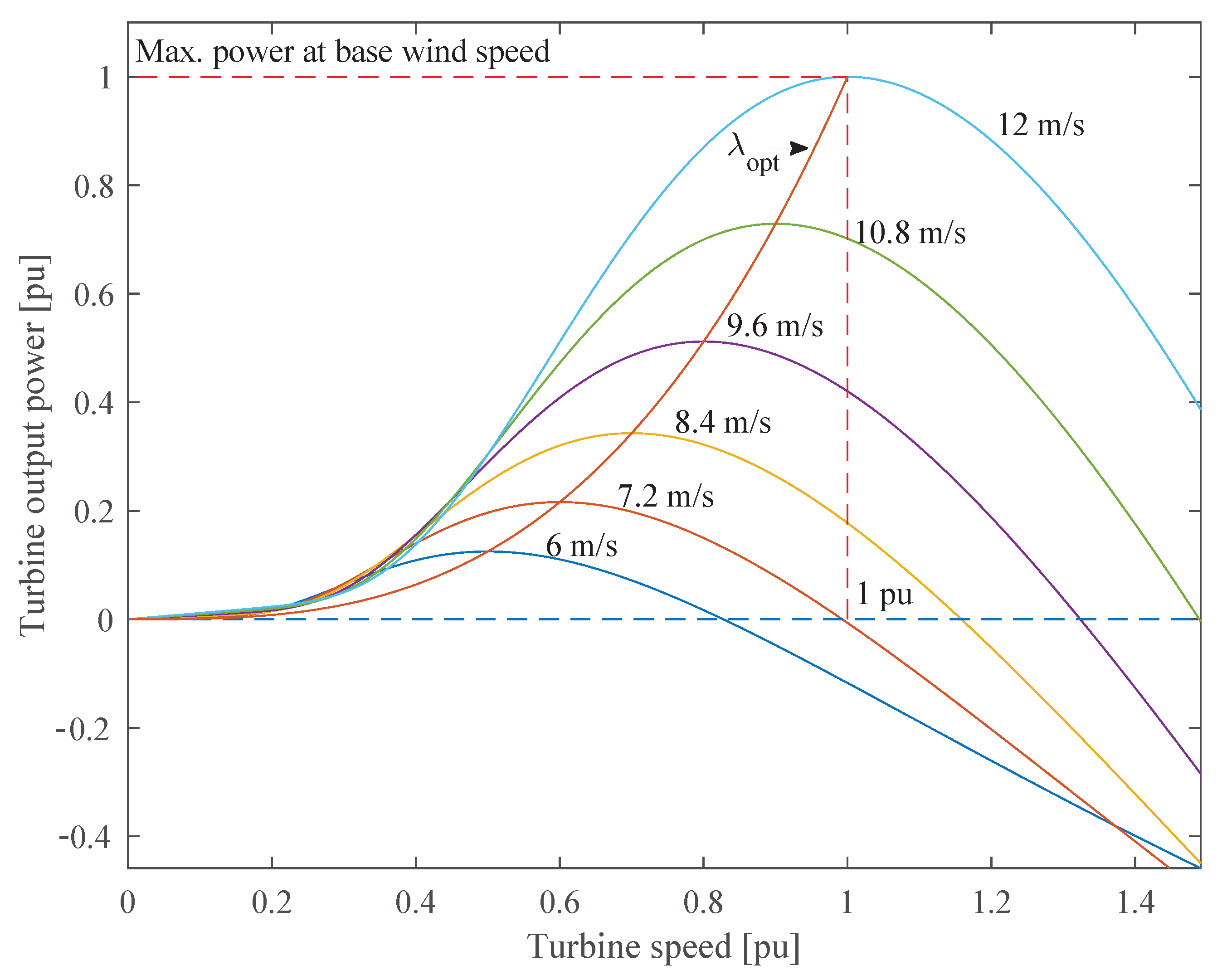
2.1. Wind Turbine Model
2.2. Permanent Magnet Synchronous Generator Model
3. Virtual Synchronous Machine Model
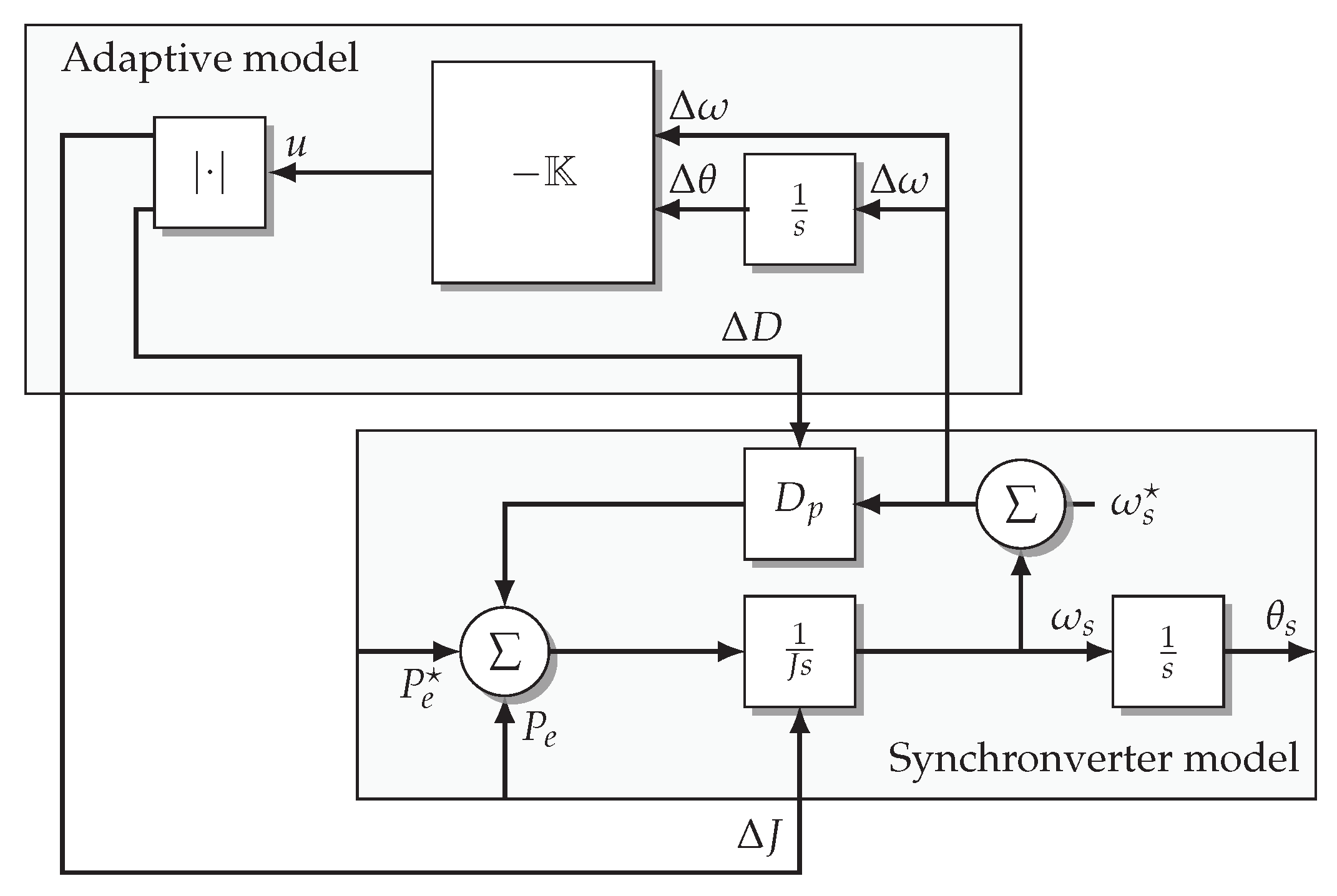
4. Adaptive Virtual Inertia
5. Test System and Simulation Results
5.1. The Test System
5.2. Simulation Cases
- Case 1: The wind speed is constant while a short-circuit at grid-side converter (bus-1) with a period of 100 ms is assumed.
- Case 2: A drop in wind speed is considered after a three-phase to ground (bus-1) with a period of 100 ms.
- Case 3: A drop in wind speed is considered during a three-phase to ground (bus-1) with a period of 100 ms.
5.3. Simulation Results
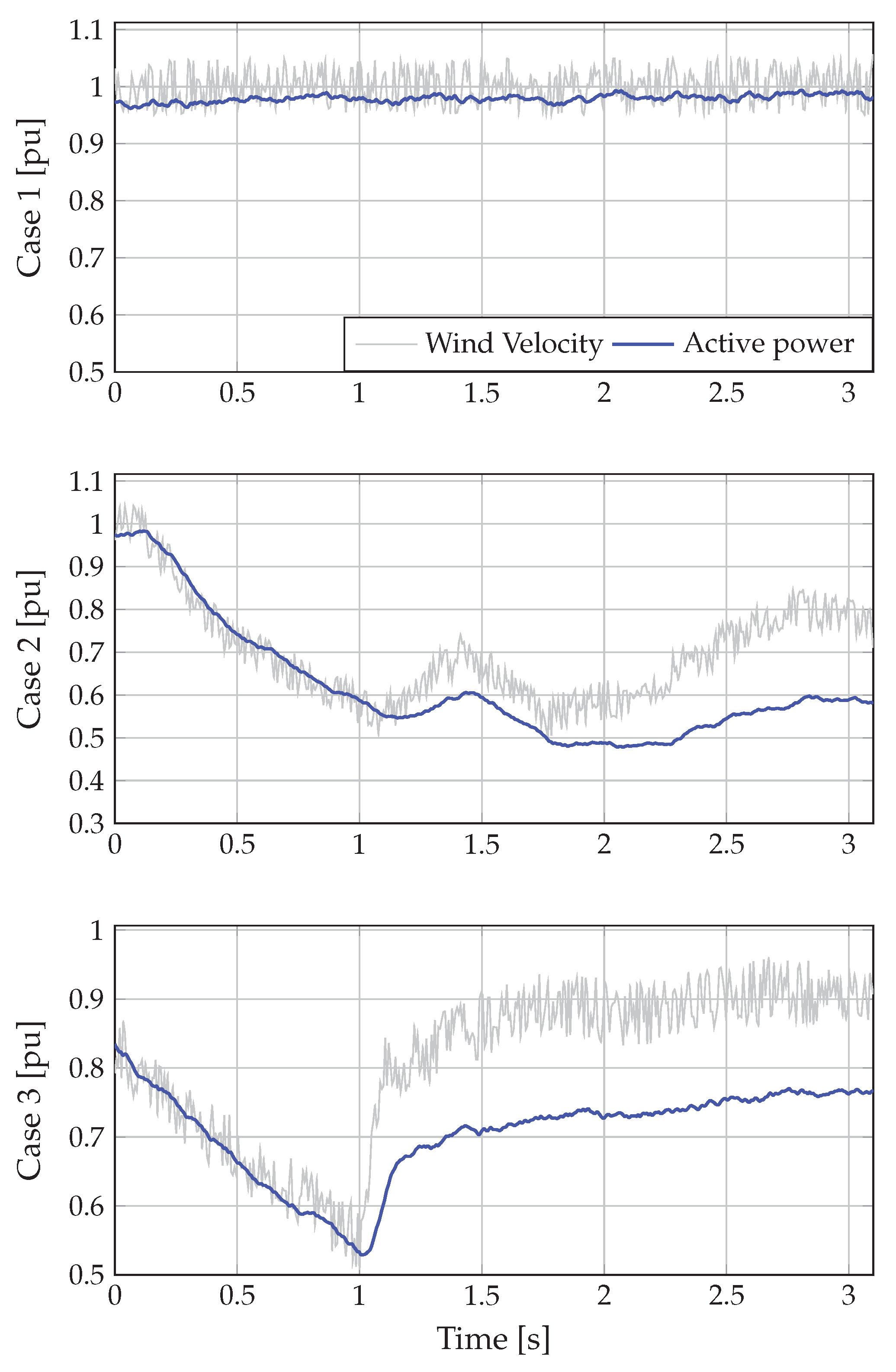
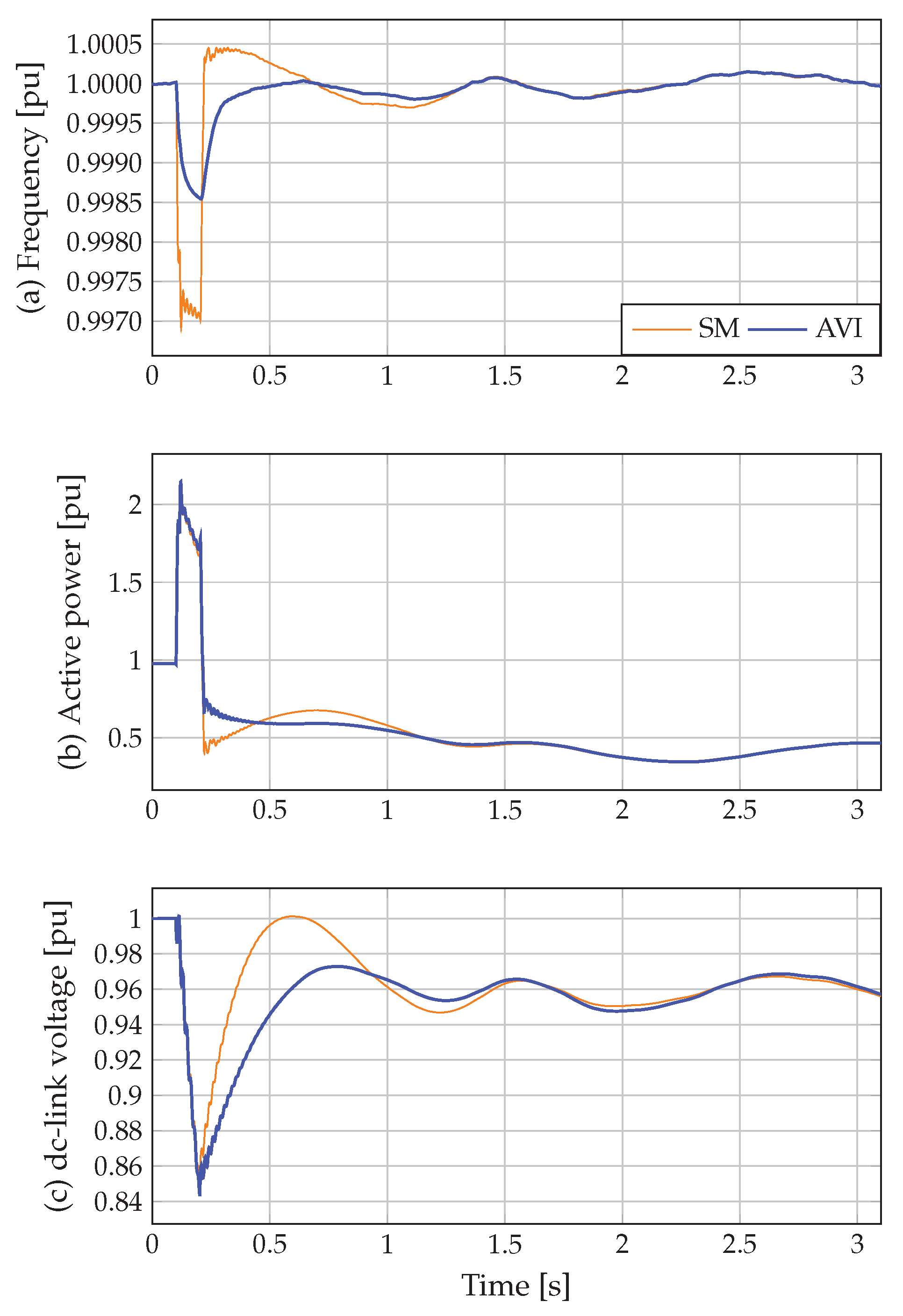
5.3.1. Case 1
5.3.2. Case 2
5.3.3. Case 3
6. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Optimum value of the speed ratio | |
| Angular speed in the PMSG shaft | |
| Angular frequency reference of the synchronverter machine | |
| Permanent magnetic flux on the PMSG | |
| Air density | |
| Time constant for the voltage droop controller | |
| A | Area covered by the turbine blades |
| Inverter filter capacitance of the system | |
| Frequency droop gain of the synchronverter machine | |
| Voltage droop gain of the synchronverter machine | |
| Initial frequency droop gain | |
| Initial voltage droop gain | |
| Rated grid frequency of the system | |
| Wind-turbine inertia time constant | |
| J | Virtual inertia of the synchronverter machine |
| Initial moment of inertia | |
| Reactive power controller integral | |
| Integral gain of the dc voltage controller | |
| Proportional gain of the dc voltage controller | |
| Inverter filter inductance of the system | |
| Stator winding’s inductance of the synchronverter machine | |
| Stator winding’s inductance of the PMSG | |
| Power torque applied to the synchronverter machine shaft | |
| Reactive power reference by synchronverter machine | |
| R | Radius of the area covered by the blades |
| Inverter filter resistance of the system | |
| Stator winding’s resistance of the synchronverter machine | |
| Stator winding’s resistance of the PMSG | |
| S | Rated power of the system |
| Output voltage magnitude reference of the synchronverter machine | |
| dc-link voltage reference | |
| Rated grid voltage line-to-line of the system | |
| Variables | |
| Pitch angle | |
| Adaptive frequency droop | |
| Adaptive virtual inertia | |
| Frequency deviation | |
| Rotor angle deviation | |
| Speed ratio | |
| Feedback matrix gain | |
| Angular frequency of the synchronverter machine | |
| Angular speed in the wind turbine | |
| Electrical angular speed of the PMSG | |
| Virtual flux of the synchronverter machine | |
| Electrical torque of the synchronverter machine | |
| Mechanical torque of the synchronverter machine | |
| Turbine output power | |
| Electrical torque of the PMSG | |
| Rotor angle of the synchronverter machine | |
| Power coefficient | |
| Electromotive force of the synchronverter machine | |
| Output phase currents vector of the synchronverter machine | |
| Stator currents of the PMSG in dq reference frame | |
| P | Real power delivered by synchronverter machine |
| Turbine power | |
| Q | Reactive power delivered by synchronverter machine |
| V | Wind speed |
| v | Output voltage magnitude of the synchronverter machine |
| dc-link voltage | |
| Stator voltages of the PMSG in reference frame |
References
- Baran, J.; Jąderko, A. An MPPT Control of a PMSG-Based WECS with Disturbance Compensation and Wind Speed Estimation. Energies 2020, 13, 6344. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B.; Sen, P.C.; Kouro, S.; Narimani, M. High-power wind energy conversion systems: State-of-the-art and emerging technologies. Proc. IEEE 2015, 103, 740–788. [Google Scholar] [CrossRef]
- Heier, S. Grid Integration of Wind Energy: Onshore and Offshore Conversion Systems; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Marin-Hurtado, A.; Escobar-Mejía, A.; Gil-González, W. Adaptive Inertia for a Virtual Synchronous Machine Using an LQR Controller Applicable to a High-Voltage DC Terminal. In Proceedings of the 2020 IEEE ANDESCON, Quito, Ecuador, 13–16 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Kashem, S.B.A.; Chowdhury, M.E.; Ahmed, J.; Ashraf, A.; Shabrin, N. Wind Power Integration with Smart Grid and Storage System: Prospects and Limitations. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 552–569. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M. Self-synchronisation of wind farm in MMC-based HVDC system. In Proceedings of the 2016 IEEE Electrical Power and Energy Conference (EPEC), Ottawa, ON, Canada, 12–14 October 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Do, T.D. Disturbance Observer-Based Fuzzy SMC of WECSs Without Wind Speed Measurement. IEEE Access 2017, 5, 147–155. [Google Scholar] [CrossRef]
- Watil, A.; Magri, A.E.; Raihani, A.; Lajouad, R.; Giri, F. Multi-objective output feedback control strategy for a variable speed wind energy conversion system. Int. J. Electr. Power Energy Syst. 2020, 121, 106081. [Google Scholar] [CrossRef]
- Beltran, B.; Benbouzid, M.E.H.; Ahmed-Ali, T. Second-Order Sliding Mode Control of a Doubly Fed Induction Generator Driven Wind Turbine. IEEE Trans. Energy Convers. 2012, 27, 261–269. [Google Scholar] [CrossRef]
- Majdoub, Y.; Abbou, A.; Akherraz, M. Variable speed control of DFIG-wind turbine with wind estimation. In Proceedings of the 2014 International Renewable and Sustainable Energy Conference (IRSEC), Ouarzazate, Morocco, 17–19 October 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Li, D.Y.; Cai, W.C.; Li, P.; Jia, Z.J.; Chen, H.J.; Song, Y.D. Neuroadaptive Variable Speed Control of Wind Turbine with Wind Speed Estimation. IEEE Trans. Ind. Electron. 2016, 63, 7754–7764. [Google Scholar] [CrossRef]
- Song, D.; Yang, J.; Dong, M.; Joo, Y.H. Model predictive control with finite control set for variable-speed wind turbines. Energy 2017, 126, 564–572. [Google Scholar] [CrossRef]
- Boukhezzar, B.; Siguerdidjane, H. Nonlinear control with wind estimation of a DFIG variable speed wind turbine for power capture optimization. Energy Convers. Manag. 2009, 50, 885–892. [Google Scholar] [CrossRef]
- Boukhezzar, B.; Siguerdidjane, H. Comparison between linear and nonlinear control strategies for variable speed wind turbines. Control Eng. Pract. 2010, 18, 1357–1368. [Google Scholar] [CrossRef]
- Calabrese, D.; Tricarico, G.; Brescia, E.; Cascella, G.L.; Monopoli, V.G.; Cupertino, F. Variable Structure Control of a Small Ducted Wind Turbine in the Whole Wind Speed Range Using a Luenberger Observer. Energies 2020, 13, 4647. [Google Scholar] [CrossRef]
- Kim, Y.S.; Chung, I.Y.; Moon, S.I. Tuning of the PI Controller Parameters of a PMSG Wind Turbine to Improve Control Performance under Various Wind Speeds. Energies 2015, 8, 1406–1425. [Google Scholar] [CrossRef]
- Li, P.; Wang, J.; Xiong, L.; Wu, F. Nonlinear Controllers Based on Exact Feedback Linearization for Series-Compensated DFIG-Based Wind Parks to Mitigate Sub-Synchronous Control Interaction. Energies 2017, 10, 1182. [Google Scholar] [CrossRef]
- Kim, K.; Kim, H.G.; Song, Y.; Paek, I. Design and Simulation of an LQR-PI Control Algorithm for Medium Wind Turbine. Energies 2019, 12, 2248. [Google Scholar] [CrossRef]
- Yang, J.; Wu, J.; Dong, P.; Yang, J. Passivity-based control in wind turbine for maximal energy capture. In Proceedings of the 2004 IEEE International Conference on Electric Utility Deregulation, Restructuring and Power Technologies Proceedings, Hong Kong, China, 5–8 April 2004; IEEE: Piscataway, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Cisneros, R.; Gao, R.; Ortega, R.; Husain, I. A PI-passivity-based control of a wind energy conversion system enabled with a solid-state transformer. Int. J. Control 2020, 1–11. [Google Scholar] [CrossRef]
- Gao, R.; Husain, I.; Cisneros, R.; Ortega, R. Passivity-based and standard PI controls application to wind energy conversion system. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Mancilla-David, F.; Ortega, R. Adaptive passivity-based control for maximum power extraction of stand-alone windmill systems. Control Eng. Pract. 2012, 20, 173–181. [Google Scholar] [CrossRef]
- Azeem, B.; Rehman, F.; Mehmood, C.; Ali, S.; Khan, B.; Saeed, S. Exact Feedback Linearization (EFL) and De-Couple Control of Doubly Fed Induction Generator Based Wind Turbine. In Proceedings of the 2016 International Conference on Frontiers of Information Technology (FIT), Islamabad, Pakistan, 19–21 December 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Jose, J.T.; Chattopadhyay, A.B. Mathematical Formulation of Feedback Linearizing Control of Doubly Fed Induction Generator Including Magnetic Saturation Effects. Math. Probl. Eng. 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Suul, J.A.; D’Arco, S.; Rodriguez, P.; Molinas, M. Extended stability range of weak grids with Voltage Source Converters through impedance-conditioned grid synchronization. In Proceedings of the 11th IET International Conference on AC and DC Power Transmission, Birmingham, UK, 10–12 February 2015. [Google Scholar]
- Amin, M.; Rygg, A.; Molinas, M. Self-synchronization of wind farm in an MMC-based HVDC system: A stability investigation. IEEE Trans. Energy Convers. 2017, 32, 458–470. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Weiss, G. Synchronverters: Inverters That Mimic Synchronous Generators. IEEE Trans. Ind. Electron. 2011, 58, 1259–1267. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Ma, Z.; Ming, W.L.; Konstantopoulos, G.C. Grid-friendly wind power systems based on the synchronverter technology. Energy Convers. Manag. 2015, 89, 719–726. [Google Scholar] [CrossRef]
- Yap, K.Y.; Sarimuthu, C.R.; Lim, J.M.Y. Grid Integration of Solar Photovoltaic System Using Machine Learning-Based Virtual Inertia Synthetization in Synchronverter. IEEE Access 2020, 8, 49961–49976. [Google Scholar] [CrossRef]
- Aouini, R.; Marinescu, B.; Kilani, K.B.; Elleuch, M. Synchronverter-based emulation and control of HVDC transmission. IEEE Trans. Power Syst. 2015, 31, 278–286. [Google Scholar] [CrossRef]
- Zhong, Q.C.; Nguyen, P.L.; Ma, Z.; Sheng, W. Self-synchronized synchronverters: Inverters without a dedicated synchronization unit. IEEE Trans. Power Electron. 2013, 29, 617–630. [Google Scholar] [CrossRef]
- Wang, C.; Meng, J.; Wang, Y.; Wang, H. Adaptive virtual inertia control for DC microgrid with variable droop coefficient. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017; IEEE: Piscataway, NJ, USA, 2017. [Google Scholar] [CrossRef]
- Blau, M.; Weiss, G. Synchronverters used for damping inter-area oscillations in two-area power systems. Renew. Energy Power Qual. J. 2018, 45–50. [Google Scholar] [CrossRef]
- Gil-González, W.; Garcés, A.; Fosso, O.B. Passivity-based control for small hydro-power generation with PMSG and VSC. IEEE Access 2020, 8, 153001–153010. [Google Scholar] [CrossRef]
- Anderson, B.D.; Moore, J.B. Optimal Control: Linear Quadratic Methods; Courier Corporation: North Chelmsford, MA, USA, 2007. [Google Scholar]




| Control Method | Control Objective | Reference |
|---|---|---|
| Fuzzy sliding mode control | Disturbance rejection without wind speed measures | [7] |
| Integral sliding mode control | Maximum power point tracking (MPPT) | [8] |
| Second-order sliding mode control | MPPT | [9] |
| Backstepping control | MPPT | [10] |
| Neuroadaptive speed controller | MPPT with uncertain dynamics | [11] |
| Model predictive control | MPPT | [12] |
| Feedback-PI controller | Speed control with disturbance rejection | [13] |
| LQG (versus linear/nonlinear control) | Speed control with disturbance rejection | [14] |
| PI control | MPPT with tip-speed ratio | [15] |
| PI control | PMSG WT | [16] |
| PI control | PMSG with variable-speed fixed-pitch | [17] |
| LQR-PI control | PMSG | [18] |
| Passivity-based control (PBC) | MPPT | [19] |
| PI-PBC | MPPT with estimator wind speed | [20] |
| Robust PI-PBC controller | MPPT | [21] |
| Adaptive standard PBC | MPPT with estimator wind speed | [22] |
| Exact feedback linearization | DIFG | [23] |
| Feedback linearization | MPPT | [24] |
| Exact feedback linearization | DIFG and voltage compensation | [17] |
| Feedback linearization | MPPT | [24] |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| DC-link voltage () | 500 V | Rated power (S) | 100 kVA |
| Rated grid voltage () | 260 V | Rated grid frequency () | 60 Hz |
| Rated angular frequency () | 376.99 rad/s | Inverter filter inductance () | 0.25 mH |
| Inverter filter resistance () | 1.885 m | Inverter filter capacitance () | 15.35 µF |
| Frequency droop gain () | 10.4 W/(rad/s) | Voltage droop gain () | 5.2 Var/V |
| Reactive power set-point () | 0 Var | Moment of inertia () | 0.104 |
| Proportional regulator gain () | 5 pu | Integral regulator gain () | 0.02 pu |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rated power of the PMSG | 100 kVA | Rated output power of the turbine | 100 W |
| Rated rotational speed | Rated wind speed (V) | 12 m/s | |
| Stator winding´s resistance () | 0.006 | Stator winding´s inductance () | 0.3 mH |
| Magnetic flux () | 0.8 Wb | Pole pairs () | 90 |
| Inertia () | 20,000 | Viscous damping | 0.01 Nms |
| Frequency | Dc-Link Voltage | |||||||
|---|---|---|---|---|---|---|---|---|
| Max. [pu] | Min. [pu] | RoCof [pu/s] | Max. [pu] | Min. [pu] | ||||
| Case 1 | SM | 0.9219 | 1.0008 | 0.9969 | 0.3513 | 70.8756 | 1.0496 | 0.8500 |
| AVI | 0.3649 | 1.0004 | 0.9985 | 0.0723 | 60.7015 | 1.0383 | 0.8443 | |
| Case 2 | SM | 0.8991 | 1.0005 | 0.9968 | 0.3505 | 57.0816 | 1.0013 | 0.8488 |
| AVI | 0.5874 | 1.0001 | 0.9985 | 0.0604 | 44.3128 | 1.0013 | 0.8431 | |
| Case 3 | SM | 1.1072 | 1.0023 | 0.9968 | 0.3614 | 105.2154 | 1.0633 | 0.9362 |
| AVI | 0.5389 | 1.0005 | 0.9984 | 0.0556 | 87.1536 | 1.0220 | 0.9344 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gil-González, W.; Montoya, O.D.; Escobar-Mejía, A.; Hernández, J.C. LQR-Based Adaptive Virtual Inertia for Grid Integration of Wind Energy Conversion System Based on Synchronverter Model. Electronics 2021, 10, 1022. https://doi.org/10.3390/electronics10091022
Gil-González W, Montoya OD, Escobar-Mejía A, Hernández JC. LQR-Based Adaptive Virtual Inertia for Grid Integration of Wind Energy Conversion System Based on Synchronverter Model. Electronics. 2021; 10(9):1022. https://doi.org/10.3390/electronics10091022
Chicago/Turabian StyleGil-González, Walter, Oscar Danilo Montoya, Andrés Escobar-Mejía, and Jesús C. Hernández. 2021. "LQR-Based Adaptive Virtual Inertia for Grid Integration of Wind Energy Conversion System Based on Synchronverter Model" Electronics 10, no. 9: 1022. https://doi.org/10.3390/electronics10091022
APA StyleGil-González, W., Montoya, O. D., Escobar-Mejía, A., & Hernández, J. C. (2021). LQR-Based Adaptive Virtual Inertia for Grid Integration of Wind Energy Conversion System Based on Synchronverter Model. Electronics, 10(9), 1022. https://doi.org/10.3390/electronics10091022








