1. Introduction
Nowadays, at least 90% of industrial systems use electric machines [
1]. They are commonly used in pumps, ventilators, mills, elevators, electric vehicles, etc. In particular, induction motors (IM) are robust, trustworthy and can be employed in hazardous environments [
2]. Different control techniques exist for IM, the most representative being voltage/frequency (
), field-oriented control (FOC) and direct torque control (DTC).
The
method provides an easy and functional way to control the IM’s velocity, which allows a satisfactory response in steady state; however, its behavior in transient state is not ideal [
3]. FOC is one of the most popular algorithms used, and there are two types: direct FOC (DFOC) and indirect FOC (IFOC). In DFOC, the magnetic flux value is measured inside the motor using at least two flux sensors. In IFOC, the rotor flux angle is observed/estimated through stator current measurements. The disadvantages of these methods are sensor fragility and sensitiveness to parameter variation, respectively [
4,
5]. On the other hand, DTC has gained popularity due to simple structure and performance in high torque applications, but its main limitation is the excessive torque ripple due to current’s hysteresis controllers [
6].
With new technological trends, recent techniques that improve the behavior of IM have been integrated into FOC and DTC. One of them is fuzzy logic (FL); this is a method that allows approximately replicating the process of human reasoning based on their previous knowledge and experience [
7]. In this technique, the overall membership functions relate human thought to the FL algorithm in a mathematical way [
8]. The general FL algorithm is based on the following procedures: fuzzification, fuzzy rules (or decision making), interference methods and defuzzification.
Another technique that has grown in importance is the model of predictive control (MPC), principally in engineering applications as a consequent of high-speed processors [
9]. This technique was developed in the 1960s and has been applied to industrial processes such as chemical plants and oil refineries [
10]. MPC features the following: the use of dynamic model system with high accuracy [
11], fast-dynamic response, multivariable control and the inclusion of non-linear constraints [
9]. MPC has a prediction horizon, i.e., the steps of future sampling based on the current one, which involves a high load of computational calculations [
12]. An optimization function is used in MPC to evaluate different inputs, the present sampling, and the input that minimize the error to be used in the next sampling [
13]. Likewise, the proposed function has a weighting factor that is tuned by a heuristic process [
14].
FL and MPC are usually compared to a traditional FOC or DTC structure for performance validation. However, in the literature, an assessment between advanced techniques is usually lacking; and many of those reported evaluations are validated only by using numerical software or real-time hardware, which, in the authors’ opinion, limits the reported conclusions. After a deep study of the literature, it was noticed that work is focused on two different paths: (1) comparing IM controllers, which mainly use real-time controllers to implement the different control techniques; and (2) developing HIL test beds to validate power electronic converter applications.
For instance, a comparison between indirect FOC and DTC for IM was reported by Hemavathy et al. [
15]. Here, speed tracking, dynamic and load disturbance response are reported. Unfortunately, only software implementation is given. In [
16], a comparison of FOC, DTC, predictive torque control (PTC) and predictive current control (PCC) was experimentally performed in 2.2 kW squirrel-cage IM. The IM was driven by a modified SERVOSTAR620 14 kVA inverter (Radford, VT, USA) and controlled by a 1.4 GHz real-time controller, which provided full control of the IGBT gates. The authors concluded that overall the strategies had good functioning in the entire speed range with or without load. However, the implementation of different control strategies in a Field-Programmable Gate Array (FPGA), digital signal processor (DSP) or advanced microcontroller was lacking, which limits the overall conclusions. Different control and optimization techniques for IM were reviewed by Hannan et al. [
17]. They reviewed the literature on conventional scalar and vector controls, focusing on biology- and physics-based optimization algorithms. However, only a qualitative description and comparison is reported. Indeed, it is reported that only genetic, lighting and quay lighting optimization algorithm are practically implemented in a DSP, and the others have only been simulated or executed in real-time controllers.
A comparison between DTC and PTC was reported by Karlovsky and Lettl [
18]. They presented numerical and experimental results. This paper reports that a smaller ripple is observed in torque waveforms using PTC compared with traditional DTC. Unfortunately, the implementation of both algorithms was carried out using a real-time controller (dSPACE ds1103 system), which limited the overall conclusions. An interesting work was reported by Nauel and Todd [
19]. They proposed an integral-proportional (IP) controller instead of a classical proportional-integral (PI) one. The proposed structure is placed in the current and speed controller of a traditional FOC squirrel cage IM. The system consists of a Typhoon HIL, a Typhoon docking station and a TI microcontroller (TMS320F28335). The PI and IP control structures were both discretized and coded. The authors reported that IP improved speed tracking without affecting the disturbance rejection. Unfortunately, the implementation of IP in other controllers’ topologies was not performed, and details about the DSP implementation are absent. A qualitatively comparison of adjustable-speed drives (ADS) for shaft powers of 20 MW or more was reported by Rauber and den Bakker [
20]. The comparison was done between voltage source inverter (VSI) and load-commutated inverters (LSI). The authors concluded that LSI topology has the highest reliability, while VSI-based drives have flexibility from the system integration point of view. However, no comparison of control techniques applied in the ADS is reported.
The second research effort is focused on PEC’s HIL applications, development and reliability studies.
For instance, stability of different power hardware-in-the-loop (PHIL) configurations was reported by Lauss and Strunz [
21]. They presented transfer functions for the entire PHIL and quantified the overall involved time delays, which enhanced simulation stability and precision. A multi-rate co-simulation architecture that integrates PHIL, a real-time quasi-static time-series, and a reduced-equivalent electromagnetic transient of the distribution feeder in a large distribution network was reported by Prabakar et al. [
22]. This co-simulation was tested in an interconnected 500-kVA advanced photovoltaic (PV) inverter in PHIL architecture. A custom real-time HIL emulator to test transients and dynamic behavior of power electronics converters was reported by Iranian et al. [
23]. A MATLAB/Simulink hardware description language (HDL) and LabVIEW environment was used to model, control and test a 2.5 MW doubly-feed induction generator.
Validation in a HIL 402 real-time emulator of a novel cubic converter was reported by Ahmad et al. [
24]. The proposed converter was compared with conventional boost and quadratic boost converter in a maximum power point tracking (MPPT) for a Solar PV array. Operation modes, component sizing, power losses, efficiency and thermal modeling was reported. Unfortunately, the control stage was missed. A real-time silicon carbide IGBT model based on the Wiener–Hammerstein configuration was reported by Liang et al. [
25]. A Beijing–Shanghai AC traction application was used as a testbed and implemented on the hybrid multiprocessor system-on-chip (MPSoC) and field-programmable gate array (FPGA) platform. Comparisons with PSCAD/EMTDC and Saber RD was done to verify system and device level performance. A scalable modeling approach, which relies on multi-objective targets between model functionalities, accuracy and execution time was reported by Chakraborty et al. [
26]. A dSPACE SCALEXIO HIL test bench was used for real-time (RT) model implementation for the EV’s HV DC/DC converter. Additionally, passive component losses were verified using Finite Element Method (FEM) software.
An example of a high bandwidth motor emulator was reported by Luo et al. [
27]. The system comprises a 2 kV, 50 A silicon carbide MOSFET six-pack full bridge module from Wolfspeed (CCS050M12CM2), inductive coupling, a reconfigurable real-time model for an interior permanent magnet machine implemented in FPGA and a hybrid predictive control method. The motor model and PWM pattern were implemented in an Avnet PicoZed, which contains a Xilinx ZYNQ-7000 (XC7Z015-1SBG485) system on chip (SoC). A systematic methodology for HIL power electronic converters by using LabVIEW software was reported by Estrada et al. [
28]. Five simple steps are proposed for HIL converters: design, modeling, solving the model using a numerical method, programming an off-line simulation of the model using fixed-point representation and implementing the solution of the model in FPGA. A buck converter and a three-phase voltage source inverter are implemented and compared with the simulation of commercial software (PSIM® v9.0) and real power converters. Finally, a new model-free controller to ameliorate the load frequency control performance of a shipboard micro grid was reported by Khooban et al. [
29], who used an OPAL-RT HIL test bed to validate the proposed controller.
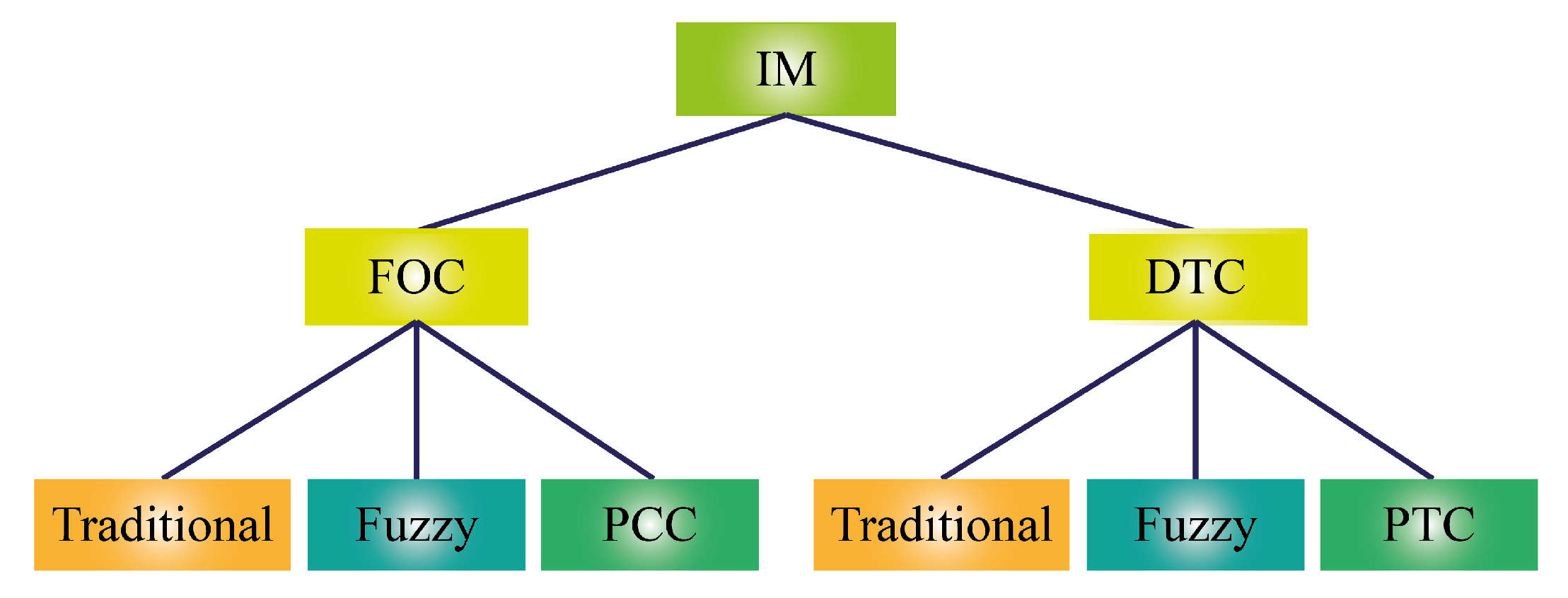
We investigated the following IM controllers: FOC, Fuzzy FOC, Predictive Current Control, DTC, Fuzzy DTC and Predictive Torque Control (
Figure 1). The goals of this investigation were to experimentally compare for the first time, to the best of the authors’ knowledge, traditional and advance controllers on HIL and DSP qualitatively and quantitively. Thus, the following contributions to the state of the art are hereby emphasized:
HIL Typhoon 402 was used to integrate the fidelity of the physical simulation and the flexibility of numerical simulations. It emulated the induction machine, inverter and sensors. Performance of the overall *.dll strategies were compared with the MATLAB SIMULINK and a good agreement among them was achieved.
The six controllers were fully implemented into a DSP TMS320F28035 considering practical implementation issues. It was found that sampling time, controller gain discretization, variable type selection and memory allocation are the parameters that must be solved to achieve a high-performance variable speed drive. The DSP implementations on the HIL board was in consonance with the MATLAB simulation.
It was concluded that predictive current control is computationally simple, it has no practical complexity and it achieves a higher performance compared with the other approaches. Indeed, in the author’s experience, the use of real time controller limits the conclusion previously reported, because real life control challenges are completely removed.
The paper is organized as follows.
Section 2 presents the different variants and their control and tuning. The experimental results of different configurations, such as their qualitative and quantitative comparison, are described in
Section 3. Finally, the most important conclusions of this work are detailed in
Section 4. The work in this paper corroborates the elasticity of digital controllers and confirms the control execution can alter the assortment of drive sections.
3. Experimental Results
This section reports the step-by-step process used to implement the several variable speed IM strategies described above. Initially, a detailed software tuning process is given, then features of the DSP-HIL test bed are reported and, finally, DSP-HIL and SIMULINK comparative results are shown. The real-time HIL system simulated in real-time the power and motor hardware, and the converter and motor under test were controlled using physical hardware, in this case, a Texas Instrument DSP TMS320F28035.
3.1. Software Tuning Process
The six variable speed strategies described above were simulated in MATLAB SIMULINK and Virtual HIL Device (a software-based emulator of the Typhoon HIL 402 real-time device). Numerical implementations were carried out in three stages. Initially, each controller was implemented by using standard SIMULINK Simscape Electrical libraries and standard block functions.
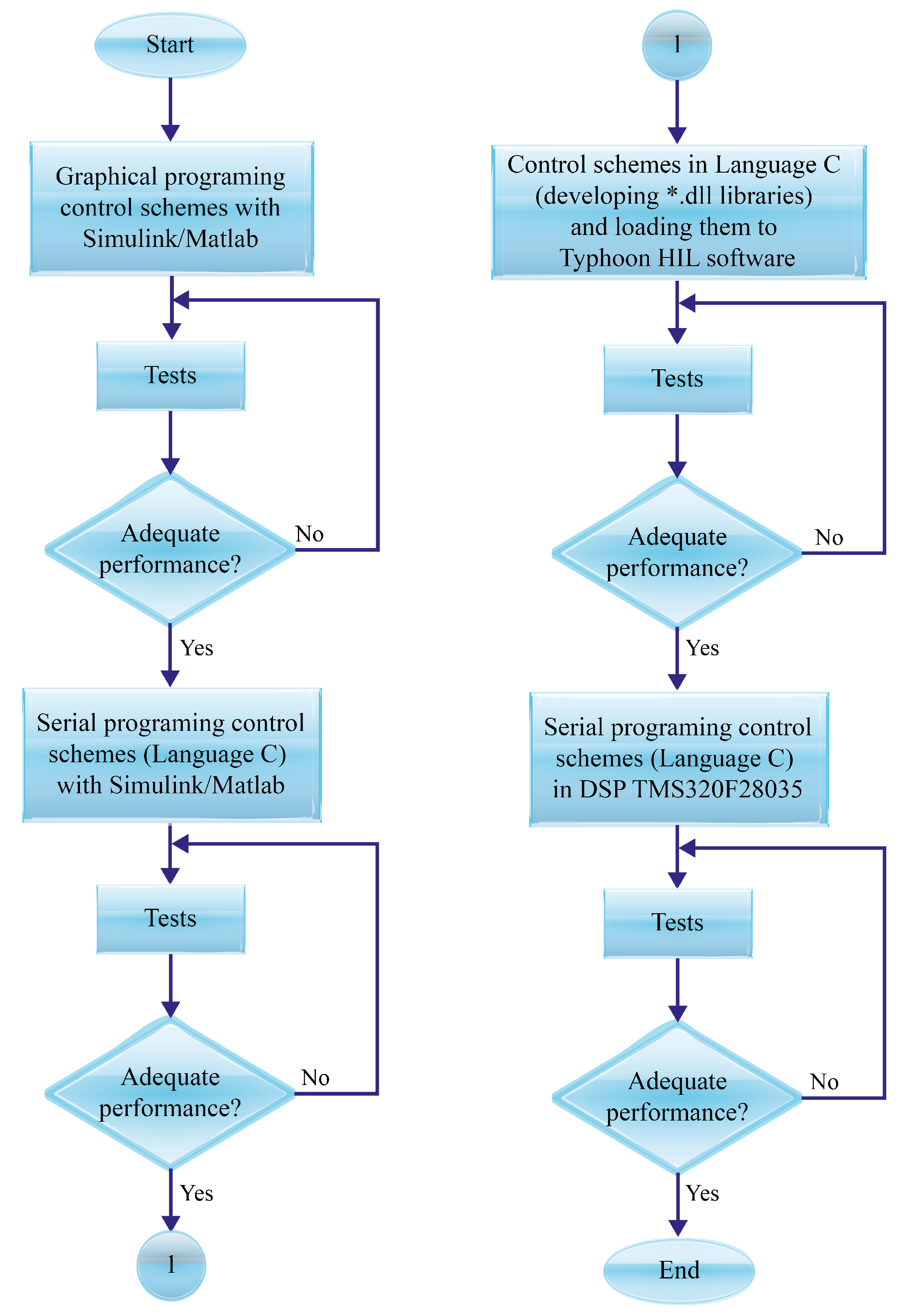
Figure 6 shows the steps to compare the overall *.dll strategies with the MATLAB SIMULINK and MATLAB SIMULINK C functions, where a good agreement between them was achieved. A control panel is also accessible to define the simulation parameters and display the system’s performance by using a virtual oscilloscope and monitoring the system’s evolvement.
This repetitive process allowed debugging the variable speed controllers in each step and incrementing the practical systems’ reliability. The six variable speed strategies with SIMULINK have C functions and the .dll libraries on the Virtual HIL Typhoon software are not reported due to space issues. The induction motor and controller parameters are shown in
Appendix A.
The drive consisted of a sinusoidal PWM controlled voltage source inverter (VSI) feeding a squirrel cage three-phase induction machine. The DC-link of the inverter was connected to an ideal DC voltage source, and the stator three-phase voltages were generated by the PWM VSI. The VSI consisted of a classical three-leg configuration, one per phase, with two switches with antiparallel diode each, and only one switch per leg was turned on at any time. The switches were controlled by sinusoidal PWM phase shifted by 120° for each phase, generated by a SIMULINK Simscape block.
3.2. HIL-DSP Test Bed Considerations
After the .dll libraries were verified on simulations, the next step was to migrate those to C, so the DSP could execute them. A backward Euler method was selected to implement the overall digital controllers. It is worth mentioning that some control techniques require smaller sampling time for execution, for instance IFOC (16 s) or DTC (15 s). Therefore, appropriate sampling time and discrete controller gains were calculated.
For the practical implementation, a HIL DSP 100 conditioning card was used between Typhoon HIL 402 and DSP TMS320F28035 (
Figure 7). The Typhoon HIL 402 handles analog outputs up to ±10 V, so the HIL DSP 100 Interface card conditioned it to DSP voltage levels of 0–3 V. It is necessary to mention that the Typhoon HIL 402 ADC’s output scaling signal can be independently adjusted between output channels. Indeed, the Typhoon HIL 402 emulates the IM dynamic and sends three-phase voltages, three-phase currents and a reference and measured speed to eight DPSs’ analog-to-digital converter inputs, ADCINA1–A4 and ADCINB1–B4, respectively. Once the DSP executes the applicable controller technique, it sends back the PWM switching signals to the HIL’s digital inputs 1–6.
Another fundamental parameter for the experimental implementation was the selection of variable type. In the numerical simulations, a float variable was used because the programmed sampling time is considered in the numerical results and there is no time delay in the mathematical operations due to the type of variable. In contrast, the DSP process must be accomplished within the sampling time. Thus, even though the float variables offer better resolution in the DSP TMS320F28035, they take a long time to execute, so a Q-format fixed point format was used for the overall experimental tests. Indeed, these fixed-point mathematical operations were executed in the DSP RAM’s memory instead of FLASH, since they require fewer clock cycles to execute.
3.3. Practical Validation
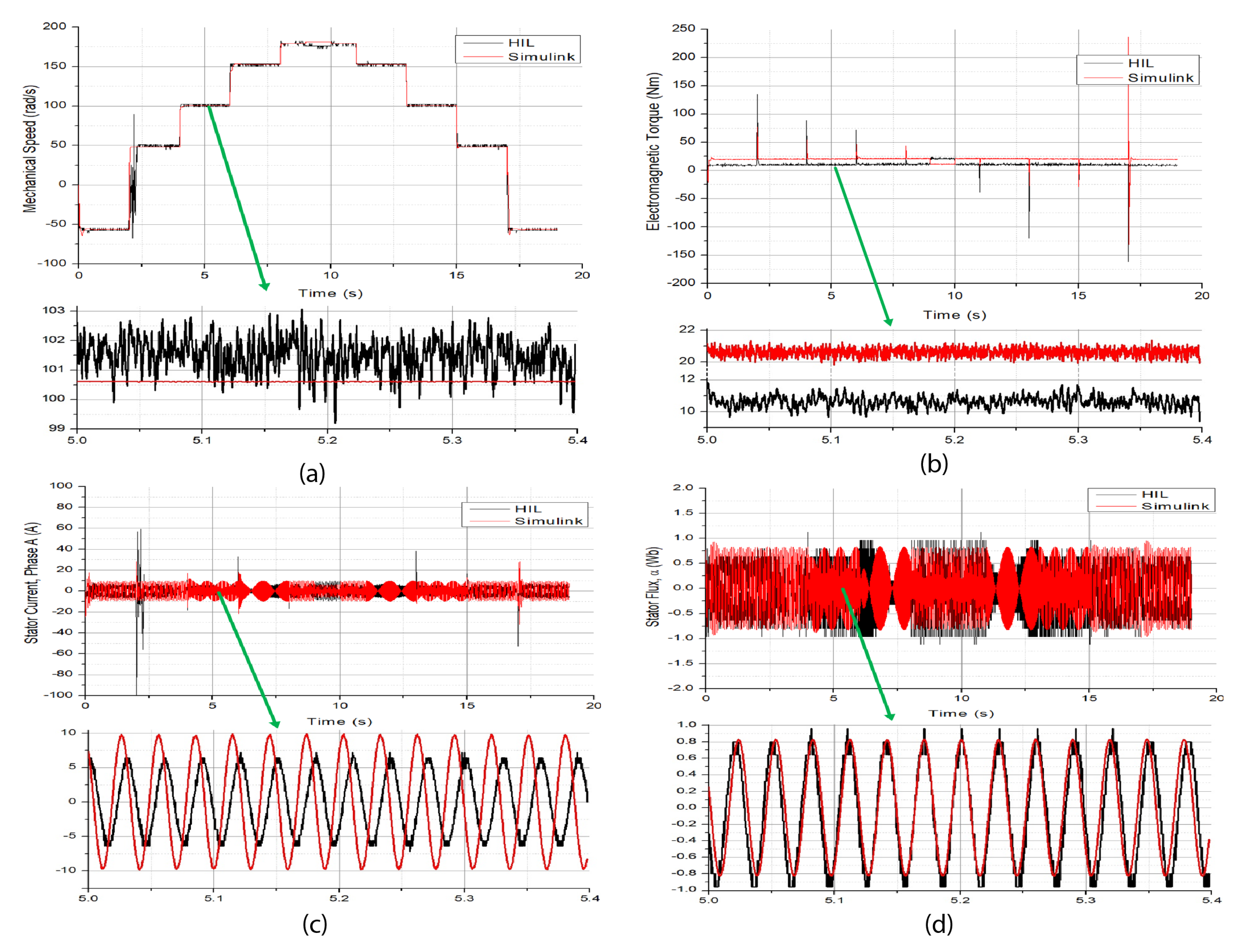
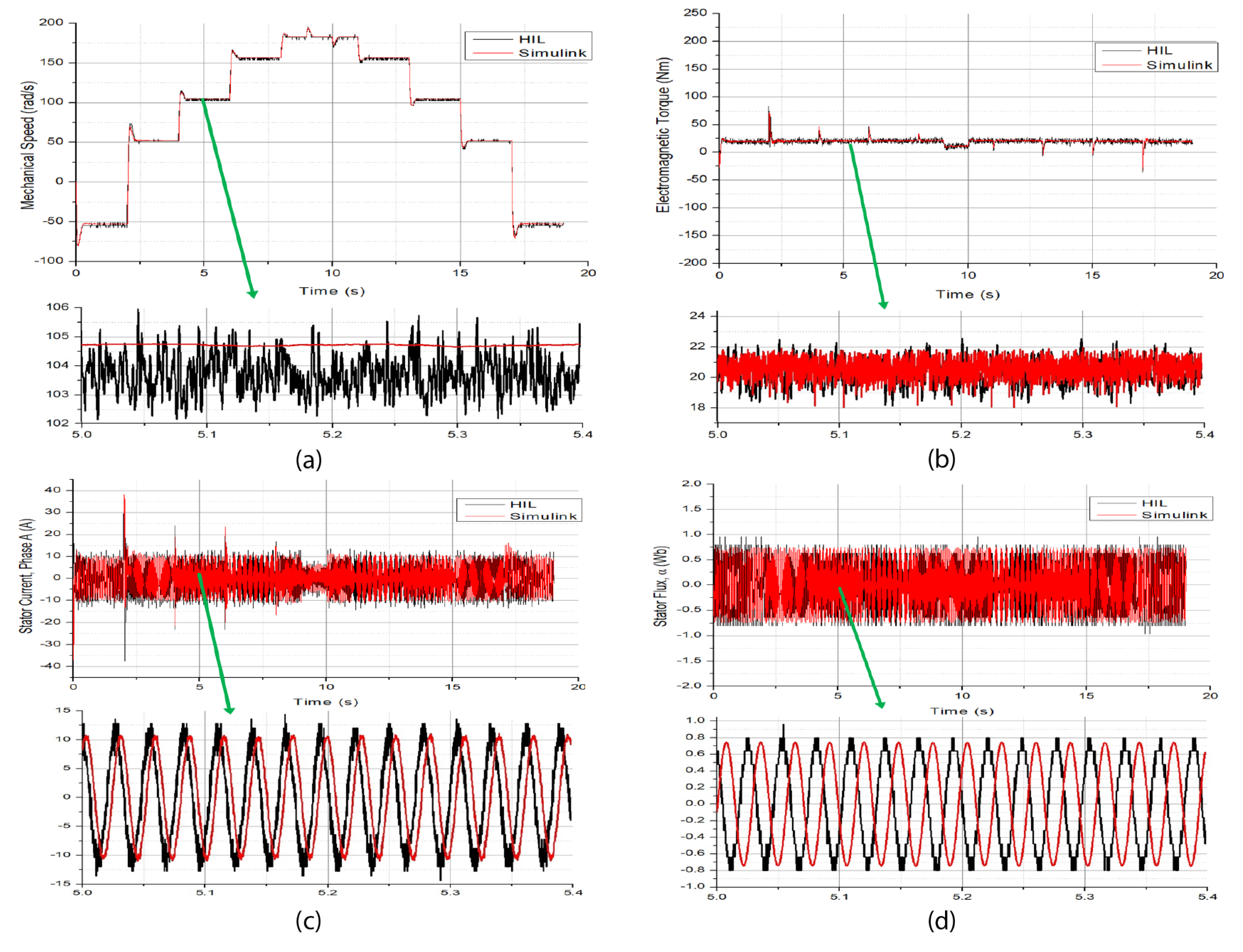
Figure 8 shows the results of the MATLAB SIMULIK block functions and DSP-HIL of traditional IFOC.
Figure 8a shows that IFOC has a good speed response for both systems during step speed transitions from clockwise to counterclockwise speed directions. The highest overshoot is achieved during a transition of 100 rad/s in 2 s. A load change of −10 Nm was applied in 9 s and removed in 10 s; as can be seen, a small overshoot is reflected in the speed. A speed zoom is also shown in the same figure; it can be noticed that a neglectable speed variation between reference and practical responses was found, and both systems follow the overall reference signal.
Figure 8b shows the torque response for the same speed reference. At 2 s, the highest step load variation and difference between SIMULINK and DSP-HIL responses can be noticed. Despite the great difference, the torque performance is not as severely affected. This last is a notorious inaccuracy caused by noise observed in the torque monitoring signal from the Typhoon HIL 402. Meanwhile, torque exhibits similar behavior on both simulation platforms, as shown in
Figure 8b (zoom).
Figure 8c,d shows the stator current phase A and stator flux, respectively. A good agreement between both platforms can be seen, with a slight time delay caused by the sampling and DSP delay time.
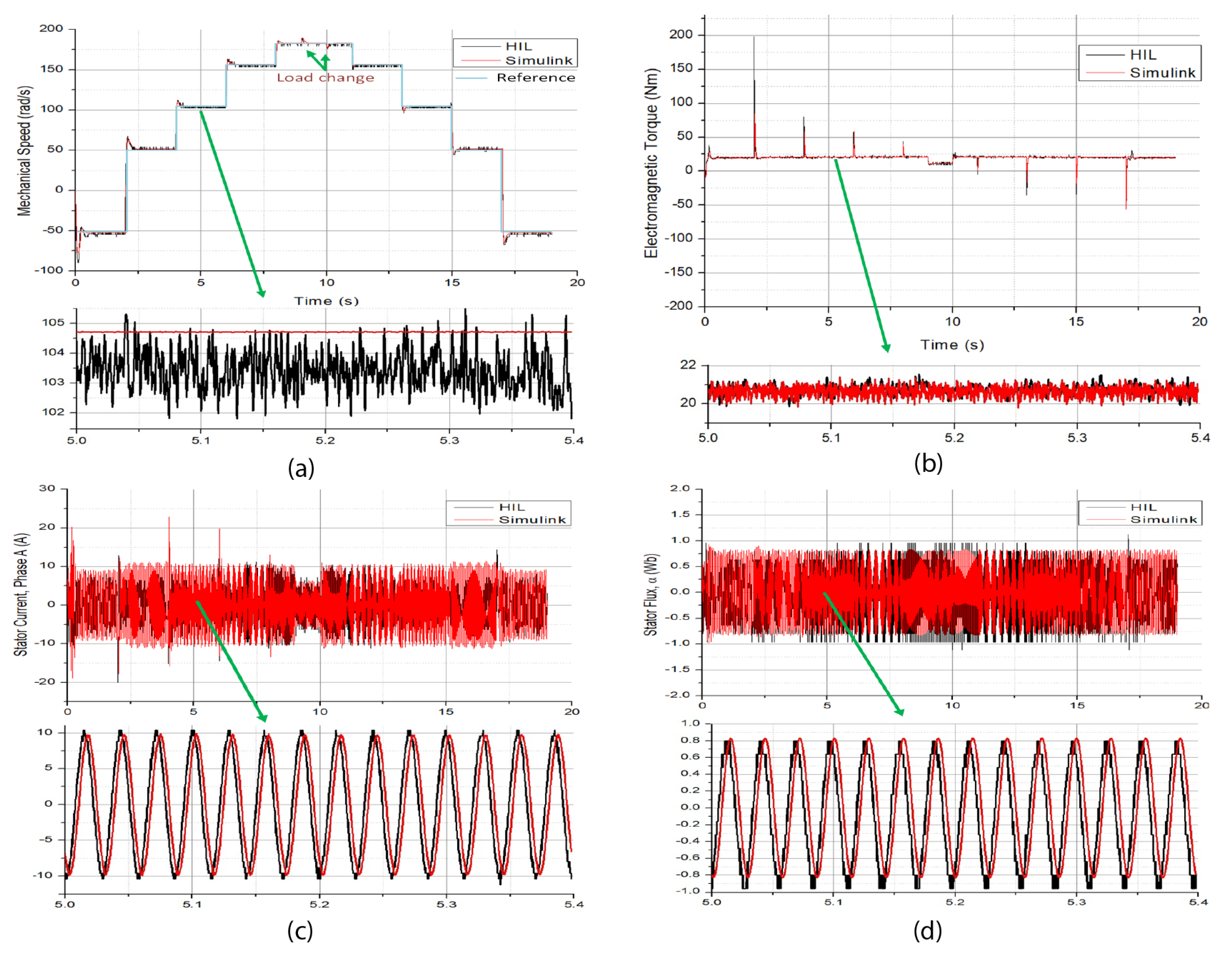
Figure 9 shows the results of the MATLAB SIMULIK block functions and DSP-HIL of DIFOC.
Figure 9a shows that DIFOC has a good speed response for both systems during step speed transitions from clockwise to counterclockwise speed directions. The highest speed error tracking is achieved during a transition of 100 rad/s in 2 s. A load change of −10 Nm was applied in 9 s and removed in 10 s; as can be seen, no overshoot is reflected in the speed. A speed zoom is also shown in the same figure. A neglectable speed variation between reference and practical responses was found, and both systems follow the overall reference signal.
Figure 9b shows the torque response for the same speed reference. At 17 s, the highest step load variation and difference between SIMULINK ad DSP-HIL responses can be noticed. Despite the notorious great difference, the torque performance is not as severely affected. This last once again is a mismatch caused by noise observed in the torque monitoring signal.
Figure 9c,d shows the stator current phase A and stator flux, respectively. A poor agreement between both platforms can be noticed. Indeed, the current in steady state is bigger in the SIMULINK compared to the DS-HIL response, with a slight time delay caused by the sampling and DSP processing time.
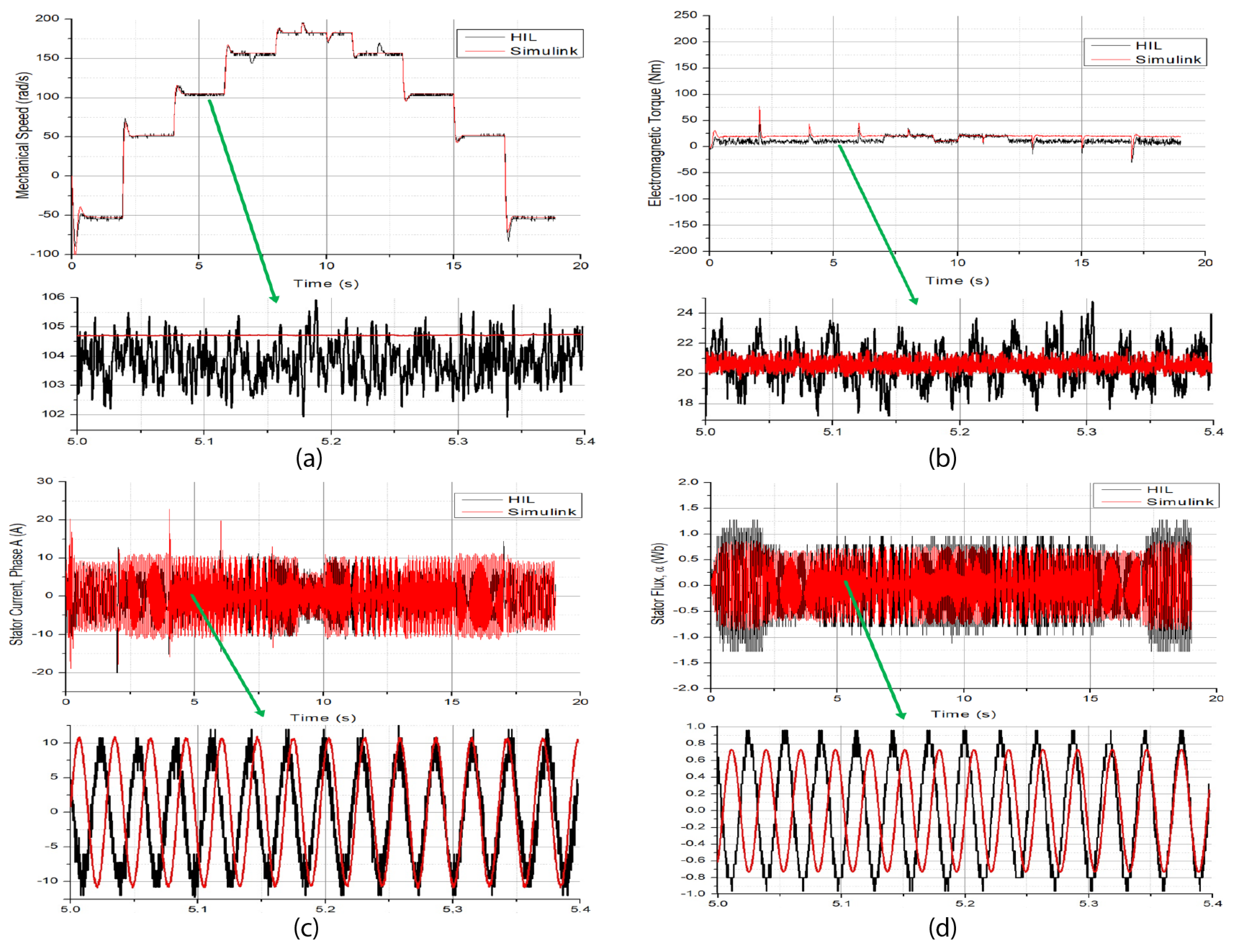
Figure 10 shows the results of the MATLAB SIMULIK block functions and DSP-HIL of PCC.
Figure 10a shows that PCC has a good speed response for both systems during step speed transitions from clockwise to counterclockwise speed directions. Similar to the previous controllers, the highest speed error tracking is achieved during a transition of 100 rad/s in 2 s. A load change of −10 Nm was applied in 9 s and removed in 10 s. The system is able to come back to the reference in less than 1 s. A speed zoom is also shown in the same figure. A low speed variation between reference and practical responses was found, and both systems follow the desired signal.
Figure 10b shows the torque response for the same speed reference. At 2 s, the highest step load variation and difference between SIMULINK ad DSP-HIL responses can be noticed. Despite the notorious difference, the torque performance follows a similar behavior.
Figure 10c,d shows the stator current phase A and stator flux, respectively. There is a modest agreement between both platforms. Indeed, the current in steady state is bigger in the SIMULINK compared to the DS-HIL response, with a slight time delay caused by the DSP’s sampling processing time.
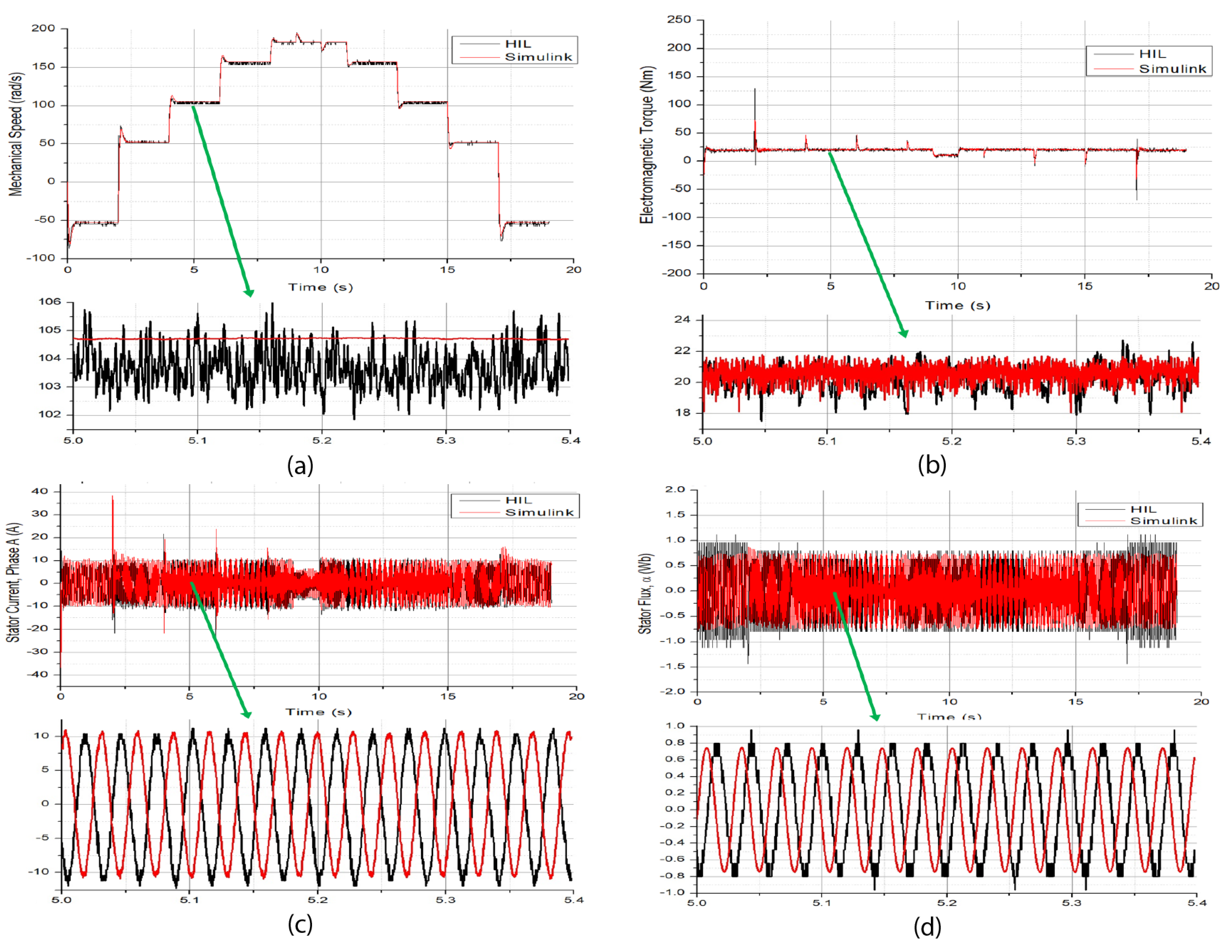
Figure 11 shows the results of the MATLAB SIMULIK block functions and DSP-HIL of DTC.
Figure 11a shows that DTC has a good speed response for both systems during step speed transitions from clockwise to counterclockwise speed directions. Similar to the previous controllers, the highest speed error tracking is achieved during a transition of 100 rad/s in 2 s. A load change of −10 Nm was applied in 9 s and removed in 10 s. The system is able to come back to the reference in less than 1 s. A speed zoom is also shown in the same figure. A low speed variation between reference and practical responses was found, and both systems follow the desired signal.
Figure 11b shows the torque response for the same speed reference. At 2 s, the highest step load variation and difference between SIMULINK ad DSP-HIL responses It can be noticed. Despite the notorious difference, the torque performance follows a similar behavior, and the DSP-HIL error, twice the expected one, is due to numerical inaccuracy.
Figure 11c,d shows the stator current phase A and stator flux, respectively. Similar to the previous results, a low equivalence between both platforms and results is observed, with a notorious phase shift delay caused by the DSP’s sampling processing time.
Figure 12 shows the results of the MATLAB SIMULIK block functions and DSP-HIL of FTC.
Figure 12a shows that FTC has a good speed response agreement for both systems during step speed transitions on both directions. In contrast to previous controllers, there is a neglectable speed error tracking in the overall speed transitions. Once again, a load change of −10 Nm was applied in 9 s and removed in 10 s, and the system came back to the reference in less than 1 s for both cases. Additionally,
Figure 12b shows the torque response for the same speed reference. A torque zoom is also shown in the same figure. There is a low torque variation between SIMULINK ad DSP-HIL responses.
Figure 12c,d shows the stator current phase A and stator flux, respectively. Similar to the previous results, a low equivalence between both platforms and results is observed, with a notorious phase shift delay in the phase caused by the DSP’s sampling processing time.
The final tests were on PTC algorithm.
Figure 13a shows that PTC also has a good speed response agreement for both systems during step speed transitions on both directions. Additionally, there is a neglectable speed error tracking in the overall speed transitions. Once again, a load change of −10 Nm was applied in 9 s and removed in 10 s, and the system came back to the reference in less than 1 s for both cases. Additionally,
Figure 13b shows the torque response for the same speed reference. Similar to FTC response, a low torque variation between SIMULINK and DSP-HIL is noticed.
Figure 13c,d shows the stator current phase A and stator flux, respectively. A low equivalence between both platforms and results is observed, with a small phase shift delay in the phase.
4. Discussion
Table 1 provides the experimental data from the six different motor controllers. The top half of the table shows some of the main characteristics of the dynamic performance, followed by the hardware resources and general characteristics on the bottom.
DIFOC has the minimum settling time compared with the others. Additionally, it is apparent from these data that very little settling time improvement is achieved by the three torque controllers compared with current controllers. The smallest overshoot is reached by DIFOC. On the other hand, a neglectable speed variation between desired and practical response was achieved, with a maximum of 3% on the six controllers. One of the most interesting aspects of this graph is the IFOC response, which obtained the minimum torque ripple in the steady state and the minimum harmonic distortion on flux and current. It is also interesting to note that only two controllers behave with a fixed switching frequency, which helps to decrease the flux and current harmonic distortion. The final dynamic performance characteristic evaluated in this table refers to low speed behavior. There is a significant difference between the six controllers, and only two attained excellent behavior and the rest poor behavior. Note that a scale of poor, good and excellent score was used to evaluate this parameter.
The next part of
Table 1 is concerned with hardware resources. IFOC and DIFOC used more resources than the others, mainly due to the PWM function. DTC has the lowest memory used and execution time, contrasting with DIFOC and PTC, which have the highest. DTC uses the minimum number of clock cycles, followed by IFOC and PTC with the maximum. To calculate the processing time, it is necessary to divide the clock cycles by the clock frequency, i.e., 879/60 MHz = 15 µS. Having discussed the dynamic performance and hardware resources, we next address the overall characteristics. For example, modulation is only needed on IFOC and DIFOC, which utilize three compensators. By contrast, FTC and PTC use only one. PCC and PTC are techniques with the most sensitive motor parameters, being DTC and FTC the most robust. IFOC, DIFOC and PCC use only current information, while DTC, FTC and PTC use torque and flux. Indeed, only one transformation is requested by the torque techniques, compared to the first three, which use two.
4.1. Main Achievements Traditional Controllers
Considering the implemented drivers in detail, IFOC presents better behavior in terms of current and electromagnetic torque. Therefore, for control that is referenced with currents, these will be very well detailed compared to other types of control. Being a function of the current, the electromagnetic torque will also have a reduced ripple. The disadvantage of IFOC is that the implementation and philosophy to carry out the control is more complex than the others, e.g., DTC, mainly due to changing the coordinates. Furthermore, equations used in its control are difficult to find in the literature with greater implementation details. On the other hand, DTC displays considerable curls, which are mainly due to hysteresis drivers. Therefore, the nature of this type of regulator always introduces oscillations in the control variables.
4.2. Main Achievements Advance Controllers
Fuzzy methods consist of different stages initiated by the rule selection, followed by membership functions, the number of input and output fuzzy sets and their degree of intersecting, association, connection operations and defuzzification method. Open research directions in fuzzy control techniques are reducing the computational load and increasing feasibility; both aims can be achieved by minimizing the number of memberships and using different defuzzification functions.
For instance, the implemented DIFOC consists of a diffuse Mamdani type with a defuzzification based on center of gravity (COG). This controller consists of a set of fuzzy “IF-THEN” rules, where the system takes as input the values of the fuzzification and applies them to the related. The AND and OR operators are used to obtain a single number that represents the evaluation result. This number (the truth value) is applied to the outcome. By using this controller, a neglectable speed variation between reference and practical responses was found and both systems follow the overall reference signal.
In contrast, the FTC has a similar behavior to DTC, that is, it practically presents the same magnitudes of current ripple and electromagnetic torque. This is because this work considers the characteristics of the DTC, that is, the limits of torque and flux hysteresis are the same as for DTC, e.g., the number of sectors, translated into the fuzzy logic philosophy. The main disadvantage of this controller is that it consumes a lot of storage memory, thus it cannot be applied if resources are limited.
On the other hand, predictive techniques are emerging in the field of power electronics, and these techniques are being adapted to conventional, DTC and IFOC controllers, with promising improvements for the future replacement of conventional control systems. Their downside is that they consume a significant processing time, and, according to our findings, for a horizon time greater than one, the response in ripple current and torque are greatly reduced in simulations. However, the calculation load grows even more, which made it impossible to use this method experimentally, at least in this DSP.
In particular, it was found experimentally that PCC has a problem with maximum load at low speeds (it gets out of control), which does not happen with simulations and has not been reported in the literature. This result suggests that the implementation considerations to adapt them to the DSP interfere with the performance of this controller. This surprising finding contrasts with previously studies [
16,
17,
18], in which PCC experiments were performed with real-time controllers. A possible explanation can involve the restricted range used in DSP.
4.3. Other Strategies
Optimization techniques for IM are emerging for use in scalar, vector and direct induction motor drives. Hannan et al. [
17] used biology- and physics-based optimization algorithms, and their numerical and real time results show promising outcomes. In general, optimization techniques can be applied to speed, current or torque controllers to find the best parameters. Indeed, it is claimed that they can be applied to minimize the error, flux changes of the torque, current ripple, noise and frequency variation. Additionally, optimization systems can achieve robustness, damping capability, enhanced transient responses and significant speed reduction responses in terms of overshoot, steady-state error and settling time [
38]. However, optimization techniques have limitations of global minimum, trial-and-error tuning procedure, local minima and optimal trapping. They also have limitations in varying the algorithms and computational time to achieve the best optimization operation. Practical implementation into a microcontroller, DSP, FPGA or other digital platforms is still limited.
A recent trend in the PE community is the application of fractional-order (FO) theory in the control of power electronic converters [
39] and, recently, motor drives. Claimed advantages of FO are its possibility to more accurately represent the nonlinear characteristic of passive element and the achievement of faster controllers compared with integers one [
40].
An interesting effort to bring FO to the engineering classrooms was reported by Khubalkar et al. [
41], who reported the FO implementation of analog fractional integrator, a digital fractional integrator, a FO-PID controller for a DC motor, a FO-PID controller for hardware in the loop MagLev system, a FO-PID controller for a brushless direct current motor and a digital FO-PID controller for a direct current motor. A five-level space vector pulse width modulated multipoint clamped (MPC) inverter fed direct torque-controlled IM drive with FO PI controllers was reported by Chandra Sekhar and Lakhimsetty [
42]. They claimed that the proposed drive system achieves full-load torque control with fast response and reduced torque ripple for a wide range of speed variations compared with traditional structure. Another FO PI controller-based direct torque control scheme for an induction motor (IM) drive was reported by Chandra Sekhar et al. [
43]. They measured the IM performance during starting, running and speed reversal along with the step change in the load torque. Numerical and practical results in a 2 HP IM are reported, but no details of the FO tuning stability or implementation details are given.
In general, a non-integer rational transfer function (RTF) can include fractional integer and fractional derivative terms, which can be positive or negative [
44]. To practically implement RTF in a physical testbed, they must first be approximated to a rational function of two polynomials with integer order inside a desired frequency band. Once the approximation process is done, the following step is synthesizing the RTF. After the approximation and synthesis process finishes, an electrical circuit can be obtained. To this end, there are two main approaches, analog and digital [
45]. The first one uses passive components and operational amplifiers (OPAM), while the second one employs FPGA boards.
FO is an interesting approach, and it can be easily integrated into traditional FOC or DTC controllers. Up to date, some brief theory and practical results are reported, but a systematic procedure to bring FO modeling and control to the motor drive community is still lacking. This topic is open, and it can be foreseen that it will be a hot topic soon in the motor drives community, mainly due to three reasons: (1) it does not require too much processing capabilities compared with optimization techniques; (2) it can be easily integrated into current motor drives techniques; and (3) traditional linear control theory can be extended to FO controllers, e.g., Laplace operators and frequency response.
5. Conclusions
This study set out to determine a fair comparison between several adjustable speed drives. It is clear from the current study that their behaviors were, in general terms, as reported in the literature. Taken together, these results suggest that the performance of FOC controllers can be better if their control scheme parameters are adjusted adequately.
The FOC and DTC fuzzy controllers are based completely on the ideology of conventional schemes, incorporating the experience and conceptualization of whoever builds them. Because of this, their implementation was not complicated. However, it required knowledge about IM dynamics to avoid a cumbersome tuning.
On the other hand, it is also well known that predictive controllers make use of the exact system model, and this can often be a limitation. However, thanks to advances in digital electronics, today their implementation is possible in a limited integration time horizon; otherwise, the hardware/software resources increase greatly. A consideration of PTC controllers is that they use a weighting value that becomes a, sometimes rustic, heuristic process.
Overall, for the schemes, it is concluded that, with a small sampling time, the response will be better. However, this choice has a limit related to the DSP’s processing speed. Similarly, the number of bits of the analog-to-digital converter directly affected the samples taken. It is important to note that, in most studies related to variable speed drives compared in this work, more powerful digital devices are used for the experimental results. However, this does not limit the ability to implement all the strategies on the DSP-HIL platform.