Wide-Range Operation of High Step-Up DC-DC Converters with Multimode Rectifiers

Abstract

This paper discusses the essence and application specifics of the multimode rectifiers in high step-up DC-DC converters. It presents an overview of existing multimode rectifiers. Their use enables operation in the wide input voltage range needed in highly demanding applications. Owing to the rectifier mode changes, the converter duty cycle can be restricted to a range with a favorable efficiency. It is shown that the performance of such converters depends on the front-end inverter type. The study considers current- and impedance-source front-end topologies, as they are the most relevant in high step-up applications. It is explained why the full- and half-bridge implementations provide essentially different performances. Unlike the half-bridge, the full-bridge implementation shows step changes in efficiency during the rectifier mode changes, which could compromise the long-term reliability of the converter. The theoretical predictions are corroborated by experimental examples to compare performance with different boost front-end inverters.

1. Introduction

Power electronics is a critical technology for the ongoing energy transition through electrification [1]. As a result, distributed energy generation systems have been proliferating in residential applications. New and existing applications impose new requirements on converter designs to improve flexibility and performance over the existing solutions. Among the modern applications of power electronics, residential dc microgrids provide significant improvements in energy efficiency in residential settings. On the other hand, they require the integration of low-voltage energy sources and battery energy storage into a dc bus operating at a considerably higher dc voltage. Therefore, residential dc microgrids require new power electronic solutions to interface with low-voltage energy sources and battery energy storage [2].

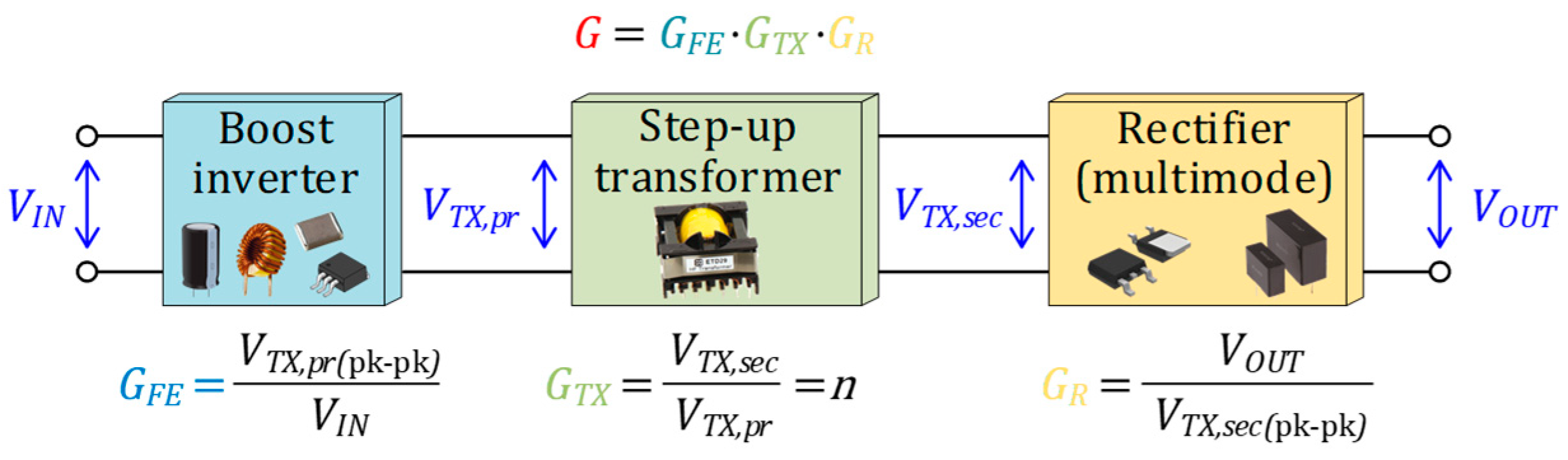
Today, high step-up DC-DC converters with a wide voltage gain range are demanded in different applications, especially in photovoltaic (PV) module-level power electronics (MLPE) [3,4], or in applications with configurable output voltages [5]. Such converters are usually comprised of three stages, according to Figure 1:

-

A boost (step-up) front-end inverter (BFEI) is fed with the input voltage V_IN. BFEI supplies pulsed high-frequency voltage V_TX,pr to the transformer primary winding. This voltage could be asymmetrical, but it is volt-second balanced to avoid transformer saturation. Considering that the peak-to-peak swing of the voltage applied to the transformer equals V_TX,pr(pk-pk), the dc-ac voltage gain of the BFEI (G_FE) could be defined as the ratio between this peak-to-peak voltage swing and the input dc voltage, as shown in Figure 1.

-

A step-up isolation transformer is used as the most efficient and low-cost technique for the voltage step-up, while galvanic isolation is an additional measure for safety and common mode current rejection. Its turns ratio could be defined as the ac-ac voltage gain G_TX equal to the ratio between the secondary winding voltage V_TX,sec and the primary winding voltage V_TX,pr in the idealized case of the lossless system.

-

A rectifier receives a high-frequency stepped-up voltage of the secondary winding V_TX,sec and converts it into the stable ripple-free output voltage V_OUT. The most straightforward way to define the ac-dc voltage gain of the rectifier (G_R) is to consider the ratio between the output voltage V_OUT and the peak-to-peak swing of the secondary winding voltage V_{TX,sec(pk-pk)}.

The overall dc voltage gain of the converter is a product of the voltage gains of these stages, as explained in Figure 1. However, a high dc voltage gain does not guarantee a wide input voltage range. An extended dc gain range could be achieved by reconfiguring one or more of the three stages, which results in a step change in the voltage gain or a gain range shift in the corresponding stage(s).

For example, the gain range of the BFEI could be additionally adjusted by the reconfiguration of its topology from a full-bridge into a half-bridge [6] or a single-switch inverter [7] with a twice lower dc-ac gain G_FE. Similarly, the equivalent turns ratio of the isolation transformer can be changed by the commutation of an auxiliary secondary winding [8] to achieve a step change in the G_TX gain. Reconfigurations in both of these two stages could also be combined using a simple control [9] or a sophisticated hardware integration [10] to extend the dc voltage gain range further. As for the challenges, the reconfiguration of the inverter can compromise the reliability of the converter, as the thermal stress of the switching semiconductor components changes significantly after a reconfiguration. Reconfiguration capability at the transformer stage would require the increased use of either magnetic core material or winding copper, which would impose limitations of converter cost and volumetric characteristics.

This study focuses on adjusting the ac-dc voltage gain G_R of the rectifier stage as a new technique that has been increasingly used in recent years. This gain could be adjusted either smoothly or stepwise by applying an ac boost [11,12] or multimode rectifiers (MMRs) [13,14] correspondingly. In general, the step changes in the gain G_R of an MMR could also be smoothed by employing a special switching sequence for a short time [15]. The concept of MMRs has recently attracted attention due to its design and control simplicity. Moreover, the application of MMR along with topology morphing control helps to achieve a balanced cost–performance tradeoff by allowing the inverter switches to be operated within the optimal conditions in a wide range of input voltages and operating powers. This could unlock the true potential of even the simplest BFEI topologies [16], which is essential for cost-sensitive applications such as PV MLPE systems. On the other hand, the application of MMR to high step-up DC-DC converters in a wide input voltage range could result in efficiency steps at the rectifier mode transitions [13,14].

The main idea of this paper is to give a short insight into the essence and application specifics of MMR in high step-up DC-DC converters with a wide input voltage range. The existing literature suggest full-bridge implementation, as this is used the most but in applications with a low dc voltage gain. This assumption could result in a DC-DC converter design with a poor performance, as will be demonstrated below. Therefore, this paper focuses on the issue of the efficiency step change occurring at the operating mode change in an MMR. This will demonstrate that the efficiency behaves differently at the step change in the gain G_R depending on the BFEI used. Some BFEI topologies cause a step change in the converter efficiency, while others avoid this issue. Therefore, this paper provides some tips on the selection of BFEI to synthesize high step-up DC-DC converters with a wide input voltage range. It is organized as follows. The second section describes known MMR topologies and selects one of them for further study. The implementation possibilities of high step-up DC-DC converters with MMR are discussed in the third section. The fourth section provides an analysis of power losses and an experimental verification of the theoretical operating principles described in the third section and justifies the difference between the BFEIs based on the full-bridge and half-bridge topologies. The conclusions are drawn in the fifth section.

2. State-of-the-Art Multimode Rectifiers

This section provides a short survey of multimode rectifiers. During the last decade, a wide variety of MMRs was proposed and validated in different applications, which clearly demonstrates the overall potential of the MMR technology. The typical applications of the MMRs today range from the sub-kW high-performance PV microconverters to multi-kW fault-tolerant power electronic transformers and energy routers. In PV microconverters, the implementation of MMRs allows keeping the control variable of the switching stage in a most favorable range, which helps to flatten the power conversion efficiency over the wide range of operating voltages and powers of the converter [16]. In fault-tolerant systems, the application of MMR along with the special control patterns of the switching stage helps us to achieve a certain level of tolerance to semiconductor failures, which might considerably improve the availability of a converter in mission-critical applications [17].

Figure 2 shows the power circuit topologies of state-of-the-art MMRs. It can be seen that the majority of MMRs are realized as passive diode rectifiers, where the mode selection is implemented by turning on or off the mode change switch S_R. Alternatively, the mode selection of an MMR could be realized by changing the static PWM pattern, as in the semiactive variable-structure rectifier shown in Figure 2d [18]. However, this approach with two high-frequency switching transistors at the high-voltage side requires more complex design and control.

In both described cases, the BFEI performs input voltage regulation as the main control action. At the same time, an MMR additionally adjusts the dc voltage gain range of the converter by the step change of the rectifier topology either from a full-bridge rectifier (FBR) to a voltage doubler rectifier (VDR) (Figure 2a,b), as in [5,19,20,21], or from a VDR to a voltage-quadrupler rectifier (VQR) (Figure 2c–e), as in [14,16,18]. Such two-mode rectifiers are characterized by the 1:2 range of the ac-dc gain G_R. The MMR topology recently proposed in [13] (Figure 2f) enables all these three modes—i.e., FBR, VDR, and VQR—thus allowing a remarkable ac-dc voltage gain range of 1:4. Figure 2g shows another approach to a three-mode MMR, which is realized by combining a VQR with a symmetrical voltage sixfolder rectifier (VSR). Even though it provides high values for the ac-dc gain G_R, which reduces the transformer turns ratio in high step-up applications, this MMR features the ac-dc voltage gain range of only 1:1.5, which renders it unsuitable for wide gain range applications.

Table 1. Main properties of the state-of-the-art MMRs.

MMR Topology	Voltage Gain GR 1					GR Range	Number of Components 2
	0.5	1	2	2.5	3		C	D	SR	S
Figure 2a [5,19]	Y	Y	N	N	N	1:2	2	4	1	-
Figure 2b [20,21]	Y	Y	N	N	N	1:2	2	4	13	-
Figure 2c [14]	N	Y	Y	N	N	1:2	4	4	13	-
Figure 2d [18]	N	Y	Y	N	N	1:2	3	2	-	2
Figure 2e [16]	N	Y	Y	N	N	1:2	4	4	1	-
Figure 2f [13]	Y	Y	Y	N	N	1:4	4	7	2	-
Figure 2g [22]	N	N	Y	Y	Y	1:1.5	6	8	2	-

¹ Y = Yes, N = No; ² C = capacitor, D = diode, S_R = static mode change switch, S = semiconductor switch (PWM modulation pattern is static in each mode).

summarizes the main properties of the existing MMR topologies, including the complexity and number of components. It shows that an MMR provides the ac-dc gain G_R in multiples of 0.5, which is the ratio between the output voltage V_OUT and the peak-to-peak swing of the secondary winding voltage V_TX,sec. Some of the topologies can achieve G_R = 3, but the range ac-dc voltage gain G_R is still 1:2 or less for most of them. It is worth mentioning that the topology proposed in [18] (Figure 2d) can be distinguished from the other MMR topologies, as it provides a low component count at the expense of applying a static PWM to the two semiconductor switches. This MMR is not suitable for low-cost high step-up applications, as it requires costly driving circuits and high-resolution PWM.

All other topologies utilize a mode change switch(es) S_R that is controlled statically. The implementation of S_R depends on its operating conditions. In most cases, S_R requires a one- or two-quadrant operation capability with a unipolar voltage blocking capability, which could be implemented using a single MOSFET. At the same time, the topologies shown in Figure 2b,c require a mode change switch with four-quadrant operation, which could increase the cost of their implementation.

Based on the comparison in Table 1, the three-mode reconfigurable rectifier topology [13] shown in Figure 2f stands out, as its range of the ac-dc gain G_R equals 1:4, while it uses fewer components than the other MMR with the three operating modes proposed in [22]. It features the best performance/complexity tradeoff and, therefore, was selected for further use in this study. The selected MMR compares favorably to the existing techniques for voltage gain range extension. For example, a 1:4 adjustment of the voltage regulation range was not demonstrated by any known concept of the reconfigurable BFEI. Only a 1:2 gain range adjustment was demonstrated in [6,7] by means of the BFEI control. On the other hand, a transformer with three output-side winding can reproduce a 1:4 gain change range with two steps by extending the concept [8] with a multi-tap secondary winding. Assuming that MMR [13] and technique [8] are modified to provide exactly the same behavior of G_TX × G_R, the following conclusions can be drawn regardless of the BFEI implementation:

-

The MMR should provide three values of G_TX × G_R—namely, n_MMR/2, n_MMR, and 2 × n_MMR, where n_MMR corresponds to the baseline turns ratio for the MMR.

-

The multi-tap transformer provides three turns ratio values: n_TX1, n_TX2, and n_TX3, which relate to n_TX3 = 2 × n_TX2 = 4 × n_TX1 to reproduce the behavior of G_TX × G_R of the MMR.

-

The assumption above yields the following relation: n_MMR = 2 × n_TX1.

-

Considering that the technique [8] is based on the full-bridge diode rectifier, the wire cross-section of multi-tap secondary winding should be rated for the maximum output current. The MMR winding should be wound with wire rated for a twice higher current but twice fewer turns.

-

Technique [8] would require four switches instead of the two used in the MMR, making it not attractive for low-power high step-up applications, where the cost of implementation is of great importance.

Considering all the aspects mentioned above, idealized transformer designs for MMR and multi-tap techniques would require the same copper cross-section area. However, in practice the multi-tap transformer design suffers from the copper cross-section area increase caused by the connection terminals to the winding taps. Despite having a similar copper cross-section area, a higher number of turns of the multi-tap winding requires more winding layers, which is a significant drawback due to the much-increased parasitic proximity and skin effects, increasing the winding losses considerably [23,24]. The final consideration in favor of the MMR approach is that the VDR mode, where the transformer winding experiences the highest current stress, is used in the range where the input current is limited, and thus the converter operates at the power levels below the rated maximum. As a result, the MMR transformer design could have a copper cross-section area much less than that of technique [8].

The mode selection in the MMR [13] is realized by turning on and off the mode selection switches S_R1 and S_R2. In the FBR mode (Figure 3a), this MMR utilizes only half of the circuit, while the other half is bypassed by diode D₇. The positive and negative half-waves of the secondary winding voltage V_TX,sec are rectified by the diode pairs D₁–D₃ and D₂–D₄, correspondingly. The VDR mode is activated when the switch S_R1 is turned on (Figure 3b). Diodes D₁ and D₃ rectify the transformer current in this mode. The diode D₇ bypasses half of the rectifier circuit similarly with the FBR mode. The VQR mode is activated when both switches S_R1 and S_R2 are turned on (Figure 3c).

The given MMR provides the widest range of gain G_R and requires only two active switches:

$$G_R=\frac{V_{OUT}}{V_{TX,\sec (\mathrm{pk}-\mathrm{pk})}}=\{\begin{array}{l}0.5, S_{R1}=OFF, S_{R2}=OFF,\\ 1, S_{R1}=ON, S_{R2}=OFF,\\ 2, S_{R1}=ON, S_{R2}=ON,\end{array},$$

(1)

where V_{TX,sec(pk-pk)} is the peak-to-peak value of the secondary winding voltage V_TX,sec. It is worth mentioning that there is a forbidden state when the switch S_R1 is turned off and the switch S_R2 is turned on. This MMR can operate with either symmetrical or asymmetrical secondary winding voltage V_TX,sec. From (1), it follows that the given MMR provides a fourfold increase in the converter gain if the FBR mode is changed to the VQR mode.

3. Implementation Possibilities of High Step-Up DC-DC Converters with MMR

This section provides a discussion on two possible implementations of high step-up DC-DC converters with MMRs. As was mentioned above, some implementations suffer from efficiency steps at the MMR mode transition. This behavior of the efficiency is not observed in DC-DC converters with a low dc voltage gain (high input voltage), which are typically realized based on the voltage-source LLC or other resonant topology using variable frequency control. Their efficiency curves intersect without a step [6,22], which is not the case in high step-up DC-DC converters with pulse-width modulation. On the other hand, both voltage- and current-source DC-DC converter topologies demonstrate a step of efficiency at the mode transition of an MMR in high step-up applications [10,13]. As the current- and impedance-source DC-DC converters are the most popular BFEI types in high step-up applications [25], this study is focused on them.

3.1. Case Study DC-DC Converter Topologies Utilizing MMR

For high step-up galvanically isolated DC-DC converters, the current- and impedance-source BFEIs are usually selected as they combine the input voltage regulation capability in a wide range with inherent voltage boost functionality and continuous input current. There are two opportunities for the implementation of the BFEI based on the full-bridge or a switching stage with a reduced number of switches such as half-bridge or single-switch. Figure 4 shows two exemplary topologies of the current- and impedance-source BFEI: the full-bridge quasi-Z-source inverter (FBqZSI, Figure 4a) and the boost half-bridge inverter (BHBI, Figure 4b). The current- and impedance-source inverters short circuit the input inductor or the impedance-source network to perform an input voltage step-up. These time intervals are highlighted with a blue color in Figure 4. For both converters, the shoot-through duty cycle depends on the input voltage as a linear function, which is advantageous for the control system design.

3.2. MMR Implementation with Full-Bridge Front-End Inverter

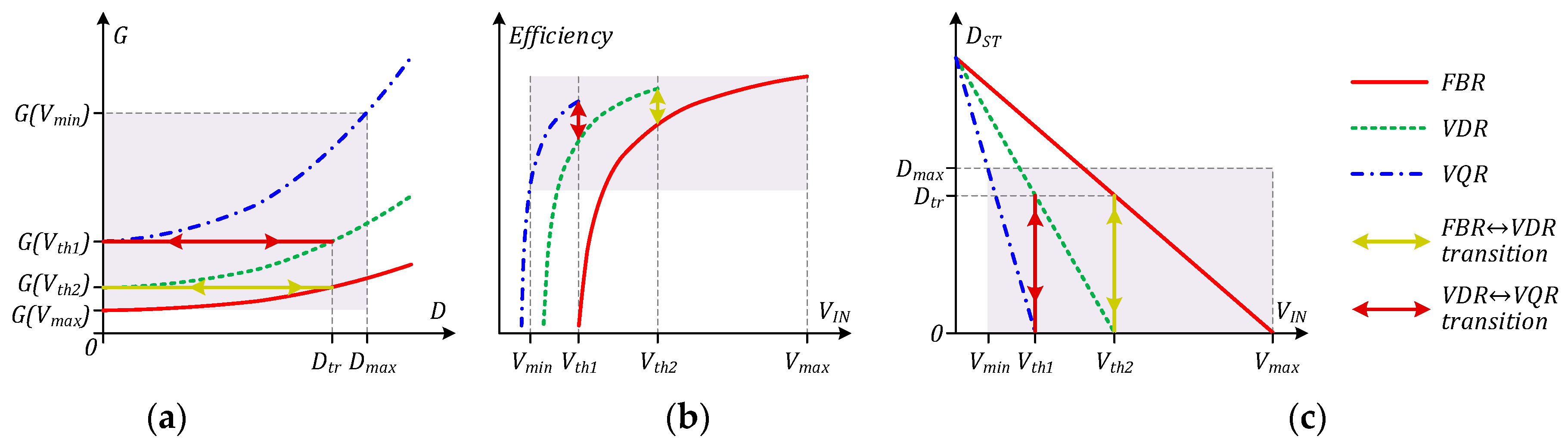
The operation of the front-end FBqZSI with the selected three-mode rectifier is presented in Figure 5 for the ideal case. The minimum value of the duty cycle D can be zero—i.e., when the FBqZSI stage implements only active states and achieves a maximum efficiency. Considering the output voltage swing, the FBqZSI provides the following dc-ac voltage gain:

$$G_{FE(qZSI)}=\frac{V_{TX,pr(\mathrm{pk}-\mathrm{pk})}}{V_{IN}}=\frac{2}{1-2\cdot D},$$

(2)

where V_TX,pr(pk-pk) is the peak-to-peak value of the voltage V_TX,pr.

Transitions between the rectifier modes appear when the shoot-through duty cycle drops down to D = 0 and further regulation using a given rectifier mode is not possible when regulating from a lower voltage to a higher, as shown in Figure 5c. When regulating voltage in the other direction, the transition happens when the gain G_FE is increased twofold at D = D_tr, which corresponds to the converter gain in the next operating mode of the MMR at D = 0. During the mode transition, the duty cycle D has to be changed in a step. Considering the linear dependence of the duty cycle D on the input voltage V_IN, it is easy to implement its step change using a feed-forward control, as the step size is easy to predict theoretically [16]. The main drawback of the full-bridge switching stage is related to a considerable change in efficiency when the converter changes the operating mode of the MMR [13], as shown in Figure 5b. As a result, the FBqZSI-based converter (Figure 4a) can switch between its three gain curves, as shown in Figure 5a.

In the ideal case, the values of the gain at the transition points are related in multiples of two: G(V_th1) = 2 × G(V_th2) = 4 × G(V_max). The maximum dc voltage gain G is achieved at the minimum input voltage V_min, which corresponds to the maximum duty cycle D = D_max. The maximum input voltage V_max corresponds to D = 0 in the FBR mode of the MMR. Due to this, the duty cycle step always happens between D = 0 (the maximum efficiency points) and D = D_tr (providing the same dc voltage gain after the step). Therefore, both threshold voltages V_th1 and V_th2 are defined by the transformer turns ratio as follows: V_th1 = V_OUT/(4n) and V_th2 = V_OUT/(2n).

Typically, the efficiency curve of a high step-up DC-DC converter with a BFEI reaches the maximum efficiency value at the maximum input voltage, which could be translated to D = 0 in each mode of the MMR. In Figure 5b, the maximum efficiency is achieved at D = 0, as the absence of the shoot-through states significantly decreases the rms currents of the switches due to the high current of the switches during the shoot-through states [26]. Moreover, the switching losses are minimum at D = 0, as the shoot-through states result in high switching currents of the main switches as well as reverse recovery losses in the synchronous switch S_qZS [27,28]. The switching losses of the FBEI semiconductors are dominant when D ≠ 0; thus, the efficiency step is inevitable between the efficiency curves, as suggested in Figure 5b. It is worth mentioning that the MMR would operate at a nearly constant output current when the converter operates at the same input power across a wide input voltage range. As a result, the conduction losses in the rectifier will depend on the number of diodes employed in each MMR mode. Hence, it could be predicted that the VQR mode will feature higher losses in the output-side diodes, resulting in a lower peak efficiency at D = 0 than that of the VDR mode with fewer diodes employed. As a result, their smooth intersections during MMR mode transitions are not feasible. The steps of the efficiency value caused by the MMR operating mode transitions could result in additional thermal cycling, thus compromising the converter reliability. Moreover, parasitic oscillations occur during zero voltage intervals when the shoot-through states are implemented, resulting in the voltage having a symmetrical shape [13]. Hence, the full-bridge BFEI implementation with MMRs is not advisable in high step-up DC-DC converters with a wide input voltage range, which is typically used in applications where high reliability is of great importance.

3.3. MMR Implementation with Half-Bridge Front-End Inverter

Considering the possible implementations of the BFEI with a reduced number of switches, the BHBI was selected as it showed a good overall performance in previous studies [19,29,30,31]. The bridge BFEI counterparts are more complicated and, thus, more costly. The dc-ac gain of the BHBI is defined by the duty cycle D of the switch S₂:

$$G_{FE(BHB)}=\frac{V_{TX,pr(\mathrm{pk}-\mathrm{pk})}}{V_{IN}}=\frac{1}{1-D}.$$

(3)

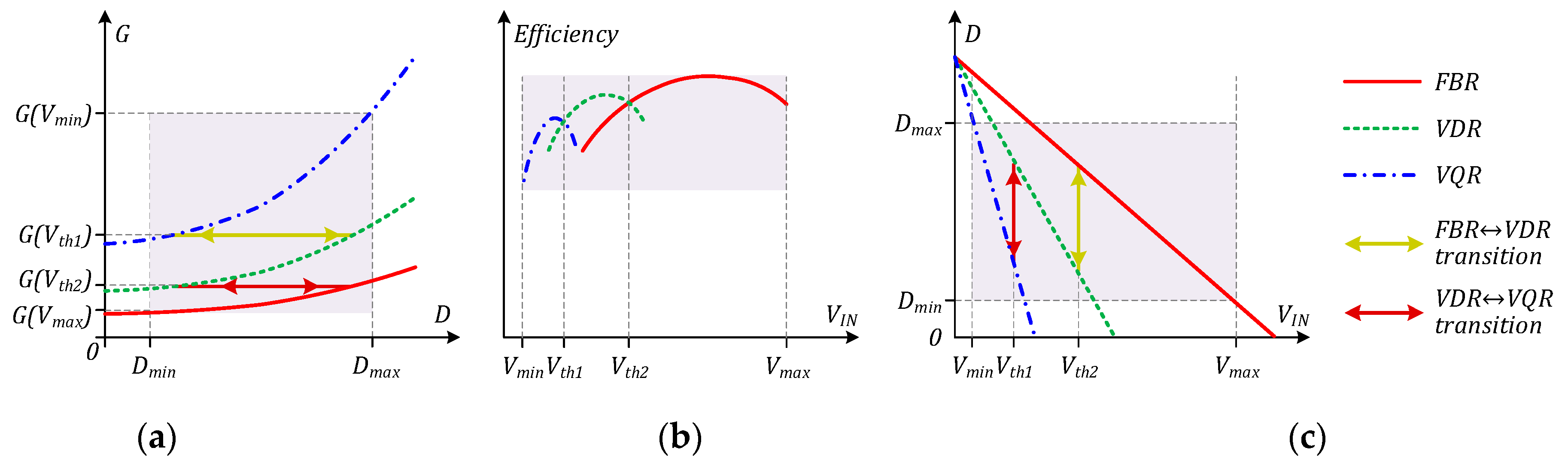
In the case of BHBI, the duty cycle of the main switch S₂ has to be constrained both from the top and bottom. Figure 6 provides an idealized explanation of BHBI operation with the three-mode rectifier. The minimum duty cycle D_min and the maximum duty cycle D_max are defined by the converter design. To achieve an acceptable efficiency in the whole input voltage range, the switch duty cycle range is typically restricted between 0.3 and 0.7 due to thermal limitations [19,29].

The MMR mode transitions could be performed at threshold voltages (V_th1 and V_th2) where the efficiency curves related to different MMR modes intersect. These intersections are feasible as the efficiency curves of converters with a reduced number of switches typically resemble a parabolic shape, as was demonstrated in [32]. This behavior is dictated by the intrinsic mechanism of losses in these converters. This symmetry results from the thermal overloading of one of the switches when the duty cycle is either too low or too high. When the duty cycle D is too close to one, the switch S₁ suffers from very short current pulses with high amplitude and rms values, causing both high conduction and switching losses. A similar issue could be observed for the switch S₂ if the duty cycle D is too close to zero. Typically, the maximum efficiency could be achieved at duty cycles close to the middle of the duty cycle regulation range [32], which corresponds to D = 0.5 for the BHBI [29]. Therefore, the efficiency curves can intersect with each other, as shown in Figure 6b. As for the losses in the MMR, they generally depend on the number of diodes used in a particular MMR mode and the output current. The efficiency intersections define the points of optimal transition between the MMR modes. They occur at points where either of the switches starts to suffer from a high rms current, and its duty cycle must be increased or decreased to return its value into the favorable range from D_min to D_max. The threshold voltages could depend on the operating power and are defined empirically. Their dependence on the input power could be approximated and used for the implementation of a feed-forward control facilitating smooth transitions between the MMR operating modes [14]. The value of the duty cycle step could also vary in a range constrained by D_min and D_max if these limits are selected to be 0.3 to 0.7 or wider.

3.4. Comparison of Two Converter Implementations

The considered implementation of wide-range DC-DC converters can be compared in several ways—first, the number of components. Considering that the input capacitor in BHBI is optional and should not be counted in the total bill of materials, both converters feature:

-

seven diodes in the output-side rectifier;

-

four capacitors in the output-side rectifier;

-

two semiconductor switches controlled statically in the output-side rectifier;

-

two-winding isolation transformer with the same turns ratio;

-

two capacitors in the BFEI operating at different voltage stress.

The differences between the two converter topologies lie in BFEI implementation:

-

FBqZSI requires five switches, while the BHBI needs only two switches but rated for twice higher blocking voltage than those of the FBqZSI;

-

FBqZSI requires two inductors (they could be coupled with flux summation) that operate at double the switching frequency, while BHBI needs only one inductor of higher inductance than that of the FBqZSI to handle higher ripple resulting from operation at the switching frequency.

The comparison between the two implementations is given in

Table 2. Comparison of the two implementations of the converter with the MMR.

BFEI	Switches		Diodes	Capacitors		Inductors	Dmin	Dmax	Efficiency Steps
	BFEI	MMR	MMR	BFEI	MMR	BFEI
FBqZSI	5	2 (static)	7	2	4	2	0	0.3	Yes
BHBI	2					1	0.3	0.7	No

.

The regulation ranges could be compared using values of D_min and D_max. Using (2) and considering D_min = 0 and D_max = 0.3, the FBqZSI range could be found as a ratio between the maximum and minimum gain G_FE as follows:

$$\frac{G_{FE(qZSI)\max }}{G_{FE(qZSI)\min }}=\frac{\frac{2}{1-2\cdot D_{\max }}}{\frac{2}{1-2\cdot D_{\min }}}=\frac{1-2\cdot D_{\min }}{1-2\cdot D_{\max }}=\frac{1}{0.4}=2.5.$$

(4)

From (4), it follows that the FBqZSI is capable of regulating the input voltage in 1:2.5 range, which corresponds to a converter dc voltage gain G_R of 1:10 considering the 1:4 gain range of the MMR. At the same time, the duty cycle will be bounded to the recommended range. However, considering the losses in the converter, the realistic range of the converter range would be narrower.

In a similar way, the range for BHBI could be calculated using (3) and considering D_min = 0.3 and D_max = 0.7:

$$\frac{G_{FE(BHB)\max }}{G_{FE(BHB)\min }}=\frac{\frac{1}{1-D_{\max }}}{\frac{1}{1-D_{\min }}}=\frac{1-D_{\min }}{1-D_{\max }}=\frac{0.7}{0.3}\approx 2.33.$$

(5)

From (5), it follows that the 1:2.33 range is feasible with the recommended duty cycle range of 0.3 to 0.7. It is worth mentioning that the BHBI efficiency is less sensitive to the duty cycle due to the twice wider range available. This means that a well-optimized design with a proper PCB layout can stretch the given duty cycle range to 0.25…0.75, which will immediately result in extending the input voltage regulation range of the BHBI to 1:3.

It is worth mentioning the main difference between the essence of control variables. FBqZSI switches are controlled with the gating signals with a duration of 0.5 or higher, depending on the duty cycle value. As a result, D_min = 0 is just a case when no shoot-through action is implemented in the switching sequence—i.e., the FBqZSI provides the lowest possible gain and the highest possible efficiency at the full power, while the main switches S₁…S₄ operate with a duty cycle of 0.5. On the other hand, at D > 0 the inverter switches experience high current stress during the shoot-through states, which equals double the average input current. The theoretical maximum duty cycle equals 0.5, but in practice it is typically limited to D_max = 0.3 to avoid excessive losses and overheating of the inverter switches, as demonstrated in [33]. At the same time, the control duty cycle of the BHBI corresponds to the actual duty cycle of the switch S₂, while the switch S₁ operates with a (1-D) duty cycle. The actual values of D_min and D_max for the BHBI are limited by the thermal performance of the converter design and the cooling of the semiconductors. Regardless of the BFEI implementation, the average switch current is proportional to the input power. However, in the BFEI with a reduced number of switches, such as BHBI or similar, a switch operation with a low duty cycle results in a significant increase in its rms current. In a generalized case, the ratio between the rms and average currents is inversely proportional to the square root of the switch duty cycle.

To conclude this section, it is essential to understand how the voltage stress of the switches differs between the selected BFEIs. The BHBI must operate at a twice higher voltage to provide the same transformer voltage swing as the FBqZSI. These stresses are summarized and tabulated in

Table 3. Voltage stress of the BFEI switches.

BFEI	MMR Mode
	FBR	VDR	VQR
FBqZSI	$\frac{V_{OUT}}{n}$	$\frac{V_{OUT}}{2\times n}$	$\frac{V_{OUT}}{4\times n}$
BHBI	$\frac{2\times V_{OUT}}{n}$	$\frac{V_{OUT}}{n}$	$\frac{V_{OUT}}{2\times n}$

. Evidently, the FBqZSI can utilize switches with a much lower voltage rating than the BHBI.

4. Experimental Results and Discussion

Two experimental prototypes of the high step-up DC-DC converter were assembled to verify theoretical assumptions regarding the efficiency curve shapes and resulting transitions between the MMR modes. Their photos are shown in Figure 7. The parameters and main components are listed in

Table 4. Specifications of the experimental prototype.

Input voltage VIN	1065 V
Output voltage VOUT	400 V
Switching frequency, fS	105 kHz
Transformer turns ratio n	6
Output capacitors C1, C3	0.47 µF
Output capacitors C2, C4	3 µF
Rectifier diodes D1…D6	Wolfspeed CSD01060E
Switch SR1	ROHM SCH2080KE
Switch SR2	Infineon IPW60R080P7
	FBqZSI	BHBI
Capacitors CqZS1 and CqZS2	25 µF	-
Inductors	2 × 22 µH	88 µH
Clamping capacitor CD	-	47 µF
Blocking capacitor CB	-	13.6 µF
Switches S1, S2	Infineon BSC035N10NS5	Infineon IPB117N20NFD
Switches S3, S4, SqZS		-

. These converters were designed to utilize as many common components as possible while providing the same input voltage range of 10 to 65 V and a peak power of 250 W. This input power and voltage range correspond to countless 60-cell silicon-based photovoltaic (PV) modules that are widely used in residential PV systems. In addition, the maximum input voltage of the BHBI-based converter theoretically could be over 65 V, but it is additionally limited by the design of the onboard auxiliary power supply. The onboard power bus of 5 V is stabilized by integrated synchronous step-down voltage converter LM46002 from Texas Instruments, which cannot accept input voltages of over 65 V. The switching frequency was selected based on general practice in the literature for this class of converters.

The MMR was implemented in the same way in both prototypes. Both prototypes were designed to cover the same input voltage range, resulting in a two-fold difference in the voltage rating of the front-end generic Si switches. The output side semiconductors are rated for 600 V or 650 V. High switching frequency requires the use of SiC Schottky barrier diodes (SBDs) at the output side, SiC MOSFET co-packed with an SBD for S_R1, but a generic Si device for S_R2. A microcontroller with a Cortex-M4 core and enhanced PWM peripherals was used to implement a simple closed-loop system employing a PI controller complemented with a feed-forward loop using theoretical calculations derived from Equations (1)–(3). Quasi-Z-source inductors were implemented as coupled inductors on a single RM14 3C95 ferrite core. The BHBI input inductor L_IN was implemented using a high-flux toroidal powder core. Both prototypes utilize same design of the isolation transformers based on an RM14 3C95 ferrite core and copper Litz wire with 0.1 mm strands.

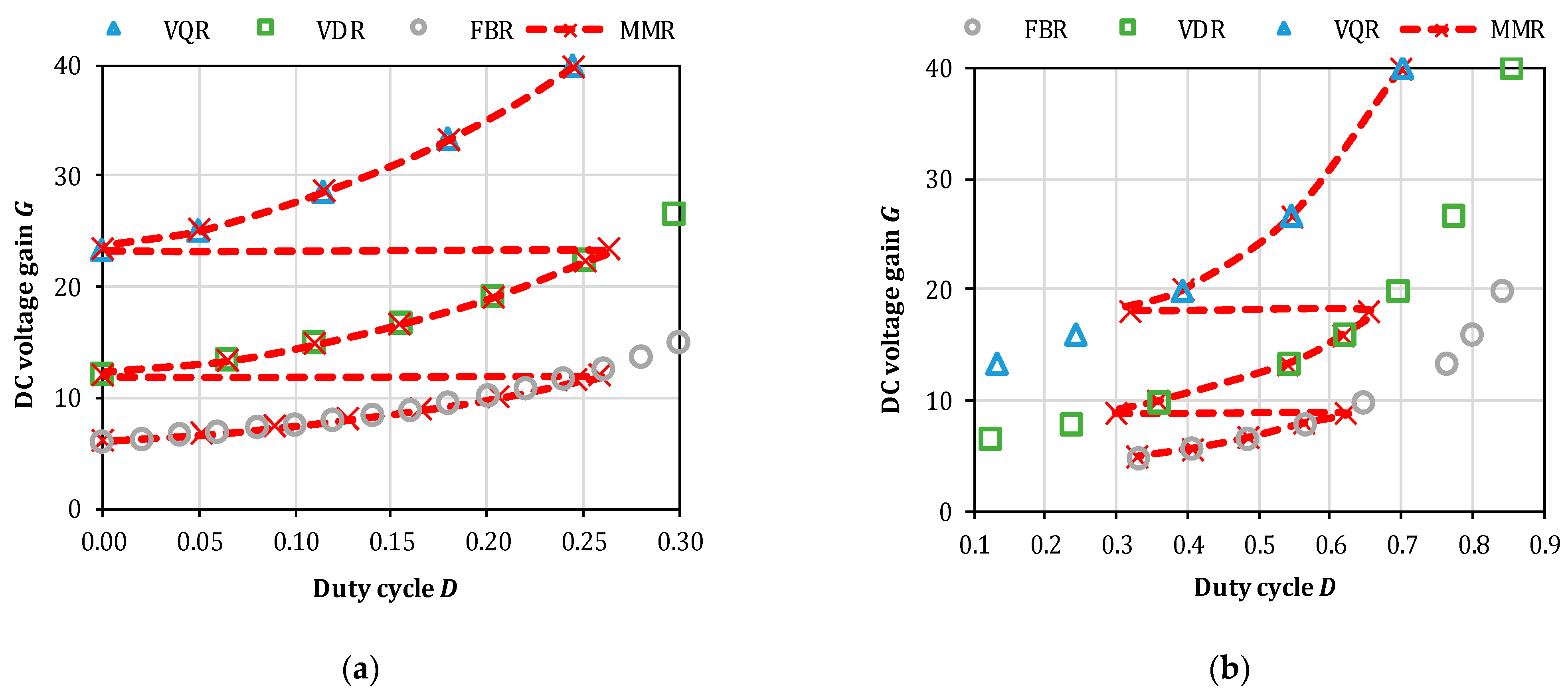
For the best efficiency, the duty cycle of the BHBI switch S₂ should be restricted within the optimal range from 0.3 to 0.7, while the FBqZSI features the optimal shoot-through duty cycle range from 0 to 0.3, as recommended in [33]. Further measurements will prove whether this is feasible with MMR reconfiguration. The measurements were performed in wider duty cycle ranges to capture converter operating behaviors for different MMR modes and compare those with the theoretical predictions. 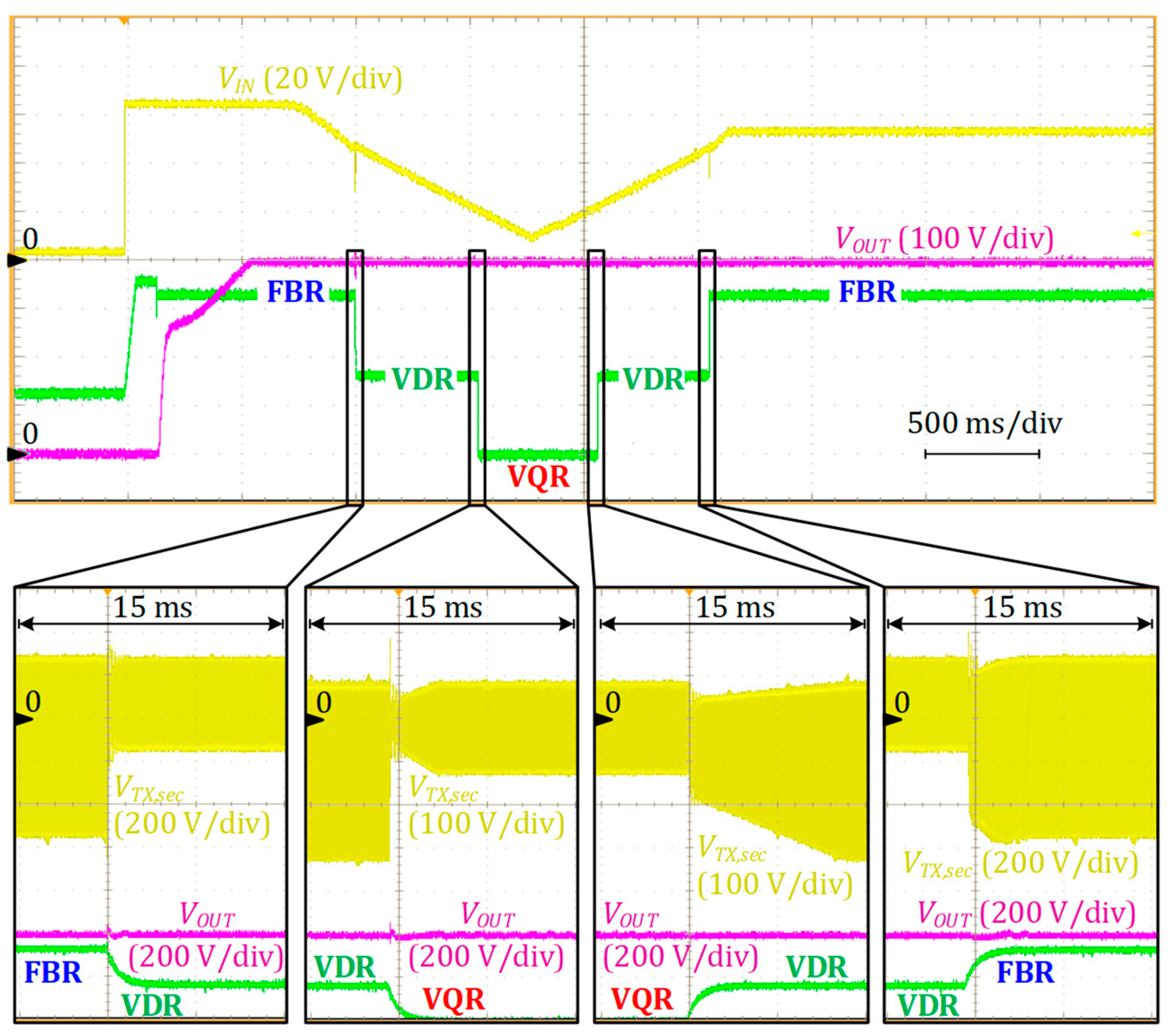As shown in Figure 8, both BFEI operate in the corresponding optimal duty cycle ranges when optimal transitions between the MMR modes are implemented. As predicted theoretically, the transition between the MMR modes happens at D = 0 in the case of FBqZSI (Figure 8a) and close to D = 0.3 for the BHBI (Figure 8b). For the FBqZSI, the theoretical value of the duty cycle step of D_tr = 0.25 is close to the experimentally observed D_tr = 0.26. The step size depends on the operating point for the BHBI. It was observed experimentally that these step values equal 0.32 and 0.36 for V_th2 = 45 V and V_th1 = 21.5 V, respectively. It is worth noting that the optimal mode transitions were observed at roughly D = 0.3, which results from the increased stress of the BHBI switch S₂ at lower duty cycle values. These control characteristics correspond to the input power of 100 W.

Similar to the control variables, the efficiency was measured at the power level of 100 W using a precision power analyzer Yokogawa WT1800. This power level was selected as it is feasible in the whole target input voltage range, as the converters cannot operate at currents above 10 A, while the isolation transformer can continuously operate at 250 W at input voltages above 25 V. The FBqZSI shows the highest efficiency at D = 0 due to the considerably reduced switching and conduction losses. Simultaneously, it drops significantly during a transition to the next adjacent mode of the MMR (Figure 9a). Stepwise changes in losses can result in the thermal cycling of the converter components and compromise their long-term reliability. At the given test conditions, the FBqZSI-based converter experiences MMR mode transitions at V_th1 = 17.2 V and V_th2 = 33.5 V. The first transition corresponds to 2.3 W of the power loss step, while the second results in a step of 6 W, which proves our prior assumption about the thermal cycling issue. For a full-bridge topology, these threshold voltages can experience small variations resulting from conduction losses variations, as shown in

Table 5. Example of thermal cycling observed in the FBqZSI-based converter at V_th1.

Input Power, W	Vth1, V	Efficiency Step			Power Loss Step, W
		From, %	To, %	Difference, %
25	16.5	86.7	95.5	8.8	2.2
50	16.8	90.3	95.7	5.4	2.7
100	17.2	92.7	95	2.3	2.3
120	17.4	92.3	94.4	2.1	2.5
175 *	17.8	92	93.5	1.5	2.6

* Corresponds to the maximum input current with the active cooling of PCB for the given thermal design.

for the first threshold voltage V_th1. Evidently, with the input power increase—i.e., an increase in the conduction losses—the efficiency step reduces in relative terms, while the absolute step of the power loss remains above 2 W. This proves the assumption that the thermal cycling issue is present and could cause reliability issues at light and full load conditions. A similar behavior could be observed for the second mode transitions at V_th2. For example, an efficiency step of 6% resulting in a power loss step of 6 W at the input power of 100 W is reduced to 2.7% at the input power of 250 W, which, however, corresponds to an even higher power loss step of 6.8 W. Therefore, the application of full-bridge BFEIs with MMR is not advisable in high step-up applications.

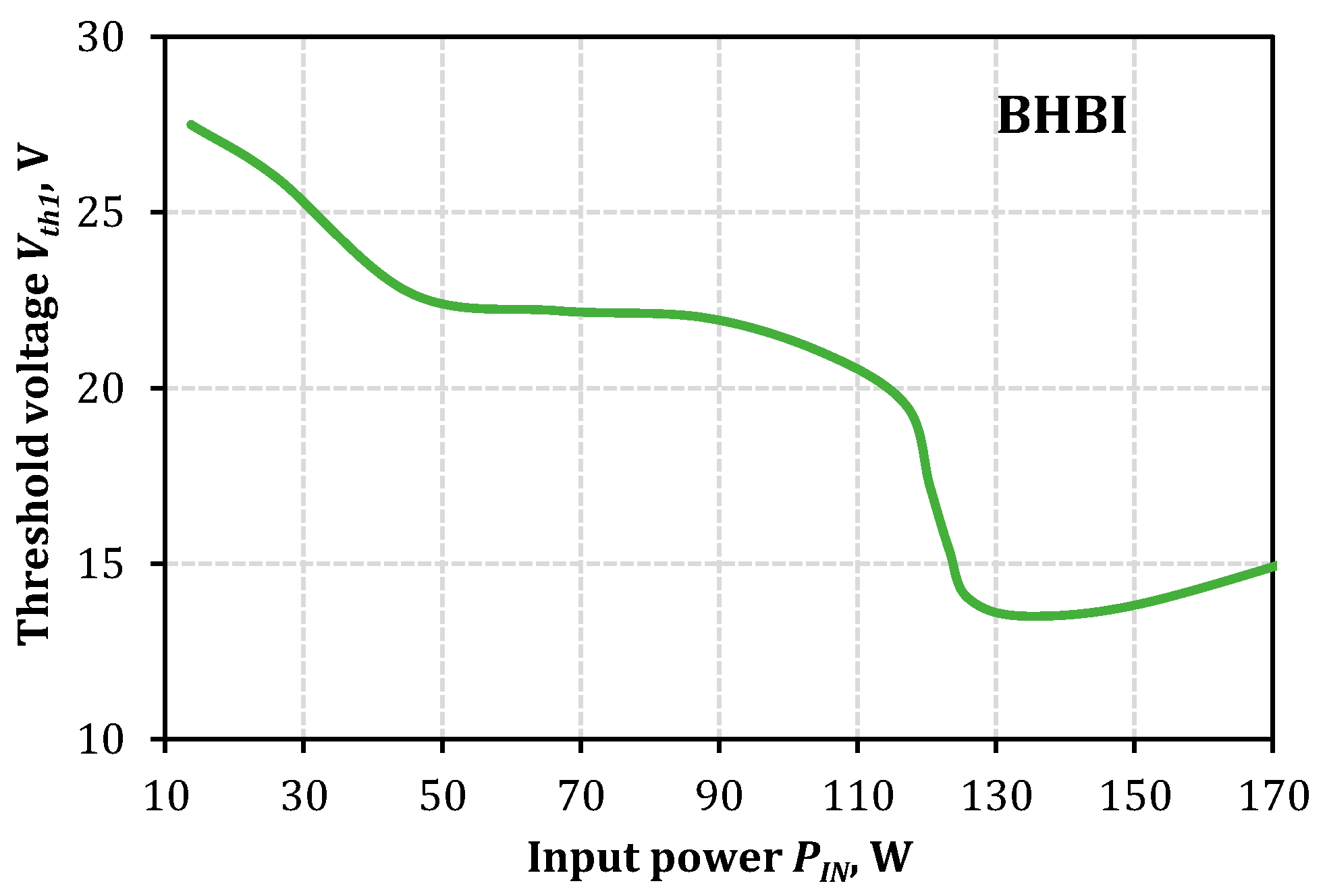
As expected, the front-end BHBI avoids this issue, as shown in Figure 9b. The parabolic shape of the BHBI efficiency curves allows for smooth transitions between the MMR modes, thus reducing the thermal cycling of the components. The overall efficiency envelope with BHBI is continuous, unlike that in the case of FBqZSI. As was mentioned, the mode transitions of the MMR occur at V_th1 = 21.5 V and V_th2 = 45 V. Compared to the FBqZSI-based converter, these threshold voltages experience a much wider variation. For comparison with the FBqZSI, the first threshold voltage position was measured as a function of the input power PIN, as shown in Figure 10. Evidently, the threshold voltage reduces when the input power is increased. Lower threshold voltages would correspond to a higher position of the mode transitions than those in Figure 8b. This could be explained by the balance between the switching and conduction losses in the BHBI-based converter. At lower power, where the conduction losses are relatively minor, the VQR mode of the MMR is beneficial in a wider voltage range, as it lowers the switching losses in the converter more than it increases the conduction losses due to a higher number of diodes at the output side. At higher power levels, the conduction losses in those extra diodes start dominating over the switching losses already at lower input voltages. In terms of intersections of the efficiency curves, the intersection point is at the falling (right) branch of the VQR mode efficiency curve at light loads, which shifts to the rising (left) branch of the VQR mode efficiency curve at higher powers.

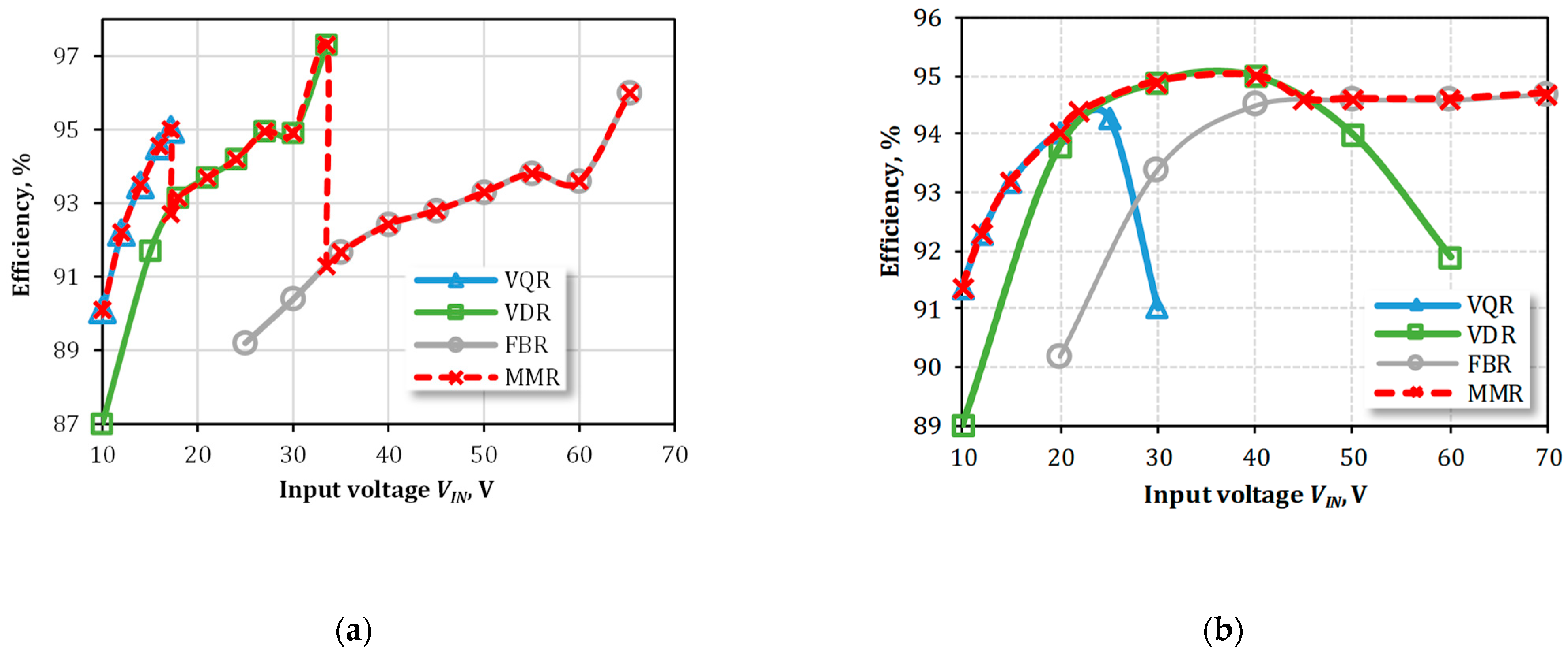
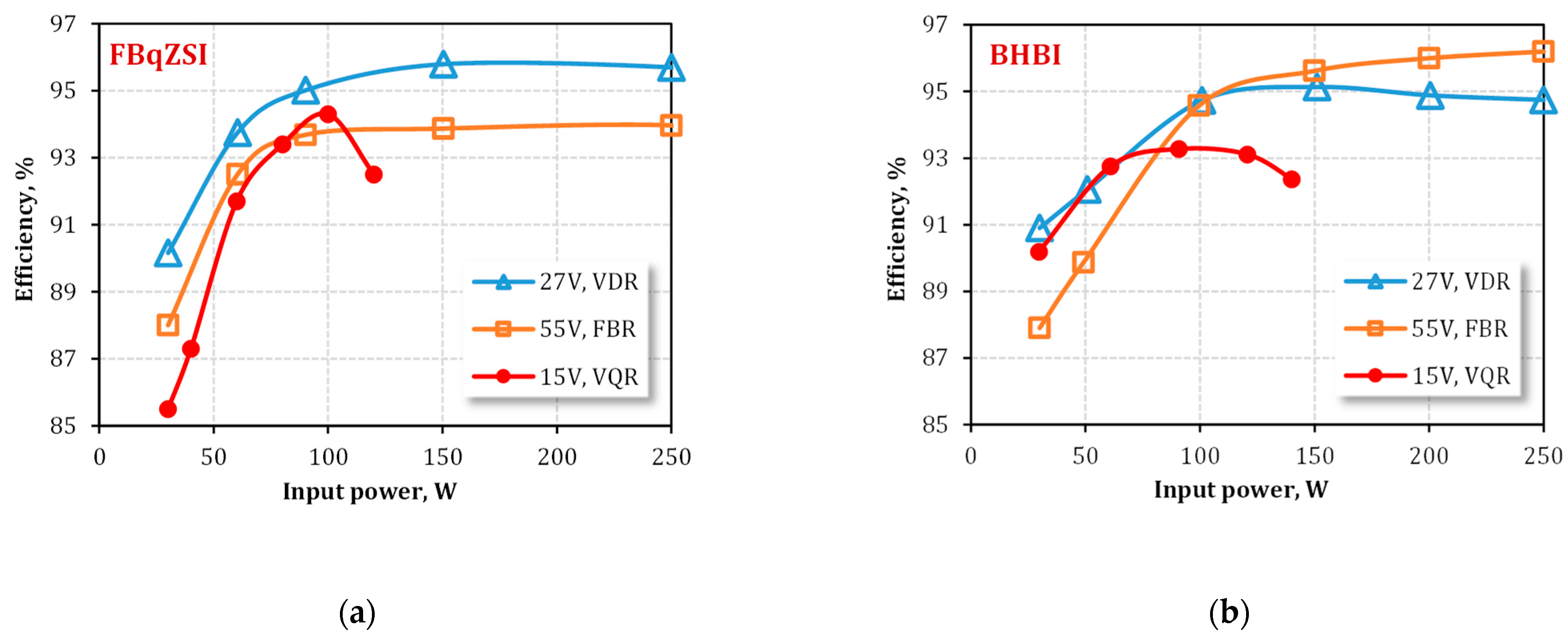
Figure 11 demonstrates how the efficiency depends on the converter operating power for different input voltages that correspond to all three operating modes of the MMR. Three operating point were selected based on observations from Figure 9. It was concluded that both converters should operate with the VQR mode of the MMR at V_IN = 15 V, the VDR mode at V_IN = 27 V, and the FBR mode at V_IN = 55 V. Moreover, these operating points closely follow the relation between the G_R values of the MMR, which allows us to keep the converter operating at nearly the same control duty cycle values: between 0.53 and 0.57 for the BHBI and between 0.06 and 0.09 for the FBqZSI. Therefore, selecting these operating points allows for a fairer comparison between the three operating modes. The operating points are referred to as, for example, “15 V, VQR” in Figure 11, where the first value corresponds to the input voltage and the second term refers to the MMR mode. The power was limited to 120 W in the case of the VQR mode to avoid the saturation of the magnetic components. As could be observed from the figures, the BHBI provides more smooth efficiency curves due to the lower number of switches that dissipate considerable switching power losses at light loads.

A closed-loop control system was implemented to demonstrate the feasibility of smooth transitions between MMR modes. It is based on the Cortex-M4 microcontroller STM32F334 with high-resolution pulse-width modulation PWM timers and a 12-bit analog-to-digital converter (ADC). The converter was loaded with electronic load in constant-voltage mode to imitate a dc microgrid. The output voltage was measured for protection using a resistive divider and differential isolation amplifier AMC1200 from Texas Instruments. The input voltage was measured using a resistive divider and an operational amplifier OPA378 from Texas Instruments. A high-accuracy hall-effect-based current sensor ACS720 from Allegro Microsystems was used for the input current measurement.

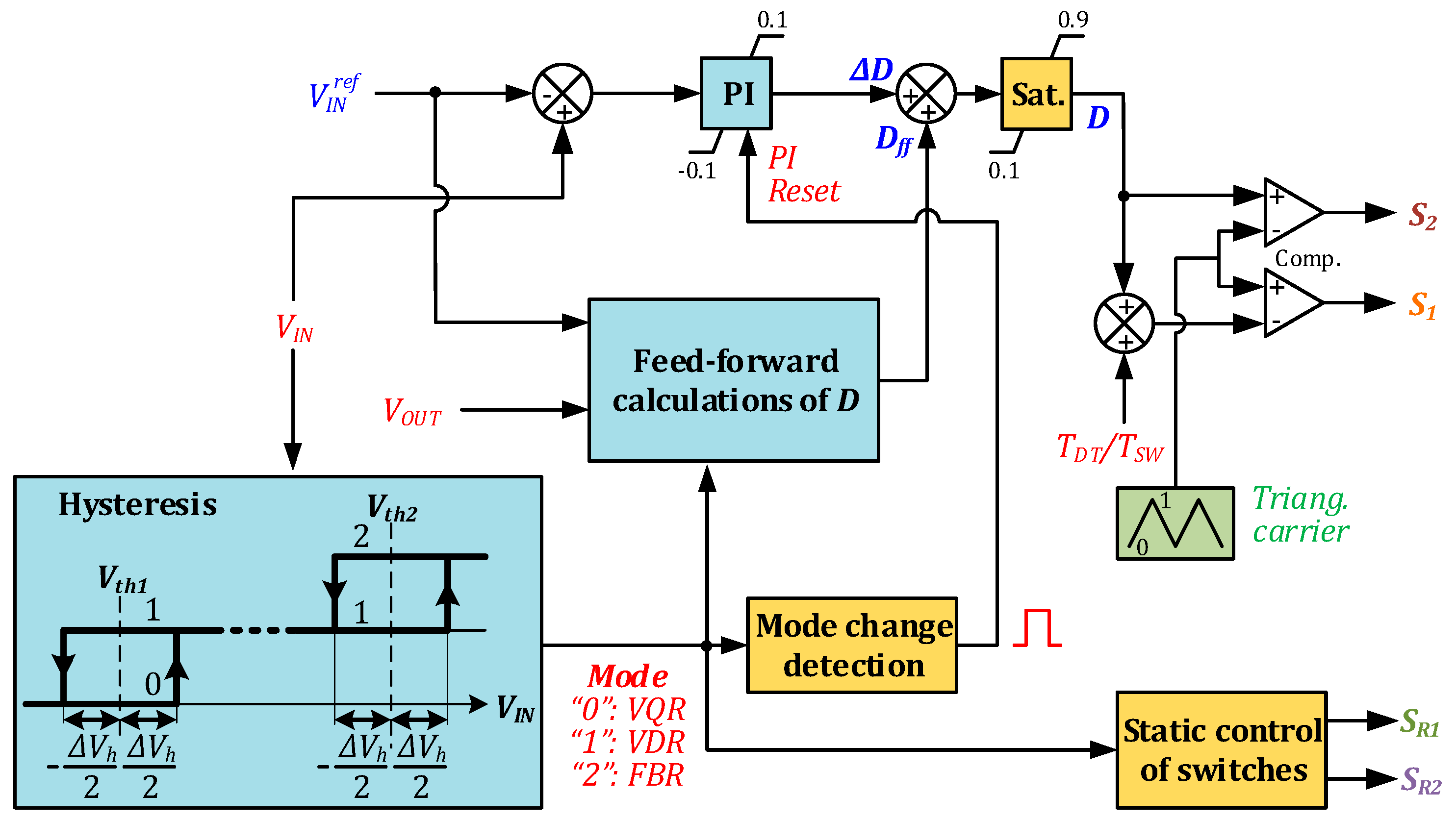
A smooth transition between the MMR modes could be achieved by employing the feed-forward control, similar to [14]. As shown in Figure 12, the feed-forward calculation of the duty cycle D calculates the main component D_ff using relations (1)–(3). The value of D_ff is calculated based on the measured V_OUT and the reference value of V_IN ($V_{IN}^{ref}$). These calculations do not take into account the losses in the converter, which results in the underestimation of the duty cycle. This means that D_ff would provide an input voltage slightly different from the reference value. To compensate for this difference, a generic PI controller with a bandwidth of 200 Hz was used to minimize the difference between the reference and measured input voltage by adding a small difference ΔD to the duty cycle D_ff. It is important to reset (nullify) the integrator each time the MMR mode changes. This approach enables fast transients during MMR mode changes, as shown in Figure 13, where the green signal for the ADC output of the microcontroller indicates the MMR operating mode. The mode change transients take a longer time at the rising input voltage ramp due to the recharging of the MMR capacitors, which is required as the voltage V_TX,sec increases its swing twofold at each transition. The reverse transitions are faster as the output current assists in discharging these capacitors. To stabilize the converter operation in the vicinity of the threshold voltages, a small hysteresis control with a bandwidth of ΔV_h = 2 V was introduced for defining mode transition points in the closed-loop control.

5. Power Loss Breakdown

The methodology for the power loss calculations is described in this section along with a power loss breakdown example.

The power losses in the inductors includes the copper losses, dc and ac, represented by an equivalent resistance r_Li. Considering the equivalent resistance and the rms current I_Li,rms, the power losses in i-th inductor are calculated by:

$$P_{Li}=r_{Li}{I}_{Li,rms}{}^2.$$

(6)

Inductor core losses can be ignored, as the ac components of the core flux density are much less than the maximum dc component.

Among the capacitors, only input-side capacitors should be considered for power loss calculation due to their high rms current stress. Similar to the inductors, the power losses in i-th capacitor are calculated based on the equivalent series resistance r_Ci and rms current I_Ci,rms as follows:

$$P_{Ci}=r_{Ci}{I}_{Ci,rms}{}^2.$$

(7)

MOSFET losses consist of conduction losses and switching losses. The conduction losses of the i-th MOSFET are calculated based on the on-state resistance R_DS(on)i and the switch rms current I_Si as follows:

$$P_{Si,cond}=R_{DS(on)i}{I}_{Si,rms}^2.$$

(8)

An improved method for the calculation of the switching losses was adopted from [34]. The switching losses of the i-th MOSFET consist of turn-on and turn-off losses:

$$P_{Si,sw}=P_{Si,on}+P_{Si,off},$$

(9)

where P_Si,on and P_Si,off are the MOSFET turn-on and turn-off losses. According to [34,35]:

$$P_{Si,on}=\frac{1}{2}{f}_s{I}_{Si,on}{V}_{Si}(t_r+t_{fu})+Q_{rr}{V}_{Si},$$

(10)

where t_r is the current rise time from the datasheet and t_fu is the voltage fall time that is calculated based on numerical integration of the C_rSS parasitic capacitance characteristics from the MOSFET datasheet from 0 V up to the switch voltage stress value V_Si corresponding to Table 3. Q_rr is the reverse-recovery charge that is typically given in the datasheet only for one out of many possible conditions, which reduces the accuracy of loss estimation.

The turn-off losses are obtained as:

$$P_{Si,off}=\frac{1}{2}{f}_s{I}_{Si,off}{V}_{Si}(t_f+t_{ru}),$$

(11)

where t_f is the current fall time from the datasheet and t_ru is the voltage rise time calculated based on the numerical integration of the C_rSS parasitic capacitance characteristics from the MOSFET datasheet from the switch voltage stress value V_Si down to 0 V.

The copper losses of the transformer are calculated based on the equivalent resistance of the windings and rms transformer current. For calculations, the equivalent resistance of the transformer windings is considered in the secondary side based on the corresponding short-circuit test taken at 100 kHz using an RLC meter HAMEG HM8118 from Rohde&Schwarz. Therefore, the copper losses of transformer could be calculated by:

$$P_{TX,Cu}=r_{TX}{I}_{TX\sec }^2,$$

(12)

where r_TX is the equivalent resistance of the windings and I_TXsec is the rms current of the secondary winding.

The improved generalized Steinmetz equation (iGSE) method [36] was adopted for the calculation of the transformer core losses:

$$P_{TX,core}=f_{s}v{k}_i{(\Delta B)}^{\beta -\alpha }{{\displaystyle \sum _m\left|\frac{B_{m+1}-B_m}{t_{m+1}-t_m}\right|}}^{\alpha }(t_{m+1}-t_m),$$

(13)

where ∆B is the peak-to-peak flux density, α and β are the Steinmetz coefficients that depend on the core material and operating frequency according to the specification from a manufacturer, B_m is the flux density at instant t_m, and v is the core volume. The constant k_i could be obtained as follows:

$$k_i=\frac{k}{2^{\beta +1}{\pi }^{\alpha -1}\left(0.2761+\frac{1.7061}{\alpha +1.354}\right)}\mathrm{m}$$

(14)

where k is the Steinmetz coefficient that is taken from the core material datasheet. As it follows from (13), the MMR mode with a lower G_R value (the FBR mode) generates higher transformer core losses due to the increased voltage swing.

The power losses of the MMR diodes are calculated based on the simple approximation of the diode volt-ampere characteristics by representing the conduction diode with a voltage source and a resistance:

$$P_{Di}=V_F{I}_{Di,av}+R_d{I}_{Di,rms}^2,$$

(15)

where V_F is the forward voltage drop of the diode, R_d is the on-state resistance of the diode that describes the slope of the volt-ampere characteristics, I_Di,av is the average current of the i-th diode, and I_Di,rms is the rms current of the i-th diode. For both BFEI, the VDR mode provides the best performance as features a good utilization of the transformer and a low number of diodes in the output-side rectifier.

The power loss breakdowns shown in Figure 14 were calculated for the operating power of 100 W and the operating voltages used in Figure 11. The input voltage corresponds to the operating points selected for Figure 11. As the input current is inversely proportional to the input voltage at a constant operating power, the power losses in the windings of the transformer and inductors would be the highest, as follows from Figure 14. The magnetic core in the transformer become recognizable only in the FBR mode. Therefore, these losses were grouped with the copper losses in Figure 14. The transformer suffers from the highest core losses in the FBR mode with the BHBI, where the flux density swing is the highest among all operating conditions. In both converters, the MMR dissipates most of the losses in the VQR mode, where eight semiconductor components (all but D₇) conduct the current. The losses in the auxiliary circuits and sensors increase with the input voltage as the efficiency of the onboard step-down power supply decreases, while the input-side voltage divider dissipates more losses at a higher input voltage. In the VQR mode, the conduction losses in the input-side semiconductors are dominant, while the switching losses are dominant in the FBR mode. Even though the BHBI operates at a twice higher voltage but lower currents than that of the FBqZSI in the same MMR mode, the high number of switches results in considerable losses in the FBqZSI switches in the FBR mode of the MMR.

Despite the attempts to balance the BFEI performance by selecting operating points with nearly the same switch duty cycles, the FBqZSI showed an unbalanced performance, and the efficiency in the VDR mode of the MMR is much better than in any other mode—i.e., the “27 V, VDR” curve is the highest in Figure 11a. This is due to the balanced switching losses of the five input-side MOSFETs and MMR conduction losses from only three diodes conducting in the MMR, while one of these semiconductor types is gets high in the VQR and FBR modes. At the same time, the BHBI shows much more balanced performance due to using only two MOSFETs, even though they operate at twice the voltage stress of that of the FBqZSI at the same operating point. Additionally, BHBI consumes less auxiliary power on-board due to the smaller driving losses.

6. Conclusions

This study shows that multimode rectifiers with static operating mode control are a promising solution in high step-up DC-DC converters that cannot achieve a wide input voltage range otherwise. The high step-up of the input voltage requires the application of boost front-end inverters, such as impedance- and current-source topologies. It could be concluded that the full-bridge boost front-end inverters tend to exhibit an efficiency curve that rises with the input voltage due to a reduction in the switching and conduction losses. The application of an MMR extends their input voltage regulation range but results in a sizable efficiency step at the point of the MMR mode change. Consequently, the heat dissipation would change stepwise inside a converter case. Therefore, the thermal cycling of the converter components can occur, which compromises the converter reliability. Therefore, this paper recommends using the half-bridge or another front-end inverter with a reduced number of switches to avoid efficiency steps during converter operation and provide a smooth efficiency curve. This approach also suits most high step-up applications well, as they typically require sub-kW converters.

These conclusions were confirmed experimentally by comparing two prototypes. The full-bridge front-end inverter shows a high peak efficiency of 97.4%, but the efficiency can change with up to a 6% step in the case of an MMR mode change. The boost half-bridge front-end inverter avoids this issue but needs switches with a twice higher voltage rating. Nevertheless, it achieves a peak efficiency of 95.2% and a higher average efficiency than the full-bridge counterpart.