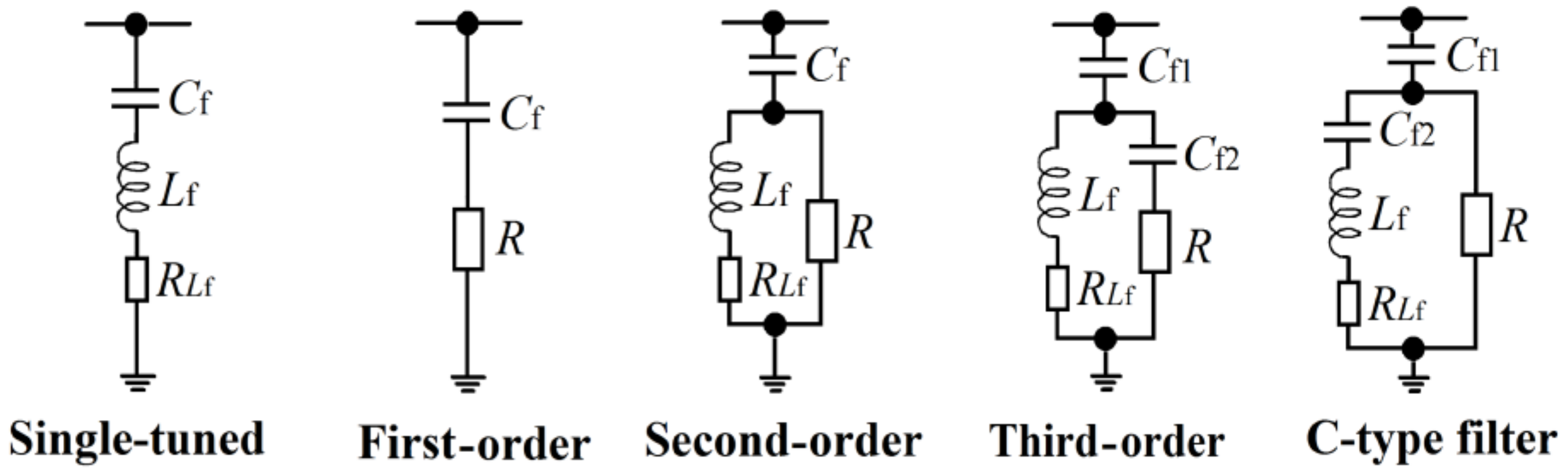
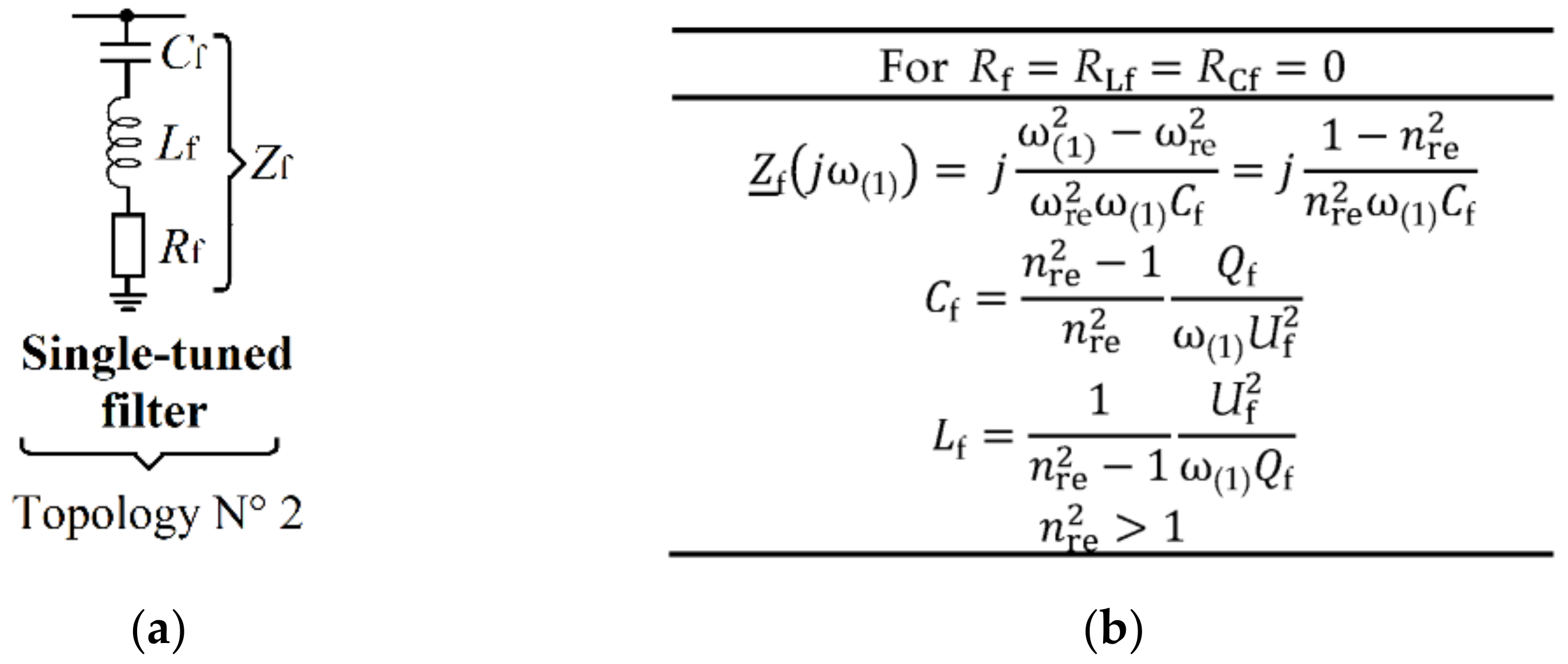Figure 1.
Simulated power system together with the passive harmonic filter (PHF) topologies.
Figure 1.
Simulated power system together with the passive harmonic filter (PHF) topologies.
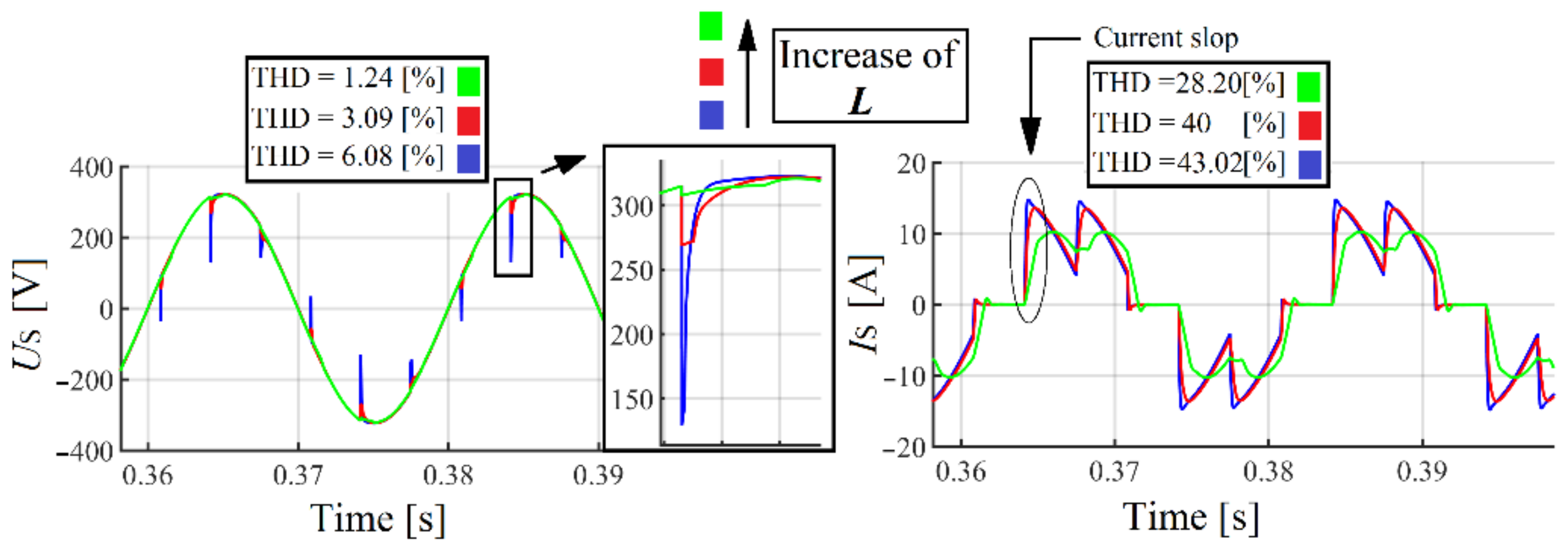
Figure 2.
PCC voltage and current waveforms (without filter connection) after the thyristor bridge input line reactor inductance (L) increase.
Figure 2.
PCC voltage and current waveforms (without filter connection) after the thyristor bridge input line reactor inductance (L) increase.
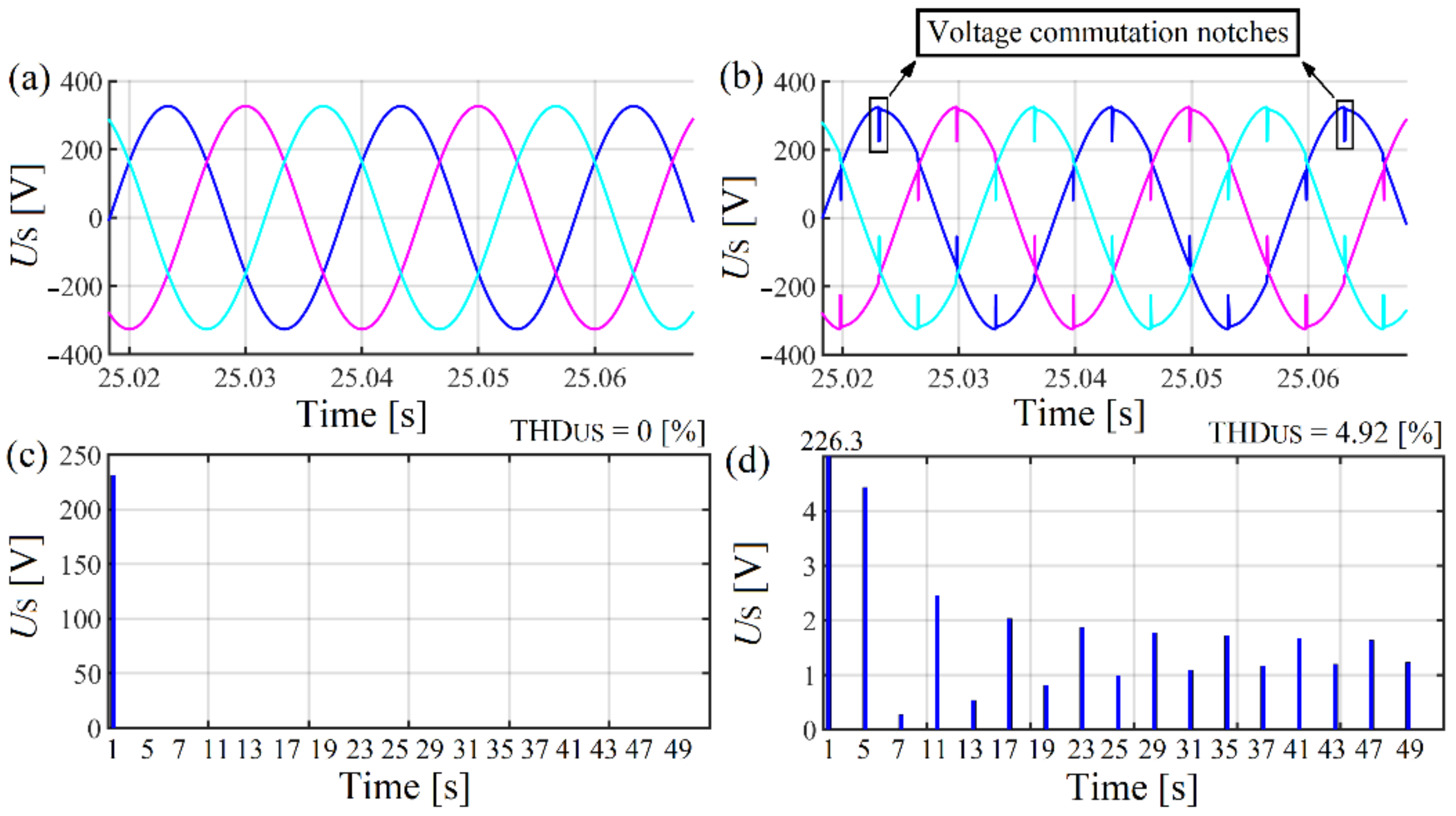
Figure 3.
Grid voltage waveforms and spectrums: (a,c) when the load is not connected to the PCC and (b,d) when the load is connected to the PCC.
Figure 3.
Grid voltage waveforms and spectrums: (a,c) when the load is not connected to the PCC and (b,d) when the load is connected to the PCC.
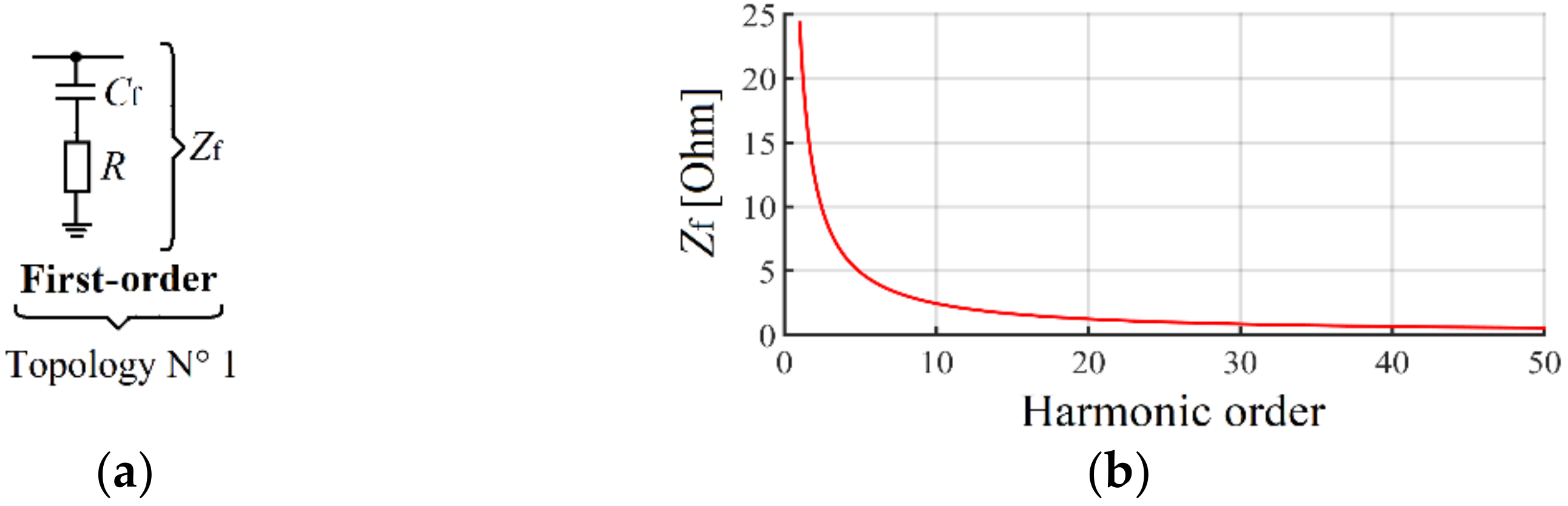
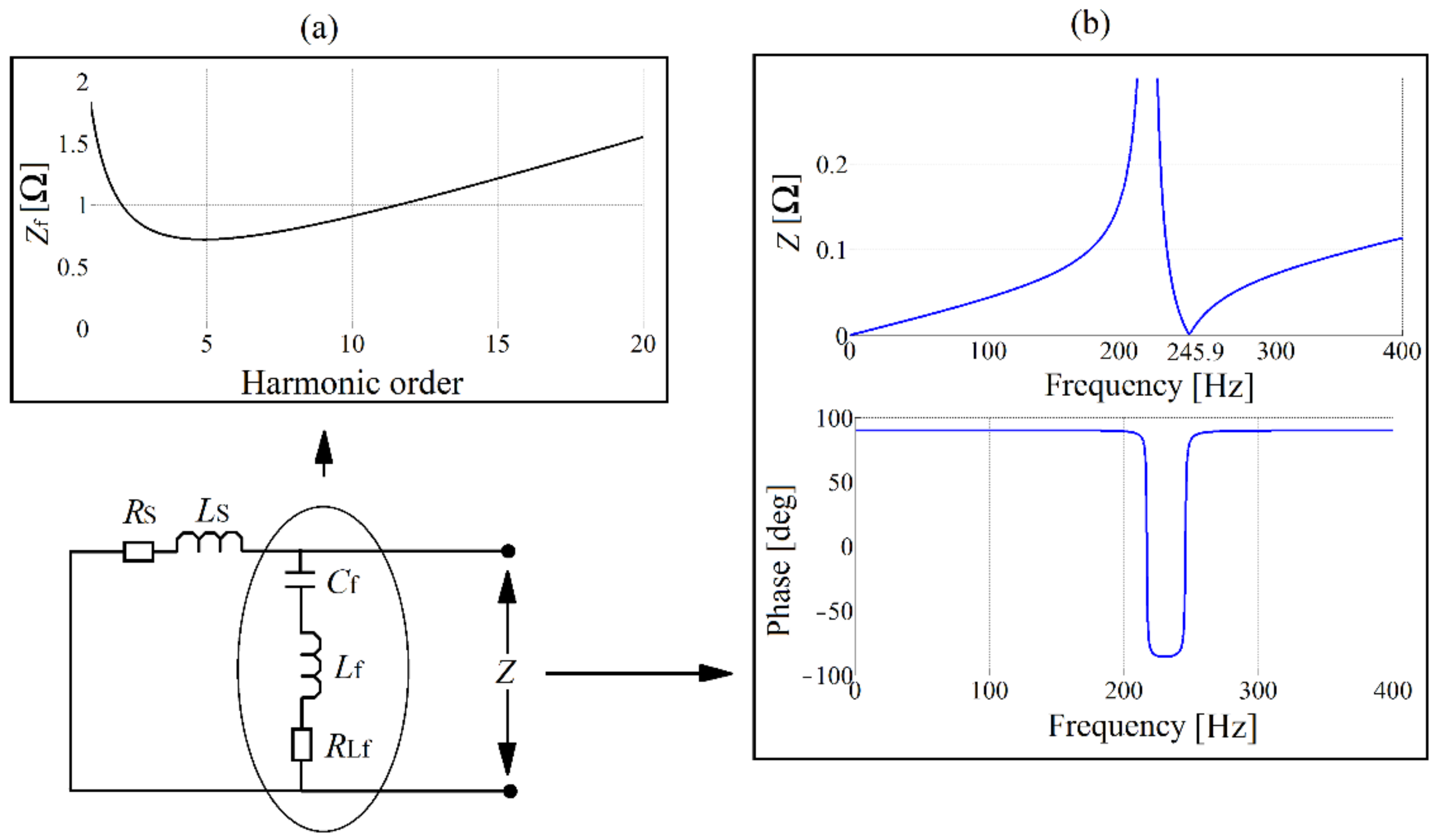
Figure 4.
(a) First-order filter, (b) impedance versus frequency characteristic of the first-order filter.
Figure 4.
(a) First-order filter, (b) impedance versus frequency characteristic of the first-order filter.
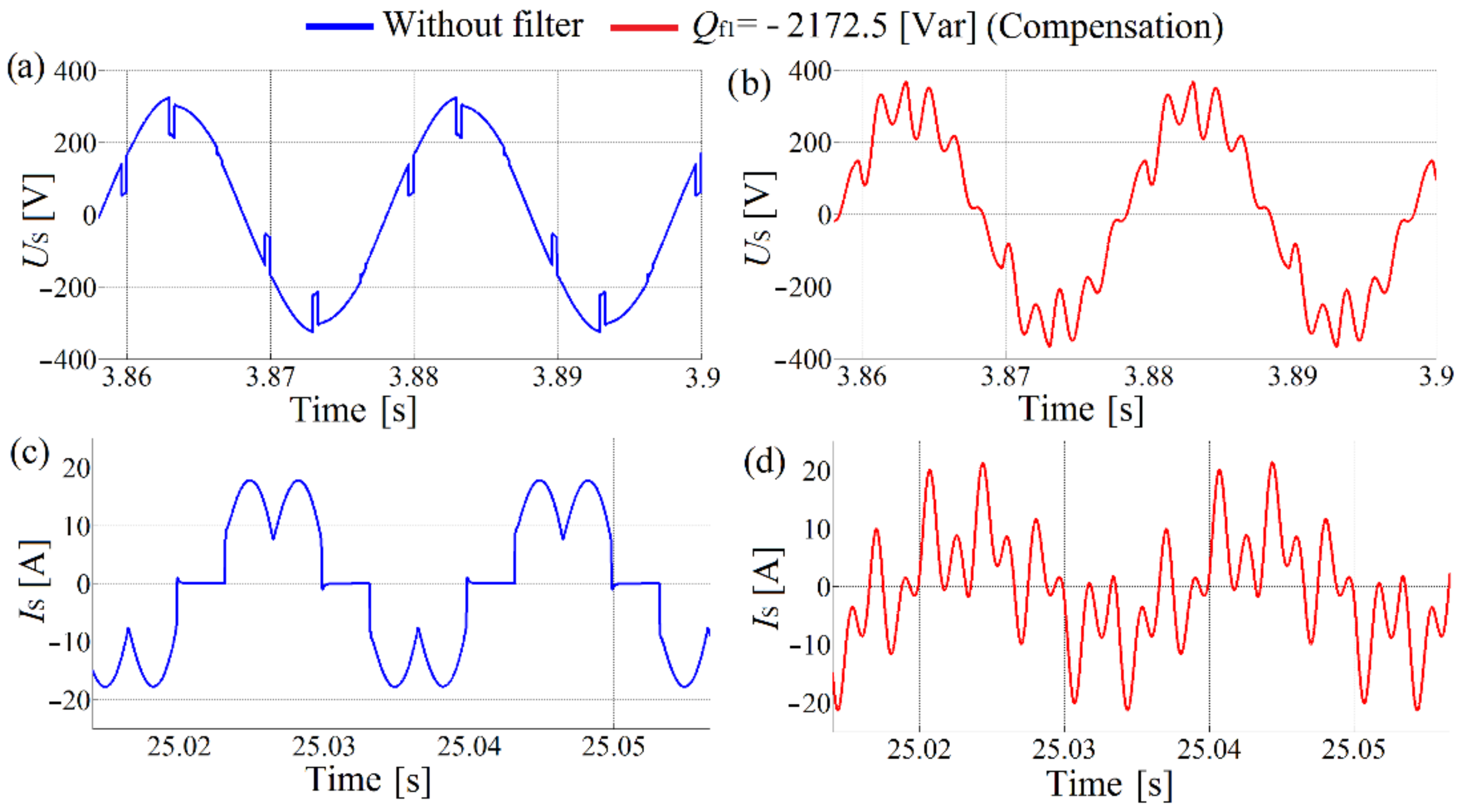
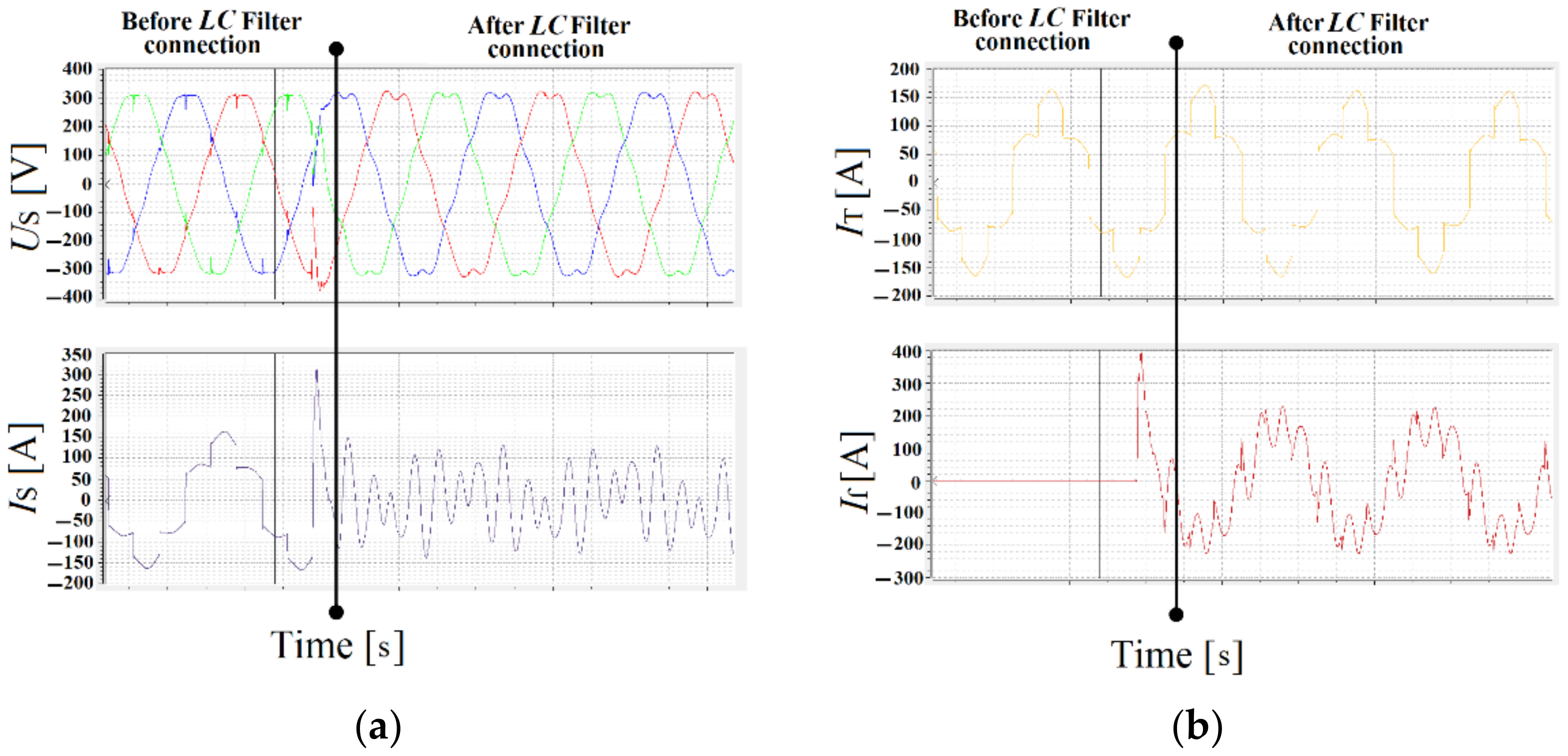
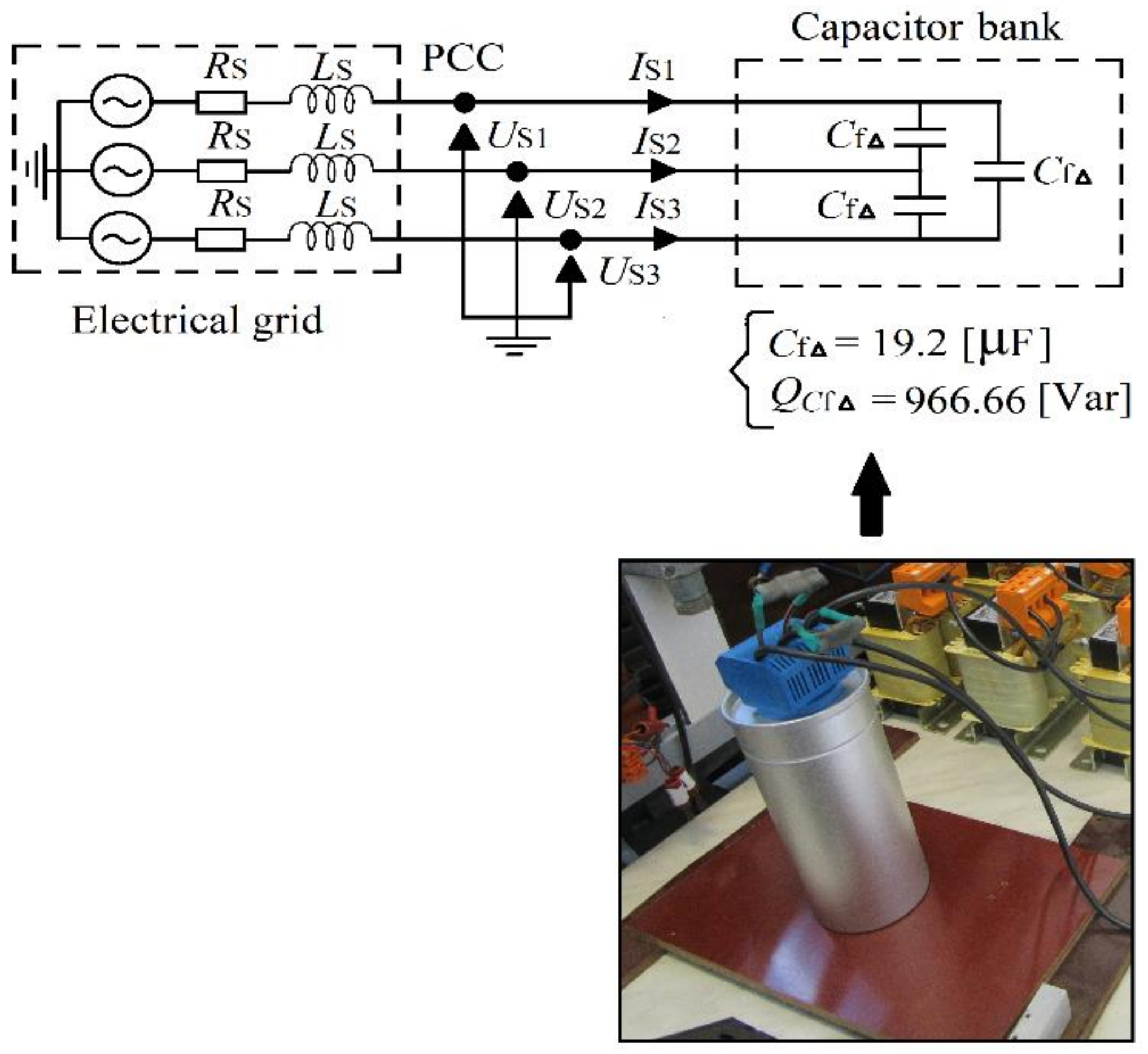
Figure 5.
Supply network voltage and current waveforms: before (a,c) and after (b,d) the capacitor bank connection.
Figure 5.
Supply network voltage and current waveforms: before (a,c) and after (b,d) the capacitor bank connection.
Figure 6.
Supply network voltage and current spectrums before (a,c) and (b,d) after the capacitor bank connection; (e) spectrum of capacitor bank current.
Figure 6.
Supply network voltage and current spectrums before (a,c) and (b,d) after the capacitor bank connection; (e) spectrum of capacitor bank current.
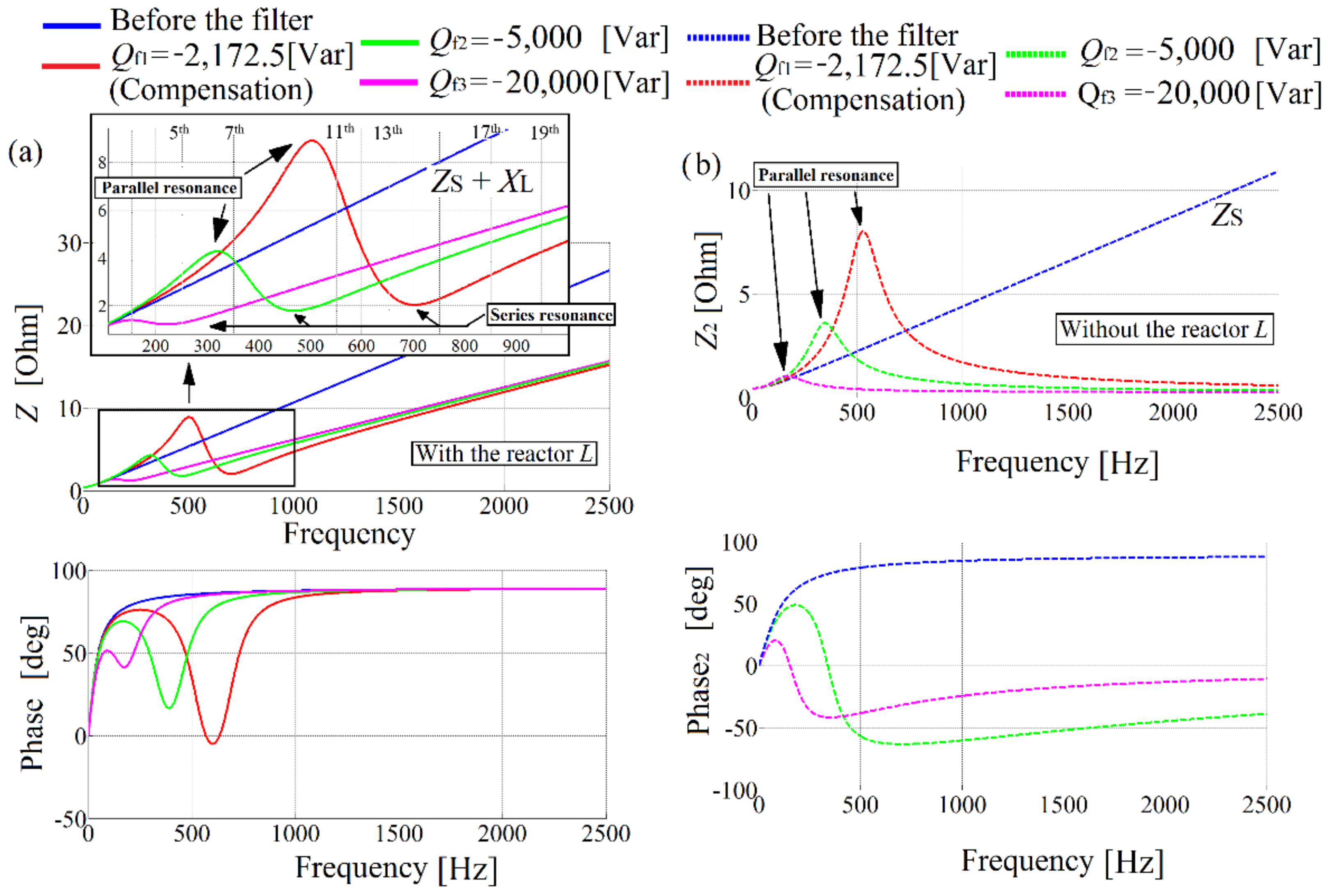
Figure 7.
Impedance versus frequency characteristics of power system measured at the input of thyristor bridge: (a) with the input reactor L; (b) without the input reactor L (just to show that the observed series resonance depends on the L presence).
Figure 7.
Impedance versus frequency characteristics of power system measured at the input of thyristor bridge: (a) with the input reactor L; (b) without the input reactor L (just to show that the observed series resonance depends on the L presence).
Figure 8.
(a) Single-tuned filter, (b) expressions used to compute the single-tuned filter parameters. ωre—resonance frequency, nre—harmonic order at the resonance.
Figure 8.
(a) Single-tuned filter, (b) expressions used to compute the single-tuned filter parameters. ωre—resonance frequency, nre—harmonic order at the resonance.
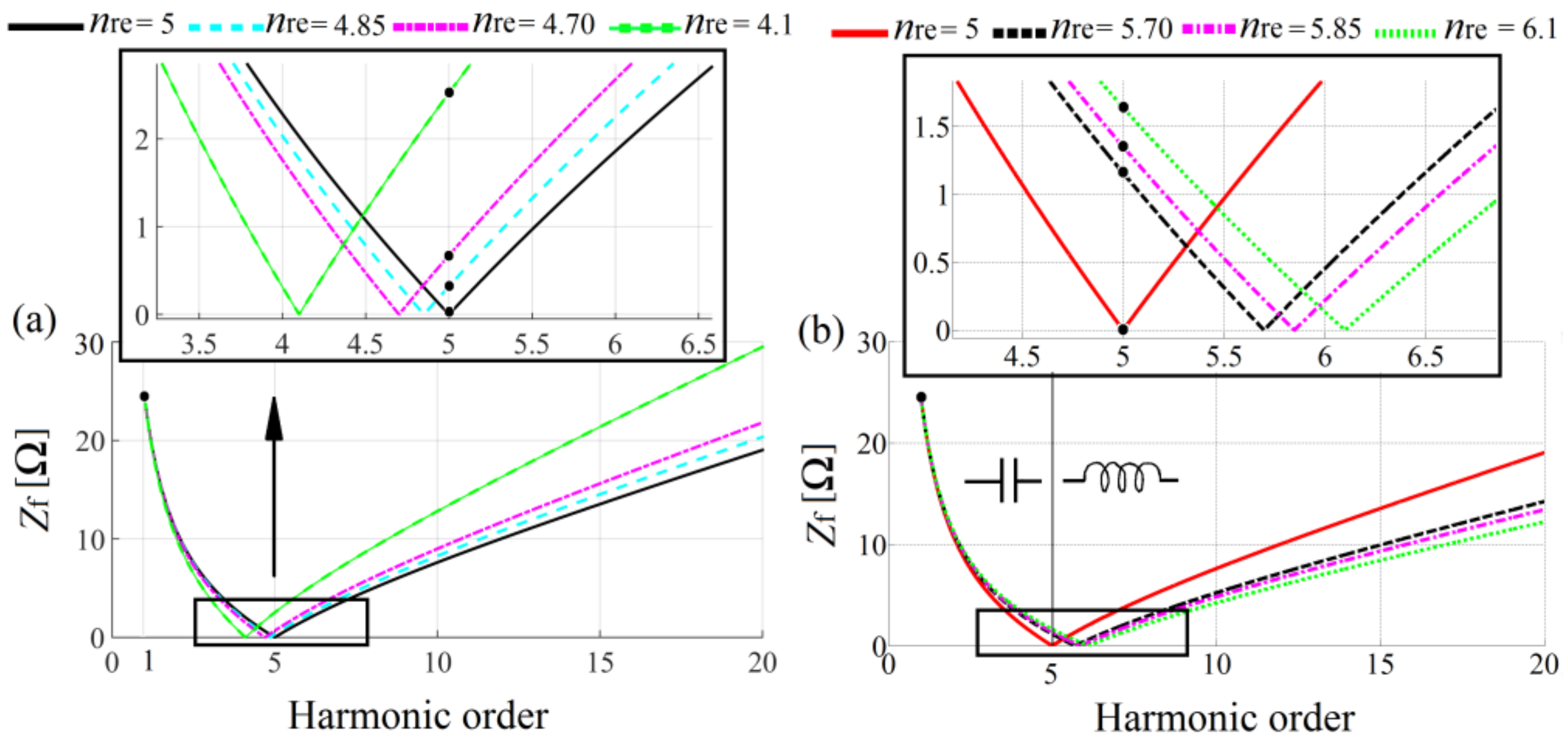
Figure 9.
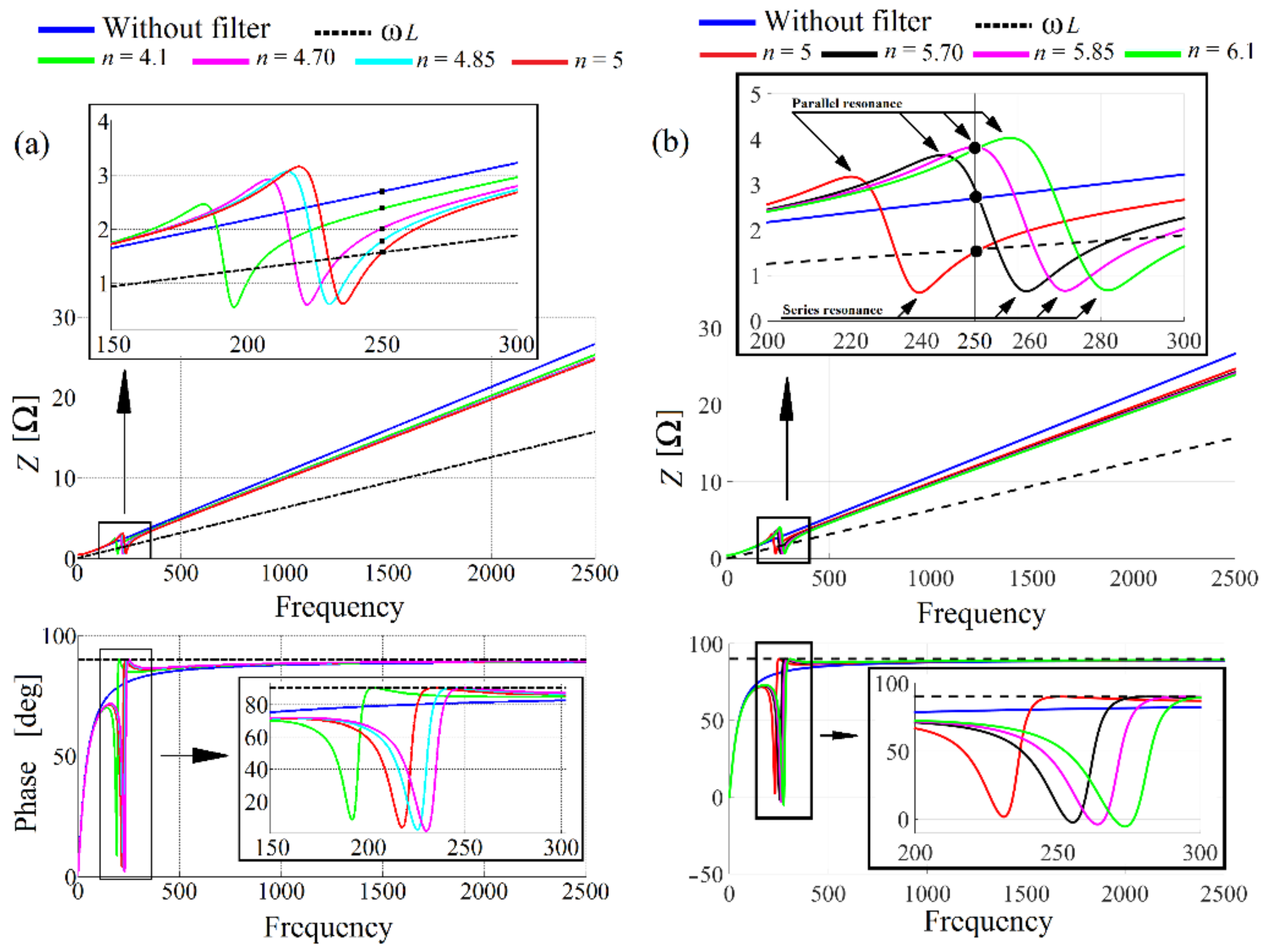
Single-tuned filter impedance versus frequency characteristics: (a) when the filter is tuned to the frequencies lower or equal to the frequency of the 5th harmonic; (b) and when it is tuned to the frequencies higher or equal to the frequency of the 5th harmonic.
Figure 9.
Single-tuned filter impedance versus frequency characteristics: (a) when the filter is tuned to the frequencies lower or equal to the frequency of the 5th harmonic; (b) and when it is tuned to the frequencies higher or equal to the frequency of the 5th harmonic.
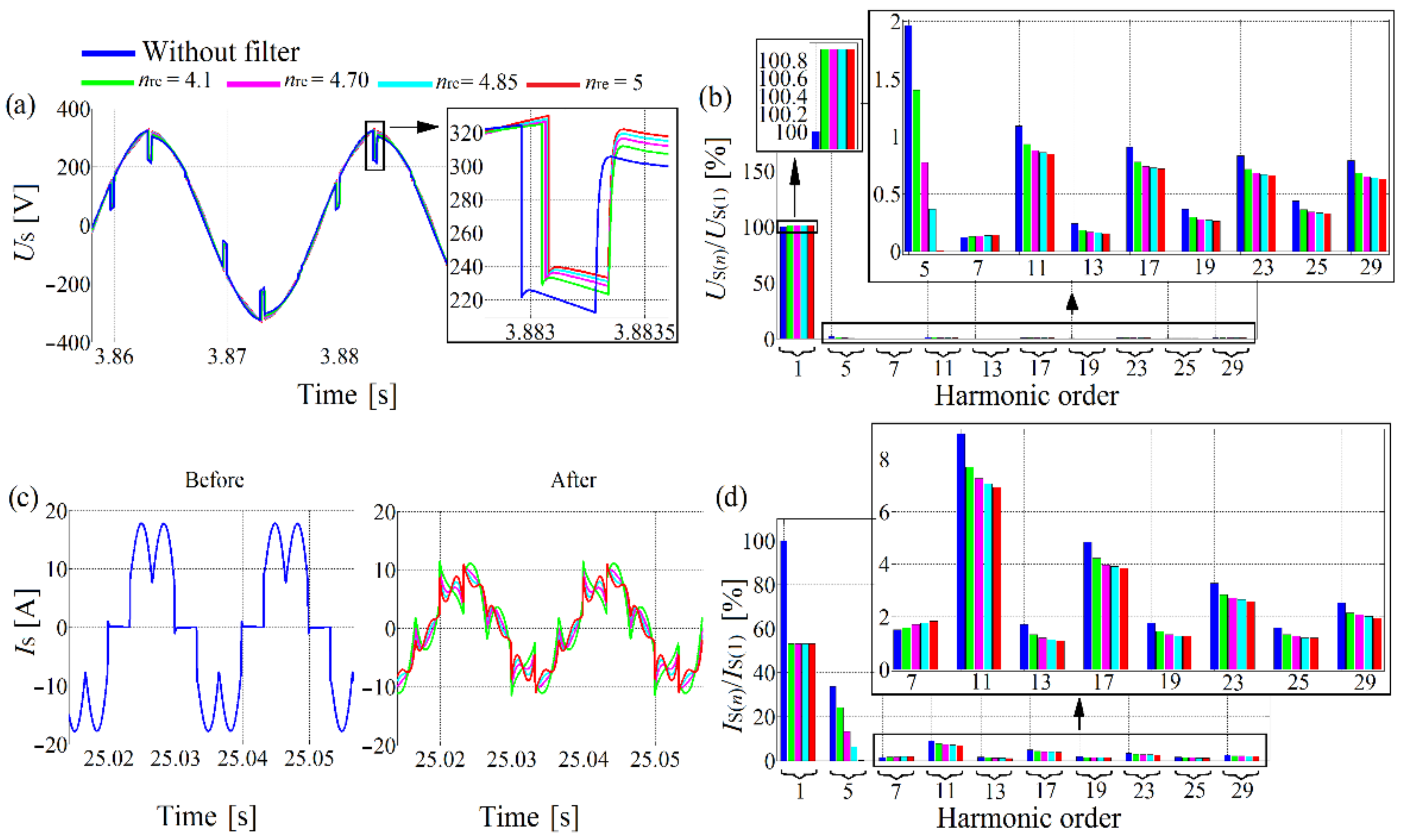
Figure 10.
The single-tuned filter is tuned to the frequencies lower or equal to the frequency of the 5th harmonic: (a) grid voltage and (b) its spectrum; (c) grid current and (d) its spectrum before and after the filter connection.
Figure 10.
The single-tuned filter is tuned to the frequencies lower or equal to the frequency of the 5th harmonic: (a) grid voltage and (b) its spectrum; (c) grid current and (d) its spectrum before and after the filter connection.
Figure 11.
The single-tuned filter is tuned to the frequencies higher or equal to the frequency of the 5th harmonic: (a) grid voltage and (b) its spectrum; (c) grid current, and (d) its spectrum before and after the filter connection.
Figure 11.
The single-tuned filter is tuned to the frequencies higher or equal to the frequency of the 5th harmonic: (a) grid voltage and (b) its spectrum; (c) grid current, and (d) its spectrum before and after the filter connection.
Figure 12.
Impedance frequency characteristics of the power system seen from the rectifier input when the single filter is tuned to the frequencies lower than 250 Hz (a) and when it is tuned to the frequency higher than 250 Hz (b).
Figure 12.
Impedance frequency characteristics of the power system seen from the rectifier input when the single filter is tuned to the frequencies lower than 250 Hz (a) and when it is tuned to the frequency higher than 250 Hz (b).
Figure 13.
(a) Second-order filter, (b) expressions used to compute the second-order filter parameters. RLf—reactor resistance.
Figure 13.
(a) Second-order filter, (b) expressions used to compute the second-order filter parameters. RLf—reactor resistance.
Figure 14.
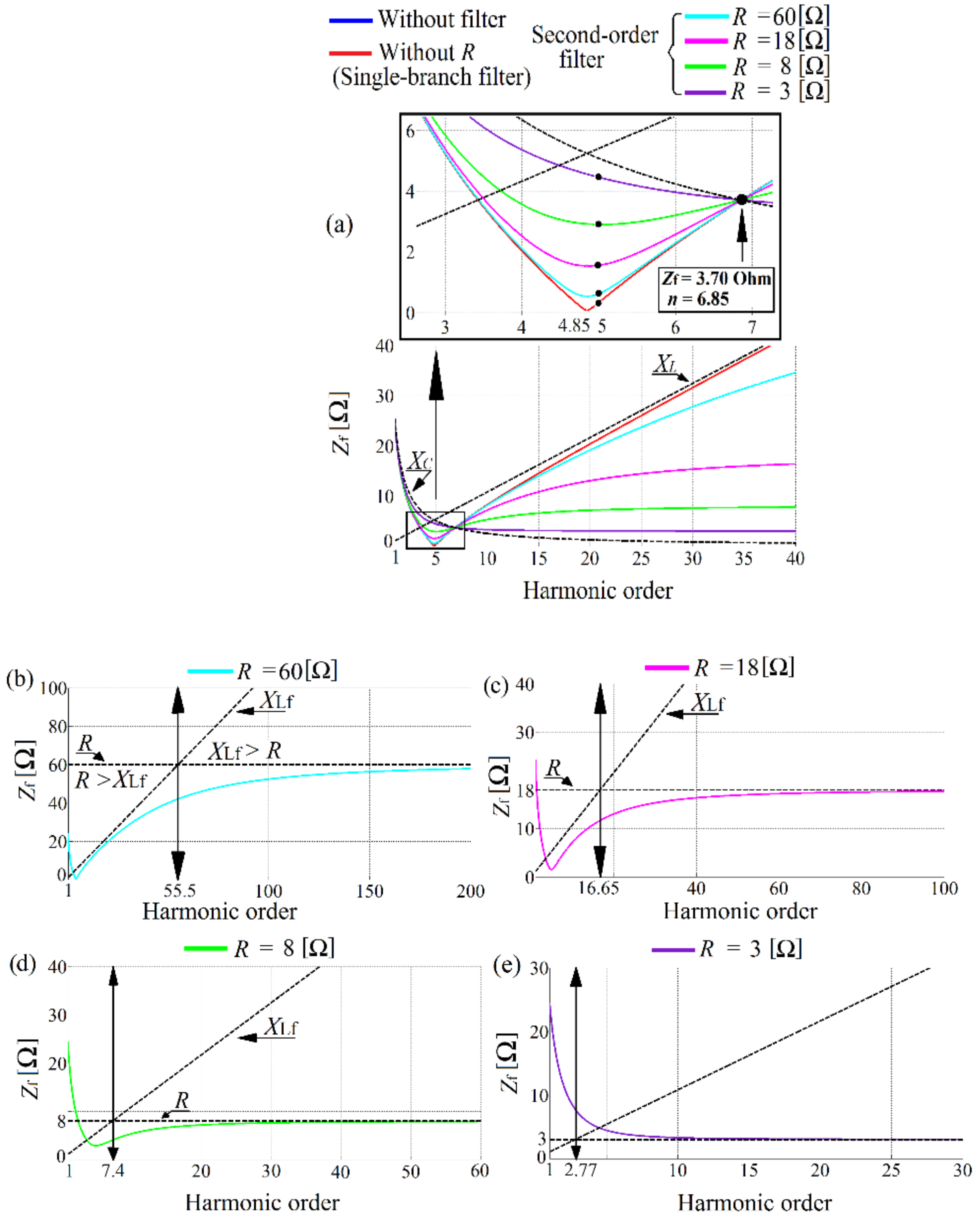
(a) Second-order filter impedance versus frequency characteristics for different damping resistance value: (b) R = 60 Ω, (c) R = 18 Ω, (d) R = 8 Ω, (e) R = 3 Ω.
Figure 14.
(a) Second-order filter impedance versus frequency characteristics for different damping resistance value: (b) R = 60 Ω, (c) R = 18 Ω, (d) R = 8 Ω, (e) R = 3 Ω.
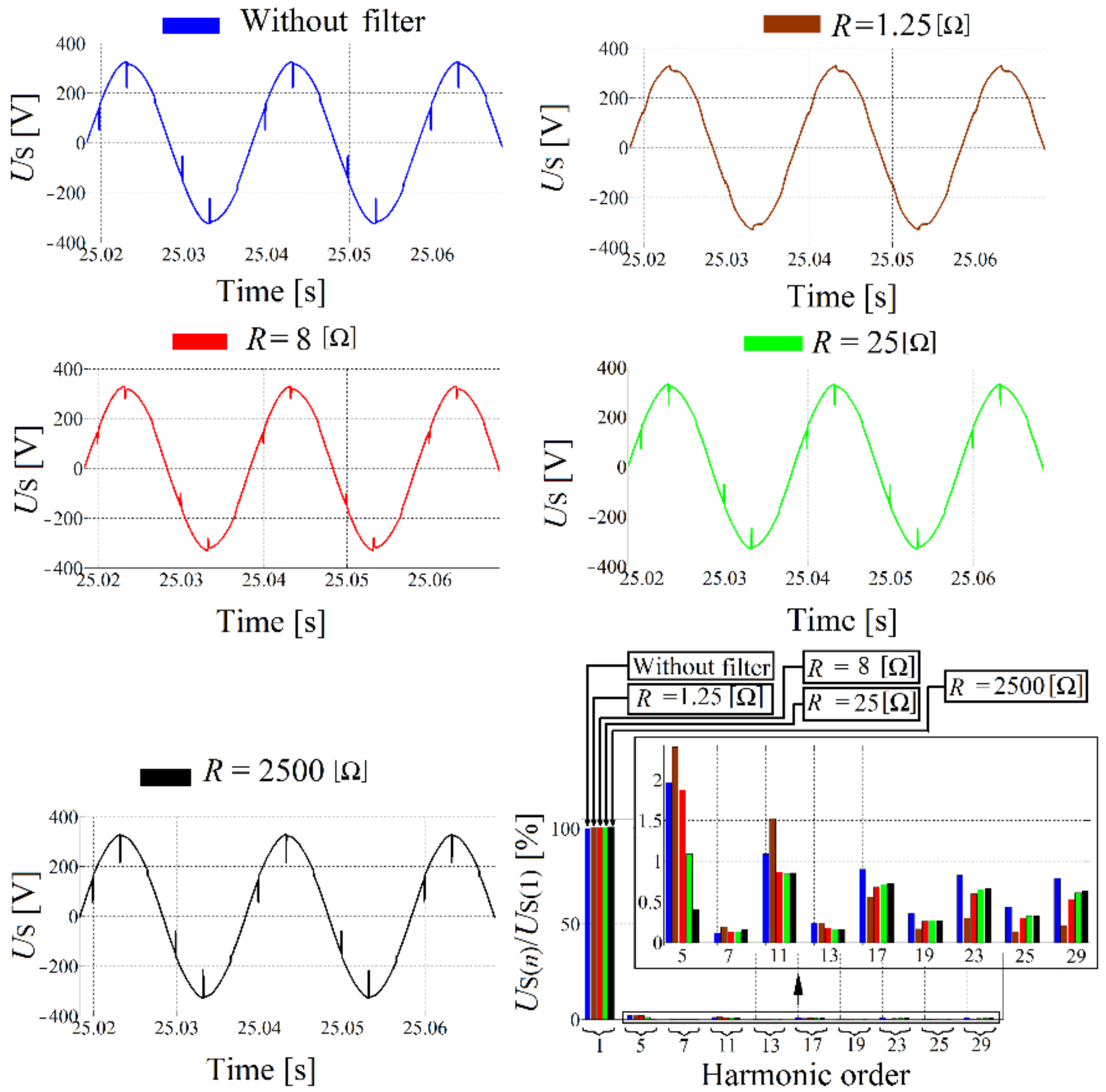
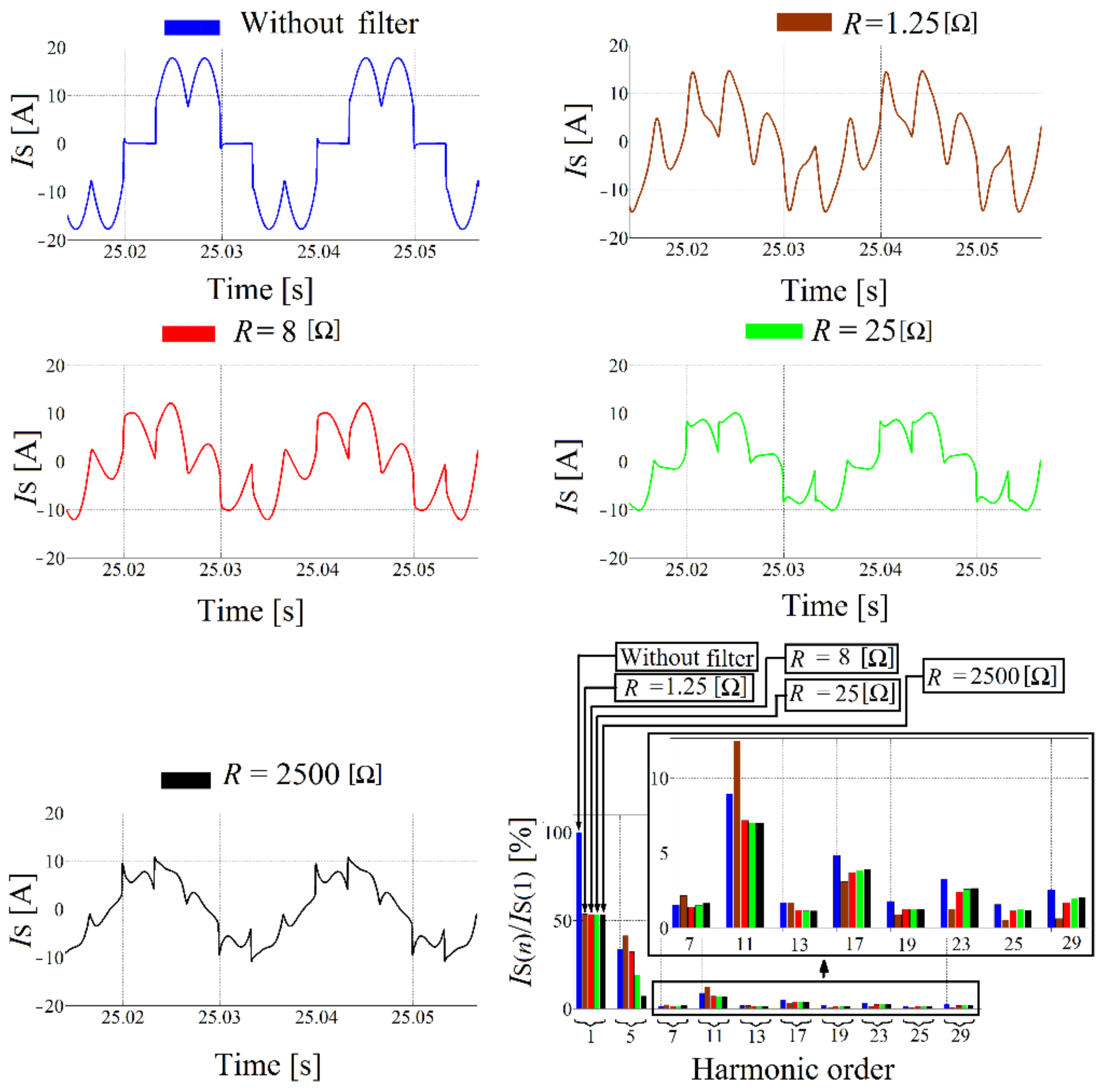
Figure 15.
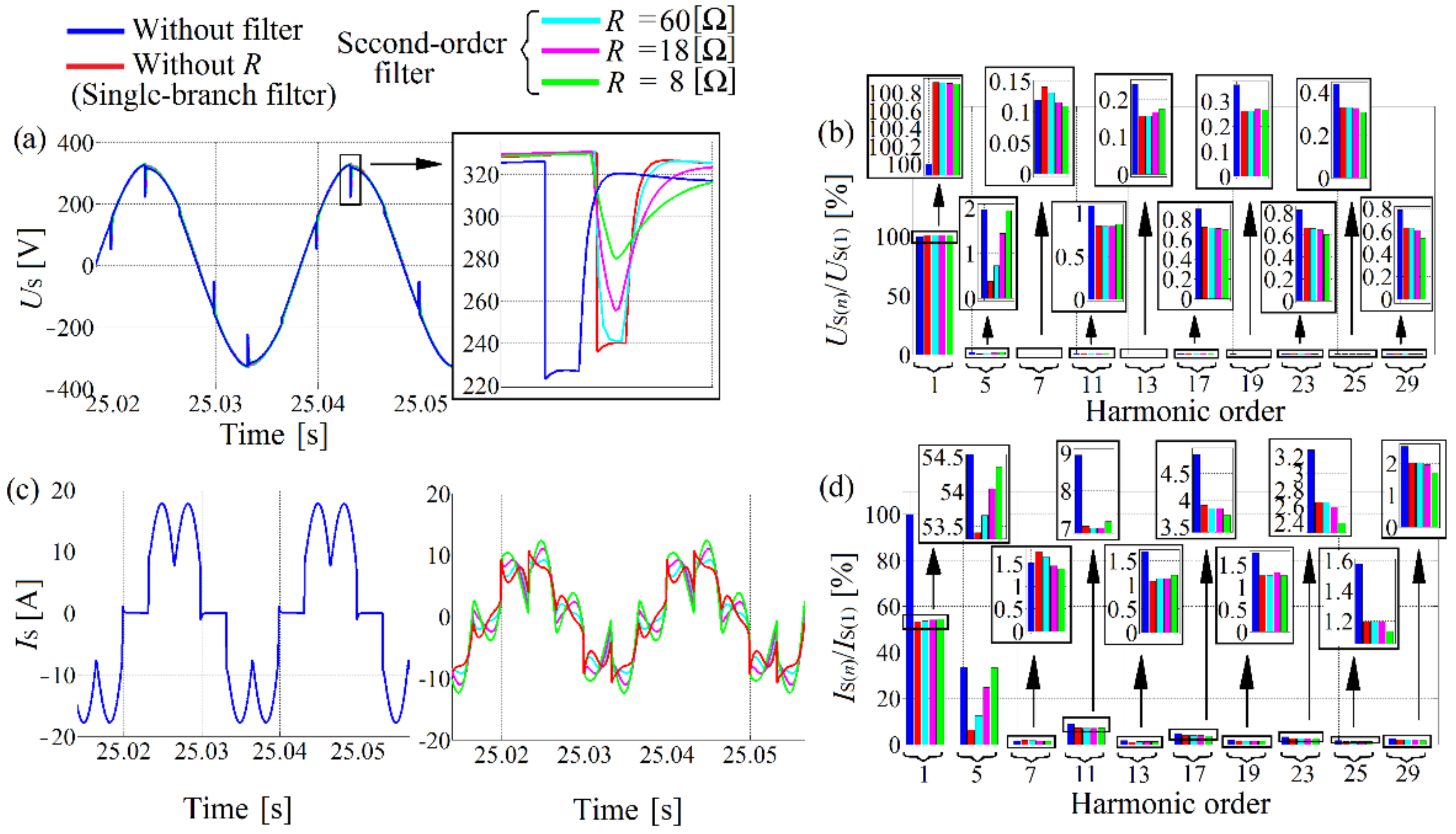
(a) Grid voltage and (b) its spectrum (p.u.); (c) grid current and (d) its spectrum (p.u.) before and after the filter connection.
Figure 15.
(a) Grid voltage and (b) its spectrum (p.u.); (c) grid current and (d) its spectrum (p.u.) before and after the filter connection.
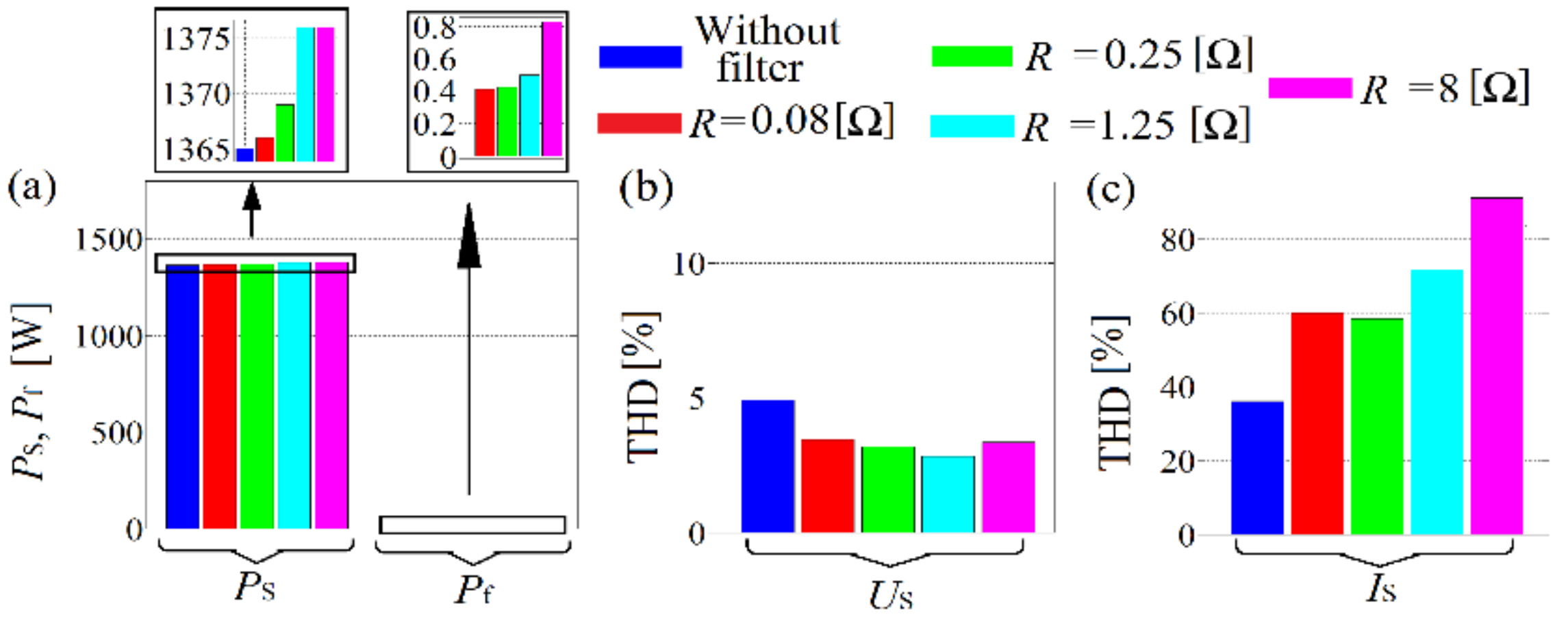
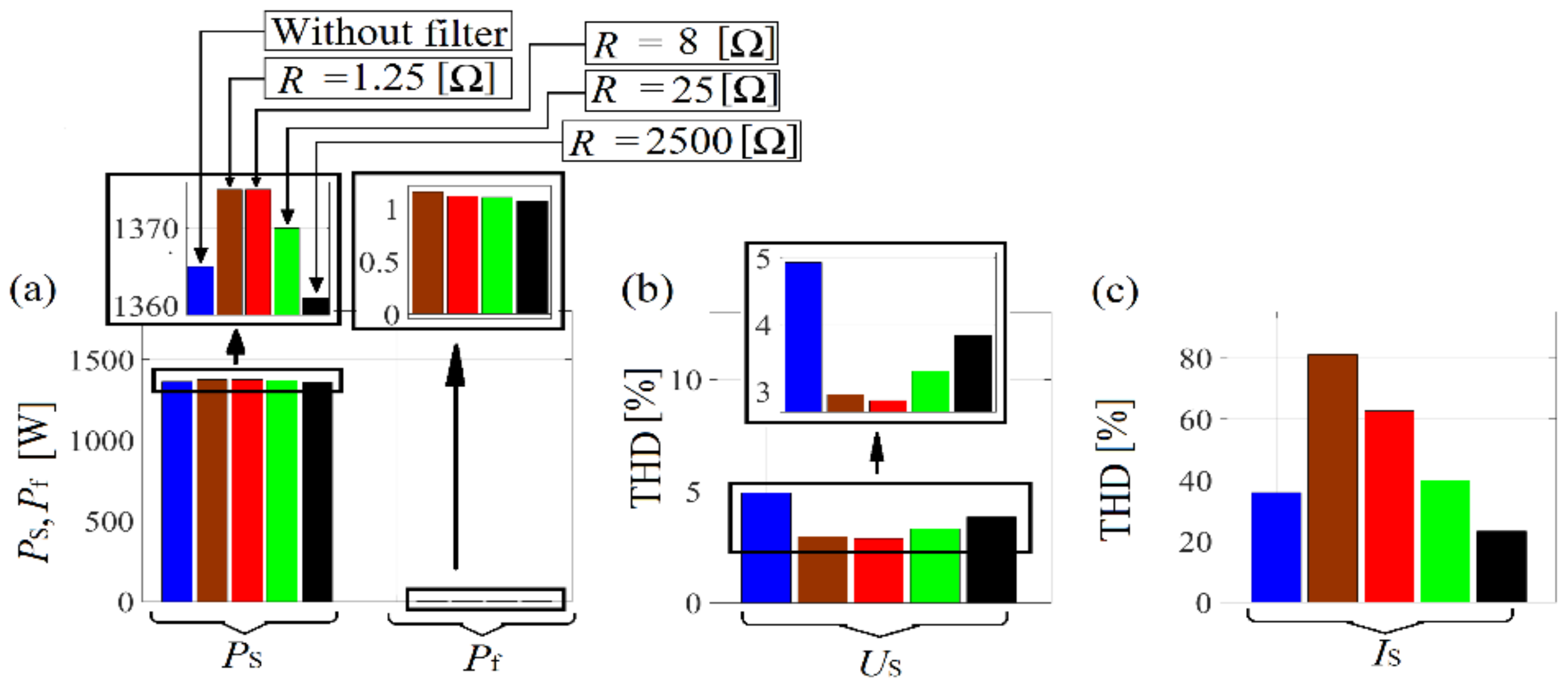
Figure 16.
(a) Active power at the PCC (PS) and filter terminals (Pf), (b) grid voltage THD, (c) grid current THD.
Figure 16.
(a) Active power at the PCC (PS) and filter terminals (Pf), (b) grid voltage THD, (c) grid current THD.
Figure 17.
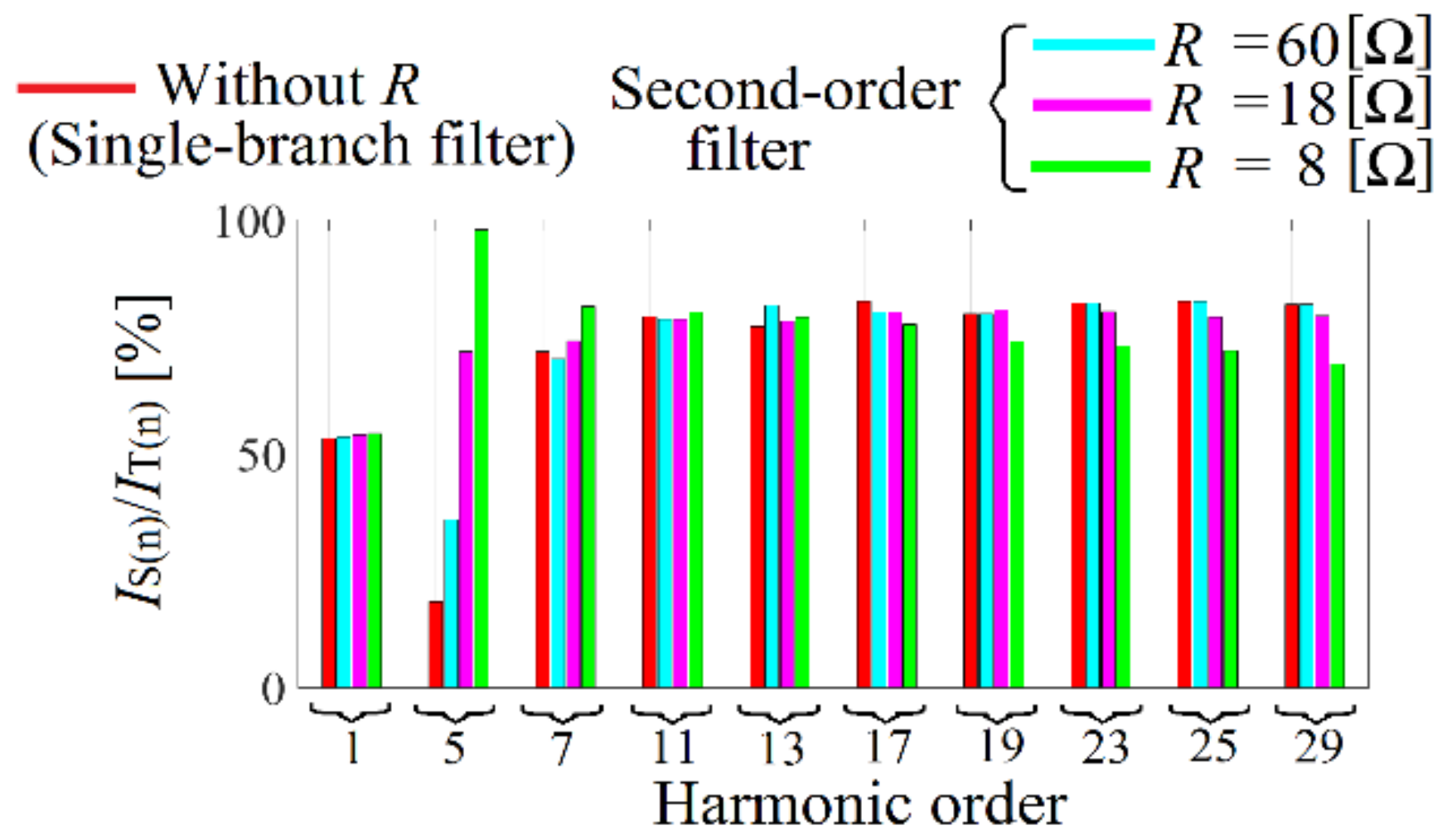
Second-order filter work efficiency in terms of harmonic mitigation.
Figure 17.
Second-order filter work efficiency in terms of harmonic mitigation.
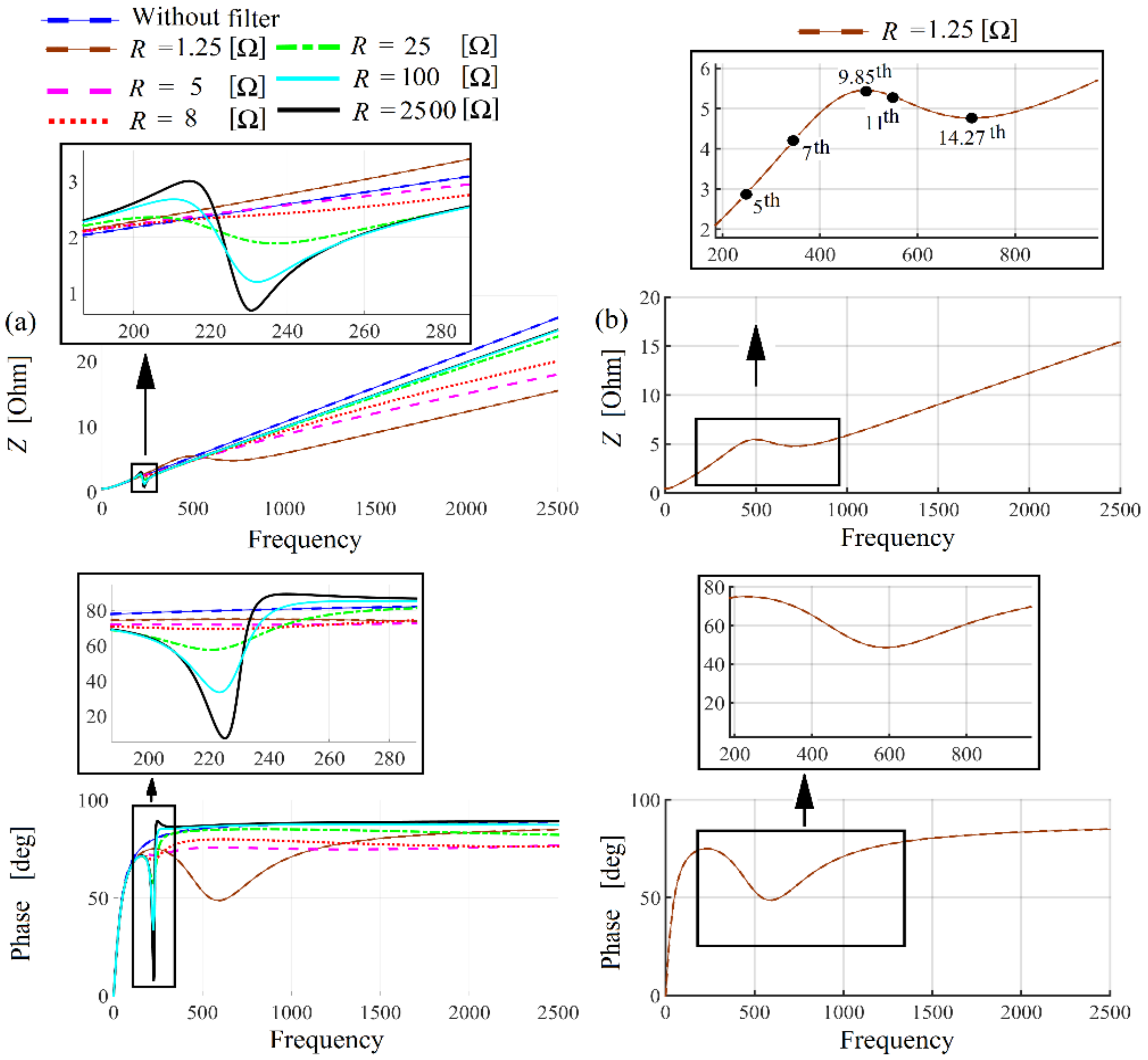
Figure 18.
Power system impedance versus frequency characteristic observed from the thyristor bridge input terminals for different values of the filter damping resistance.
Figure 18.
Power system impedance versus frequency characteristic observed from the thyristor bridge input terminals for different values of the filter damping resistance.
Figure 19.
(a) Third-order filter, (b) expressions used to compute the third-order filter parameters. nre1—harmonic order at the series resonance, nre2—harmonic order at the parallel resonance.
Figure 19.
(a) Third-order filter, (b) expressions used to compute the third-order filter parameters. nre1—harmonic order at the series resonance, nre2—harmonic order at the parallel resonance.
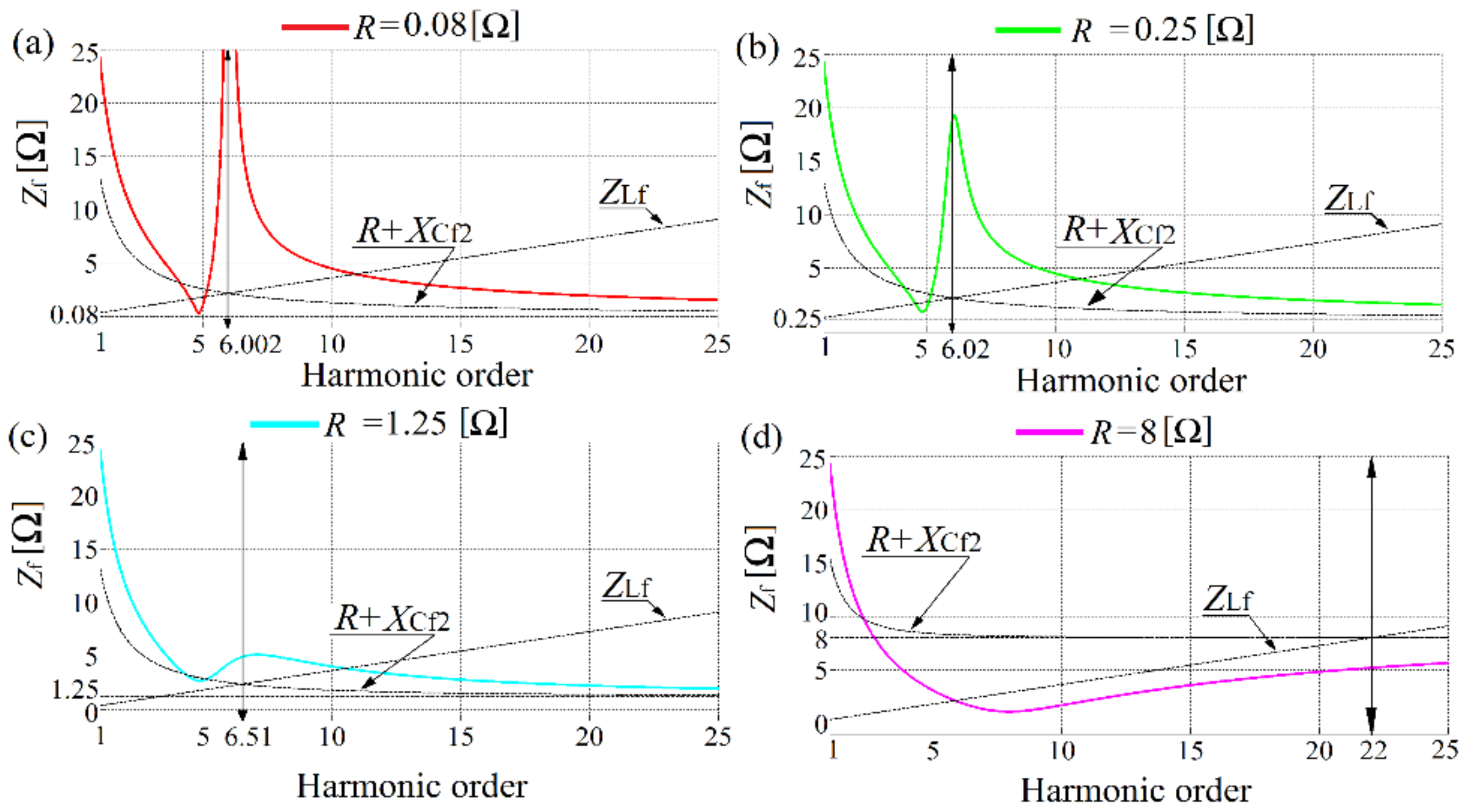
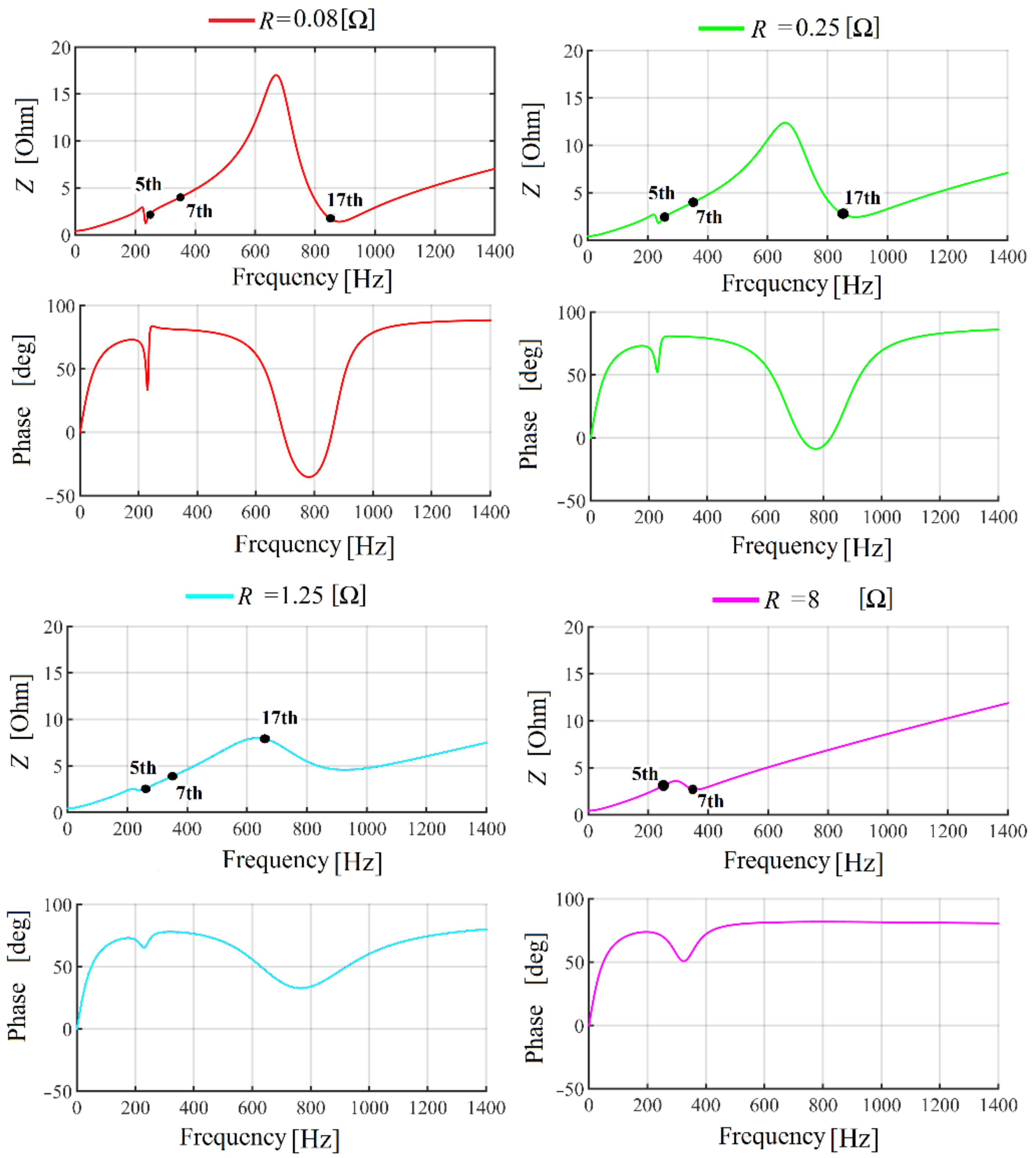
Figure 20.
Third-order filter impedance versus frequency characteristics for different damping resistance value: (a) R = 0.08 Ω, (b) R = 0.25 Ω, (c) R = 1.25 Ω, (d) R = 8 Ω.
Figure 20.
Third-order filter impedance versus frequency characteristics for different damping resistance value: (a) R = 0.08 Ω, (b) R = 0.25 Ω, (c) R = 1.25 Ω, (d) R = 8 Ω.
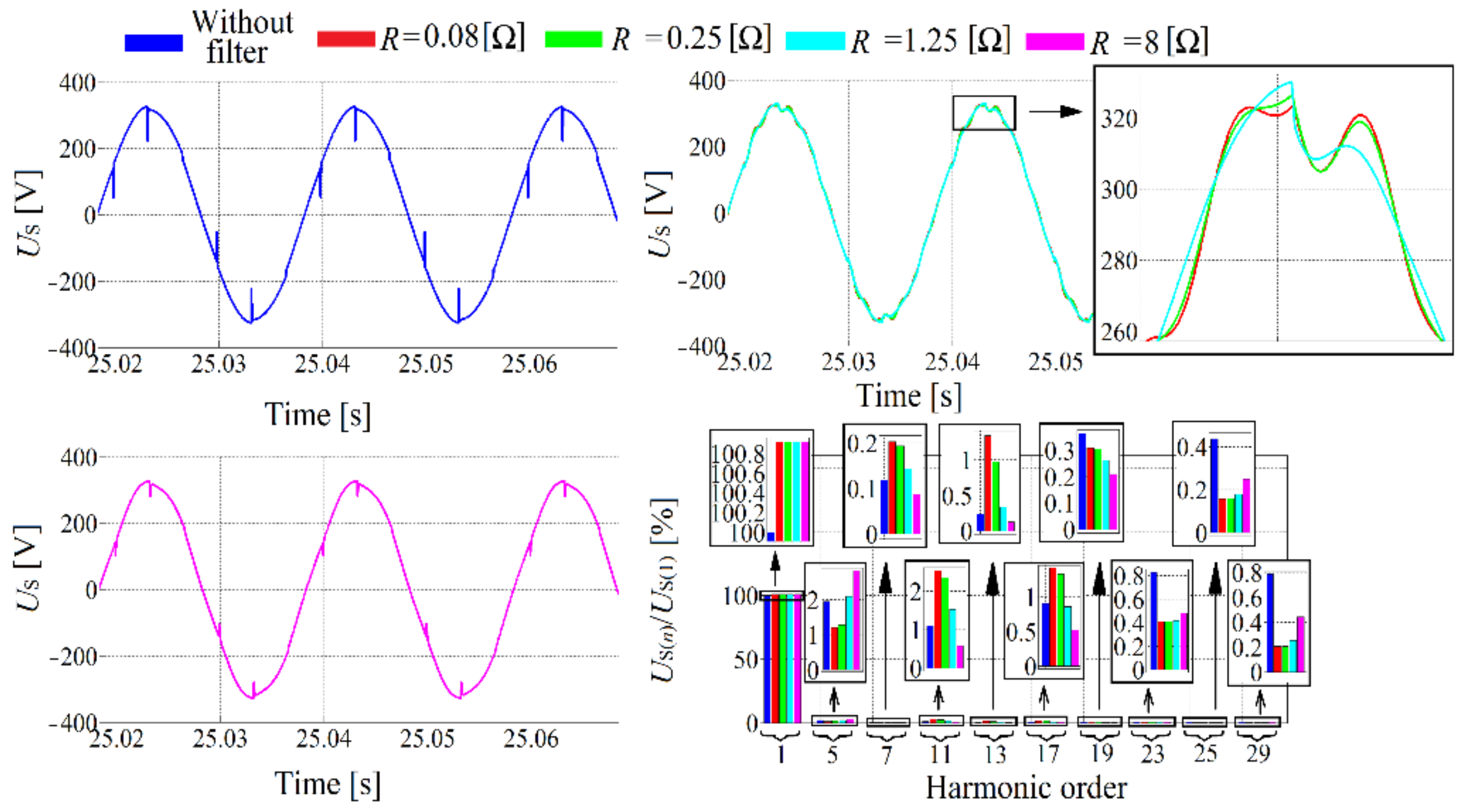
Figure 21.
Grid voltage waveforms and spectrums after the 3rd order filter connection with different value of damping resistance.
Figure 21.
Grid voltage waveforms and spectrums after the 3rd order filter connection with different value of damping resistance.
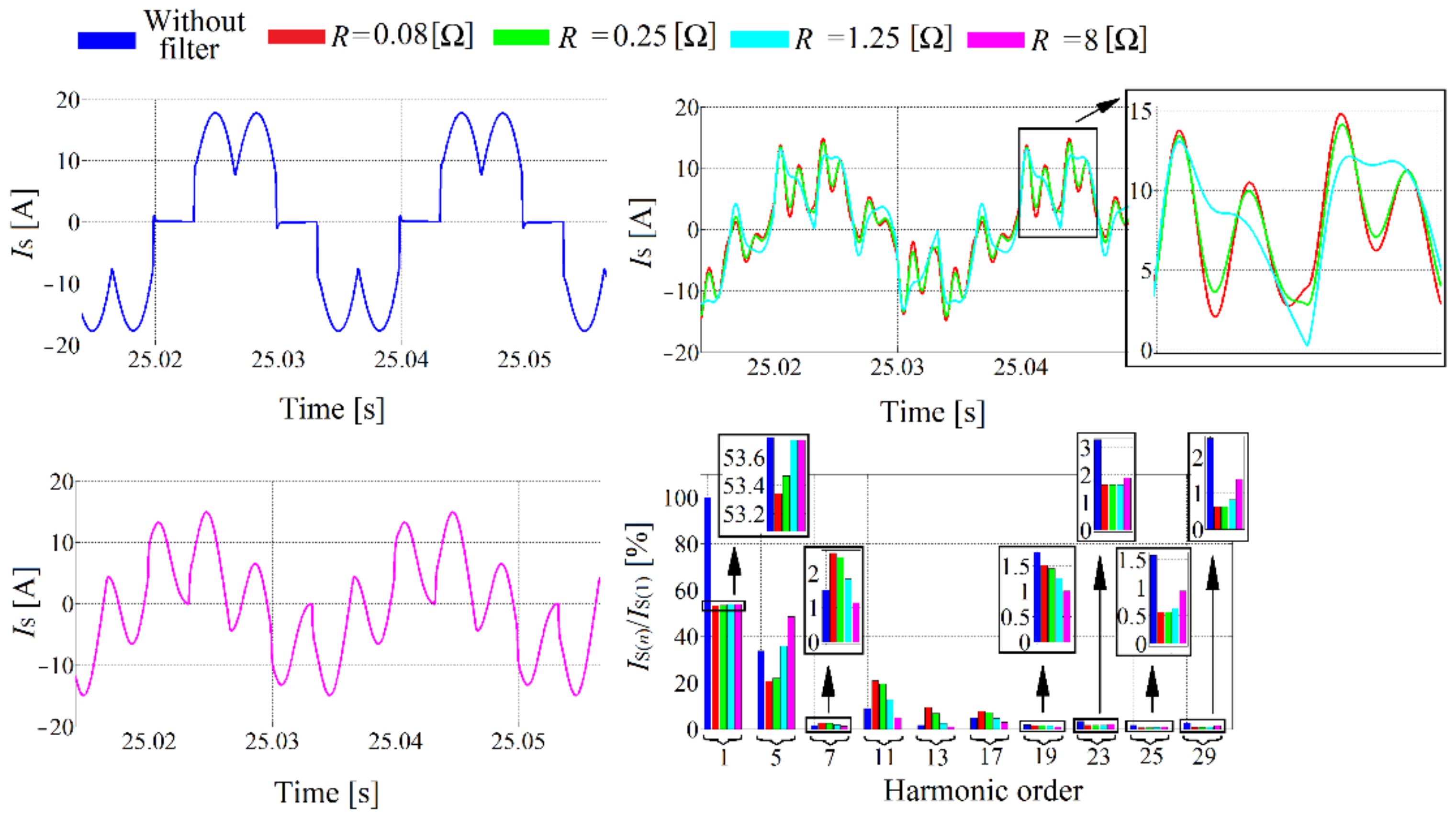
Figure 22.
Grid current waveforms and spectrums after the 3rd order filter connection with different value of damping resistance.
Figure 22.
Grid current waveforms and spectrums after the 3rd order filter connection with different value of damping resistance.
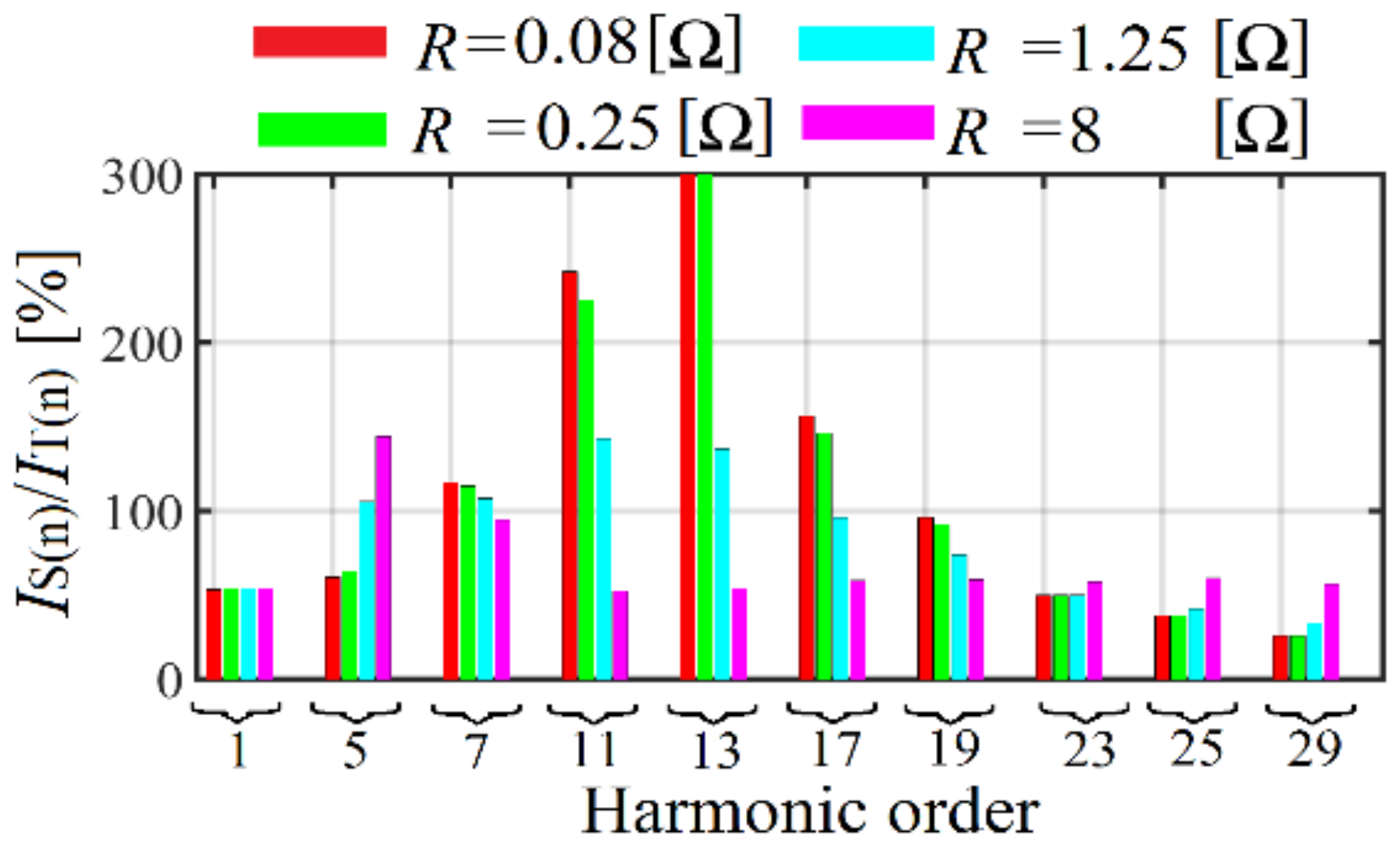
Figure 23.
Third-order filter work efficiency.
Figure 23.
Third-order filter work efficiency.
Figure 24.
(a) Active power at the PCC (PS) and filter terminals (Pf), (b) grid voltage THD, (c) grid current THD.
Figure 24.
(a) Active power at the PCC (PS) and filter terminals (Pf), (b) grid voltage THD, (c) grid current THD.
Figure 25.
Power system impedance versus frequency characteristics observed at the thyristor bridge input for different values of the third-order filter damping resistance (R).
Figure 25.
Power system impedance versus frequency characteristics observed at the thyristor bridge input for different values of the third-order filter damping resistance (R).
Figure 26.
(a) C-type filter, (b) expressions used to compute its parameters.
Figure 26.
(a) C-type filter, (b) expressions used to compute its parameters.
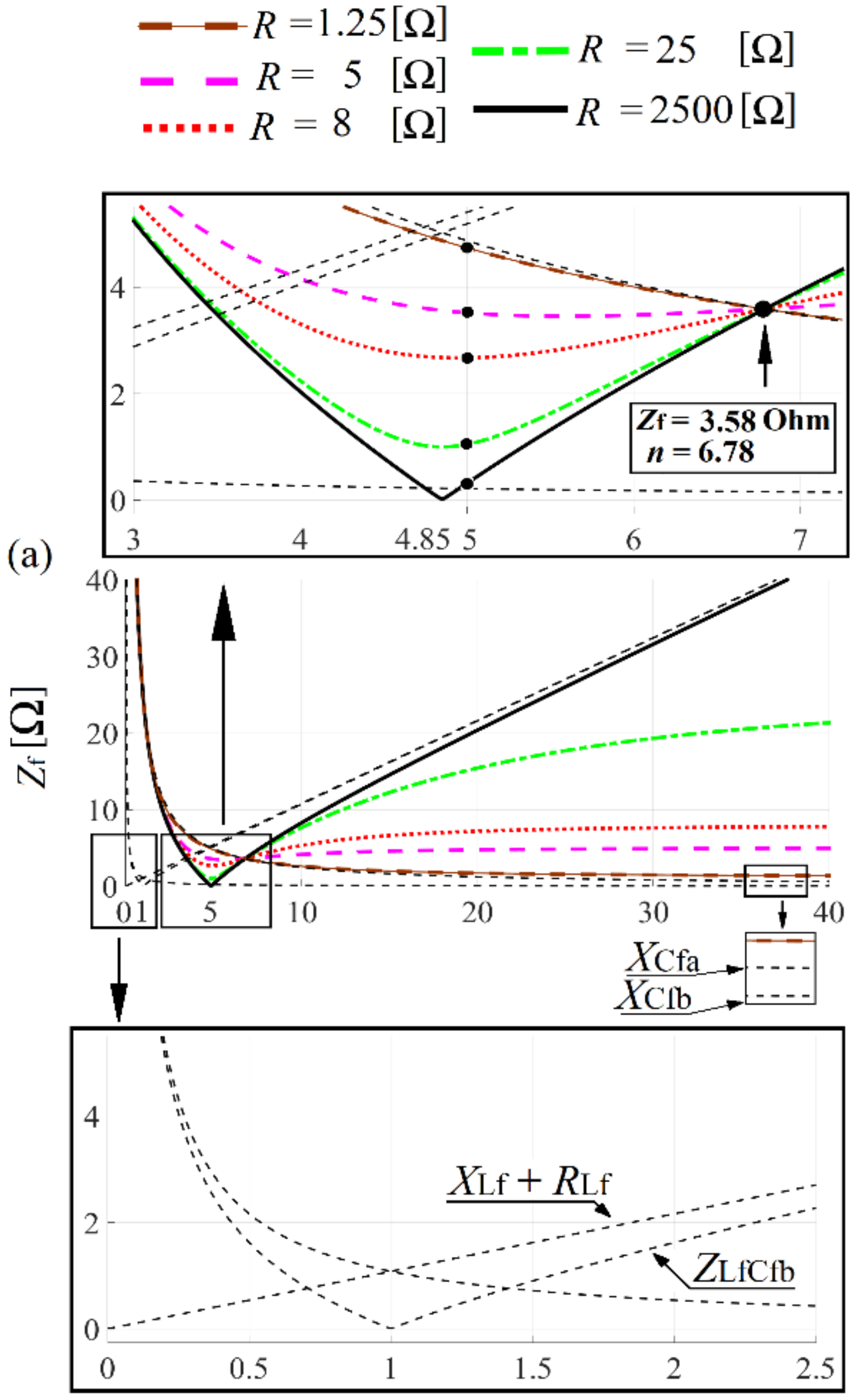
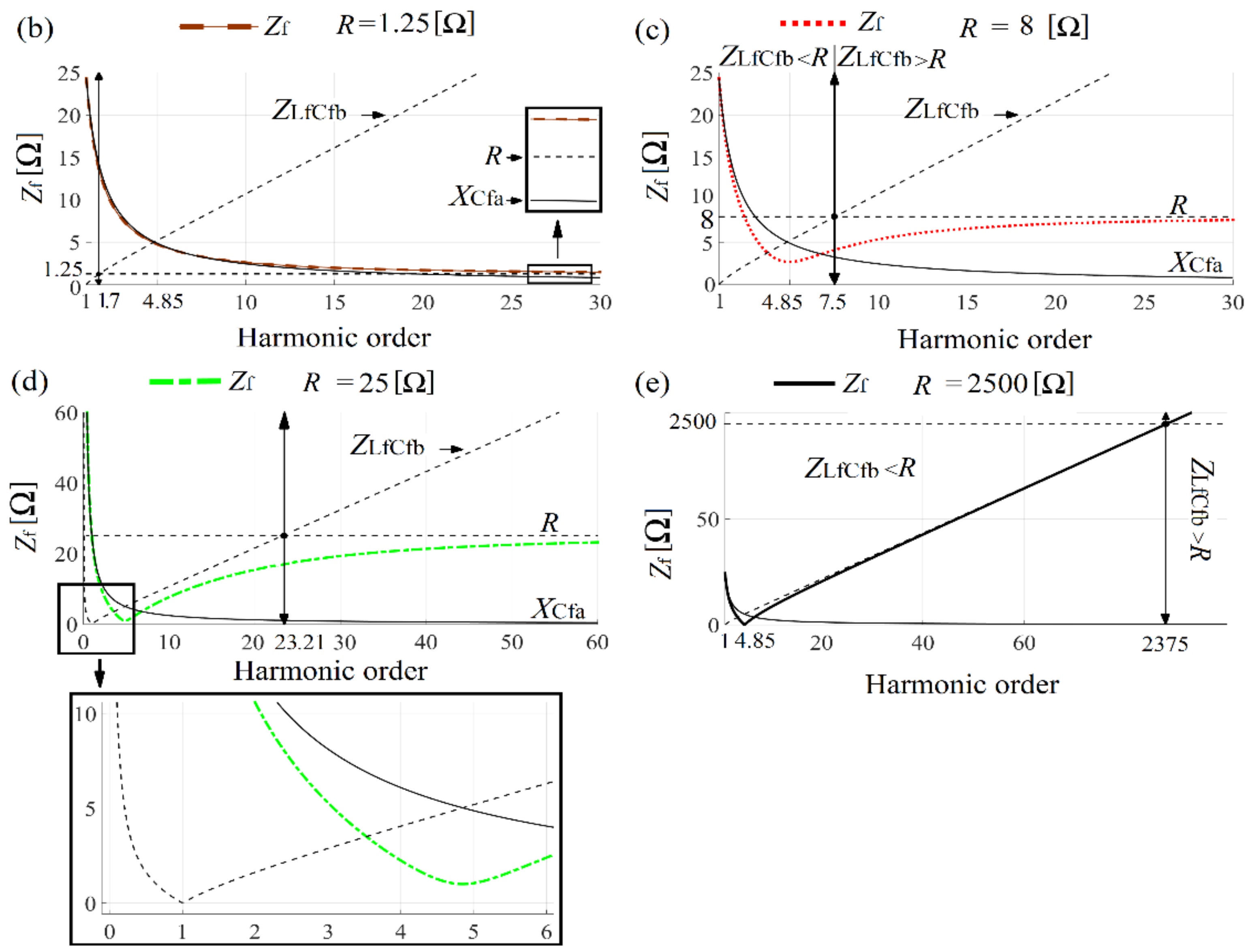
Figure 27.
(a) C-type filter impedance versus frequency characteristics for different damping resistance value: (b) R = 1.25 Ω, (c) R = 8 Ω, (d) R = 25 Ω, (e) R = 2500 Ω.
Figure 27.
(a) C-type filter impedance versus frequency characteristics for different damping resistance value: (b) R = 1.25 Ω, (c) R = 8 Ω, (d) R = 25 Ω, (e) R = 2500 Ω.
Figure 28.
Grid voltage waveforms and spectrums after the C-type filter connection with different value of damping resistance.
Figure 28.
Grid voltage waveforms and spectrums after the C-type filter connection with different value of damping resistance.
Figure 29.
Grid current waveforms and spectrums after the C-type filter connection with different value of damping resistance.
Figure 29.
Grid current waveforms and spectrums after the C-type filter connection with different value of damping resistance.
Figure 30.
Active power at the PCC (PS) and filter terminals (Pf) (a), grid voltage THD (b), grid current THD (c) obtained before and after the C-type filter connection with different damping resistance value.
Figure 30.
Active power at the PCC (PS) and filter terminals (Pf) (a), grid voltage THD (b), grid current THD (c) obtained before and after the C-type filter connection with different damping resistance value.
Figure 31.
(a,b) Power system impedance versus frequency characteristics observed at the input of thyristor bridge for different values of the C-type filter resistance.
Figure 31.
(a,b) Power system impedance versus frequency characteristics observed at the input of thyristor bridge for different values of the C-type filter resistance.
Figure 32.
C-type filter work efficiency on the harmonic mitigation.
Figure 32.
C-type filter work efficiency on the harmonic mitigation.
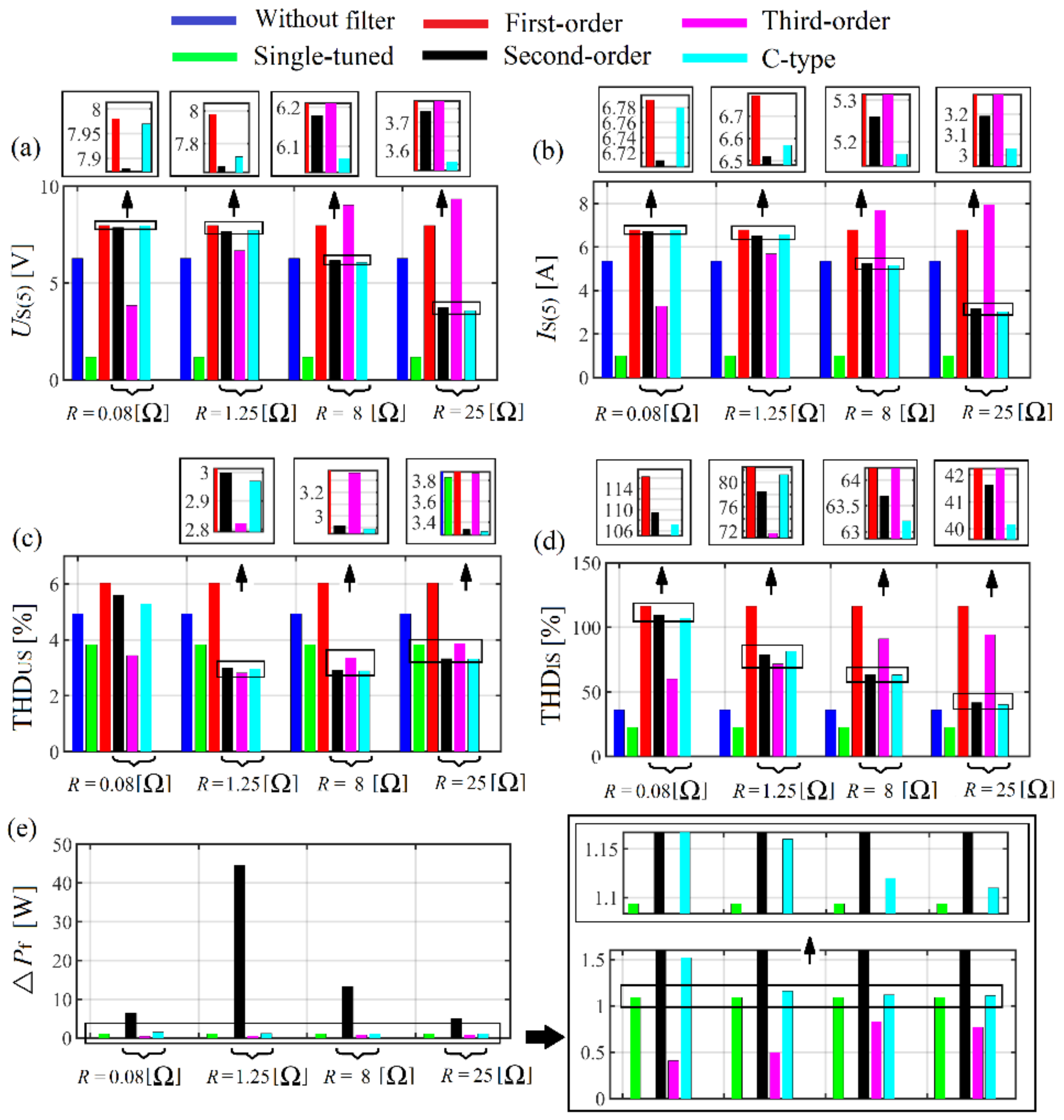
Figure 33.
Compared topologies of PHF.
Figure 33.
Compared topologies of PHF.
Figure 34.
Comparison spectrums: (a,b) grid voltage and current 5th harmonic; (c,d) grid voltage and current THD; (e) filter power losses.
Figure 34.
Comparison spectrums: (a,b) grid voltage and current 5th harmonic; (c,d) grid voltage and current THD; (e) filter power losses.
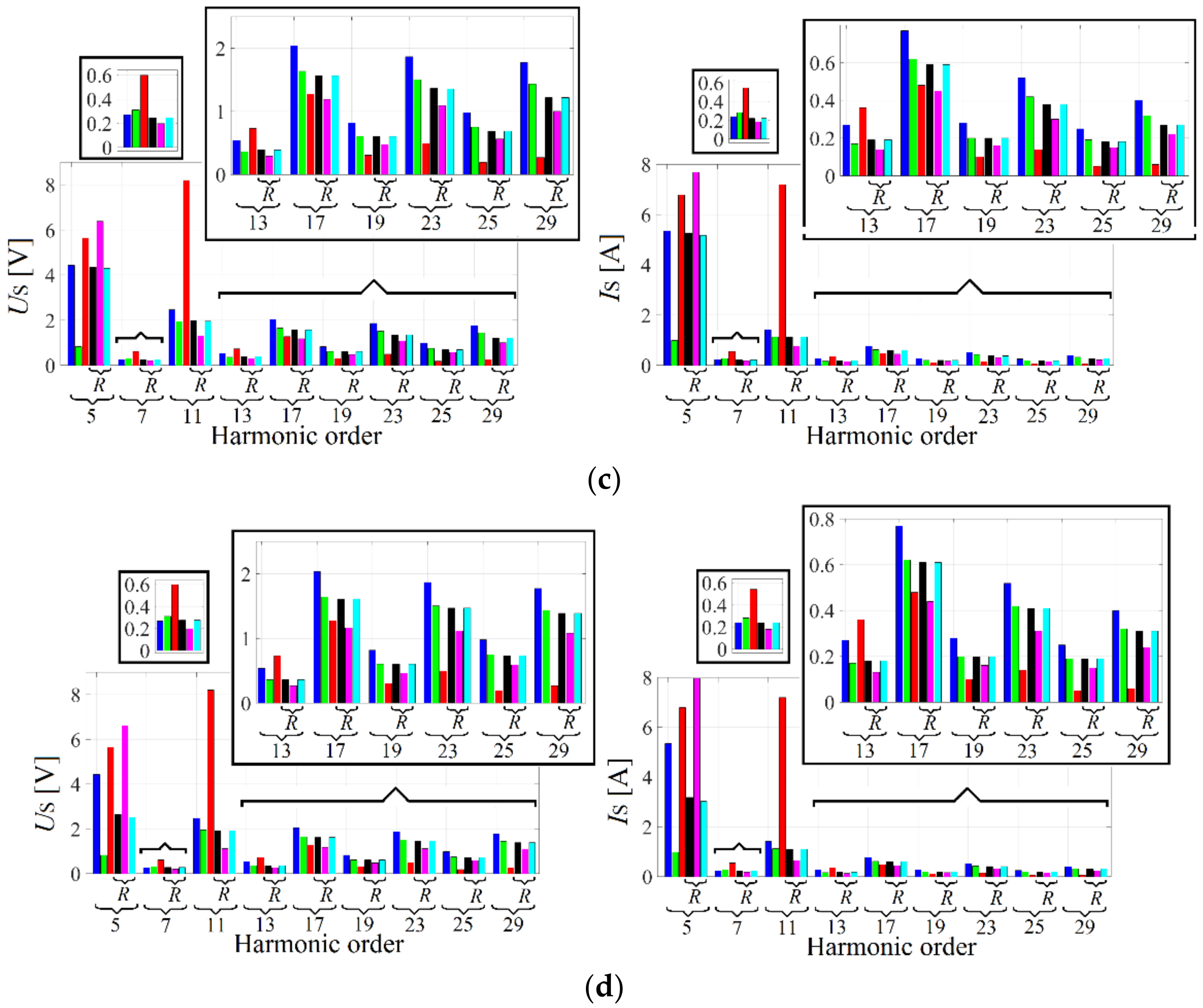
Figure 35.
Grid voltage and current spectrums before and after the filter connection. The filter damping resistance has the value of: (a) 0.08 Ω, (b) 1.5 Ω, (c) 8 Ω, (d) 25 Ω.
Figure 35.
Grid voltage and current spectrums before and after the filter connection. The filter damping resistance has the value of: (a) 0.08 Ω, (b) 1.5 Ω, (c) 8 Ω, (d) 25 Ω.
Figure 36.
(a) Laboratory set-up, (b) equivalent circuit of the laboratory set-up.
Figure 36.
(a) Laboratory set-up, (b) equivalent circuit of the laboratory set-up.
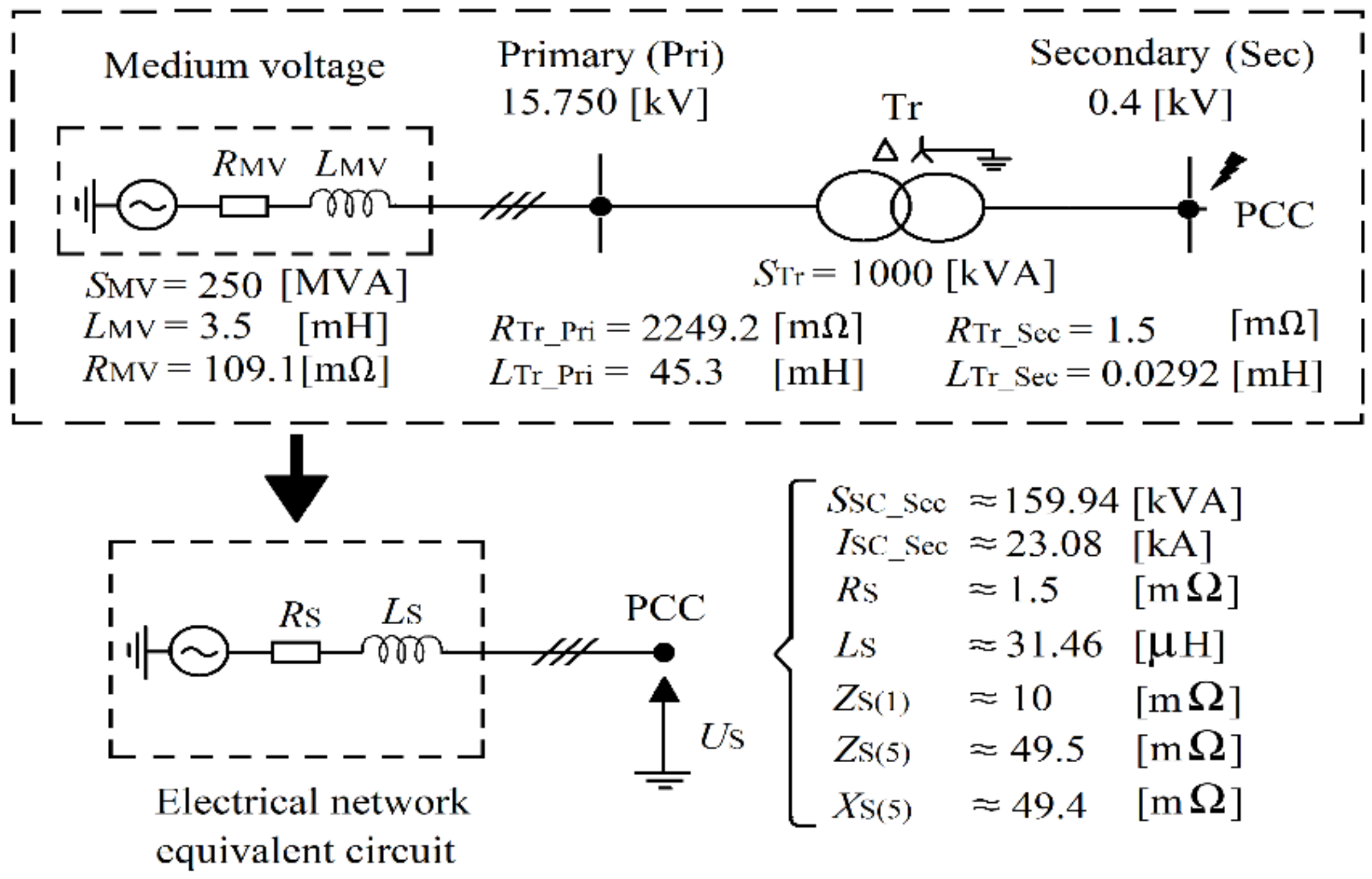
Figure 37.
Electrical network (grid) equivalent circuit with the parameters.
Figure 37.
Electrical network (grid) equivalent circuit with the parameters.
Figure 38.
PCC voltage waveforms (a) together with the spectrum (b) when the filter and load are not connected.
Figure 38.
PCC voltage waveforms (a) together with the spectrum (b) when the filter and load are not connected.
Figure 39.
(a) Frequency characteristic of the laboratory investigated single-tuned filter, (b) simulated impedance versus frequency characteristic seen from the transformer input.
Figure 39.
(a) Frequency characteristic of the laboratory investigated single-tuned filter, (b) simulated impedance versus frequency characteristic seen from the transformer input.
Figure 40.
Measured waveforms of: (a) the grid voltage and current waveforms, (b) transformer input and single-tuned filter terminals.
Figure 40.
Measured waveforms of: (a) the grid voltage and current waveforms, (b) transformer input and single-tuned filter terminals.
Figure 41.
Measured waveforms and spectrums of the PCC voltage before (a) and after (b) the filter connection.
Figure 41.
Measured waveforms and spectrums of the PCC voltage before (a) and after (b) the filter connection.
Figure 42.
Measured waveforms and spectrums of the grid current before (a) and after (b) the filter connection.
Figure 42.
Measured waveforms and spectrums of the grid current before (a) and after (b) the filter connection.
Figure 43.
Laboratory equivalent circuit with the capacitors bank connected to the PCC.
Figure 43.
Laboratory equivalent circuit with the capacitors bank connected to the PCC.
Figure 44.
(a) PCC voltage and (b) its spectrum, (c) grid current waveforms, and (d) its spectrum.
Figure 44.
(a) PCC voltage and (b) its spectrum, (c) grid current waveforms, and (d) its spectrum.
Table 1.
Computed equivalent parameters of the simulated electrical grid see from the point of common coupling (PCC) when no load is connected.
Table 1.
Computed equivalent parameters of the simulated electrical grid see from the point of common coupling (PCC) when no load is connected.
| SSC_PCC [MVA] | ISC_PCC [A] | LS [µH] | RS [mΩ] | ZS [Ω] | ZS(5) [Ω] |
|---|
| 0.33 | 481.12 | 681.82 | 425.5 | 0.480 | 1.15 |
Table 2.
First-order filter parameters together with expressions used to compute these parameters.
Table 2.
First-order filter parameters together with expressions used to compute these parameters.
|
|---|
| Qf [Var] | Cf [µF] | Zf(1) [Ω] | Zf(5) [Ω] | Zf(7) [Ω] | Rf [Ω] |
|---|
| −2172.5 | 130.72 | 24.35 | 4.87 | 3.48 | 0.25 |
Table 3.
Single-tuned filter parameters. The filter is tuned to the frequencies lower or equal to the frequency of the harmonic to be eliminated (5th).
Table 3.
Single-tuned filter parameters. The filter is tuned to the frequencies lower or equal to the frequency of the harmonic to be eliminated (5th).
| fre [Hz] | nre | Cf [µF] | Lf [mH] | Zf(5) [Ω] | Zf(1) [Ω] | Qf [Var] |
|---|
| 205 | 4.1 | 122.95 | 4.9 | 2.52 | 24.35 | −2172.5 |
| 235 | 4.70 | 124.81 | 3.7 | 0.67 |
| 245.5 | 4.85 | 125.17 | 3.4 | 0.32 |
| 250 | 5 | 125.49 | 3.2 | 0.00 |
Table 4.
Single-tuned filter parameters. The filter is tuned to the frequencies higher or equal to the frequency of the harmonic to be eliminated (5th).
Table 4.
Single-tuned filter parameters. The filter is tuned to the frequencies higher or equal to the frequency of the harmonic to be eliminated (5th).
| fre [Hz] | nre | Cf [µF] | Lf [mH] | Zf(5) [Ω] | Zf(1) [Ω] | Qf [Var] |
|---|
| 250 | 5 | 125.49 | 3.2 | 0 | 24.35 | −2172.5 |
| 285 | 5.70 | 126.70 | 2.5 | 1.16 |
| 292.5 | 5.85 | 127 | 2.3 | 1.35 |
| 305 | 6.1 | 127.21 | 2.1 | 1.64 |
Table 5.
Influence of the single-tuned filter detuning phenomenon on the grid voltage and current THD.
Table 5.
Influence of the single-tuned filter detuning phenomenon on the grid voltage and current THD.
| (a) Grid Voltage and Current THD When the Single-Tuned Filter Is Tuned to the Frequencies Lower or Equal to the Frequency of the 5th Harmonic | (b) Grid Voltage and Current THD When the Single-Tuned Filter Is Tuned to the Frequencies Higher or Equal to the Frequency of the 5th Harmonic |
|---|
| nre | THD(Us) [%] | THD(Is) [%] | nre | THD(Us) [%] | THD(Is) [%] |
|---|
| Without filter | 4.93 | 36 | Without filter | 4.93 | 36 |
| 4.1 | 4.24 | 49.7 | 5 | 3.79 | 18.74 |
| 4.70 | 3.94 | 31.54 | 5.70 | 6.49 | 172.17 |
| 4.85 | 3.84 | 22.35 | 5.85 | 6.42 | 169.08 |
| 5 | 3.79 | 18.74 | 6.1 | 5.77 | 146.29 |
Table 6.
Parameters of 2nd order filter (Qf = −2172.5Var).
Table 6.
Parameters of 2nd order filter (Qf = −2172.5Var).
| R [Ω] | Zf(5) [Ω] | Zf(1) [Ω] | Rf [mΩ] | Cf [µF] | Lf [mH] | nre | q′ |
|---|
| inf | 0.32 | 24.35 | 74.9 | 125.17 | 3.4 | 4.85 | 14.25 |
| 60 | 0.61 | 24.35 |
| 18 | 1.55 | 24.36 |
| 8 | 2.89 | 24.38 |
| 3 | 4.46 | 24.52 |
Table 7.
Parameters of the 3rd order filter (Qf = −2172.5Var).
Table 7.
Parameters of the 3rd order filter (Qf = −2172.5Var).
| R [mΩ] | Zf(5) [Ω] | Zf(1) [mΩ] | RLf [mΩ] | Cf1 [µF] | Cf2 [µF] | Lf [mH] | nre1 | nre2 |
|---|
| 80 | 1.07 | 24349.8 | 4.3 | 128.74 | 242.70 | 1.2 | 4.85 | 6 |
| 250 | 1.36 | 24349.8 |
| 750 | 2.28 | 24349.9 |
| 1250 | 2.70 | 24350.0 |
| 8000 | 3.11 | 24352.9 |
Table 8.
Parameters of C-type filter (Qf = −2172.5Var).
Table 8.
Parameters of C-type filter (Qf = −2172.5Var).
| R [Ω] | Zf(5) [mΩ] | Zf(1) [mΩ] | RLf [mΩ] | Cfa [µF] | Cfb [µF] | Lf [mH] | nre |
|---|
| 1.25 | 4.73 | 24.34 | 12.7 | 130.72 | 2900 | 3.4 | 4.85 |
| 5 | 3.51 |
| 8 | 2.67 |
| 25 | 1.04 |
| 2500 | 0.32 |
Table 9.
Comparison assumptions.
Table 9.
Comparison assumptions.
| | Qf = −2172.5Var, θ = 57º, nre = 4.85, q’= 85 |
|---|
| First-Order | Single-Tuned | Second-Order | Third-Order | C-Type |
|---|
| R [Ω] | - | - | 0.08 | 0.08 | 0.08 |
| - | - | 1.25 | 1.25 | 1.25 |
| - | - | 8 | 8 | 8 |
| - | - | 25 | 25 | 25 |
| RLf [Ω] | - | 0.0127 | 0.0127 | 0.0043 | 0.0127 |
Table 10.
Measured parameters of the investigated single-tuned filter.
Table 10.
Measured parameters of the investigated single-tuned filter.
| Zf(5) [mΩ] | Zf(1) [mΩ] | RLf [mΩ] | Cf∆ [µF] | Lf [µF] | Qf [kvar] | nre | q′ |
|---|
| 718.5 | 1839 | 1.68 | 600.84 | 232.49 | −27.87 | 4.91 | 43.47 |
Table 11.
Measured powers before and after the filter connection.
Table 11.
Measured powers before and after the filter connection.
| Grid (PCC) | Transformer Input | Filter |
|---|
| PS [kW] | QS [kVar] | PT [kW] | QT [kVar] | Pf [kW] | Qf [kVar] |
|---|
| Before the filter connection |
| 2.52 | 23.29 | 2.52 | 23.29 | - | - |
| After the filter connection |
| 2.30 | −3.56 | 2.46 | 24.44 | −0.15 | −28.00 |
Table 12.
Measured grid voltage and current parameters before the single-tuned filter connection.
Table 12.
Measured grid voltage and current parameters before the single-tuned filter connection.
| n | US [V] | IS [A] |
|---|
| Ampl | [°] | Ampl | [°] |
|---|
| 1st | 223.49 | −90.72 | 104.84 | −174.54 |
| 3rd | 3.33 | 47.96 | 1.42 | −99.53 |
| 5th | 6.33 | 85.39 | 20.18 | −160.96 |
| 7th | 4.86 | −87.65 | 8.36 | 30.13 |
| 9th | 1.18 | −31.38 | 1.06 | 126.86 |
| 11th | 1.86 | −63.59 | 6.08 | 47.50 |
| 13th | 0.26 | −156.65 | 5.24 | −128.10 |
| TTHD [%] | 5.74 | 25.18 |
Table 13.
Measured grid voltage and current parameters after the single-tuned filter connection.
Table 13.
Measured grid voltage and current parameters after the single-tuned filter connection.
| n | US [V] | IS [A] | If [A] | IT [A] |
|---|
| Ampl | [°] | Ampl | [°] | Ampl | [°] | Ampl | [°] |
|---|
| 1st | 227.38 | −89.29 | 18.68 | −32.12 | 123.15 | 1.03 | 108.04 | −173.52 |
| 3rd | 3.77 | 53.88 | 1.91 | −114.61 | 0.86 | 155.63 | 2.09 | −90.97 |
| 5th | 8.64 | 82.21 | 42.37 | −174.11 | 23.34 | 169.16 | 21.15 | −155.31 |
| 7th | 10.93 | −116.56 | 49.68 | −19.30 | 46.61 | −28.71 | 8.46 | 44.35 |
| 9th | 2.23 | −102.75 | 1.89 | 54.78 | 2.65 | 8.55 | 1.90 | 142.74 |
| 11th | 1.15 | 178.92 | 6.78 | −25.97 | 9.54 | −71.33 | 6.80 | 63.45 |
| 13th | 0.63 | 28.27 | 3.96 | −126.15 | 1.75 | 104.06 | 5.27 | −111.42 |
| TTHD [%] | 6.92 | 356.21 | 44.67 | 25.06 |