Abstract
The channel of the broadband wireless communications system can be modeled as a dynamic sparse channel. Such a channel is difficult to reconstruct by using linear channel estimators that are normally employed for dense channels’ estimation because of their lack of capacity to use the inherent channel’s sparsity. This paper focuses on reconstructing this type of time-varying sparse channel by extending a recently proposed dynamic channel estimator. Specifically, variable step size’s mechanism and variable momentum parameter are incorporated into traditional Iterative Hard Thresholding-based channel estimator to develop the proposed Iterative Hard Thresholding with Combined Variable Step Size and Momentum (IHT-wCVSSnM)-based estimator. Computer simulations carried out in the context of a wireless communication system operating in a dynamic sparse channel, show that the proposed IHT-wCVSSnM-based estimator performs better than all the other estimators significantly. However, the computational complexity cost of the proposed estimator is slightly higher than the closely performing channel estimator. Nevertheless, the inherent complexity cost of the proposed estimator could be compromised in a situation where the system’s performance is of higher priority when compared with the computational complexity cost.
1. Introduction
Most of the emerging wireless communication systems can be classified as broadband systems. In general, broadband wireless networks operate over frequency and time selective channels. Many experimental studies have established that in a realistic scenario broadband channels display sparsity in the delay domain. In such channels, the delay spread is very large in comparison with the small numbers of distinguishable multipath delays [1,2,3]. Hence, these channels are modeled as being sparse. Moreover, these sparse channels can be categorized as either static or time-varying (dynamic) sparse channels. In terms of sparse signals in general, some studies [4,5] have shown that such signals can be estimated using a small number of observations under some conditions. Consequently, exploitation of the structure of sparse channels can enhance the designing of less complex and efficient algorithms for dynamic sparse channel reconstruction. In the works presented in [6,7], the authors established that spatial non-stationarity can be considered as a vital propagation property of massive multiple-input multiple-output (MIMO) channels. It has been shown that the presence of the antenna array with a large physical size in massive MIMO systems results in some of its properties (such as angle spread, delay spread, power, and the number of clusters associated with the MIMO wireless channel) not being static over large scale array. Some other authors established in [8] that the delay-domain channel sparse structures are different because some clusters are detectable to a certain degree of the antenna array. Millimeter-wave (mmWave)’s band is indicated in [9] to possess a very large unlicensed bandwidth. Consequently, these can be employed as a means of providing data rate services. The directional features associated with MmWave’s bands make them sparse in the spatial domain [10]. In comparison with static sparse channel models, dynamic sparse channels are very difficult to estimate or reconstruct. This is due to their time-varying path delays and their non-zero taps that appear and disappear sporadically.
In dense channels, channel estimators based on linear algorithms have been found useful. However, these estimators are inefficient when employed for reconstructions of dynamic wireless sparse channels. This is because it has been established that they failed to take advantage of the associated sparsity in the channel for the channel estimation procedure. This is one of the main motivations behind this paper. Some previously proposed methods for reconstructing dynamically varying sparse wireless communication channels are detailed as follows.
The authors in [11] proposed a flexible complexity-based recursive least-squares-based estimator for underwater acoustic (UWA) channels. The channel impulses’ responses are said to possess large delays and Doppler spreads with few significant echoes. The proposed method employed single-carrier waveforms for estimation of doubly-selective single antenna channels, while neglecting the weakest taps. In [12] and [13], the authors employed matching pursuit (MP) algorithm to developed a channel estimator for frequency-selective single-antenna channels. The proposed method was hinged on the understanding that both the broadband channels and digital television channels and in hilly terrains show sparse features. In [14] an estimation technique that is based on the polynomial basis expansion model of [15] is proposed for time-varying OFDM sparse channels. The authors in [16] exploited the Orthogonal Matching Pursuit (OMP) algorithm to develop an extended Orthogonal Matching Pursuit (OMP)-based channel estimation. This channel estimation scheme is said to bring the required number of measurements for OMP closer to Basic Pursuit (BP)-based estimator. Subspace pursuit (SP)-based estimator and OMP-based estimator are developed for estimations of sparse channels of wireless communication systems in [17] and [18], respectively. However, in [19] and [20], the inherent temporal correlation in a wireless channel is exploited in developing the adaptive simultaneous OMP (A-SOMP)-based estimator and structured SP (SSP)-based channel estimator respectively, for tracking of dynamic channels. In [21], the Bayesian compressive sensing technique was proposed for the reconstruction of signals from compressible signals hinged on some linear basis. The reconstruction of the signal is achieved by using a small number of basis-function coefficients associated with the linear basis. A Hierarchical Bayesian Kalman (HBK) filter-based estimator is used by the authors in [22] for the reconstruction of a time-varying sparse channel. By using structured matching pursuit (SMP), the authors in [23] exploited temporal correlations associated with time-varying sparse channels for the reconstruction of the time-varying sparse channels in wireless communication systems. However, in [24] the same authors employed differential orthogonal matching pursuit (D-OMP)-based estimator for estimations of the time-varying sparse channel. In [25], a joint multi-symbol channel estimator was proposed for the estimation of a time-varying sparse channel. The estimator is based on differential simultaneous orthogonal matching pursuit (DSOMP) algorithm, while in [26] the same authors proposed another estimator that is based on differential block simultaneous orthogonal matching pursuit (DBSOMP) algorithm for massive MIMO systems. A greedy-based channel tracking algorithm that is capable of tracking the dynamic sparse signals, such as the time-varying angle of departure (AoD), angle of arrival (AoA), and channel gain amplitudes of mmWave channel, is developed for a millimeter wave (mmWave) communication system in [27]. Kalman filter-based compressed sensing estimator is employed in [28] to control a time-reversal receiver to enhance the underwater acoustic communication systems’ performance. In [29], the problem of estimation based on the maximization of a modified likelihood function is investigated. The modified likelihood function’s maximization is performed with the aid of the Expectation–Maximization (EM) algorithm. By considering transmission over the time-varying channel in downlink orthogonal frequency division multiplexing (OFDM)-massive MIMO system, quasi-block simultaneous orthogonal matching pursuit (QBSO) algorithm is employed in [30] to recover the sparse MIMO channels. For rapidly changing dynamic and frequency selective scenarios, as we have in aeronautical systems and high-speed trains, Space Alternated Generalized Expectation Maximization Maximum a Posteriori (SAGE-MAP) based channel estimator is proposed in [31] for tracking of the Autoregressive (AR) modeled dynamic sparse channels. A Variable Step Size Sign Data Sign Error NLMS (VSS-SDSENLMS)-based estimator is developed in [32] by exploiting the time-varying broadband wireless channel’s sparsity for tracking of sparse channels. In [33] the dynamic massive MIMO channel is reconstructed as one simultaneously sparse signal vector. Thereafter, the authors designed sparse Bayesian learning (SBL) framework for estimation of the temporal dynamic features of the sparse virtual channel and spatial signatures. The authors in [34] investigated the estimation of the sparse multi-user massive MIMO channels via multi-task (MT)-sparse Bayesian learning (SBL) that is employed in learning dynamic sparse channels in the uplink paths of multi-user massive MIMO-OFDM systems. By exploiting sparsity and the associated temporal correlation of the dynamic wireless channel, the authors in [35] proposed a technique for estimation of the channels in space-time block coding MIMO-OFDM (STBC MIMO-OFDM) systems. The technique is based on amended mean square error (MSE) optimal threshold (IMOT) and adaptive multi-frame averaging (AMA) schemes. The authors in [36] proposed a decision-directed-based sparse adaptive predictor that works in the delay-Doppler domain for dynamic UWA channels. To track the dynamic sparse wireless communication channels, the authors in [37] exploited associated temporal correlations of channels to develop the proposed iterative hard thresholding with memory (IHT_wM)-based estimator for broadband communication systems. A summary of some of the above reviewed relevant works is presented in Table 1. The other motivations for this paper are as follows. Most of the above estimation methods perform well but are highly expensive in terms of computational complexity costs. Some others perform poorly with low computational complexity costs. There are some of these techniques that show both disadvantages.

Table 1.
Summary of the reviewed relevant works.
In this paper, the work presented in [37] is revisited. As an extension of this work, the main contributions of this paper are summarized as follows.
- We propose an efficient dynamic channel estimator that is developed by deriving a combined variable step size mechanism and variable momentum and incorporating this into the traditional iterative hard thresholding. The estimator is named Iterative Hard Thresholding with Combined Variable Step Size and Momentum (IHT-wCVSSnM)-based estimator.
- We present a comparative study of the proposed IHT-wCVSSnM-based estimator with some other estimators when employed in a broadband wireless communication system that is operating in a dynamic sparse wireless channel.
Though the channel estimator proposed in this paper is built on the same traditional Iterative Hard Thresholding algorithm employed in [37], however, the main distinctions between this work and the one presented in [37] include the following. In 37, a constant step size parameter is employed in the operation of the channel estimator. In this paper, a variable step size mechanism is developed for the proposed IHT-wCVSSnM)-based estimator.
Consequently, reference [37] employed variable momentum step size in combination with fixed step size in the dynamic channel estimation procedure. On the other hand, the proposed IHT-wCVSSnM-based estimator’s operation is based on the combined variable step size and variable momentum step size mechanisms. Insight about time to computation in terms of CPU running time for all the estimators is presented in this paper but not in [37].
The remainder of this paper assumes the following order. Section 2 details the considered typical wireless system model with a sparse channel. The proposed IHT-wCVSSnM-based estimator is described in Section 3. Section 4 focuses on simulation results and computational complexities of the proposed IHT-wCVSSnM-based estimator in comparison with some other estimators considered in this paper. Finally, the conclusion and future research focuses are presented in Section 5.
2. Wireless System Model with Sparse Channel
The system model considered in this paper and presented in this section is similar to the one employed in [37]. It is a wideband wireless communication system’s model with sparse channels in the time domain. In such systems, the effective channels’ tap coefficients are very few in comparison with the approximately zero taps’ coefficients. An example of such a sparse wireless channel is illustrated in Figure 1 [38]. The corresponding linear measurement for such system is expressed as
with representing the dynamic sparse channel that is to be estimated from the under-sampled measurements in continuous time slots, and . The channel coefficients has a sparsity level of , the total number of non-zero taps’ coefficients. By considering the -th time slot’s window, the -th measurement vector from (1) can be expanded having length of size. From (1), the time-varying dynamic channel coefficient vector that has number of taps can be expanded as . The operation stands for the transpose and parameter is assumed to be greater than parameter , that is . The parameter in (1) represents the -th component vector of the Gaussian noise (AWGN) that is both complex and white with zero mean and variance , where is identity matrix. The last parameter in (1), denotes the measurement matrix, and it is assumed to be static for simplicity, which is . The -th component of the measurement matrix, can be expressed as follows.
where is Toeplitz matrix. The columns of are semi-orthogonal, i.e., for all , and . The operator represents the conjugate transpose.
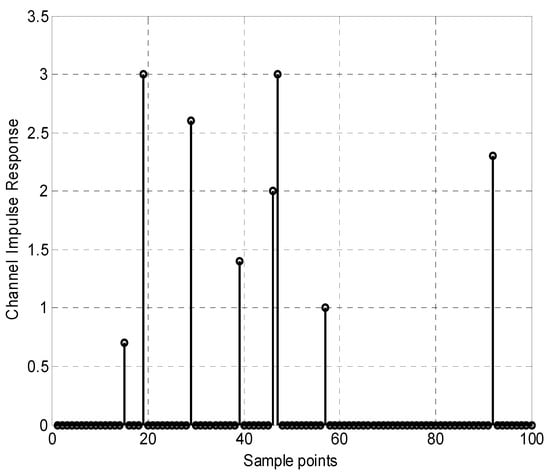
Figure 1.
Typical Sample Spaced Sparse Multipath Channel. Reprinted with permission from [38]. Copyright 2018 Elsevier.
The most common use channel model in wireless communication systems is the Rayleigh fading channel. For the system model considered in this paper, a time-varying Rayleigh fading channel that has a velocity between 100 km/h and 120 km/h [24] is considered. In this channel model, there are variations of the velocity within three to four consecutive time slots. Consequently, the corresponding channel impulse response changes rapidly while the path delays change slowly. To depict the temporal correlations of a channel with this type of channel model, similarly to [37], the corresponding path delay set, , is given as
In (3), the parameter stands for the path delay set of wireless channel coefficients , and this is expressed as . The size of the similar path delay set is denoted as P. The following relationship exists between the size of the similar path delay set P, the temporal correlation degree of the dynamic sparse channel , and the sparsity level of the dynamic wireless channel. This relationship is expressed as , and it is a constraint that is enforced on the number of the time-varying sparse channel taps’ coefficients between two succeeding time slots. In the next section, the procedure for reconstructing these dynamic sparse channel coefficients is detailed.
3. The Proposed IHT-wCVSSnM-Based Estimator for Dynamic Sparse Wireless Channel
This section presents the detail of the proposed Iterative Hard Thresholding with Combined Variable Step Size and Momentum (IHT-wCVSSnM)-based estimator. The developed estimator is based on the traditional Iterative Hard Thresholding that minimizes the following error function
to reconstruct the dynamic sparse wireless channel . In (4), parameter is a constant. Remember that denotes the level of the sparsity of the dynamic channel coefficients so that . Consequently, in a bid to define the structure of combinatorial sparsity model can be used. As a result, the sparse channel coefficients can be re-constructed by minimizing the error function of (4) that is now re-written in the following form:
Finally, the traditional iterative thresholding procedure for solving (5) is expressed as
where is a constant step size and , and is a signum function. Given the estimate of the -sparse dynamic channel coefficients as with its corresponding known path delay set at kth iteration given as , then the non-zero components of the dynamic channel coefficients , for the subsequent estimate is expected to fulfill the following conditions:
for the fixed step size . The path delay support set vector of denoted as , is the index path delay set of non-zero coefficients vector . The connection between and support set is given as . The complement of the support set is denoted as . Therefore, the -sparse path delay support set denoted as can be expressed as
Provided that there is the availability of the a-prior knowledge of at the kth iteration, then the smallest index set contains a-prior knowledge in such a way for the following inequality to hold
In (9), operator is a combinatorial projection onto the subspace that is defined by the combinatorial sparsity model . In Equations (6), (7), and (9), it can be seen that a constant step size parameter is incorporated. Generally, in most of the estimators that use the step-size parameter in the estimation procedure, a smaller value of step size usually leads to faster convergence of the estimator’s tracking speed, but with poor mean square error (MSE) at a steady state. However, a larger value step size will result in a reasonably small MSE at a steady state with the downside of very slow tracking and convergence speed. In a bid to achieve more of both advantages: high tracking and convergence speed with low MSE, the mechanism of variable step size is introduced into the traditional Iterative Hard Thresholding-based estimator as follows. By following the principle presented in [39], (7) and (9) are re-written by incorporating a variable step-size parameter as follows:
Then, it follows that the Iterative Hard Thresholding-based estimator with variable step size will track and estimate the dynamic sparse wireless channel as
where and .
The variable step size is then obtained by performing the following argument of the minimum function:
The variable step size in (13) will minimize the objective function expressed in (4), and as a results of restricted isometry property (RIP), with constant .
Further, by following the accelerated gradient principles presented in [40] and memory idea employed in [37], let the -th vector , expressed as
set all but the largest components, say of to zero. The function stands for linear operator as earlier defined. Hence, the combinatorial projection onto the subspace describes by combinatorial sparsity model is therefore expressed as
Then,
The parameter is the momentum step size that the IHT-wM-based estimator technique presented in [37] employed “memory” to attain. The variable momentum step size mechanism is combined with the variable step size in this paper to develop the proposed IHT-wCVSSnM-based estimator. Usually, the parameter uses constant value within the following range . Its adaptive format is computed by minimization of the following objective function:
The variable momentum step size in (17) simply involves a vector-vector inner product operation and it is less computationally costly.
Finally, the proposed IHT-wCVSSnM-based estimator for dynamic sparse wireless communication systems is summarized in Algorithm 1. It comprises three stages. At the initialization stage, all the various parameters that required initialization are set to initial values. Stage 2 is the iteration stage where the core operations of the proposed IHT-wCVSSnM-based estimator occur. The kth -sparse path delay support set , is computed at step 2. Step 3 computes the variable step size as given in (13). Momentum step size , is obtained in step 4 as presented in (17). The reconstruction of the dynamic sparse coefficients takes place in step 6, an update of the residual signal is obtained in step 7. The final Stage 3 is the stopping criterion phase. Immediately the stopping criterion condition in step 8 is satisfied, the reconstructed sparse channel coefficients are returned by the algorithm. In the next section, the comparative computer simulation results are presented in terms of Mean square error (MSE) that is defined as
4. Computer Simulation Results and Computational Complexity Costs
In this section, the comparative computer simulation results are presented for the proposed IHT-wCVSSnM-based estimator and some other estimators from the literature. Some of the recent channel estimator proposed for reconstruction of dynamic sparse channels considered in this paper include the IHT-wM-based estimator [37], traditional OMP-based estimator [16], traditional OMP-based estimator [17], A-SOMP-based estimator [19], SMP-based estimator [23], IHT-wM-based estimator [37], and linear channel estimator based on least square algorithm [41]. Some of the parameters’ settings for the simulations are as follows: the size of the measurement matrix is set as , the sparsity level is initially set as = 15, but its variations are employed for some other simulations. The number of continuous-time slots is set to 10.
The initial set of results are illustrated in Figure 2 and show achievable comparative MSE performance of the proposed IHT-wCVSSnM-based estimator and other estimators while, the degree of temporal correlation of the time-varying sparse channel, is set at 8. Both the proposed IHT-wCVSSnM-based estimator and the IHT-wM-based estimator of [37] perform exceptionally well with all the other estimators. However, at the higher signal to noise ratio (SNR), the proposed IHT-wCVSSnM-based estimator outperforms its counterpart, the IHT-wM-based estimator of [37]. In Figure 3, the performances of all the estimators are evaluated when the temporal correlation degree of the dynamic channel (L) varies between 2 and 14. The performances are evaluated at both SNR of 5 dB and SNR of 15 dB. The corresponding results are illustrated in both Figure 3a,b, respectively. Most of the estimators exhibit constant MSE performance as the value of increases at SNR of 5 dB. Slightly improved MSE performances can be observed in both the proposed IHT-wCVSSnM-based estimator and the IHT-wM-based estimator of [37]. The results at SNR = 15 dB, however, suggest that only the A-SOMP-based estimator of [19] seems to be significantly improved by increasing the value of . Nonetheless, it shows the poorest performance, whereas the proposed IHT-wCVSSnM-based estimator shows the best performance with slightly improved performance as the value of increases from 2 to 14.
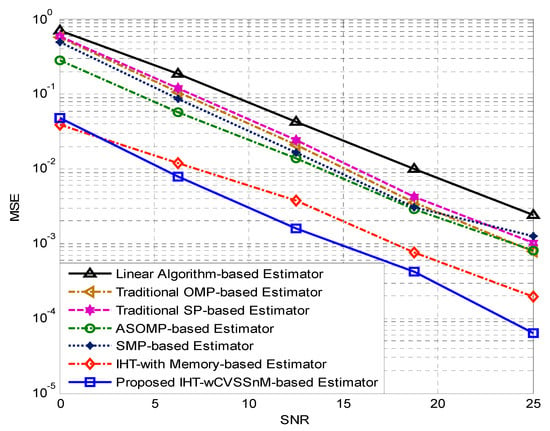
Figure 2.
Achievable comparative MSE versus signal to noise ratio (SNR) performance of the proposed IHT-wCVSSnM-based estimator with other channel estimators when the degree of temporal correlation is set as .
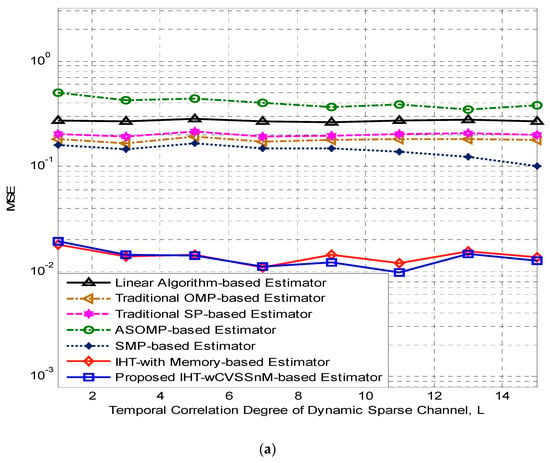
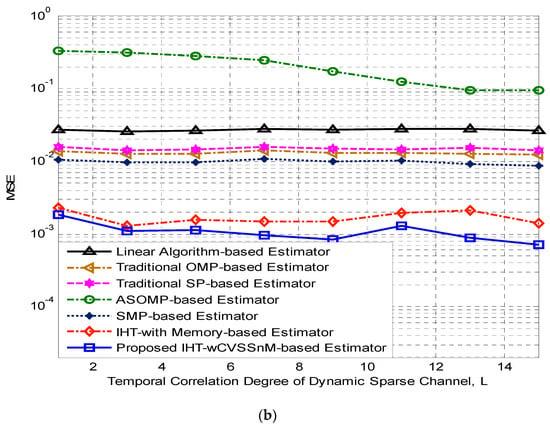
Figure 3.
Achievable comparative MSE versus temporal correlation degree of dynamic sparse channel performance of the proposed IHT-wCVSSnM-based estimator with other channel estimators (a) SNR = 5 dB, (b) SNR = 15 dB.
In terms of computational complexity cost requirements of each of the considered estimators and the proposed IHT-wCVSSnM-based estimator, the linear estimator of [41] exhibits the least computational complexity cost of order , the conventional OMP-based estimator involves complexity cost of , conventional SP-based estimator requires computational complexity cost of . The ASOMP-based estimator involves the computational complexity cost of about while the SMP-based estimator requires the complexity cost of . The IHT-wM-based estimator of [37] requires computational complexity cost of order , and the proposed IHT-wCVSSnM-based estimator’s operation requires computational complexity cost of order . To quantify the effects of computational complexities on the proposed estimator and other estimators in terms of the time to computation, CPU running time for all the estimators is obtained and illustrated in Figure 4. Figure 4a illustrates the running time results when the SNR is at 5 dB; and when the SNR is set at 15 B, the corresponding results are shown in Figure 4b. In these two results, it is obvious that the proposed IHT-wCVSSnM-based estimator requires more time for computations (including computations of both variable step size and momentum parameter) than all the other estimators. Its computational complexity cost is also slightly higher than its closely performing counterpart, the IHT-wM-based estimator of [37]. In the scenario where the dynamic sparse channel estimation is executed at the base station (BS), the slightly higher computational complexity cost of the proposed IHT-wCVSSnM-based estimator will be immaterial. This is because the performance is of high priority at this instance. Hence, the additional computational complexity cost can be borne at the BS. If the channel estimation is performed at the user equipment, the higher computational complexity will be undesirable. However, such high computational complexity cost can be easily accommodated due to the current advancement in the integrated circuit (IC)’s developments. This will allow high priority to be placed on the overall system’s performance to enhance users’ experiences.
| Algorithm 1 Proposed IHT-wCVSSnM-based Estimator for Wireless Communication systems with Dynamic Sparse Channels |
| Input:; ; ; ; ; Itr-Max; : stopping tolerance; : step size Output: Reconstructed sparse channel: Stage 1, Initialization of the Proposed IHT-wCVSSnM-based estimator: ; : Iteration counter : residue error; : Path delay support set of ; Stage 2, Iteration section of the Proposed IHT-wCVSSnM-based estimator: for do 1. While 2. 3. 4. 5. 6. 7. Stage 3, Stopping Criterion for the Proposed IHT-wCVSSnM-based estimator: 8. Until the stopping criterion is met: 9. or Itr-Max 10. end while 11. Return |
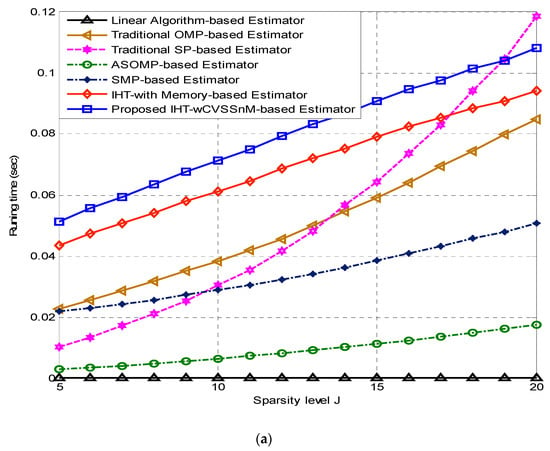
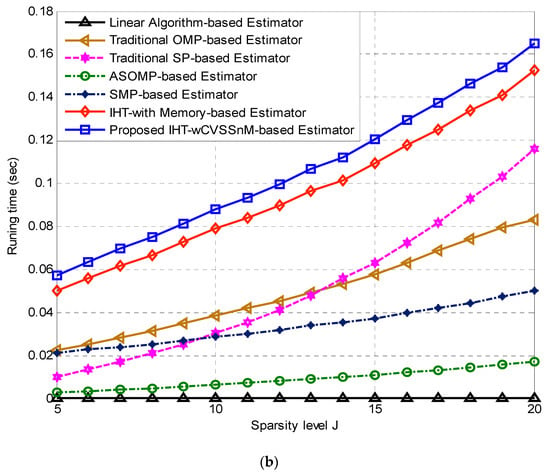
Figure 4.
CPU running time versus temporal correlation degree of dynamic sparse channel comparison for all the channel estimators (a) SNR = 5 dB, (b) SNR = 15 dB.
5. Conclusions and Future Research Directions
This paper extended the work presented in [37] to propose a new dynamic sparse channel estimator for wireless communication systems. Specifically, the proposed estimator incorporates both variable step size and variable momentum parameters into the traditional Iterative Hard Thresholding-based channel estimator to develop the proposed Iterative Hard Thresholding with Combined Variable Step Size and Momentum (IHT-wCVSSnM)-based estimator presented in this paper. The comparative performances of the proposed IHT-wCVSSnM-based estimator and other estimator considered in this paper are documented in terms of a wireless communication system operating in a dynamic sparse wireless channel environment. The simulation results suggest that the proposed IHT-wCVSSnM-based estimator outperforms all the other estimators including the IHT-wM-based estimator of [37]. It is seen that the proposed IHT-wCVSSnM-based estimator exhibits an inherent high computational complexity cost than all the other estimators. However, this could be negligible when operating at the BS and could be compromised for higher performance when deployed at user equipment due to advancement in the development of IC being used in the user’s equipment.
Future research direction will immediately focus on reducing the computational complexity cost of the proposed IHT-wCVSSnM-based estimator without compromising its corresponding performance. Further, it will be worthwhile to investigate the proposed IHT-wCVSSnM-based estimator’s performance in a specific 5G and beyond 5G wireless communication systems.
Author Contributions
Conceptualization, O.O.O.; methodology; O.O.O., investigation; O.O.O., original draft preparation, O.O.O.; writing—review and editing, A.F. and T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the National Research Foundation (NRF) of South Africa in terms of both NRF Competitive Program (funding) for Rated Researchers with grant number 118547 and funding based on the NRF, South Africa/NCBR, Poland joint science and technology research collaboration with grant number 118678.
Conflicts of Interest
The authors declare no conflict of interest.
References
- He, X.; Song, R.; Zhu, W.-P. Pilot Allocation for Distributed-Compressed-Sensing-Based Sparse Channel Estimation in MIMO-OFDM Systems. IEEE Trans. Veh. Technol. 2016, 65, 2990–3004. [Google Scholar] [CrossRef]
- Qi, C.; Yue, G.; Wu, L.; Huang, Y.; Nallanathan, A. Pilot Design Schemes for Sparse Channel Estimation in OFDM Systems. IEEE Trans. Veh. Technol. 2014, 64, 1493–1505. [Google Scholar] [CrossRef]
- Masood, M.; Afify, L.H.; Al-Naffouri, T.Y. Efficient Coordinated Recovery of Sparse Channels in Massive MIMO. IEEE Trans. Signal Process. 2014, 63, 104–118. [Google Scholar] [CrossRef]
- Candes, E. Compressive Sampling. Int. Congr. Math. 2006, 3, 1433–1452. [Google Scholar]
- Candes, E.; Tao, T. The Dantzig Selector: Statistical estimation when p is much larger than n. Ann. Stat. 2007, 35, 2313–2351. [Google Scholar]
- Li, J.; Ai, B.; He, R.; Yang, M.; Zhong, Z.; Hao, Y.; Shi, G. The 3D Spatial Non-Stationarity and Spherical Wavefront in Massive MIMO Channel Measurement. In Proceedings of the 2018 10th International Conference on Wireless Communications and Signal Processing (WCSP), Hangzhou, China, 18–20 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Chen, J.; Yin, X.; Cai, X.; Wang, S. Measurement-Based Massive MIMO Channel Modeling for Outdoor LoS and NLoS Environments. IEEE Access 2017, 5, 2126–2140. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, J.; Yang, X.; Ma, N.; Zhang, Z. Recent Research on Massive MIMO Propagation Channels: A Survey. IEEE Commun. Mag. 2018, 56, 22–29. [Google Scholar] [CrossRef]
- Rappaport, T.S.; Heath, R.W., Jr.; Daniels, R.C.; Murdock, J.N. Book Millimeter-Wave Wireless Communications; Pearson Education: London, UK, 2014. [Google Scholar]
- Heath, R.W.; Gonzalez-Prelcic, N.; Rangan, S.; Roh, W.; Sayeed, A.M. An Overview of Signal Processing Techniques for Millimeter Wave MIMO Systems. IEEE J. Sel. Top. Signal Process. 2016, 10, 436–453. [Google Scholar] [CrossRef]
- Kocic, M.; Brady, D.; Merriam, S. Reduced-complexity RLS estimation for shallow-water channels. In Proceedings of the IEEE Symposium on Autonomous Underwater Vehicle Technology, Cambridge, MA, USA, 5–6 June 1994; pp. 165–170. [Google Scholar]
- Cotter, S.F.; Rao, B. Matching pursuit based decision-feedback equalizers. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing (Cat. No.00CH37100), Istanbul, Turkey, 19–24 April 2002; Volume 5, pp. 2713–2716. [Google Scholar] [CrossRef]
- Cotter, S.; Rao, B. Sparse channel estimation via matching pursuit with application to equalization. IEEE Trans. Commun. 2002, 50, 374–377. [Google Scholar] [CrossRef]
- Hu, D.; Wang, X.; He, L. A New Sparse Channel Estimation and Tracking Method for Time-Varying OFDM Systems. IEEE Trans. Veh. Technol. 2013, 62, 4648–4653. [Google Scholar] [CrossRef]
- Hijazi, H.; Ros, L. Polynomial Estimation of Time-Varying Multipath Gains with Intercarrier Interference Mitigation in OFDM Systems. IEEE Trans. Veh. Technol. 2009, 58, 140–151. [Google Scholar] [CrossRef]
- Sahoo, S.K.; Makur, A. Signal Recovery from Random Measurements via Extended Orthogonal Matching Pursuit. IEEE Trans. Signal Process. 2015, 63, 2572–2581. [Google Scholar] [CrossRef]
- Dai, W.; Milenkovic, O. Subspace Pursuit for Compressive Sensing Signal Reconstruction. IEEE Trans. Inf. Theory 2009, 55, 2230–2249. [Google Scholar] [CrossRef]
- Needell, D.; Tropp, J. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl. Comput. Harmon. Anal. 2009, 26, 301–321. [Google Scholar] [CrossRef]
- Dai, L.; Wang, J.; Wang, Z.; Tsiaflakis, P.; Moonen, M. Spectrum- and Energy-Efficient OFDM Based on Simultaneous Multi-Channel Reconstruction. IEEE Trans. Signal Process. 2013, 61, 6047–6059. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Wang, Z. Structured compressive sensing based superimposed pilot design in downlink large-scale MIMO systems. Electron. Lett. 2014, 50, 896–898. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian Compressive Sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Karseras, E.; Leung, K.; Dai, W. Tracking dynamic sparse signals using Hierarchical Bayesian Kalman filters. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6546–6550. [Google Scholar] [CrossRef]
- Zhu, X.; Dai, L.; Gui, G.; Dai, W.; Wang, Z.; Adachi, F. Structured Matching Pursuit for Reconstruction of Dynamic Sparse Channels. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Zhu, X.; Dai, L.; Dai, W.; Wang, Z.; Moonen, M. Tracking a dynamic sparse channel via differential orthogonal matching pursuit. In Proceedings of the 2015 IEEE Military Communications Conference (MILCOM), Tampa, FL, USA, 26–28 October 2015; pp. 792–797. [Google Scholar] [CrossRef]
- Zhang, X.; Gui, L.; Qin, Q.; Gong, B. Dynamic sparse channel estimation over doubly selective channels: Differential simultaneous orthogonal matching pursuit. In Proceedings of the 2016 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Nara, Japan, 1–3 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, X.; Gui, L.; Gong, B.; Xiong, J.; Qin, Q. Dynamic sparse channel estimation over doubly selective channels for large-scale MIMO systems. In Proceedings of the 2017 IEEE International Symposium on Broadband Multimedia Systems and Broadcasting (BMSB), Cagliari, Italy, 7–9 June 2017; pp. 1–7. [Google Scholar] [CrossRef]
- Lim, S.H.; Choi, J.W.; Shim, B. Greedy Sparse Channel Estimation for Millimeter Wave Communications. In Proceedings of the 2018 IEEE Region 10 Conference (TENCON), Jeju, Korea, 28–31 October 2018; pp. 1628–1632. [Google Scholar] [CrossRef]
- Jiang, W.; Wang, X.; Tong, F. Dynamic compressed sensing estimation of time varying underwater acoustic channel. In Proceedings of the 2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, China, 22–25 October 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Carvajal, R.; Godoy, B.I.; Agüero, J.C.; Goodwin, G.C. EM-based sparse channel estimation in OFDM systems. In Proceedings of the 2012 IEEE 13th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Cesme, Turkey, 4–6 November 2015; pp. 530–534. [Google Scholar] [CrossRef]
- Qin, Q.; Gui, L.; Gong, B.; Luo, S. Sparse Channel Estimation for Massive MIMO-OFDM Systems over Time-Varying Channels. IEEE Access 2018, 6, 33740–33751. [Google Scholar] [CrossRef]
- Buyuksar, A.B.; Senol, H.; Erkucuk, S.; Cirpan, H.A. Data-aided autoregressive sparse channel tracking for OFDM systems. In Proceedings of the 2016 International Symposium on Wireless Communication Systems (ISWCS), Poznan, Poland, 20–23 September 2016; pp. 424–428. [Google Scholar] [CrossRef]
- Beena, A.O.; Pillai, S.S.; Vijayakumar, N. An Improved Adaptive Sparse Channel Estimation Method for Next Generation Wireless Broadband. In Proceedings of the 2018 International Conference on Wireless Communications, Signal Processing and Networking (WiSPNET), Chennai, India, 22–24 March 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Ma, J.; Zhang, S.; Li, H.; Gao, F.; Jin, S. Sparse Bayesian Learning for the Time-Varying Massive MIMO Channels: Acquisition and Tracking. IEEE Trans. Commun. 2018, 67, 1925–1938. [Google Scholar] [CrossRef]
- Shahmansoori, A. Sparse Bayesian Multi-Task Learning of Time-Varying Massive MIMO Channels with Dynamic Filtering. IEEE Wirel. Commun. Lett. 2020, 9, 871–874. [Google Scholar] [CrossRef]
- Zhang, M.; Zhou, X.; Wang, C. Time-Varying Sparse Channel Estimation Based on Adaptive Average and MSE Optimal Threshold in STBC MIMO-OFDM Systems. IEEE Access 2020, 8, 177874–177895. [Google Scholar] [CrossRef]
- Zhang, Y.; Venkatesan, R.; Dobre, O.A.; Li, C. Efficient Estimation and Prediction for Sparse Time-Varying Underwater Acoustic Channels. IEEE J. Ocean. Eng. 2019, 45, 1112–1125. [Google Scholar] [CrossRef]
- Oyerinde, O.O.; Flizikowski, A.; Marciniak, T. Iterative Hard Thresholding with Memory-based Dynamic Sparse Wireless Channel Estimator. In Proceedings of the 14th International Conference on Signal Processing and Communication Systems (ICSPCS), Adelaide, Australia, 14–16 December 2020; pp. 1–5. [Google Scholar]
- Oyerinde, O.O. An overview of channel estimation schemes based on regularized adaptive algorithms for OFDM-IDMA systems. Digit. Signal Process. 2018, 75, 168–183. [Google Scholar] [CrossRef]
- Kyrillidis, A.; Cevher, V. Recipes on hard thresholding methods. In Proceedings of the 2011 4th IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP), San Juan, PR, USA, 13–16 December 2011; pp. 353–356. [Google Scholar] [CrossRef]
- Cevher, V. On accelerated hard thresholding methods for sparse approximation. In Wavelets and Sparsity XIV; International Society for Optics and Photonics: Bellingham, WA, USA, 2011; Volume 8138, pp. 1–6. [Google Scholar]
- Vithanage, C.; Denic, S.; Sandell, M. Robust Linear Channel Estimation Methods for Per-Subcarrier Transmit Antenna Selection. IEEE Trans. Commun. 2011, 59, 2018–2028. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).