An FPGA-Based Four-Channel 128k-Point FFT Processor Suitable for Spaceborne SAR
Abstract
:1. Introduction
- A proposed FFT processor implemented on FPGA for on-orbit SAR processing is one that supports up to 128k fixed-point FFT operations, which further meets the needs of on-orbit SAR processing for ultra-long point FFT. The high-speed parallel 128k-point FFT processor is suitable for high-precision SAR real-time processing.
- A radix-23 algorithm and a mixed-radix algorithm are combined with the advantages of low hardware resources and high real-time performance.
- A word length adjustment strategy is proposed that can better ensure the accuracy of fixed-point calculations.
- The designed processor is implemented on the Virtex-7 series FPGA device, and the calculation results are compared with the MATLAB double-precision floating point calculation results, showing that the relative error of the FPGA calculation results was maintained at about 10−4. We compared the designed processor with previous work, showing that the designed FFT processor requires fewer hardware resources.
2. Fast Fourier Transform (FFT) Operation Analysis and Principle Introduction
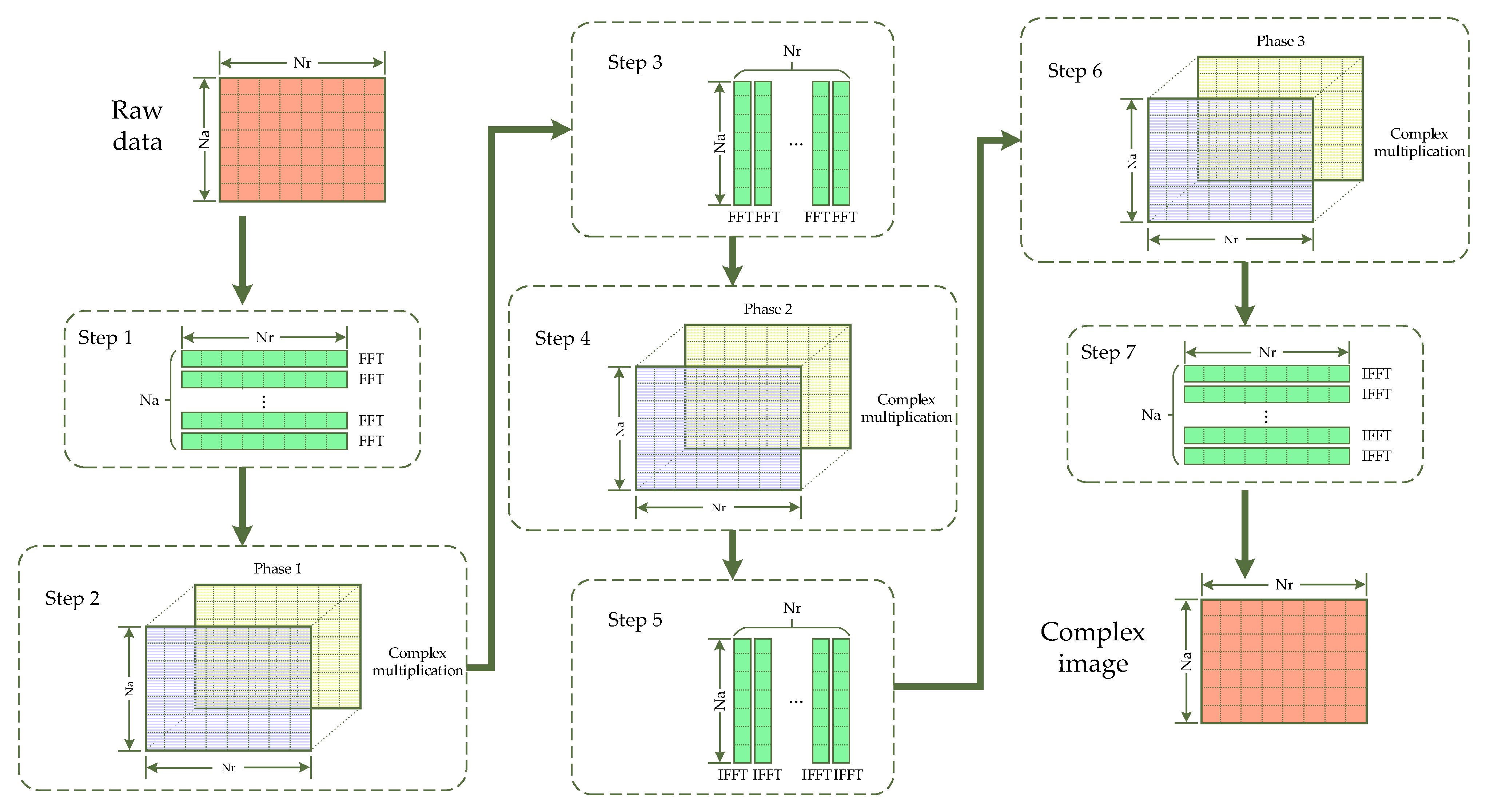
2.1. Operation Proportion Analysis of FFT in the Standard Chirp-Scaling (CS) Algorithm
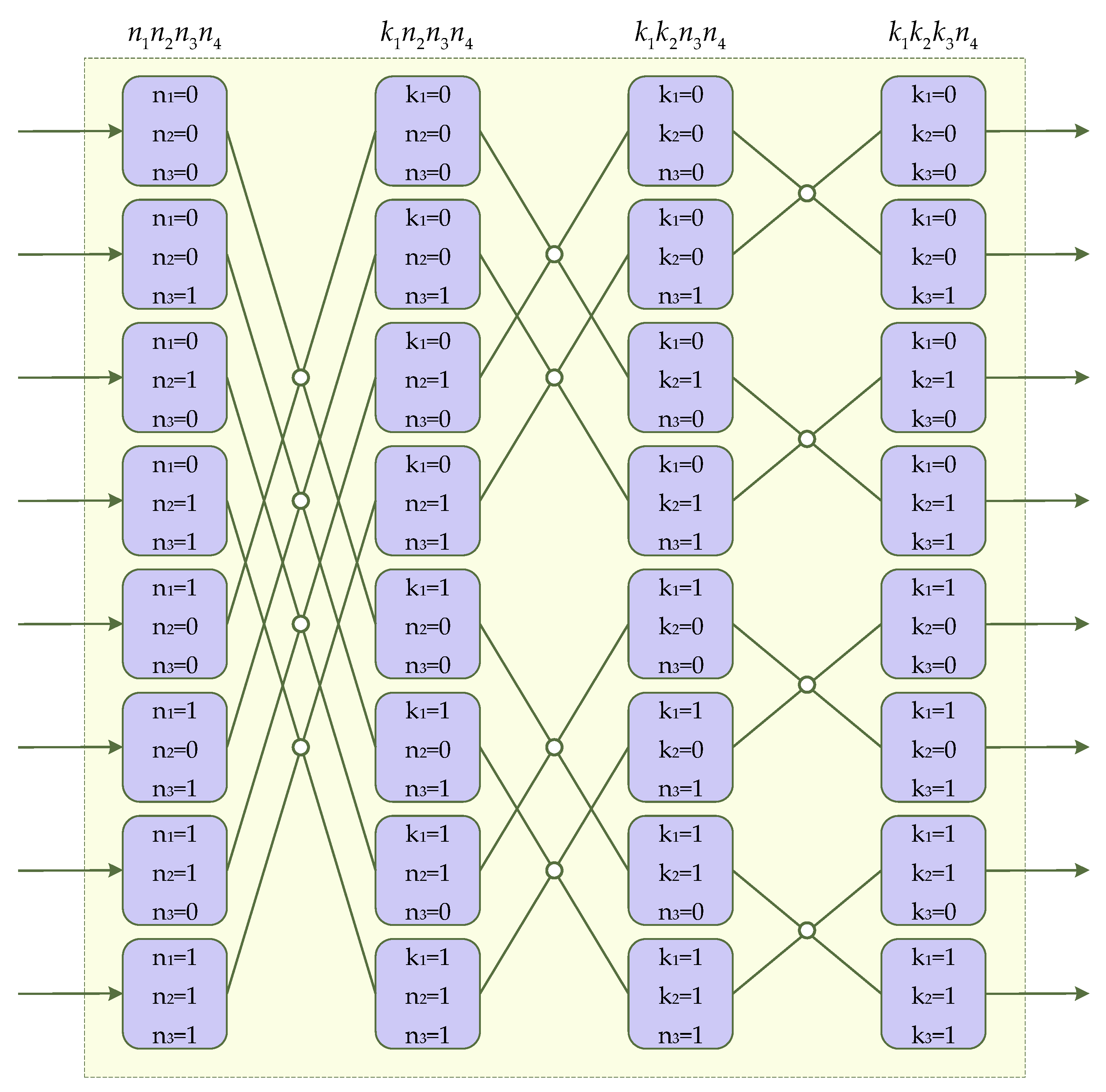
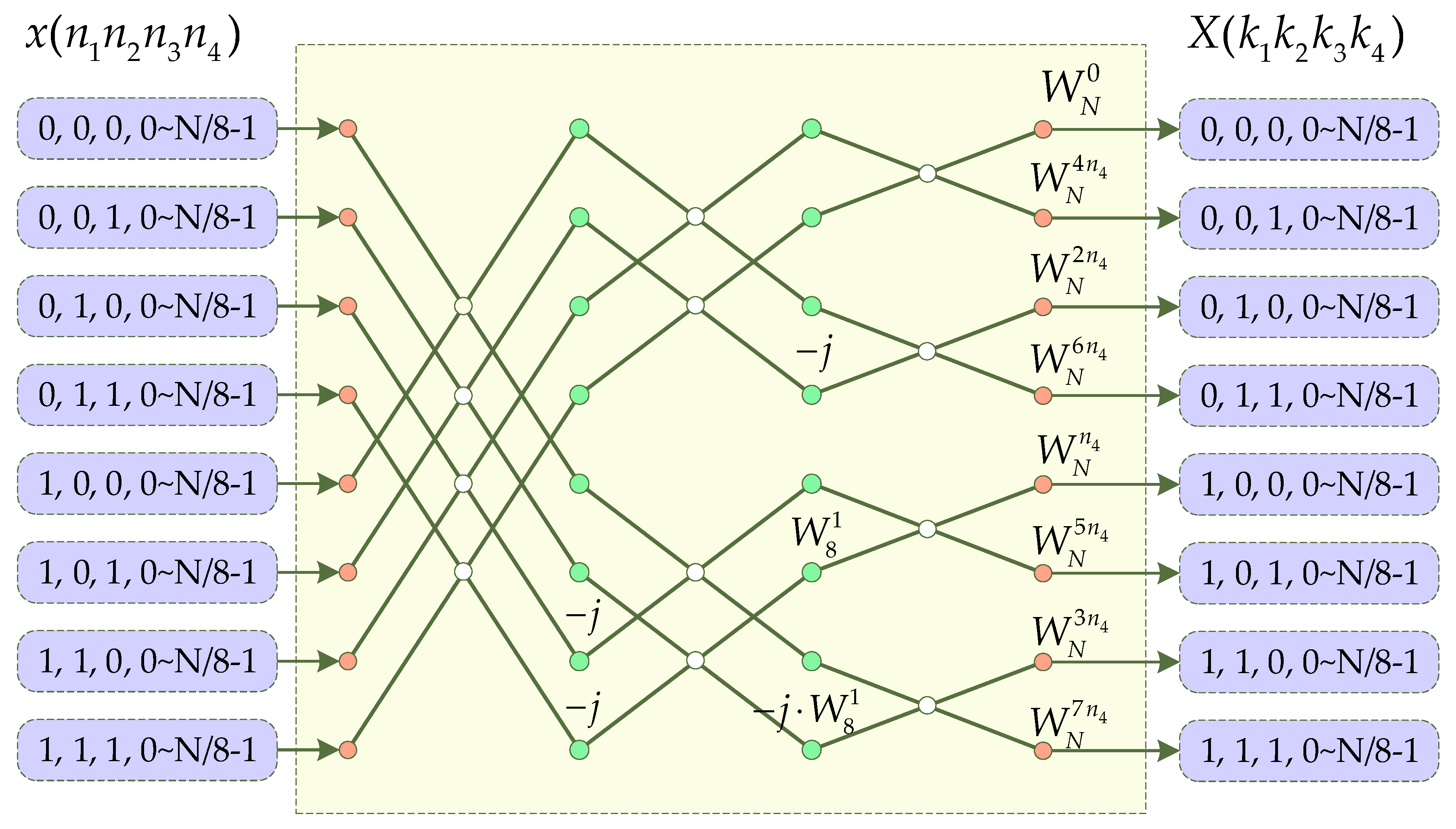
2.2. Introduction of the Radix-23 Algorithm
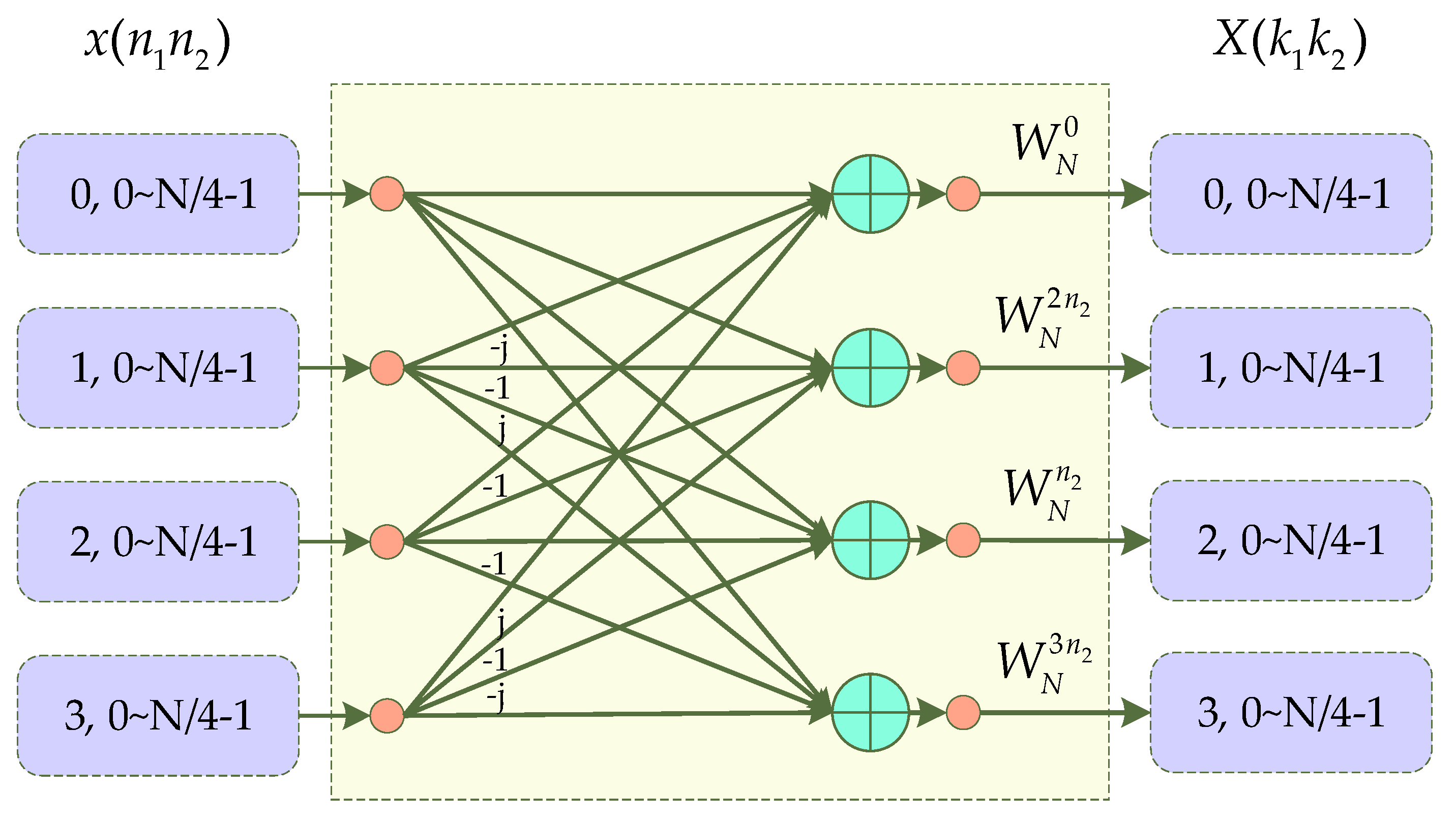
2.3. Introduction of Mixed-Radix Algorithm
3. Hardware Implementation of the FFT Processor
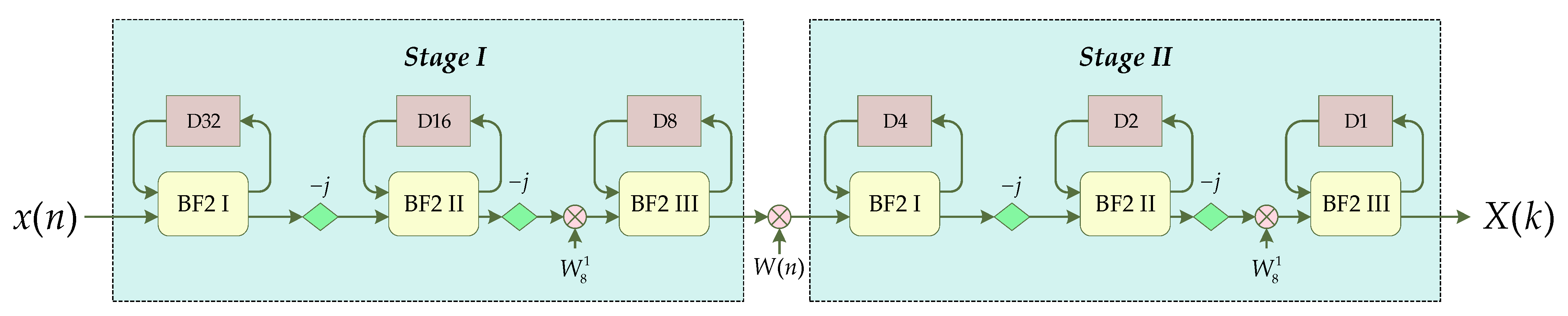
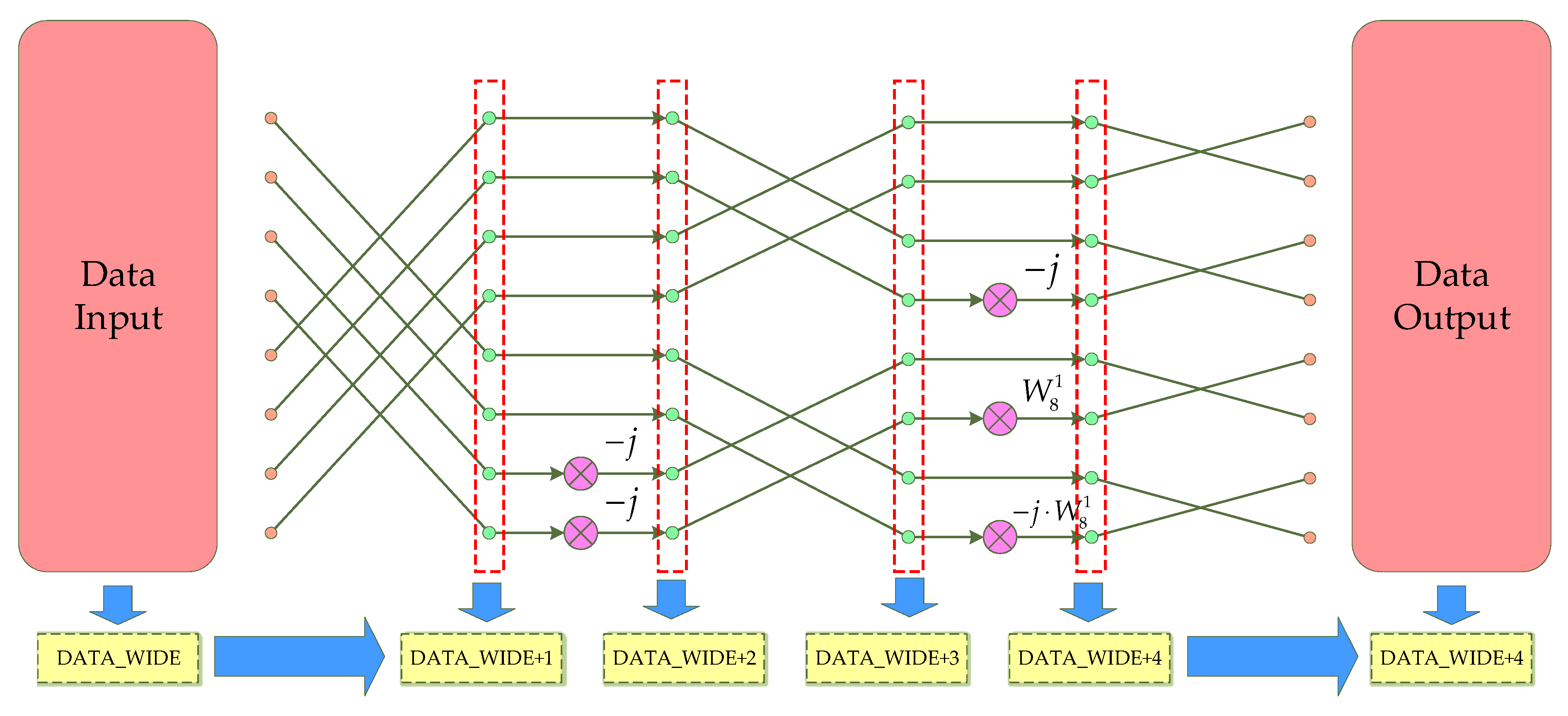
3.1. Implementation of the Radix-23 Algorithm under Single-Path Delay Feedback (SDF) Structure
3.2. Strategy of Fixed-Point FFT Word Length Adjustment
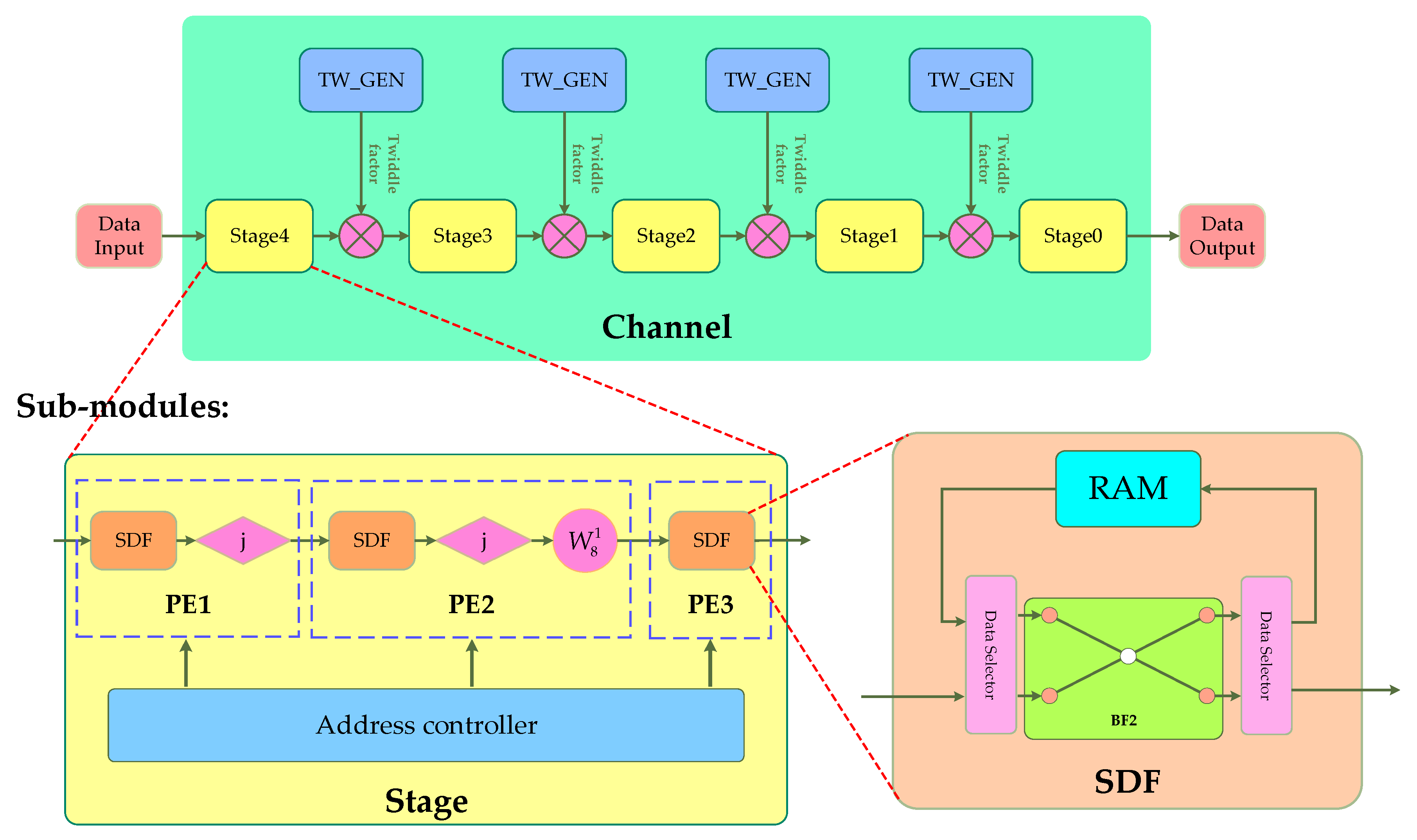
3.3. Single Channel FFT Processor Structure
- ⮚
- The radix-2 butterfly unit (BF2) realizes a complex butterfly operation, which contains logic circuits for the addition and subtraction of complex numbers.
- ⮚
- The data selector is used to determine the inflow and outflow direction of data, which contain address control logic to control RAM and work with the BF2.
- ⮚
- The SDF module implements a pipeline to receive input data, and a pipeline to output the data after the radix-2 butterfly calculation. The SDF module contains a piece of RAM, which can be easily implemented by calling the IP core Block Memory Generator.
- ⮚
- The processing unit modules (PE1, PE2, and PE3) are used to rotate the data in a specific direction after the SDF structure, that is, to multiply the factors −j and .
- ⮚
- The address controller is used to provide the three SDF structures with the address values of the current read and write operations on the RAM in each clock cycle, and indicate the current operation of the SDF structure on the RAM (cache the newly input data or cache the BF2 settlement result). The logic of the address controller is completely based on the sequence value of the current incoming time domain data, and therefore it can also be considered a data flow controller.
- ⮚
- The function of the operation–stage module (stage) is to complete the processing of data at an operation stage and output the results and their corresponding addresses in a pipeline.
- ⮚
- The TW_GEN module is used to generate the twiddle multiplication factor required for each clock to be used as the input of the non-constant factor multiplier. In this module, the CORDIC IP core in the FPGA needs to be called. The IP core is used to generate the sin(x) value and the cos(x) value when the input is x; the value of x can be summarized as Equation (11) using Equation (4) and Figure 4. We name the TW_GEN connected after Stage 4 as TW_GEN4, and so on. For Equation (11), the numerical change rule of each parameter in each TW_GEN module is shown in Table 5. Except for N, which is a fixed value, other values change in each clock cycle with the value in Table 5 using Equation (11) as follows:
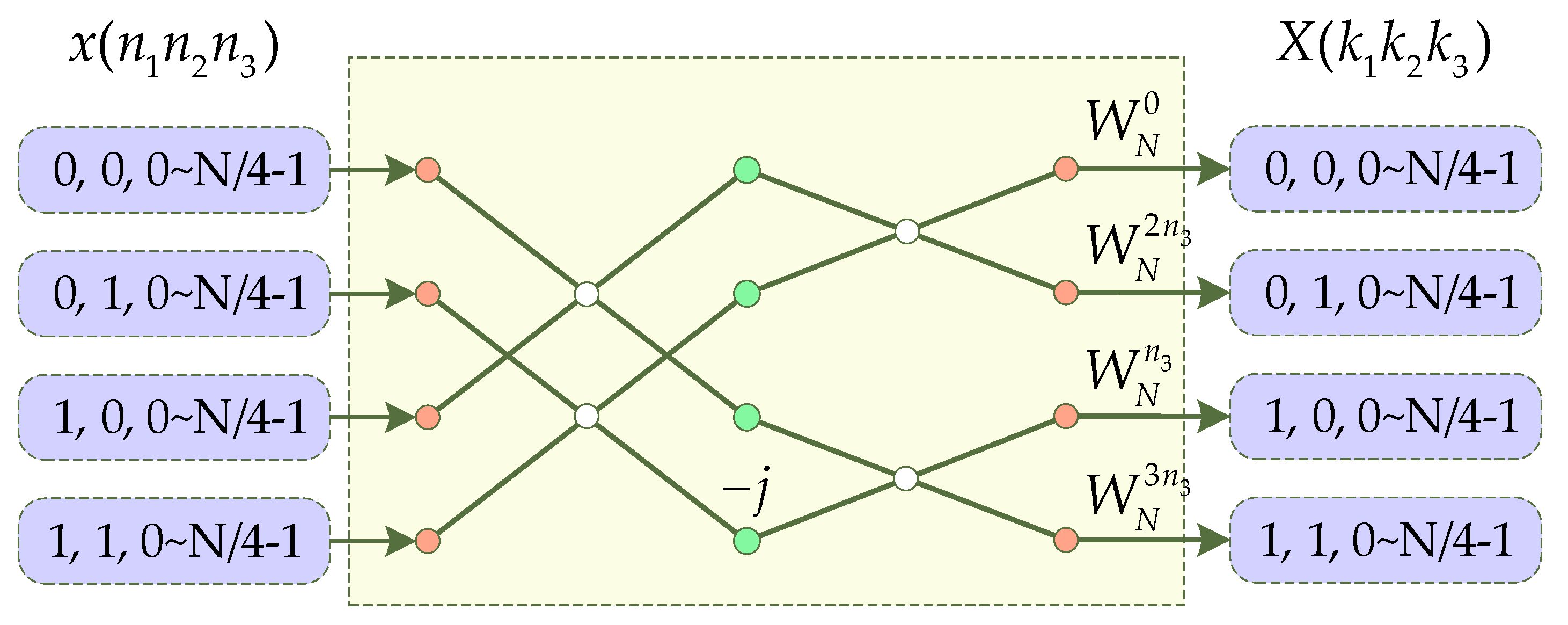
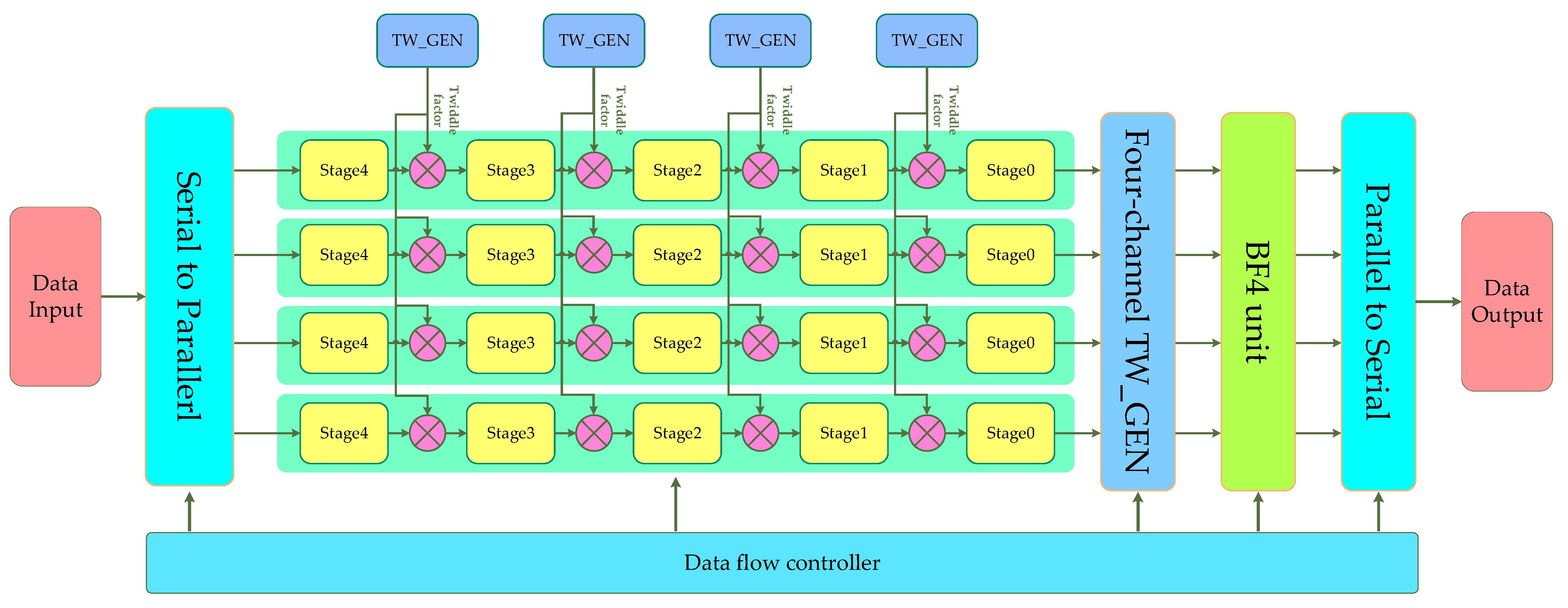
3.4. Four-Channel FFT Processor Structure
- ⮚
- The serial to parallel module is used to decompose the serial data from a single channel into four channels, which can be realized by a multiplexer. In order to ensure the synchronization of the four channels, a buffer unit needs to be set up so that the data of the four channels are sent at the same time. The decomposition rules are shown in Figure 13.
- ⮚
- The stage module and TW_GEN are identical to those in the single-channel structure. Since the structure of the four channels is identical, the required twiddle factor after the operation level at the same position is the same, so the four channels can share one TW_GEN after the same operation stage.
- ⮚
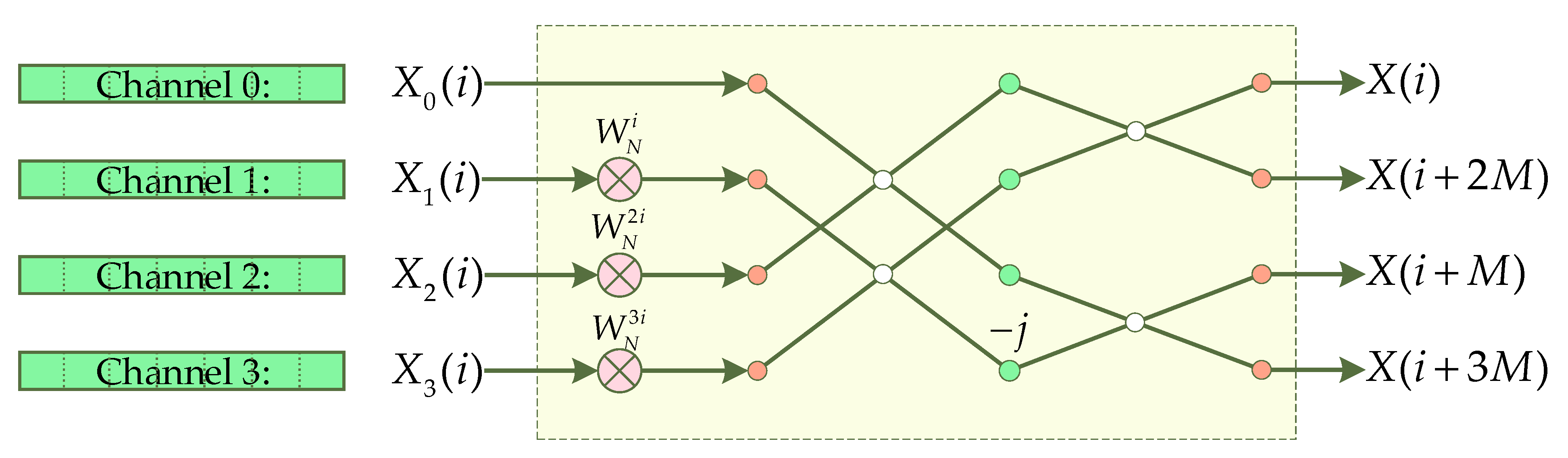
- The four-channel TW_GEN module is used to generate the twiddle factor in Figure 7, and three CORDIC IP cores need to be called for implementation. Four multipliers are provided in the four-channel TW_GEN module, which is different from the TW_GEN module.
- ⮚
- The R4 unit is used to implement the radix-4 algorithm, which integrates the data of the four channels and is implemented by logic circuits.
- ⮚
- The parallel-to-serial module is used to combine four channels of data into one channel, and its operation rules are opposite to those of the serial-to-parallel module and can be realized by register groups.
- ⮚
- The data flow controller is used to control the data flow in the processor. Its functions include the following: continue to input zero after the end of the data to drive the processor; provide operation addresses for the register groups in the serial-to-parallel module and parallel-to-serial module; provide the x value for the CORDIC core in all TW_GEN modules (including four-channel TW_GEN module), that is, there is no need to set the address controller in each TW_GEN module; and provide the operating address and instructions for the RAM provided in the SDF, and there is also no need to set the address controller separately in the SDF.
4. Experimental Evaluation and Results
4.1. Experimental Settings
4.1.1. Experimental Data Settings
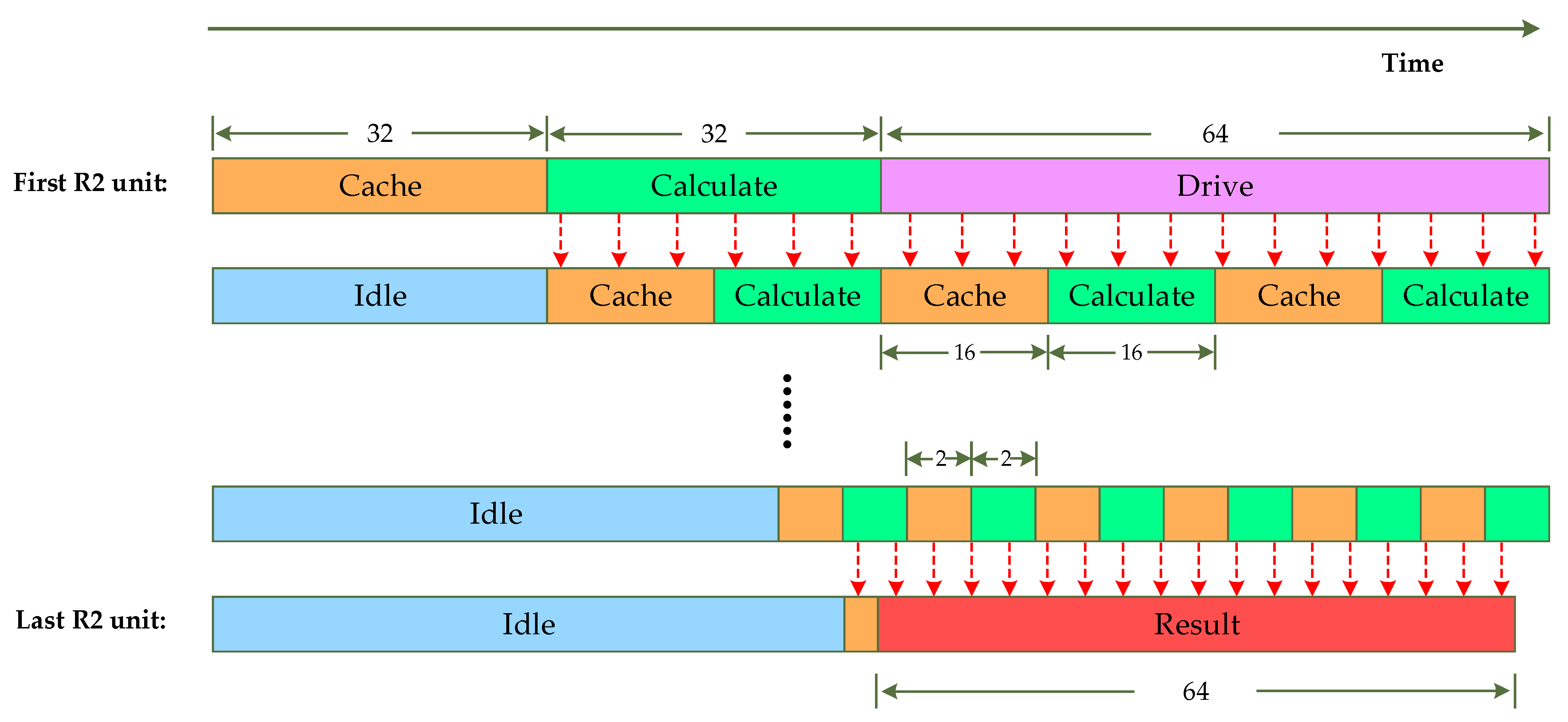
4.1.2. Experimental Procedure
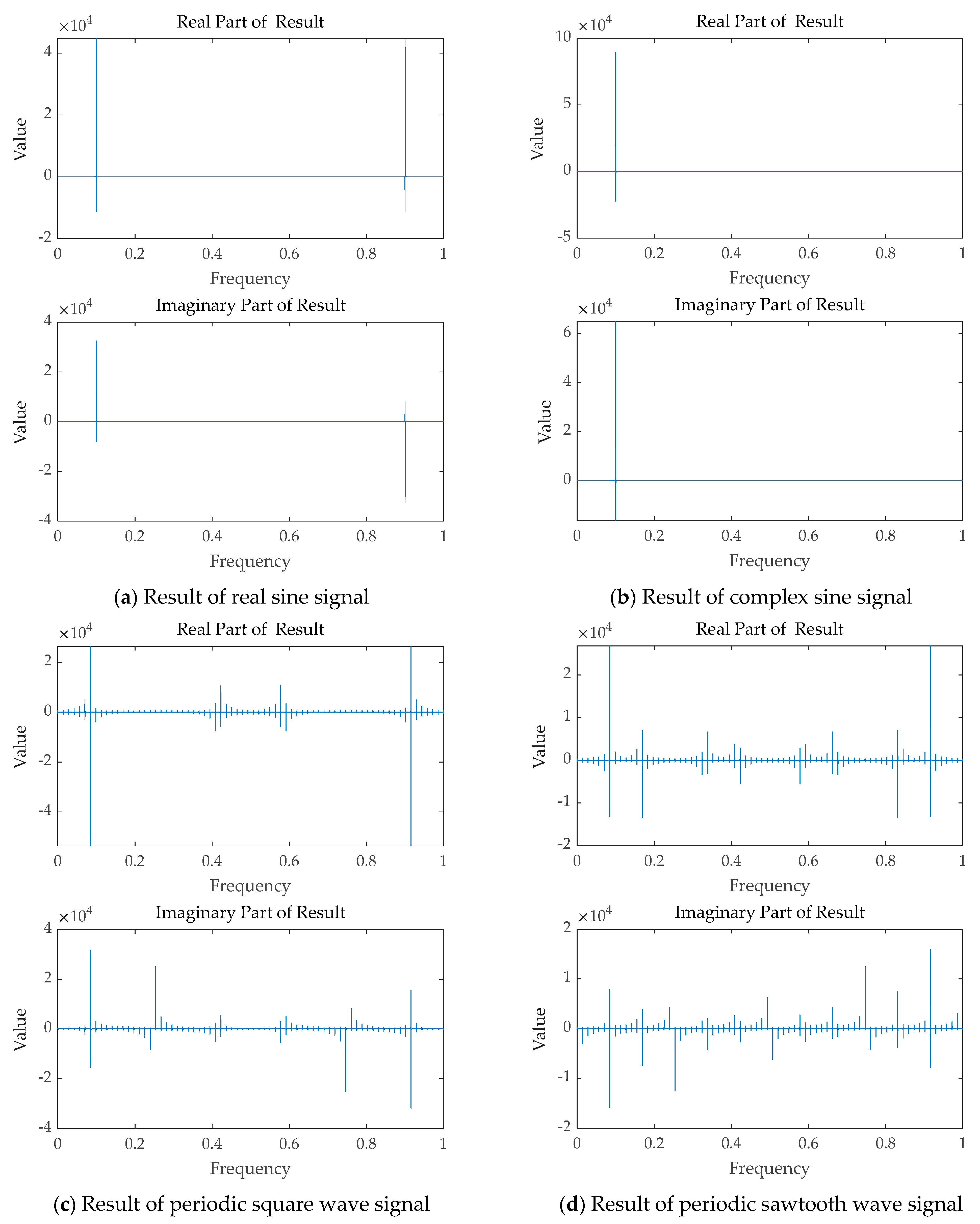
4.2. Performance Evaluation
4.3. Hardware Performance Comparison
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wu, C.; Liu, K.Y.; Jin, M. Modeling and a Correlation Algorithm for Spaceborne SAR Signals. IEEE Trans. Aerosp. Electron. Syst. 1982, AES-18, 563–575. [Google Scholar] [CrossRef]
- Raney, R.K.; Runge, H.; Bamler, R.; Cumming, I.G.; Wong, F.H. Precision SAR processing using chirp scaling. IEEE Trans. Geosci. Remote Sens. 1994, 32, 786–799. [Google Scholar] [CrossRef]
- Meng, J. Research on Vibration and Lever-Arm Effect Influence to Onboard SAR Centre Motion Parameters. In Proceedings of the 2011 Second International Conference on Digital Manufacturing & Automation, Zhangjiajie, China, 5–7 August 2011; pp. 1050–1054. [Google Scholar]
- Lou, Y.; Clark, D.; Marks, P.; Muellerschoen, R.J.; Wang, C.C. Onboard Radar Processor Development for Rapid Response to Natural Hazards. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 2770–2776. [Google Scholar] [CrossRef]
- Yan, X.; Chen, J.; Nies, H.; Yang, W.; Loffeld, O. Doppler Parameter Estimation Model Using Onboard Orbit Determination and Inter-satellite Distance Measurement for Spaceborne Bistatic SAR Real-time Imaging. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019; pp. 1–4. [Google Scholar]
- Seasat. Available online: https://en.wikipedia.org/wiki/Seasat (accessed on 11 February 2021).
- KOMPSAT 5 (Arirang 5). Available online: https://space.skyrocket.de/doc_sdat/kompsat-5.htm (accessed on 7 July 2020).
- PAZ SAR Satellite Mission of Spain. Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/p/paz (accessed on 1 January 2021).
- RCM (RADARSAT Constellation Mission). Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/r/rcm (accessed on 1 January 2021).
- China Launches Remote Sensing Satellite Yaogan-33. Available online: https://www.businesstoday.in/current/world/china-launches-remote-sensing-satellite-yaogan-33/story/426233.html (accessed on 29 December 2020).
- Capella X-SAR (Synthetic Aperture Radar) Constellation. Available online: https://directory.eoportal.org/web/eoportal/satellite-missions/content/-/article/capella-x-sar (accessed on 1 January 2021).
- Synthetic Aperture Radar Gets Boost From Small Satellites. Available online: https://www.csrwire.com/press_releases/708016-synthetic-aperture-radar-gets-boost-small-satellites (accessed on 13 November 2020).
- Suess, M.; Schaefer, C.; Zahn, R. Discussion of the introduction of on-board SAR data processing to spaceborne SAR instruments. In Proceedings of the IGARSS 2000—IEEE 2000 International Geoscience and Remote Sensing Symposium. Taking the Pulse of the Planet: The Role of Remote Sensing in Managing the Environment, Proceedings (Cat. No.00CH37120), Honolulu, HI, USA, 24–28 July 2000; Volume 5, pp. 2331–2333. [Google Scholar]
- Green, R.C.; Wang, L.; Alam, M. Applications and Trends of High Performance Computing for Electric Power Systems: Focusing on Smart Grid. IEEE Trans. Smart Grid 2013, 4, 922–931. [Google Scholar] [CrossRef]
- Hu, W.; Zhang, Y.; Fu, J. An introduction to CPU and DSP design in China. Sci. China Inf. Sci. 2016, 59, 1–8. [Google Scholar] [CrossRef]
- ASIC or FPGA? Each Solution Has Advantages and Disadvantages. Available online: https://www.swindonsilicon.com/asic-fpga-advantages-and-disadvantages/ (accessed on 12 October 2018).
- Ploeg, A.V.D. Why Use an FPGA Instead of a CPU or GPU? Available online: https://blog.esciencecenter.nl/why-use-an-fpga-instead-of-a-cpu-or-gpu-b234cd4f309c (accessed on 14 August 2018).
- Paek, S.W.; Balasubramanian, S.; Kim, S.; De Weck, O. Small-Satellite Synthetic Aperture Radar for Continuous Global Biospheric Monitoring: A Review. Remote Sens. 2020, 12, 2546. [Google Scholar] [CrossRef]
- Fu, W.; Ma, J.; Chen, P.; Chen, F. Remote Sensing Satellites for Digital Earth. In Manual of Digital Earth; Guo, H., Goodchild, M.F., Annoni, A., Eds.; Springer: Singapore, 2020; pp. 55–123. [Google Scholar]
- Zhou, X.; Xie, Y.; Yang, C.; Du, Q.; Deng, Y. Fixed-point simulation technology for SAR real-time imaging system. In Proceedings of the IET International Radar Conference 2015, Hangzhou, China, 14–16 October 2015; pp. 1–5. [Google Scholar]
- Palsodkar, P.; Gurjar, A. Improved fused floating point add-subtract and multiply-add unit for FFT implementation. In Proceedings of the 2014 2nd International Conference on Devices, Circuits and Systems (ICDCS), Coimbatore, India, 6–8 March 2014; pp. 1–5. [Google Scholar]
- Chen, J.; Lei, Y.; Peng, Y.; He, T.; Deng, Z. Configurable floating-point FFT accelerator on FPGA based multiple-rotation CORDIC. Chin. J. Electron. 2016, 25, 1063–1070. [Google Scholar] [CrossRef]
- Prabhu, E.; Mangalam, H.; Karthick, S. Design of area and power efficient Radix-4 DIT FFT butterfly unit using floating point fused arithmetic. J. Cent. South Univ. 2016, 23, 1669–1681. [Google Scholar] [CrossRef]
- Shaditalab, M.; Bois, G.; Sawan, M. Self-sorting radix-2 FFT on FPGAs using parallel pipelined distributed arithmetic blocks. In Proceedings of the IEEE Symposium on FPGAs for Custom Computing Machines (Cat. No.98TB100251), Napa Valley, CA, USA, 17 April 1998; pp. 337–338. [Google Scholar]
- Sun, Z.; Liu, X.; Ji, Z. The Design of Radix-4 FFT by FPGA. In Proceedings of the 2008 International Symposium on Intelligent Information Technology Application Workshops, Shanghai, China, 21–22 December 2008; pp. 765–768. [Google Scholar]
- Chandu, Y.; Maradi, M.; Manjunath, A.; Agarwal, P. Optimized High Speed Radix-8 FFT Algorithm Implementation on FPGA. In Proceedings of the 2018 2nd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, 11–12 May 2018; pp. 430–435. [Google Scholar]
- Santhosh, L.; Thomas, A. Implementation of radix 2 and radix 22 FFT algorithms on Spartan6 FPGA. In Proceedings of the 2013 Fourth International Conference on Computing, Communications and Networking Technologies (ICCCNT), Tiruchengode, India, 4–6 July 2013; pp. 1–4. [Google Scholar]
- Tang, J.; Li, X.; Zhang, G.; Lai, Z. Design of high-throughput mixed-radix MDF FFT processor for IEEE 802.11.3c. In Proceedings of the 2012 IEEE 11th International Conference on Solid-State and Integrated Circuit Technology, Xi’an, China, 29 October–1 November 2012; pp. 1–3. [Google Scholar]
- Chen, Y.; He, C. A efficient design of a real-time FFT architecture based on FPGA. In Proceedings of the IET International Radar Conference, Xi’an, China, 14–16 April 2013; pp. 1–5. [Google Scholar]
- Cumming, I.; Wong, F.; Raney, K. A SAR Processing Algorithm with No Interpolation. In Proceedings of the IGARSS′92 International Geoscience and Remote Sensing Symposium, Houston, TX, USA, 26–29 May 1992; pp. 376–379. [Google Scholar]
- Yang, C.; Xie, Y.; Chen, L.; Chen, H.; Deng, Y. Design of a configurable fixed-point FFT processor. In Proceedings of the IET International Radar Conference, Hangzhou, China, 14–16 October 2015; pp. 1–4. [Google Scholar]
- Zhou, J.; Dong, Y.; Dou, Y.; Lei, Y. Dynamic Configurable Floating-Point FFT Pipelines and Hybrid-Mode CORDIC on FPGA. In Proceedings of the 2008 International Conference on Embedded Software and Systems, Chengdu, China, 29–31 July 2008; pp. 616–620. [Google Scholar]


| Satellite Name | Country | Launch Time | Working Mode and Resolution |
|---|---|---|---|
| ERS-1 | ESA | 1991 | Stripmap mode, 20 m |
| ALOS | Japan | 2006 | Spotlight mode, 2.5 m |
| Yaogan14 | China | 2012 | Spotlight mode, 0.5 m |
| KOMPSat-5 | Korea | 2013 | Spotlight mode, 1 m Strip mode, 3 m Scan mode, 10 m |
| ALOS-2 | Japan | 2014 | Spotlight mode, 1 × 3 m Stripmap mode, 3/6/10 m Scan model, 100 m |
| Paz | Spain | 2016 | Spotlight mode, 2 m Stripmap mode, 6 m Scan model, 15 m |
| Capela1 | USA | 2018 | Spotlight mode, 0.3–1 m |
| RCM 1, 1, 2 | Canada | 2019 | Spotlight mode, 1–1.3 m |
| Capella 2, 3, 4 | USA | 2021 | Spotlight mode, 0.3–1 m |
| Step | Number of Multiplication | Number of Addition | Number of Computation |
|---|---|---|---|
| Step 1 | |||
| Step 3 | |||
| Step 5 | |||
| Step 7 | |||
| Total |
| Step | Number of Multiplication | Number of Addition | Number of Computation |
|---|---|---|---|
| Step 2 | |||
| Step 4 | |||
| Step 6 | |||
| Total |
| Algorithm | Occupancy for Multiplier | Occupancy for Memory | Occupancy for Butterfly Unit |
|---|---|---|---|
| R-2 SDF | |||
| R-4 SDF | |||
| R-23 SDF |
| Parameter | TW_GEN4 | TW_GEN3 | TW_GEN2 | TW_GEN1 |
|---|---|---|---|---|
| 32,758 | 4096 | 512 | 64 | |
| 0, 1, 2, …, 4095 | 0, 1, 2, …, 511 | 0, 1, 2, …, 63 | 0, 1, 2, …, 7 | |
| 0, 4, 2, 6, 1, 5, 3, 7 | 0, 4, 2, 6, 1, 5, 3, 7 | 0, 4, 2, 6, 1, 5, 3, 7 | 0, 4, 2, 6, 1, 5, 3, 7 |
| Name of Test Signal | Function Expressions of Test Signal |
|---|---|
| Real sine signal | |
| Complex sine signal | |
| Periodic square wave signal | |
| Periodic sawtooth signal |
| Real Sine Signal | Complex Sine Signal | Square Save Signal | Sawtooth Wave Signal | |
|---|---|---|---|---|
| 32-bit Fixed-point | 1.84 × 10−4 | 6.05 × 10−4 | 4.18 × 10−4 | 3.05 × 10−4 |
| Single-precision Floating-point | 1.25 × 10−4 | 5.1 × 10−4 | 4.8 × 10−4 | 2.2 × 10−4 |
| Proposed | Pipelined | Radix-4 | Radix-2 | Radix-2 Lite | |
|---|---|---|---|---|---|
| Transform cycles | 131,218 | 131,284 | 262,367 | 655,741 | 1,179,691 |
| Our Design | Xilinx IP | [29] | [31] | [32] | |
|---|---|---|---|---|---|
| Transform length | 128k | 64k | 256 | 1024 | 4k |
| Data type | 32-bit fixed | 32-bit fixed | 24-bit fixed | 16-bit fixed | 32-bit floating |
| Transform cycles | 131,218 | 131,284 | 298 | 48 | - |
| Slice LUTs | 39,519 | 11,182 | 6043 | 5174 | 44,071 |
| BRAM Tiles | 282 | 147.5 | 8 | 4 | 179 |
| DSPs | 146 | 102 | 24 | 16 | 200 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Chen, H.; Xie, Y. An FPGA-Based Four-Channel 128k-Point FFT Processor Suitable for Spaceborne SAR. Electronics 2021, 10, 816. https://doi.org/10.3390/electronics10070816
Li Y, Chen H, Xie Y. An FPGA-Based Four-Channel 128k-Point FFT Processor Suitable for Spaceborne SAR. Electronics. 2021; 10(7):816. https://doi.org/10.3390/electronics10070816
Chicago/Turabian StyleLi, Yongrui, He Chen, and Yizhuang Xie. 2021. "An FPGA-Based Four-Channel 128k-Point FFT Processor Suitable for Spaceborne SAR" Electronics 10, no. 7: 816. https://doi.org/10.3390/electronics10070816
APA StyleLi, Y., Chen, H., & Xie, Y. (2021). An FPGA-Based Four-Channel 128k-Point FFT Processor Suitable for Spaceborne SAR. Electronics, 10(7), 816. https://doi.org/10.3390/electronics10070816





