PD-Type Iterative Learning Control with Adaptive Learning Gains for High-Performance Load Torque Tracking of Electric Dynamic Load Simulator

Abstract

To realize the high-performance load torque tracking of an electric dynamic load simulator system with random measurement noises and strong position disturbances, a PD-type iterative learning control (ILC) algorithm with adaptive learning gains is proposed in this paper. With the principle of system analyzing, a nonlinear discrete state-space model is established. The adaptive learning gains is used to suppress the effects of periodic disturbances and random measurement noises on the load torque tracking performance. A traditional PD feedback controller in parallel with the proposed ILC is designed to stabilize the system and render the ILC converge quickly. The convergence analysis of the proposed control method ensures the stability of the system. Compared with the fixed learning gains, the experiment results show that the proposed control method has better load torque tracking performance and can effectively suppress the adverse effects of periodic and aperiodic disturbances on tracking accuracy.

1. Introduction

In recent years, with the development of more electric aircraft (MEA) technology, many actuators of medium and large unmanned aerial vehicle (UAV) have been gradually replaced by an electromechanical actuator (EMA), which can eliminate the hydraulic mechanism, reduce weight, and simplify the system structure [1,2,3]. The electrical dynamic load simulator (EDLS) is an important piece of equipment for testing the EMA [4,5,6], which can accurately simulate the alternating load characteristics and effectively test the dynamic and static performance of the EMA.

The EDLS is a passive torque servo system with strong motion disturbance [7]. Nonlinear factors, such as inertia, friction, backlash, elastic deformation, and random measurement noises, can be summarized as periodic and aperiodic disturbances of the system. It is difficult to ensure the synchronous movement of the loading motor and EMA, and the active movement of the EMA will lead to surplus torque in the system [8]. The existence of surplus torque seriously affects the accuracy of torque loading and reduces the sensitivity and stability of EDLS. Therefore, the vital problem to ensure the performance of EDLS is to realize the suppression of surplus torque [6].

Scholars have proposed many advanced control strategies to eliminate the surplus torque of EDLS. The existing control strategies mainly include feed-forward compensation based on position or speed [9], adaptive neural network compensation method [10], adaptive robust control [7], novel robust control [11], proportional resonance (PR) control [6], iterative learning control (ILC) [12], etc. Jiao et al. [13] proposed a compensation control strategy based on the structure invariance principle to eliminate the surplus torque, but this method requires an accurate system model. There are unknown nonlinearity and time-varying parameters in the actual system, which makes it difficult to achieve the ideal control effect. In [5], Li et al. developed a new high-performance control scheme based on neural networks and a linear difference inclusion model to deal with the nonlinear factors and external disturbance of EDLS. Using H∞ performance criterion and parallel distributed compensation, the external disturbances can be attenuated, and the load torque reference can be completely tracked. In [6], Wang et al. proposed a PR-based loading control strategy for EDLS to effectively eliminate surplus torque and track sinusoidal curves with high precision. Yang et al. [14] proposed a robust hybrid control law containing a proportional–derivative (PD) controller and a novel cerebellar model articulation controller (CMAC). The control algorithm is easy to implement, which improves the approximation accuracy and capability of EDLS to sinusoidal signals, and eliminates surplus torque. However, the lack of theoretical guidance in the design of CMAC network structure makes it difficult to be popularized and applied. Although these controllers mentioned above have improved the load torque tracking accuracy of EDLS to some extent, there are still some limitations. For example, the controller structure is complex, and it is difficult to apply in practical engineering and hard to completely eliminate surplus torque.

Iterative learning control was proposed by Arimoto et al. [15] in 1984, and it has been widely studied and applied since then [16]. The ILC has advantages of being a simple algorithm, having good convergence performance, and being independent of the precise mathematical model of the controlled plant. It has been well applied to the control system with periodic and repetitive motion characteristics. Wang et al. [17] explored an ILC strategy based real-time recurrent neural networks (RTRNN) to make the EDLS track any desired load torque with high accuracy. Wang et al. proposed a compound torque controller based on the ILC and EMA position feed-forward compensation. The ILC is used to restrain the influence of surplus torque, and the feed-forward compensator combined with a traditional load torque feedback controller ensures torque tracking performance. However, most of the existing EDLS control strategies based on ILC are parallel with the traditional feedback controller. The traditional ILC controller is very sensitive to random measurement noise and aperiodic disturbances, which makes it difficult to ensure high accuracy.

In order to improve the tracking accuracy of load torque and eliminate the influence of surplus torque and other aperiodic disturbances on the system, this paper presents a novel control algorithm, combining a traditional PD feedback controller with a PD-type ILC with adaptive learning gains (PDILC-ALG) [18]. The proposed feedback controller can be used to stabilize the system so that the output of the system does not deviate too far from the expected trajectory [19], so as to ensure that the iterative learning controller can realize the tracking task quickly. The learning gains of the PD-type ILC are adjusted according to the system errors and errors rate to reduce the influence of random measurement noise on the system performance. Also, the ILC is used to improve the tracking accuracy even though the system has modeled and unmolded periodic disturbances.

This paper is organized as follows. Following the introduction, Section 2 describes the subsection system architecture and the discrete state-space model of the studied EDLS system. Section 3 presents the design and theoretical analysis of the EDLS controller based on the PD-type ILC with adaptive learning gains and the traditional PD feedback controller. Section 4 shows the experimental results that demonstrate the effectiveness of the proposed control scheme. Finally, Section 5 draws conclusions.

2. Dynamic Model of Electric Dynamic Load Simulator

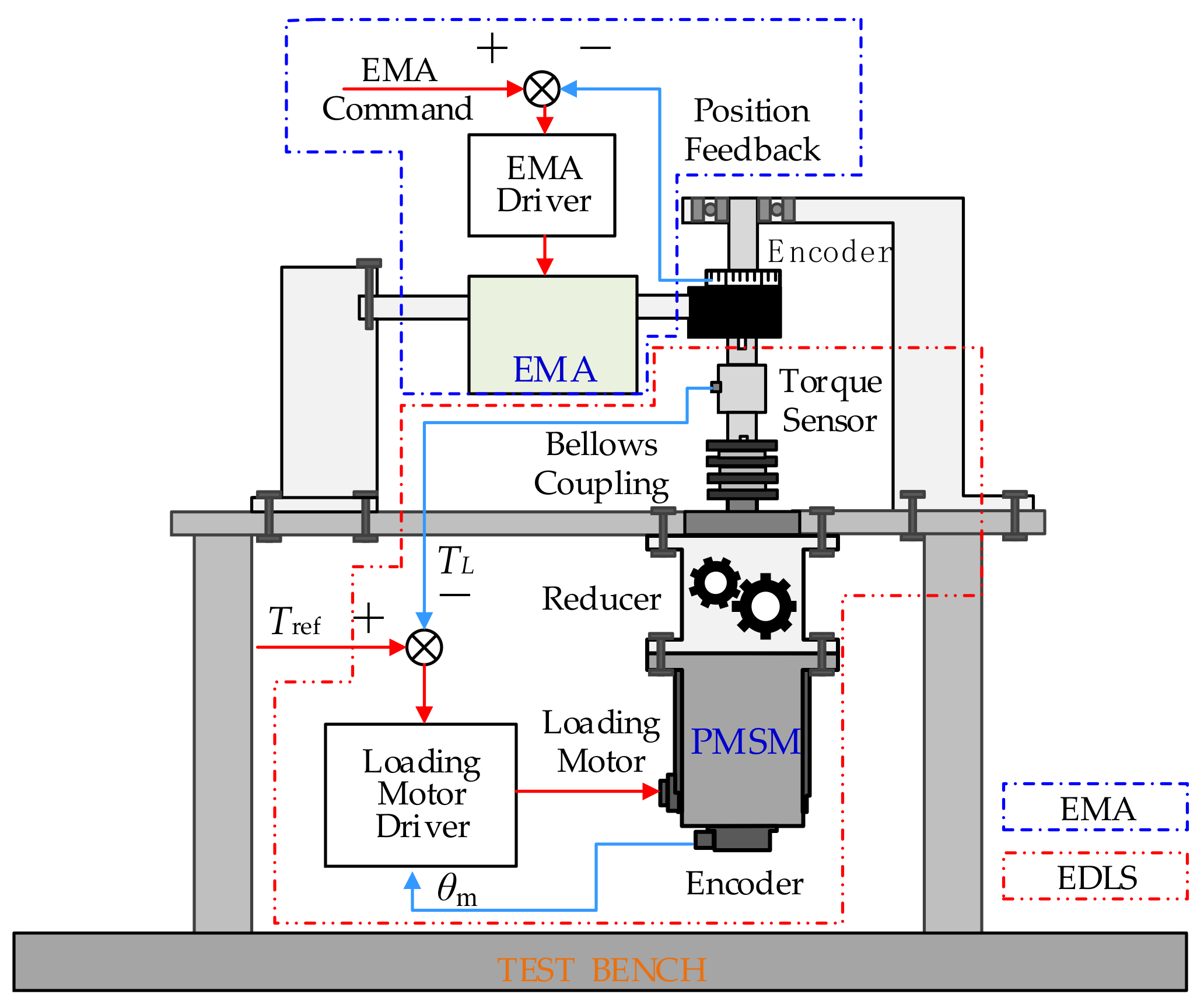
2.1. Subsection System Architecture of Electric Dynamic Load Simulator

The arrangement of the considered EDLS in this paper used to simulate the dynamic load torque of EMA is presented in Figure 1. The mechanical structure of the EDLS system can be divided into two major parts according to different functions: one is the EMA under test worked in a position servo mode treated as the position servo system, and the other is the EDLS, consisting of a permanent magnet synchronous motor (PMSM) and its driver system treated as a torque servo system. As shown in Figure 1, the EDLS system consists of a servo motor, a reducer, two encoders, and the loaded EMA servo system. As the driving element of the EDLS, the PMSM is connected with a reducer, the torque sensor, and the loaded EMA through the coupling. The reducer is used to magnify the electromagnetic torque output of the PMSM to achieve large mechanical torque output. The torque sensor measures the torque signal on the transmission mechanism and transmits it to the control equipment to form a torque feedback loop.

2.2. Mathematical Model of Electric Dynamic Load Simulator

The loading motor (PMSM) generates the dynamic load torque applied to the EMA under test. Since the direct torque control (DTC) technique has high dynamic torque response and excellent speed control characteristics, the DTC scheme is adopted to PMSM drives to obtain the load torque with small time delay, high dynamic, and high reliability [20]. In normal conditions, EDLS operates within 10 Hz, while the electromagnet torque of PMSM is updated at up to 4 KHz. Therefore, the driver of the PMSM loading motor can be modeled as an ideal electromagnetic torque generator. The dynamic characteristics of the PMSM driver can be neglected in practice. Thus, the input–output relationship of the control input $u(t)$ versus the output electromagnetic torque $T_e(t)$ is given by [7]:

$$T_e(t)=K_{m}u(t)$$

(1)

where $K_m$ is the equivalent gain of the PMSM driver.

According to the torque balance principle, the mechanical dynamic model of the PMSM is described as follows [7]:

$$T_e(t)=J_m\frac{d{\omega }_m}{dt}+B_m{\omega }_m+\frac{T_L}{n_g}+T_d$$

(2)

$${\omega }_m(t)=\frac{d{\theta }_m(t)}{dt}$$

(3)

where ${\theta }_m$ and ${\omega }_m$ are the rotation angle and angular velocity of PMSM, respectively. $J_m$ is the total moment inertia of realized at PMSM, $B_m$ is the viscosity coefficient, $T_L$ represents the simulated load torque of EMA under test, $n_g$ is the reduction ratio of the reducer, and $T_d$ represents the lumped disturbance torque caused by frictions, backlash, etc.

A torque sensor mounted on the drive shaft is used to measure the transmission and load torque. According to Hooke’s law, the mathematical model of the torque sensor is given by:

$$T_L(t)=K_G(\frac{{\theta }_m}{n_g}-{\theta }_a)$$

(4)

where $K_G$ is the stiffness coefficient of the torque sensor, ${\theta }_a$ is the angular position of EMA. Differentiating Equation (4), the dynamic of the torque sensor can be obtained as follows:

$$\frac{d}{dt}{T}_L(t)=K_G(\frac{{\omega }_m}{n_g}-{\omega }_a)$$

(5)

where ${\omega }_a$ denotes the angular velocity of EMA.

Based on the above analysis, select the load torque $T_L$ and angular velocity ${\omega }_m$ of PMSM as state states, i.e., $x(t)={[x_1(t),x_2(t)]}^{\mathrm{T}}={[T_L(t),{\theta }_m(t)]}^{\mathrm{T}}$. Define $\eta (t)$ as the random measurement noise of torque sensor. By combining Equations (1), (2), (4) and (5), the dynamics of the EDLS can be described by the following state space.

$$\left\{\begin{array}{c}{\dot{x}}_1(t)=K_G(\frac{1}{n_g}{x}_2(t)-{\omega }_a)\\ {\dot{x}}_2(t)=-\frac{1}{J_m{n}_g}{x}_1(t)-\frac{B_m}{J_m}{x}_2(t)+\frac{K_m}{J_m}u(t)-\frac{1}{J_m}{T}_d\\ y(t)=x_1(t)+\eta (t)\end{array}\right.$$

(6)

Equation (6) can be rewritten as:

$$\left\{\begin{array}{c}\dot{x}(t)=Ax(t)+Bu(t)+Ed\\ y(t)=Cx(t)+\eta (t)\end{array}\right.$$

(7)

where $A=\left[\begin{array}{cc}0& \frac{K_G}{n_g}\\ -\frac{1}{J_m{n}_g}& -\frac{B_m}{J_m}\end{array}\right]$, $B=\left[\begin{array}{c}0\\ \frac{K_m}{J_m}\end{array}\right]$, $E=\left[\begin{array}{c}-K_G\\ -\frac{1}{J_m}\end{array}\right]$, $d=\left[\begin{array}{c}{\omega }_a(t)\\ T_d(t)\end{array}\right]$, $C=\left[\begin{array}{cc}1& 0\end{array}\right]$.

In general, the control algorithms of an EDLS are implemented using digital microcomputers and are formulated as a discrete-time system. The controller that should be designed needs a discrete-time model of the EDLS, thus requiring the use of Tustin’s discretization method [21], and $h$ is the sample period. The discrete model of the EDLS can be described as follows:

$$\left\{\begin{array}{c}x(i+1)={(I-\frac{h}{2}A)}^{-1}[(I+\frac{h}{2}A)x(i)+hBu(i)+hEd(i)]\\ y(i)=Cx(i)+\eta (i)\end{array}\right.$$

(8)

where i is an integer that denotes the discrete time step index, $x(i+1)$ is the value of $x$ at $(i+1)h$ and $x(i)$ is the value of $x$ at $ih$. $u(i)$, $d(i)$, $y(i)$, and $\eta (i)$ denote the value of $u$, $d$, $y$, and $\eta$ at $ih$, respectively. $I$ is an identify matrix of appropriate dimension.

With reference to Equation (8), define the following state space matrices.

$$A_d={(I-\frac{h}{2}A)}^{-1}(I+\frac{h}{2}A)$$

(9)

$$B_d={(I-\frac{h}{2}A)}^{-1}hB$$

(10)

$$E_d={(I-\frac{h}{2}A)}^{-1}hE$$

(11)

$$C_d=C$$

(12)

Then, the discrete model of the EDLS described by Equation (8) can be rewritten as:

$$\left\{\begin{array}{c}x(i+1)=A_{d}x(i)+B_{d}u(i)+E_{d}d(i)\\ y(i)=C_{d}x(i)+\eta (i)\end{array}\right.$$

(13)

Obviously, system states are adjusted by the electromagnetic torque of the loading motor, which is driven by a PMSM under DTC. It can also be seen from Equation (13) that the system states will be strongly affected by the angular velocity of the loaded EMA system. The active movement of the EMA is the main factor that generates surplus torque, so the angular velocity of EMA can be regarded as the strong motion disturbance of the EDLS system. Given a bounded periodical load torque trajectory $T_{ref}(t)$, the objective of this paper is to design a input torque command $u(t)$ for the PMSM driver so that the output load torque $T_L(t)$ tracks $T_{ref}(t)$ as closely as possible despite the strong motion disturbance, random measurement noise of the torque sensor, and other aperiodic disturbances. The development of the load torque controller will be proposed in the following section.

3. Controller Design for Electric Dynamic Load Simulator

As mentioned previously, the EDLS system is a typical multivariate system with a variety of disturbances. For an EDLS that performs the same load torque tracking task multiple times, the primary task of controller design is to provide control signals to the actuator accurately, so as to achieve high-performance tracking of the desired trajectory. The traditional ILC scheme can achieve the desired high-performance tracking within a finite interval despite the existence of repeated disturbances, such as the strong motion disturbance induced by EMA and unmolded periodic dynamics in the system. However, the traditional ILC scheme is difficult to deal with the random measurement noise without repeated characteristics. In order to obtain high performance for repetitive loading torque tracking of an EDLS with uncertainties, measurement noise, and periodic external disturbances, a novel PD-type ILC with adaptive learning gains combined with a PD feedback controller is proposed in this paper.

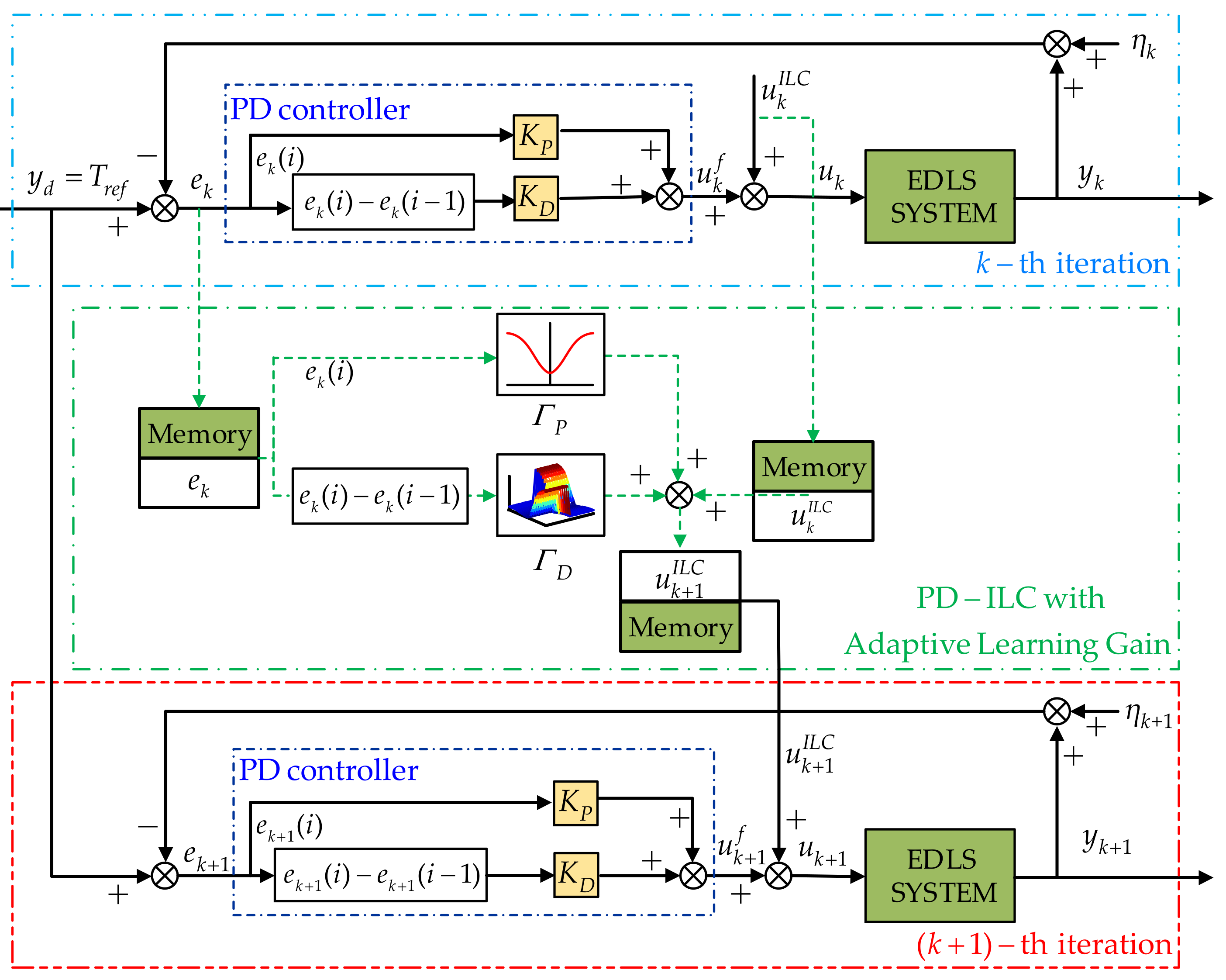
3.1. The Framework of PD-Type Iterative Learning Control Law with Adaptive Learning Gains

The ILC uses the input signals and error signals gained from previous iterations to continuously correct the inaccurate control signals, so as to get an appropriate control input that can achieve the desired tracking performance from trail-to-trail [22]. However, the conventional PD-type ILC with fixed learning gains can hardly deal with the aperiodic measurement noise of a nonlinear system [23]. In order to improve the torque tracking performance of the EDLS, the schematic diagram of proposed controller is shown in Figure 2.

The following notations are used; see also Figure 2: the proposed learning control algorithm is a PD-type ILC with adaptive learning gains and the feedback controller is a traditional PD controller. The subscript $k$ indicates the present iteration with $k\in \left\{0,1,2,\cdots \right\}$; $i$ is the time index and $i\in \{0,1,\dots ,N\}$, where $(N+1)$ is the number of discrete time steps in each iteration; $y_d=T_{ref}$ is the desired periodical loading torque trajectory; $e_k$ and $y_k$ are the tracking error and the system practical output on $k-\mathrm{th}$ iteration, respectively; $u_k^f$ is the output of the PD feedback controller with $K_P$ and $K_D$ being the proportional gain and derivative gain, respectively; $u_k^{ILC}$ is the output of the PD-type ILC controller in the $k-\mathrm{th}$ iteration; ${\mathrm{\Gamma }}_P$ and ${\mathrm{\Gamma }}_D$ are the proportional learning gain and derivative learning gain, respectively; ${\eta }_k$ denotes the measurement noise of the torque sensor on $k-\mathrm{th}$ iteration. Considering the measurement noise of the torque sensor, as shown in Figure 2, one can calculate the tracking errors as:

$$e_k(i)=y_d(i)-y_k(i)-{\eta }_k(i).$$

(14)

Thus, the selected hybrid PD-type ILC with adaptive leaning gains and a standard PD feedback controller can be described as follows:

$$u_k(i)=u_k^f(i)+u_k^{ILC}(i).$$

(15)

The feedback controller of the system is a standard PD controller, as mentioned above, which is used to stabilize the system and compensate the EDLS for nonrepeating disturbances, so that the initial errors of the system at the beginning of each iteration are within the allowable range. The PD feedback control law on $k-\mathrm{th}$ iteration is given as follows:

$$u_k^f(i+1)=K_P{e}_k(i+1)+K_D[e_k(i+1)-e_k(i)].$$

(16)

The functions of each parameter of PD feedback controller are as follows:

• $K_P$: The proportional control gain $K_P$ can reflect the error signal $e_k(i)$ of the control system proportionally. When the error is generated, the controller will immediately exert control action to reduce the error.
• $K_D$: The derivative term is used to reflect the change rate of the error signal, which can introduce an effective early correction signal into the system before the error signal becomes too big, so as to accelerate the response speed of the system and reduce the adjustment time.

An easy way to obtain reasonable control parameters $K_P$ and $K_D$ is to use the manual tuning method. The development of the PD-type ILC with adaptive learning gains $u_k^{ILC}$ will be described in Section 3.2.

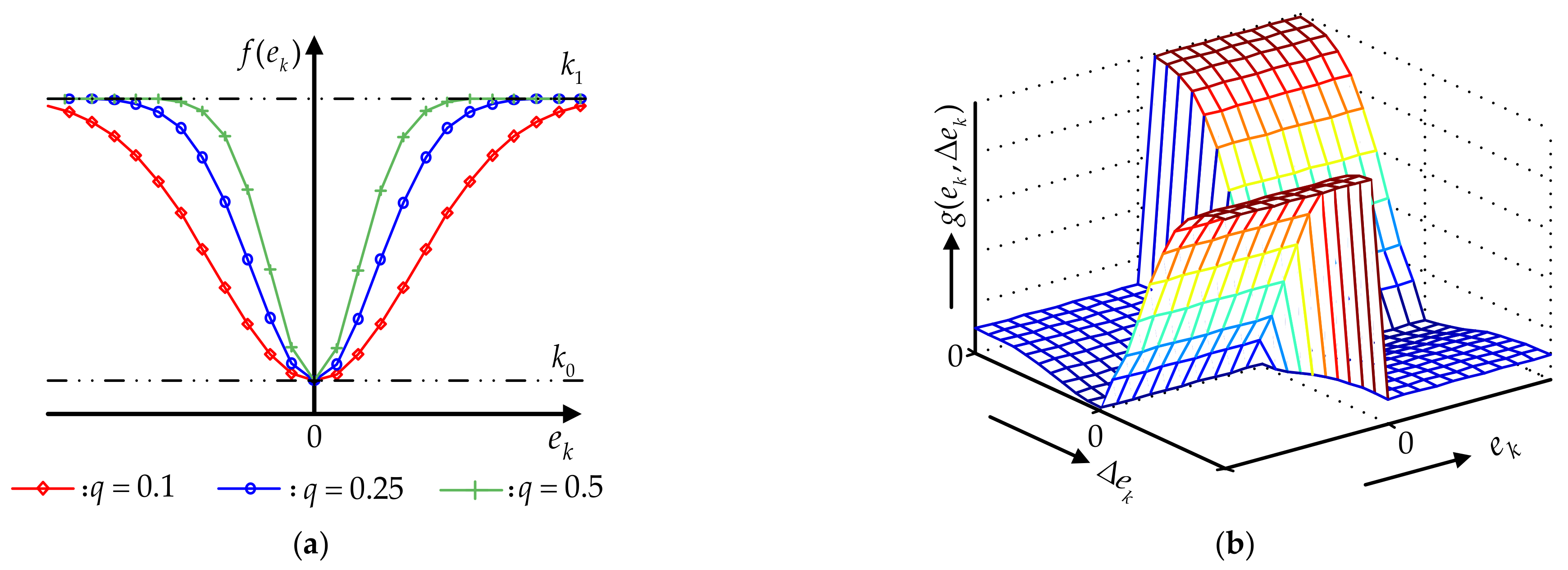
3.2. The PD-Type Iterative Learning Control Adaptive with Learning Gains Controller Design

From Equation (13) and Figure 2, one can see that the system has periodic disturbance and random measurement noise. The standard PD feedback controller proposed in Section 3.1 can be used to eliminate the influence of nonrepeating disturbances on the system. However, the output of the proposed PD control method is determined by the current error, and when the system continues to be subjected to the periodic disturbance, it is often difficult for the proposed PD control method to make the system error converge smoothly, and there are still periodic errors in the system’s response to the periodic drive reference signal.

The standard PD feedback controller has many disadvantages such as the trade-off between overshoot and the system rapidity, and the poor ability to deal with periodic disturbances. To overcome this shortcoming, the ILC law introduces human learning behavior into the control law design. The control system can modify the control input during the next iteration by the control input and error stored during the previous iterations of the same task, and finally achieve better tracking results through continuous iteration and learning.

Many ILC design algorithms, such as the plant inversion method [24], norm-optimal ILC method [25] and PD-type ILC method [26,27], have been proposed to improve the output tracking performance of systems that are often required to operate the same task multiple times. Among these methods, the PD-type ILC method has the characteristics of a simple structure, low design cost, and good robustness, and it does not need an accurate system model. The PD-type learning law has been the most widely used type of iterative learning controller at present. However, the conventional PD-type ILC with fixed learning gains can hardly deal with the aperiodic measurement noise of a nonlinear system. In order to improve the torque tracking performance of the EDLS and suppress the influence of random measurement noise on the control system, as shown in Figure 2, a PD-type ILC with adaptive learning gains is proposed. The learning gains can be adjusted adaptively according to the system errors and can be used to suppress measurement noise. Without loss of generality, on the $k-\mathrm{th}$ iteration, the PD-type ILC with adaptive learning gains can be described as follows:

$$u_{k+1}^{ILC}(i)=u_k^{ILC}(i)+{\Gamma }_{P,k}(e_k)e_k(i)+{\Gamma }_{D,k}(e_k,\Delta e_k)[e_k(i)-e_k(i-1)]$$

(17)

with proportional and derivative learning gains given by:

$${\Gamma }_{P,k}(e_k)={\tau }_{P}f(e_k)$$

(18)

$${\Gamma }_{D,k}={\tau }_{D}g(e_k,\mathsf{\Delta }{e}_k)$$

(19)

and the first difference of tracking error is given by:

$$\mathsf{\Delta }{e}_k(i)=e_k(i)-e_k(i-1)$$

(20)

where ${\tau }_P$ and ${\tau }_D$ are positive constant gains, and the nonlinear function $f(e_k)$ and $g(e_k,\mathsf{\Delta }{e}_k)$ are given, respectively, as follows [28]:

$$f(e_k)=k_1-(k_1-k_0)e^{-q{e}_k^2}$$

(21)

$$g(e_k,\mathsf{\Delta }{e}_k)=\lambda s(e_k\cdot \mathsf{\Delta }{e}_k)f(e_k)+(1-\lambda )f(e_k)$$

(22)

where $s(\ast )$ is the step function and satifies

$$s(e_k\cdot \Delta e_k)=\left\{\begin{array}{c}1, \mathrm{for} e_k\cdot \Delta e_k>0\\ 0, \mathrm{for} e_k\cdot \Delta e_k\ge 0\end{array}\right.$$

(23)

where $k_1$ and $k_0$ are the upper and lower bounds of nonlinear function $f(\ast )$, respectively, and $k_1>k_0\ge 0$. $q$ is used to determine the concavity openness of $f(\ast )$, so as to adjust the transition process of $f(\ast )$ and enhance the adaptability of $f(\ast )$ to errors $e_k$. $\lambda$ is a positive constant with $0\le \lambda <1$.

Remark 1.

For the PD-type ILC with adaptive learning gains (17), it is clear that, for$\forall k\in \left\{0,1,2,\cdots \right\}$,

$$\left\{\begin{array}{l}{\Gamma }_{P,k}\in [{\tau }_P{k}_0,{\tau }_P{k}_1]\\ {\Gamma }_{D,k}\in [0,{\tau }_D{k}_1]\end{array}\right..$$

(24)

Remark 2.

The selection principle of parameter$q$is as follows: A larger$q$leads to$f(\ast )$with a larger opening concavity, so that a small amplitude of error$e_k$can get a small value of$f(\ast )$. Therefore, one should determine the value of$q$according to the amplitude of random measurement noise, that is to say, an error with small amplitude needs a large$q$to suppress.

The effect of different parameters on the shape of the nonlinear function $f(\ast )$ and the relationship between $f(\ast )$ and the error $e_k$ can be seen in Figure 3a. The typical nonlinear function $g(\ast )$ versus the error $e_k$ and its first difference are shown in Figure 3b.

From Figure 3a and Equation (18), one can calculate that the function $f(\ast )$ is a bounded smooth function with values that vary with error magnitude. The greater the error amplitude, the larger the function value, and the greater the proportional learning gain ${\Gamma }_P$ for the proposed PD-type ILC. Since the measurement noise present in the system is generally concentrated in a range of small amplitudes, small learning gains of a PD-type ILC can weaken the impact of noise on the system when the error magnitude is small. From Figure 3b and Equation (19), one can calculate that the function $s(\ast )$ is used to adjust the system damping. Then, ${\Gamma }_D$ is directly used to mitigate the adverse effects of control inertia. In this method, the selected adjustment rule of learning gains can achieve both the desired tracking accuracy and system performance. The values of ${\Gamma }_P$ and ${\Gamma }_D$ have to be determined according to the monotonic convergence condition, which will be analyzed in Section 3.3.

3.3. Convergence Analysis

As mentioned in Section 2.2, the load torque of EDLS system output $T_L(t)$ is a function of ${\theta }_m(t)$ and ${\theta }_a(t)$. Since the EDLS system described by Equation (13) is required to move along a pre-determined trajectory repeatedly, without loss of generality, the EDLS system can be treated as a linear time-varying system with respective disturbance and random measurement noise. Then, the state-space model of the EDLS system (13) in the $k-\mathrm{th}$ iteration can be rewritten:

$$\left\{\begin{array}{c}{x}_k(i+1)=A_d{x}_k(i)+B_d{u}_k(i)+E_d{d}_k(i)\\ y_k(i)=C_d{x}_k(i)+{\eta }_k(i)\end{array}\right..$$

(25)

To restrict the analysis, the following assumptions are used for the system:

• The ideal control input set $u_d(i)$ can make the system state $x(i)$ and system output $y(i)$ track the ideal states $x_d(i)$ and the desired output $y_d(i)$, respectively;
• The initial state error of each iteration satisfies $x_{k+1}(0)-x_k(0)={\zeta }_k$, and ${\zeta }_k$ satisfies $\left|{\zeta }_k\right|\le \epsilon$ with $\epsilon >0$;
• The periodic disturbance $d_k(i)$ and the output measurement noise ${\eta }_k(i)$ are bounded as follows: $\forall k\in \left\{0,1,2,\cdots \right\}$ and $\underset{i\in [0,N]}{\sup }\left|d_k(i)\right|\le b_d$; $\underset{i\in [0,N]}{\sup }\left|{\eta }_k(i)\right|\le b_{\eta }$; $b_d$ and $b_{\eta }$ are known positive constants;
• The periodic disturbance $d_k(i)$ satisfies: $\forall k\in \left\{0,1,2,\cdots \right\}$ and $i\in \{0,1,\dots ,N\}$, $d_k(i)=d_{k+1}(i)$;

Theorem 1.

For the linear time-varying system with respective disturbance and random measurement noise (25) which satisfies assumptions 1–4, if the hybrid adaptive gain-scheduled PD with ILC control law (15) is used, the adaptive gain-scheduled algorithm (16) and the PD-type ILC scheme (24) are adopted. Given a desired trajectory $y_d(i)$, $i\in \{0,1,\dots ,N\}$ and the sample interval $h$, the monotonic convergence condition for all frequencies up to the Nyquist frequency can be given by:

$${‖1-\frac{G(z)[{\Gamma }_{P,k}+{\Gamma }_{D,k}(1-z^{-1})]}{G(z)[K_P+K_D(1-z^{-1})]+1}‖}_{\infty }\le \rho <1;z=e^{j\omega h} \mathrm{with} \omega \in [0,{\omega }_N]$$

(26)

where${\omega }_N=1/(2h)$is the Nyquist frequency.

Proof of Theorem 1.

Taking the $z$ transform of Equation (25) and the learning law given by Equations (15)–(17) for the $k-\mathrm{th}$ iteration, it follows:

$$Y_k(z)=G(z)U_k(z)+{\mathsf{\Phi }}_k(z)+{\mathsf{\Pi }}_k(z)$$

(27)

$$\left\{\begin{array}{c}{U}_k(z)=U_k^f(z)+U_k^{ILC}(z)\\ U_k^f(z)=K_P{E}_k(z)+K_D{E}_k(z)(1-z^{-1})\\ U_k^{ILC}(z)=U_{k-1}^{ILC}(z)+{\Gamma }_{P,k}{E}_{k-1}(z)+{\Gamma }_{D,k}{E}_{k-1}(z)(1-z^{-1})\end{array}\right.$$

(28)

where ${\mathsf{\Pi }}_k(z)$ is the z-transform of the sequence $\left\{{\eta }_k\right\}$, and

$$G(z)=C_d{(zI-A_d)}^{-1}{B}_d$$

(29)

$${\mathsf{\Phi }}_k(z)=C_d{(zI-A_d)}^{-1}z{x}_k(0)+C_d{(zI-A_d)}^{-1}{E}_d{D}_k(z)$$

(30)

$$E_k(z)=Y_d(z)-Y_k(z)-{\mathsf{\Pi }}_k(z).$$

(31)

Then, one can get

$$\begin{array}{l}{Y}_{k+1}(z)-Y_k(z)=G(z)[U_{k+1}(z)-U_k(z)]+[{\mathsf{\Phi }}_{k+1}(z)-{\mathsf{\Phi }}_k(z)]+[{\mathsf{\Pi }}_{k+1}(z)-{\mathsf{\Pi }}_k(z)]\\ =G(z)[U_{k+1}^f(z)-U_k^f(z)]+G(z)E_k(z)[{\Gamma }_{P,k}+{\Gamma }_{D,k}(1-z^{-1})]\\ +[{\mathsf{\Pi }}_{k+1}(z)-{\mathsf{\Pi }}_k(z)]\end{array}$$

(32)

since

$${\mathsf{\Phi }}_{k+1}(z)-{\mathsf{\Phi }}_k(z)=C_d{(zI-A_d)}^{-1}z[x_{k+1}(0)-x_k(0)]+C_d{(zI-A_d)}^{-1}{E}_d[D_{k+1}(z)-D_k(z)]\approx 0$$

(33)

$$U_{k+1}^f(z)-U_k^f(z)=[K_P+K_D(1-z^{-1})][E_{k+1}(z)-E_k(z)]$$

(34)

$$\begin{array}{cc}\hfill Y_{k+1}(z)-Y_k(z)& =[Y_d(z)-E_{k+1}(z)]-[Y_d(z)-E_k(z)]\hfill \\ & =-E_{k+1}(z)+E_k(z)\hfill \end{array}.$$

(35)

From these equations, one can get:

$$\begin{array}{l}[G(z)K_P+G(z)K_D(1-z^{-1})+1]E_{k+1}(z)\\ +[G(z){\Gamma }_{P,k}+G(z){\Gamma }_{D,k}(1-z^{-1})-G(z)K_P-G(z)K_D(1-z^{-1})-1]E_k(z)\\ ={\mathsf{\Pi }}_k(z)-{\mathsf{\Pi }}_{k+1}(z)\end{array}.$$

(36)

The homogeneous equation [1] of Equation (36) is

$$E_{k+1}(z)=E_k(z)-\frac{G(z)[{\Gamma }_{P,k}+{\Gamma }_{D,k}(1-z^{-1})]}{G(z)[K_P+K_D(1-z^{-1})]+1}{E}_k(z).$$

(37)

If the sample interval of system (25) is $h$, then the Nyquist frequency is ${\omega }_N=1/(2h)$. Taking the infinity norm on both sides of Equation (37), the output error monotonically decreasing can be reached for all frequencies under Nyquist frequency [29] if

$${‖\frac{E_{k+1}(z)}{E_k(z)}‖}_{\infty }={‖1-\frac{G(z)[{\Gamma }_{P,k}+{\Gamma }_{D,k}(1-z^{-1})]}{G(z)[K_P+K_D(1-z^{-1})]+1}‖}_{\infty }\le \rho <1;z=e^{j\omega h} \mathrm{with} \omega \in [0,{\omega }_N].$$

(38)

Since $K_P$ and $K_D$ can be obtained by the manual tuning method, by substituting proper $K_P$ and $K_D$ into the right-hand side of Equation (38), one can get:

$${‖1-\frac{G(e^{j\omega h})[{\Gamma }_{P,k}+{\Gamma }_{D,k}(1-e^{-j\omega h})]}{G(e^{j\omega h})[K_P+K_D(1-e^{-j\omega h})]+1}‖}_{\infty }<1;\forall \omega \in [0,{\omega }_N].$$

(39)

The adaptive learning gains ${\Gamma }_{P,k}$ and ${\Gamma }_{D,k}$ are determined by ${\tau }_P$, ${\tau }_D$, $k_1$, $k_0$, and $q$, and as mentioned in Remark 1, ${\Gamma }_{P,k}\in [{\tau }_P{k}_0,{\tau }_P{k}_1]$, and ${\Gamma }_{D,k}\in [0,{\tau }_D{k}_1]$. Hence, the parameters design of adaptive learning gains ${\Gamma }_{P,k}$ and ${\Gamma }_{D,k}$ can be formulated as:

$$\underset{({\tau }_P,{\tau }_D,k_0,k_1)}{\sup }\left|1-\frac{G(e^{j\omega h})[{\Gamma }_{P,k}+{\Gamma }_{D,k}(1-e^{-j\omega h})]}{G(e^{j\omega h})[K_P+K_D(1-e^{-j\omega h})]+1}\right|<1;\forall \omega \in [0,{\omega }_N].$$

(40)

Clearly, when $K_P$ and $K_D$ are known, it is always possible to find ${\tau }_P$, ${\tau }_D$, $k_0$, $k_1$, and $q$ such that the Equation (40) is satisfied for all frequencies up to the Nyquist frequency ${\omega }_N$.

Then, according to Equations (31), (36), and (38), and the assumption 5, one can get the final error of the system, which can be described as:

$$\underset{k\to \infty }{\lim }{E}_k(z)=\frac{{\mathsf{\Pi }}_k(z)-{\mathsf{\Pi }}_{k-1}(z)}{G(z)[K_P+K_D(1-z^{-1})]+1}\le \frac{b_{\eta }}{G(z)[K_P+K_D(1-z^{-1})]+1}.$$

(41)

According to assumption 5, if the tracking error signals of the first iteration, $E_0$, is finite, and there is no uncertainty and disturbance in (26), then one can get that ${‖E_k(z)‖}_{\infty }\le {\rho }^k{‖E_0(z)‖}_{\infty }\to 0$ as $k\to \infty$. In order to fulfill the monotonic convergence condition (41), one should choose the proper feedback gains and learning gains of the proposed controller in this paper. □

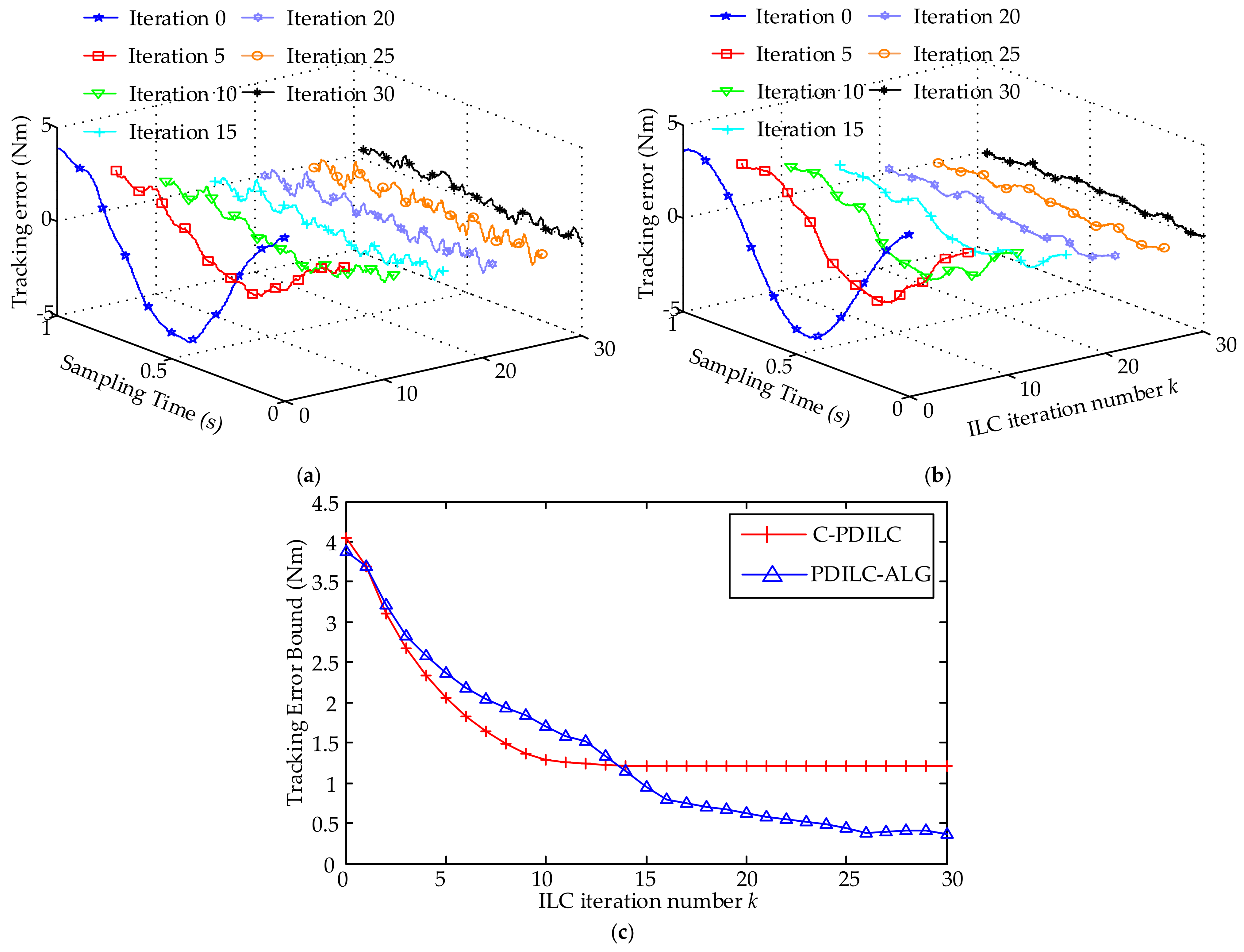
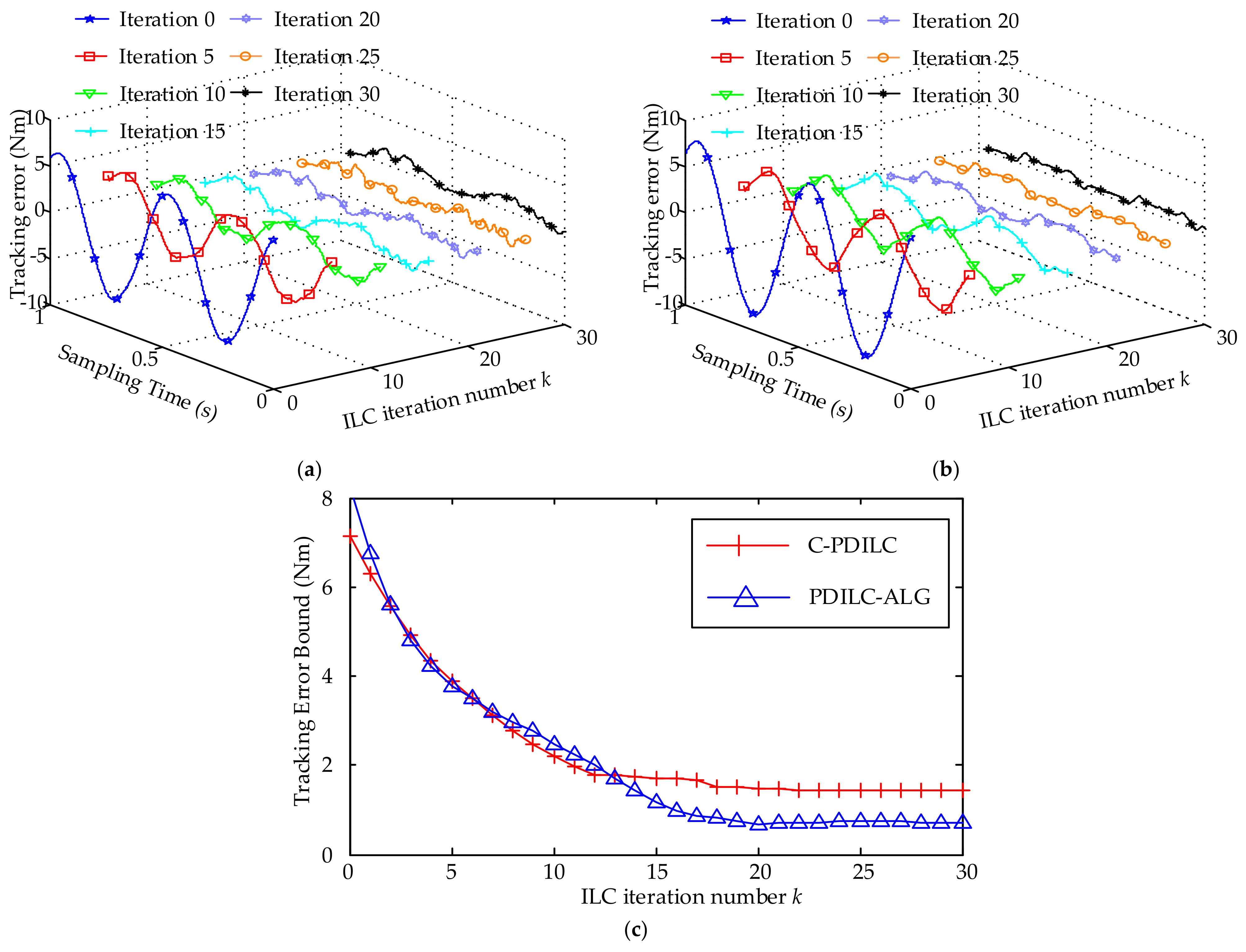
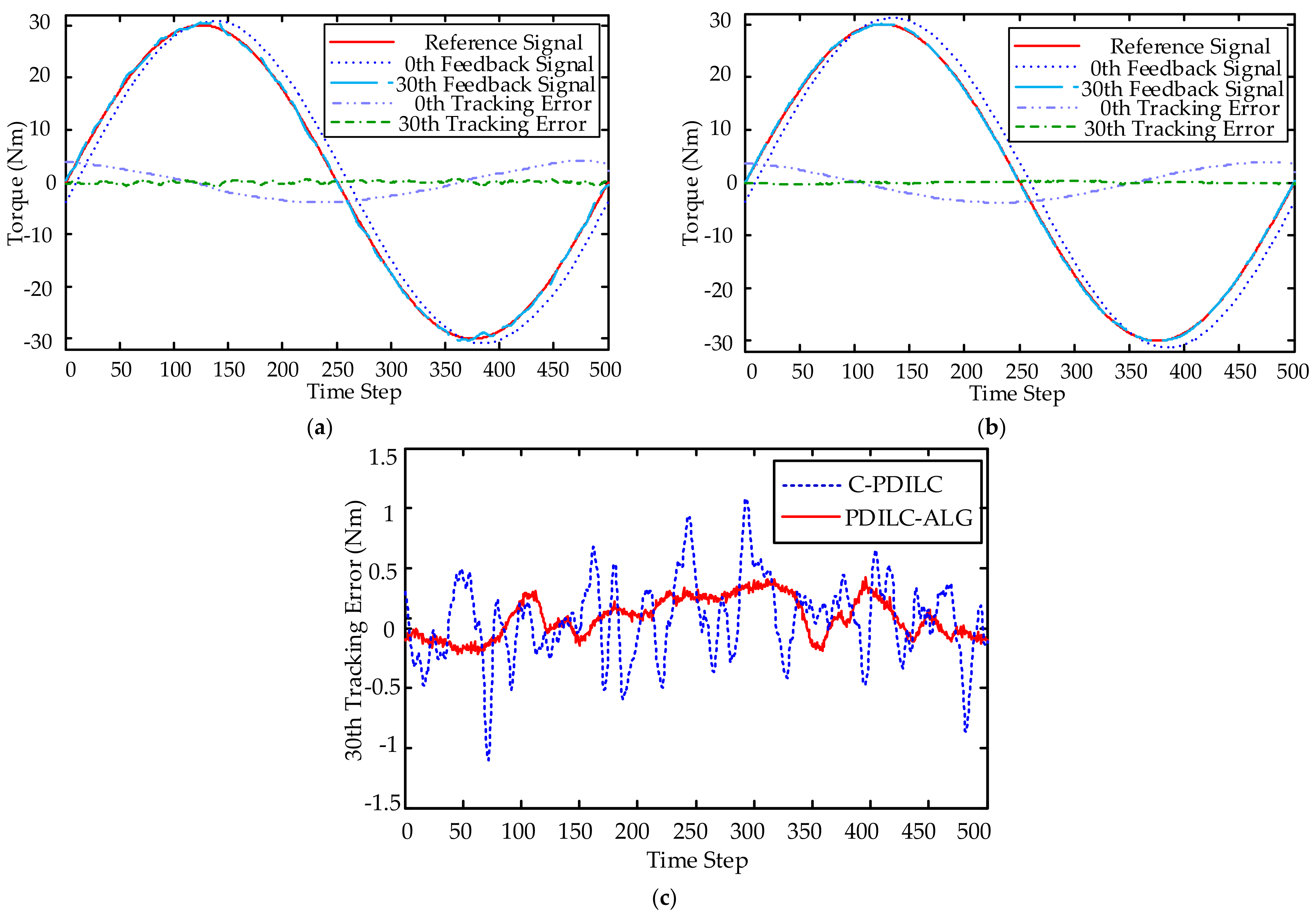
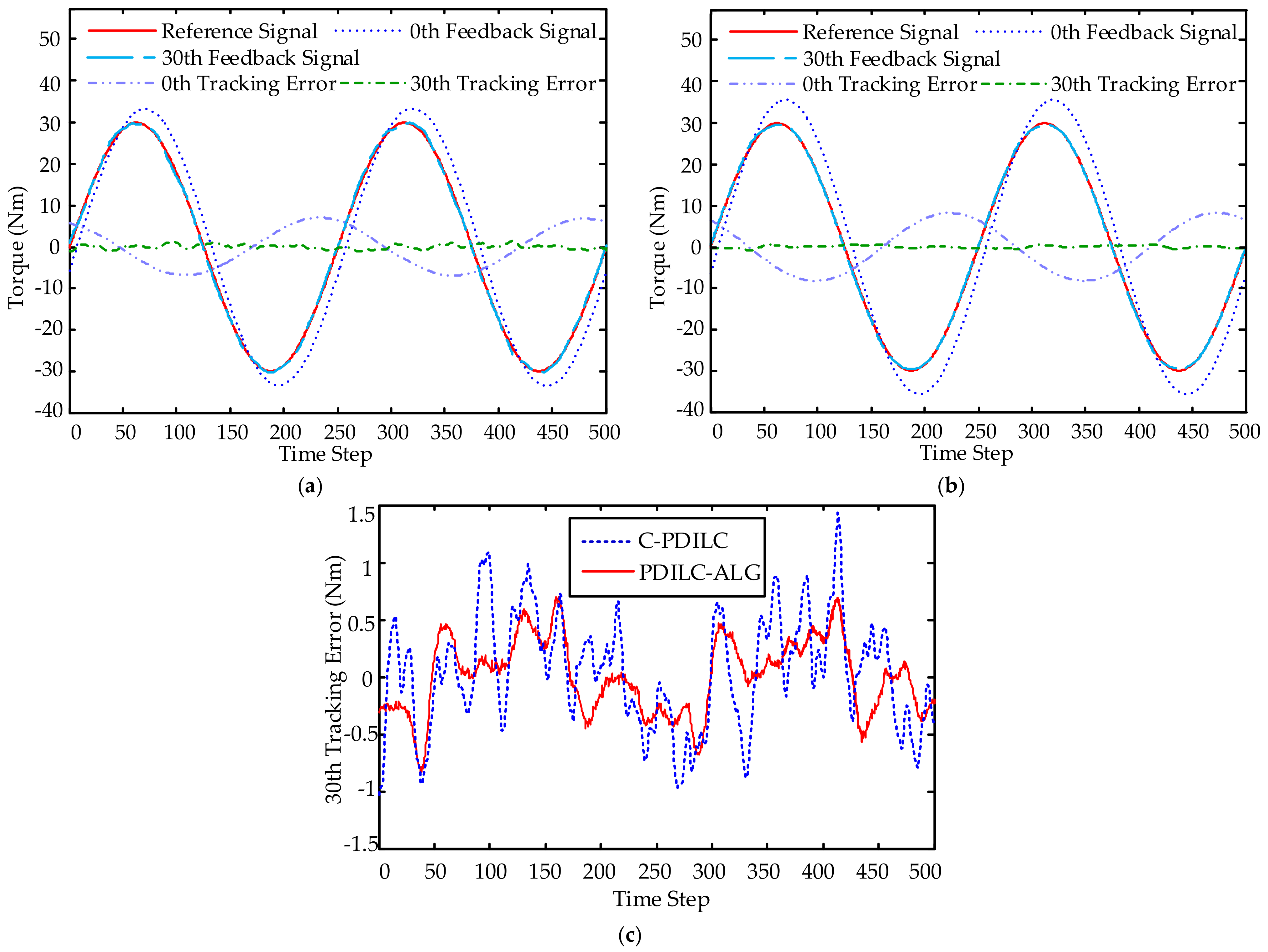
4. Experimental Evaluation

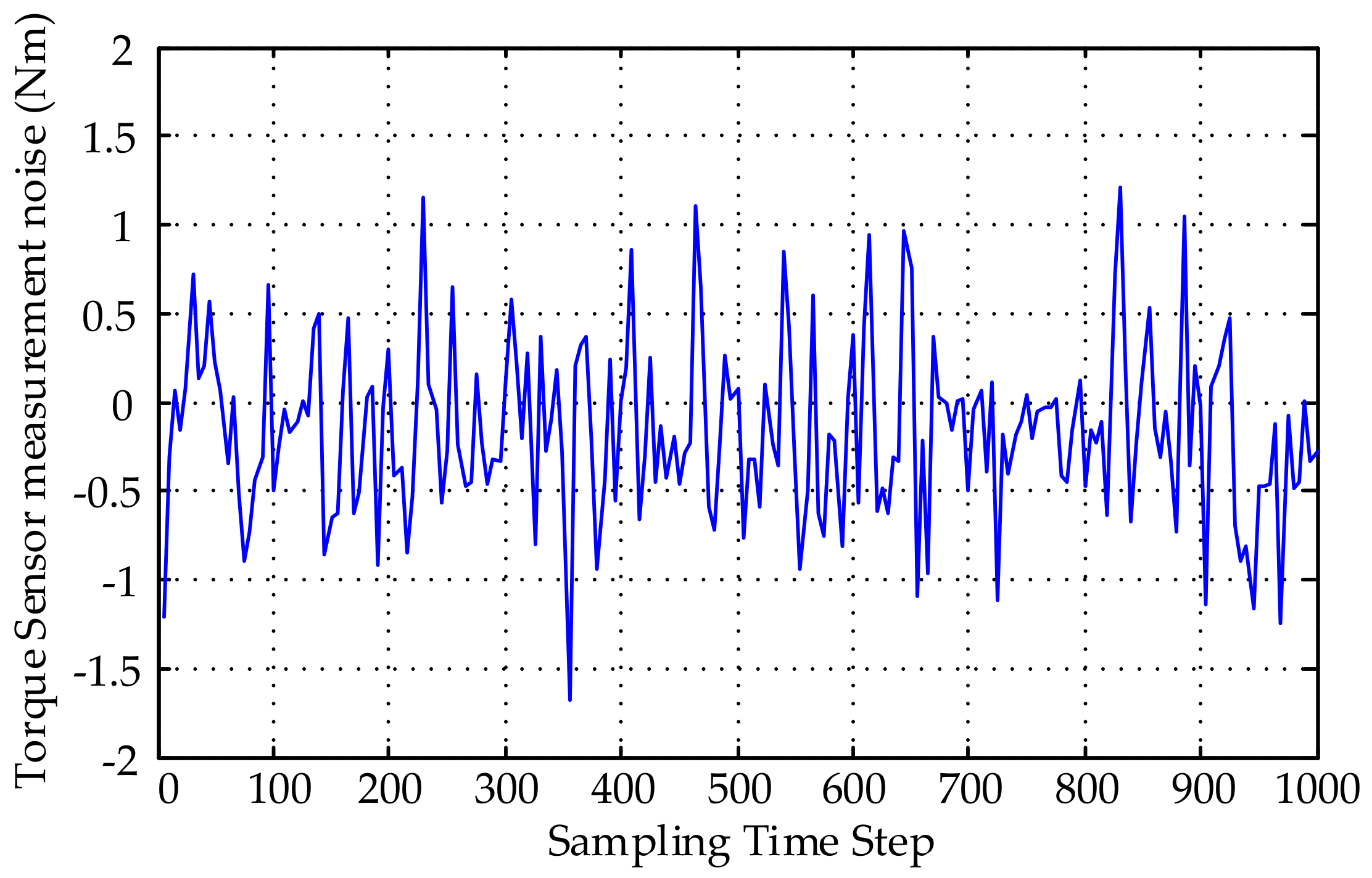
4.1. Experimental Setup

In order to demonstrate the effectiveness of the proposed robust adaptive iterative learning control scheme, experiments were conducted on an experimental laboratory test bench, shown in Figure 4. A PMSM was selected as a loading motor that was used to generate the loading torque of the tested EMA. Two high-precision encoders were used to obtain the position of the drive shaft. A torque sensor was used to measure the dynamic loading torque of the EDLS. An EDLS controller was used to implement the proposed robust adaptive iterative learning control scheme. In order to improve the dynamic response and stability accuracy of the loading torque, the driver of the loading motor is based on the direct torque control strategy to achieve high-precision torque output. The tested EMA was driven by a position servo driver. The main parameters of the loading motor drive system and EDLS are given in

Table 1. The main indicators of permanent magnet synchronous motor (PMSM) loading motor.

Rated Power	Rated Speed	Rated Torque	Rated Voltage
$3 (\mathrm{KW})$	$3000 (\mathrm{r}/\min )$	$9.55 (\mathrm{N}\cdot \mathrm{m})$	$380 (\mathrm{V})$

and

Table 2. Parameters of the electric dynamic load simulator.

Parameter	Value	Unit
$K_m$	0.955	$(\mathrm{N}\cdot \mathrm{m})/\mathrm{V}$
$J_m$	0.000697	$\mathrm{K}\mathrm{g}\cdot {\mathrm{m}}^2$
$B_m$	0.00018	$(\mathrm{N}\cdot \mathrm{m})/(\mathrm{rad}/\mathrm{s})$
$n_g$	35	dimensionless
$K_G$	8500	$(\mathrm{N}\cdot \mathrm{m})/\mathrm{rad}$

, respectively.

4.2. Experimental Results

To evaluate the effectiveness of the proposed ILC schemes, performances of conventional PD-type ILC with fixed learning gains have been carried out as comparison. By setting the sample period $h=0.002 s$, and submitting $h$ into Equations (9)–(12), the system matrices can be described as:

$$A_d=\left[\begin{array}{cc}0.9803& 0.4808\\ -0.0812& 0.9798\end{array}\right]; B_d=\left[\begin{array}{c}0.3294\\ 1.3563\end{array}\right]; E_d=\left[\begin{array}{c}-8.7611\\ -1.0753\end{array}\right]; C_d=\left[\begin{array}{cc}1& 0\end{array}\right].$$

The Nyquist frequency of the EDLS system is ${\omega }_N=250 \mathrm{Hz}$. Then, the following two controllers are proposed for comparison.

(1)

Conventional PD-type ILC (C-PDILC): this is a combination of a standard PD feedback controller and a conventional PD-type ILC. The conventional PD-type ILC with fixed learning gains can be seen as a special case of the proposed method in this paper, for all $k\in \left\{0,1,2,\cdots \right\}$. ${\Gamma }_P$ and ${\Gamma }_D$ are restricted to be constant scalars. To satisfy the condition of Equation (38), the control gains of PD feedback controller are chosen as $K_P=2.25$ and $K_D=0.02$, and the PD-type learning gains are chosen as ${\Gamma }_P=1.5$ and ${\Gamma }_D=0.6$. For all frequencies up to the Nyquist frequency, one can get:

$${‖1-\frac{G(z)[{\Gamma }_P+{\Gamma }_D(1-z^{-1})]}{G(z)[K_P+K_D(1-z^{-1})]+1}‖}_{\infty }\in [0.5592,0.6035]<1;z=e^{j\omega h} \mathrm{for} \forall \omega \in [0,250].$$

(42)

(2)

PD-type ILC with adaptive learning gains (PDILC-ALG): this is the proposed method in this paper. In order to satisfy the condition of Equation (38), the parameters of adaptive learning gains are chosen as ${\tau }_P=1.5$, ${\tau }_D=0.6$, $k_0=0.1$, $k_1=1$, $\lambda =0.75$, and $q=0.5$. The proportional gain of the feedback controller is the same as the conventional PD-type ILC; i.e., $K_P=2.25$ and $K_D=0.02$. Then, for all frequencies up to the Nyquist frequency and all $k\in \left\{0,1,2,\cdots \right\}$, one can get:

$${‖1-\frac{G(z)[{\Gamma }_{P,k}+{\Gamma }_{D,k}(1-z^{-1})]}{G(z)[K_P+K_D(1-z^{-1})]+1}‖}_{\infty }\in [0.5592,0.9604]<1; z=e^{j\omega h} \mathrm{for} \forall \omega \in [0,250] \mathrm{and} \forall k\in \left\{0,1,2,\cdots \right\}.$$

(43)

Two experimental test cases were conducted to evaluate the performance of the two comparison controllers.

Case 1: The tested EMA revolves according to the sine command, which was described as ${\theta }_a^{\ast }(t)=8^{\circ }\sin (2\pi ih)$, while the exerted loading torque is given by a sinusoidal signal as $y_d(t)=30\sin (2\pi ih)$.

Case 2: The tested EMA revolves according to the sine command, which was described as ${\theta }_a^{\ast }(t)=4^{\circ }\sin (4\pi ih)$, while the exerted loading torque is given by a sinusoidal signal as $y_d(t)=30\sin (4\pi ih)$.

Furthermore, $i\in \{0,1,\dots ,N\}$, $N=500$ in each iteration.

The following infinite norm of the loading torque tracking error bound $b_e$, which is used to make quantitative comparisons for the loading torque tracking accuracy of the two controllers, is defined as follows:

$$b_{e,k}=\underset{i\in [0,500]}{\sup }\left|e_k(i)\right|, \mathrm{for} \forall k\in \left\{0,1,2,\cdots \right\}$$

(44)

where $k$ is the number of iterations.

Here, the measurement noise of the torque sensor is shown in Figure 5. The loading torque tracking error results of the two comparison controllers in different experimental test cases are shown in Figure 6 and Figure 7, respectively.

It can be seen that after enough iterations, the proposed PD-type ILC with adaptive learning gains has a better tracking accuracy, which leads to a smaller output error. Under different experimental cases, the error bounds of the two proposed methods are shown in Figure 6c and Figure 7c, respectively. Due to the influence of the random measurement noise, it is difficult for the two control methods of comparison to guarantee the tracking accuracy and convergence speed simultaneously. The Case 1 quantitative comparison results are listed in

Table 3. Case 1 (${\theta }_a^{\ast }(t)=8^{\circ }\sin (2\pi ih)$, $y_d(t)=30\sin (2\pi ih)$) experimental results of the two controllers.

Strategy	$\mathbf{Error} \mathbf{Bound} {\mathit{b}}_{\mathit{e}} \mathbf{in} \mathbf{Different} \mathbf{Iteration}$
	8th	18th	28th
C-PDILC	$1.43 \mathrm{N}\cdot \mathrm{m}$	$1.21 \mathrm{N}\cdot \mathrm{m}$	$1.21 \mathrm{N}\cdot \mathrm{m}$
PDILC-ALG	$1.97 \mathrm{N}\cdot \mathrm{m}$	$0.76 \mathrm{N}\cdot \mathrm{m}$	$0.41 \mathrm{N}\cdot \mathrm{m}$

, and the Case 2 quantitative comparison results are listed in

Table 4. Case 2 (${\theta }_a^{\ast }(t)=4^{\circ }\sin (4\pi ih)$, $y_d(t)=30\sin (4\pi ih)$) experimental results of the two controllers.

Strategy	$\mathbf{Error} \mathbf{Bound} {\mathit{b}}_{\mathit{e}} \mathbf{in} \mathbf{Different} \mathbf{Iteration}$
	8th	18th	28th
C-PDILC	$3.12 \mathrm{N}\cdot \mathrm{m}$	$1.67 \mathrm{N}\cdot \mathrm{m}$	$1.43 \mathrm{N}\cdot \mathrm{m}$
PDILC-ALG	$3.25 \mathrm{N}\cdot \mathrm{m}$	$0.87 \mathrm{N}\cdot \mathrm{m}$	$0.74 \mathrm{N}\cdot \mathrm{m}$

.

From Table 3 and Figure 6c, it can be seen that the conventional PD-type ILC with fixed learning gains has an error bound of $1.21 \mathrm{N}\cdot \mathrm{m}$ and converges to the convergence domain after about 13 iterations. The convergence rate of the proposed PD-type ILC with an adaptive learning gain is slightly slower, but the error range is $0.41 \mathrm{N}\cdot \mathrm{m}$ after the 28th iteration. From Table 4 and Figure 7c, it can be seen that the conventional PD-type ILC with fixed learning gains has an error bound of $1.43 \mathrm{N}\cdot \mathrm{m}$ and converges to the convergence domain after about 23 iterations. The convergence rate of the proposed PD-type ILC with adaptive learning gain is slightly slower, but the error range is $0.74 \mathrm{N}\cdot \mathrm{m}$ after the 28th iteration.

The tracking performance of the conventional PD-type ILC and the PD-type ILC with adaptive learning gains in different experimental test cases are shown in Figure 8 and Figure 9, respectively.

This study considers not only the unmolded dynamic, parameter uncertainty, and the periodic external disturbance but also the random measurement noise. Due to the $0\mathrm{th}$ control input $u_0$ of the two compared control methods being derived from the output value of the feedback PD controller with same parameters, they have the same tracking performance on iteration 0. Under different experimental cases, the $30\mathrm{th}$ error signals of the two proposed methods are shown in Figure 8c and Figure 9c, respectively. The Case 1 quantitative comparison results are listed in

Table 5. Case 1 (${\theta }_a^{\ast }(t)=8^{\circ }\sin (2\pi ih)$, $y_d(t)=30\sin (2\pi ih)$) experimental results of the two controllers.

Strategy	Maximum Error	Minimum Error	${\mathit{b}}_{\mathit{e}}/\mathbf{max}\left|{\mathit{y}}_{\mathit{d}}\right|$
C-PDILC	$1.07 \mathrm{N}\cdot \mathrm{m}$	$-1.21 \mathrm{N}\cdot \mathrm{m}$	$4.03\%$
PDILC-ALG	$0.29 \mathrm{N}\cdot \mathrm{m}$	$-0.32 \mathrm{N}\cdot \mathrm{m}$	$1.07\%$

, and the Case 2 quantitative comparison results are listed in

Table 6. Case 2 (${\theta }_a^{\ast }(t)=4^{\circ }\sin (4\pi ih)$, $y_d(t)=30\sin (4\pi ih)$) experimental results of the two controllers.

Strategy	Maximum Error	Minimum Error	${\mathit{b}}_{\mathit{e}}/\mathbf{max}\left|{\mathit{y}}_{\mathit{d}}\right|$
C-PDILC	$1.39 \mathrm{N}\cdot \mathrm{m}$	$-1.43 \mathrm{N}\cdot \mathrm{m}$	$4.77\%$
PDILC-ALG	$0.68 \mathrm{N}\cdot \mathrm{m}$	$-0.73 \mathrm{N}\cdot \mathrm{m}$	$2.43\%$

.

From Table 5 and Figure 8c, it is obvious that the PD-type ILC with adaptive learning gains has a smaller tracking error whose tracking error bound during the 30th iteration is about $0.32 \mathrm{N}\cdot \mathrm{m}$, whilst the tracking error bound based on conventional PD-type ILC is about $1.21 \mathrm{N}\cdot \mathrm{m}$. From Table 6 and Figure 9c, it can be seen that the PD-type ILC with adaptive learning gains has a smaller tracking error whose tracking error bound during the 30th iteration is about $0.73 \mathrm{N}\cdot \mathrm{m}$, whilst the tracking error bound based on conventional PD-type ILC is about $1.43 \mathrm{N}\cdot \mathrm{m}$. Due to the presence of the random measurement noise, the conventional PD-type ILC cannot ensure accurate loading torque tracking. The proposed PD-type ILC with adaptive learning gains can obviously improve the tracking performance, although the convergence rate is compromised.

5. Conclusions

Periodic and aperiodic disturbances have been the main factors affecting the stability of the EDLS system, which limit the tracking control performance for a given trajectory. This is because the presence of a variety of disturbances in the system will reduce the tracking accuracy of the EDLS and increase the complexity of the controller. Thus, a PD-type ILC with adaptive learning gains is proposed in this paper and designed to obtain satisfactory control input by learning the information of previous system operation. Meanwhile, a standard PD feedback controller is designed to suppress some uncertain disturbances and stabilize the system, so that the PD-type ILC with adaptive learning gains can realize the tracking task quickly. The theoretical analysis and the comparison of experimental results showed that the proposed control law can guarantee the accurate load torque tracking despite of periodic and aperiodic disturbances for the EDLS.

Furthermore, in the modeling of EDLS, the influence of nonlinear characteristics such as friction and backlash on the loading accuracy are ignored, and only the strong position disturbance of EMA and the measurement noise of torque sensor are considered. However, in practical working conditions, especially in the process of high-precision load torque tracking, the influence of friction and backlash are inevitable. In the following research, we will consider the friction model and backlash model, perfect the mathematical model of EDLS, so as to enhance the engineering application of the research.