Abstract
A realistic performance assessment of any wireless communication system requires the use of a fading channel model that reflects its main characteristics. The traditional Rayleigh and Nakagami-m models have been (and still are) the basis of most theoretical research on wireless technologies today, even for emerging technologies, such as millimeter-wave communications (mm-Wave). In this article, we show that the fluctuating multiple-ray (FMR) and - shadowed models had a better fit (i.e., lowest mean square error statistical test) to field measurements in outdoor environments at 28 GHz than the conventional channel models. Therefore, these generalized models are feasible alternatives that can be used as a benchmark when evaluating communication performance in mm-Wave scenarios.
1. Introduction
The increasing demands for new wireless applications/services and the rapid growth of connected intelligent “things” (also known as the internet of things (IoT) [1]) will saturate the capacity of current mobile communication systems in the coming years. Building on this background, network designers and researchers search for novel emerging technologies to ensure ultra-high data rates, energy efficiency, ultra-wide radio coverage, and connectivity, as well as ultra-low latencies and high reliability [2]. In this context, the fifth generation of wireless networks (5G) emerges as a solution to satisfy these strict requirements through intelligent and environmentally friendly technologies [3]. The key to 5G communications’ successful operation will be unifying different technologies that coexist in the same environment. Among these 5G technologies, the following stand out: massive multiple-input multiple-output (MIMO), heterogeneous networks (HetNets), non-orthogonal multiple access (NOMA), full-duplex (FD) transmission/reception, direct beamforming (BF), and millimeter-wave (mm-Wave) communications [4,5].
Specifically, mm-Wave communication has attracted broad interest in academia and industry, as it will the very crowded and scarce spectrum of current networks to be overcome [6]. In this sense, several research studies have focused on mm-Wave communications, where the taking of empirical measurements of the propagation channels of wireless communication systems has been carried out by both industrial and research groups [7,8,9]. However, the basis of most theoretical research on mm-Wave communications uses the Rayleigh and Rician distributions as channel models to capture small-scale fading in non-line-of-sight (NLOS) and line-of-sight (LOS) scenarios [10]. Recently, in [11], the small-scale fading cumulative distribution function (CDF) obtained from an empirical 28 GHz outdoor measurement demonstrated that Rician fading was more suitable than Rayleigh, even for NLOS environments. An exhaustive analysis of the results in [11,12] shows that the traditional fading models (Rayleigh, Rician, and Nakagami-m) fail to accurately capture the random fluctuations suffered in the dominant components of the received signal. Furthermore, since the mm-Wave radio channel’s propagation characteristics are different from those of frequency bands below 3 GHz, most of the existing characteristic channel measurements and models are not relevant for the mm-Wave bands. Therefore, fundamental knowledge of mm-Wave channel propagation features, including accurate and reliable fading channel models, is essential for developing 5G mobile communications [13]. To overcome these limitations in the small-scale channel characterization in the mm-Wave bands, new fading channel models have been proposed in recent years. In this context, based on the small-scale fading measurements given in [11], the authors in [14] prove that the fluctuating two-ray (FTR) fading model provides a much better fit than the conventional fading models at 28 GHz outdoor mm-Wave bands. In [15], the researchers, through indoor mm-Wave measurement campaigns, provide strong evidence that the two-wave with diffuse power (TWDP) channel model is more accurate than the Rician model in characterizing mm-Wave indoor channels at 60 GHz. The results in [16] demonstrated that the statistical TWDP model is a suitable channel model for mm-Wave train-to-infrastructure wireless communications. The TWDP channel model has also successfully been applied in recent publications to model vehicle-to-infrastructure channel measurement data in the mm-Wave band [17,18]. Recently, other popular stochastic fading models were investigated in [19] to characterize propagation conditions encountered in mm-Wave communications. Specifically, measurement campaigns were carried out in various indoor mm-Wave scenarios with frequencies ranging from 55 to 65 GHz for LOS and NLOS conditions. The findings in [19] reveal that the -, -, and - fading channel models are satisfactory for modeling short-term fading in the mm-Wave band. Other interesting results for modeling small-scale fading in mm-Wave communications can be found in [20,21,22]. In our work, we focus on two fading channel models to characterize mm-Wave scenarios in 5G networks and beyond. We briefly describe each of these models in the following: (1) - shadowed model [23]: In this fading model, the received power signal is structured by a finite sum of multipath clusters. Each cluster is modeled by a dominant component and scattered diffuse waves. All the specular components are subject to the shadowing fluctuation caused by obstacles or human body movements, and (2) fluctuating multiple-ray (FMR) model [24]: In this channel model, the receiver signal can be expressed as a superposition of multiple dominant waves, plus additional waves associated with diffuse scattering. In addition, a fluctuation in the amplitude of the dominant rays is assumed. This fact is due to blockage by obstacles or by various electromagnetic disturbances.
In light of the above considerations, in this paper, we investigate the performance of both the FMR and - shadowed fading channel models to fit the field measurement in mm-Wave communications. Two important points related to the fading models mentioned above are highlighted: (1) The number of channel models obtainable from the - shadowed distribution as particular cases is abundant, as shown in ([23] Table I). In particular, the - and - that have proven to be suitable for modeling mm-Wave channels are special cases of the - shadowed model; (2) the FMR encompasses the popular general models—namely, TWDP and FTR, which are the most widely used to model the propagation channel in mm-Wave frequencies. Based on the open literature and to the best of the authors’ knowledge, the - shadowed and FMR fading models’ performance in fitting experimental measurements in mm-Wave communications is still unexplored.
In addition to the main contribution, we compare the new generalized channel models’ performance with that of traditional fading models generally used in the literature (e.g., Rayleigh, Rice, Nakagami-m) to evaluate mobile communication systems’ behavior in mm-Wave bands. Based on the results presented in this paper, we show that classical fading channel models lack the versatility to model propagation characteristics in mm-Wave environments. Conversely, the FMR and - shadowed channel models provide an excellent fit to channel measurements of a 28 GHz communication system. The remainder of this paper is organized as follows. Section 2 presents a brief overview of the FMR, and the - shadowed fading distributions are given. In Section 3, the fading parameters of the - shadowed and FMR models are adjusted to the empirical measurements of communications at 28 GHz given in [11] through the use of a learning algorithm—namely, particle swarm optimization (PSO). Section 4 shows illustrative numerical results and discussions. Finally, concluding remarks are provided in Section 5.
Notation: Throughout this paper, and denote the probability density function (PDF) and the CDF of a random variable Z, respectively. is the expectation operator, and is the absolute value. In addition, denotes the gamma function [25] (Equation (6.1.1)), is the lower incomplete gamma function [25] (Equation (6.5.2)), is the upper incomplete gamma function [25] (Equation (6.5.3)), is the confluent hypergeometric function [25] (Equation (13.1.3)), denotes the Laguerre polynomial of z order [25] (Equation (22.2.13)), is the Pochhammer symbol [25] (Equation (6.1.222)), and is the bivariate confluent hypergeometric function [26] (Equation (4.19)).
2. Preliminaries
Here, we begin by reviewing the main statistics (i.e., PDF and CDF) of the - shadowed and FMR fading channel models.
2.1. FMR Channel Model
In this model, the envelope, R, of the signal can be structured as a superposition of multipath waves arising from dominant reflections and L additional waves associated with diffuse scattering, so
where denotes the n-th specular component with amplitude and a uniformly distributed random phase , and represents the random fluctuation in the specular components, which follows a Gamma random variable (RV) with scale parameter and . On the other hand, based on the assumption that , the diffuse components follow a Gaussian RV, i.e., . Hence, is Rayleigh distributed with .
The FMR model in (1) encompasses very important fading channel models as particular cases. For instance, the FMR model reduces to the N-wave with diffuse power (NWDP) distribution when becomes deterministic, i.e., . A complete list of popular fading channel models derived from the FMR model can be found in ([10] Table I). Let be the instantaneously received signal-to-noise ratio (SNR) through an FMR fading channel, where is defined as the transmit SNR, with being the transmit power and being the mean power of the additive white Gaussian noise. According to [24], the PDF and CDF of the received SNR of the FMR model can be expressed as
where the corresponding fading parameters (i.e., the power, number, and amplitudes of the specular components) are embedded in the coefficient , and is the average received SNR, given by
where is the number of dominant components. In addition, the coefficient can be computed recursively by [24]
wherein , and
where the initial value is set as , and
2.2. - Shadowed Channel Model
The - shadowed model considers a signal composed of clusters of multipath waves propagating in a nonhomogeneous environment. Within each cluster, the multipath waves have scattered diffuse waves with identical power and a specular component with certain arbitrary power. The envelope signal of the - shadowed RV can be expressed as [23]
where is the number of the multipath clusters, and and are mutually independent zero-mean Gaussian RVs with variance, i.e., . Hence, the total power of the scattered components for each cluster is . Moreover, represents the dominant component of the i-th cluster with a power given by , where and are real numbers. The parameter defined as the ratio between the total power of the dominant components and the total power of the scattered waves can be computed as , where . The specular components for each cluster are subject to the same common shadowing fluctuation, denoted by the random amplitude , which follows a Gamma RV with scale parameter and spreading parameter . The classical fading channel models that are included in the - shadowed distribution can be found in ([23] Table I). Again, let be the instantaneous SNR for the signal under the - shadowed model. So, the PDF and CDF of the RV are given as in [23] by
where is the average SNR of the RV , i.e, . Finally, the PDF of the RV , which follows a Gamma distribution, is given by [24]
where for denotes the shadowing severity index of either the FMR or the - shadowed fading channels, respectively. Here, it is worth pointing out that shadowing effects are a paramount factor to be taken into account in the performance analysis of dense networks or mm-Wave communications. Based on these channel characteristics, the - shadowed fading model finds applicability in several real-world applications, including underwater acoustic communications (UAC), body-centric fading channels, unmanned aerial vehicle (UAV) systems, land mobile satellite (LMS), device-to-device (D2D) communications, and 5G heterogeneous cellular systems [27].
3. Empirical Validation
In this section, we introduce the methodology used to validate the goodness of fit between the theoretical CDFs of the fading models and the empirical measurements of the small-scale fading for mm-Wave outdoor communications in the 28 GHz band. Details on the specific measurement configuration can be found in [11]. As in [11], we use the CDF envelope of the received signal for performance comparisons between different fading channel models. Furthermore, the mean square error (MSE) was adopted to define the error factor, , in order to quantify the goodness of fit between the empirical data and the theoretical CDFs, denoted by , respectively. Therefore, mathematically, can be formulated as
where
is the empirical CDF data obtained from [11], and can be obtained from (3) or (10) through a standard change of variables, i.e., . It is worth mentioning that the error factor given in (12) is used to obtain the estimated parameters for the following channel models: (i) Rayleigh, (ii) Nakagami-m, (iii) - shadowed, and (iv) FMR. Now, in order to find the optimal values of the theoretical CDF fading parameters in (3) and (10) for the different channel models, we use the iterative PSO algorithm. Next, we briefly describe the background of PSO, which builds up the foundation for the proposed estimation of the CDF parameters.
3.1. Overview of PSO
PSO is a learning technique based on the social behavior of birds flocking or fish schooling—it is an evolutionary computing method focused on the biological form of evolution [28].
In typical PSO, a set of candidate solutions called “particles” are placed in the search space of some problem, and each evaluates the objective function (OF) at its current location. Each particle defines its movement through the search space by using some historical aspects of its own current and best locations with those of one or more swarm members. The next iteration takes place after all the particles have moved, following the same pattern. After a specified number of iterations, the swarm as a whole will likely approach the OF’s optimal value, just like a flock of birds collectively foraging for food [29].
Each particle in the swarm comprises three components—namely, current position , the previous best position , and the velocity . On each iteration of the PSO algorithm, is evaluated in the OF. If is better than any that have been evaluated in the OF so far, the coordinates of are stored in . The value of the best OF so far is stored in a variable named for comparison on subsequent iterations. The aim is to keep finding better and then updating and pbest. In addition, each particle interacts with some other particles and is affected by the best global position, , found by any particle of its topological neighborhood. A new is chosen by adding coordinates to , and the PSO algorithm operates by adjusting , which can be interpreted as a search step size. Each particle’s velocity is iteratively adjusted so that the particle stochastically oscillates around the and locations [29].
Based on the above, the velocity and position rules of each particle are given, respectively, by [28]
where pop is the size of the population, and denotes random numbers sampled from a uniform distribution on the interval . w is the inertia or habit term—the particle continues to move in the direction in which it had previously moved. is the memory—the particle is attracted to the best location in its trajectory. is the cooperation—the particle is attracted to all particles’ best location in the swarm.
All parameters in the PSO algorithm, i.e., pop, number of iterations (iter), and , are fixed values at the beginning of the process. In this context, pop and iter are often set empirically based on the difficulty of a problem at hand [29]. For our optimization problem, several tests were carried out for different values of both pop and iter. Here, we found that the minimum values for ensuring convergence were and . Concerning the w coefficient, high values (e.g., 2) correspond to a system where particles perform extensive exploration. However, once the particles find the optimal possible position, w should gradually decrease in each iteration to avoid leaving the desired solution space [29]. Finally, and , also known as acceleration coefficients, are typically set to a value of [30], although assigning different values to and sometimes leads to improved performance [31]. Based on our exhaustive tests, we found that the configuration enhances our optimization problem’s convergence speed. An informative flowchart with the steps for implementing PSO is given in Figure 1. Here, it can be observed that, in the PSO algorithm, the search space is influenced by both the movements and positions of the particles.
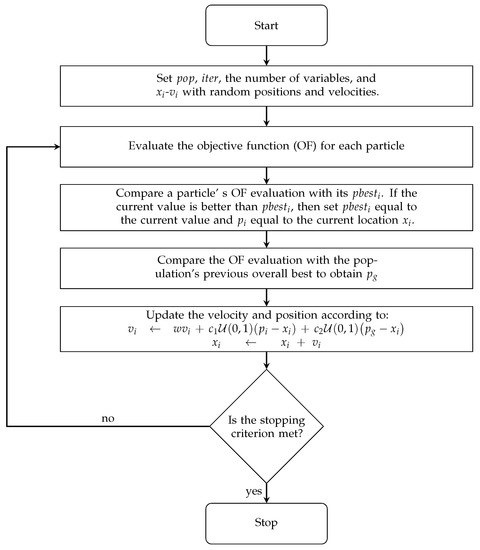
Figure 1.
Basic flowchart of PSO.
3.2. Optimization Procedure
Based on the procedure given in Figure 1, we implement the PSO method inAlgorithm 1 to solve the formulated optimization problem in (12) for each fading channel model. Specifically, we set the following parameters: (i) Rayleigh: , , , ; (ii) Nakagami-m: , , , . For notation convenience, we denote vectors by lowercase bold letters and matrices by uppercase bold letters.
For informative purposes, we detail the procedure to obtain the generalized fading models’ OF below.
From (3), the envelope CDF of the FMR distribution, i.e., , is given by
Note that by substituting (16) in (12), the optimization problem is given in terms of well-known functions in the communication theory literature (e.g., lower incomplete gamma function). By truncating (16) up to the first terms, this yields
The truncation error of to the first terms can be expressed as
Here, the number of terms needed in (18) to achieve a accuracy was . Concerning the - shadowed model, departing from (10), the envelope CDF distribution, i.e., is given by
Unfortunately, there are no mathematical packages available in MATLAB or Mathematica Wolfram to compute the bivariate confluent hypergeometric function, . To overcome this issue, we resort to an alternative representation of , expressed as [23] (Equation (34))
Here, by substituting (20) into (19), and then by truncating the resulting expression up to the first terms, we get
Applying the truncation error, i.e., substituting (19) and (21) into (18), the number of necessary terms to achieve a relative error of less than 2% is .
On the other hand, in order to obtain the empirical results presented in [11] (Figure 6), i.e., in (12), we use the WebPlotDigitizer. For instance, with the software’s help, the empirical data corresponding to the CDF for the LOS case comprise two vectors of the same length M (see (12)). The first vector denotes extracted values in decibels (r-axis), and the second represents empirical CDF values on a linear scale. Then, by replacing the empirical data vectors in the OF given in (12), this yields
where is given by (17) or (21) depending on the fading model at hand. In this context, for the FMR model, after putting (17) into (22), the elapsed time in the PSO method for estimating the fading parameters, i.e., , takes some minutes (e.g., ≈12 min for LOS and ≈13 min for the NLOS case). Likewise, after inserting (21) into (22) for the - shadowed case, the average time demanded by the PSO algorithm for adjusting is several minutes (e.g., ≈22 min for LOS and ≈25 min for the NLOS case).
Finally, we provide a quick explanation of the functions implemented in Algorithm 1. The PSO function returns the following results: (1) fobest: minimum value of the objective function, i.e., , in (12); (2) xgbest: optimal values of the fading parameters (e.g, for the - shadowed model) of the the theoretical CDF that minimize (12). It is worth pointing out that the number of optimal values returned by the PSO algorithm depends on the fading channel model. For instance, for the Nakagami-m case, the number of optimal values returned in xgbest is two, namely, and .
| Algorithm 1 PSO | ||
| functionOBJECTIVEFUNC() | ||
| 2: | ▹ Signal level vector in dB | |
| 3: | ||
| 4: | ▹ Empirical data [11] (Figure 6) | |
| 5: Equation (17) or Equation (21) | ▹ Substituting and is given by (13). | |
| 6: | ||
| 7: for to aux do | ||
| 8: | ||
| 9: end for | ||
| 10: Y ← | ▹ Objective Function, i.e., , given in Equation(22) | |
| 11: return | ||
| 12:end function | ||
| 13:function PSO | ||
| 14: | ▹ Number of iterations | |
| 15: | ▹ Set population size | |
| 16: | ▹ Weighting coefficient for personal best position | |
| 17: | ▹ Weighting coefficient for global best position | |
| 18: | ▹ Set inertia weigh | |
| 19: | ▹ Set number of variables (i.e., fading parameters) | |
| 20: | ▹ Set min values | |
| 21: | ▹ Set max values | |
| 22: for to do | ▹ Set initial position | |
| 23: ; | ||
| 24: end for | ||
| 25: OBJECTIVEFUN | ▹ Evaluation of the objective function (OF) | |
| 26: [, ] ← min() ▹: min value of the OF; : index of the min OF | ||
| 27: | ▹ best values that minimize the OF | |
| 28: | ||
| 29: | ||
| 30: | ▹ Set initial velocity of the particles | |
| 31: for to do | ||
| 32: ; ▹ Update particle velocity | ||
| 33: | ▹ Update particle positions | |
| 34: OBJECTIVEFUN | ▹ Update the value of the OF | |
| 35: ▹ MEMORY | ||
| 36: (find ) ← (find ); | ||
| 37: (find ) ← (find ); | ||
| 38: ▹ COOPERATION | ||
| 39: [, ] ← min() | ||
| 40: | ||
| 41: ▹ Decrease inertia weigh | ||
| 42: | ||
| 43: end for | ||
| 44: return | ||
| 45:end function | ||
4. Numerical Results and Discussion
This section first shows how the fading parameters of the - and FMR fading models affect the PDF’s shape. All PDF curves are presented as a function of the envelope r; these can be easily derived from (2) and (9) by a simple change of variables, i.e., . In addition, for the FMR case, we define a power ratio parameter similar to the well-known Rician K parameter, i.e., , with being the total average power of the specular components. Secondly, by using the MSE metric, we investigate which of the channel models’ theoretical CDFs best fit the experimental data of the envelope CDF obtained in [11]. Specifically, the curves labeled as “measured” in the figures below were obtained from [11] (Figure 6) by using software tools for extracting the underlying numerical data from figure plots—we used WebPlotDigitizer to accomplish this task. In our analysis, the channel models’ fading parameters (i.e., Rayleigh, Nakagami-m, FMR, and - shadowed) were estimated in the previous section with the help of the PSO algorithm, as shown in Table 1.

Table 1.
Cumulative distribution function (CDF) fitting parameters for the line-of-sight (LOS) and non-line-of-sight (NLOS) scenarios.
For the sake of comparison, the theoretical CDF of the FTR given in [14] is also included as a reference in our analysis. Notice that the FTR model is a particular case of the FMR when the number of specular dominant components in (3) is equal to two, i.e., . It is worth mentioning that in [14], the optimal values of the FTR model’s fading parameters were calibrated through the empirical measurements of [11] using the Kolmogorov–Smirnov (KS) statistical tool.
Figure 2 and Figure 3 plot the PDF curves for different fading parameter combinations of both the - shadowed and FMR distributions. From all traces, the versatility of the fading models mentioned above is clear. For instance, in Figure 2, we verify that the - shadowed model provides a unification of a variety of important fading distributions, including Rayleigh, Rice (Nakagami-n), Nakagami-m, Hoyt (Nakagami-q), Rician shadowed, -, and - distributions, to name a few (see ([23] Table 1) for more details). Because of the - shadowed generality, this model can characterize small-scale fading, which appears due to LOS or NLOS conditions, dominant specular components, and multipath clustering. In Figure 3, we plot the PDF curves of the FMR model by varying the number of specular rays for dB, , and . In addition, to seek readability, yet without loss of generality, the amplitudes of successive rays are expressed in terms of the amplitude of the first dominant component, that is, for , with . Considering this, we set: and for . Here, it can be observed that the FMR model exhibits an inherent multimodal behavior for small values of .
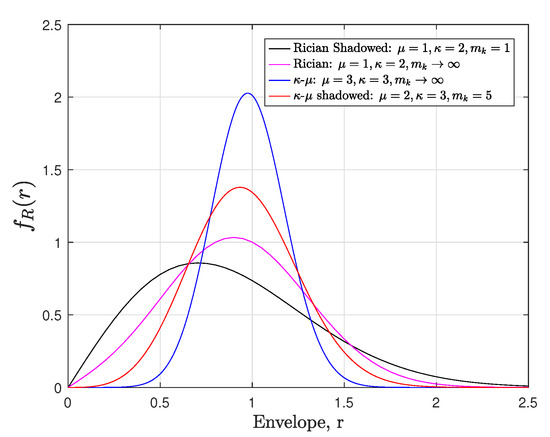
Figure 2.
Probability density function (PDF) curves of the - shadowed distribution for fixed .
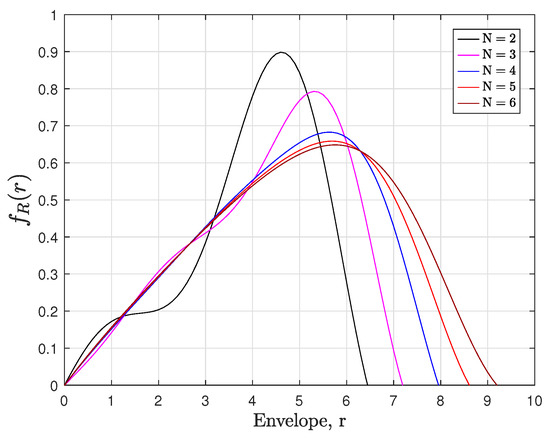
Figure 3.
PDF of the fluctuating multiple-ray (FMR) envelope for different numbers of dominant specular waves ().
Nevertheless, as the number of dominant components increases (e.g., ), the central limit theorem holds, and the PDF curves reduce to unimodal distributions (e.g., Rician for and Rayleigh for ).
In Figure 4 and Figure 5, we compare the theoretical CDFs with the empirical CDF for the cross-polarized LOS and NLOS scenarios described in [11]. From all curves in the LOS scenarios, we observe that the - shadowed model is the one that best fits the measured data, providing values closer to the true CDF than the other fading models. This performance is because this channel model offers more degrees of freedom of adjustment (i.e., ) compared to the conventional distributions. Notice that the factor for the LOS case () is larger than that for the NLOS () scenario, as expected. Based on this fact, we can infer that the Rayleigh and Nakagami-m models’ poor fit is because, in these models, . Furthermore, for the LOS scenario illustrated in Figure 4, an interesting observation can be made: The theoretical CDF - shadowed model makes a slight change in concavity (see the range from −10 to 5 dB) to continue the trend of the empirical CDF curve.
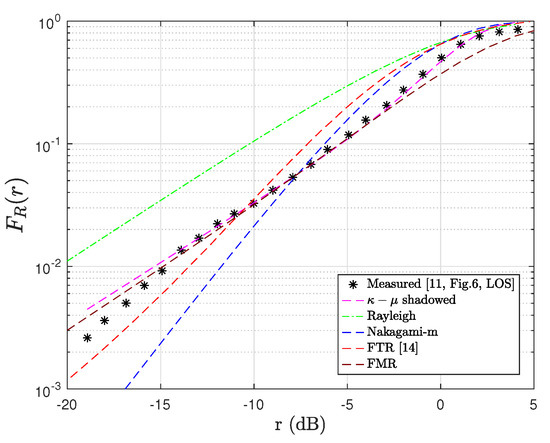
Figure 4.
Empirical vs. theoretical CDFs of the received signal amplitude in LOS scenarios.
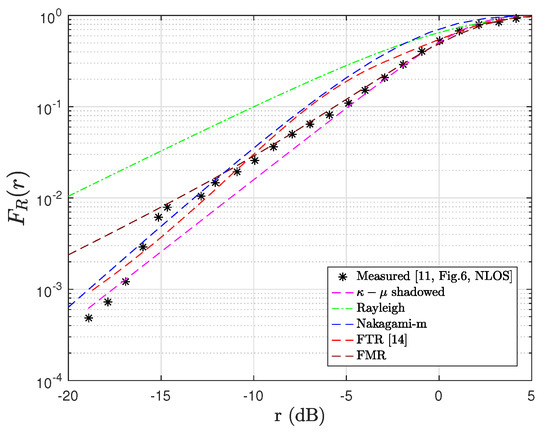
Figure 5.
Empirical vs. theoretical CDFs of the received signal amplitude in NLOS scenarios.
This flexibility of adjustment is because the parameter plays a key role in the goodness of fit, as it enables the theoretical CDF to modify its concavity or convexity (i.e., inflection points). On the other hand, for NLOS scenarios, it is clear that the FMR model with rays provides the best fit performance. In the same way as the - shadowed distribution, the FMR model can also modify the concavity and convexity of the theoretical curve through the parameter in order to achieve a better fit to the measured data. Regarding the performance of the FTR model, it can be seen that this distribution offers a better fit to the experimental data than the Rayleigh and Nakagami-m counterparts. In short, from all curves, it is clear that the generalized fading channel models provide a better fit than the classical models for modeling small-scale fading in mm-Wave wireless links. On the other hand, it is worth mentioning that both the - shadowed and FMR models are mathematically much more intricate than the traditional fading channels. This aspect increases the computational cost of the PSO process for estimating the CDF parameters (see Section 3.2). Therefore, we point out some ideas for overcoming these mathematical limitations of generalized fading models in the following. The FMR distribution has a comparable mathematical complexity to that of models obtained as special cases, such as TWDP and FTR. Based on this, using either the FTR or TWDP would not significantly improve the PSO’s performance in terms of time consumption. In light of this, an interesting research field is the approximation of the FMR model by a finite mixture of Nakagami-m distributions where the parameters can be adjusted by using learning algorithms (e.g., unsupervised expectation maximization [32]). This fact will undoubtedly improve the mathematical tractability of the FMR model. Concerning the - shadowed model, it is noteworthy that simple approximations of the the model can be used with the aim of reducing the time required by the PSO method and the mathematical complexity. In particular, the - shadowed CDF can be represented as (i) an infinite series in terms of Laguerre polynomials [27], and (ii) an infinite [33] and finite [34] mixture of gamma distributions. However, some constraints need to be considered when using such approximations (e.g., only integer fading parameters and convergence issues in the Laguerre polynomial). An alternative to these issues is that, as in the FMR case, the CDF distribution of the - shadowed model can be approximated using learning algorithms.
Finally, Table 2 summarizes the MSE values for the statistical channel models in all of the scenarios under study. From the tabulated results, it can be confirmed that the best goodness of fit (highlighted in bold) between the empirical and theoretical CDFs is achieved with the - shadowed and FMR models for the LOS and NLOS cases, respectively. Finally, it is worth mentioning that in the current literature, several research works have been developed under the premise of the use of both - shadowed and FMR models. For instance, we can state the following: (1) heterogeneous 5G cellular systems over - shadowed fading channels [27]; (2) physical layer security over - shadowed [35] and FMR [36] fading channels; (3) cooperative networks over FTR channels [37]; (4) the next mobile communications over FTR channels [38].

Table 2.
Mean square error (MSE) between the theoretical and empirical CDFs for the LOS and NLOS scenarios.
5. Conclusions
The lack of information on statistical channel modeling for future wireless communication networks has motivated researchers to carry out measurement campaigns to understand the channels’ behavior in mm-Wave frequencies more accurately. This paper has contributed to this research direction by investigating the goodness of fit between the experimental CDFs and theoretical CDFs of traditional/generalized fading channel models for LOS and NLOS scenarios. The fading models (i.e., - shadowed and FMR models) that best fit the empirical data were chosen by using the MSE statistical tool. Based on the numerical results, it was possible to verify that the generalized models—namely, the - shadowed and FMR models—provides the smallest MSE estimation error compared to the conventional models in all analyzed scenarios. All in all, we conclude that the generalized fading models examined in this paper can be satisfactorily used in this hard mm-Wave band.
Author Contributions
Conceptualization, J.D.V.S.; methodology, L.U.-A. and M.C.P.P.; writing—original draft preparation, J.D.V.S.; writing—review and editing, L.U.-A. and M.C.P.P.; supervision, L.U.-A. and M.C.P.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Escuela Politécnica Nacional for development of the project PIGR-19-06-“Seguridad en comunicaciones móviles cooperativas de 5G usando tecnologías de capa física”.
Acknowledgments
José David Vega Sánchez is the recipient of a teaching assistant fellowship from Escuela Politécnica Nacional for doctoral studies in Electrical Engineering.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, S.; Xiao, L.; Han, Z.; Tang, Y. Eliminating NB-IoT Interference to LTE System: A Sparse Machine Learning-Based Approach. IEEE Internet Things J. 2019, 6, 6919–6932. [Google Scholar] [CrossRef]
- Vega Sánchez, J.D.; Urquiza-Aguiar, L.; Paredes Paredes, M.C.; Moya Osorio, D.P. Survey on physical layer security for 5G wireless networks. Ann. Telecommun. 2020. [Google Scholar] [CrossRef]
- Liu, D.; Hong, W.; Rappaport, T.S.; Luxey, C.; Hong, W. What will 5G Antennas and Propagation Be? IEEE Trans. Antennas Propag. 2017, 65, 6205–6212. [Google Scholar] [CrossRef]
- Wu, Y.; Khisti, A.; Xiao, C.; Caire, G.; Wong, K.; Gao, X. A Survey of Physical Layer Security Techniques for 5G Wireless Networks and Challenges Ahead. IEEE J. Sel. Areas Commun. 2018, 36, 679–695. [Google Scholar] [CrossRef]
- Moya Osorio, D.P.; Vega Sánchez, J.D.; Alves, H. Physical-Layer Security for 5G and Beyond. In The Essential 5G Reference Online; John Wiley & Sons: Hoboken, NJ, USA, 2019; Chapter 1; pp. 1–19. [Google Scholar] [CrossRef]
- Yang, N.; Wang, L.; Geraci, G.; Elkashlan, M.; Yuan, J.; Di Renzo, M. Safeguarding 5G wireless communication networks using physical layer security. IEEE Commun. Mag. 2015, 53, 20–27. [Google Scholar] [CrossRef]
- Koymen, O.H.; Partyka, A.; Subramanian, S.; Li, J. Indoor mm-Wave Channel Measurements: Comparative Study of 2.9 GHz and 29 GHz. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, C.; Ghazal, A.; Ai, B.; Liu, Y.; Fan, P. Channel Measurements and Models for High-Speed Train Communication Systems: A Survey. IEEE Commun. Surv. Tutor. 2016, 18, 974–987. [Google Scholar] [CrossRef]
- Hur, S.; Baek, S.; Kim, B.; Chang, Y.; Molisch, A.F.; Rappaport, T.S.; Haneda, K.; Park, J. Proposal on Millimeter-Wave Channel Modeling for 5G Cellular System. IEEE J. Sel. Top. Signal Process. 2016, 10, 454–469. [Google Scholar] [CrossRef]
- Romero-Jerez, J.M.; Lopez-Martinez, F.J.; Paris, J.F.; Goldsmith, A.J. The Fluctuating Two-Ray Fading Model: Statistical Characterization and Performance Analysis. IEEE Trans. Wirel. Commun. 2017, 16, 4420–4432. [Google Scholar] [CrossRef]
- Samimi, M.K.; MacCartney, G.R.; Sun, S.; Rappaport, T.S. 28 GHz Millimeter-Wave Ultrawideband Small-Scale Fading Models in Wireless Channels. In Proceedings of the 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15–18 May 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Mavridis, T.; Petrillo, L.; Sarrazin, J.; Benlarbi-Delaï, A.; De Doncker, P. Near-Body Shadowing Analysis at 60 GHz. IEEE Trans. Antennas Propag. 2015, 63, 4505–4511. [Google Scholar] [CrossRef]
- Lin, Z.; Du, X.; Chen, H.; Ai, B.; Chen, Z.; Wu, D. Millimeter-Wave Propagation Modeling and Measurements for 5G Mobile Networks. IEEE Wirel. Commun. 2019, 26, 72–77. [Google Scholar] [CrossRef]
- Romero-Jerez, J.M.; Lopez-Martinez, F.J.; Paris, J.F.; Goldsmith, A. The Fluctuating Two-Ray Fading Model for mm-Wave Communications. In Proceedings of the 2016 IEEE Globecom Workshops (GC Wkshps), Washington, DC, USA, 4–8 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Zochmann, E.; Caban, S.; Mecklenbr, C.F.; Pratschner, S.; Lerch, M.; Schwarz, S.; Rupp, M. Better than Rician: Modelling millimetre wave channels as two-wave with diffuse power. EURASIP J. Wirel. Commun. Netw. 2019, 3, 1–21. [Google Scholar] [CrossRef]
- Zöchmann, E.; Blumenstein, J.; Marsalek, R.; Rupp, M.; Guan, K. Parsimonious Channel Models for Millimeter Wave Railway Communications. In Proceedings of the 2019 IEEE Wireless Communications and Networking Conference (WCNC), Marrakesh, Morocco, 15–18 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zöchmann, E.; Hofer, M.; Lerch, M.; Pratschner, S.; Bernadó, L.; Blumenstein, J.; Caban, S.; Sangodoyin, S.; Groll, H.; Zemen, T.; et al. Position-Specific Statistics of 60 GHz Vehicular Channels During Overtaking. IEEE Access 2019, 7, 14216–14232. [Google Scholar] [CrossRef]
- Groll, H.; Zöchmann, E.; Pratschner, S.; Lerch, M.; Schützenhöfer, D.; Hofer, M.; Blumenstein, J.; Sangodoyin, S.; Zemen, T.; Prokeš, A.; et al. Sparsity in the Delay-Doppler Domain for Measured 60 GHz Vehicle-to-Infrastructure Communication Channels. In Proceedings of the 2019 IEEE International Conference on Communications Workshops (ICC Workshops), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Marins, T.R.R.; dos Anjos, A.A.; Peñarrocha, V.M.R.; Rubio, L.; Reig, J.; de Souza, R.A.A.; Yacoub, M.D. Fading Evaluation in the mm-Wave Band. IEEE Trans. Commun. 2019, 67, 8725–8738. [Google Scholar] [CrossRef]
- Dos Anjos, A.A.; Marins, T.R.R.; Da Silva, C.R.N.; Peñarrocha, V.M.R.; Rubio, L.; Reig, J.; De Souza, R.A.A.; Yacoub, M.D. Higher Order Statistics in a mmWave Propagation Environment. IEEE Access 2019, 7, 103876–103892. [Google Scholar] [CrossRef]
- Zöchmann, E.; Groll, H.; Pratschner, S. A Small-Scale Fading Model for Overtaking Vehicles in a Millimeter Wave Communication Link. In Proceedings of the 2019 IEEE 20th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Cannes, France, 2–5 July 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Romero-Jerez, J.M.; Lopez-Martinez, F.J.; Pena-Martin, J.P.; Abdi, A. Stochastic Fading Channel Models with Multiple Dominant Specular Components for 5G and Beyond. arXiv 2019, arXiv:1905.03567. [Google Scholar]
- Paris, J.F. Statistical Characterization of κ-μ Shadowed Fading. IEEE Trans. Veh. Technol. 2014, 63, 518–526. [Google Scholar] [CrossRef]
- Chun, Y.J. A Generalized Fading Model with Multiple Specular Components. arXiv 2018, arXiv:1810.05258. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 10th ed.; Dover: New York, NY, USA, 1972. [Google Scholar]
- Brychkov, Y.A.; Saad, N. Some formulas for the Appell function F1a,b,b′;c;w,z. Integral Transform. Spec. Funct. 2012, 23, 793–802. [Google Scholar] [CrossRef]
- Chun, Y.J.; Cotton, S.L.; Dhillon, H.S.; Lopez-Martinez, F.J.; Paris, J.F.; Yoo, S.K. A Comprehensive Analysis of 5G Heterogeneous Cellular Systems Operating Over κ – μ Shadowed Fading Channels. IEEE Trans. Wirel. Commun. 2017, 16, 6995–7010. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. An overview. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Simpson, P.; Dobbins, R. Computational Intelligence PC Tools; Academic Press Professional: San Diego, CA, USA, 1996; Chapter 6; pp. 212–226. [Google Scholar]
- Suganthan, P.N. Particle swarm optimiser with neighbourhood operator. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1958–1962. [Google Scholar] [CrossRef]
- Sánchez, J.D.V.; Urquiza-Aguiar, L.; Paredes, M.C.P. An Accurate, Fast Approximation for the Sum of Fading Random Variables via Expectation Maximization Applications to Diversity Systems. IEEE Access 2018, 6, 42616–42630. [Google Scholar] [CrossRef]
- Ramirez-Espinosa, P.; Lopez-Martinez, F.J. On the Utility of theInverse Gamma Distribution in Modeling Composite Fading Channels. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, USA, 9–13 December 2019. [Google Scholar]
- Lopez-Martinez, F.J.; Paris, J.F.; Romero-Jerez, J.M. The κ- μ Shadowed Fading Model With Integer Fading Parameters. IEEE Trans. Veh. Technol. 2017, 66, 7653–7662. [Google Scholar] [CrossRef]
- Vega Sánchez, J.D.; Moya Osorio, D.P.; Lopez-Martinez, J.; Paredes Paredes, M.C.; Urquiza-Aguiar, L. Information-Theoretic Security of MIMO Networks under κ-μ Shadowed Fading Channels. arXiv 2020, arXiv:2005.02441. [Google Scholar]
- Vega Sánchez, J.D.; Moya Osorio, D.P.; Lopez-Martinez, J.; Paredes Paredes, M.C.; Urquiza-Aguiar, L. On the Secrecy Performance Over N-Wave with Diffuse Power Fading Channel. IEEE Trans. Veh. Technol. 2020, 69, 15137–15148. [Google Scholar] [CrossRef]
- Hashemi, H.; Haghighat, J.; Eslami, M.; Navaie, K. Amplify-and-Forward Relaying With Maximal Ratio Combining Over Fluctuating Two-Ray Channel: Non-Asymptotic and Asymptotic Performance Analysis. IEEE Trans. Commun. 2020, 68, 7446–7459. [Google Scholar] [CrossRef]
- Shi, B.; Pallotta, L.; Giunta, G.; Hao, C.; Orlando, D. Parameter Estimation of Fluctuating Two-Ray Model for Next Generation Mobile Communications. IEEE Trans. Veh. Technol. 2020, 69, 8684–8697. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).