Robust Autoregression with Exogenous Input Model for System Identification and Predicting
Abstract
1. Introduction
2. Materials and Methods
2.1. SISO ARX
2.2. MISO ARX
2.3. Lp (p ≤ 1) Norm-Based ARX Model
| Algorithm 1 Lp (p ≤ 1) BFGS |
| Require: Iteration number n, termination error , initialize W as a random nonzero 2q-dimensional vector, initial pseudo-Hessian matrix . For k from 1 to n do Compute the gradient by if then break end if Solve the coupled linear equations , and calculate Find the optimal learning velocity by Update ARX parameter W by Update by Equation (16) end for |
3. Results
3.1. Simulation Study
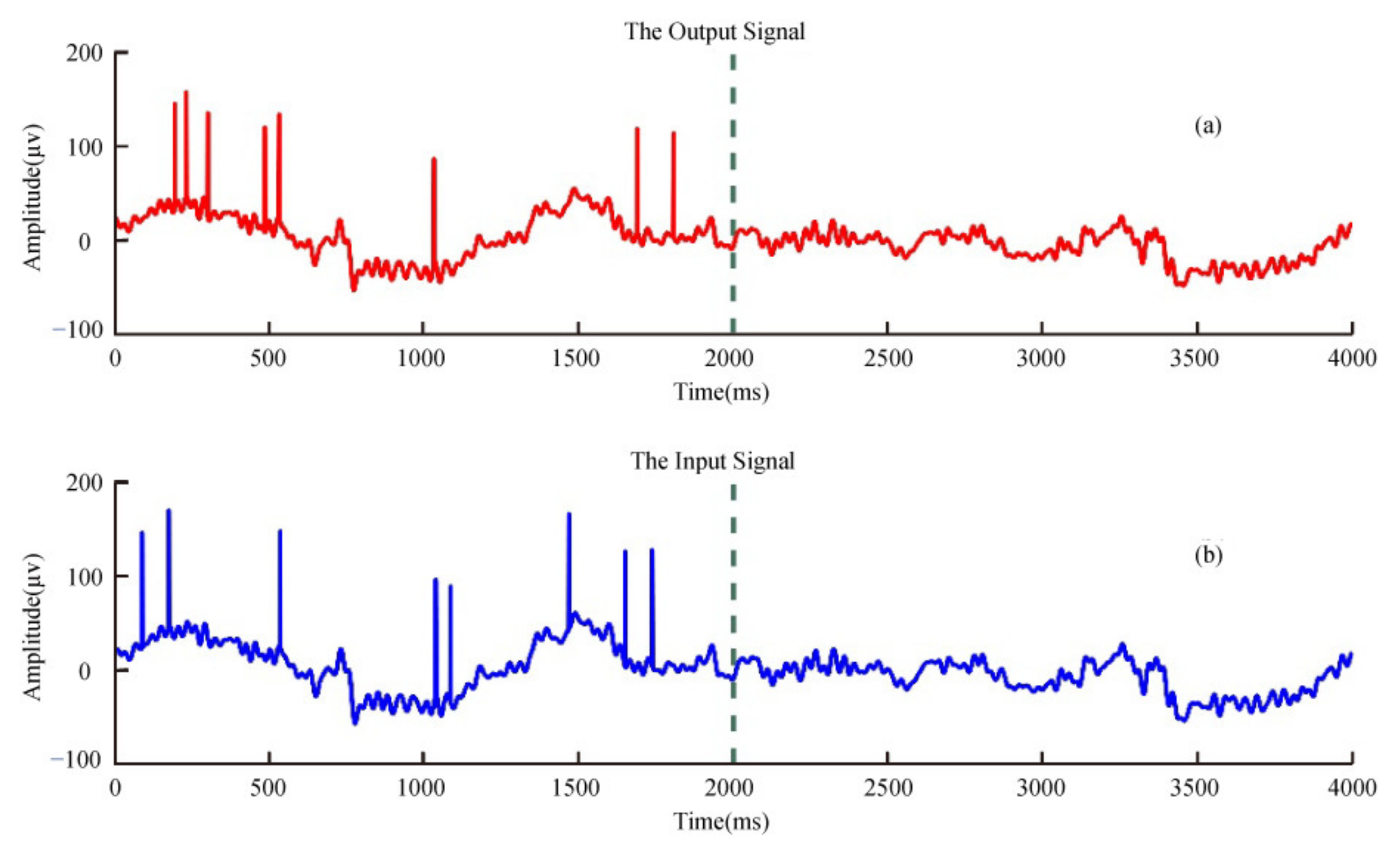
3.1.1. Experimental Dataset
3.1.2. Effect of Outlier Occurrence Rate
3.1.3. Effect of Outlier Strength
3.2. Real Data Studies
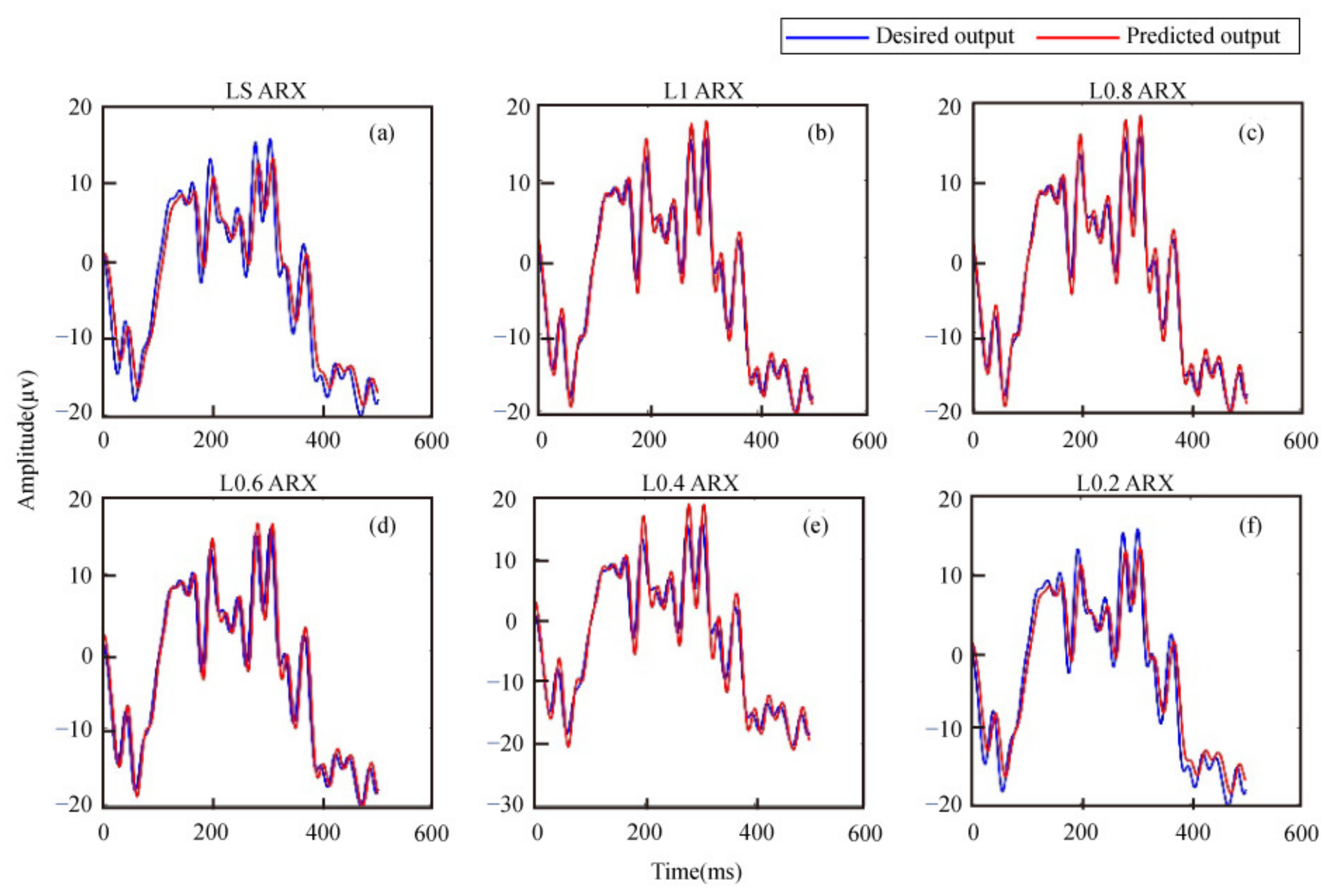
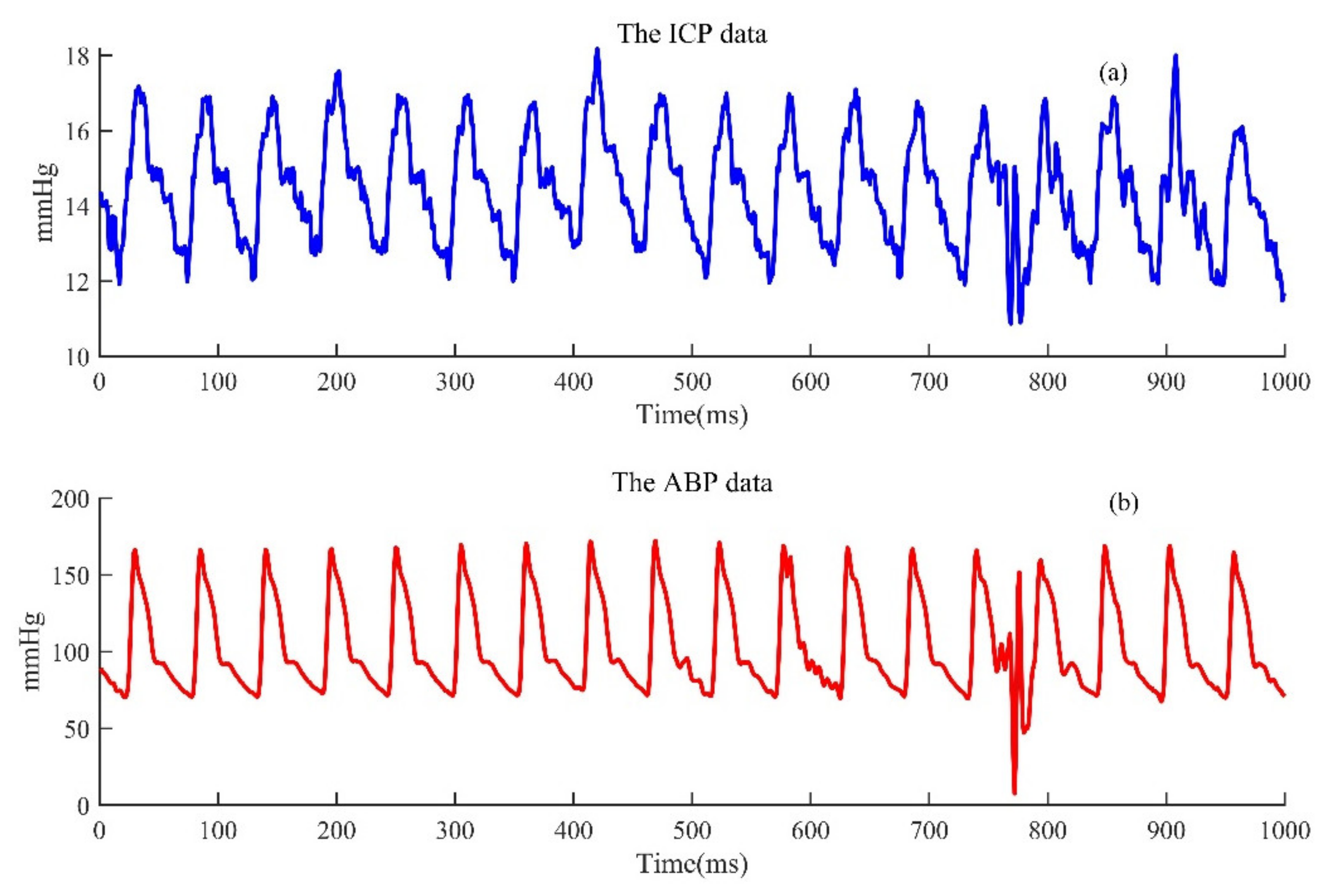
3.2.1. Application to Actual EEG Recordings
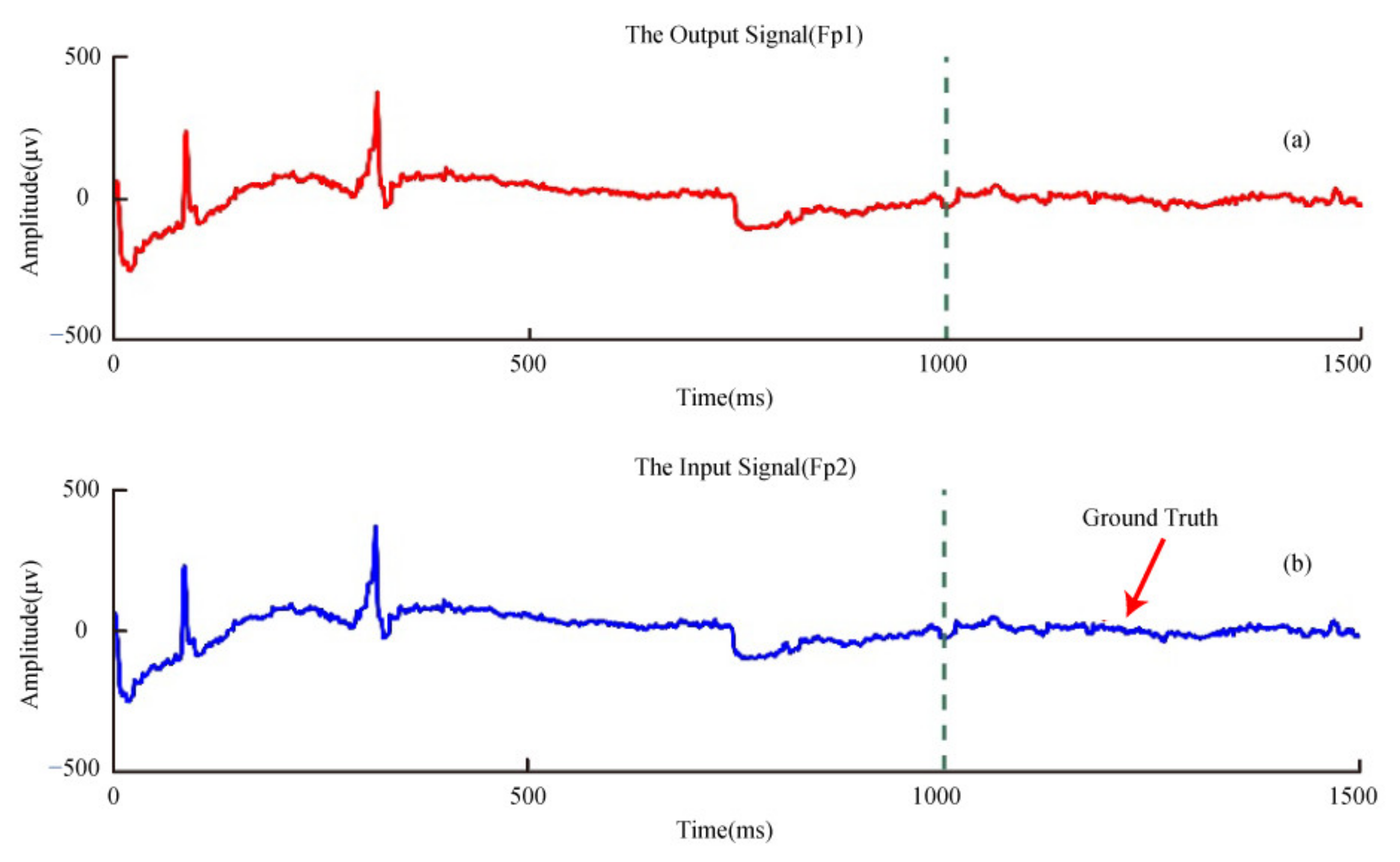
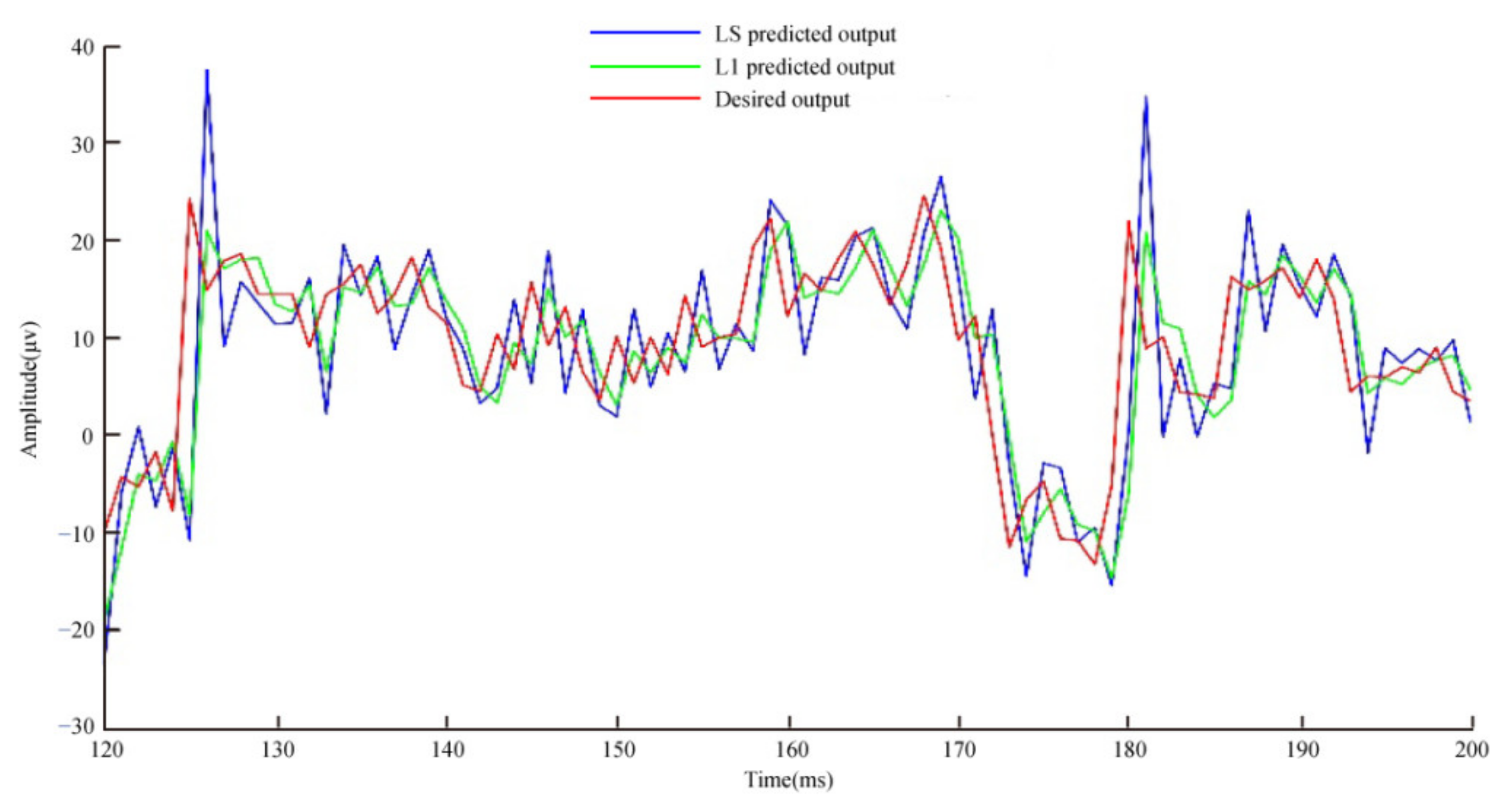
3.2.2. Application to Actual EEG Recordings
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Monden, Y.; Yamada, M.; Arimoto, S. Fast Algorithm for Identification of an Arx Model and Its Order Determination. IEEE Trans. Acoust. Speech Signal Proces. 1982, 30, 390–399. [Google Scholar] [CrossRef]
- Isaksson, A.J. Identification of Arx-Models Subject to Missing Data. IEEE Trans. Autom. Control 2002, 38, 813–819. [Google Scholar] [CrossRef]
- Jin, G.D.; Lu, L.B.; Zhu, X.F. A Method of Order Determination for Arx and Arma Models Based on Nonnegative Garrote. Appl. Mech. Mater. 2014, 721, 496–499. [Google Scholar] [CrossRef]
- Nelles, O. Nonlinear System Identification: From Classical Approaches to Neuralnetworks and Fuzzy Models. Appl. Ther. 2001, 6, 717–721. [Google Scholar]
- Xu, P.; Kasprowicz, M.; Bergsneider, M.; Hu, X. Improved Noninvasive Intracranial Pressure Assessment with Nonlinear Kernel Regression. IEEE Trans. Inform. Technol. Biomed. 2010, 14, 971–978. [Google Scholar]
- Wang, Z.; Xu, P.; Liu, T.; Tian, Y.; Lei, X.; Yao, D. Robust Removal of Ocular Artifacts by Combining Independent Component Analysis and System Identification. Biomed. Signal Proces. Control 2014, 10, 250–259. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Breakspear, M.; Cunnington, R. Fusing Concurrent Eeg–Fmri with Dynamic Causal Modeling: Application to Effective Connectivity During Face Perception. NeuroImage 2013, 102, 60–70. [Google Scholar] [CrossRef]
- Gourévitch, B.; Kay, L.M.; Martin, C. Directional Coupling from the Olfactory Bulb to the Hippocampus During a Go/No-Go Odor Discrimination Task. J. Neurophysiol. 2010, 103, 2633–2641. [Google Scholar] [CrossRef]
- Zhao, Y.; Billings, S.A.; Wei, H.-L.; Sarrigiannis, P.G. A Parametric Method to Measure Time-Varying Linear and Nonlinear Causality with Applications to Eeg Data. IEEE Trans. Biomed. Eng. 2013, 60, 3141–3148. [Google Scholar] [CrossRef]
- Siuly, S.; Li, Y. Discriminating the Brain Activities for Brain–Computer Interface Applications through the Optimal Allocation-Based Approach. Neural Comput. Appl. 2015, 26, 799–811. [Google Scholar] [CrossRef]
- Burke, D.P.; Kelly, S.P.; De Chazal, P.; Reilly, R.B.; Finucane, C. A Parametric Feature Extraction and Classification Strategy for Brain-Computer Interfacing. IEEE Trans. Neural Syst. Rehabil. Eng. 2005, 13, 12–17. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wei, H.-L.; Billings, S.A.; Sarrigiannis, P. Time-Varying Model Identification for Time–Frequency Feature Extraction from Eeg Data. J. Neurosci. Meth. 2011, 196, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Qidwai, U.; Shakir, M.; Malik, A.S.; Kamel, N. Parametric Modeling of Eeg Signals with Real Patient Data for Simulating Seizures and Pre-Seizures. In Proceedings of the 2013 International Conference on Human Computer Interactions, Chennai, India, 23–24 August 2013; pp. 1–5. [Google Scholar]
- Yu, H.; Guo, X.; Qin, Q.; Deng, Y.; Wang, J.; Liu, J.; Cao, Y. Synchrony Dynamics Underlying Effective Connectivity Reconstruction of Neuronal Circuits. Phys. Stat. Mech. Appl. 2017, 471, 674–687. [Google Scholar] [CrossRef]
- Yu, H.; Wu, X.; Cai, L.; Deng, B.; Wang, J. Modulation of Spectral Power and Functional Connectivity in Human Brain by Acupuncture Stimulation. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 977–986. [Google Scholar] [CrossRef]
- Liao, W.; Mantini, D.; Zhang, Z.; Pan, Z.; Ding, J.; Gong, Q.; Yang, Y.; Chen, H. Evaluating the Effective Connectivity of Resting State Networks Using Conditional Granger Causality. Biol. Cybern. 2010, 102, 57–69. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Putrino, D.; Ghosh, S.; Brown, E.N. A Granger Causality Measure for Point Process Models of Ensemble Neural Spiking Activity. PLoS Comput. Biol. 2011, 7, e1001110. [Google Scholar] [CrossRef] [PubMed]
- Kwak, N. Principal Component Analysis Based on L1-Norm Maximization. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1672–1680. [Google Scholar] [CrossRef]
- Xu, P.; Tian, Y.; Chen, H.; Yao, D. Lp Norm Iterative Sparse Solution for Eeg Source Localization. IEEE Trans. Biomed. Eng. 2007, 54, 400–409. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Xu, P.; Zhang, R.; Guo, L.; Yao, D. L1 Norm Based Common Spatial Patterns Decomposition for Scalp Eeg Bci. Biomed. Eng. Online 2013, 12, 77. [Google Scholar] [CrossRef]
- Mattsson, P.; Zachariah, D.; Stoica, P. Recursive Identification Method for Piecewise Arx Models: A Sparse Estimation Approach. IEEE Trans. Signal Proces. 2016, 64, 5082–5093. [Google Scholar] [CrossRef]
- Guo, S.; Wang, Z.; Ruan, Q. Enhancing Sparsity Via ℓp (0<P<1) Minimization for Robust Face Recognition. Neurocomputing 2013, 99, 592–602. [Google Scholar]
- Chartrand, R.; Staneva, V. Restricted Isometry Properties and Nonconvex Compressive Sensing. Inverse Probl. 2008, 24, 035020. [Google Scholar] [CrossRef]
- Chartrand, R. Exact Reconstruction of Sparse Signals Via Nonconvex Minimization. IEEE Signal Process. Lett. 2007, 14, 707–710. [Google Scholar] [CrossRef]
- Foucart, S.; Lai, M.-J. Sparsest Solutions of Underdetermined Linear Systems Via ℓq-Minimization for 0 <Q ⩽ 1. Comput. Harmon. Anal. 2009, 26, 395–407. [Google Scholar]
- Nie, F.; Huang, Y.; Wang, X.; Huang, H. New Primal Svm Solver with Linear Computational Cost for Big Data Classifications. In Proceedings of the 31st International Conference on International Conference on Machine Learning, Beijing, China, 22–24 June 2014; Volume 32, pp. II-505–II-513. [Google Scholar]
- Ye, Q.; Fu, L.; Zhang, Z.; Zhao, H.; Naiem, M. Lp-and Ls-Norm Distance Based Robust Linear Discriminant Analysis. Neural Netw. 2018, 105, 393–404. [Google Scholar] [CrossRef]
- Wang, H.; Nie, F.; Cai, W.; Huang, H. Semi-Supervised Robust Dictionary Learning Via Efficient L-Norms Minimization. In Proceedings of the IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013; pp. 1145–1152. [Google Scholar]
- Lustig, M.; Donoho, D.; Pauly, J.M. Sparse Mri: The Application of Compressed Sensing for Rapid Mr Imaging. Magn. Reson. Med. 2007, 58, 1182–1195. [Google Scholar] [CrossRef]
- Chartrand, R. Fast Algorithms for Nonconvex Compressive Sensing: Mri Reconstruction from Very Few Data. In Proceedings of the 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Boston, MA, USA, 28 June–1 July 2009; pp. 262–265. [Google Scholar]
- Li, P.; Wang, X.; Li, F.; Zhang, R.; Ma, T.; Peng, Y.; Lei, X.; Tian, Y.; Guo, D.; Liu, T. Autoregressive Model in the Lp Norm Space for Eeg Analysis. J. Neurosci. Methods 2015, 240, 170–178. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Huang, X.; Li, F.; Wang, X.; Zhou, W.; Liu, H.; Ma, T.; Zhang, T.; Guo, D.; Yao, D. Robust Granger Analysis in Lp Norm Space for Directed Eeg Network Analysis. IEEE Trans. Neural Syst. Rehabil. Eng. 2017, 25, 1959–1969. [Google Scholar] [CrossRef] [PubMed]
- Rahim, M.A.; Ramasamy, M.; Tufa, L.D.; Faisal, A. Iterative Closed-Loop Identification of Mimo Systems Using Arx-Based Leaky Least Mean Square Algorithm. In Proceedings of the 2014 IEEE International Conference on Control System, Computing and Engineering, Penang, Malaysia, 28–30 November 2014; pp. 611–616. [Google Scholar]
- Broyden, C.G. Quasi-Newton Methods and Their Application to Function Minimisation. Math. Comput. 1993, 21, 368–381. [Google Scholar] [CrossRef]
- Pavon, M. A Variational Derivation of a Class of Bfgs-Like Methods. Optimization 2018, 67, 2081–2089. [Google Scholar] [CrossRef]
- Goldfarb, D. A Family of Variable-Metric Methods Derived by Variational Means. Math. Comput. 1970, 24, 23–26. [Google Scholar] [CrossRef]
- Fletcher, R. A New Variational Result for Quasi-Newton Formulae. SIAM J. Optim. 1991, 1, 18–21. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of Quasi-Newton Methods for Function Minimization. Math. Comput. 1970, 24, 647–656. [Google Scholar] [CrossRef]
- Broyden, C.G. A Class of Methods for Solving Nonlinear Simultaneous Equations. Math. Comput. 1965, 19, 577–593. [Google Scholar] [CrossRef]
- Robitaille, B.; Marcos, B.; Veillette, M.; Payre, G. Quasi-Newton Methods for Training Neural Networks. WIT Trans. Inform. Commun. Technol. 1993, 2. [Google Scholar] [CrossRef]
- Broyden, C.G. The Convergence of a Class of Double-Rank Minimization Algorithms 1. General Considerations. IMA J. Appl. Math. 1970, 6, 76–90. [Google Scholar] [CrossRef]
- Nagasaka, Y.; Shimoda, K.; Fujii, N. Multidimensional Recording (Mdr) and Data Sharing: An Ecological Open Research and Educational Platform for Neuroscience. PLoS ONE 2011, 6, e22561. [Google Scholar] [CrossRef]
- Hardin, J.W. Generalized Estimating Equations (Gee); John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2005. [Google Scholar]
- Wu, H.; Sun, D.; Zhou, Z. Model Identification of a Micro Air Vehicle in Loitering Flight Based on Attitude Performance Evaluation. IEEE Trans. Robot. 2004, 20, 702–712. [Google Scholar] [CrossRef]


| Method | Number of Outliers | ||||
|---|---|---|---|---|---|
| 8 | 12 | 16 | 20 | 24 | |
| LS | 0.9961 ± 0.012 | 0.9977 ± 0.008 | 0.9986 ± 0.008 | 0.9985 ± 0.008 | 0.9991 ± 0.008 |
| Huber | 0.9626 ± 0.055 | 0.9614 ± 0.059 | 0.9424 ± 0.070 | 0.9981 ± 0.061 | 0.9999 ± 0.064 |
| L1 | 0.9754 ± 0.012 * | 0.9739 ± 0.011 * | 0.9709 ± 0.011 * | 0.9684 ± 0.010 * | 0.9675 ± 0.011 * |
| L0.8 | 0.9912 ± 0.007 * | 0.9884 ± 0.009 * | 0.9855 ± 0.008 * | 0.9815 ± 0.008 * | 0.9773 ± 0.010 * |
| L0.6 | 0.9929 ± 0.007 * | 0.9918 ± 0.008 * | 0.9906 ± 0.007 * | 0.9881 ± 0.008 * | 0.9863 ± 0.009 * |
| L0.4 | 0.9935 ± 0.007 * | 0.9927 ± 0.008 * | 0.9922 ± 0.007 * | 0.9906 ± 0.007 * | 0.9900 ± 0.009 * |
| L0.2 | 0.9940 ± 0.007 * | 0.9936 ± 0.008 * | 0.9936 ± 0.008 * | 0.9929 ± 0.008 * | 0.9923 ± 0.009 * |
| Method | Number of Outliers | ||||
|---|---|---|---|---|---|
| 8 | 12 | 16 | 20 | 24 | |
| LS | 2.8701 ± 0.128 | 3.1407 ± 0.156 | 3.3440 ± 0.152 | 3.4941 ± 0.149 | 3.5629 ± 0.173 |
| Huber | 3.7933 ± 1.624 | 4.7454 ± 5.712 | 3.0067 ± 0.826 | 3.3647 ± 2.065 | 2.8149 ± 0.861 |
| L1 | 1.4601 ± 0.339 * | 1.6705 ± 0.268 * | 1.8201 ± 0.218 * | 1.9369 ± 0.187 * | 2.0424 ± 0.213 * |
| L0.8 | 2.1322 ± 0.284 * | 2.0543 ± 0.288 * | 2.0326 ± 0.243 * | 2.0279 ± 0.217 * | 2.0043 ± 0.233 * |
| L0.6 | 2.3604 ± 0.151 * | 2.3212 ± 0.227 * | 2.3171 ± 0.207 * | 2.2776 ± 0.243 * | 2.2330 ± 0.293 * |
| L0.4 | 2.4589 ± 0.177 * | 2.4635 ± 0.227 * | 2.4936 ± 0.258 * | 2.4601 ± 0.276 * | 2.4058 ± 0.336 * |
| L0.2 | 2.5288 ± 0.220 * | 2.5825 ± 0.280 * | 2.6723 ± 0.319 * | 2.7355 ± 0.393 * | 2.6981 ± 0.491 * |
| Method | Number of Outliers | ||||
|---|---|---|---|---|---|
| 8 | 12 | 16 | 20 | 24 | |
| LS | 1.1100 ± 0.024 | 1.1488 ± 0.043 | 1.1619 ± 0.046 | 1.1779 ± 0.041 | 1.1893 ± 0.042 |
| Huber | 0.4743 ± 0.671 | 0.5245 ± 0.742 | 0.5490 ± 0.776 | 0.5860 ± 0.829 | 0.6524 ± 0.923 |
| L1 | 0.8564 ± 0.062 * | 0.9028 ± 0.060 * | 0.9172 ± 0.059 * | 0.9282 ± 0.062 * | 0.9214 ± 0.065 * |
| L0.8 | 0.9539 ± 0.110 * | 0.9779 ± 0.115 * | 1.0017 ± 0.096 * | 1.0333 ± 0.076 * | 1.0432 ± 0.063 * |
| L0.6 | 1.0828 ± 0.042 * | 1.0926 ± 0.060 * | 1.1043 ± 0.056 * | 1.1107 ± 0.047 * | 1.1146 ± 0.059 * |
| L0.4 | 1.1001 ± 0.028 * | 1.1376 ± 0.054 * | 1.1464 ± 0.051 * | 1.1713 ± 0.046 * | 1.1824 ± 0.047 * |
| L0.2 | 1.1076 ± 0.025 * | 1.1444 ± 0.047 * | 1.1553 ± 0.050 * | 1.1768 ± 0.046 * | 1.1887 ± 0.046 * |
| Method | Number of Outliers | ||||
|---|---|---|---|---|---|
| 8 | 12 | 16 | 20 | 24 | |
| LS | 10.3674 ± 0.171 | 11.6089 ± 0.253 | 12.6547 ± 0.466 | 13.3863 ± 0.461 | 14.1104 ± 0.549 |
| Huber | 10.0984 ± 0.470 | 10.9375 ± 0.470 | 11.5306 ± 0.495 | 11.9261 ± 0.389 | 11.4484 ± 0.625 |
| L1 | 10.2015 ± 0.406 * | 10.4782 ± 0.421 * | 10.7154 ± 0.501 * | 11.1291 ± 0.616 * | 11.3014 ± 0.640 * |
| L0.8 | 10.5792 ± 1.750 * | 11.0256 ± 1.770 * | 11.4188 ± 1.823 * | 12.6198 ± 2.701 * | 12.9624 ± 2.641 * |
| L0.6 | 10.7649 ± 2.207 * | 11.3840 ± 2.504 * | 11.2274 ± 2.540 * | 11.4422 ± 2.738 * | 12.0195 ± 3.306 * |
| L0.4 | 10.3466 ± 2.070 * | 10.1870 ± 1.922 * | 10.4557 ± 1.920 * | 10.6500 ± 1.153 * | 10.7433 ± 0.843 * |
| L0.2 | 9.8747 ± 1.312 * | 9.9064 ± 0.753 * | 10.3452 ± 1.039 * | 10.6899 ± 1.406 * | 10.7704 ± 0.852 * |
| Method | Outliers Strengths | ||||
|---|---|---|---|---|---|
| 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | |
| LS | 0.9949 ± 0.008 | 0.9972 ± 0.007 | 0.9989 ± 0.007 | 1.0002 ± 0.007 | 1.0011 ± 0.007 |
| Huber | 0.9674 ± 0.056 | 0.9734 ± 0.063 | 0.9838 ± 0.070 | 0.9908 ± 0.074 | 0.9880 ± 0.082 |
| L1 | 0.9720 ± 0.014 * | 0.9720 ± 0.013 * | 0.9723 ± 0.010 * | 0.9718 ± 0.008 * | 0.9714 ± 0.008 * |
| L0.8 | 0.9899 ± 0.008 * | 0.9880 ± 0.008 * | 0.9863 ± 0.008 * | 0.9846 ± 0.008 * | 0.9818 ± 0.009 * |
| L0.6 | 0.9927 ± 0.007 * | 0.9914 ± 0.007 * | 0.9904 ± 0.007 * | 0.9903 ± 0.007 * | 0.9897 ± 0.008 * |
| L0.4 | 0.9933 ± 0.008 * | 0.9922 ± 0.008 * | 0.9914 ± 0.008 * | 0.9911 ± 0.008 * | 0.9909 ± 0.008 * |
| L0.2 | 0.9936 ± 0.008 * | 0.9932 ± 0.008 * | 0.9926 ± 0.008 * | 0.9919 ± 0.008 * | 0.9922 ± 0.009 * |
| Method | Outliers Strengths | ||||
|---|---|---|---|---|---|
| 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | |
| LS | 2.7784 ± 0.149 | 3.1592 ± 0.155 | 3.4438 ± 0.162 | 3.6502 ± 0.168 | 3.8041 ± 0.173 |
| Huber | 3.9342 ± 1.399 | 3.6513 ± 0.925 | 3.1422 ± 0.570 | 3.0822 ± 0.459 | 3.0151 ± 0.444 |
| L1 | 1.4513 ± 0.353 * | 1.6540 ± 0.282 * | 1.8031 ± 0.226 * | 1.9235 ± 0.194 * | 2.0272 ± 0.193 * |
| L0.8 | 2.1394 ± 0.316 * | 2.0702 ± 0.305 * | 2.0400 ± 0.256 * | 2.0166 ± 0.247 * | 2.0053 ± 0.210 * |
| L0.6 | 2.3761 ± 0.200 * | 2.3551 ± 0.221 * | 2.3181 ± 0.228 * | 2.2893 ± 0.224 * | 2.2462 ± 0.274 * |
| L0.4 | 2.4730 ± 0.203 * | 2.4843 ± 0.234 * | 2.4732 ± 0.269 * | 2.4393 ± 0.262 * | 2.4093 ± 0.276 * |
| L0.2 | 2.5262 ± 0.201 * | 2.6099 ± 0.274 * | 2.6290 ± 0.329 * | 2.5707 ± 0.335 * | 2.6121 ± 0.392 * |
| Method | Outliers Strengths | ||||
|---|---|---|---|---|---|
| 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | |
| LS | 1.1100 ± 0.024 | 1.1488 ± 0.043 | 1.1619 ± 0.046 | 1.1779 ± 0.041 | 1.1893 ± 0.042 |
| Huber | 0.5642 ± 0.798 | 0.5820 ± 0.823 | 0.5899 ± 0.834 | 0.5859 ± 0.829 | 0.5774 ± 0.817 |
| L1 | 0.8564 ± 0.062 * | 0.9028 ± 0.060 * | 0.9172 ± 0.059 * | 0.9282 ± 0.062 * | 0.9214 ± 0.065 * |
| L0.8 | 0.9539 ± 0.110 * | 0.9779 ± 0.115 * | 1.0017 ± 0.096 * | 1.0333 ± 0.076 * | 1.0432 ± 0.063 * |
| L0.6 | 1.0828 ± 0.042 * | 1.0926 ± 0.060 * | 1.1043 ± 0.056 * | 1.1107 ± 0.047 * | 1.1146 ± 0.059 * |
| L0.4 | 1.1001 ± 0.028 * | 1.1376 ± 0.054 * | 1.1464 ± 0.051 * | 1.1713 ± 0.046 * | 1.1824 ± 0.047 * |
| L0.2 | 1.1076 ± 0.025 * | 1.1444 ± 0.047 * | 1.1553 ± 0.050 * | 1.1768 ± 0.046 * | 1.1887 ± 0.046 * |
| Method | Outliers Strengths | ||||
|---|---|---|---|---|---|
| 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | |
| LS | 11.2180 ± 0.294 | 12.6363 ± 0.419 | 13.9806 ± 0.577 | 15.3493 ± 0.762 | 16.7532 ± 0.924 |
| Huber | 10.7821 ± 0.425 | 11.5455 ± 0.484 | 11.5870 ± 0.561 | 11.2759 ± 0.759 | 11.4137 ± 0.712 |
| L1 | 10.5468 ± 0.595 * | 10.7873 ± 0.498 * | 11.0528 ± 0.538 * | 11.3524 ± 0.634 * | 11.6935 ± 0.668 * |
| L0.8 | 11.6983 ± 0.803 * | 12.0348 ± 0.472 * | 12.5147 ± 0.415 * | 12.9623 ± 0.586 * | 13.1487 ± 0.549 * |
| L0.6 | 9.6700 ± 0.185 * | 10.2408 ± 0.240 * | 10.7195 ± 0.306 * | 11.0724 ± 0.376 * | 11.2908 ± 0.374 * |
| L0.4 | 9.6880 ± 0.178 * | 10.2577 ± 0.244 * | 10.7121 ± 0.253 * | 11.0420 ± 0.304 * | 11.2194 ± 0.277 * |
| L0.2 | 9.7605 ± 0.283 * | 10.3073 ± 0.278 * | 10.7745 ± 0.369 * | 11.1013 ± 0.423 * | 11.3517 ± 0.561 * |
| Subject | Method | |
|---|---|---|
| LS-ARX | L1-ARX | |
| 1 | 9.2295 | 7.7953 |
| 2 | 7.3647 | 6.4325 |
| 3 | 7.3430 | 6.4876 |
| 4 | 5.0670 | 4.0245 |
| 5 | 4.3612 | 3.3372 |
| 6 | 5.5014 | 4.5819 |
| 7 | 6.8686 | 5.4962 |
| 8 | 7.5475 | 6.5210 |
| 9 | 5.3146 | 4.1594 |
| 10 | 5.6730 | 4.5378 |
| 11 | 9.7528 | 8.3152 |
| Average | 6.7294 ± 1.73 | 5.6081 ± 1.62 * |
| Subject | Method | ||
|---|---|---|---|
| LS (mmHg) | L1 (mmHg) | Real (mmHg) | |
| 1 | 13.7831 | 13.8759 | 14.2000 |
| 2 | 18.5624 | 18.6203 | 19.0778 |
| 3 | 8.6183 | 8.7711 | 9.3489 |
| 4 | 23.7407 | 23.8564 | 24.4172 |
| 5 | 17.1373 | 17.2725 | 17.8372 |
| 6 | 24.0823 | 24.2048 | 25.0012 |
| 7 | 19.7513 | 19.7813 | 20.8477 |
| 8 | 19.8864 | 19.9744 | 20.7015 |
| 9 | 21.5216 | 21.5523 | 21.9293 |
| 10 | 17.0425 | 17.0672 | 17.1580 |
| 11 | 14.9890 | 15.1406 | 16.3673 |
| 12 | 7.8933 | 7.9316 | 8.4423 |
| 13 | 3.9604 | 4.0621 | 4.5802 |
| 14 | 7.7528 | 7.9307 | 8.5877 |
| 15 | 9.3349 | 9.5021 | 10.0645 |
| Subject | Method | |||
|---|---|---|---|---|
| LS ARX | L1 ARX | |||
| Error | CC | Error | CC | |
| 1 | 0.4482 | 0.9152 | 0.3754 | 0.9766 |
| 2 | 0.5306 | 0.9502 | 0.4794 | 0.9839 |
| 3 | 0.6162 | 0.8519 | 0.4943 | 0.9790 |
| 4 | 0.6807 | 0.9894 | 0.5715 | 0.9989 |
| 5 | 0.3293 | 0.9151 | 0.2718 | 0.9936 |
| 6 | 0.9217 | 0.9484 | 0.8011 | 0.9951 |
| 7 | 1.0964 | 0.9024 | 1.0664 | 0.9347 |
| 8 | 0.3779 | 0.8940 | 0.3384 | 0.9954 |
| 9 | 0.4364 | 0.9610 | 0.4118 | 0.9936 |
| 10 | 0.2154 | 0.9127 | 0.2069 | 0.9525 |
| 11 | 1.3784 | 0.9018 | 1.2268 | 0.9776 |
| 12 | 0.3072 | 0.8706 | 0.2888 | 0.9895 |
| 13 | 0.3116 | 0.8814 | 0.2654 | 0.9251 |
| 14 | 0.5458 | 0.8570 | 0.4354 | 0.9846 |
| 15 | 0.4512 | 0.9392 | 0.3528 | 0.9871 |
| Mean Result | 0.5765 ± 0.32 | 0.9127 ± 0.04 | 0.5057 ± 0.30 * | 0.9778 ± 0.02 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Li, C.; Li, N.; Li, P.; Wang, X.; Gao, D.; Yao, D.; Xu, P.; Yin, G.; Li, F. Robust Autoregression with Exogenous Input Model for System Identification and Predicting. Electronics 2021, 10, 755. https://doi.org/10.3390/electronics10060755
Xie J, Li C, Li N, Li P, Wang X, Gao D, Yao D, Xu P, Yin G, Li F. Robust Autoregression with Exogenous Input Model for System Identification and Predicting. Electronics. 2021; 10(6):755. https://doi.org/10.3390/electronics10060755
Chicago/Turabian StyleXie, Jiaxin, Cunbo Li, Ning Li, Peiyang Li, Xurui Wang, Dongrui Gao, Dezhong Yao, Peng Xu, Gang Yin, and Fali Li. 2021. "Robust Autoregression with Exogenous Input Model for System Identification and Predicting" Electronics 10, no. 6: 755. https://doi.org/10.3390/electronics10060755
APA StyleXie, J., Li, C., Li, N., Li, P., Wang, X., Gao, D., Yao, D., Xu, P., Yin, G., & Li, F. (2021). Robust Autoregression with Exogenous Input Model for System Identification and Predicting. Electronics, 10(6), 755. https://doi.org/10.3390/electronics10060755





