The Application of Classical Control in the Design and Analysis of Power Amplifiers for Driving Piezoelectric Stack Actuators
Abstract
1. Introduction
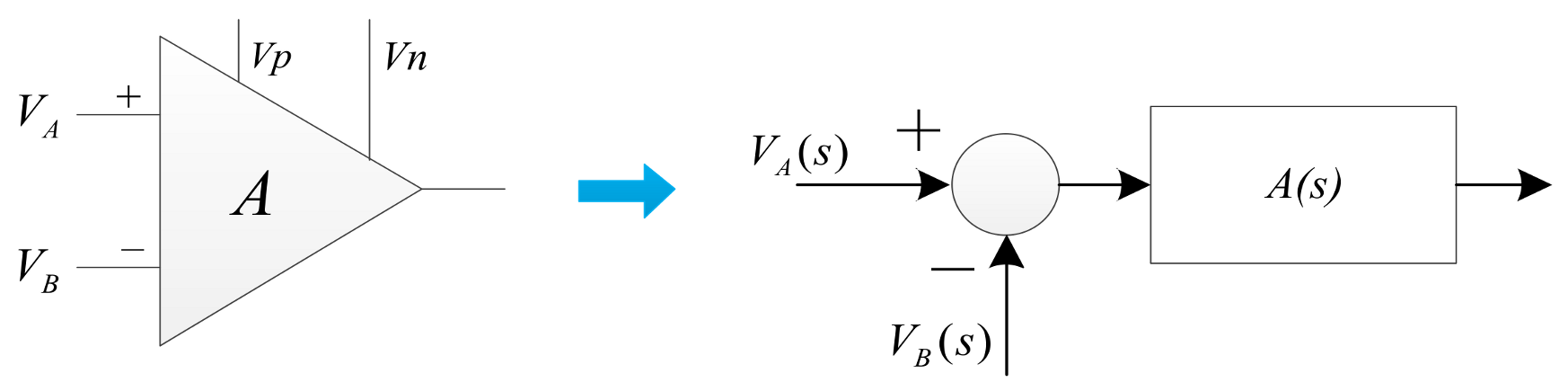
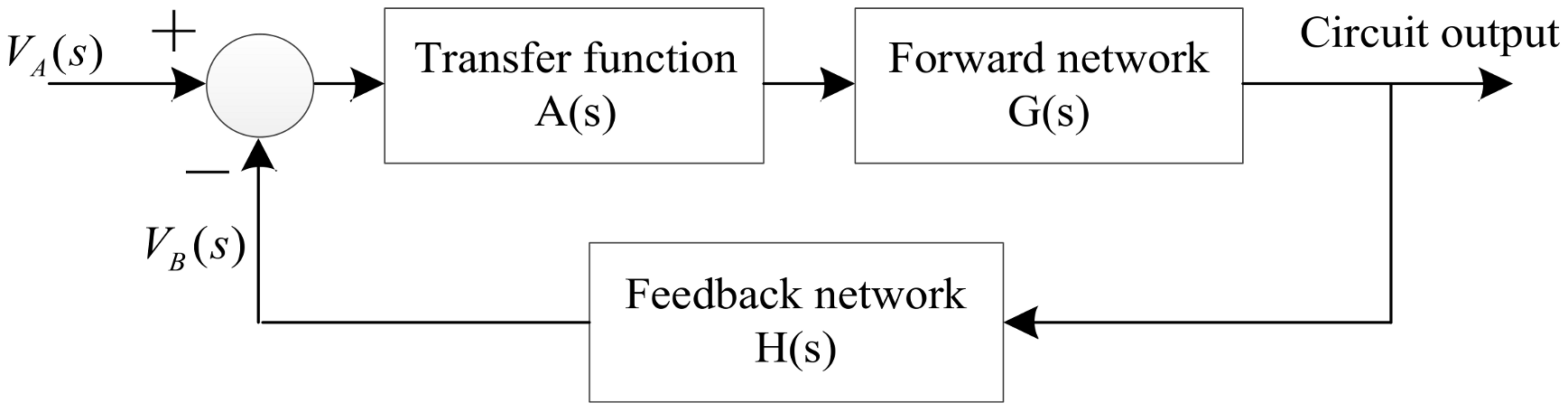
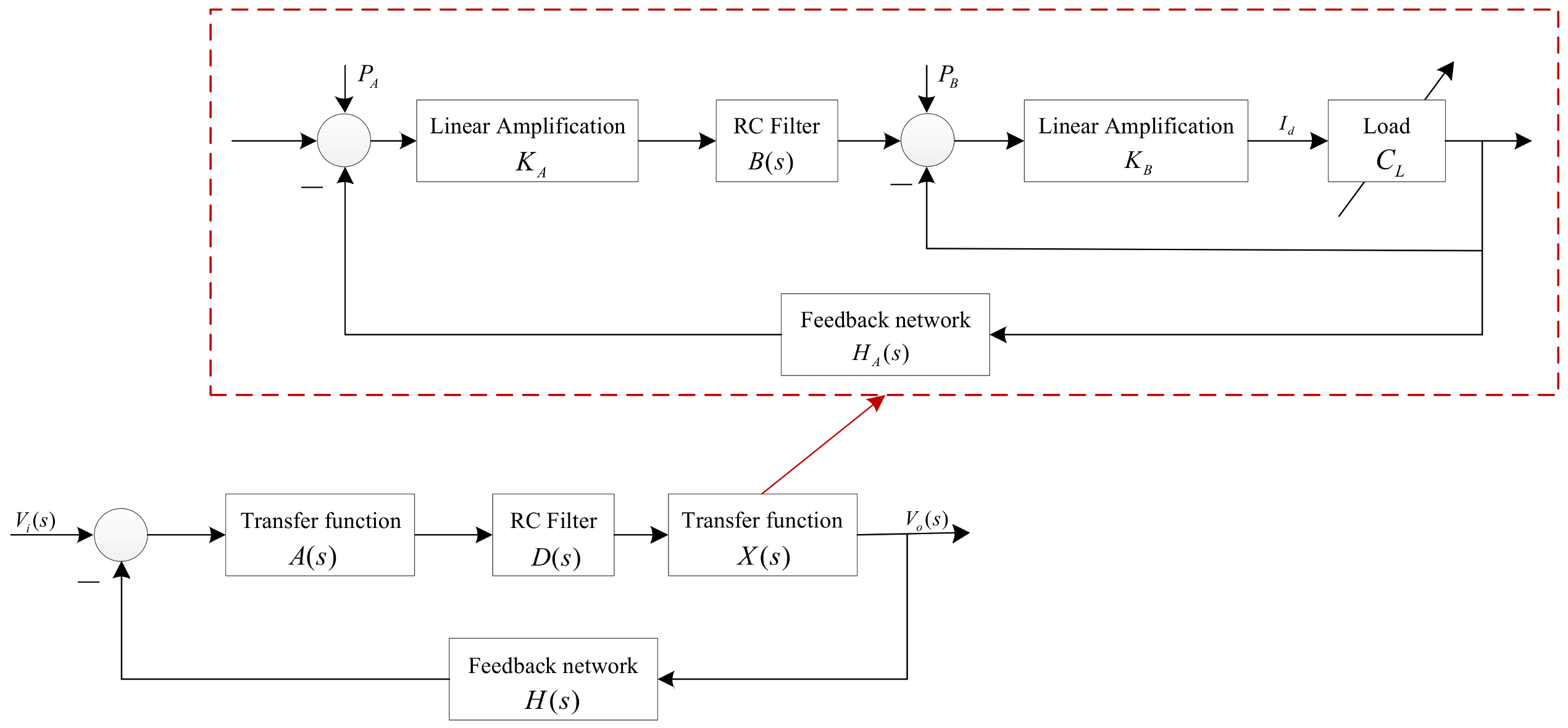
2. The Proposed Approach
3. Power Amplifiers Using High-Voltage Operational Amplifiers
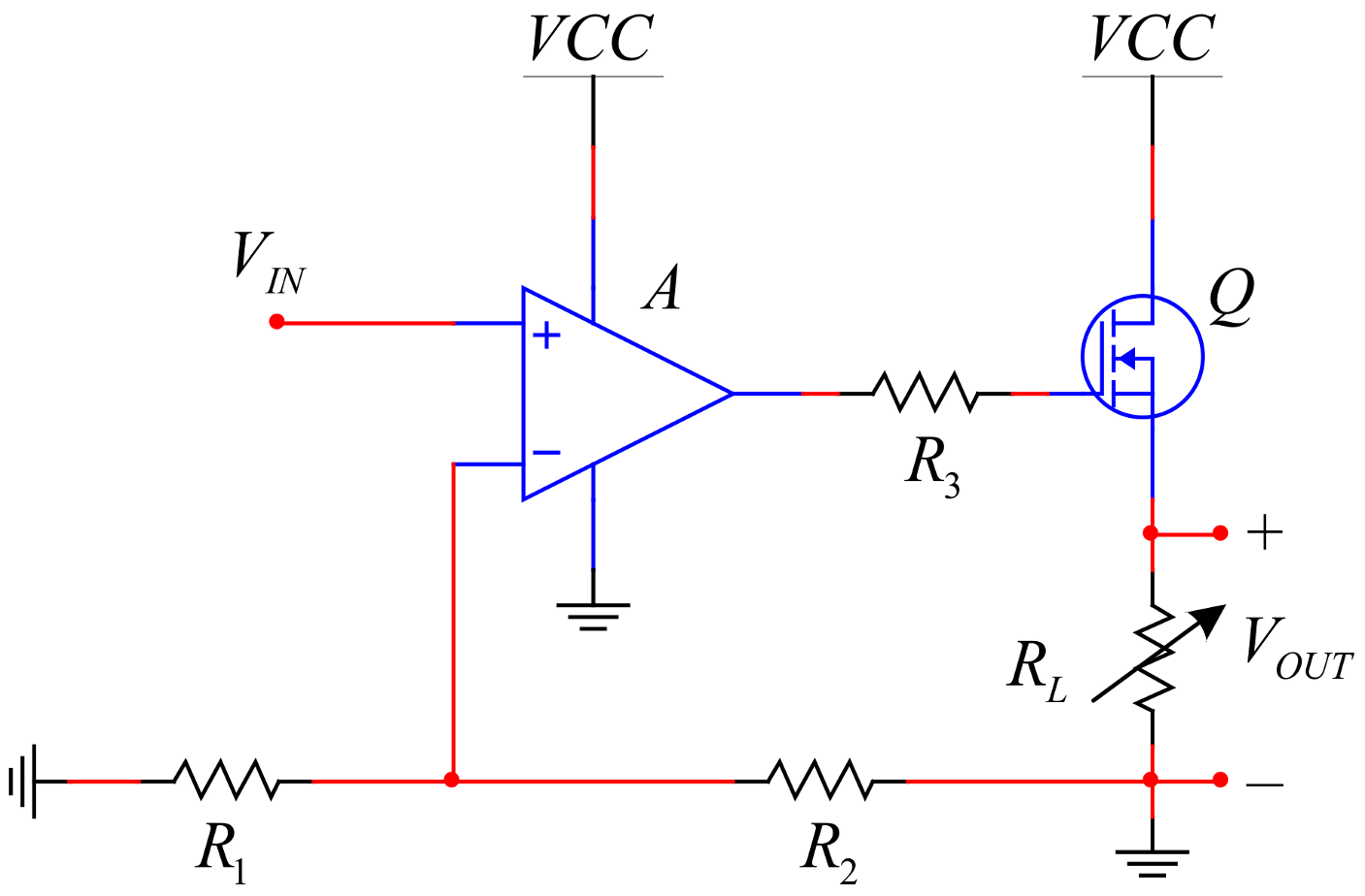
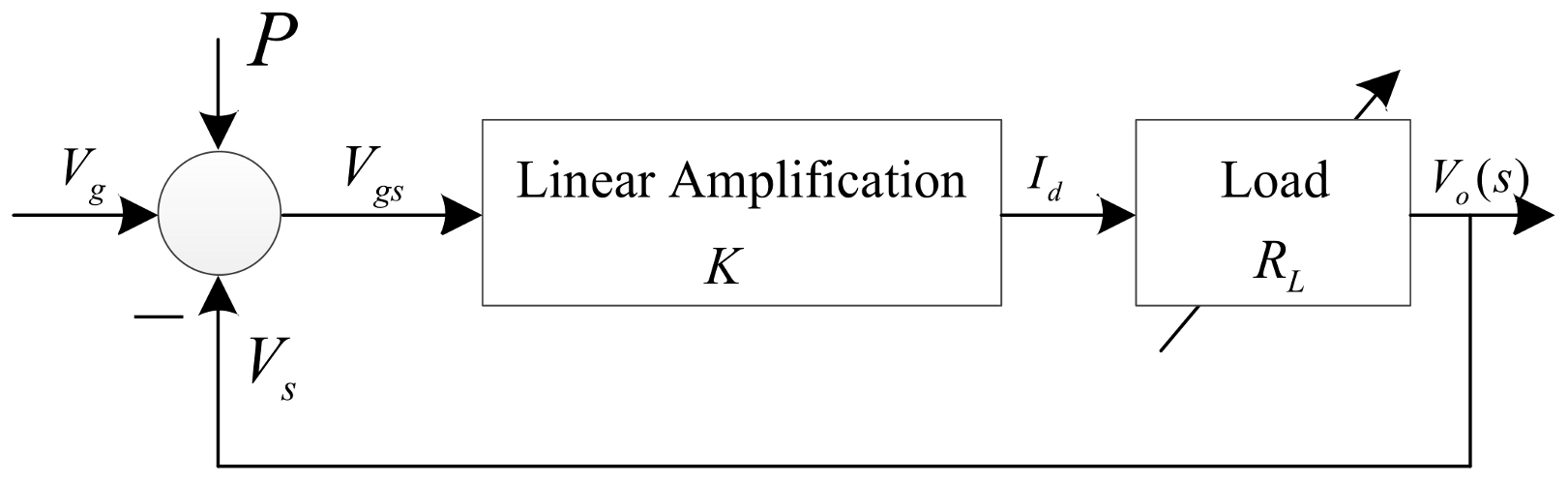
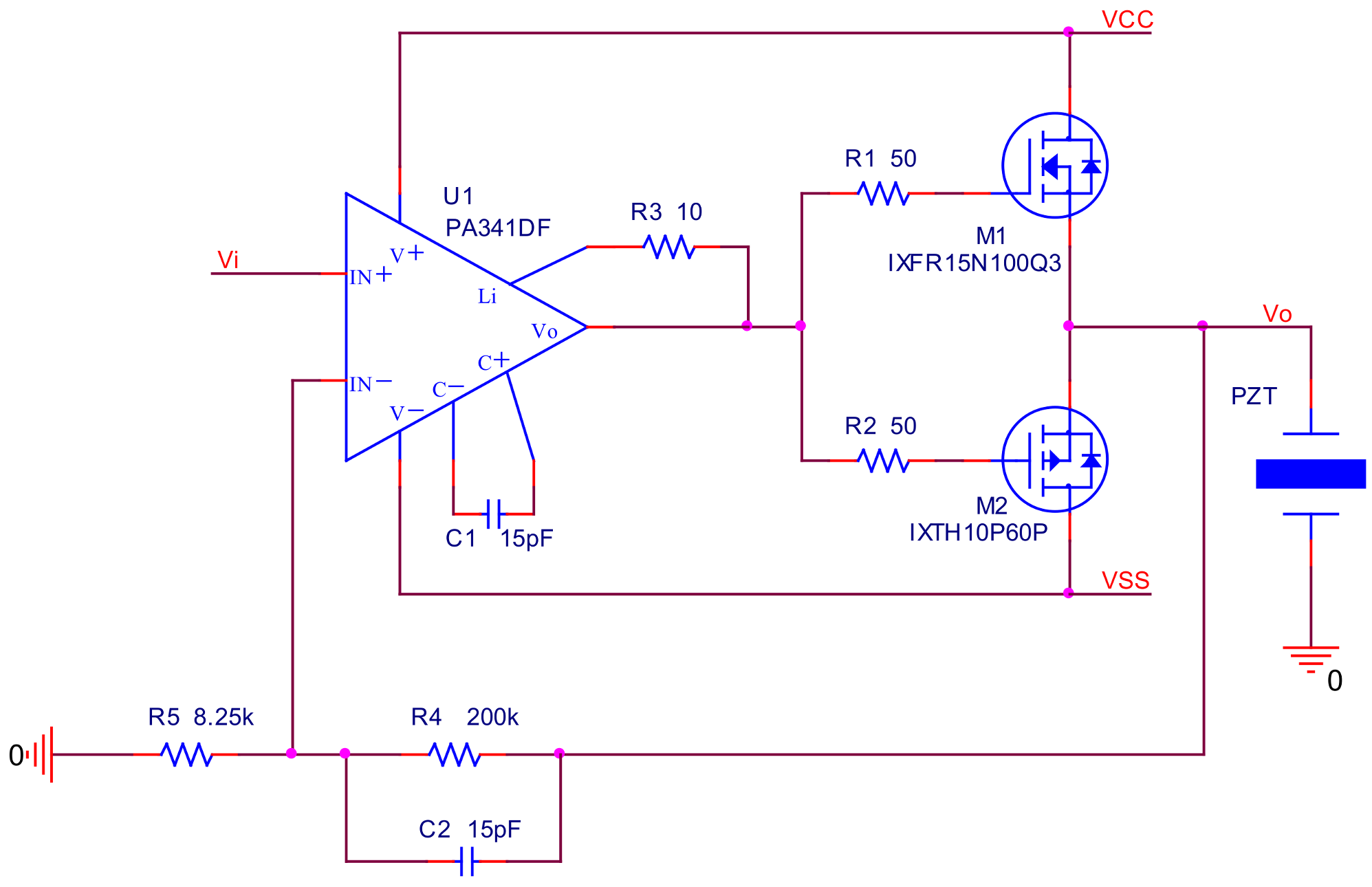
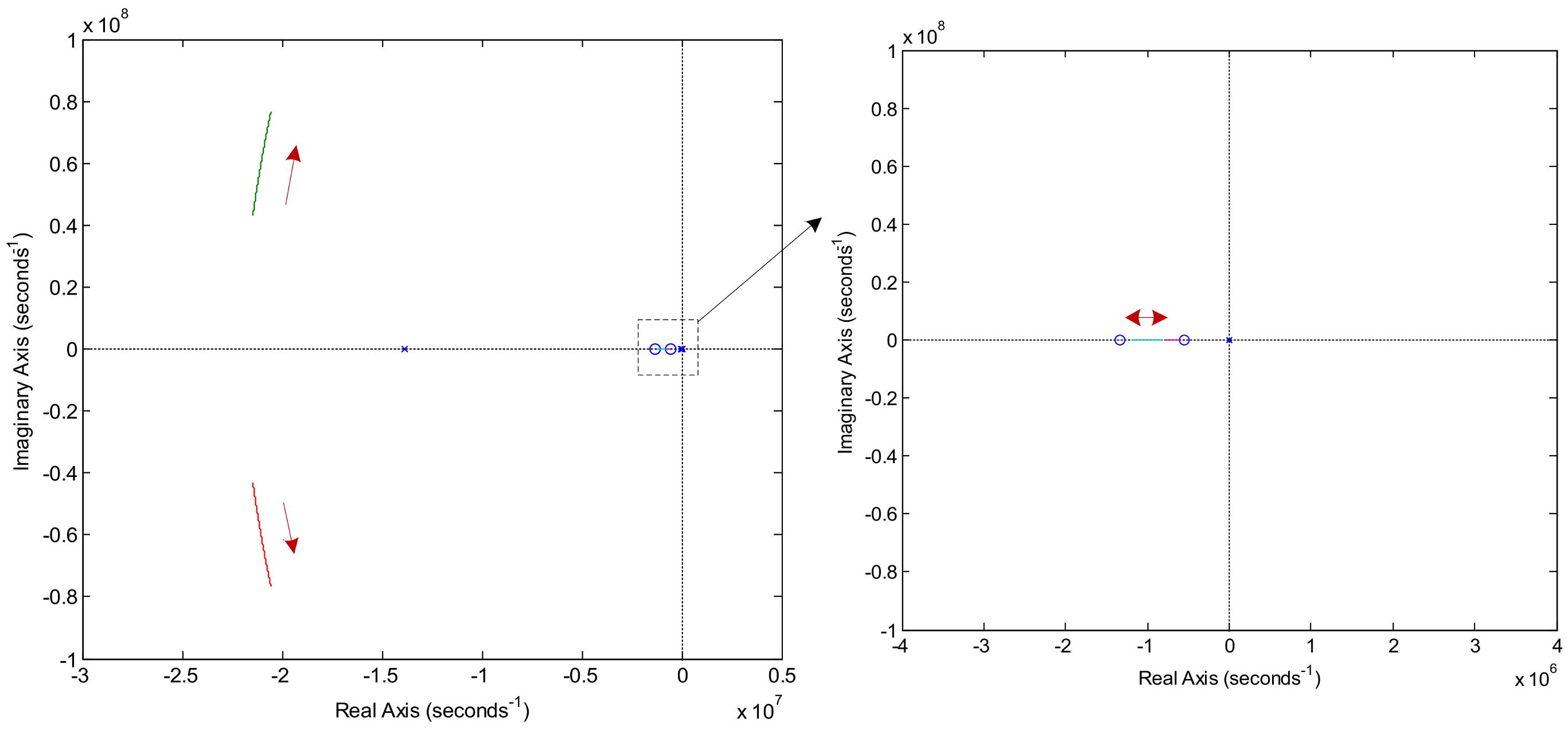
3.1. The Model of the Power Amplifier and Its Stability Analysis
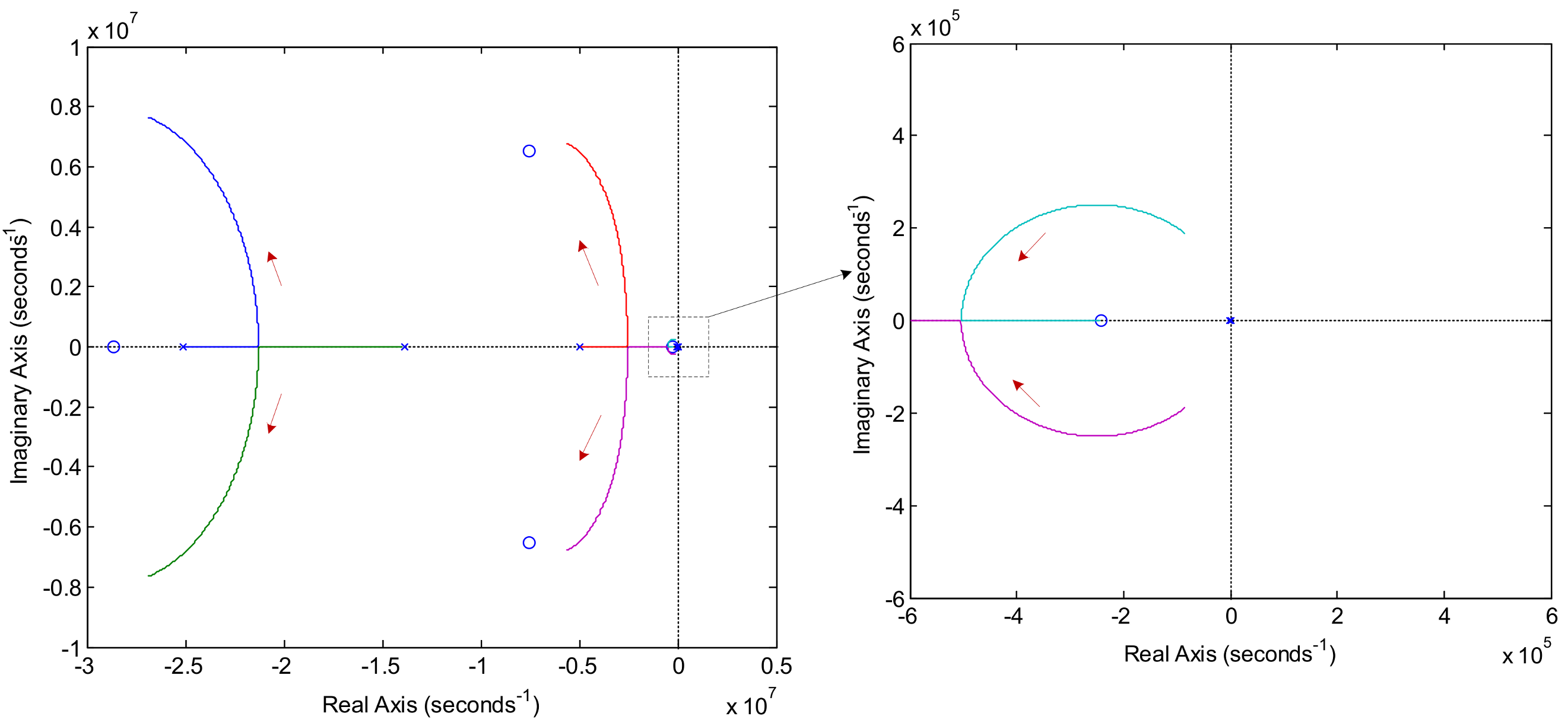
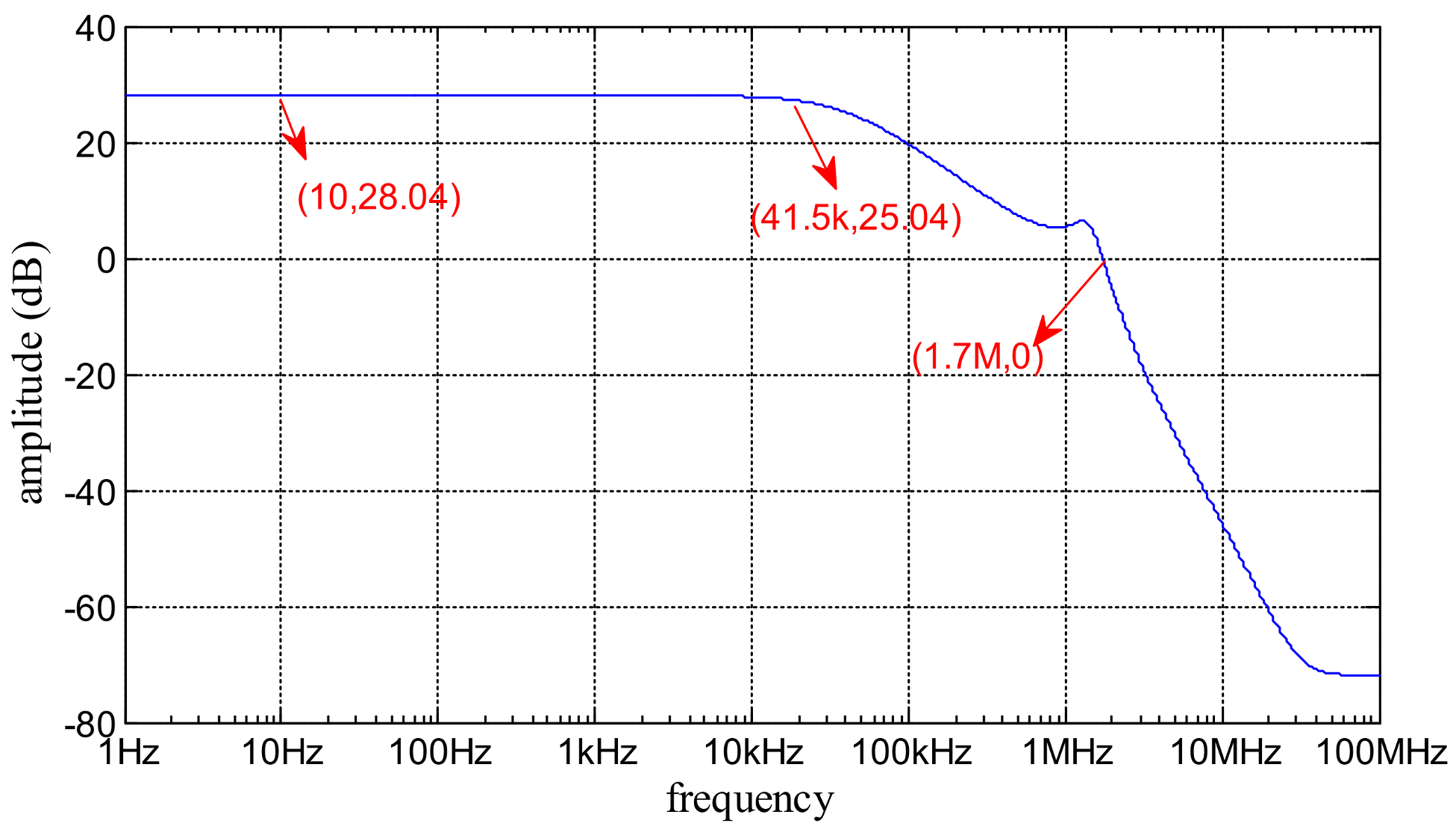
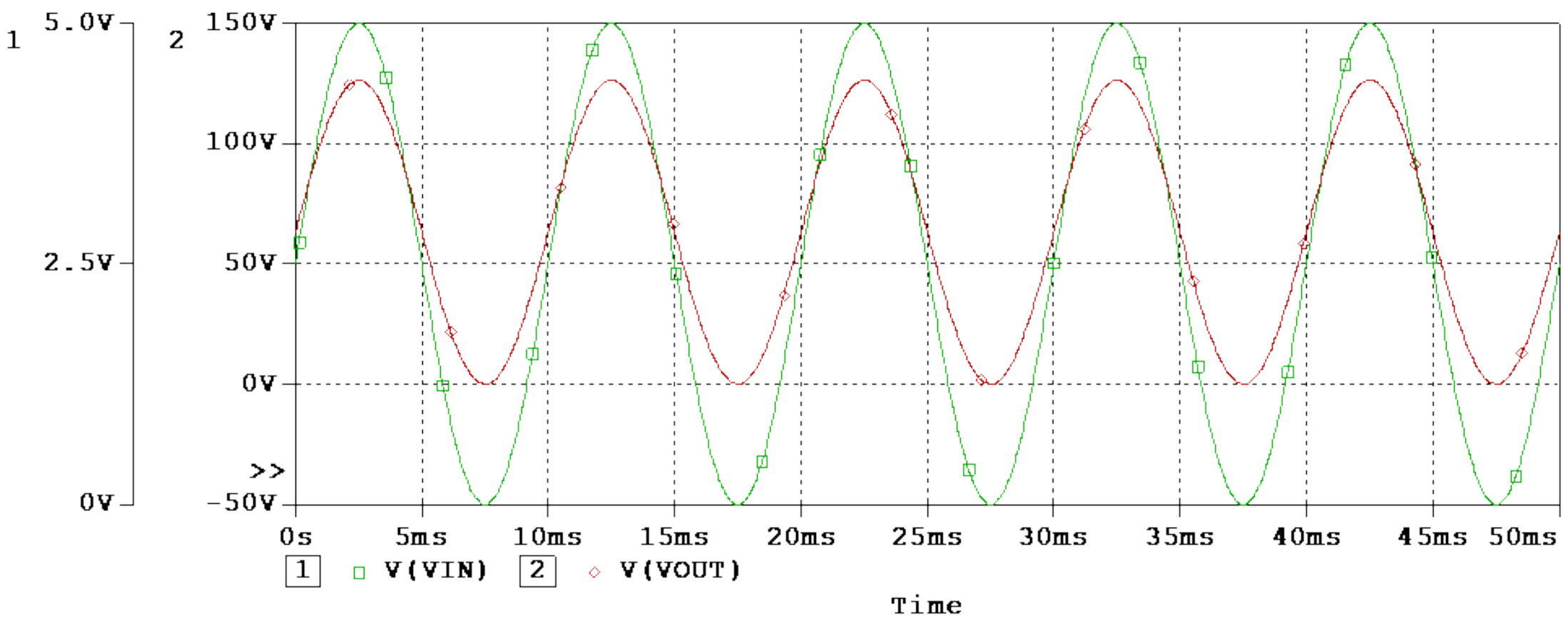
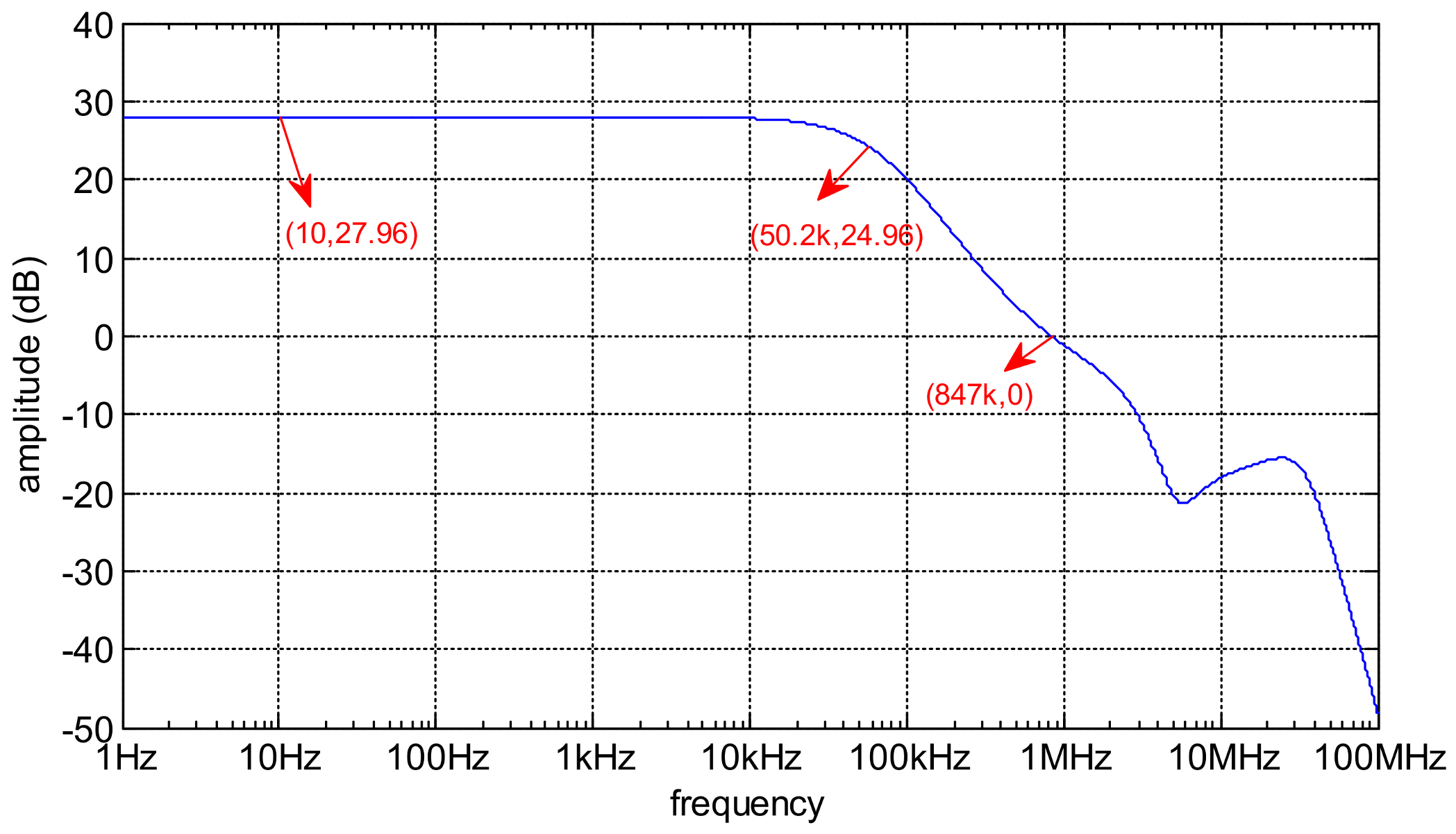
3.2. Simulation and Analysis
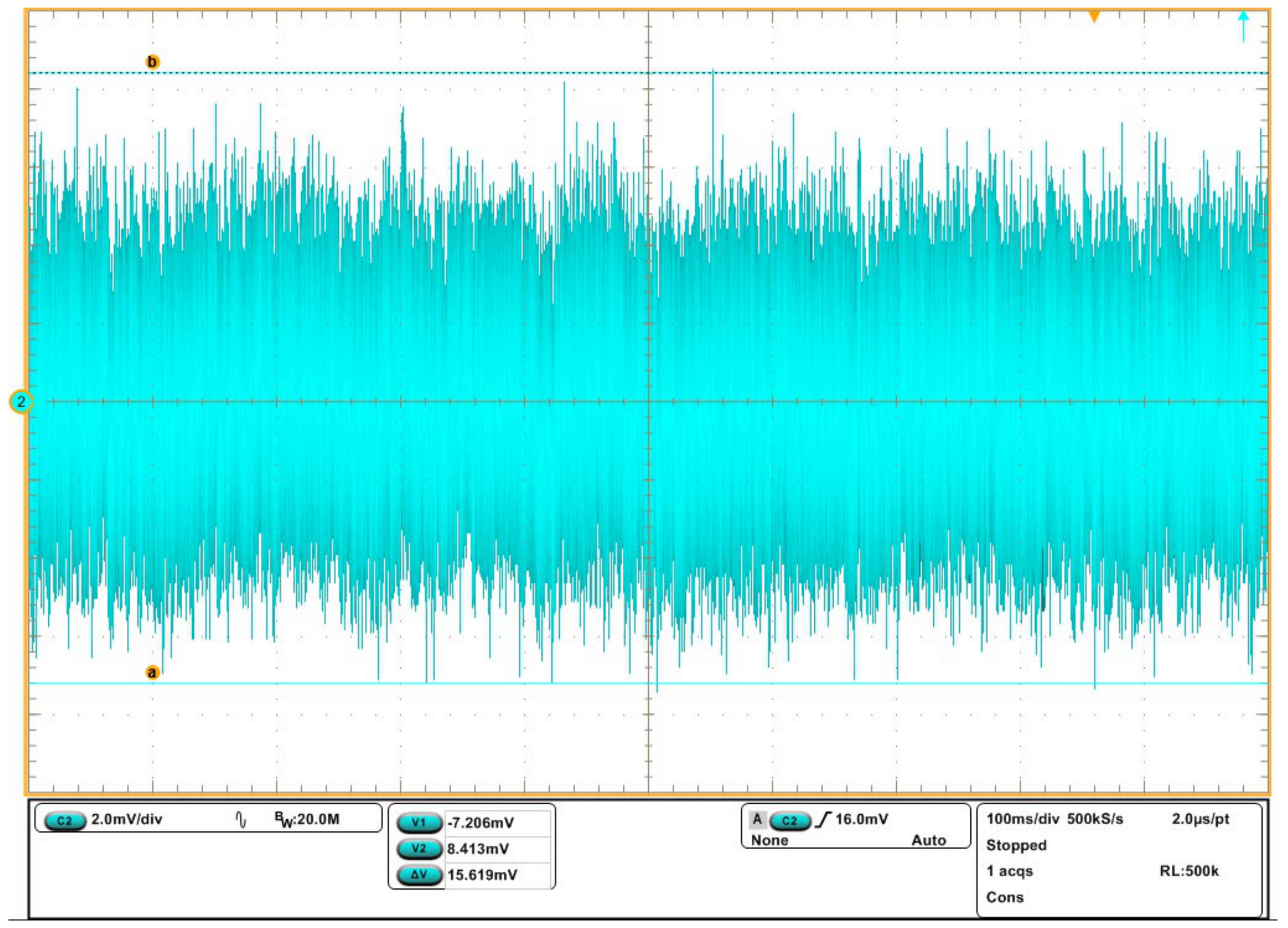
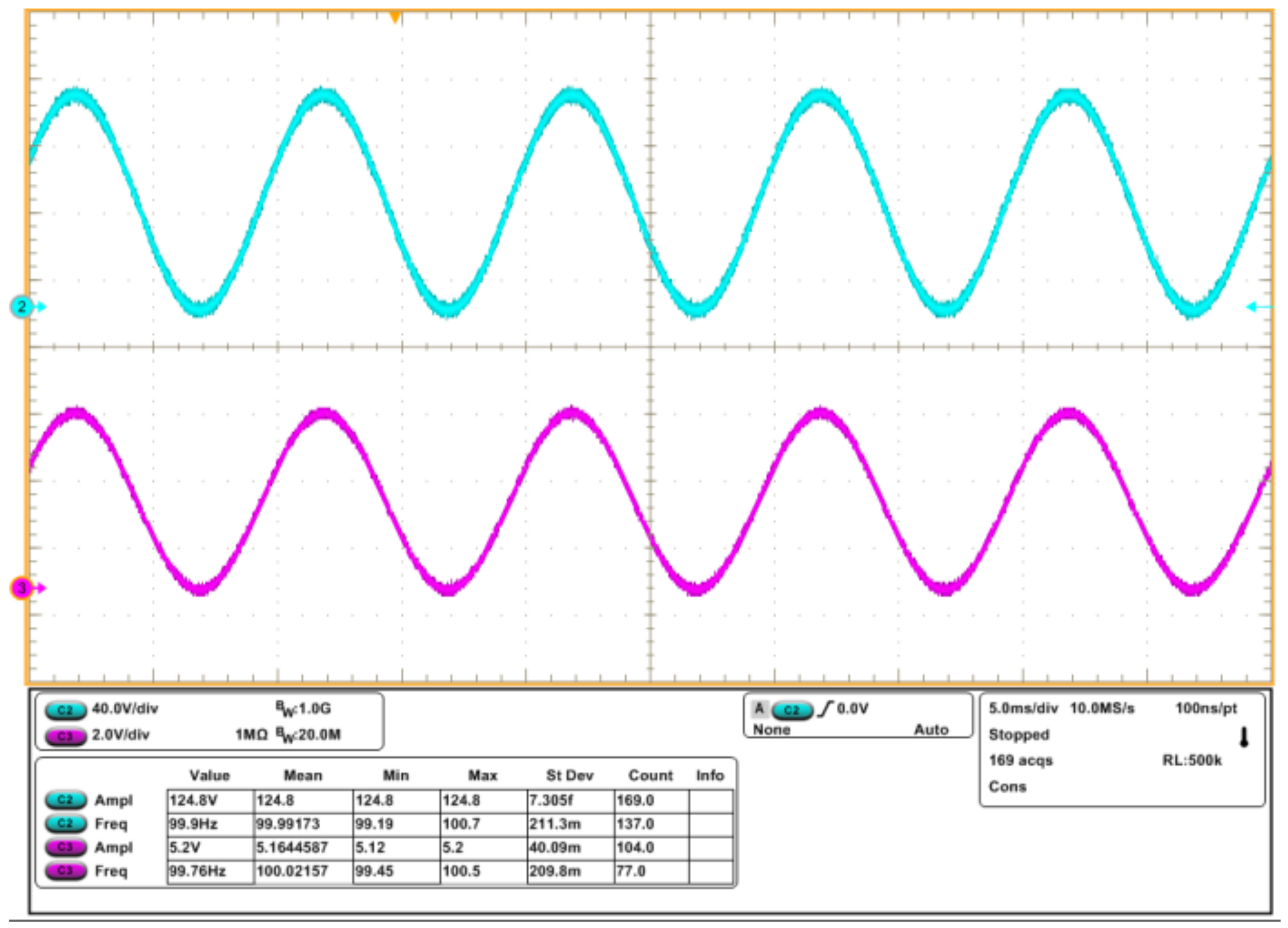
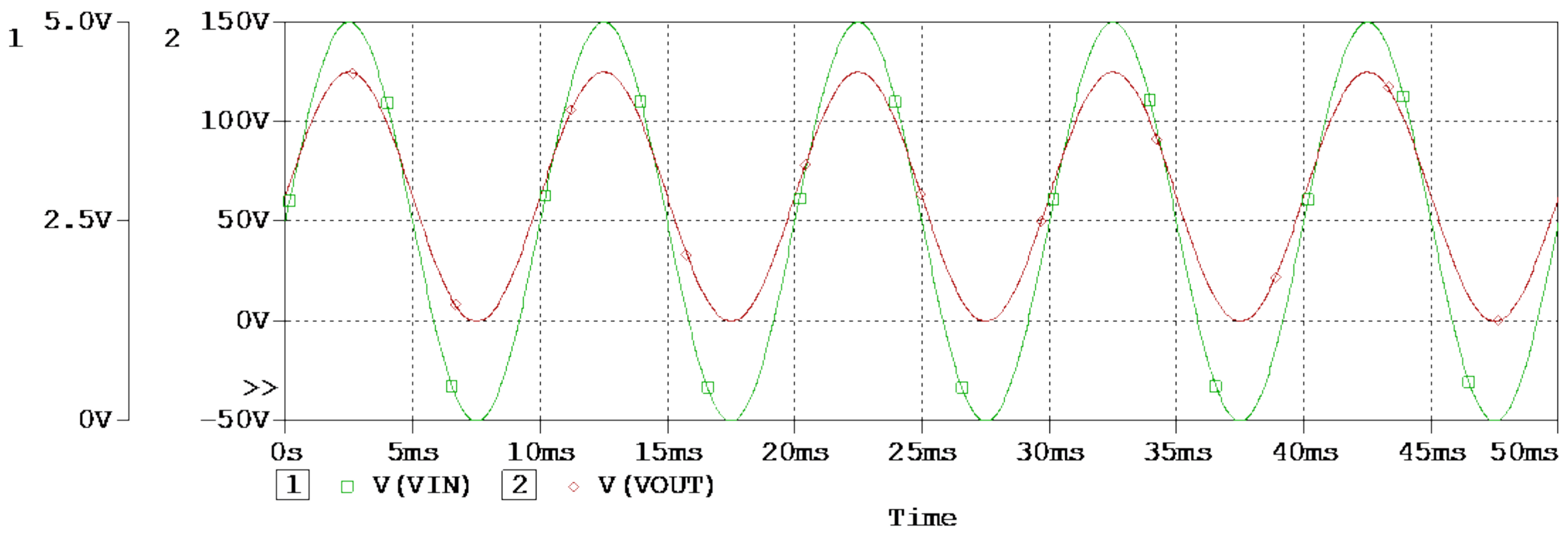
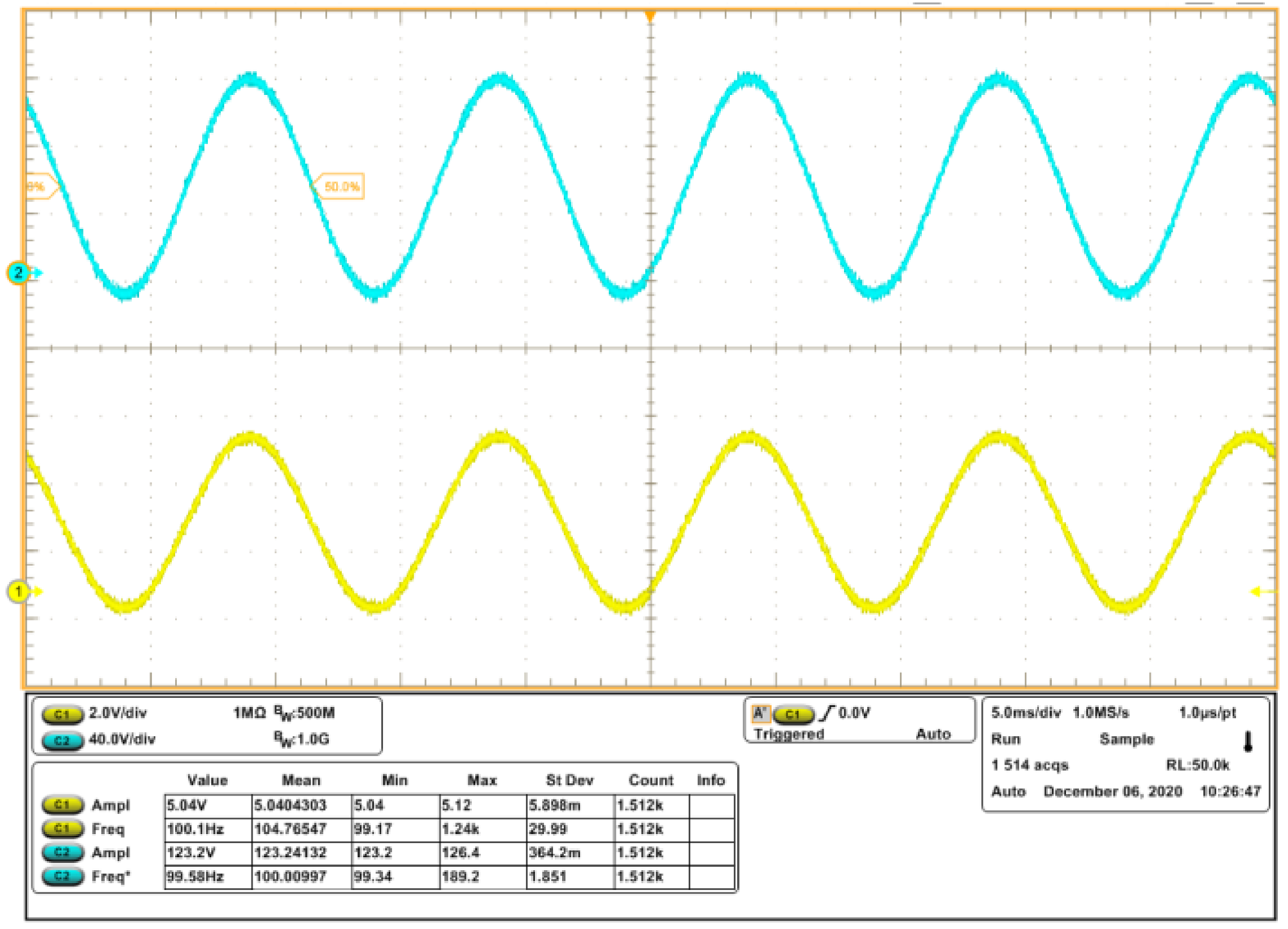
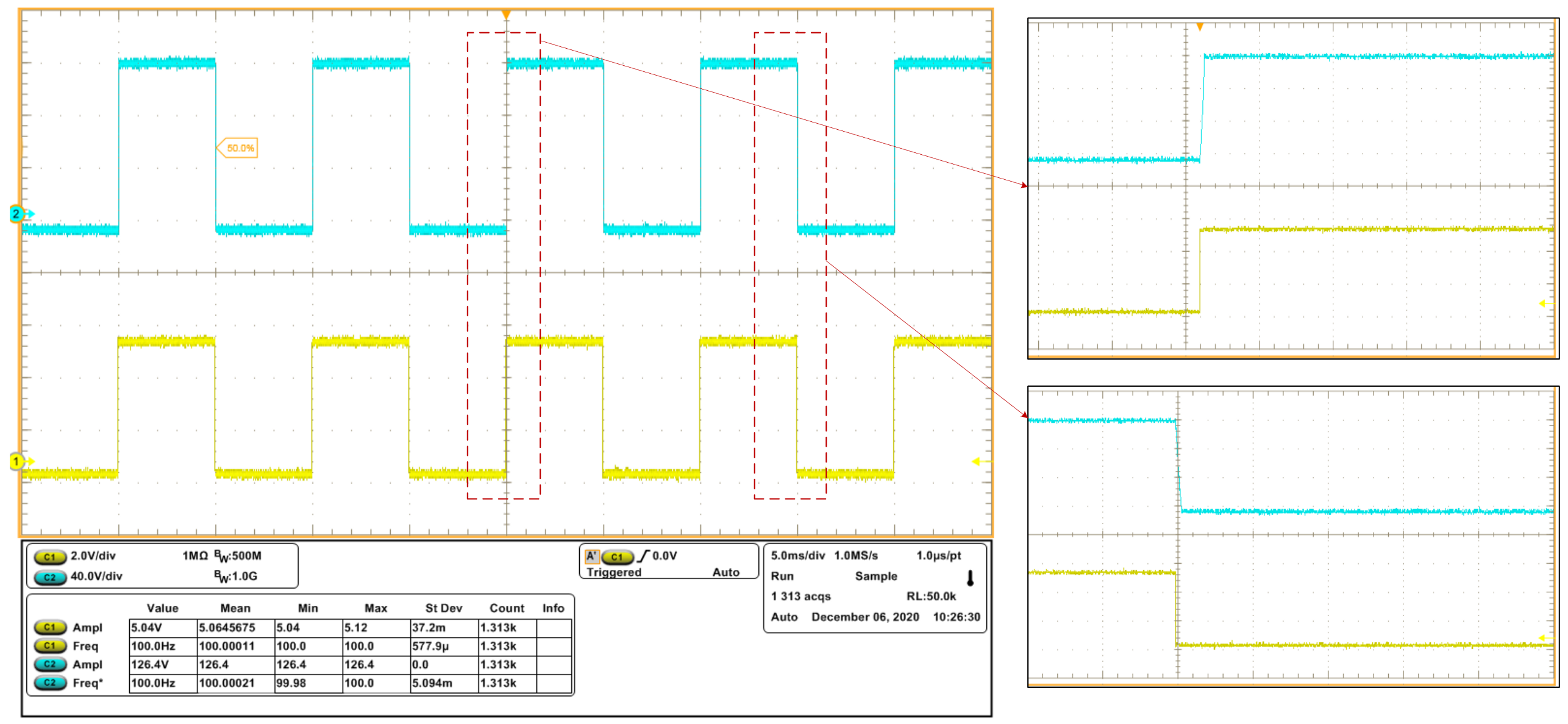
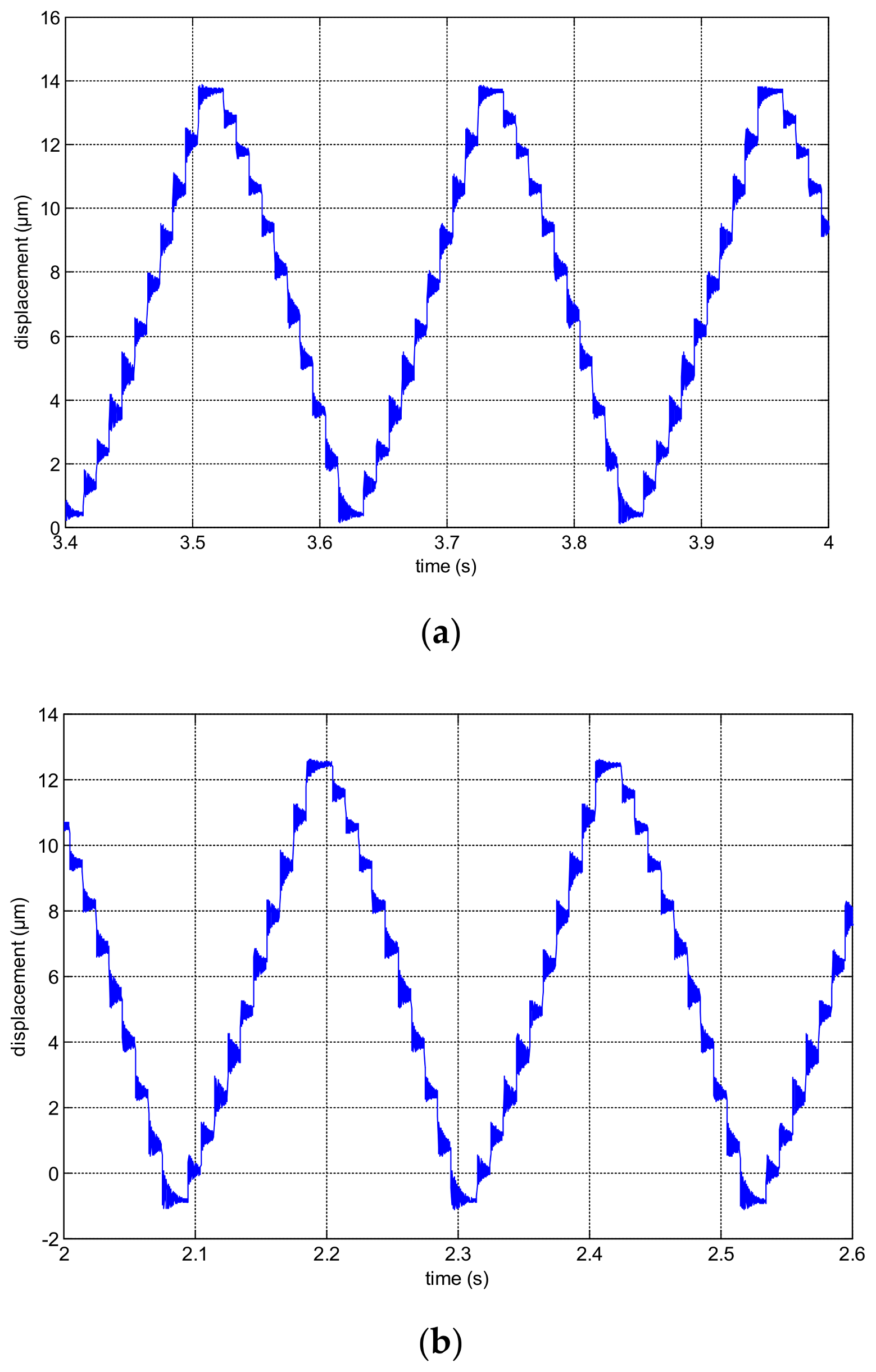
3.3. Experimental Results and Comments
4. Power Amplifiers Using General Operational Amplifiers
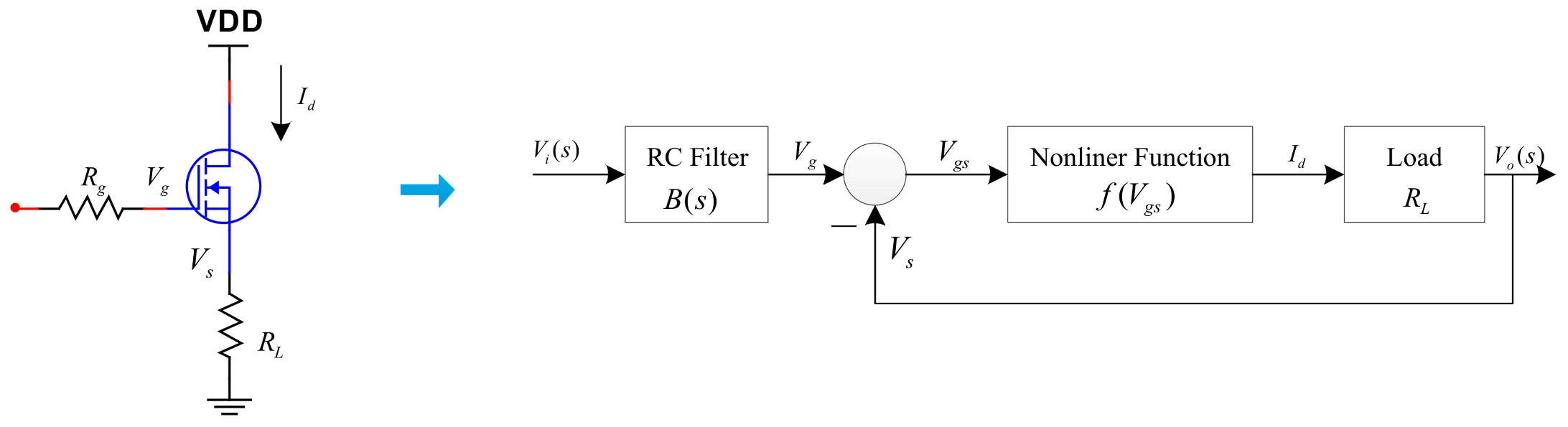
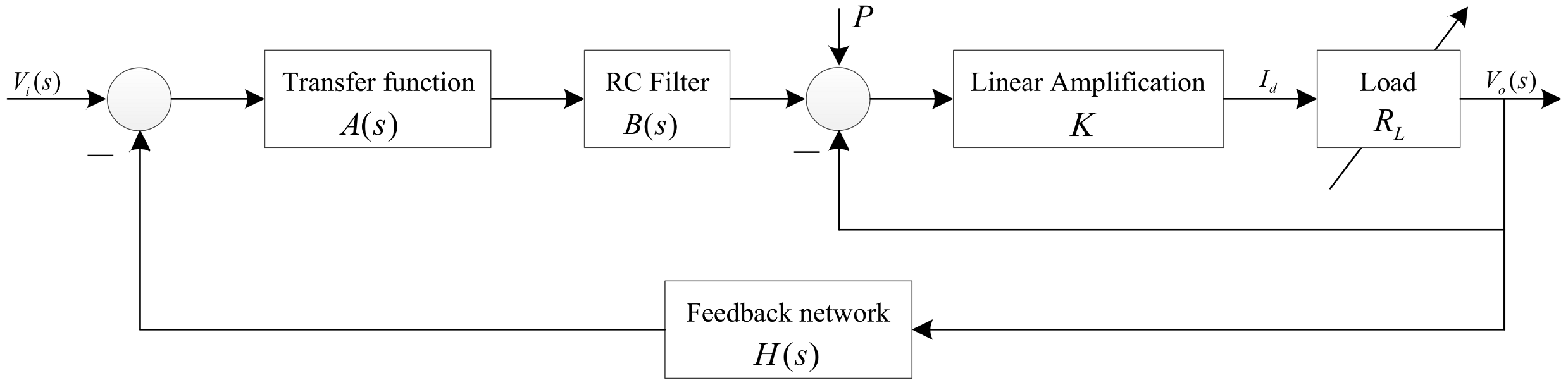
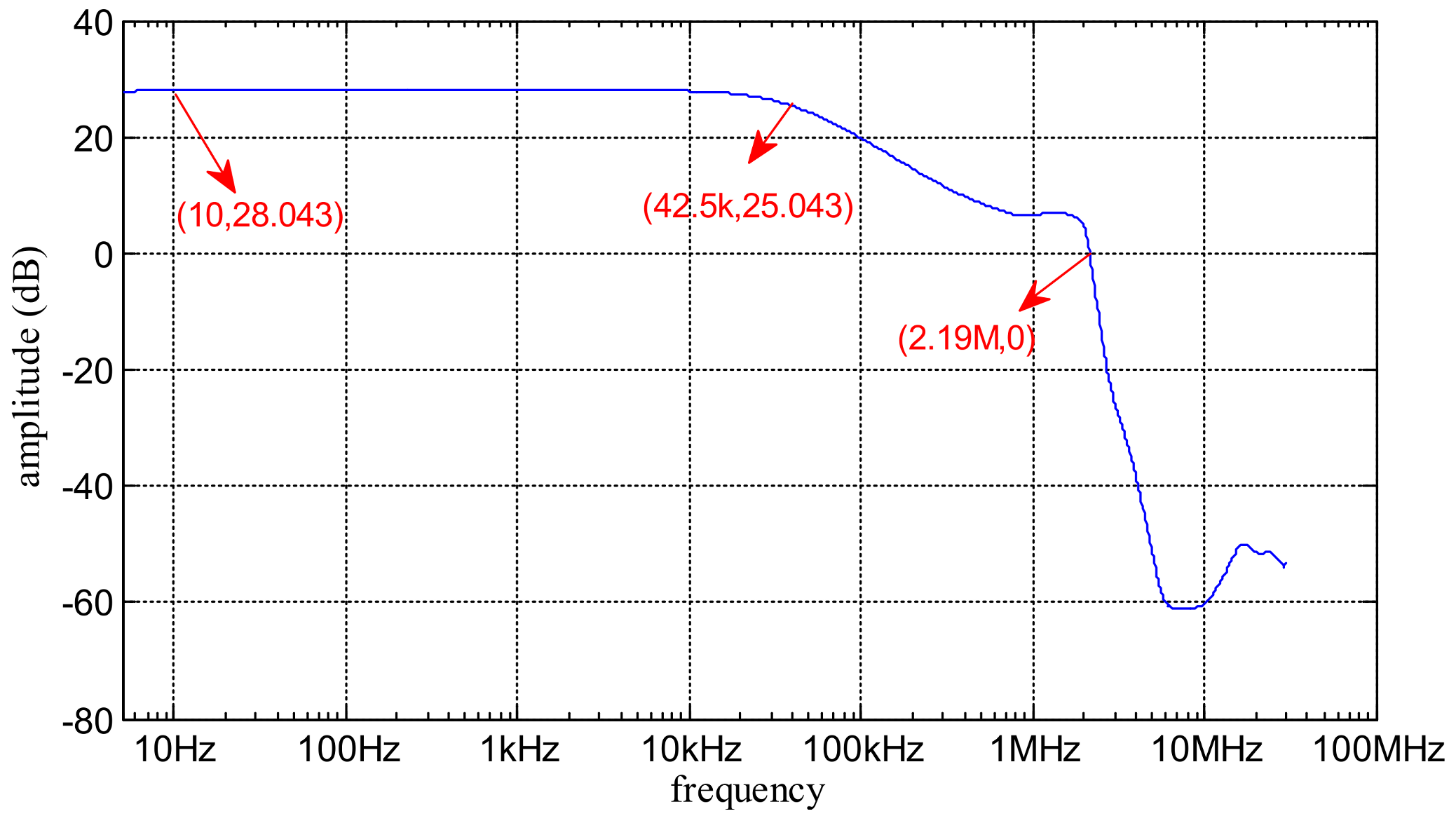
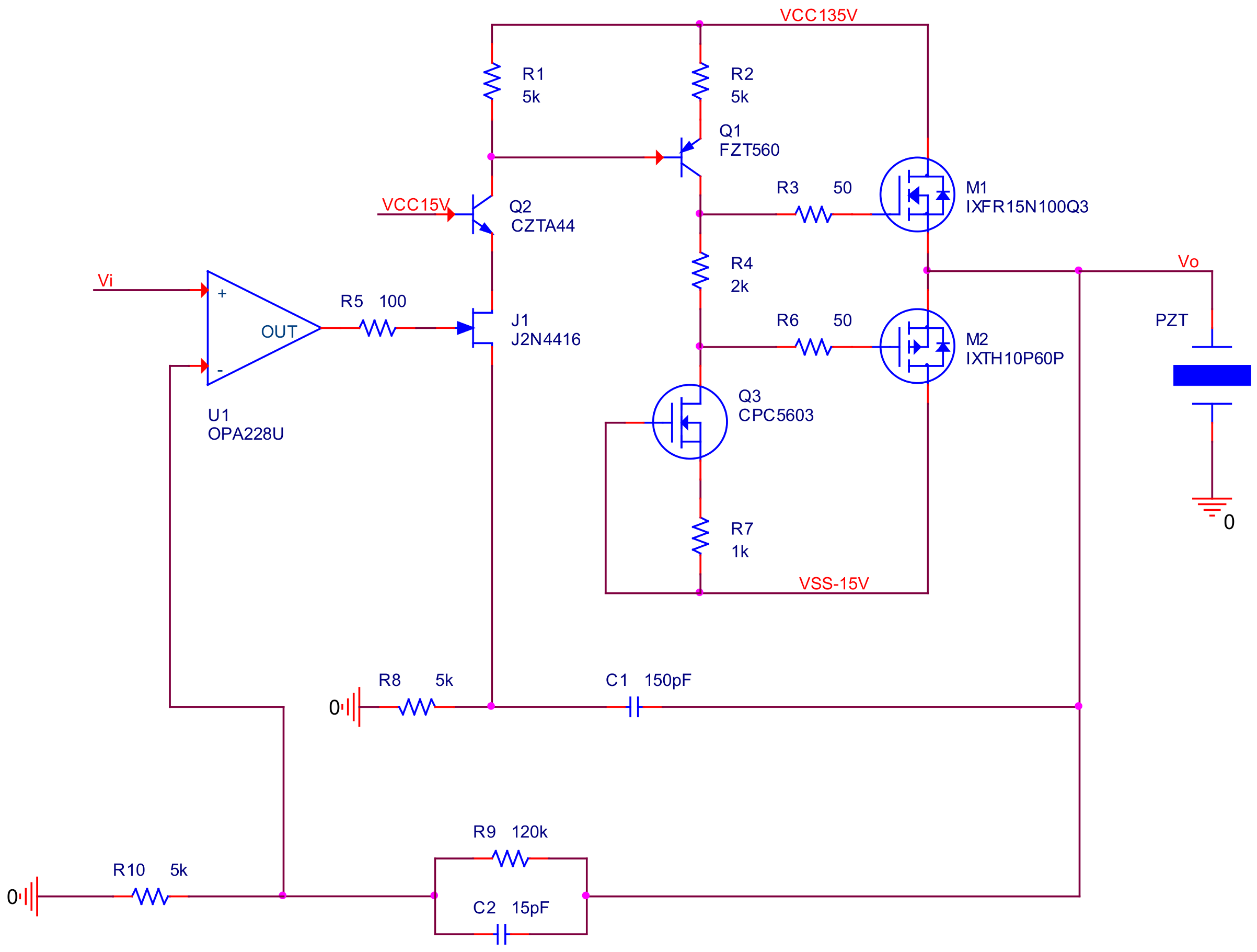
4.1. The Model of the Power Amplifier and Its Stability Analysis
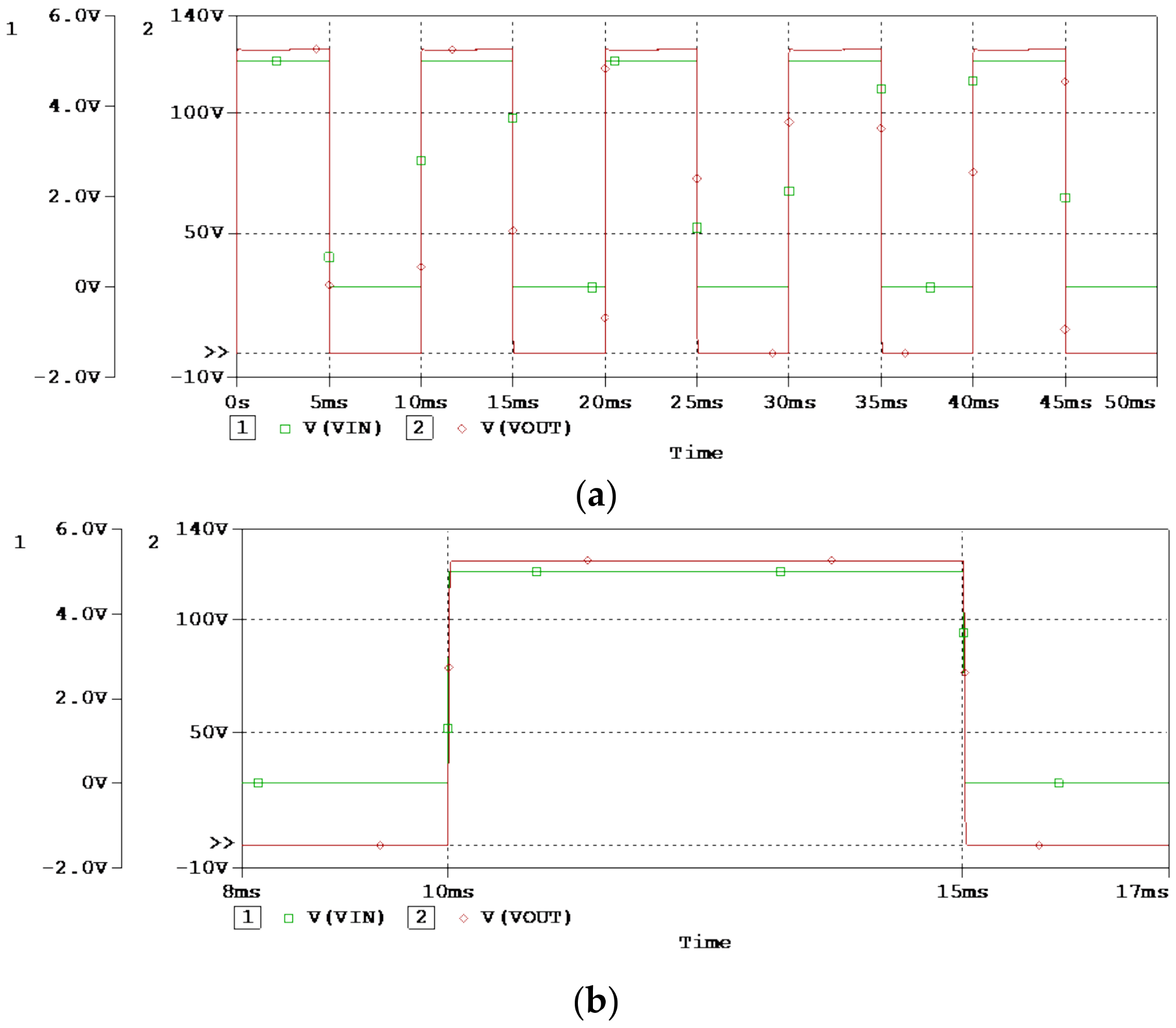
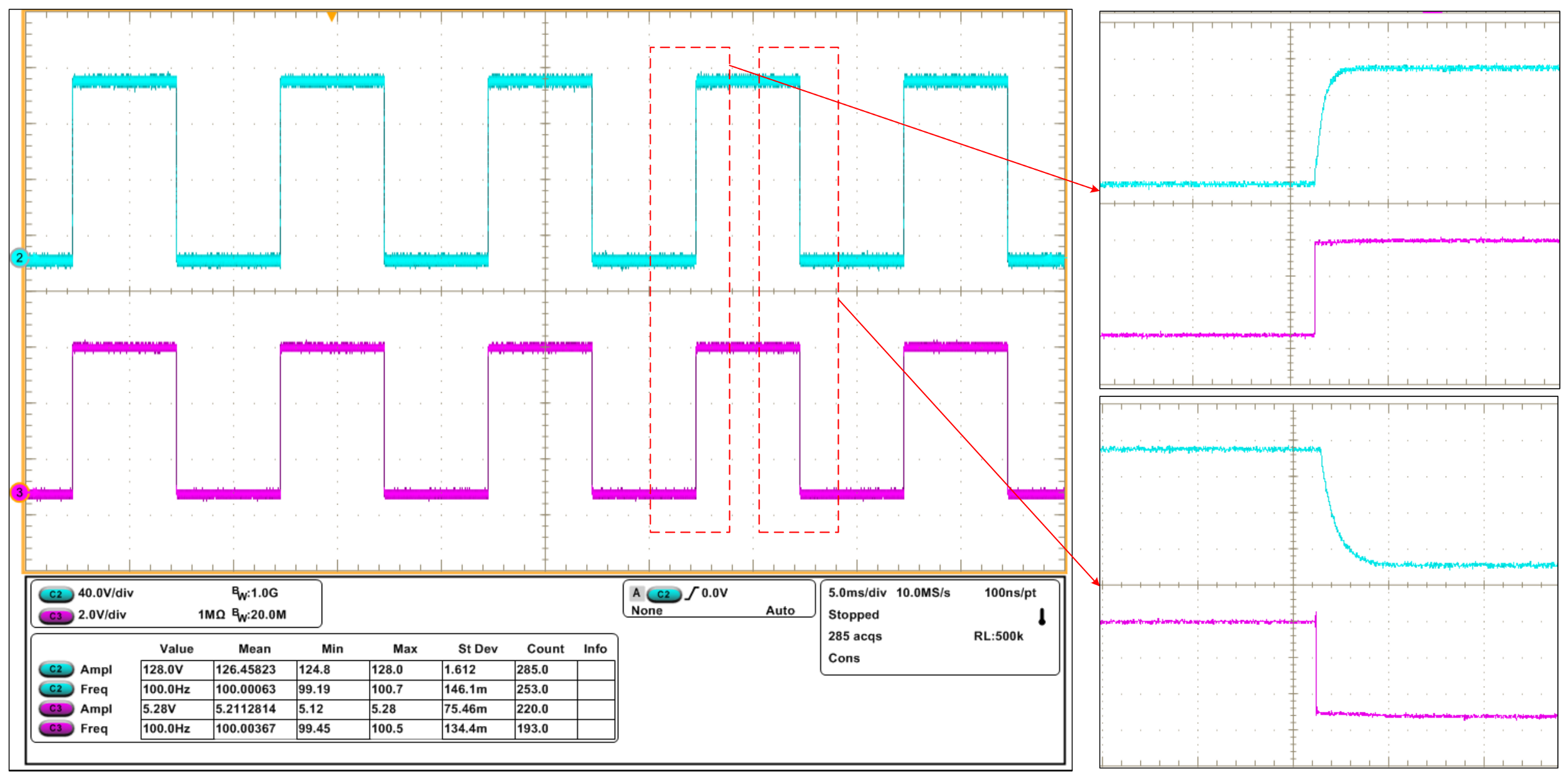
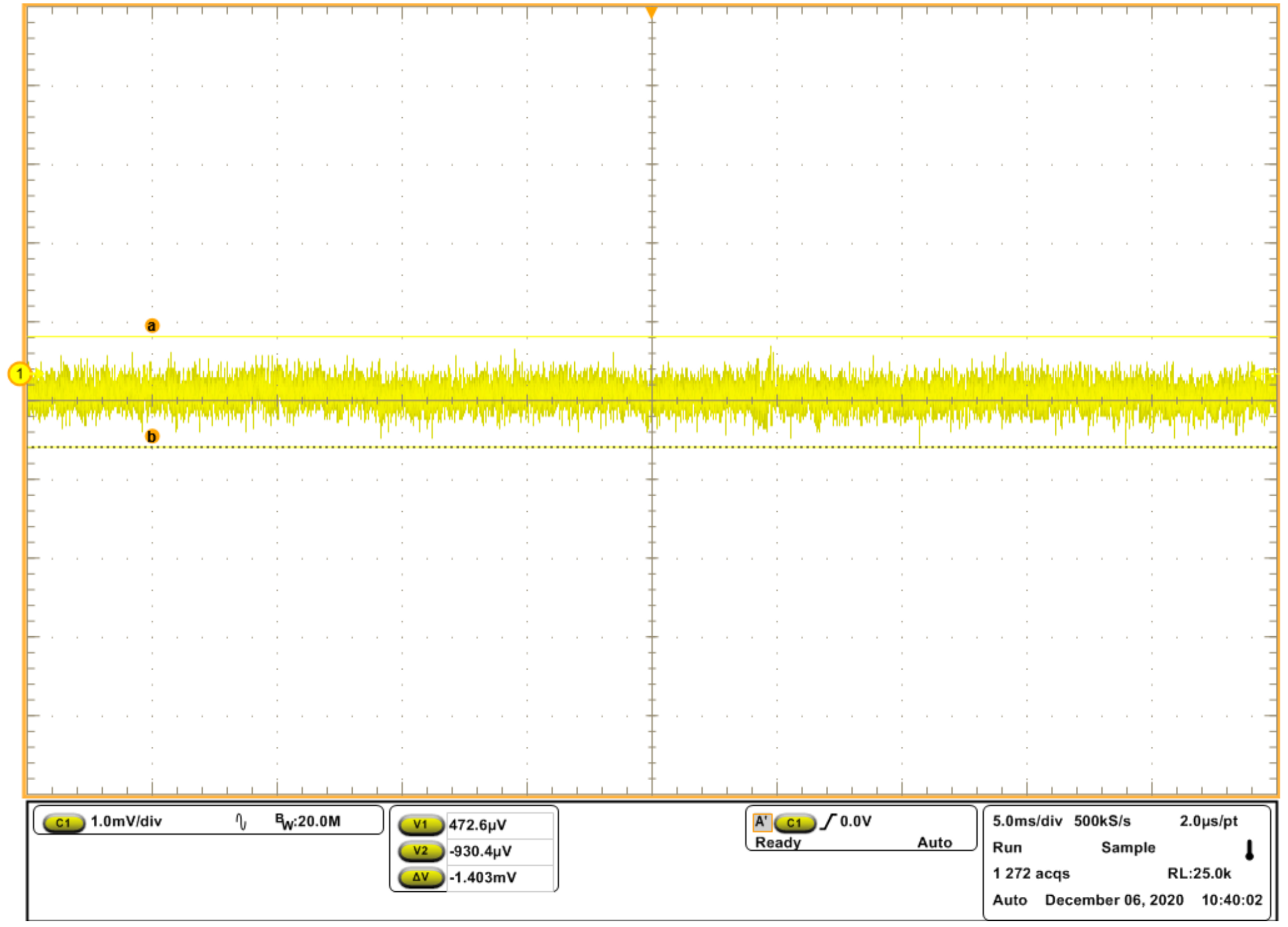
4.2. The Simulated and Experimental Results
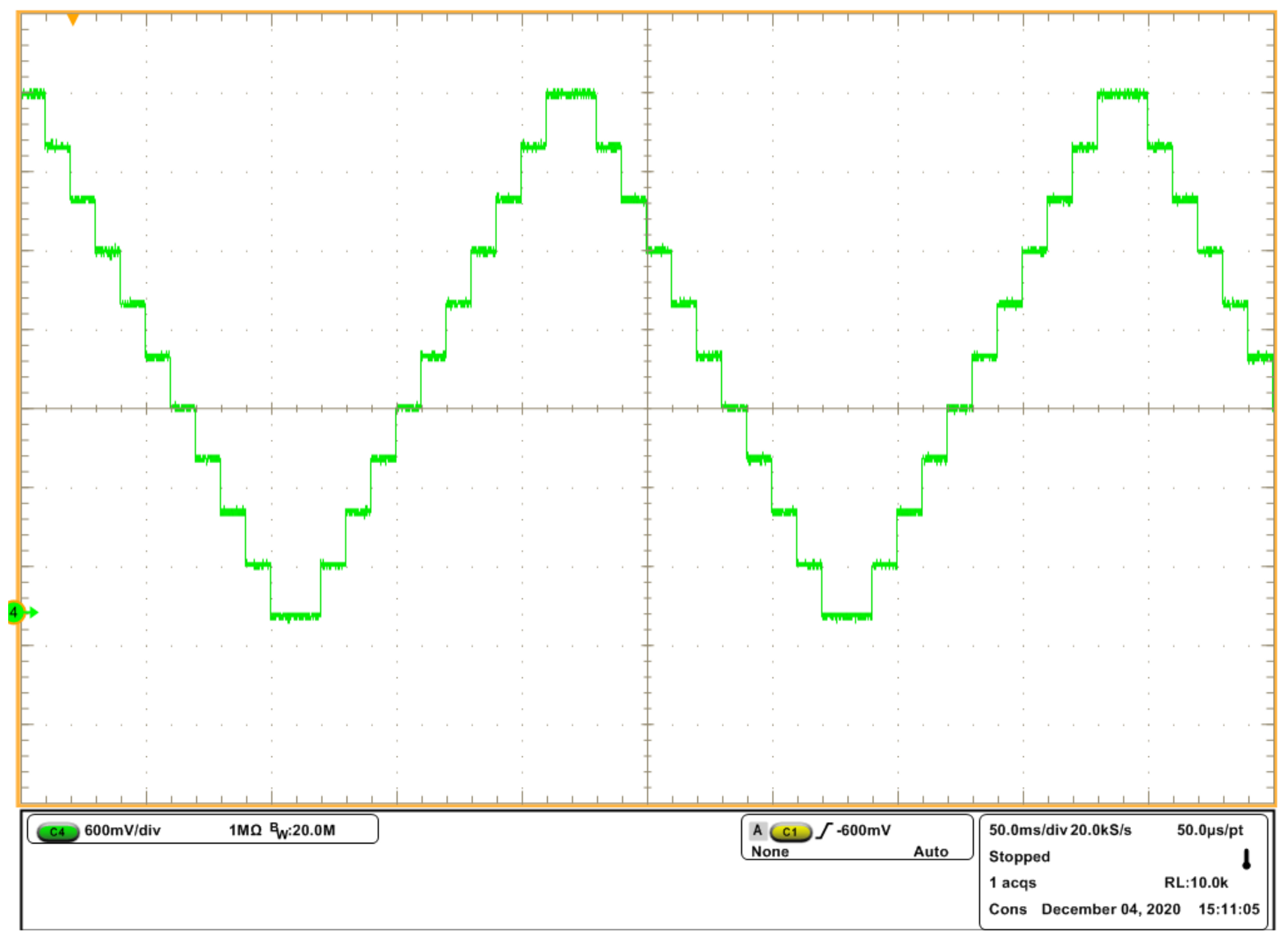
5. Tests with Mechanical Stage and Some Comparisons
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Romero, E.; Peretti, G.; Marqués, C. An operational amplifier model for evaluating test strategies at behavioural level. Microelectron. J. 2007, 38, 1082–1094. [Google Scholar] [CrossRef]
- Giusi, G.; Crupi, F.; Pace, C.; Magnone, P. Full Model and Characterization of Noise in Operational Amplifier. IEEE Trans. Circuits Syst. I Regul. Pap. 2009, 56, 97–102. [Google Scholar] [CrossRef]
- Spinelli, E.M.; Haberman, M.A.; Guerrero, F.N.; García, P.A. A High Input Impedance Single-Ended Input to Balanced Differential Output Amplifier. IEEE Trans. Instrum. Meas. 2020, 69, 1682–1689. [Google Scholar] [CrossRef]
- Fang, S.; Wang, X. Modeling and analysis method of fractional-order buck–boost converter. Int. J. Circuit Theory Appl. 2020, 48, 1493–1510. [Google Scholar] [CrossRef]
- Xu, S.; Wang, C.; Lu, S.; Sun, W. Small-signal modelling for time-length compensation algorithm in current controlled converters. Int. J. Circuit Theory Appl. 2020, 48, 148–155. [Google Scholar] [CrossRef]
- Maundy, B.J.; Elwakil, A.S.; Gift, S.J. Enhancing the improved Howland circuit. Int. J. Circuit Theory Appl. 2019, 47, 532–541. [Google Scholar] [CrossRef]
- Imam, A.A.; Sreerama Kumar, R.; Al-Turki, Y.A. Modeling and Simulation of a PI Controlled Shunt Active Power Filter for Power Quality Enhancement Based on P-Q Theory. Electronics 2020, 9, 637. [Google Scholar] [CrossRef]
- Zaman, H.; Zheng, X.; Wu, X.; Khan, S.; Ali, H. A Fixed-Frequency Sliding-Mode Controller for Fourth-Order Class-D Amplifier. Electronics 2018, 7, 261. [Google Scholar] [CrossRef]
- Cheng, Q.; Li, W.; Tang, X.; Guo, J. Design and Analysis of Three-Stage Amplifier for Driving pF-to-nF Capacitive Load Based on Local Q-Factor Control and Cascode Miller Compensation Techniques. Electronics 2019, 8, 572. [Google Scholar] [CrossRef]
- Shao, Y.; Xu, M.; Shao, S.; Song, S. Effective dynamical model for piezoelectric stick-slip actuators in bi-directional motion. Mech. Syst. Signal Process. 2020, 145, 106964. [Google Scholar] [CrossRef]
- Deng, J.; Chen, W.; Li, K.; Wang, L.; Liu, Y. A sandwich piezoelectric actuator with long stroke and nanometer resolution by the hybrid of two actuation modes. Sens. Actuators A Phys. 2019, 296, 121–131. [Google Scholar] [CrossRef]
- Xu, Z.; Huang, H.; Dong, J. A stick-slip piezoelectric actuator with measurable contact force. Mech. Syst. Signal Process. 2020, 144, 106881. [Google Scholar] [CrossRef]
- Lin, C.Y.; Tampubolon, M.; Lo, Y.K.; Lin, J.Y.; Wu, Y.C.; Chiu, H.J. Study and implementation of a 15-W driver for piezoelectric actuators. Int. J. Circuit Theory Appl. 2017, 45, 439–454. [Google Scholar] [CrossRef]
- Milecki, A.; Regulski, R. Investigations of electronic amplifiers supplying a piezobimorph actuator. Mech. Syst. Signal Process. 2016, 78, 43–54. [Google Scholar] [CrossRef]
- Wang, D.H.; Zhu, W.; Yang, Q. A High-voltage and High-power Amplifier for Driving Piezoelectric Stack Actuators. J. Intell. Mater. Syst. Struct. 2009, 20, 1987–2001. [Google Scholar] [CrossRef]
- Tung, Y.C.; Jeng, S.L.; Chieng, W.H. Multi-level balanced isolated floating difference amplifier. IEEE Trans. Ind. Electron. Circuits Syst. I Regul. Pap. 2008, 55, 3016–3022. [Google Scholar] [CrossRef][Green Version]
- Xu, L.; Li, H.; Li, P.; Ge, C. A High-Voltage and Low-Noise Power Amplifier for Driving Piezoelectric Stack Actuators. Sensors 2020, 20, 6528. [Google Scholar] [CrossRef] [PubMed]
- Rios, S.A.; Fleming, A.J. Design of a Charge Drive for Reducing Hysteresis in a Piezoelectric Bimorph Actuator. IEEE/Asme Trans. Mechatron. 2016, 21, 51–54. [Google Scholar] [CrossRef]
- Yang, C.; Li, C.; Xia, F.; Zhu, Y.; Zhao, J.; Youcef-Toumi, K. Charge Controller with Decoupled and Self-Compensating Configurations for Linear Operation of Piezoelectric Actuators in a Wide Bandwidth. IEEE Trans. Ind. Electron. 2019, 66, 5392–5402. [Google Scholar] [CrossRef]
- Dahua Radio Instrument Factory. Available online: http://www.dhelec.com.cn/ (accessed on 23 January 2021).
- Keysight Technologies. Available online: https://www.keysight.com (accessed on 23 January 2020).
- Tektronix Corporation. Available online: https://www.tek.com.cn (accessed on 23 January 2020).
- Physik Instrumente. Available online: www.physikinstrumente.com (accessed on 23 January 2020).








| Circuit | Model | Parameters of the Model |
|---|---|---|
| operational amplifier | A = 3.16 × 105, S1 = 10 π, S2 = 8 π × 106 | |
| RC filter | R = 50 Ω and C = 4 nF | |
| magnification of the inner-loop | KB | the conductance of the MOSFET |
| load (variable capacitance) | CL | 4.7 μF which is the maximum load capacitance for the circuit |
| feedback network | R4 = 200 k, R5 = 8.25 k, C2 = 15 pF |
| Circuit | Model | Parameters of the Model |
|---|---|---|
| operational amplifier | A = 1.0 × 108, S1 = 0.4 π, S2 = 10 π × 106 | |
| RC filter | R = 100 Ω and C = 4 pF | |
| inner loop transfer function | TA = R8C1, R8 = 5 k, C1 = 150 pF | |
| load (variable capacitance) | CL | 4.7 μF which is the maximum load capacitance for the circuit |
| feedback network | R9 = 120 k, R10 = 5 k, C2 = 15 pF |
| References | Ripple | Bandwidth | Cost | Size | Circuit Complexity |
|---|---|---|---|---|---|
| [13] | 40 mV | Not given | Low | Medium | Complex |
| [14] | Not given | 20 kHz | Medium | Medium | Simple |
| [15] | 20 mV | About 20 kHz | Medium | Big | Medium |
| [17] | 2 mV | 57 kHz | Low | small | Complex |
| E-618 ([23]) | 20 mV | About 15 kHz | High | Big | Not given |
| This work A | 16 mV | 43 kHz | Medium | Small | Simple |
| This work B | 2 mV | 53 kHz | Low | Small | Simple |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.; Li, H.; Li, P.; Ge, C. The Application of Classical Control in the Design and Analysis of Power Amplifiers for Driving Piezoelectric Stack Actuators. Electronics 2021, 10, 720. https://doi.org/10.3390/electronics10060720
Xu L, Li H, Li P, Ge C. The Application of Classical Control in the Design and Analysis of Power Amplifiers for Driving Piezoelectric Stack Actuators. Electronics. 2021; 10(6):720. https://doi.org/10.3390/electronics10060720
Chicago/Turabian StyleXu, Lisong, Hongwen Li, Pengzhi Li, and Chuan Ge. 2021. "The Application of Classical Control in the Design and Analysis of Power Amplifiers for Driving Piezoelectric Stack Actuators" Electronics 10, no. 6: 720. https://doi.org/10.3390/electronics10060720
APA StyleXu, L., Li, H., Li, P., & Ge, C. (2021). The Application of Classical Control in the Design and Analysis of Power Amplifiers for Driving Piezoelectric Stack Actuators. Electronics, 10(6), 720. https://doi.org/10.3390/electronics10060720






