A Machine Learning Workflow for Tumour Detection in Breasts Using 3D Microwave Imaging
Abstract
1. Introduction
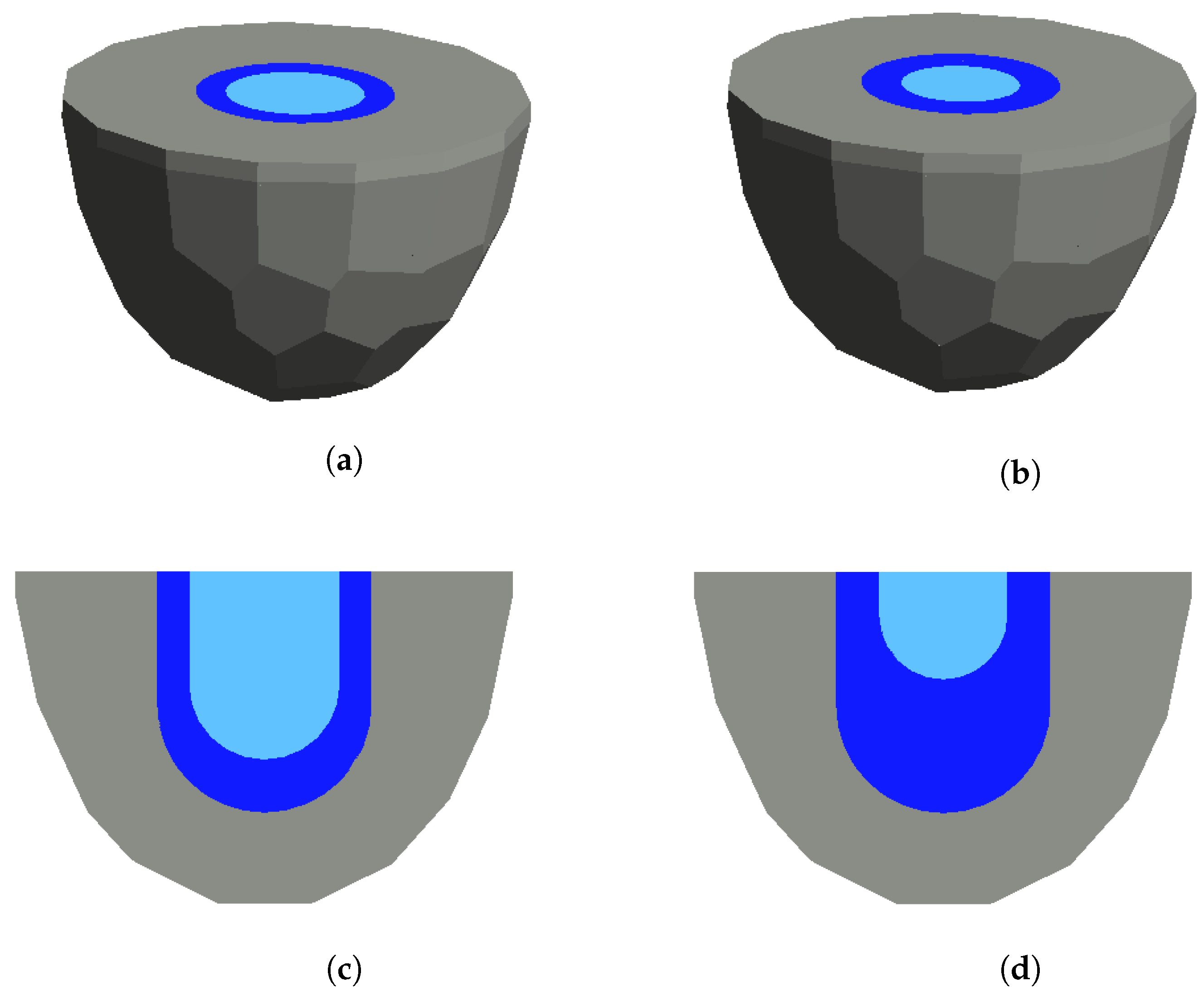
2. Faceted Air-Filled Chamber and Its Model for Microwave Breast Imaging
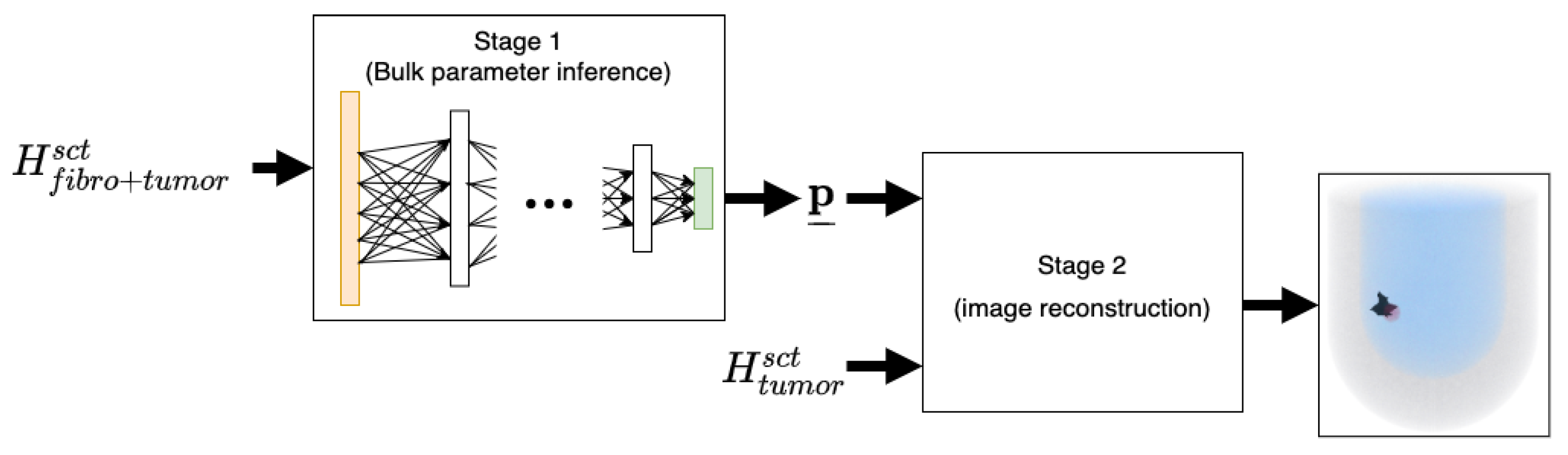
3. A Two-Stage Workflow for Prior Information Extraction and Data Inversion
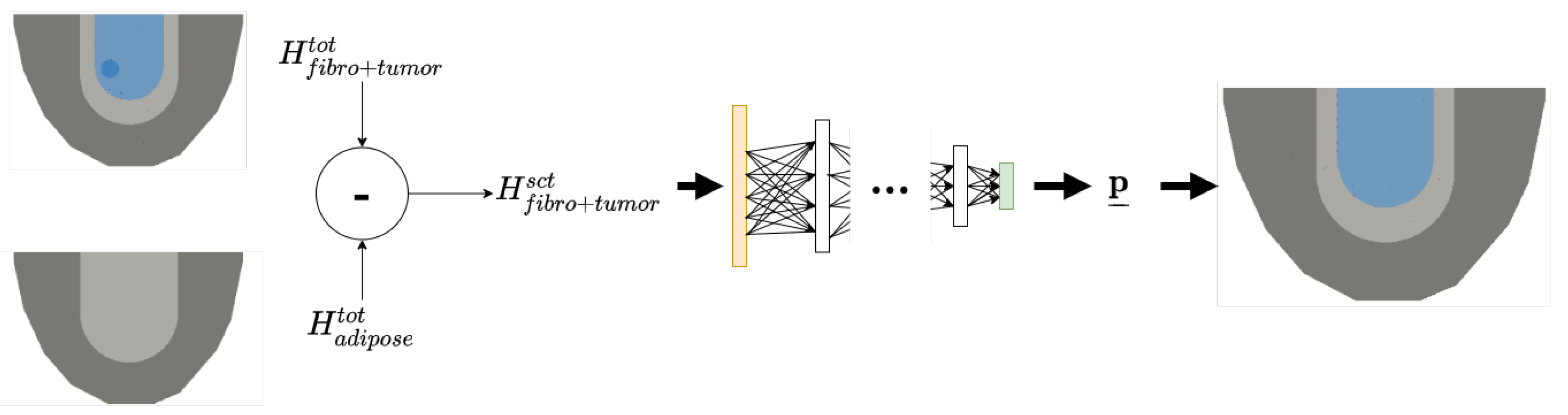
3.1. Stage 1: Bulk Parameter Inference using Neural Networks
3.1.1. Labelled Data
3.1.2. Stage 1 Network Architecture
3.1.3. Sample Pre-Processing
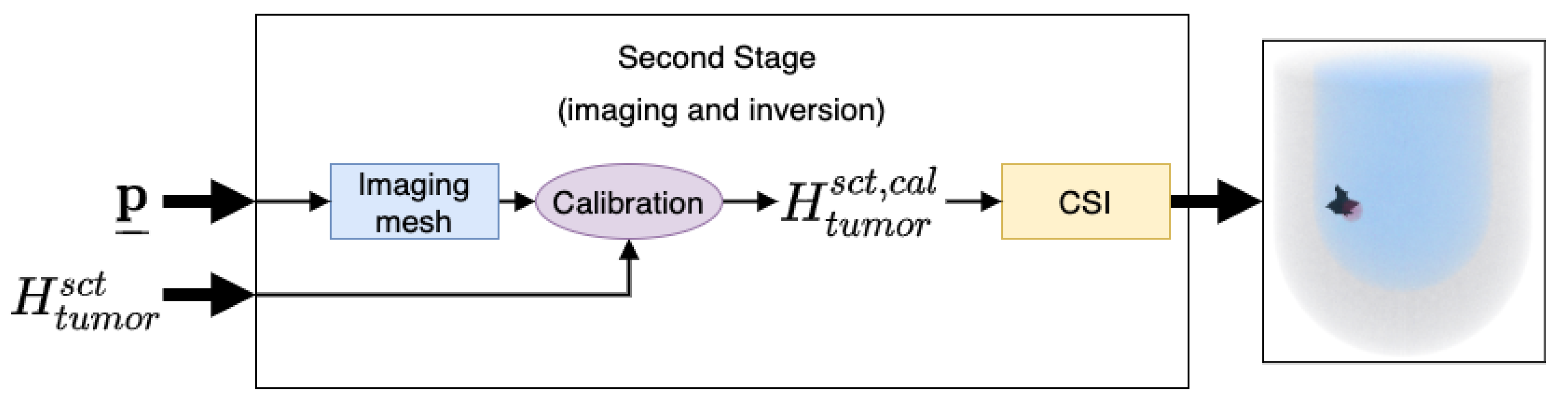
3.2. Stage 2: 3D Image Reconstruction and Tumour Detection
Contrast Source Inversion
3.3. Calibration
4. Results
4.1. Data Generation
4.2. Tumor Detection Test Samples
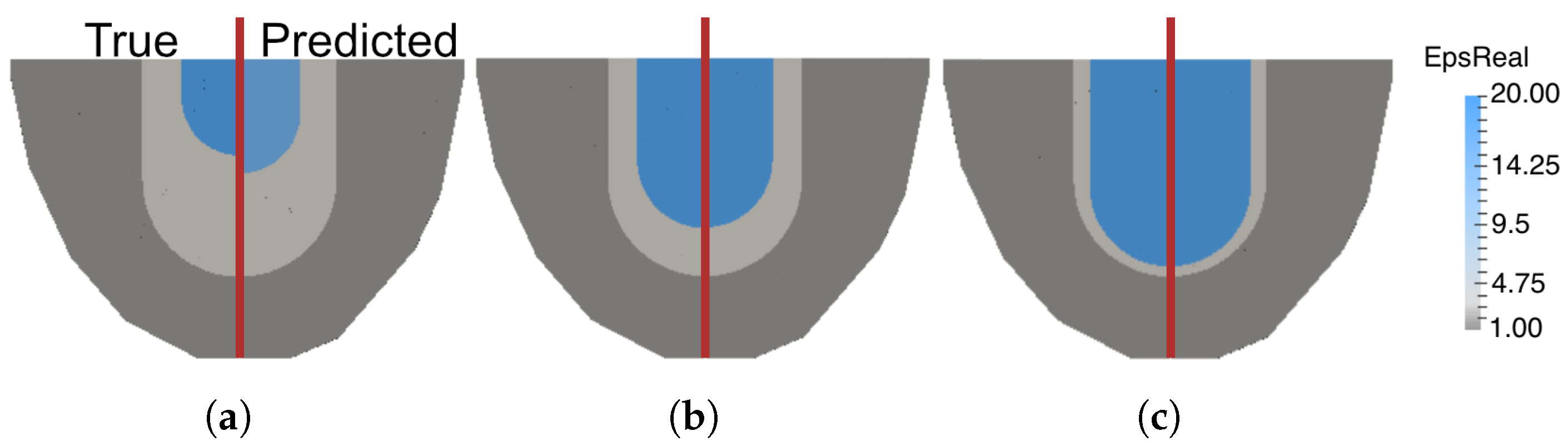
4.3. Parametric Inference of Fibroglandular Region Parameters
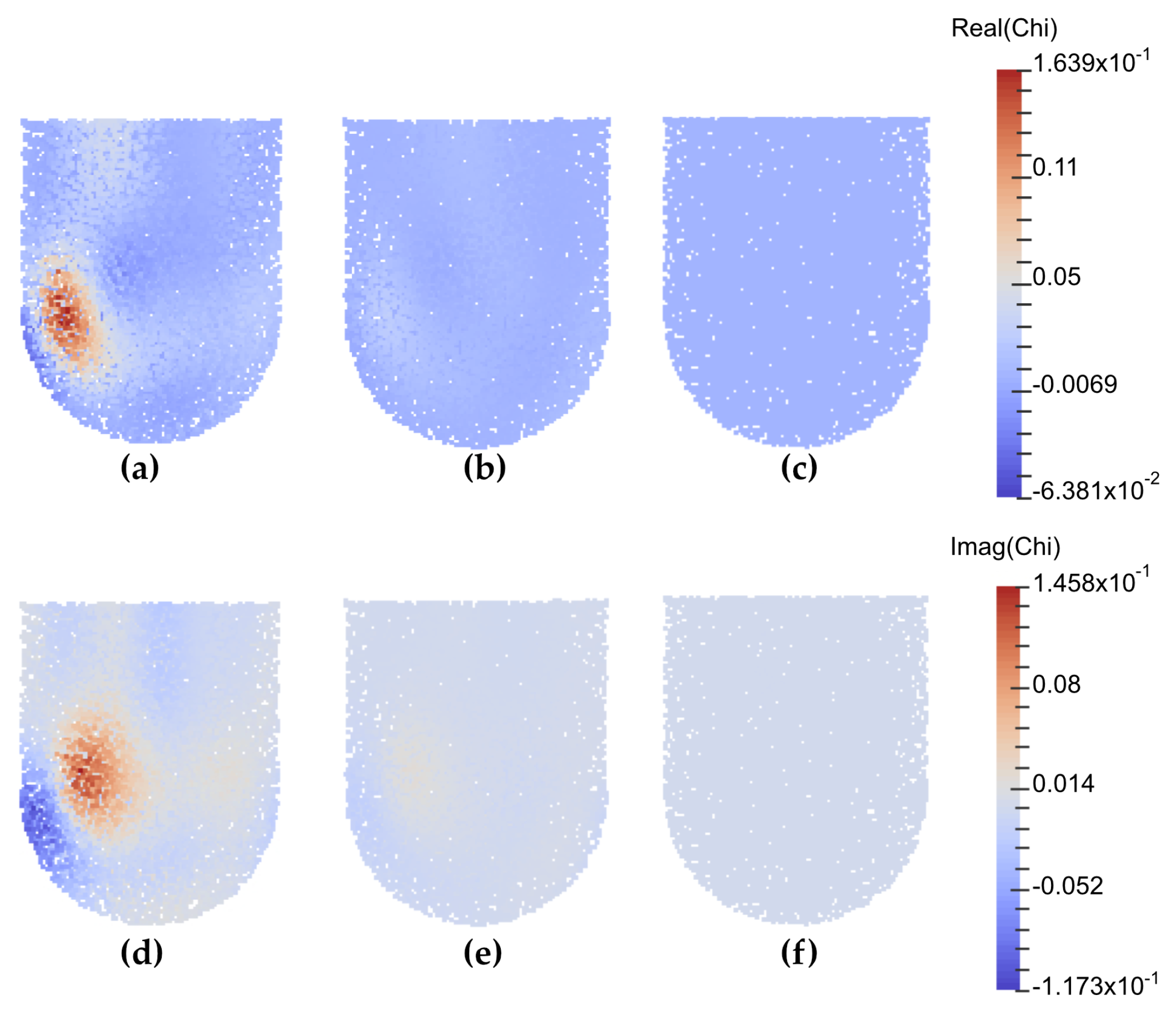
4.4. CSI-Based Tumor Detection from Predicted Prior Information
4.5. Monitoring Response to Tumor Treatment
4.6. Preliminary Bulk Parameter Inference Results on Experimental Data
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Conceição, R.C.; Mohr, J.J.; O’Halloran, M. An Introduction to Microwave Imaging for Breast Cancer Detection; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Nikolova, N.K. Microwave imaging for breast cancer. IEEE Microw. Mag. 2011, 12, 78–94. [Google Scholar] [CrossRef]
- Omer, M.; Mojabi, P.; Kurrant, D.; LoVetri, J.; Fear, E. Proof-of-concept of the incorporation of ultrasound-derived structural information into microwave radar imaging. IEEE J. Multiscale Multiphys. Comput. Tech. 2018, 3, 129–139. [Google Scholar] [CrossRef]
- Neira, L.M.; Van Veen, B.D.; Hagness, S.C. High-resolution microwave breast imaging using a 3-D inverse scattering algorithm with a variable-strength spatial prior constraint. IEEE Trans. Antennas Propag. 2017, 65, 6002–6014. [Google Scholar] [CrossRef]
- Poplack, S.P.; Tosteson, T.D.; Wells, W.A.; Pogue, B.W.; Meaney, P.M.; Hartov, A.; Kogel, C.A.; Soho, S.K.; Gibson, J.J.; Paulsen, K.D. Electromagnetic breast imaging: Results of a pilot study in women with abnormal mammograms. Radiology 2007, 243, 350–359. [Google Scholar] [CrossRef]
- Catapano, I.; Di Donato, L.; Crocco, L.; Bucci, O.M.; Morabito, A.F.; Isernia, T.; Massa, R. On quantitative microwave tomography of female breast. Prog. Electromagn. Res. 2009, 97, 75–93. [Google Scholar] [CrossRef]
- Abdollahi, N.; Kurrant, D.; Mojabi, P.; Omer, M.; Fear, E.; LoVetri, J. Incorporation of ultrasonic prior information for improving quantitative microwave imaging of breast. IEEE J. Multiscale Multiphys. Comput. Tech. 2019, 4, 98–110. [Google Scholar] [CrossRef]
- Ambrosanio, M.; Kosmas, P.; Pascazio, V. A Multithreshold Iterative DBIM-Based Algorithm for the Imaging of Heterogeneous Breast Tissues. IEEE Trans. Biomed. Eng. 2019, 66, 509–520. [Google Scholar] [CrossRef]
- Benny, R.; Anjit, T.A.; Mythili, P. An overview of microwave imaging for breast tumor detection. Prog. Electromagn. Res. 2020, 87, 61–91. [Google Scholar] [CrossRef]
- Lazebnik, M.; Popovic, D.; McCartney, L.; Watkins, C.B.; Lindstrom, M.J.; Harter, J.; Sewall, S.; Ogilvie, T.; Magliocco, A.; Breslin, T.M.; et al. A large-scale study of the ultrawideband microwave dielectric properties of normal, benign and malignant breast tissues obtained from cancer surgeries. Phys. Med. Biol. 2007, 52, 6093. [Google Scholar] [CrossRef]
- Shea, J.D.; Kosmas, P.; Hagness, S.C.; Van Veen, B.D. Three-dimensional microwave imaging of realistic numerical breast phantoms via a multiple-frequency inverse scattering technique. Med. Phys. (Lancaster) 2010, 37, 4210–4226. [Google Scholar] [CrossRef]
- Brown, K.G.; Geddert, N.; Asefi, M.; LoVetri, J.; Jeffrey, I. Hybridizable discontinuous Galerkin method contrast source inversion of 2-D and 3-D dielectric and magnetic targets. IEEE Trans. Microw. Theory Tech. 2019, 67, 1766–1777. [Google Scholar] [CrossRef]
- Asefi, M.; Baran, A.; LoVetri, J. An Experimental Phantom Study for Air-Based Quasi-Resonant Microwave Breast Imaging. IEEE Trans. Microw. Theory Tech. 2019, 67, 3946–3954. [Google Scholar] [CrossRef]
- Zakaria, A.; Jeffrey, I.; LoVetri, J.; Zakaria, A. Full-vectorial parallel finite-element contrast source inversion method. Prog. Electromagn. Res. 2013, 142, 463–483. [Google Scholar] [CrossRef]
- Tournier, P.H.; Bonazzoli, M.; Dolean, V.; Rapetti, F.; Hecht, F.; Nataf, F.; Aliferis, I.; El Kanfoud, I.; Migliaccio, C.; De Buhan, M.; et al. Numerical Modeling and High-Speed Parallel Computing: New Perspectives on Tomographic Microwave Imaging for Brain Stroke Detection and Monitoring. IEEE Antennas Propag. Mag. 2017, 59, 98–110. [Google Scholar] [CrossRef]
- Kurrant, D.; Baran, A.; LoVetri, J.; Fear, E. Integrating prior information into microwave tomography Part 1: Impact of detail on image quality. Med. Phys. 2017, 44, 6461–6481. [Google Scholar] [CrossRef]
- Kurrant, D.; Fear, E.; Baran, A.; LoVetri, J. Integrating prior information into microwave tomography part 2: Impact of errors in prior information on microwave tomography image quality. Med. Phys. (Lancaster) 2017, 44, 6482–6503. [Google Scholar] [CrossRef]
- Golnabi, A.H.; Meaney, P.M.; Paulsen, K.D. Tomographic microwave imaging with incorporated prior spatial information. IEEE Trans. Microw. Theory Tech. 2013, 61, 2129–2136. [Google Scholar] [CrossRef]
- Bevacqua, M.T.; Bellizzi, G.G.; Isernia, T.; Crocco, L. A method for effective permittivity and conductivity mapping of biological scenarios via segmented contrast source inversion. Prog. Electromagn. Res. 2019, 164, 1–15. [Google Scholar] [CrossRef]
- Abdollahi, N.; Jeffrey, I.; LoVetri, J. Improved Tumor Detection via Quantitative Microwave Breast Imaging Using Eigenfunction-Based Prior. IEEE Trans. Comput. Imaging 2020, 6, 1194–1202. [Google Scholar] [CrossRef]
- Hughson, M.; Jeffrey, I.; LoVetri, J. Ultrasound and Microwave Imaging with Prior Property Dependencies. In Proceedings of the 2019 IEEE MTT-S International Conference on Numerical Electromagnetic and Multiphysics Modeling and Optimization (NEMO), Boston, MA, USA, 29–31 May 2019; pp. 1–4. [Google Scholar]
- Obermeier, R.; Martinez-Lorenzo, J.A. Compressive sensing unmixing algorithm for breast cancer detection. IET Microw. Antennas Propag. 2018, 12, 533–541. [Google Scholar] [CrossRef]
- Chen, X. Computational Methods for Electromagnetic Inverse Scattering; John Wiley & Sons Pte. Ltd.: Singapore, 2018. [Google Scholar]
- Wei, Z.; Chen, X. Deep-learning schemes for full-wave nonlinear inverse scattering problems. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1849–1860. [Google Scholar] [CrossRef]
- Li, L.; Wang, L.; Teixeira, F.; Che, L.; Cui, T. DeepNIS: Deep Neural Network for Nonlinear Electromagnetic Inverse Scattering. IEEE Trans. Antennas Propag. 2018. [Google Scholar] [CrossRef]
- Guo, R.; Song, X.; Li, M.; Yang, F.; Xu, S.; Abubakar, A. Supervised descent learning technique for 2-D microwave imaging. IEEE Trans. Antennas Propag. 2019, 67, 3550–3554. [Google Scholar] [CrossRef]
- Oktay, O.; Ferrante, E.; Kamnitsas, K.; Heinrich, M.P.; Bai, W.; Caballero, J.; Guerrero, R.; Cook, S.A.; de Marvao, A.; Dawes, T.; et al. Anatomically Constrained Neural Networks (ACNN): Application to Cardiac Image Enhancement and Segmentation. IEEE Trans. Med. Imaging 2017, 37, 384–395. [Google Scholar] [CrossRef]
- Shao, W.; Du, Y. Microwave Imaging by Deep Learning Network: Feasibility and Training Method. IEEE Trans. Antennas Propag. 2020, 68, 5626–5635. [Google Scholar] [CrossRef]
- Chen, X.; Wei, Z.; Li, M.; Rocca, P. A Review of Deep Learning Approaches for Inverse Scattering Problems (Invited Review). Prog. Electromagn. Res. 2020, 167, 67–81. [Google Scholar] [CrossRef]
- Khoshdel, V.; Ashraf, A.; LoVetri, J. Enhancement of Multimodal Microwave-Ultrasound Breast Imaging Using a Deep-Learning Technique. Sensors 2019, 19, 4050. [Google Scholar] [CrossRef]
- Mojabi, P.; Khoshdel, V.; LoVetri, J. Tissue-Type Classification With Uncertainty Quantification of Microwave and Ultrasound Breast Imaging: A Deep Learning Approach. IEEE Access 2020, 8, 182092–182104. [Google Scholar] [CrossRef]
- Khoshdel, V.; Asefi, M.; Ashraf, A.; LoVetri, J. Full 3D Microwave Breast Imaging Using a Deep-Learning Technique. J. Imaging 2020, 6, 80. [Google Scholar] [CrossRef]
- Gilmore, C.; Jeffrey, I.; Asefi, M.; Geddert, N.T.; Brown, K.G.; LoVetri, J. Phaseless Parametric Inversion for System Calibration and Obtaining Prior Information. IEEE Access 2019, 7, 128735–128745. [Google Scholar] [CrossRef]
- Edwards, K.; Krakalovich, K.; Kruk, R.; Khoshdel, V.; LoVetri, J.; Gilmore, C.; Jeffrey, I. The implementation of neural networks for phaseless parametric inversion. In Proceedings of the 2020 XXXIIIrd General Assembly and Scientific Symposium of the International Union of Radio Science, Rome, Italy, 29 August–5 September 2020; pp. 1–3. [Google Scholar]
- Edwards, K.; Geddert, N.; Krakalovich, K.; Kruk, R.; Asefi, M.; Lovetri, J.; Gilmore, C.; Jeffrey, I. Stored Grain Inventory Management Using Neural-Network-Based Parametric Electromagnetic Inversion. IEEE Access 2020, 8, 207182–207192. [Google Scholar] [CrossRef]
- Nemez, K.; Asefi, M.; Baran, A.; LoVetri, J. A faceted magnetic field probe resonant chamber for 3D breast MWI: A synthetic study. In Proceedings of the 2016 17th International Symposium on Antenna Technology and Applied Electromagnetics (ANTEM), Montreal, QC, Canada, 10–13 July 2016; pp. 1–3. [Google Scholar]
- Nemez, K.; Baran, A.; Asefi, M.; LoVetri, J. Modeling error and calibration techniques for a faceted metallic chamber for magnetic field microwave imaging. IEEE Trans. Microw. Theory Tech. 2017, 65, 4347–4356. [Google Scholar] [CrossRef]
- Geddert, N. An electromagnetic hybridizable discontinuous Galerkin method forward solver with high-order geometry for inverse problems. Master’s Thesis, Department of Electrical and Computer Engineering, University of Manitoba, Winnipeg, MB, Canada, 2020. [Google Scholar]
- Gilmore, C.; Zakaria, A.; Pistorius, S.; LoVetri, J. Microwave imaging of human forearms: Pilot study and image enhancement. Int. J. Biomed. Imaging 2013, 2013, 673027. [Google Scholar] [CrossRef]
- Van Den Berg, P.M.; Kleinman, R.E. A contrast source inversion method. Inverse Probl. 1997, 13, 1607. [Google Scholar] [CrossRef]
- Zakaria, A.; Gilmore, C.; LoVetri, J. Finite-element contrast source inversion method for microwave imaging. Inverse Probl. 2010, 26, 115010. [Google Scholar] [CrossRef]


| Radius Range [cm] | Height Range [cm] | Range | Range |
|---|---|---|---|
| [2.85, 4.10] | [5.30, 9.80] | [15, 25] | [−25, −15] |
| Metric | Error in | Error in | Error in | Error in |
|---|---|---|---|---|
| Radius [mm] | Height [mm] | |||
| Average absolute error | 0.0280 | 0.0248 | 0.0866 | 0.0963 |
| Average absolute error (%) | 0.97% | 0.83% | 0.58% | 0.39% |
| Standard deviation | 0.0204 | 0.0194 | 0.0670 | 0.0765 |
| Position | Tumor Radius | Radius | Height | ||
|---|---|---|---|---|---|
| [mm] | [cm] | [cm] | |||
| Small fibroglandular case: | |||||
| True values: | 2.90 | 5.35 | 20.0 | −21.6 | |
| No tumor | - | 3.06 | 6.04 | 16.02 | −21.85 |
| T1 | 9 | 3.05 | 6.09 | 16.66 | −22.08 |
| T2 | 9 | 3.06 | 6.13 | 16.03 | −22.07 |
| Medium fibroglandular case: | |||||
| True values: | 3.40 | 8.50 | 20.0 | −21.6 | |
| No tumor | - | 3.39 | 8.46 | 19.90 | −21.60 |
| T1 | 9 | 3.39 | 8.47 | 19.71 | −21.72 |
| T1 | 4.5 | 3.40 | 8.44 | 20.03 | −21.57 |
| T2 | 9 | 3.39 | 8.45 | 20.48 | −21.58 |
| Large fibroglandular case: | |||||
| True values: | 4.05 | 9.75 | 20.0 | −21.6 | |
| No tumor | - | 4.07 | 9.71 | 19.81 | −21.55 |
| T1 | 9 | 4.07 | 9.73 | 19.74 | −21.36 |
| T2 | 9 | 4.06 | 9.72 | 19.79 | −21.58 |
| Noise | Metric | Error in | Error in | Error in | Error in |
|---|---|---|---|---|---|
| Radius [mm] | Height [mm] | ||||
| Average | 0.0545 | 0.0251 | 1.28 | 0.167 | |
| (−80 dB) | Max | 0.161 | 0.775 | 3.98 | 0.478 |
| Average | 0.0549 | 0.0250 | 1.41 | 0.283 | |
| (−60 dB) | Max | 0.180 | 0.779 | 4.56 | 0.679 |
| Average | 0.115 | 0.444 | 4.06 | 2.92 | |
| (−40 dB) | Max | 0.233 | 1.31 | 7.47 | 10.1 |
| Position | Tumor Radius | Radius | Height | ||
|---|---|---|---|---|---|
| [mm] | [cm] | [cm] | |||
| True values: | 3.40 | 8.50 | 20.0 | −21.6 | |
| No tumor 1 | - | 3.50 | 8.39 | 13.37 | −14.24 |
| No tumor 2 | - | 3.47 | 8.29 | 13.38 | −14.85 |
| T1 | 9 | 3.56 | 8.56 | 11.83 | −15.38 |
| T2 | 9 | 3.55 | 8.25 | 11.61 | −16.35 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Edwards, K.; Khoshdel, V.; Asefi, M.; LoVetri, J.; Gilmore, C.; Jeffrey, I. A Machine Learning Workflow for Tumour Detection in Breasts Using 3D Microwave Imaging. Electronics 2021, 10, 674. https://doi.org/10.3390/electronics10060674
Edwards K, Khoshdel V, Asefi M, LoVetri J, Gilmore C, Jeffrey I. A Machine Learning Workflow for Tumour Detection in Breasts Using 3D Microwave Imaging. Electronics. 2021; 10(6):674. https://doi.org/10.3390/electronics10060674
Chicago/Turabian StyleEdwards, Keeley, Vahab Khoshdel, Mohammad Asefi, Joe LoVetri, Colin Gilmore, and Ian Jeffrey. 2021. "A Machine Learning Workflow for Tumour Detection in Breasts Using 3D Microwave Imaging" Electronics 10, no. 6: 674. https://doi.org/10.3390/electronics10060674
APA StyleEdwards, K., Khoshdel, V., Asefi, M., LoVetri, J., Gilmore, C., & Jeffrey, I. (2021). A Machine Learning Workflow for Tumour Detection in Breasts Using 3D Microwave Imaging. Electronics, 10(6), 674. https://doi.org/10.3390/electronics10060674








