Abstract
In this paper, we adapt a recently proposed U-net deep neural network architecture from melody to bass transcription. We investigate pitch shifting and random equalization as data augmentation techniques. In a parameter importance study, we study the influence of the skip connection strategy between the encoder and decoder layers, the data augmentation strategy, as well as of the overall model capacity on the system’s performance. Using a training set that covers various music genres and a validation set that includes jazz ensemble recordings, we obtain the best transcription performance for a downscaled version of the reference algorithm combined with skip connections that transfer intermediate activations between the encoder and decoder. The U-net based method outperforms previous knowledge-driven and data-driven bass transcription algorithms by around five percentage points in overall accuracy. In addition to a pitch estimation improvement, the voicing estimation performance is clearly enhanced.
1. Introduction
The transcription of melodies and bass lines from complex music recordings is a challenging task for both human experts and machine algorithms. If musical notes are simultaneously played on different instruments within a certain interval relationship, a subset of the resulting overtones overlap. This can result in pitch estimation mistakes such as octave errors. Both melodies and bass lines are typically monophonic and their estimation from audio recordings is therefore considered as single-pitch estimation problems. In both scenarios, the transcription process involves two subproblems. The first subproblem is activity detection (often referred to as voicing estimation), where the goal is to estimate for each frame whether the targeted instrument is active or not. The second subproblem is pitch estimation, where the fundamental frequency and its corresponding pitch is computed for each active frame.
In contrast to melody lines, bass lines are rarely predominant. Particularly in jazz recordings, melodic instruments such as saxophones and trumpets often dominate the audio mix whereas rhythm section instruments such as upright bass and drums are playing in the background. Walking bass lines, which are most common in jazz, provide a steady pulse by emphasizing strong metrical positions (beat). At the same time, these bass lines give harmonic support by including important chord tones such as roots, thirds, and fifths of the played chords [1]. The main objective of this paper is to develop an algorithm to automatically transcribe jazz bass lines, which provide important rhythmic and harmonic cues for jazz ensemble performance analysis.
As the main contribution of this paper, we adapt a fully convolutional neural network based on the U-net architecture, which was previously used for melody transcription [2], for the task of bass transcription. In particular, we are investigating the influence of different hyperparameters such as the type of skip connections between encoder and decoder layers, the overall model capacity, as well as two different data augmentation strategies.
The remainder of the paper is structured as follows. Related work on data-driven bass and melody estimation is summarized in Section 2.1. Special focus is put on the application of U-net neural network architectures for Music Information Retrieval (MIR) tasks in Section 2.2. Section 3 introduces the proposed bass transcription method and details the applied audio processing and data augmentation techniques as well as the underlying neural network architecture. After introducing the applied datasets in Section 4, the experimental procedure and results are summarized in Section 5. Finally, in Section 6, we give a short conclusion of this work.
2. Related Work
2.1. Data-Driven Melody and Bass Transcription
Existing algorithms for bass and melody transcription share many techniques and can be divided into data-driven and knowledge-based methods. Data-driven transcription algorithms usually include machine learning models, which are trained in a supervised fashion. More traditionally, knowledge-based methods include specialized signal processing algorithms, which are often combined with heuristics informed by musical knowledge. With the rapid proliferation of deep learning techniques, data-driven methods have become the primary focus of research in recent years. In the subsequent discussion, we mainly focus on these approaches.
Most methods based on deep learning require large amounts of training data. However, in MIR, even for the popular task of melody transcription, only a limited number of public datasets such as MedleyDB [3], iKala (http://mac.citi.sinica.edu.tw/ikala/(accessed on 11 March 2021)) and MIR1k (https://sites.google.com/site/unvoicedsoundseparation/mir-1k (accessed on 11 March 2021)) exist, which include audio recordings and corresponding pitch annotations. For bass transcription, publicly available datasets with score-based bass annotations include the Real World Computing (RWC) dataset [4], MDB-bass-synth [5], and parts of the Weimar Jazz Database (WJD) [1,6]. A common approach to increase the amount and variability of potential training data is to apply data augmentation techniques such as time stretching and pitch shifting [7].
Different types of signal representations are used as input. While end-to-end-learning models directly process signal blocks [8,9], other networks process time-frequency representations obtained from a Short-Time Fourier Transform (STFT) [10], a constant-Q transform (CQT), or a harmonic CQT (HCQT) [11,12,13].
Various model architectures ranging from fully-connnected neural networks (FCNN) [1,14,15,16], over convolutional neural networks (CNN) [8,17], to recurrent neural networks (RNN) [10,14] are used and combined for the tasks of pitch estimation and voicing detection. Bittner et al. [11] propose a CNN model for multitask learning, which is trained to simultaneously perform melody, bass, and vocal transcription. The main rationale is that these tasks rely on and benefit from shared internal feature representations. Previously proposed data-driven bass transcription methods have used fully connected neural networks to predict pitches on a semitone resolution [1,16].
2.2. U-Nets
The U-net is a fully convolutional neural network architecture, which was originally proposed for biomedical image segmentation in computer vision [18]. The network structure resembles a convolutional autoencoder and consists of a contractive part (encoder) and an expansive part (decoder). In the encoder, the spatial resolution of the two-dimensional signal representation is gradually reduced while the number of feature channels is increased at the same time. Similarly, the decoder gradually increases the spatial resolution (using a sequence of upsampling operations), while reducing the number of feature channels. As the main improvements towards autoencoders, skip connections are introduced on different resolution levels within the network. This way, signal representations can be learnt at different resolutions.
Image segmentation algorithms aim to detect object as closes surfaces. By analogy, musical notes can be considered as objects in time-frequency representations with a sparse distribution since most of their concentrates at the fundamental frequency and its overtone frequencies. As a consequence, U-net based neural network architectures have not just been used for image segmentation but were also successfully applied for various MIR tasks such as source separation [19,20], multi-instrument music transcription [21], and lyrics-to-music alignment [22]. In addition to [2], other melody transcription algorithms using U-nets were proposed, among others, by Lu and Su [23] as well as Doras et al. [13].
3. Methodology
In this section, the different processing stages of the proposed bass transcription algorithm are detailed.
3.1. Audio Processing
Audio signals are mixed to mono and downsampled to a sample rate of 22.05 kHz. A constant-Q transformation (CQT) is computed with a hopsize of 512 samples, 12 bins per semitone resolution, and a core MIDI pitch range of [25:88] (E1 to F5). This range consists of 64 pitches and was chosen in order to replicate the network architecture proposed in [2]. Around this core MIDI pitch range, we add a lower and upper pitch margin of 5 semitones to allow for on-the-fly pitch shift data augmentation as will be explained in Section 3.2. This results in a CQT spectrogram with T denoting the number of time frames. For each audio recording, we normalize the values of C to a range of by subtracting the global minimum value and dividing by the resulting global maximum value. A bass line is encoded as vector , where a component encodes a MIDI pitch number and encodes an inactive frame (for frame indices ). The final target matrix that is used to train the network consists of two parts. The first 64 columns contain the one-hot encoded pitch values and the last column the voicing information.
3.2. Data Augmentation
In this paper, we evaluate two approaches for data augmentation in order to enrich the variability of the training data. As a first data augmentation strategy, we randomly sample a pitch shift of semitones. Since the CQT spectrogram C was extract with a pitch margin of five semitones, pitch shifting can be performed efficiently by extracting the feature as a submatrix of C according to the pitch shift s. At the same time, the frame-level targets are shifted accordingly as for all voiced frames and the target matrix Y is generated accordingly.
As a second data augmentation strategy, we propose “randomEQ”, i.e., a random multiplicative equalization of the CQT magnitude spectrogram C before applying the normalization as discussed in Section 3.1. The main motivation is to simulate variations of microphone characteristics and acoustic recording conditions. We use a simple parametric equalization function for with controlling the opening width of the parabola and controlling the frequency position of the function maximum. For each file and each epoch during training, we randomly sample and with for all . The derived equalization function is multiplied element-wise with each spectral frame in the feature matrix X. Figure 1 shows five randomly created examples of such equalization functions . Schlüter and Grill used a similar approach and applied random frequency filters to the linear spectrogram [24] using Gaussian functions instead of quadratic functions. In total, we compare four configurations—no data augmentation, pitch shifting, randomEQ, as well as both pitch shifting and randomEQ.
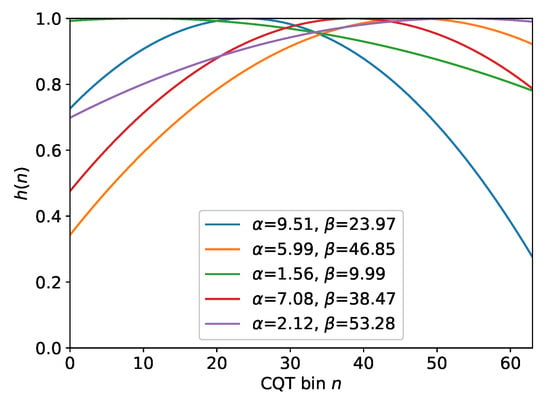
Figure 1.
Five examples of random equalization functions over .
3.3. Network Architecture
In this work, we take the U-net neural network used by Hsieh et al. in [2] as our reference system. Figure 2 summarizes the architecture of this fully convolutional neural network that consists of an encoder (left column) and a decoder (right column). The convolutional blocks CB(N) include a batch normalization layer (BatchNorm), a convolutional layers with N kernels (Conv2D(N)), and a scaled exponential linear units (SELU) activation function. In our experiments, we control the capacity of the U-net using a multiplicative scaling factor , which allows for the reduction of the number of kernels in the convolutional layers (apart from those layers with one convolutional layer) as shown in Figure 2. In the decoder, the number of frequency bins is gradually reduced from 64 to 1 using three max-pooling operations () while the number of convolutional kernels (N) is increased from to . Intermediate tensor dimensions are shown with orange backgrounds. T indicates the number of time frames of the input CQT spectrogram.
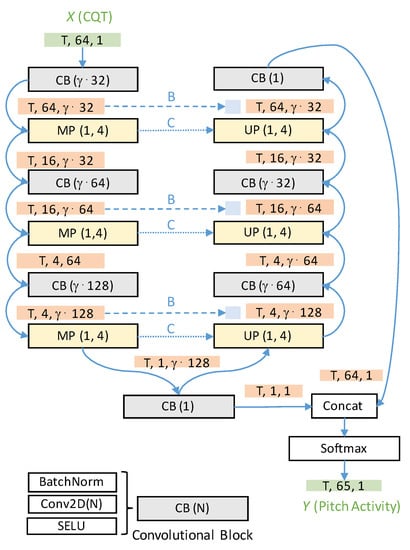
Figure 2.
U-net network architecture includes a decoder (left column) and an encoder (right column) with a sequence of convolutional blocks (CB), max pooling layers (MP), and unpooling layers (UP). Input and output variable dimensions are shown in green. Intermediate tensor dimensions are shown in orange. Solid blue lines show layer connections. Dashed and dotted blue lines indicate different skip connection strategies (compare Section 3.4). Number of kernels in the convolutional layers can be scaled with a factor (compare Section 3.3).
One of the main contributions of the model proposed by Hsieh et al. [2] is the introduction of the concatenation layer (“Concat” in Figure 2), which adds an additional column to the reconstructed feature tensor after the decoder. As explained in Section 3.1, the last row in the target matrix Y encodes the nonactivity of the bass instrument (unvoiced frames). Therefore, all unvoiced frames are encoded with a value of 1 in the last row. This way, the model can be trained to solve pitch detection and activity detection simultaneously. As a result, in the final prediction matrix, a simple argmax operation can be applied to decode the final bass pitch track and no additional thresholding operation is required. During training, we use the Adam optimizer with a learning rate of and the categorical crossentropy as loss functions.
3.4. Skip Connection Strategies
We compare four different skip connection strategies in this paper. As first approach (A), we avoid all skip connections, which converts the U-net into a deep convolutional autoencoder. As shown in Figure 2, the second approach (B) involves transferring intermediate activations after the convolutional blocks from the encoder to the decoder and stacking those with the intermediate activations in the decoder along the channel dimension [18]. In this approach, the unpooling layers perform a simple upsampling operation. As a third approach (C), the indices of the identified maxima in the max pooling (MP) layers are transferred to the unpooling (UP) layers [2]. The intuition is to obtain a more precise reconstruction while increasing the spatial resolution in the decoder. Finally, we also test the combination of the two skip-connection strategies B and C as fourth approach (D).
4. Datasets
Table 1 summarizes two sets that we assembled for this study. The Mixed Genre Set (MGS) comprises 137 recordings from four different datasets and covers multiple music genres such as pop, rock, and jazz. We included 70 recordings of the MDB-bass-synth database [5]. In these recordings, the bass track has been resynthesized to achieve a perfect correspondence to a previously estimated bass pitch track. The second subset includes 21 recordings from the MedleyDB dataset with manually transcribed bass lines. The third subset comprises of 16 files from the Popular Music Database of the RWC Database [25]. Finally, we have bass score annotations for 66 jazz ensemble recordings mostly coming from the Weimar Jazz Database (WJD) [6]. A subset of 30 of these files is included in the MGS.

Table 1.
Composition of the Mixed Genre Set (MGS) and Jazz Set (JS).
The Jazz Set (JS) includes the remaining 36 WJD files. It includes the 10 files previously used as test set in [16]. This set covers various artists, jazz styles, and recording decades and therefore allows for a realistic evaluation within the targeted application scenario.
We compare two data partition strategies as described in Table 2 to split the MGS and JS into training and validation sets. In the first strategy (Mixed), we aim for a bass transcription algorithm, which performs well for multiple music styles. Here, we randomly split the MGS into a training set (80%) and a validation set (20%). In the second strategy (Jazz), we aim to optimize the bass transcription algorithm to perform well on jazz ensemble recordings, which are in the focus of this paper. Here, we use the full MGS as training data and a random split of 20% of the JS as validation set. The remaining 80% of the files in JS are used as final test set for both strategies.

Table 2.
Two data partition strategies to split the two datasets introduced in Table 1 into training, validation, and test sets. The validation sets are used for the parameter optimization (Section 5.1) and the test set is used for the final evaluation study (Section 5.2).
5. Evaluation
5.1. Parameter Optimization Study
As discussed in Section 4, we investigate two different data partition strategies. In this experiment, we want to study the influence of the data augmentation method, the skip connection type, as well as the network capacity of the U-net approach to the transcription performance on the validation set. For each strategy, we compare 64 hyperparameter configurations based on the parameter settings defined in Table 3. The sets of hyperparameters for the best performing models in both scenarios are listed in Table 4.

Table 3.
Settings for the parameter optimization study described in Section 5.1.

Table 4.
Parameter optimization results: optimal hyperparameter configurations for both data partition strategies.
For the mixed data partition, skip connection strategy B, where the intermediate activations are transferred, outperforms strategy C, which involves transferring the max pooling indices. This finding goes in line with the proposed method for melody transcription in [2]. Larger models with combined with RandomEQ data augmentation consistently showed the best results. The highest overall accuracy value achieved was 0.82. We conjecture that this relatively high number is due to model overfitting to the Mixed Genre Set, where both the training and the validation set were drawn from it.
For the Jazz data partition, the highest overall accuracy is 0.6 and therefore significantly lower compared to the mixed data partition. Note that, in this case, the validation set only contains jazz ensemble recordings while the training set includes various music genres. Presumably, this shows that the bass transcription task is more complex due to the predominance of the melody instruments. Skip connection strategy B and pitch shifting data augmentation seem beneficial for this data partition although no clear trends could be observed across different hyperparameter configurations. The best models BassUNet and BassUNet obtained from the Mixed and Jazz data partition strategy, respectively, will be evaluated in the comparative study against three state-of-the-art bass transcription algorithms as will be described in the following section.
After identifying the optimal models BassUNet and BassUNet, we report in Table 5 the results of an ablation study. This table shows how the overall model accuracy values decrease when data augmentation and skip connections are neglected separately and jointly during the model training. The results show that both components are important for the performance of the U-net model. Similar findings were reported for the skip connections in U-nets for singing voice separation [26] as well as for the use of data augmentation for singing voice detection [24] and music transcription [27]. The sets of hyperparameters for the best performing models in both scenarios are listed in Table 4.

Table 5.
Ablation study results. Overall accuracy (OA) values on the validation sets reported for the optimal configuration (first row) and training configurations derived by removing data augmentation and skip connections separately and jointly from the model training (remaining rows).
5.2. Comparison to the State of the Art
In this experiment, we compare the two best configurations of the proposed method BassUNet and BassUNet as identified in Section 5.1 with three reference bass transcription algorithms as listed in Table 6. We use the remaining 80% of the Jazz Set (compare Section 4 and Table 2), i.e., the full Jazz Set without the validation set of the Jazz data partition as test set.

Table 6.
Brief description of all evaluated bass transcription algorithms (top) and average file-level scores on the test set (bottom). Optimal minimum salience thresholds for BI18 and AB17 obtained on the validation set are given in brackets.
The first reference algorithm (BI18) is encapsulated in a deep neural network for joint estimation of melody, multiple F0, and bass estimation as proposed by Bittner et al. [11]. The network processes harmonic CQT representations of audio signals with a cascade of multiple convolutional layers for multitask feature learning. We use an available online implementation (https://github.com/marl/superchip/blob/master/superchip/transcribe_f0.py (accessed on 11 March 2021)).
The second reference algorithm ({AB07) was proposed by Abeßer et al. in [1]. Here, a fully-connected neural network maps a CQT spectrogram to a bass pitch activity representation. Again, we use an available online implementation (https://github.com/jakobabesser/walking_bass_transcription_dnn (accessed on 11 March 2021)). Both algorithms AB17 and BI18 output independent pitch salience values for different F0 candidates on a frame level. Voicing estimation is implemented by using a fixed minimum salience threshold . Each time frame is considered to be unvoiced if all pitch salience values are below this threshold. We optimize this threshold independently for both algorithms on the full training set.
The third reference algorithm (SA12) is based on a version of the Melodia melody estimation algorithm [28], which is modified to transcribe lower fundamental frequencies as described in [29]. In contrast to the before-mentioned data-driven algorithms, this algorithm combines music domain knowledge with several audio signal processing steps. Furthermore, it analyzes only two octaves from 27.5 Hz to 110.0 Hz. Therefore, it only makes sense to compare the pitch estimation performance of SA12 with the other algorithm based on the raw chroma accuracy (RCA), which disregards the detected octave positions.
We use five common evaluation measures to evaluate the pitch estimation and voicing estimation as defined in [30]. Raw pitch accuracy (RPA) equals the fraction of the number of frames with correctly estimated pitches (within a given tolerance) and the number of voiced frames, i.e., frames with an annotated pitch. Raw chroma accuracy (RCA) additionally maps all frequency into one octave and therefore focuses on pitch class estimation. In order to evaluate the voicing estimation quality, voicing recall (VR) measures the fraction of correctly identified voiced frames and voicing false alarm rate (VFA) measures the fraction of frames which are incorrectly estimated to be voiced. A well-performing transcription algorithm should have high VR values and low VFA values as indicated by upwards and downwards arrows in Table 6. Finally, overall accuracy (OA) measures the percentage of frames with correctly estimated voicing and pitch.
Table 6 lists the five evaluation scores for each investigated bass transcription algorithm averaged over all test set files. While the proposed method BassUNet showed a lower OA value on the validation set of the Jazz data partition strategy (see Section 5.1), it outperforms all other algorithm on the test set by around 5 percent in overall accuracy (OA). The algorithm represents a model configuration, which is optimized for transcribing bass lines in jazz ensemble recordings. We believe that the main reason for that is the similar data distribution between its validation set, which guided the model training process, and the final test set.
The BassUNet model on the other hand, which was not optimized for the jazz scenario, shows a lower overall accuracy of , which results from both lower voicing and pitch detection scores. While the RPA improvement of between BassUNet and the best performing reference algorithm AB17 is only of minor size, the main improvement was achieved in voicing detection especially which is particularly evident in the reduced voicing false alarm rate of (VFA) from (AB17) to (BassUNet). We consider this to be the main contribution of the proposed U-net architecture since it explicitly learns to predict the frame-level instrument activity (voicing) without any additional thresholding operation. Similar findings were reported for the melody estimation task for some of the evaluated datasets in [2]. When looking at the pitch estimation performance (RPA, RCA), the BassUNet model performs similar to the reference methods BI18 and AB17. Notably, the reference algorithm SA12 achieves the highest VR and an almost similar raw chroma accuracy RCA as the proposed method.
6. Conclusions
In this paper, we adapt a recently proposed U-net deep neural network architecture for bass transcription of jazz ensemble recordings. Based on a constant-Q spectrogram representation of the audio signal, the network jointly predicts instrument activity (voicing) and pitch on a frame-level without requiring an additional thresholding operation. In our experiments, we perform an in-depth analysis of the influence of the applied data augmentation techniques, skip connection strategy between the encoder and decoder, as well as the overall model capacity on the model performance. In addition to the commonly used pitch shifting, we propose a simple random equalization technique (randomEQ), which increases the timbral variety of the training data. We investigate two different data partition strategy with one aiming at training a U-net model, which is optimized for transcribing bass lines in jazz ensemble recordings.
Our results show that the proposed model outperforms previous bass transcription algorithms based on fully-connected and convolutional neural network architectures as well as classical audio signal processing chains. In addition to minor pitch estimation improvements, the U-net model shows significantly lower voicing false alarms. Our findings also confirm that, especially for smaller amounts of available annotated training data, data-driven methods can be powerful but also highly sensitive to the choice of training and validation set. Our experiments confirm that the validation set should represent the expected data distribution in a given application scenario.
As discussed in Section 1, the presented bass transcription algorithm can be used to assist musicological corpus analyses. As one example, we plan to transcribe bass lines underlying all instrumental solo parts in the Weimar Jazz Database (WJD). In combination with manually transcribed beat times, we can derive beat-level bass note estimates. By combining these bass notes with the annotated harmonic changes of the lead-sheet, clues about the performed harmonic changes can be derived, which allow for a more in-depth analysis of the solo melodies.
Author Contributions
M.M. and J.A. substantially contributed to this work, including the formalization of the problem, the development of the ideas, and the writing of the paper. J.A. implemented the approaches and conducted the experiments. Both authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the German Research Foundation (AB 675/2-1, MU 2686/11-1).
Data Availability Statement
The trained models have been made publicly available to support further research https://github.com/jakobabesser/bassunet (accessed on 11 March 2021).
Acknowledgments
The International Audio Laboratories Erlangen are a joint institution of the Friedrich-Alexander-Universität Erlangen-Nürnberg (FAU) and Fraunhofer Institut für Integrierte Schaltungen IIS. The authors would like to thank Rachel Bittner and Justin Salamon for sharing datasets and supporting our evaluation with their bass transcription algorithms. In addition, our gratitude goes to Thomas Bugert for his transcription work on the Weimar Jazz Dataset bass lines and the Jazzomat Research Project for publishing the WJD dataset.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abeßer, J.; Balke, S.; Frieler, K.; Pfleiderer, M.; Müller, M. Deep Learning for Jazz Walking Bass Transcription. In Proceedings of the AES Conference on Semantic Audio, Erlangen, Germany, 22–24 June 2017; pp. 202–209. [Google Scholar]
- Hsieh, T.H.; Su, L.; Yang, Y.H. A Streamlined Encoder/Decoder Architecture for Melody Extraction. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 156–160. [Google Scholar]
- Bittner, R.M.; Salamon, J.; Tierney, M.; Mauch, M.; Cannam, C.; Bello, J.P. MedleyDB: A Multitrack Dataset for Annotation-Intensive MIR Research. In Proceedings of the 15th International Society for Music Information Retrieval Conference (ISMIR), Taipei, Taiwan, 27–31 October 2014; pp. 155–160. [Google Scholar]
- Goto, M. A real-time music scene description system: Predominant-F0 estimation for detecting melody and bass lines in real-world audio signals. Speech Commun. 2004, 43, 311–329. [Google Scholar] [CrossRef]
- Salamon, J.; Bittner, R.M.; Bonada, J.; Bosch, J.J.; Gómez, E.; Bello, J.P. An Analysis/Synthesis Framework for Automatic F0 Annotation of Multitrack Datasets. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Suzhou, China, 23–27 October 2017; pp. 71–78. [Google Scholar]
- Pfleiderer, M.; Frieler, K.; Abeßer, J.; Zaddach, W.G.; Burkhart, B. (Eds.) Inside the Jazzomat—New Perspectives for Jazz Research; Schott Campus: Santa Barbara, CA, USA, 2018. [Google Scholar]
- McFee, B.; Humphrey, E.J.; Bello, J.P. A Software Framework for Musical Data Augmentation. In Proceedings of the 16th International Society for Music Information Retrieval Conference (ISMIR), Málaga, Spain, 26–30 October 2015; pp. 248–254. [Google Scholar]
- Kim, J.W.; Salamon, J.; Li, P.; Bello, J.P. Crepe: A Convolutional Representation for Pitch Estimation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 161–165. [Google Scholar]
- Singh, S.; Wang, R.; Qiu, Y. DEEPF0: End-To-End Fundamental Frequency Estimation for Music and Speech Signals. arXiv 2021, arXiv:2102.06306. [Google Scholar]
- Park, H.; Yoo, C.D. Melody Extraction and Detection through LSTM-RNN with Harmonic Sum Loss. In Proceedings of the 42nd IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 2766–2770. [Google Scholar]
- Bittner, R.M.; McFee, B.; Bello, J.P. Multitask Learning for Fundamental Frequency Estimation in Music. arXiv 2018, arXiv:1809.00381. [Google Scholar]
- Bittner, R.M.; McFee, B.; Salamon, J.; Li, P.; Bello, J.P. Deep Salience Representations for F0 Estimation in Polyphonic Music. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Suzhou, China, 23–27 October 2017; pp. 63–70. [Google Scholar]
- Doras, G.; Esling, P.; Peeters, G. On the use of U-Net for dominant melody estimation in polyphonic music. In Proceedings of the International Workshop on Multilayer Music Representation and Processing (MMRP), Milano, Italy, 24–25 January 2019; pp. 66–70. [Google Scholar]
- Rigaud, F.; Radenen, M. Singing Voice Melody Transcription using Deep Neural Networks. In Proceedings of the 17th International Society for Music Information Retrieval Conference (ISMIR), New York, NY, USA, 7–11 August 2016; pp. 737–743. [Google Scholar]
- Balke, S.; Dittmar, C.; Abeßer, J.; Müller, M. Data-Driven Solo Voice Enhancement for Jazz Music Retrieval. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 196–200. [Google Scholar]
- Abeßer, J.; Balke, S.; Müller, M. Improving Bass Saliency Estimation Using Label Propagation and Transfer Learning. In Proceedings of the 19th International Society for Music Information Retrieval Conference (ISMIR), Paris, France, 23–27 September 2018; pp. 306–312. [Google Scholar]
- Kum, S.; Nam, J. Classification-Based Singing Melody Extraction Using Deep Convolutional Neural Networks. Preprints 2017. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. Lect. Notes Comput. Sci. 2015, 9351, 234–241. [Google Scholar]
- Jansson, A.; Humphrey, E.; Montecchio, N.; Bittner, R.; Kumar, A.; Weyde, T. Singing Voice Separation with Deep U-Net CNN. In Proceedings of the 18th International Society for Music Information Retrieval Conference (ISMIR), Suzhou, China, 23–27 October 2017. [Google Scholar]
- Stoller, D.; Ewert, S.; Dixon, S. Wave-U-Net: A multi-scale neural network for end-to-end audio source separation. In Proceedings of the 19th International Society for Music Information Retrieval Conference (ISMIR), Paris, France, 23–27 September 2018; pp. 334–340. [Google Scholar]
- Wu, Y.T.; Chen, B.; Su, L. Polyphonic Music Transcription with Semantic Segmentation. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 166–170. [Google Scholar]
- Stoller, D.; Durand, S.; Ewert, S. End-to-end Lyrics Alignment for Polyphonic Music Using an Audio-to-character Recognition Model. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019; pp. 181–185. [Google Scholar]
- Lu, W.T.; Su, L. Vocal melody extraction with semantic segmentation and audio-symbolic domain transfer learning. In Proceedings of the 19th International Society for Music Information Retrieval Conference (ISMIR), Paris, France, 23–27 September 2018; pp. 521–528. [Google Scholar]
- Schlüter, J.; Grill, T. Exploring Data Augmentation for Improved Singing Voice Detection with Neural Networks. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Málaga, Spain, 26–30 October 2015; pp. 121–126. [Google Scholar]
- Goto, M.; Hashiguchi, H.; Nishimura, T.; Oka, R. RWC Music Database: Popular, Classical, and Jazz Music Databases. In Proceedings of the International Society for Music Information Retrieval Conference (ISMIR), Paris, France, 13–17 October 2002; pp. 287–288. [Google Scholar]
- Cohen-Hadria, A.; Roebel, A.; Peeters, G. Improving singing voice separation using deep u-net and wave-u-net with data augmentation. arXiv 2019, arXiv:1903.01415. [Google Scholar]
- Thickstun, J.; Harchaoui, Z.; Foster, D.P.; Kakade, S.M. Invariances and Data Augmentation for Supervised Music Transcription. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2241–2245. [Google Scholar]
- Salamon, J.; Gómez, E. Melody Extraction From Polyphonic Music Signals Using Pitch Contour Characteristics. IEEE Trans. Audio, Speech Lang. Process. 2012, 20, 1759–1770. [Google Scholar] [CrossRef]
- Salamon, J.; Serrà, J.; Gómez, E. Tonal representations for music retrieval: From version identification to query-by-humming. Int. J. Multimed. Inf. Retr. 2013, 2, 45–58. [Google Scholar] [CrossRef]
- Salamon, J.; Gómez, E.; Ellis, D.P.; Richard, G. Melody Extraction from Polyphonic Music Signals. IEEE Signal Process. Mag. 2014, 31, 118–134. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).