A Wireless Covert Channel Based on Dirty Constellation with Phase Drift
Abstract
1. Introduction
- First, a DCM-based novel dirty constellation has been proposed, which can be used in N-ary PSK and QAM signals. The previous DCM solution [33] was dedicated to watermarking audio signals using the OFDM.
- Second, based on simulation studies, the impact of the parameter variability of the developed method on its detection possibility using statistical analysis techniques has been shown.
- Third, the efficiency of the developed method and its comparison with another dirty constellation technique [30] have been presented.
- Lastly, the possibility of the practical implementation of the proposed solution has been shown, which gives a premise for its practical use in hidden data layer creation in SDN for the SOFTANET project and in future wireless systems and networks.
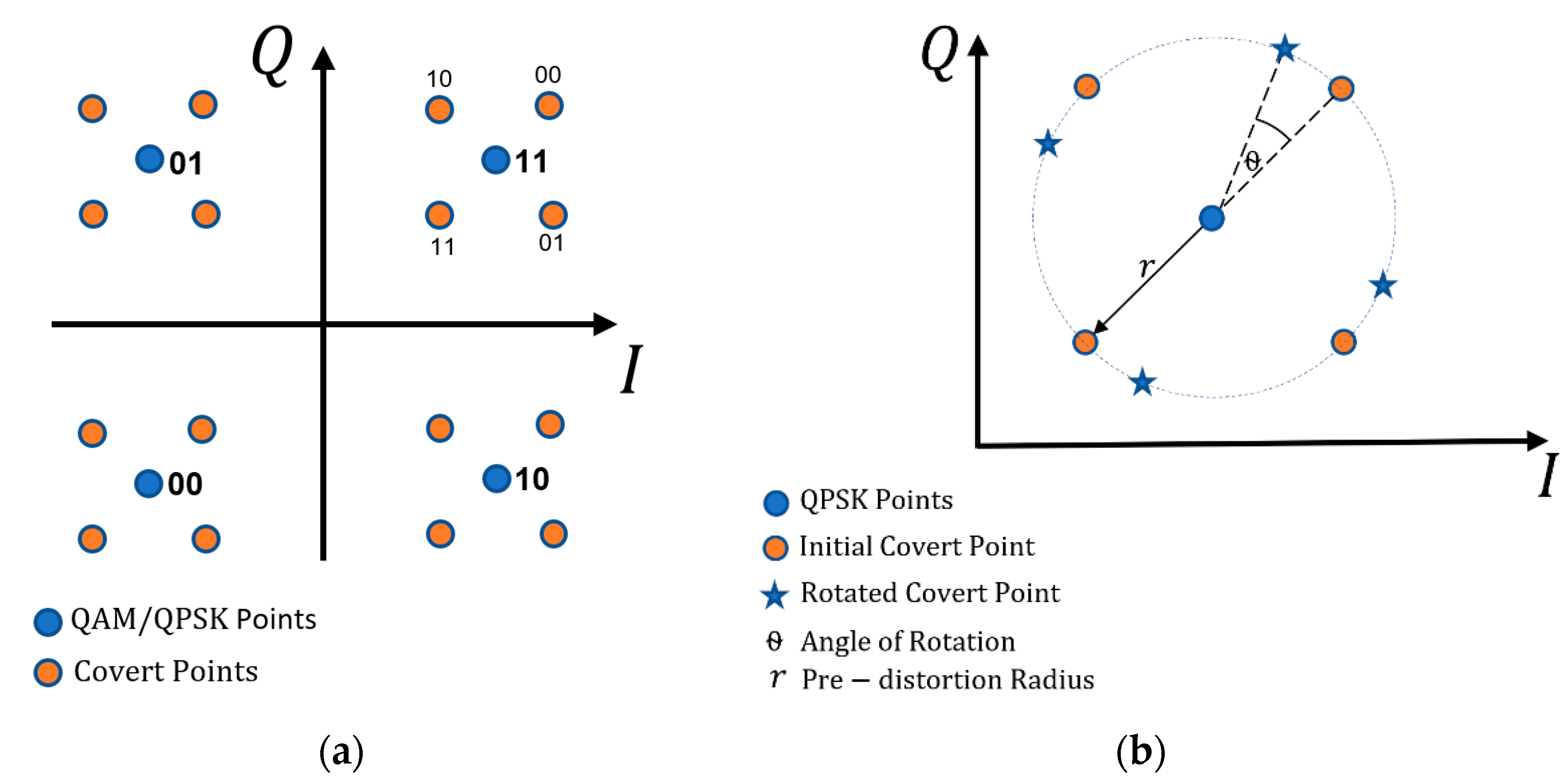
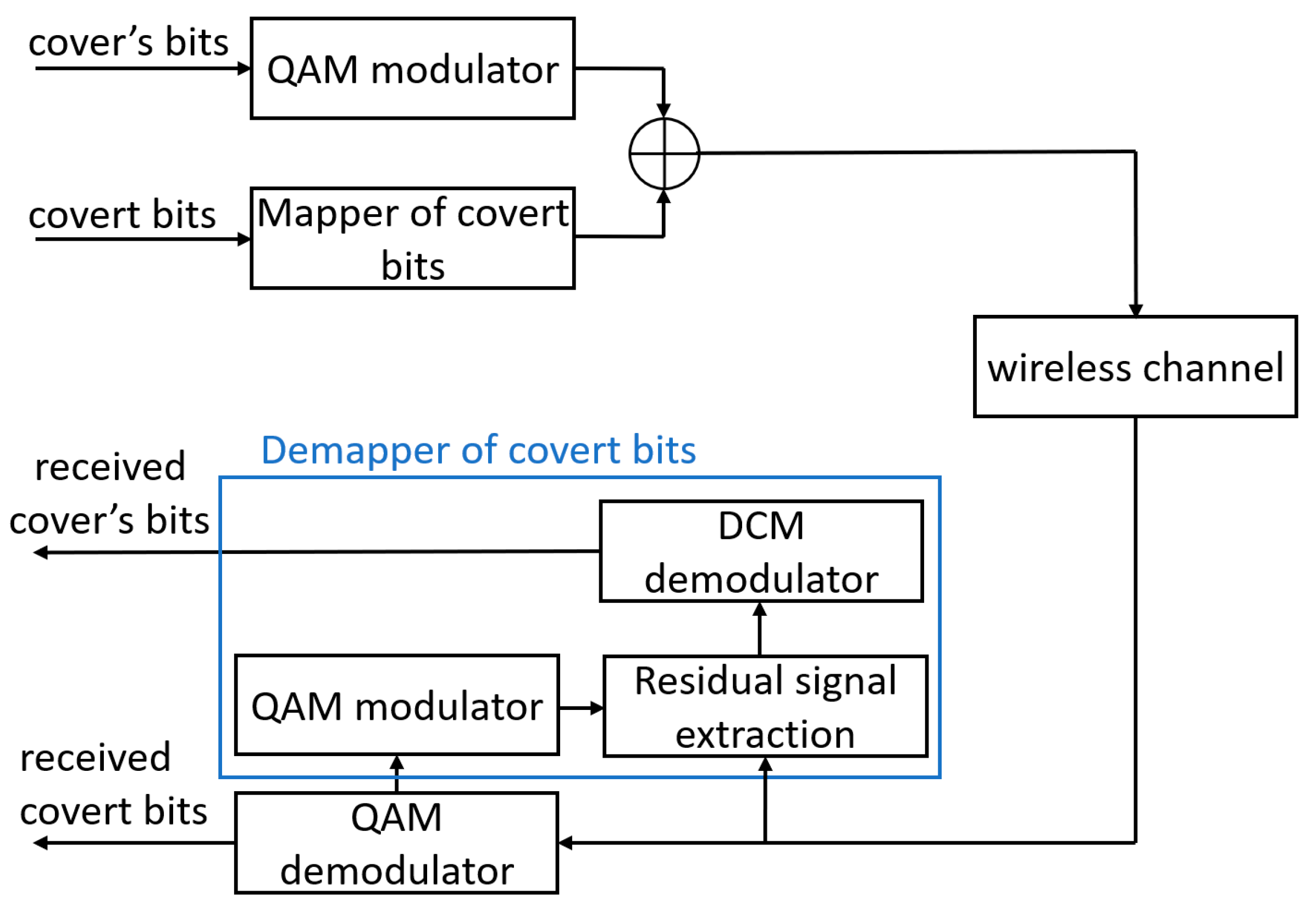
2. Concept of Dirty Constellation
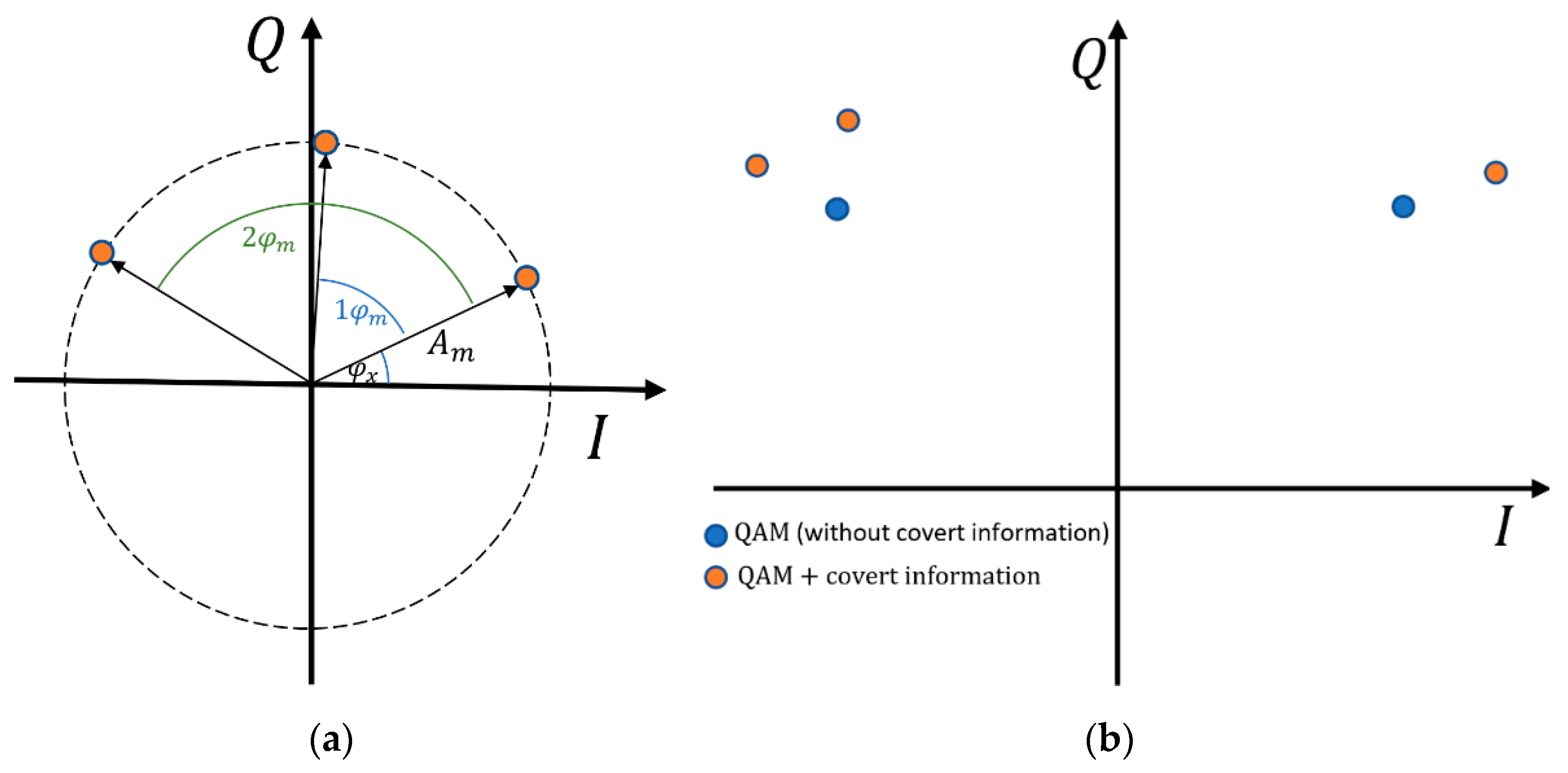
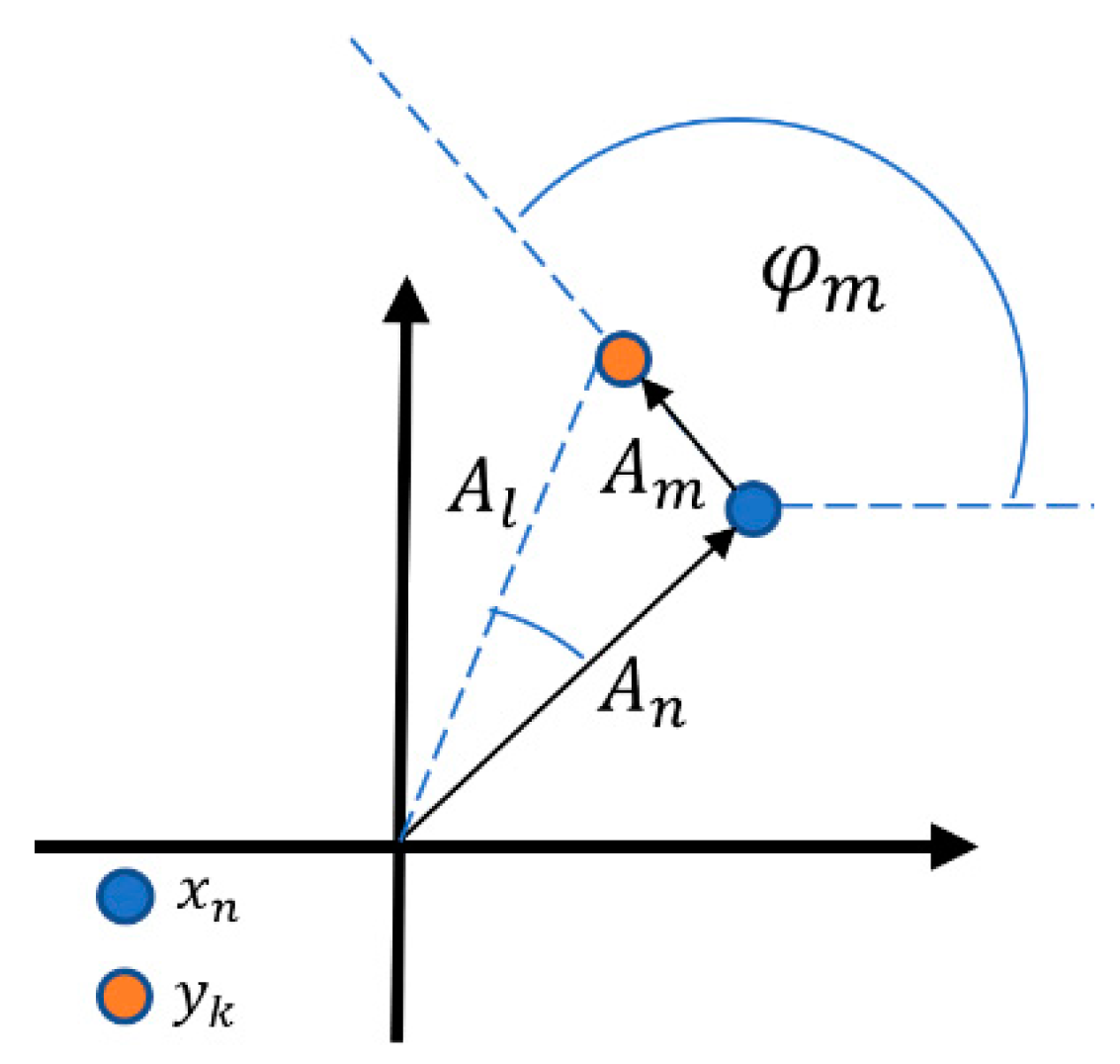
3. Phase Drift-Based Dirty Constellation
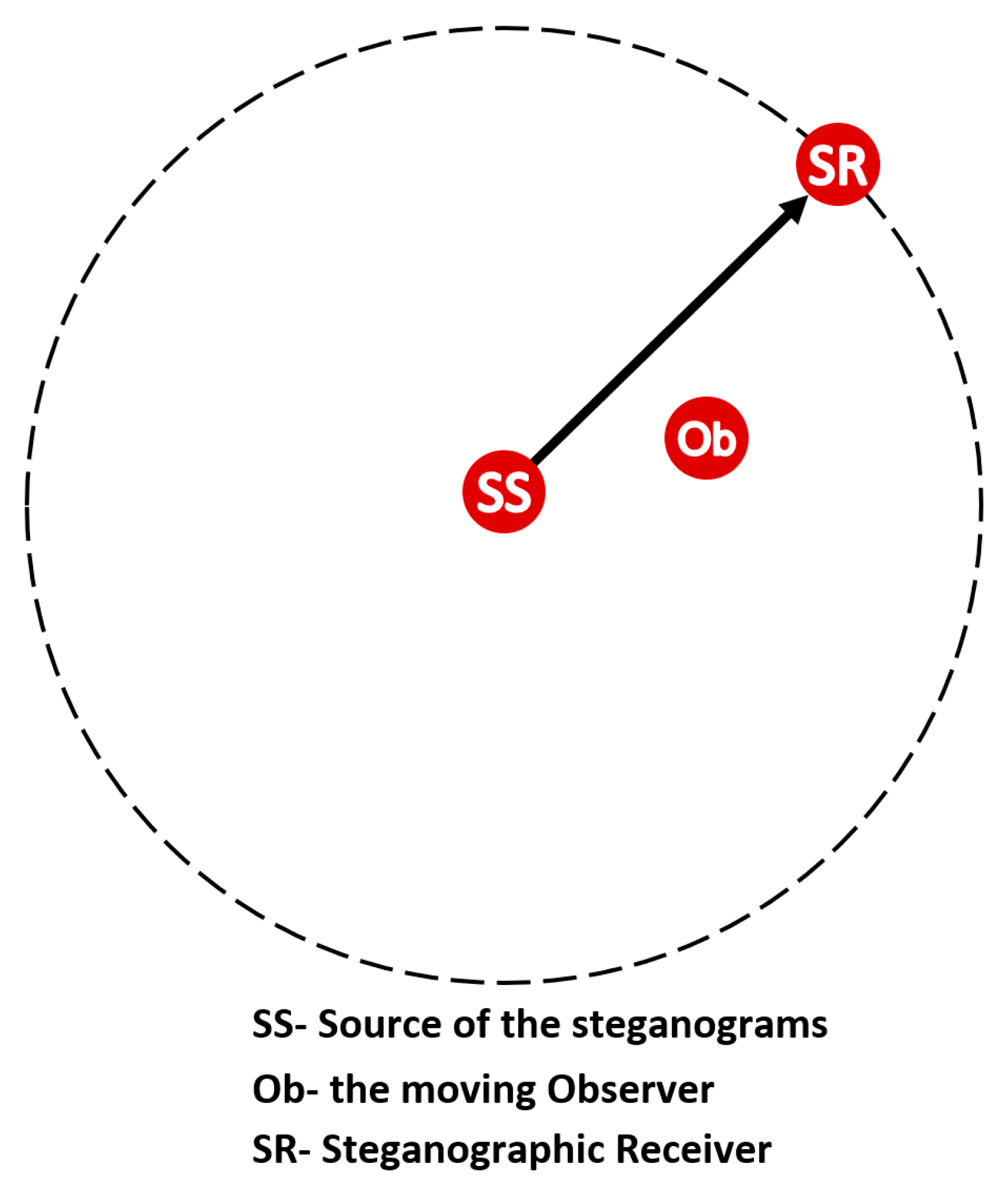
4. Evaluation Criteria for Covert Channels
- Covert channel detectability defined by the detection probability,
- Cost understood as the carrier signal distortion,
- Transmission rate and BER in the covert channel.
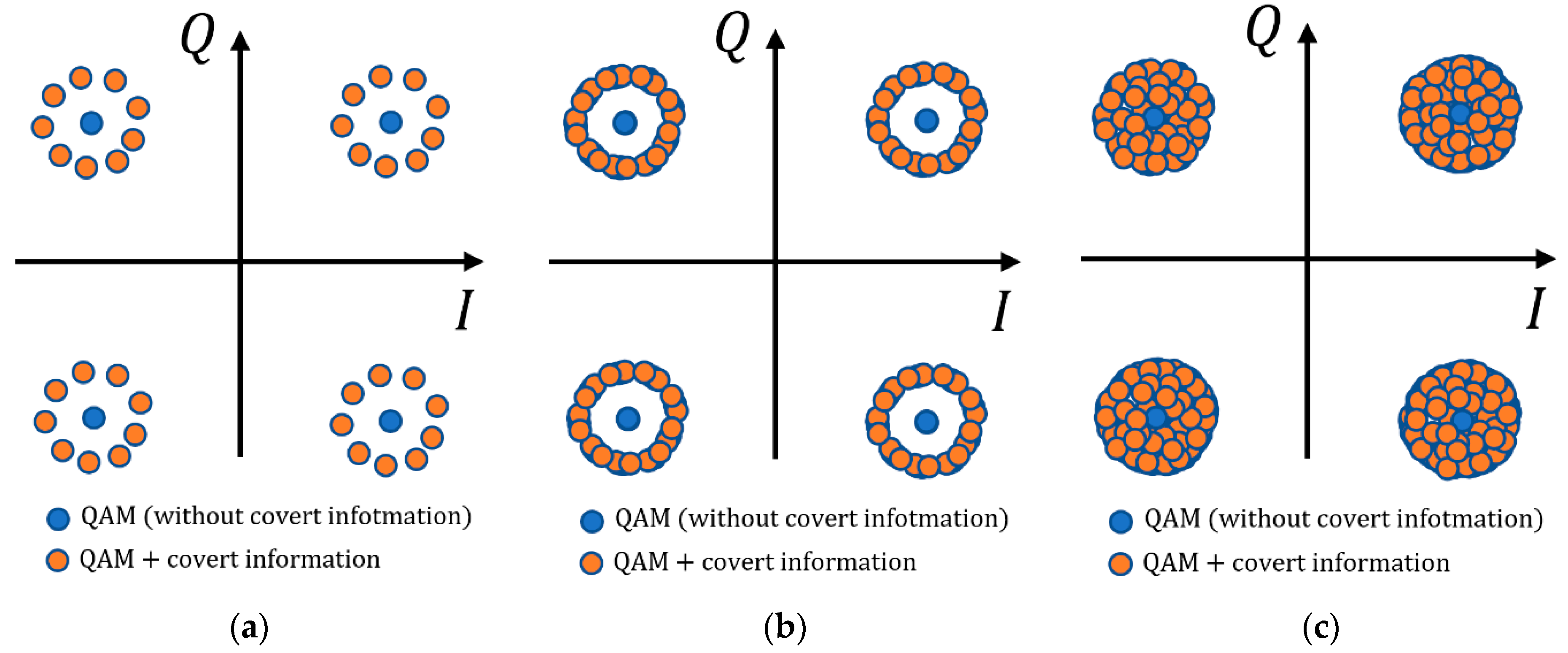
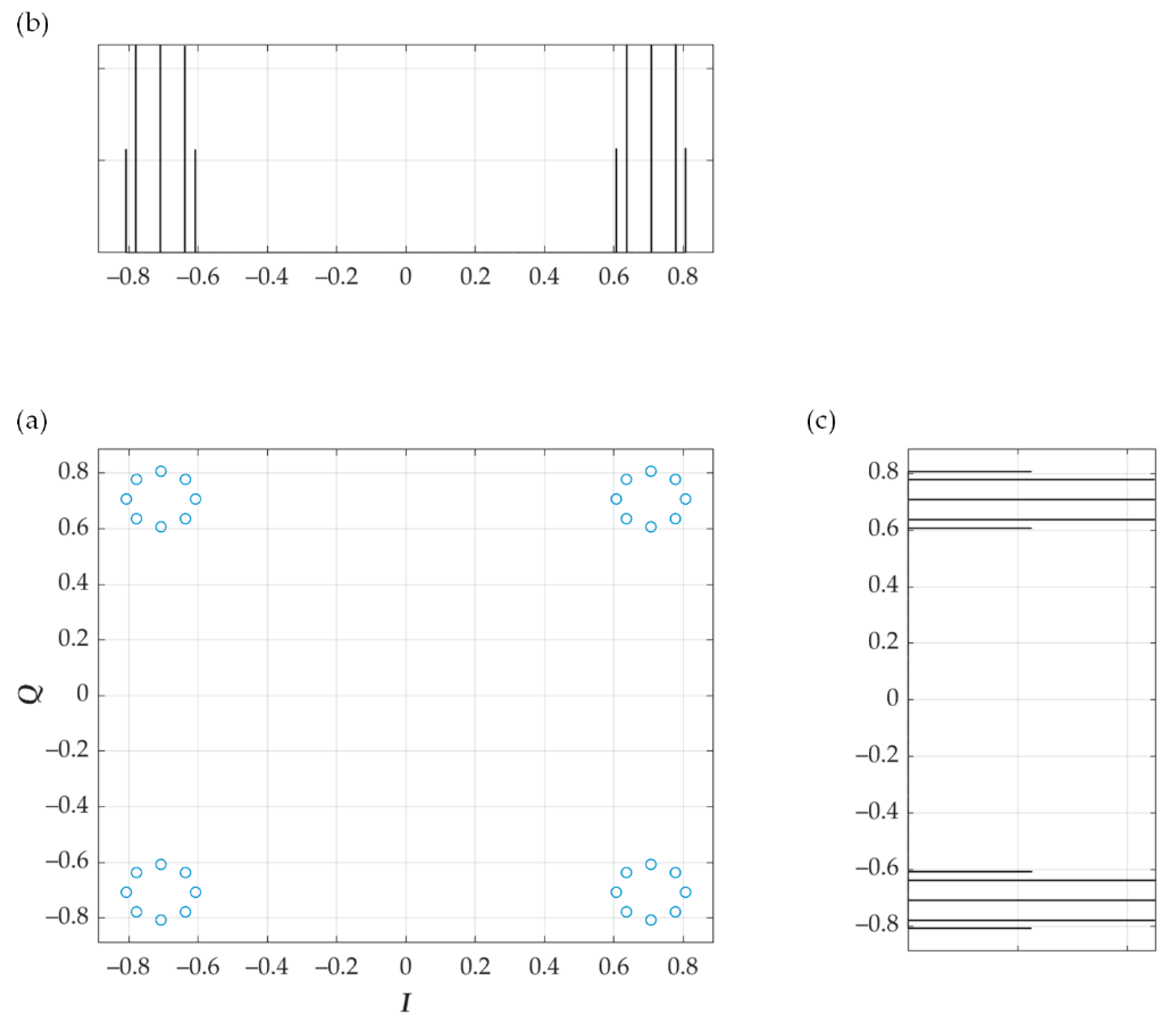
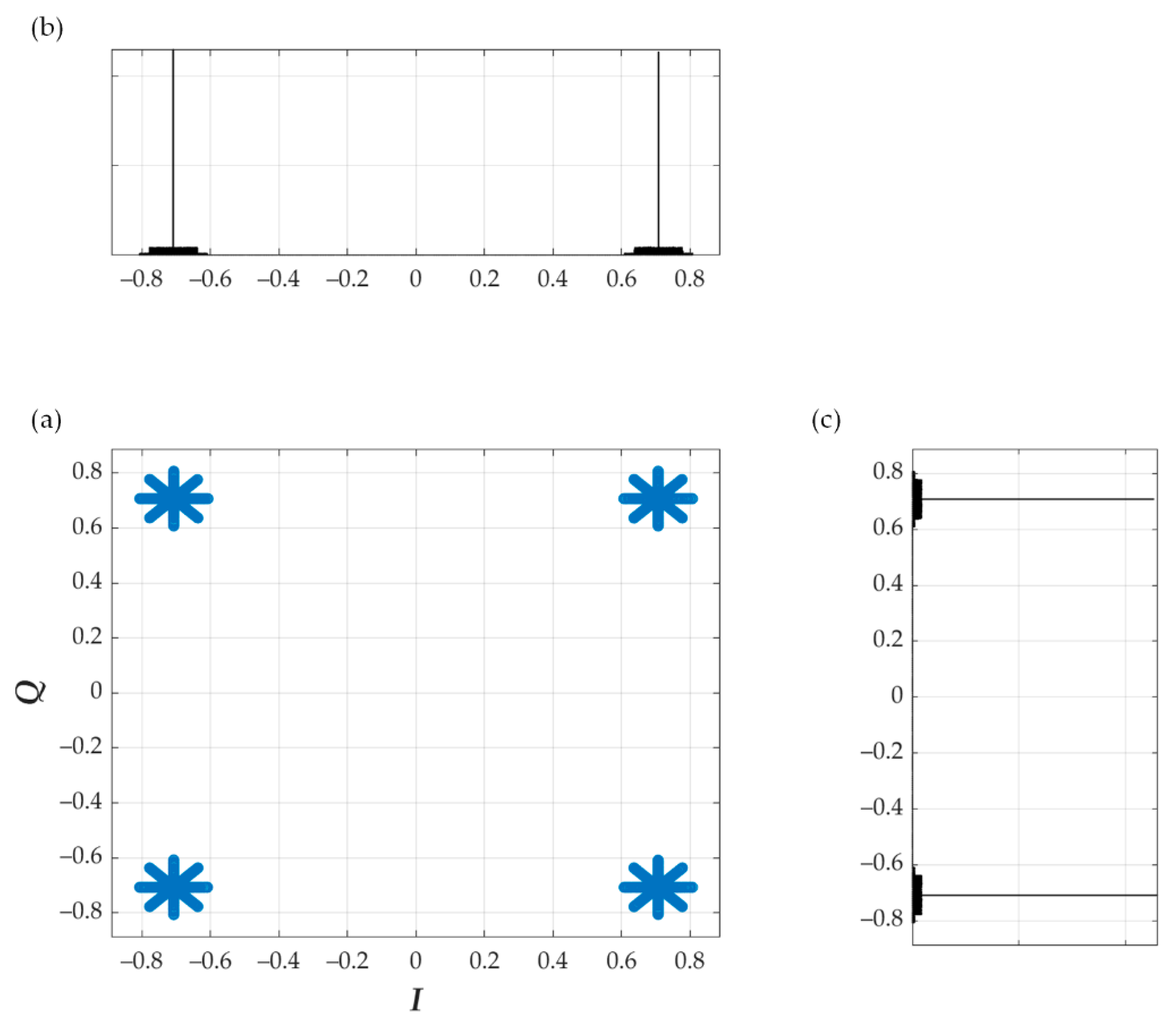
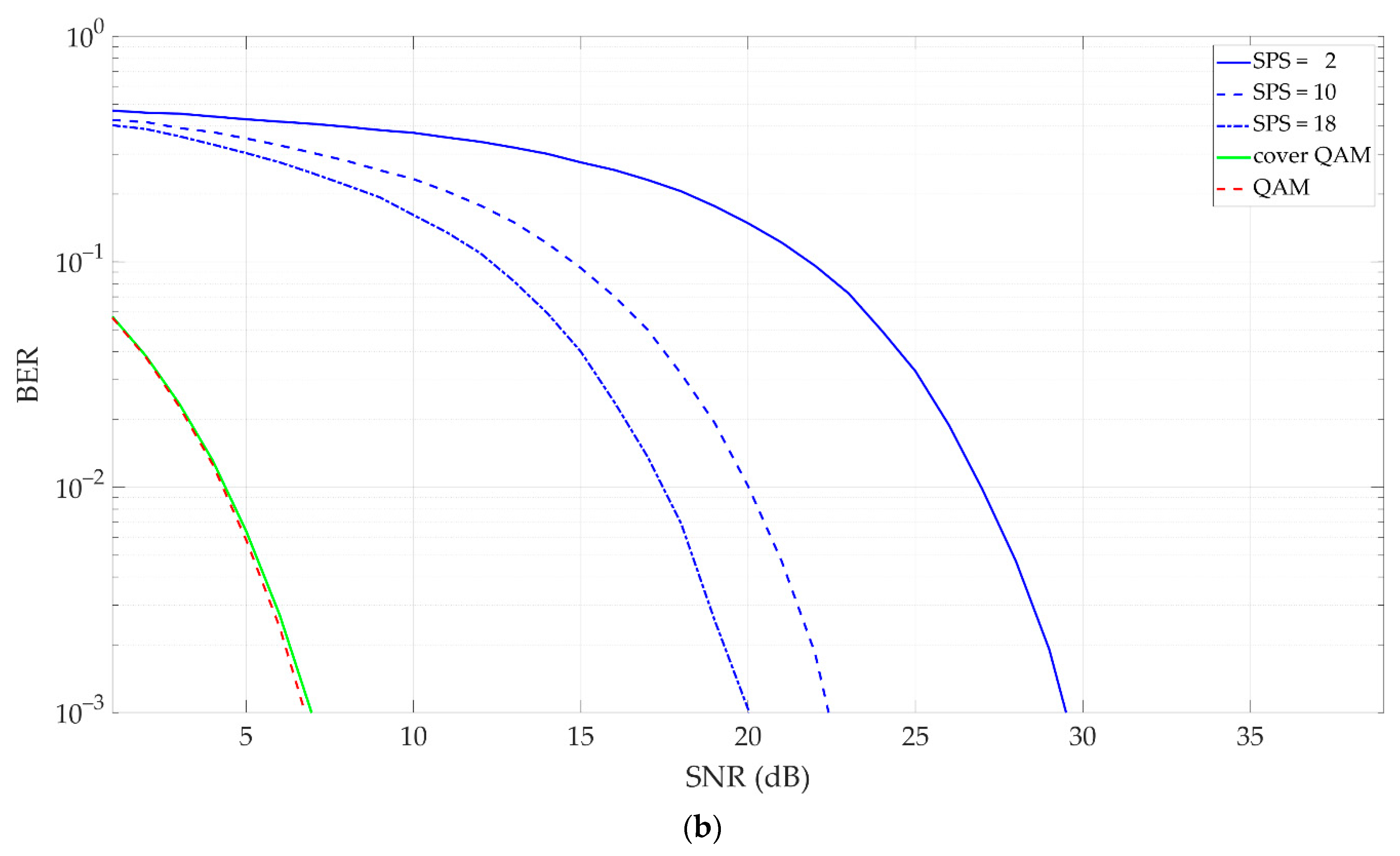
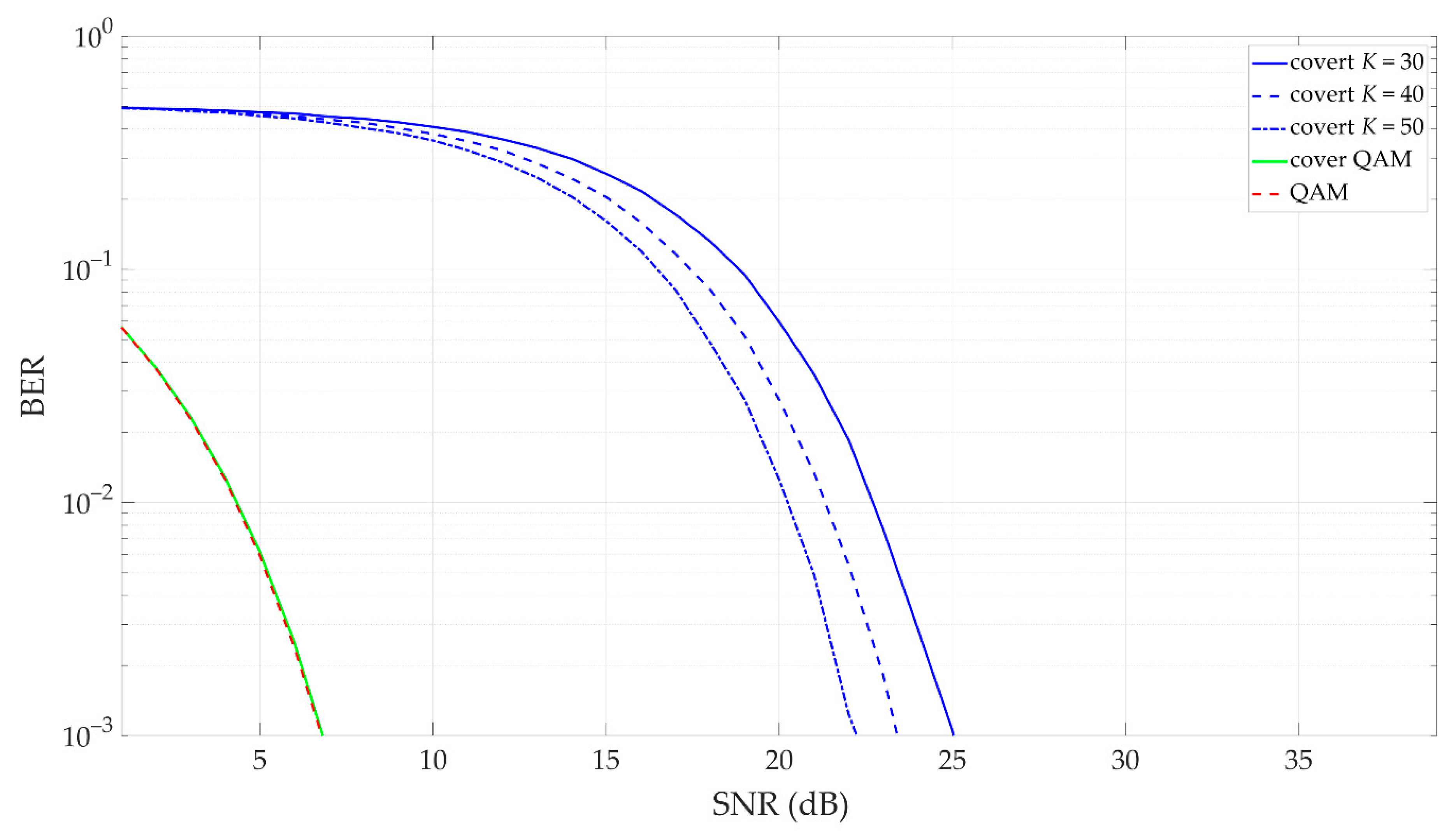
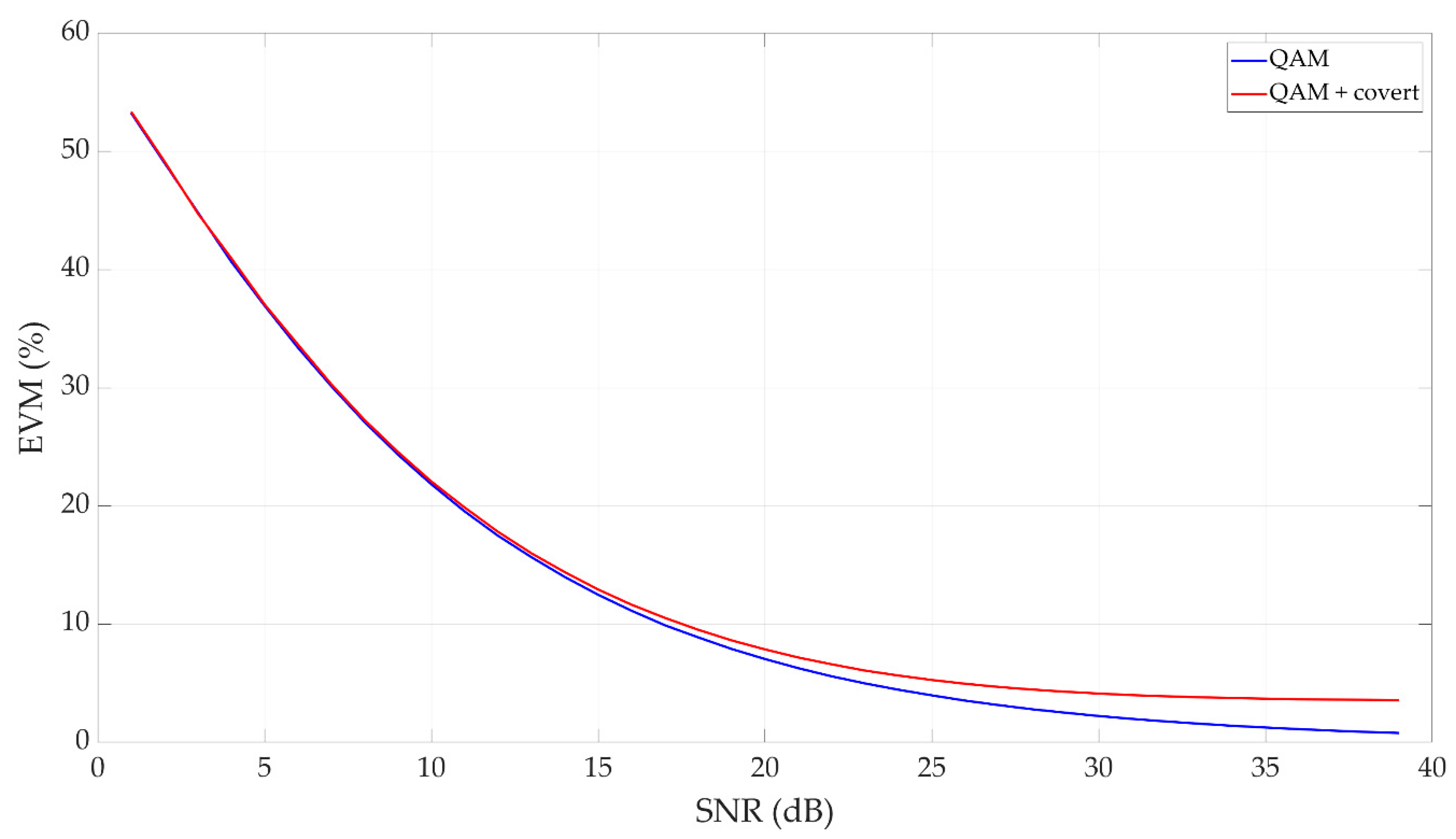
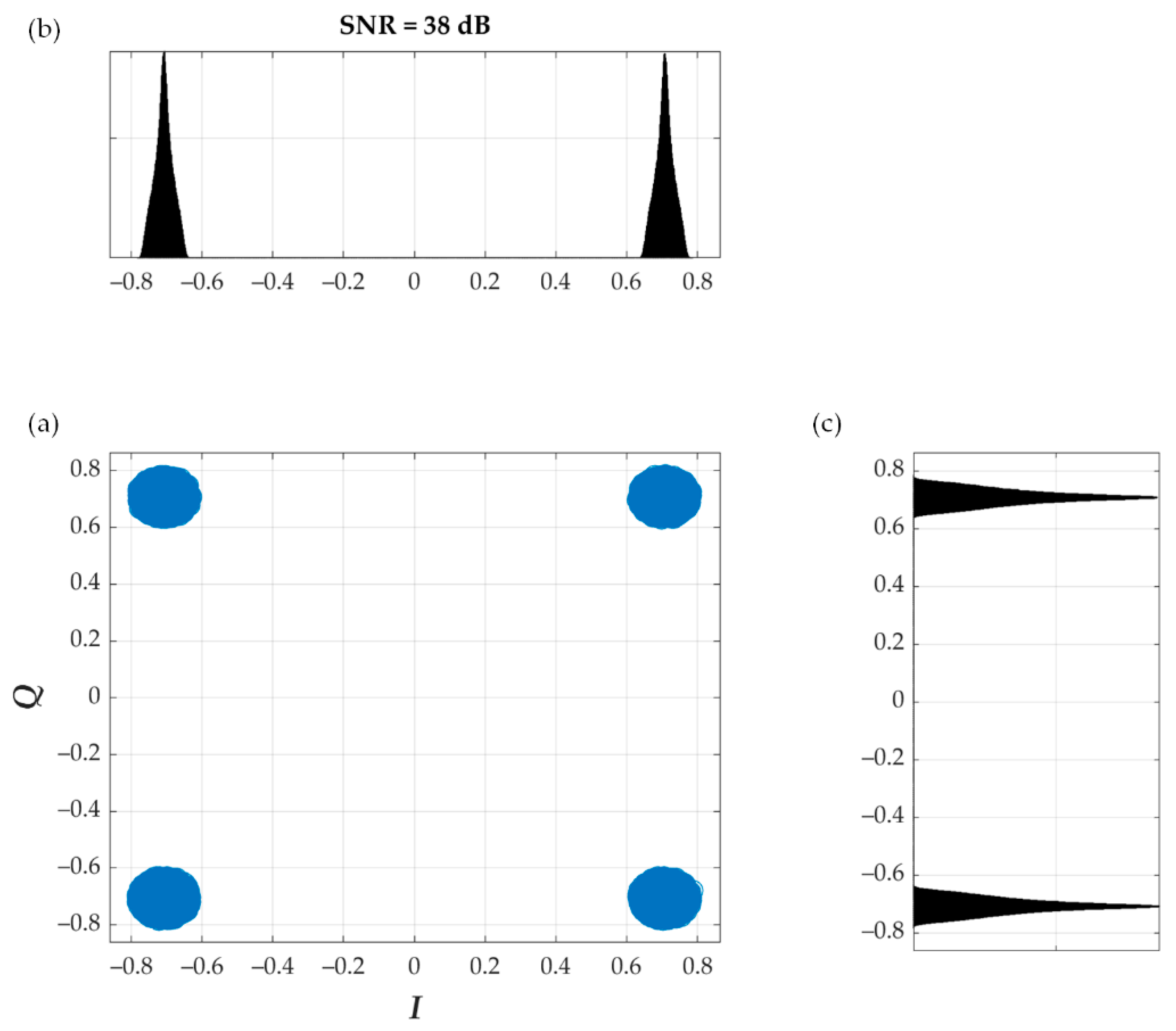
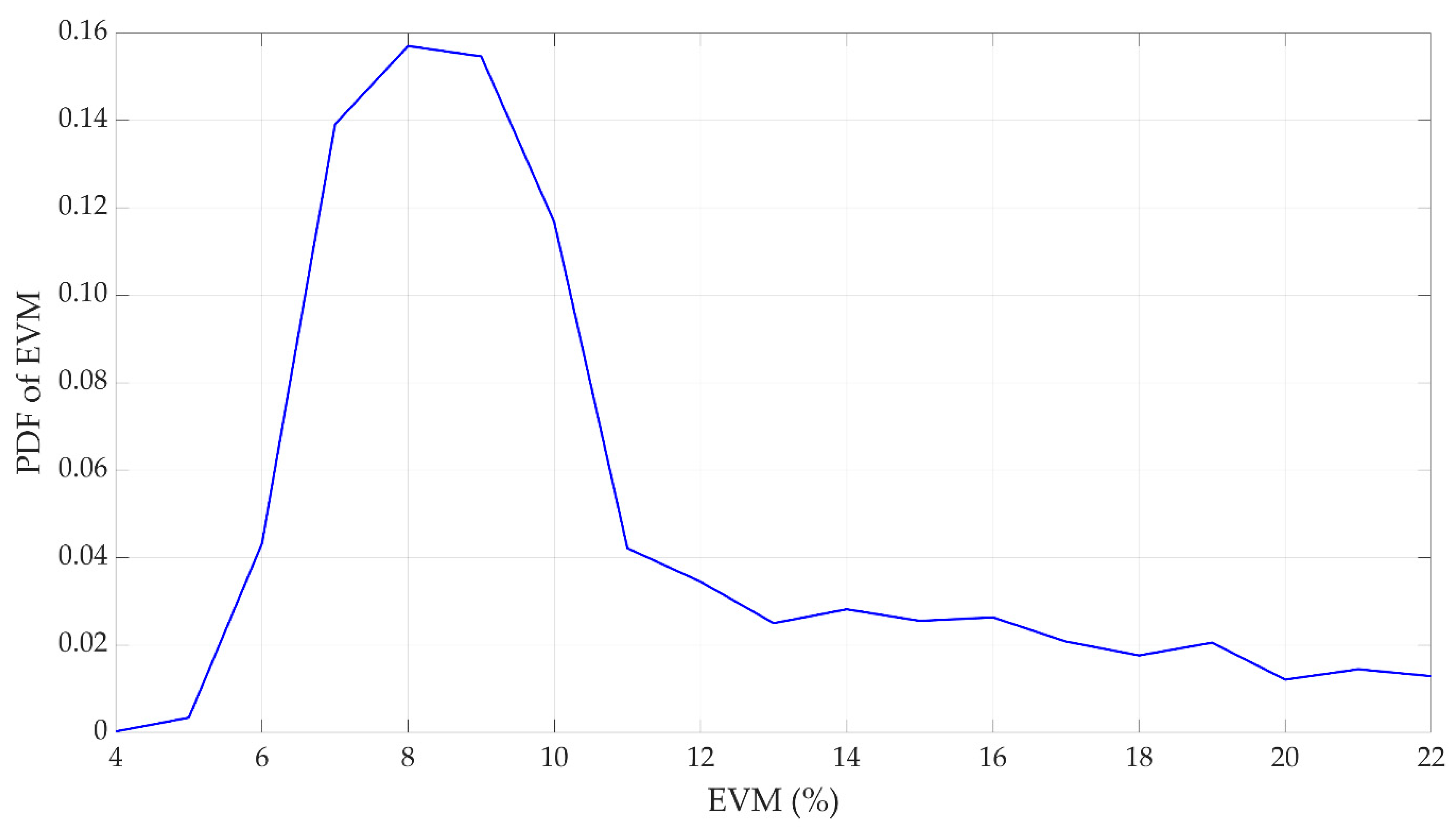
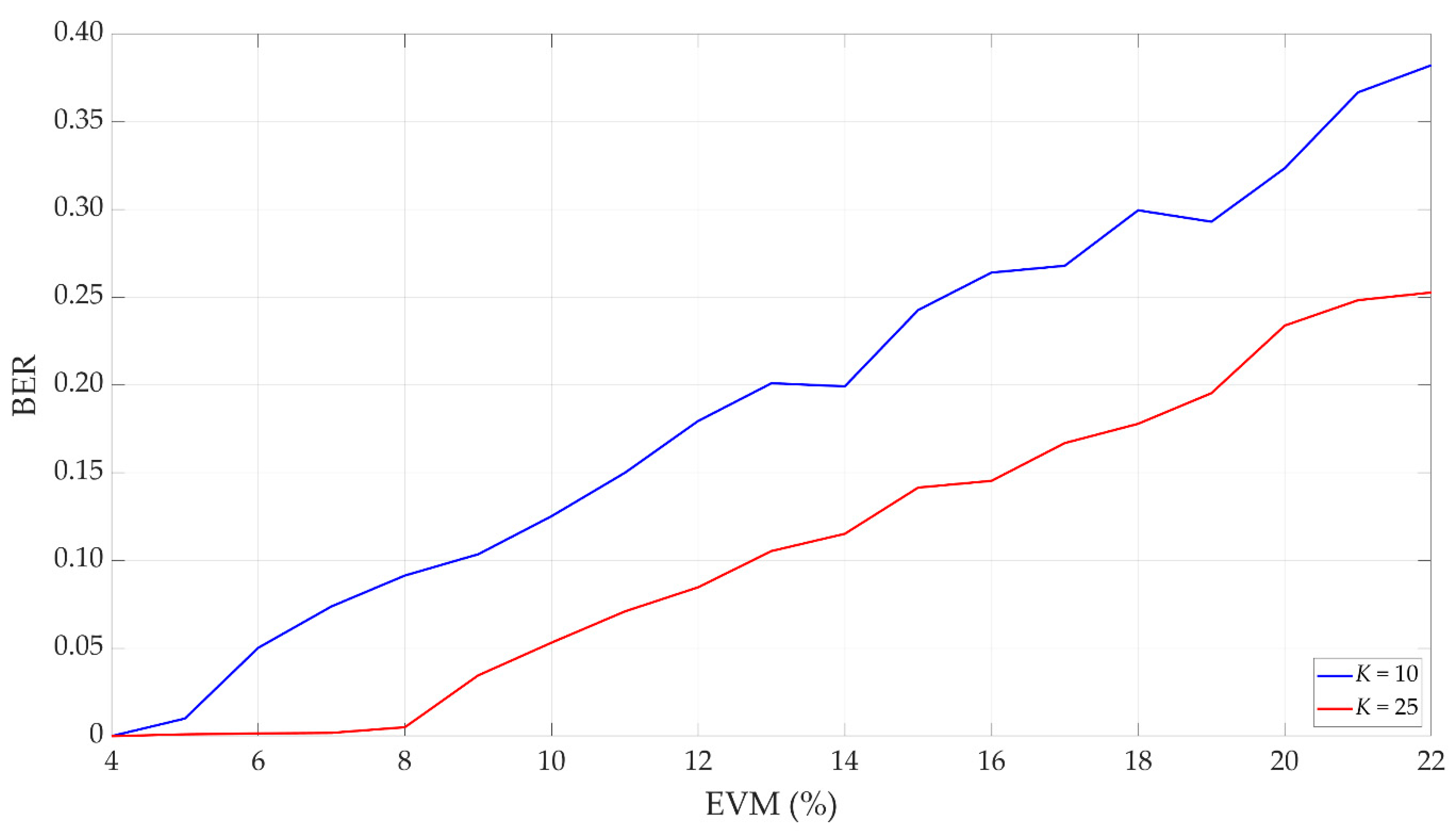
5. Simulation Analysis of Dirty Constellations
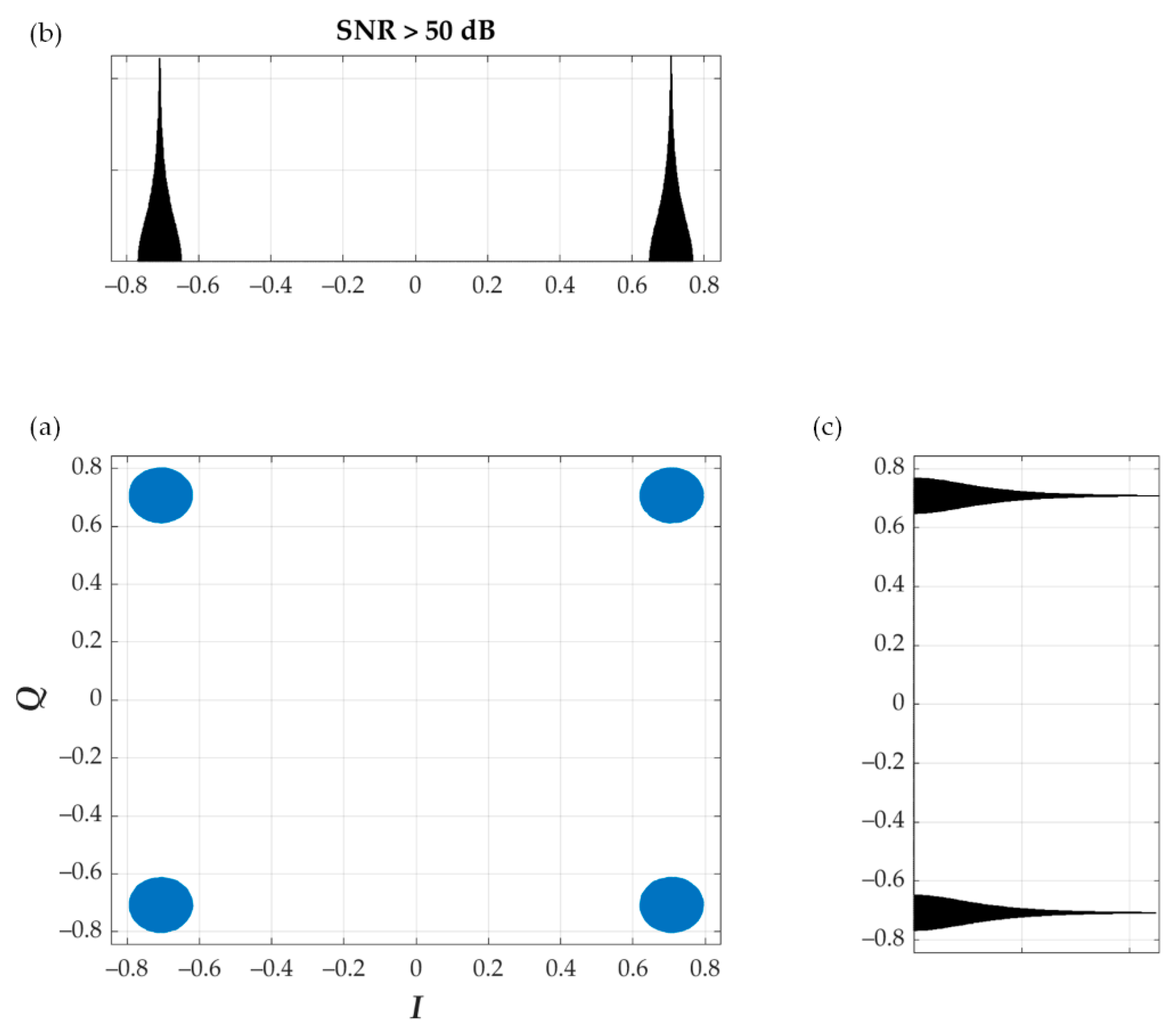
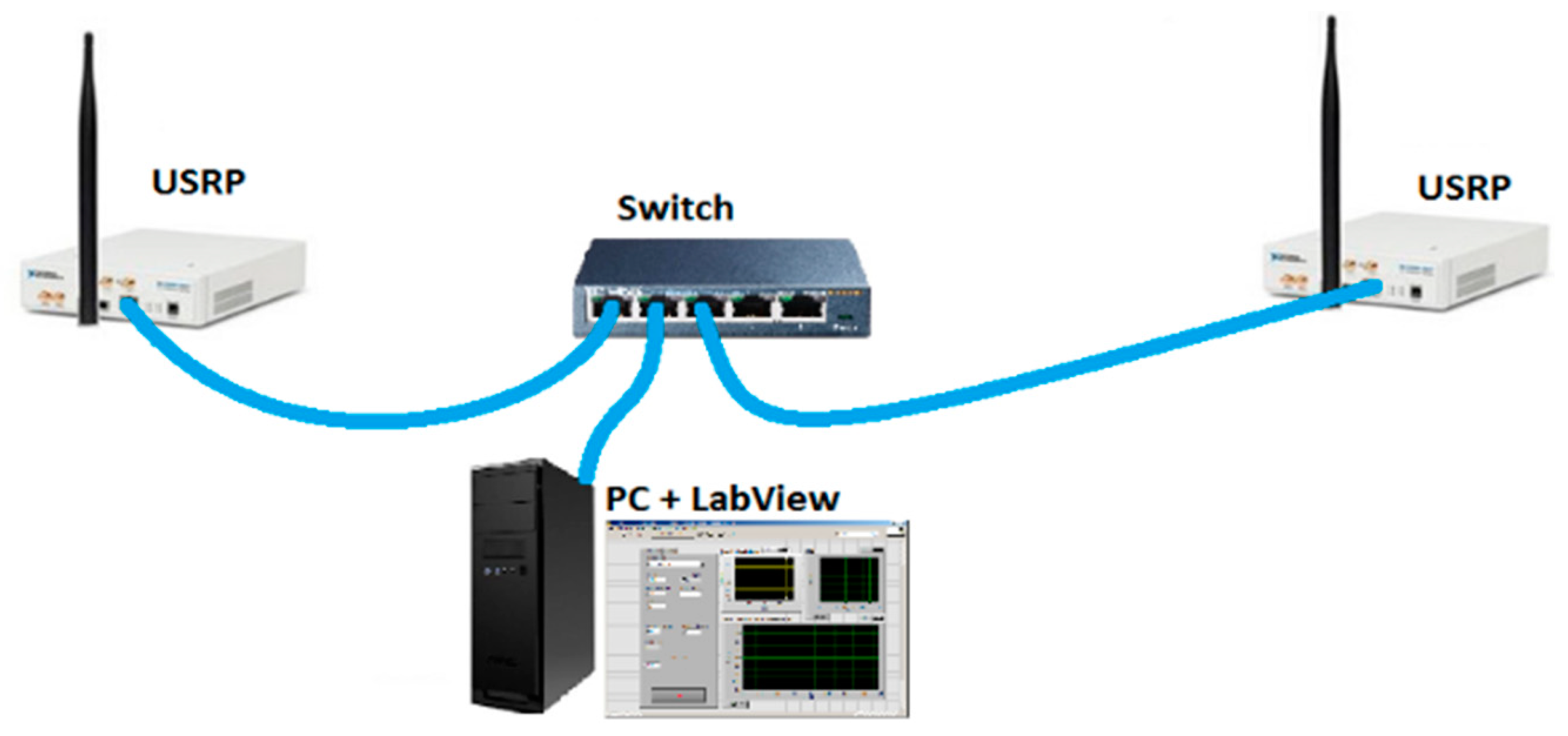
6. Hardware Implementation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| 5G | fifth generation |
| 6G | sixth generation |
| AI | artificial intelligence |
| BER | bit error rate |
| CSI | channel state information |
| DCM | drift correction modulation |
| DNS | Domain Name System |
| DSSS | direct sequence spread spectrum |
| EDA | European Defense Agency |
| EVM | error vector magnitude |
| FHSS | frequency-hopping spread spectrum |
| FSK | frequency-shift keying |
| HTTP | Hypertext Transfer Protocol |
| IEEE | Institute of Electrical and Electronics Engineers |
| IP | Internet Protocol |
| LPD | low probability of detection |
| LPI | low probability of intercept |
| MAC | medium access control |
| MIMO | multiple-input multiple-output |
| ML | machine learning |
| Ob | observer |
| OFDM | orthogonal frequency-division multiplexing |
| PC | personal computer |
| probability density function | |
| PDSCH | physical downlink shared channel |
| PN-ASK | pseudo-noise asymmetric shift keying |
| PSK | phase-shift keying |
| QAM | quadrature amplitude modulation |
| QPSK | quadrature phase-shift keying |
| SDN | software-defined network |
| SNR | signal-to-noise ratio |
| SPS | covert symbols per carrier symbol |
| SR | steganographic receiver |
| SS | steganographic source |
| TCP | Transmission Control Protocol |
| USRP | Universal Software Radio Peripheral |
References
- Zielińska, E.; Mazurczyk, W.; Szczypiorski, K. Trends in steganography. Commun. ACM 2014, 57, 86–95. [Google Scholar] [CrossRef]
- Duan, X.; Gou, M.; Liu, N.; Wang, W.; Qin, C. High-Capacity Image Steganography Based on Improved Xception. Sensors 2020, 20, 7253. [Google Scholar] [CrossRef]
- Järpe, E.; Weckstén, M. Velody 2—Resilient High-Capacity MIDI Steganography for Organ and Harpsichord Music. Appl. Sci. 2021, 11, 39. [Google Scholar] [CrossRef]
- Cao, M.; Tian, L.; Li, C. A Secure Video Steganography Based on the Intra-Prediction Mode (IPM) for H264. Sensors 2020, 20, 5242. [Google Scholar] [CrossRef] [PubMed]
- Lampson, B.W. A note on the confinement problem. Commun. ACM 1973, 16, 613–615. [Google Scholar] [CrossRef]
- Gianvecchio, S.; Wang, H.; Wijesekera, D.; Jajodia, S. Model-based covert timing channels: Automated modeling and evasion. In Proceedings of the Recent Advances in Intrusion Detection; Lippmann, R., Kirda, E., Trachtenberg, A., Eds.; Springer: Cambridge, MA, USA, 2008; Volume RAID 2008, pp. 211–230. [Google Scholar]
- Kothari, K.; Wright, M. Mimic: An active covert channel that evades regularity-based detection. Comput. Netw. 2013, 57, 647–657. [Google Scholar] [CrossRef]
- Walls, R.J.; Kothari, K.; Wright, M. Liquid: A detection-resistant covert timing channel based on IPD shaping. Comput. Netw. 2011, 55, 1217–1228. [Google Scholar] [CrossRef]
- Liu, G.; Zhai, J.; Dai, Y. Network covert timing channel with distribution matching. Telecommun. Syst. 2012, 49, 199–205. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, X.; Xu, X.; Tan, Y. A Robust Packet-Dropout Covert Channel over Wireless Networks. IEEE Wirel. Commun. 2020, 27, 60–65. [Google Scholar] [CrossRef]
- Mileva, A.; Panajotov, B. Covert channels in TCP/IP protocol stack—Extended version. Cent. Eur. J. Comput. Sci. 2014, 4, 45–66. [Google Scholar] [CrossRef]
- Frikha, L.; Trabelsi, Z.; El-Hajj, W. Implementation of a covert channel in the 802.11 header. In Proceedings of the 2008 6th International Wireless Communications and Mobile Computing Conference (IWCMC), Crete Island, Greece, 6–8 August 2008; pp. 594–599. [Google Scholar]
- Szczypiorski, K.; Mazurczyk, W. Steganography in IEEE 802.11 OFDM symbols. Secur. Commun. Netw. 2011, 9, 118–129. [Google Scholar] [CrossRef]
- Shaukat, K.; Iqbal, F.; Hameed, I.A.; Hassan, M.U.; Luo, S.; Hassan, R.; Younas, A.; Ali, S.; Adeem, G.; Rubab, A.; et al. MAC protocols 802.11: A comparative study of throughput analysis and improved LEACH. In Proceedings of the 2020 17th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Phuket, Thailand, 24–27 June 2020; pp. 421–426. [Google Scholar]
- Hassan, M.U.; Shahzaib, M.; Shaukat, K.; Hussain, S.N.; Mubashir, M.; Karim, S.; Shabir, M.A. DEAR-2: An energy-aware routing protocol with guaranteed delivery in wireless ad-hoc networks. In Recent Trends and Advances in Wireless and IoT-Enabled Networks; Jan, M.A., Khan, F., Alam, M., Eds.; EAI/Springer Innovations in Communication and Computing; Springer International Publishing: Cham, Germany, 2019; pp. 215–224. ISBN 978-3-319-99966-1. [Google Scholar]
- Frączek, W.; Szczypiorski, K. Perfect undetectability of network steganography. Secur. Commun. Netw. 2016, 9, 2998–3010. [Google Scholar] [CrossRef]
- Graniszewski, W.; Krupski, J.; Szczypiorski, K. The covert channel over HTTP protocol. In Proceedings of the Photonics Applications in Astronomy, Communications, Industry, and High-Energy Physics Experiments 2016, Wilga, Poland, 29 May–6 June 2016; SPIE: Washington, DC, USA, 2016; Volume 10031, p. 100314Z. [Google Scholar]
- Szczypiorski, K.; Drzymała, M.; Urbański, M.Ł. Network Steganography in the DNS Protocol. Int. J. Electron. Telecommun. 2016, 62, 343–346. [Google Scholar] [CrossRef]
- Smolarczyk, M.; Szczypiorski, K.; Pawluk, J. Multilayer Detection of Network Steganography. Electronics 2020, 9, 2128. [Google Scholar] [CrossRef]
- Chen, O.; Meadows, C.; Trivedi, G. Stealthy protocols: Metrics and open problems. In Concurrency, Security, and Puzzles; Lecture Notes in Computer Science; Springer: Cham, Germany, 2017; pp. 1–17. ISBN 978-3-319-51045-3. [Google Scholar]
- Bordel Sánchez, B.; Alcarria, R.; Robles, T.; Jara, A. Protecting Physical Communications in 5G C-RAN Architectures through Resonant Mechanisms in Optical Media. Sensors 2020, 20, 4104. [Google Scholar] [CrossRef] [PubMed]
- Yen, C.-T.; Huang, J.-F.; Zhang, W.-Z. Hiding Stealth Optical CDMA Signals in Public BPSK Channels for Optical Wireless Communication. Appl. Sci. 2018, 8, 1731. [Google Scholar] [CrossRef]
- Moskowitz, I.S.; Safier, P.N.; Cotae, P. Pre-Nodulation Physical Layer Steganography 2013. U.S. Patent Application 13/573,671, 25 April 2013. [Google Scholar]
- Szczepaniak, E.; Piotrowski, Z. Radio transmission masking on the example of FSK modulation. In Proceedings of the 2017 21st International Conference on Signal Processing Algorithms, Architectures, Arrangements, and Applications (SPA), Poznan, Poland, 20–22 September 2017; pp. 394–399. [Google Scholar]
- Hijaz, Z.; Frost, V.S. Exploiting OFDM systems for covert communication. In Proceedings of the 2010 Military Communications Conference (MILCOM), San Jose, CA, USA, 31 October–3 November 2010; pp. 2149–2155. [Google Scholar]
- Classen, J.; Schulz, M.; Hollick, M. Practical covert channels for WiFi systems. In Proceedings of the 2015 IEEE Conference on Communications and Network Security (CNS), Florence, Italy, 28–30 September 2015; pp. 209–217. [Google Scholar]
- Bash, B.A.; Goeckel, D.; Towsley, D.; Guha, S. Hiding information in noise: Fundamental limits of covert wireless communication. IEEE Commun. Mag. 2015, 53, 26–31. [Google Scholar] [CrossRef]
- Hero, A.O. Secure space-time communication. IEEE Trans. Inf. Theory 2003, 49, 3235–3249. [Google Scholar] [CrossRef]
- Cao, P.; Liu, W.; Liu, G.; Zhai, J.; Ji, X.; Dai, Y. A novel wireless covert channel for MIMO system. In Proceedings of the 2020 6th International Conference on Artificial Intelligence and Security (ICAIS), Hohhot, China, 17–20 July 2020; Sun, X., Wang, J., Bertino, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2020; Volume 3, pp. 351–362. [Google Scholar]
- Dutta, A.; Saha, D.; Grunwald, D.; Sicker, D. Secret agent radio: Covert communication through dirty constellations. In Proceedings of the Information Hiding, Berkeley, CA, USA, 15–18 May 2012; Kirchner, M., Ghosal, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume IH 2012, pp. 160–175. [Google Scholar]
- Cao, P.; Liu, W.; Liu, G.; Ji, X.; Zhai, J.; Dai, Y. A Wireless Covert Channel Based on Constellation Shaping Modulation. Secur. Commun. Netw. 2018, 2018, 1–15. [Google Scholar] [CrossRef]
- D’Oro, S.; Restuccia, F.; Melodia, T. Hiding data in plain sight: Undetectable wireless communications through pseudo-noise asymmetric shift keying. In Proceedings of the 2019 38th IEEE Conference on Computer Communications (INFOCOM), Paris, France, 29 April–2 May 2019; IEEE: New York, NY, USA; pp. 1585–1593. [Google Scholar]
- Piotrowski, Z. Drift Correction Modulation scheme for digital signal processing. Math. Comput. Model. 2013, 57, 2660–2670. [Google Scholar] [CrossRef]
- Lyons, R.G. Understanding Digital Signal Processing, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2010; ISBN 978-0-13-702741-5. [Google Scholar]
- Zaidi, Z.; Friderikos, V.; Yousaf, Z.; Fletcher, S.; Dohler, M.; Aghvami, H. Will SDN Be Part of 5G? IEEE Commun. Surv. Tutor. 2018, 20, 3220–3258. [Google Scholar] [CrossRef]
- Leonardi, L.; Lo Bello, L.; Aglianò, S. Priority-based bandwidth management in virtualized software-defined networks. Electronics 2020, 9, 1009. [Google Scholar] [CrossRef]
- Semong, T.; Maupong, T.; Anokye, S.; Kehulakae, K.; Dimakatso, S.; Boipelo, G.; Sarefo, S. Intelligent Load Balancing Techniques in Software Defined Networks: A Survey. Electronics 2020, 9, 1091. [Google Scholar] [CrossRef]
- Alhaddad, M.J.; Alkinani, M.H.; Atoum, M.S.; Alarood, A.A. Evolutionary Detection Accuracy of Secret Data in Audio Steganography for Securing 5G-Enabled Internet of Things. Symmetry 2020, 12, 2071. [Google Scholar] [CrossRef]
- Shaukat, K.; Luo, S.; Varadharajan, V.; Hameed, I.A.; Xu, M. A Survey on Machine Learning Techniques for Cyber Security in the Last Decade. IEEE Access 2020, 8, 222310–222354. [Google Scholar] [CrossRef]
- Shaukat, K.; Luo, S.; Varadharajan, V.; Hameed, I.A.; Chen, S.; Liu, D.; Li, J. Performance Comparison and Current Challenges of Using Machine Learning Techniques in Cybersecurity. Energies 2020, 13, 2509. [Google Scholar] [CrossRef]
- Roetteler, M.; Svore, K.M. Quantum Computing: Codebreaking and Beyond. IEEE Secur. Priv. 2018, 16, 22–36. [Google Scholar] [CrossRef]
- Zhang, H.; Ji, Z.; Wang, H.; Wu, W. Survey on quantum information security. China Commun. 2019, 16, 1–36. [Google Scholar] [CrossRef]
- Chaumont, M. Deep learning in steganography and steganalysis. In Digital Media Steganography; Hassaballah, M., Ed.; Academic Press: Cambridge, MA, USA, 2020; pp. 321–349. ISBN 978-0-12-819438-6. [Google Scholar]
- Li, F.; Tang, H.; Zou, Y.; Huang, Y.; Feng, Y.; Peng, L. Research on information security in text emotional steganography based on machine learning. Enterp. Inf. Syst. 2020, 1–18. [Google Scholar] [CrossRef]
- Sutherland, C.; Brun, T.A. Quantum steganography over noiseless channels: Achievability and bounds. Phys. Rev. A 2020, 101, 052319. [Google Scholar] [CrossRef]
- Chaharlang, J.; Mosleh, M.; Rasouli-Heikalabad, S. A novel quantum steganography-Steganalysis system for audio signals. Multimed. Tools Appl. 2020, 79, 17551–17577. [Google Scholar] [CrossRef]
- Alam, T.M.; Shaukat, K.; Hameed, I.A.; Luo, S.; Sarwar, M.U.; Shabbir, S.; Li, J.; Khushi, M. An Investigation of Credit Card Default Prediction in the Imbalanced Datasets. IEEE Access 2020, 8, 201173–201198. [Google Scholar] [CrossRef]
- ETSI. NR; Base Station (BS) Radio Transmission and Reception (3GPP TS 38.104 Version 15.5.0 Release 15); European Telecommunications Standards Institute (ETSI), 3rd Generation Partnership Project (3GPP): Sophia-Antipolis, France, 2019. [Google Scholar]
- Simmons, G.J. The prisoners’ problem and the subliminal channel. In Proceedings of the Advances in Cryptology, Santa Barbara, CA, USA, 22–24 August 1983; Chaum, D., Ed.; Springer: Berlin/Heidelberg, Germany, 1984; pp. 51–67. [Google Scholar]
- Szczypiorski, K.; Janicki, A.; Wendzel, S.; Wendzel, S. “The Good, the Bad and The Ugly”: Evaluation of Wi-Fi steganography. J. Commun. 2015, 10, 747–752. [Google Scholar] [CrossRef][Green Version]
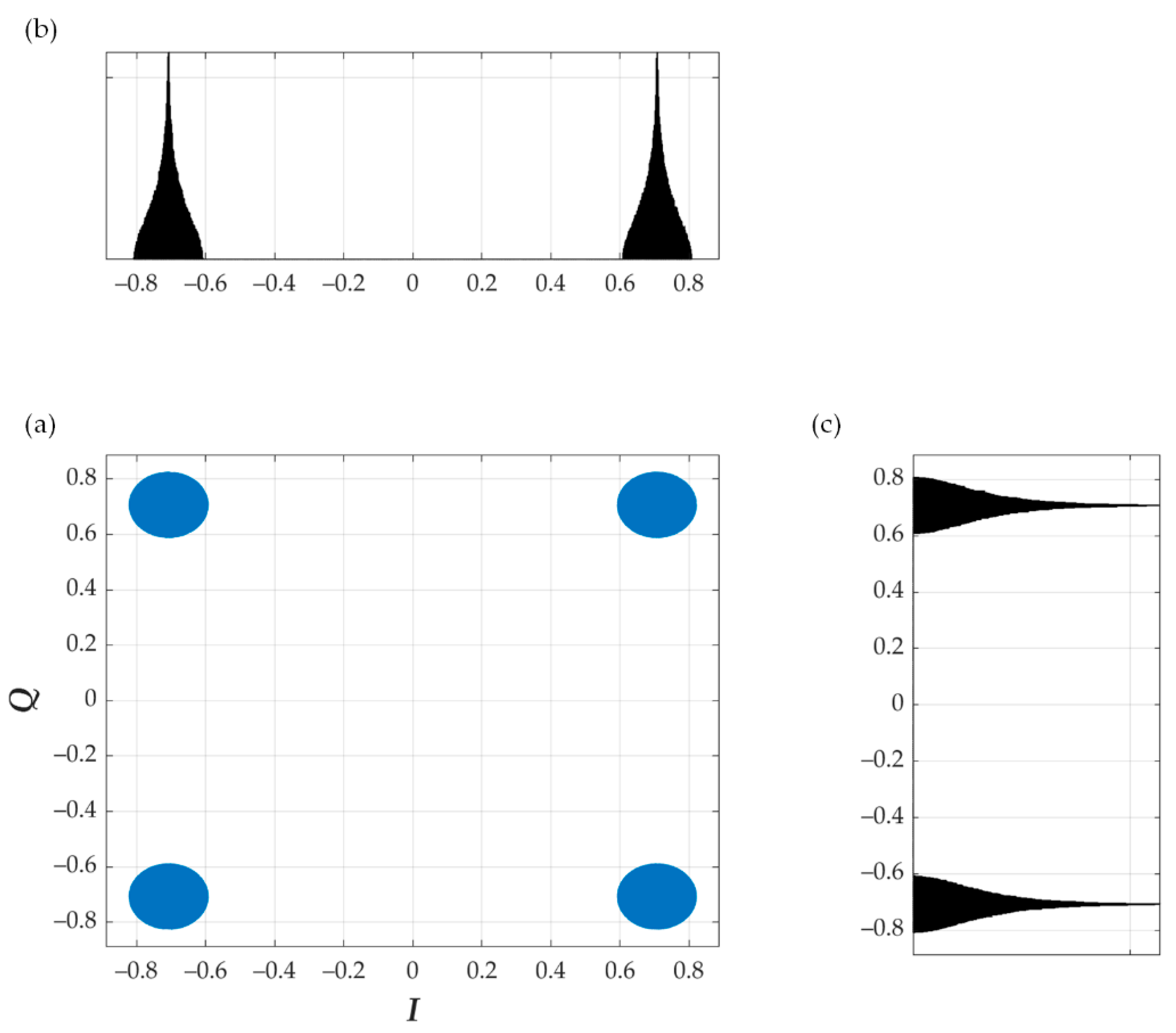
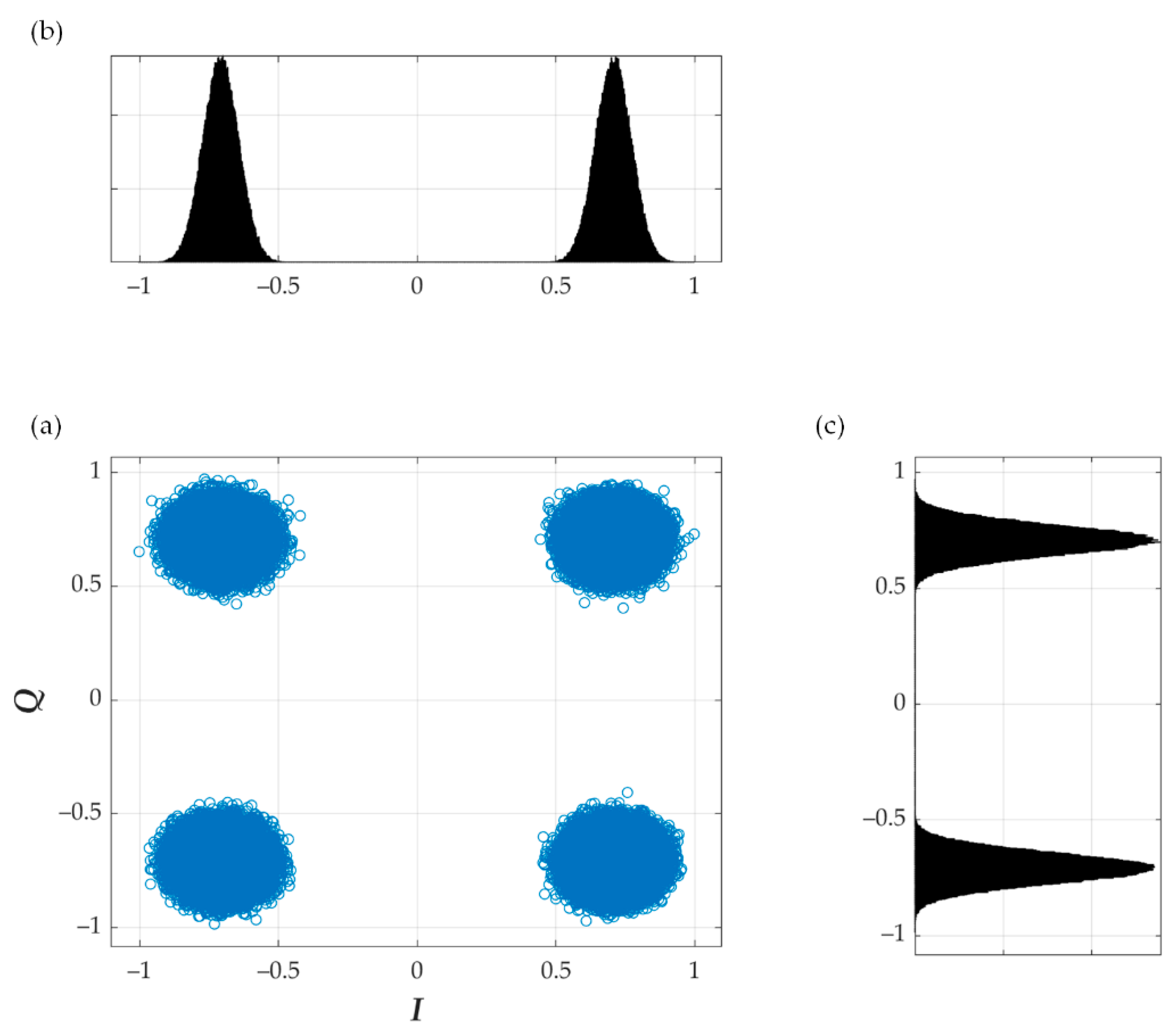
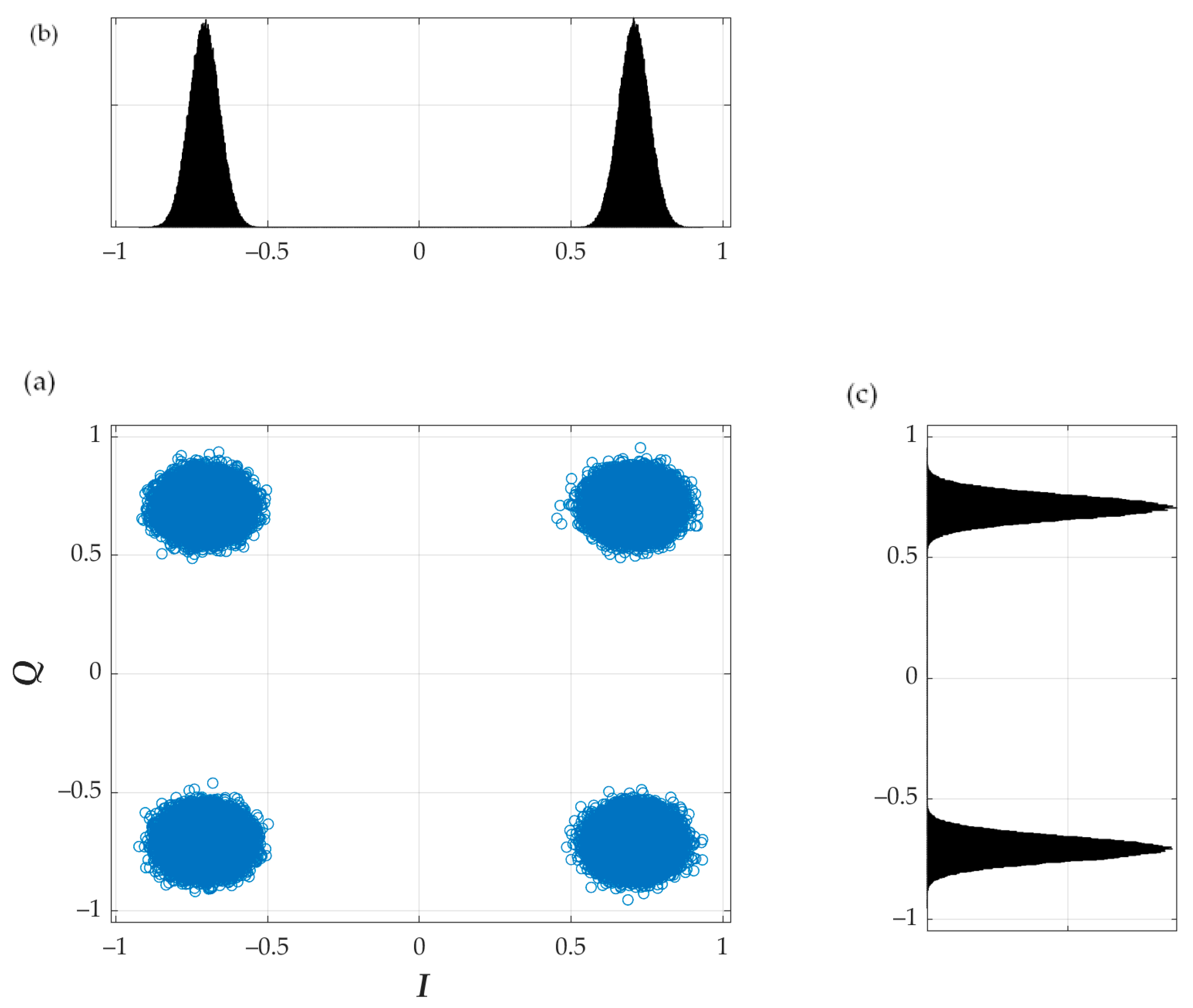
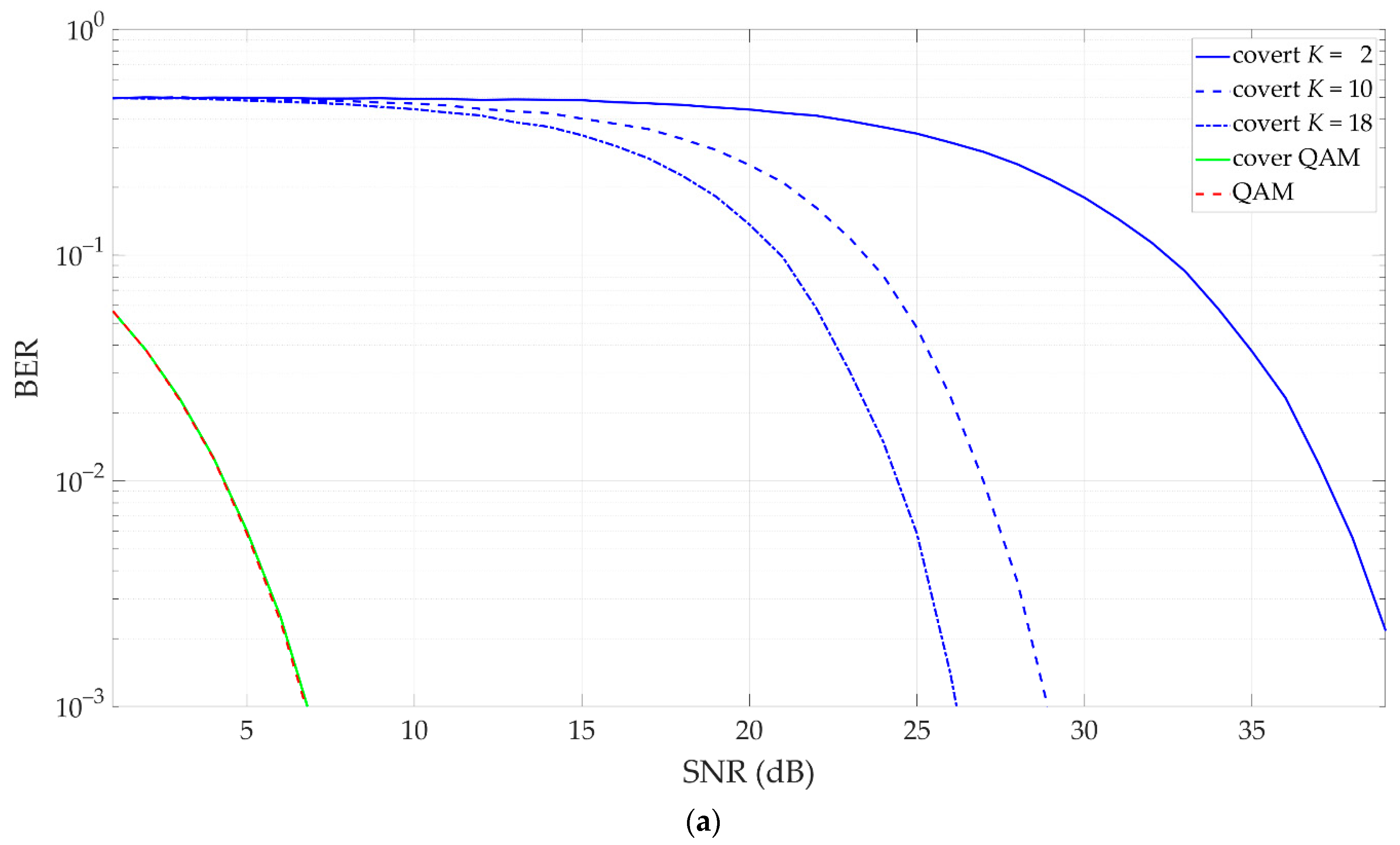
| Modulation Scheme for Physical Downlink Shared Channel (PDSCH) | Required EVM (%) |
|---|---|
| QPSK | 17.5 |
| 16 QAM | 12.5 |
| 64 QAM | 8.0 |
| 256 QAM | 3.5 |
| Signal | Parameters | Value |
|---|---|---|
| Cover (carrier) | Modulation type | 4 QAM |
| Carrier frequency | 850 MHz | |
| Bandwidth | 1 MHz | |
| Transmission rate | 4 MHz | |
| Covert information | M | 4 |
| Am | 0.05·An | |
| φm | ±π/4, ±3π/4 | |
| K | 10 and 25 | |
| Transmission rate | 400 kb/s (for K = 10) | |
| 160 kb/s (for K = 25) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grzesiak, K.; Piotrowski, Z.; Kelner, J.M. A Wireless Covert Channel Based on Dirty Constellation with Phase Drift. Electronics 2021, 10, 647. https://doi.org/10.3390/electronics10060647
Grzesiak K, Piotrowski Z, Kelner JM. A Wireless Covert Channel Based on Dirty Constellation with Phase Drift. Electronics. 2021; 10(6):647. https://doi.org/10.3390/electronics10060647
Chicago/Turabian StyleGrzesiak, Krystian, Zbigniew Piotrowski, and Jan M. Kelner. 2021. "A Wireless Covert Channel Based on Dirty Constellation with Phase Drift" Electronics 10, no. 6: 647. https://doi.org/10.3390/electronics10060647
APA StyleGrzesiak, K., Piotrowski, Z., & Kelner, J. M. (2021). A Wireless Covert Channel Based on Dirty Constellation with Phase Drift. Electronics, 10(6), 647. https://doi.org/10.3390/electronics10060647








