An SVD Approach for Estimating the Dimension of Phaseless Data on Multiple Arcs in Fresnel Zone
Abstract
1. Introduction
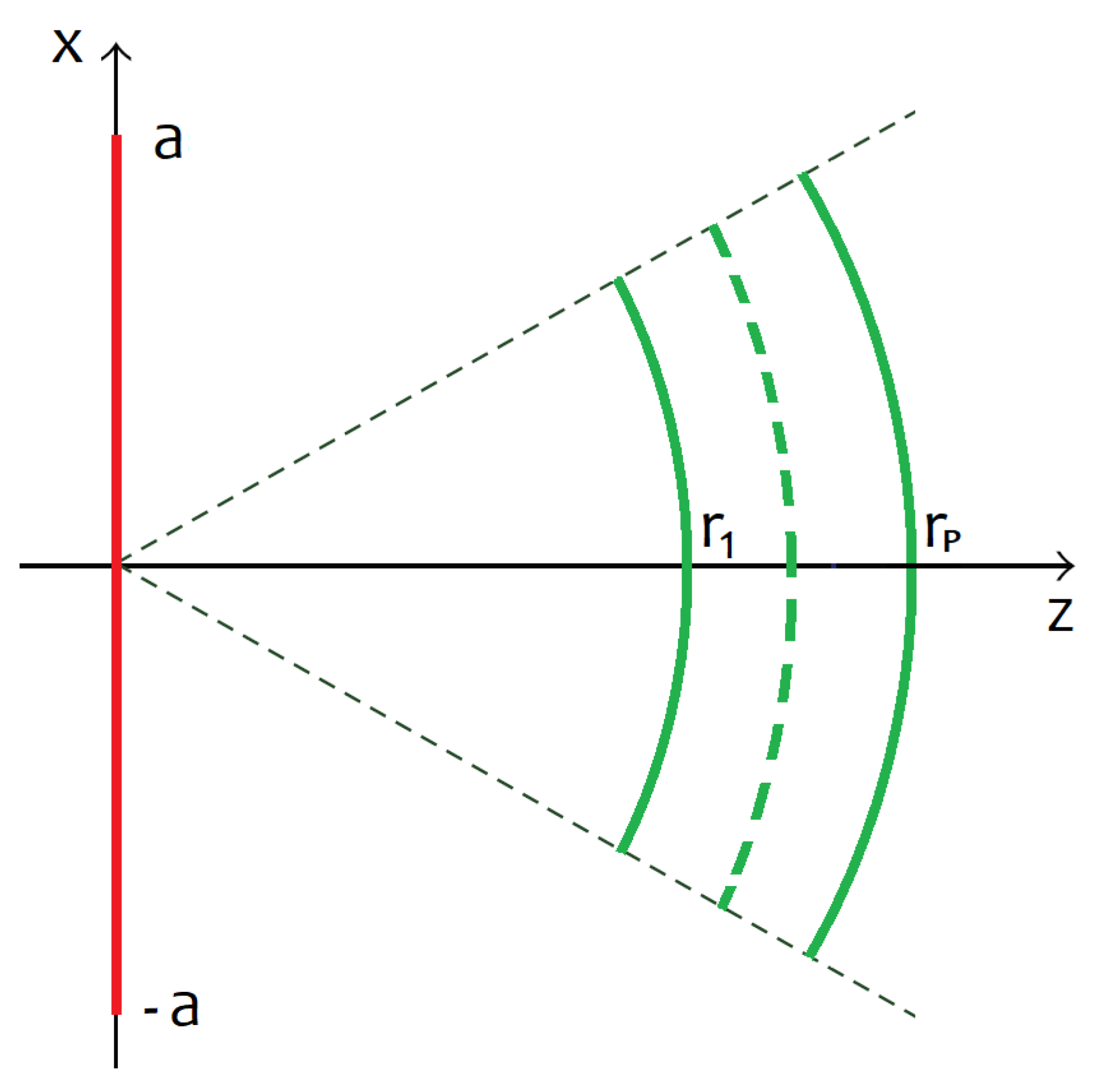
2. Geometry of the Problem and Preliminary Results
3. Singular Values of the Lifting Operator in the Case of One Observation Arc
4. Singular Values of the Lifting Operator in the Case of Observation Arcs
- the operators along the main diagonal of (30) and those off-diagonal are both convolutions.
- the kernel of becomes more and more similar to when approaches .
- the parameter p decreases,
- the parameter q increases.
5. Numerical Verification of the Theoretical Results
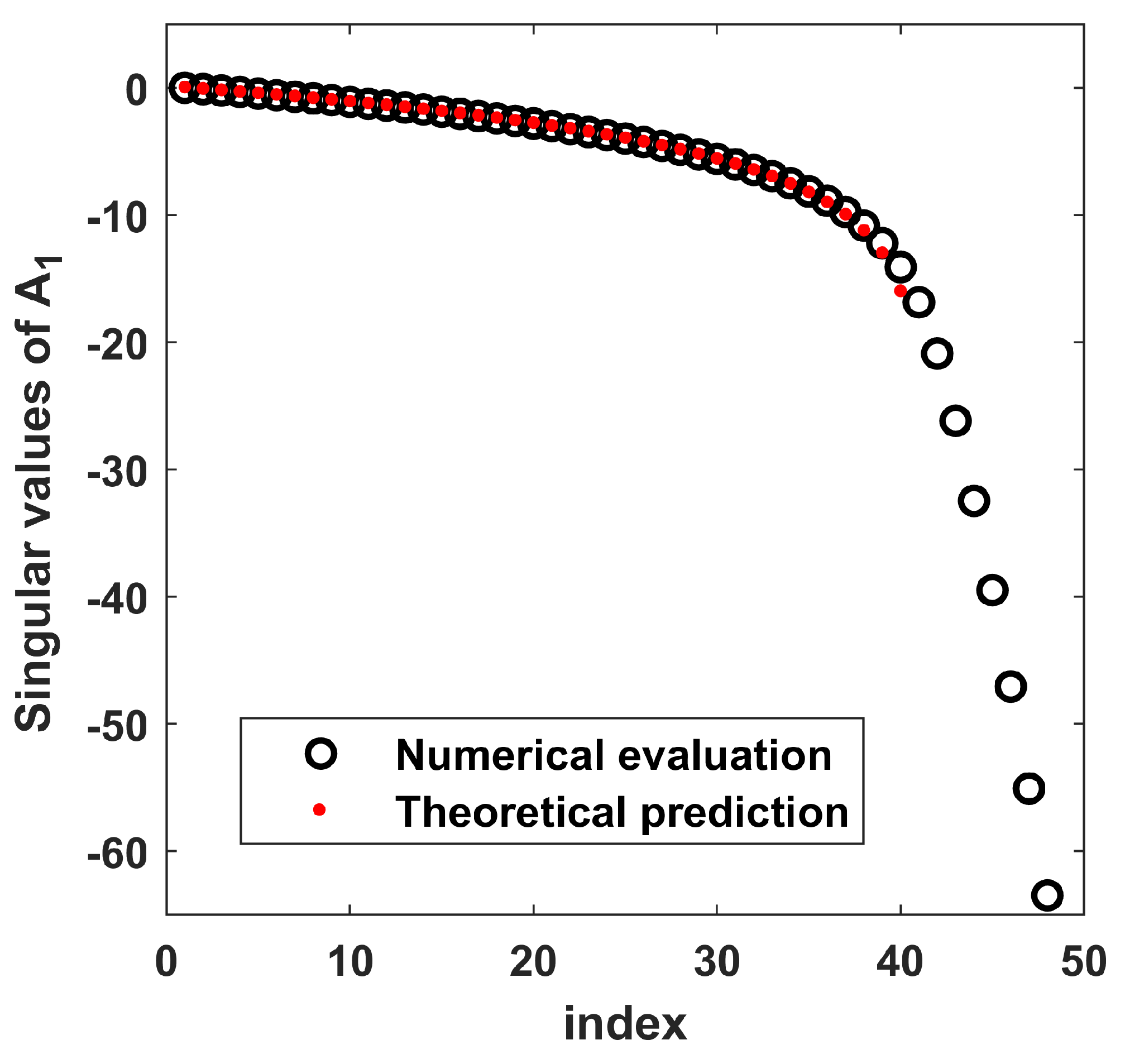
5.1. Numerical Verification in the Case of One Observation Arc
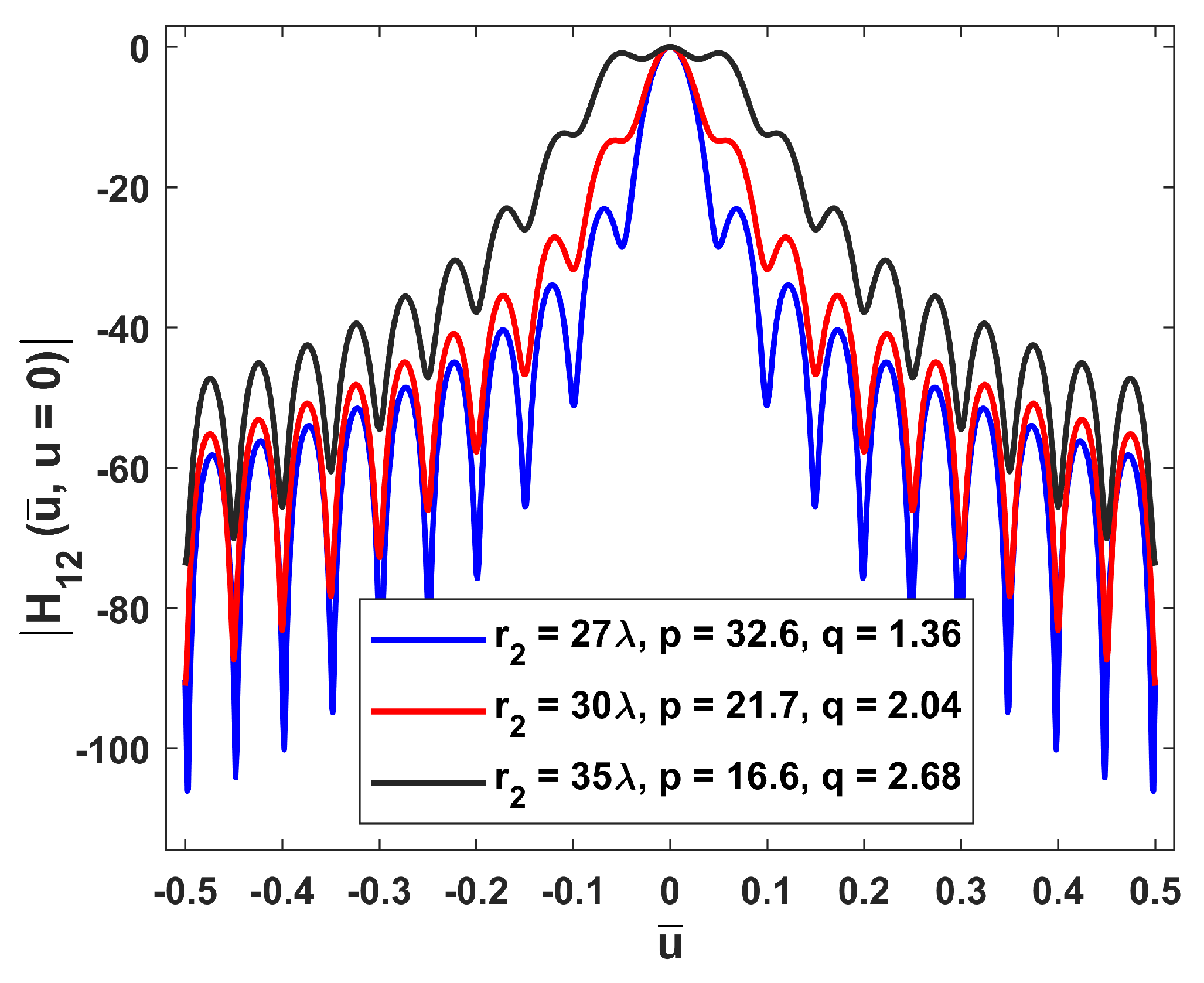
5.2. Numerical Verification in the Case of Two Observation Arcs
- a cut of the kernel of ,
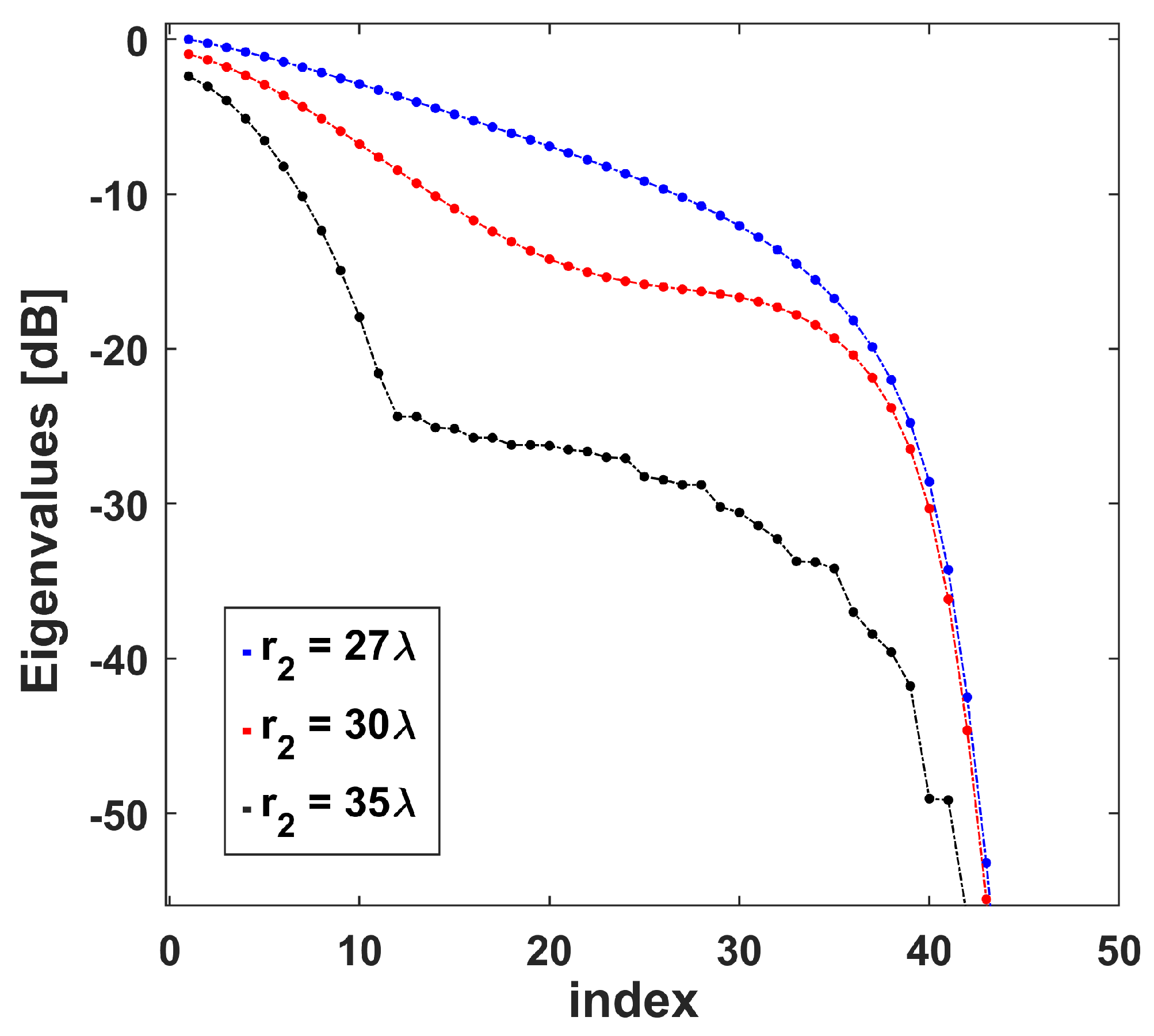
- the eigenvalues of ,
- 1.
- the width of the main lobe of is larger,
- 2.
- the eigenvalues of decay more quickly, and consequently, is lower.
5.3. Numerical Verification in the Case of Three Observation Arcs
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Bertero, M. Linear inverse and ill-posed problems. Adv. Electron. Electron Phys. 1989, 75, 1–120. [Google Scholar]
- Leone, G. Source geometry optimization for hemispherical radiation pattern coverage. IEEE Trans. Antennas Propag. 2016, 64, 2033–2038. [Google Scholar] [CrossRef]
- Brancaccio, A.; Solimene, R. Fault detection in dielectric grid scatterers. Opt. Express 2015, 23, 8200–8215. [Google Scholar] [CrossRef] [PubMed]
- Marengo, E.A.; Devaney, A.J. The inverse source problem of electromagnetics: Linear inversion formulation and minimum energy solution. IEEE Trans. Antennas Propag. 1999, 47, 410–412. [Google Scholar] [CrossRef]
- Dell’Aversano, A.; Leone, G.; Ciaramaglia, F.; Solimene, R. A Strategy for Reconstructing Simple Shapes From Undersampled Backscattered Data. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1757–1761. [Google Scholar] [CrossRef]
- Brancaccio, A.; Dell’Aversano, A.; Leone, G.; Solimene, R. Subsurface detection of shallow targets by undersampled multifrequency data and a non-cooperative source. Appl. Sci. 2019, 9, 5383. [Google Scholar] [CrossRef]
- Knapp, J.; Paulus, A.; Eibert, T.F. Reconstruction of squared field magnitudes and relative phases from magnitude-only near-field measurements. IEEE Trans. Antennas Propag. 2019, 67, 3397–3409. [Google Scholar] [CrossRef]
- Las-Heras, F.; Sarkar, T.K. Planar NF-FF with direct optimization-source reconstruction using amplitude only data. In Proceedings of the IEEE Antennas and Propagation Society International Symposium, Boston, MA, USA, 8–13 July 2001. [Google Scholar]
- Paulus, A.; Knapp, J.; Eibert, T.F. Phaseless near-field far-field transformation utilizing combinations of probe signals. IEEE Trans. Antennas Propag. 2017, 65, 5492–5502. [Google Scholar] [CrossRef]
- Arboleya, A.; Laviada, J.; Ala-Laurinaho, J.; Álvarez, Y.; Las-Heras, F.; Räisänen, A.V. Phaseless Characterization of Broadband Antennas. IEEE Trans. Antennas Propag. 2016, 64, 484–495. [Google Scholar] [CrossRef]
- Fuchs, B.; Mattes, M.; Rondineau, S.; Le Coq, L. Phaseless Near-Field Antenna Measurements From Two Surface Scans—Numerical and Experimental Investigations. IEEE Trans. Antennas Propag. 2020, 68, 2315–2322. [Google Scholar] [CrossRef]
- Pierri, R.; Leone, G.; Moretta, R. Phaseless near-field techniques from a random starting point. In Proceedings of the XXXIIIrd General Assembly and Scientific Symposium of the International Union of Radio Science, Rome, Italy, 29 August–5 September 2020; pp. 1–4. [Google Scholar]
- Costanzo, S.; Di Massa, G.; Migliore, M.D. A novel hybrid approach for far-field characterization from near-field amplitude-only measurements on arbitrary scanning surfaces. IEEE Trans. Antennas Propag. 2005, 53, 1866–1874. [Google Scholar] [CrossRef]
- Yaccarino, R.G.; Rahmat-Samii, Y. Phaseless bi-polar planar near-field measurements and diagnostics of array antennas. IEEE Trans. Antennas Propag. 1999, 47, 574–583. [Google Scholar] [CrossRef]
- Fuchs, B.; Le Coq, L. Excitation Retrieval of Microwave Linear Arrays From Phaseless Far-Field Data. IEEE Trans. Antennas Propag. 2015, 63, 748–754. [Google Scholar] [CrossRef]
- Laviada Martínez, J.; Arboleya-Arboleya, A.; Álvarez-López, Y.; García-González, C.; Las-Heras, F. Phaseless Antenna Diagnostics Based on Off-Axis Holography with Synthetic Reference Wave. IEEE Antennas Wirel. Propag. Lett. 2014, 13, 43–46. [Google Scholar] [CrossRef]
- Álvarez, Y.; Las-Heras, F.; Pino, M.R. Antenna diagnostics using phaseless NF information. In Proceedings of the 2010 Conference Proceedings ICECom, 20th International Conference on Applied Electromagnetics and Communications, Dubrovnik, Croatia, 20–23 September 2010; pp. 1–4. [Google Scholar]
- Xiong, C.; Xiao, G. Excitation Retrieval for Phased Arrays With Magnitude-Only Fields Measured at a Fixed Location. IEEE Antennas Wirel. Propag. Lett. 2021, 20, 264–268. [Google Scholar] [CrossRef]
- Maisto, M.A.; Moretta, R.; Solimene, R.; Pierri, R. Phaseless arrays diagnostic by phaselift in near zone: Numerical experiments. In Proceedings of the 2017 Progress in Electromagnetics Research Symposium (PIERS), Saint Petersburg, Russia, 22–25 May 2017; pp. 1217–1221. [Google Scholar]
- Laviada, J.; Álvarez-López, Y.; Arboleya-Arboleya, A.; García-González, C.; Las-Heras, F. Interferometric Technique With Nonredundant Sampling for Phaseless Inverse Scattering. IEEE Trans. Antennas Propag. 2014, 62, 739–746. [Google Scholar] [CrossRef]
- Crocco, L.; D’Urso, M.; Isernia, T. Inverse scattering from phaseless measurements of the total field on a closed curve. J. Opt. Soc. A 2004, 21, 622–631. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Li, L.; Li, F. Multifrequency imaging from intensity-only data using the phaseless data distorted rytov iterative method. IEEE Trans. Antennas Propag. 2009, 57, 290–295. [Google Scholar] [CrossRef]
- Estatico, C.; Fedeli, A.; Pastorino, M.; Randazzo, A.; Tavanti, E. A Phaseless Microwave Imaging Approach Based on a Lebesgue-Space Inversion Algorithm. IEEE Trans. Antennas Propag. 2020, 68, 8091–8103. [Google Scholar] [CrossRef]
- Narendra, C.; Mojabi, P. Phaseless Gauss-Newton Inversion for Microwave Imaging. IEEE Trans. Antennas Propag. 2021, 69, 443–456. [Google Scholar] [CrossRef]
- Isernia, T.; Pierri, R.; Leone, G. Phaseless near field techniques: Formulation of the problem and field properties. J. Electromagn. Waves Appl. 1994, 8, 871–888. [Google Scholar] [CrossRef]
- Isernia, T.; Leone, G.; Pierri, R. The phase retrieval by a reference source. In Proceedings of the Digest on Antennas and Propagation Society International Symposium, San Jose, CA, USA, 26–30 June 1989; pp. 64–67. [Google Scholar]
- Candès, E.J.; Li, X.; Soltanolkotabi, M. Phase Retrieval via Wirtinger Flow: Theory and Algorithms. IEEE Trans. Inf. Theory 2015, 61, 1985–2007. [Google Scholar] [CrossRef]
- Ghods, R.; Lan, A.; Goldstein, T.; Studer, C. Linear Spectral Estimators and an Application to Phase Retrieval. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1734–1743. [Google Scholar]
- Yonel, B.; Yazici, B. A Deterministic Theory for Exact Non-Convex Phase Retrieval. IEEE Trans. Signal Process. 2020, 68, 4612–4626. [Google Scholar] [CrossRef]
- Soldovieri, F.; Liseno, A.; D’Elia, G.; Pierri, R. Global convergence of phase retrieval by quadratic approach. IEEE Trans. Antennas Propag. 2005, 53, 3135–3141. [Google Scholar] [CrossRef]
- Pierri, R.; Moretta, R. On Data Increasing in Phase Retrieval via Quadratic Inversion: Flattening Manifold and Local Minima. IEEE Trans. Antennas Propag. 2020, 68, 8104–8113. [Google Scholar] [CrossRef]
- Sun, J.; Qu, Q.; Wright, J. A geometric analysis of phase retrieval. Found. Comput. Math. 2018, 18, 1131–1198. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Cadima, J. Principal component analysis: A review and recent developments. Philos. Trans. R. Soc. A 2016, 374, 20150202. [Google Scholar] [CrossRef]
- Bouwmans, T.; Zahzah, E. Robust PCA via Principal Component Pursuit: A Review for a Comparative Evaluation in Video Surveillance. Comput. Vis. Image Underst. 2014, 122, 22–34. [Google Scholar] [CrossRef]
- Moretta, R.; Pierri, R. Performance of Phase Retrieval via Phaselift and Quadratic Inversion in Circular Scanning Case. IEEE Trans. Antennas Propag. 2019, 67, 7528–7537. [Google Scholar] [CrossRef]
- Solimene, R.; Mola, C.; Gennarelli, G.; Soldovieri, F. On the singular spectrum of radiation operators in the non-reactive zone: The case of strip sources. J. Opt. 2015, 17, 025605. [Google Scholar] [CrossRef]
- Leone, G.; Munno, F.; Pierri, R. Radiation properties of conformal antennas: The elliptical source. Electronics 2019, 8, 531. [Google Scholar] [CrossRef]
- Maisto, M.A.; Solimene, R.; Pierri, R. Valid angle criterion and radiation pattern estimation via singular value decomposition for planar scanning. IET Microw. Antennas Propag. 2019, 13, 2342–2348. [Google Scholar] [CrossRef]
- Gori, F.; Palma, C. On the eigenvalues of the sinc2 kernel. J. Phys. A Math. Gen. 1975, 8, 1709. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- Pierri, R.; Moretta, R. An evaluation of the data space dimension in phase retrieval: Results in Fresnel zone. In Proceedings of the XXXIVth General Assembly and Scientific Symposium of the International Union of Radio Science, Rome, Italy, 28 August–4 September 2021; Available online: www.techrxiv.org/articles/preprint/13828169 (accessed on 16 February 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pierri, R.; Moretta, R. An SVD Approach for Estimating the Dimension of Phaseless Data on Multiple Arcs in Fresnel Zone. Electronics 2021, 10, 606. https://doi.org/10.3390/electronics10050606
Pierri R, Moretta R. An SVD Approach for Estimating the Dimension of Phaseless Data on Multiple Arcs in Fresnel Zone. Electronics. 2021; 10(5):606. https://doi.org/10.3390/electronics10050606
Chicago/Turabian StylePierri, Rocco, and Raffaele Moretta. 2021. "An SVD Approach for Estimating the Dimension of Phaseless Data on Multiple Arcs in Fresnel Zone" Electronics 10, no. 5: 606. https://doi.org/10.3390/electronics10050606
APA StylePierri, R., & Moretta, R. (2021). An SVD Approach for Estimating the Dimension of Phaseless Data on Multiple Arcs in Fresnel Zone. Electronics, 10(5), 606. https://doi.org/10.3390/electronics10050606






