On Multi-Scalar Multiplication Algorithms for Register-Constrained Environments
Abstract
1. Introduction
1.1. Previous Work
1.2. Motivation and Contribution
2. Adaptive Window Method
3. A Case Study: Adaptive Window Method for Five Registers
3.1. Using NAF Representation
3.2. Using JSF Representation
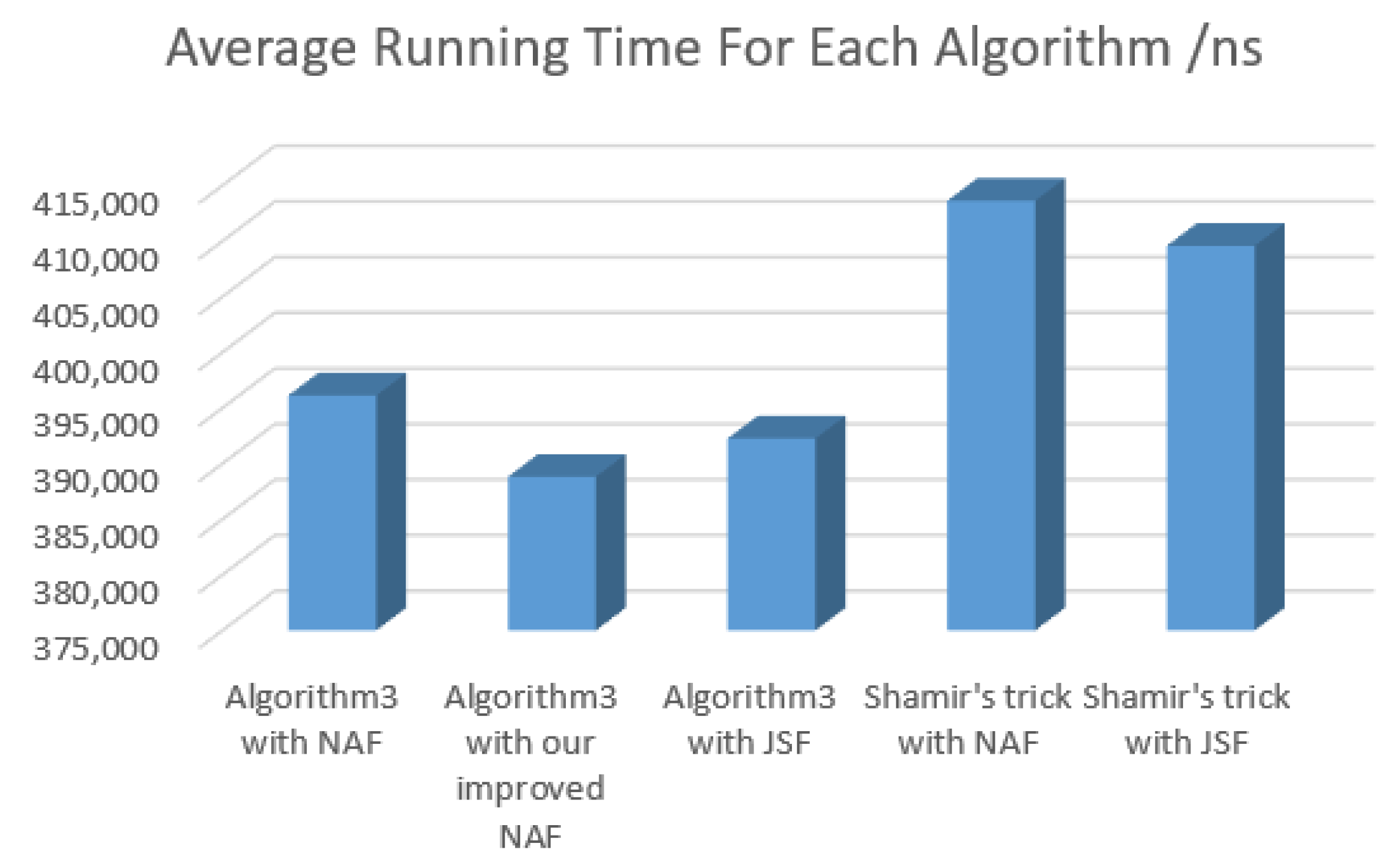
4. Experiments and Comparison
5. Future Work
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Some Notations Using in the Appendixes
Appendix B. Some Facts of NAF Representation
Appendix C. Proof of Theorem 1
Appendix D. Proof of Theorem 2
Appendix E. Some Facts of JSF Representation
Appendix F. Proof of Theorem 3
References
- National Institute of Standards and Technology. Federal Information Processing Standards Publication 186-3: Digital Signature Standard (DSS). 2009. Available online: https://csrc.nist.gov/csrc/media/publications/fips/186/3/archive/2009-06-25/documents/fips_186-3.pdf (accessed on 5 November 2020).
- American National Standards Institute. ANSI X9.62: Public Key Cryptography for the Financial Services Industry: The Elliptic Curve Digital Signature Algorithm (ECDSA); American National Standards Institute: New York, NY, USA, 2005. [Google Scholar]
- Schnorr, C.P. Efficient signature generation by smart cards. J. Cryptol. 1991, 4, 161–174. [Google Scholar] [CrossRef]
- Fuchsbauer, G.; Orrù, M.; Seurin, Y. Aggregate Cash Systems: A Cryptographic Investigation of Mimblewimble. In Proceedings of the 38th Annual International Conference on the Theory and Applications of Cryptographic Techniques Selected Areas in Cryptography (EUROCRYPT 2019), Part I, Darmstadt, Germany, 19–23 May 2019; Ishai, Y., Rijmen, V., Eds.; Lecture Notes in Computer Science. Springer: Cham, Switzerland, 2019; Volume 11476, pp. 657–689. [Google Scholar]
- Sun, D.Z.; Sun, L.; Yang, Y. On secure simple pairing in Bluetooth standard v5.0-part II: Privacy analysis and enhancement for low energy. Sensors 2019, 19, 3259. [Google Scholar] [CrossRef]
- Zhang, Y.D.; He, D.B.; Zhang, M.W.; Choo, K.K.R. A provable-secure and practical two-party distributed signing protocol for SM2 signature algorithm. Front. Comput. Sci. China 2020, 14, 143803. [Google Scholar] [CrossRef]
- Chen, E.; Zhu, Y.; Lin, C.L.; Lv, K.W. Zero-pole cancellation for identity-based aggregators: A constant-size designated verifier-set signature. Front. Comput. Sci. China 2020, 14, 144806. [Google Scholar] [CrossRef]
- Gordon, D.M. A survey of fast exponentiation methods. J. Algorithms 1998, 27, 129–146. [Google Scholar] [CrossRef]
- ElGamal, T. A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 1985, 31, 469–472. [Google Scholar] [CrossRef]
- Dimitrov, V.S.; Jullien, G.A.; Miller, W.C. Complexity and fast algorithms for multiexponentiations. IEEE Trans. Comput. 2000, 49, 141–147. [Google Scholar] [CrossRef]
- Solinas, J.A. Low-Weight Binary Representations for Pairs of Integers; Combinatorics and Optimization Research Report CORR 2001-41, Centre for Applied Cryptographic Research, University of Waterloo. 2001. Available online: http://www.cacr.math.uwaterloo.ca/techreports/2001/corr2001-41.ps (accessed on 5 November 2020).
- Grabner, P.J.; Heuberger, C.; Prodinger, H. Distribution results for low-weight binary representations for pairs of integers. Theor. Comput. Sci. 2004, 319, 307–331. [Google Scholar] [CrossRef][Green Version]
- Yang, W.C.; Guan, D.J.; Laih, C.S. Algorithm of asynchronous binary signed-digit recoding on fast multiexponentiation. Appl. Math. Comput. 2005, 167, 108–117. [Google Scholar] [CrossRef]
- Ruan, X.Y.; Katti, R.S. Left-to-right optimal signed-binary representation of a pair of integers. IEEE Trans. Comput. 2005, 54, 124–131. [Google Scholar] [CrossRef]
- Sun, D.Z.; Huai, J.P.; Sun, J.Z.; Zhang, J.W. Computational efficiency analysis of Wu et al.’s fast modular multi-exponentiation algorithm. Appl. Math. Comput. 2007, 190, 1848–1854. [Google Scholar] [CrossRef]
- Sun, D.Z.; Huai, J.P.; Sun, J.Z.; Li, J.X. Analysis of multi-exponentiation algorithm using binary signed-digit representations. Int. J. Comput. Methods 2009, 6, 307–315. [Google Scholar] [CrossRef]
- Yang, W.C.; Hung, C.P. Analysis of the Dimitrov-Jullien-Miller recoding algorithm. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 2016, E99A, 139–144. [Google Scholar] [CrossRef]
- Arno, S.; Wheeler, F.S. Signed digit representations of minimal hamming weight. IEEE Trans. Comput. 1993, 42, 1007–1010. [Google Scholar] [CrossRef]
- Menezes, A.; van Oorschot, P.; Vanstone, S. Handbook of Applied Cryptography; CRC Press: Boca Raton, FL, USA, 1997; pp. 627–628. [Google Scholar]
- Yen, S.M.; Laih, C.S.; Lenstra, A.K. Multi-exponentiation. IEE Proc. Comp. Digit. Tech. 1994, 141, 325–326. [Google Scholar] [CrossRef]
- Möller, B. Algorithms for Multi-exponentiation. In Proceedings of the Selected Areas in Cryptography (SAC 2001), Toronto, ON, Canada, 16–17 August 2001; Vaudenay, S., Youssef, A.M., Eds.; Lecture Notes in Computer Science. Springer: Berlin/Heidelberg, Germany, 2001; Volume 2259, pp. 165–180. [Google Scholar]
- Avanzi, R.M. The complexity of certain multi-exponentiation techniques in cryptography. J. Cryptol. 2005, 18, 357–373. [Google Scholar] [CrossRef]
- Yang, W.C.; Guan, D.J.; Laih, C.S. Fast multicomputation with asynchronous strategy. IEEE Trans. Comput. 2007, 56, 234–242. [Google Scholar] [CrossRef]
- Sun, D.Z.; Huai, J.P.; Li, J.X. A note on asynchronous multi-exponentiation algorithm using binary representation. Inf. Process. Lett. 2012, 112, 876–879. [Google Scholar] [CrossRef]
- Chevalier, C.; Laguillaumie, F.; Vergnaud, D. Privately outsourcing exponentiation to a single server: Cryptanalysis and optimal constructions. Algorithmica 2020, 83, 72–115. [Google Scholar] [CrossRef]
- Borges, F.; Lara, P.; Portugal, R. Parallel algorithms for modular multi-exponentiation. Appl. Math. Comput. 2017, 292, 406–416. [Google Scholar] [CrossRef]
- Topcuoglu, C.; Kaya, K.; Savas, E. A generic private information retrieval scheme with parallel multi-exponentiations on multicore processors. Concurr. Comput. Pract. Exp. 2018, 30, e4685. [Google Scholar] [CrossRef]
- Tao, R.; Liu, J.; Su, H.; Sun, Y.; Liu, X. Combination in Advance Batch Multi-exponentiation on Elliptic Curve. In Proceedings of the 2015 IEEE 2nd International Conference on Cyber Security and Cloud Computing (CSCloud 2015), New York, NY, USA, 3–5 November 2015; Qiu, M.K., Zhang, T., Das, S., Eds.; IEEE Computer Society: Washington, DC, USA, 2015; pp. 411–416. [Google Scholar]
- Wu, Q.H.; Sun, Y.; Qin, B.; Hu, J.K.; Liu, W.R.; Liu, J.W.; Ding, Y. Batch public key cryptosystem with batch multi-exponentiation. Futur. Gener. Comp. Syst. 2016, 62, 196–204. [Google Scholar] [CrossRef]
- Atmel Corporation. 8-Bit AVR Microcontroller with 128K Bytes In-System Programmable Flash. 2007. Available online: http://ww1.microchip.com/downloads/en/DeviceDoc/doc0945.pdf (accessed on 5 February 2021).
- ARM. ARM7TDMI Technical Reference Manual (Rev 3). 2017. Available online: http://ww1.microchip.com/downloads/en/DeviceDoc/DDI0029G_7TDMI_R3_trm.pdf (accessed on 5 February 2021).
- Hankerson, D.; Menezes, A.; Vanstone, S. Guide to Elliptic Curve Cryptography; Springer: New York, NY, USA, 2004; pp. 109–113. [Google Scholar]
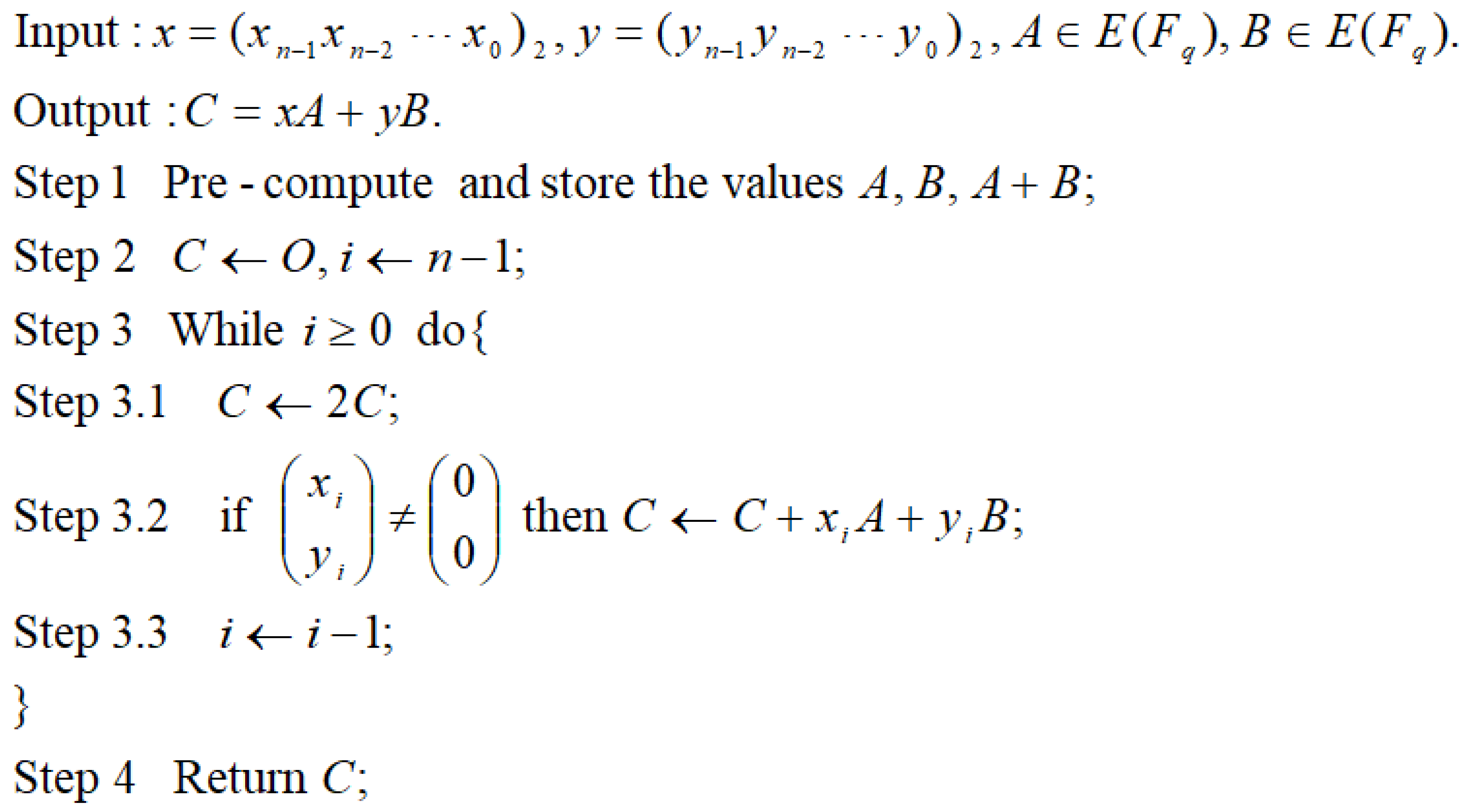

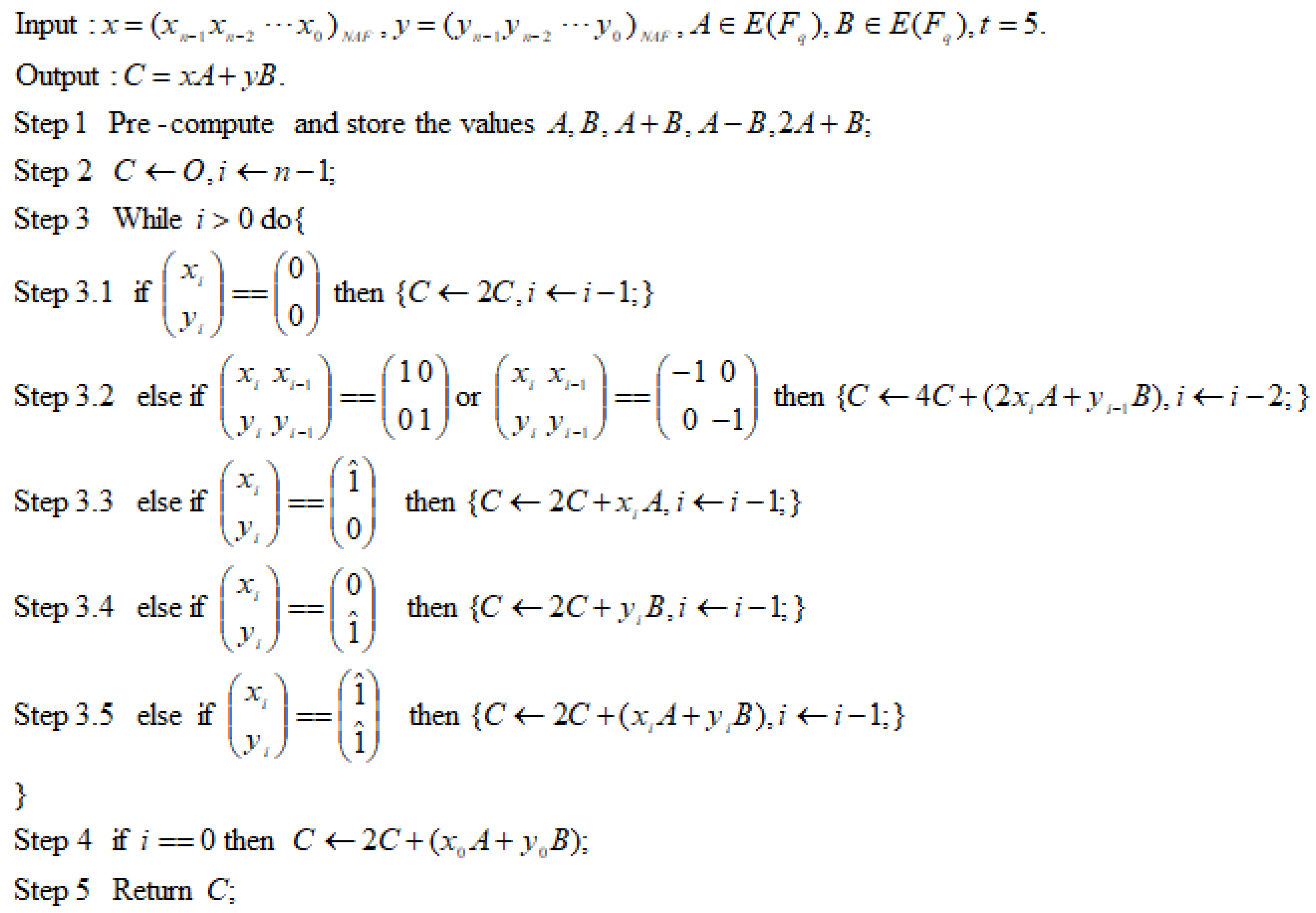
| Term | Definition |
|---|---|
| Finite field with elements | |
| Elliptic curve group E defined over a finite field | |
| O | The point at infinity on |
| Any two points on | |
| The point addition applied to and | |
| The point doubling applied to , i.e., | |
| The scalar multiplication by an integer x applied to , i.e., | |
| , | The binary representations of the integers and |
| , | Any signed binary representations of the integers and , i.e., |
| , | The non-adjacent form (NAF) representations of the integers and |
| The signed sequence pair of the integers and , where and are, respectively, the certain signed binary representations of the integers and | |
| The bit length of the integers and using the binary representations or the signed binary representations | |
| Any bit or | |
| The performance factor of a certain multi-scalar multiplication algorithm, i.e., the number of point additions required by the algorithm | |
| The performance factor of Shamir’s trick using the binary representation | |
| The performance factor of Shamir’s trick using the NAF representation | |
| The performance factor of Shamir’s trick using the joint sparse form (JSF) representation | |
| The performance factor of the -register adaptive window method using the NAF representation | |
| The performance factor of the -register adaptive window method using the improved NAF representation | |
| The performance factor of the -register adaptive window method using the JSF representation | |
| The probability that the event occurs | |
| The conditional probability of the event given the event |
| Algorithms | Number of Registers | Performance Factor Constant Theoretical Value | Performance Factor Constant Experimental Value |
|---|---|---|---|
| Figure 3 | 5 | 1/2 = 0.5 | 0.499962 |
| Figure 3 with our improved NAF | 5 | 209/432 ≈ 0.483796 | 0.483781 |
| Figure 3 using JSF | 5 | 31/64 = 0.484375 | 0.484313 |
| Shamir’s trick with NAF | 4 | 5/9 = 0.555556 | 0.555466 |
| Shamir’s trick with JSF | 4 | 1/2 = 0.5 | 0.500036 |
| Shamir’s trick with 3-NAF interleaving [32] | 4 | 1/2 = 0.5 | 0.500014 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, D.-Z.; Zhong, J.-D.; Zhang, H.-D.; Guo, X.-Y. On Multi-Scalar Multiplication Algorithms for Register-Constrained Environments. Electronics 2021, 10, 605. https://doi.org/10.3390/electronics10050605
Sun D-Z, Zhong J-D, Zhang H-D, Guo X-Y. On Multi-Scalar Multiplication Algorithms for Register-Constrained Environments. Electronics. 2021; 10(5):605. https://doi.org/10.3390/electronics10050605
Chicago/Turabian StyleSun, Da-Zhi, Ji-Dong Zhong, Hong-De Zhang, and Xiang-Yu Guo. 2021. "On Multi-Scalar Multiplication Algorithms for Register-Constrained Environments" Electronics 10, no. 5: 605. https://doi.org/10.3390/electronics10050605
APA StyleSun, D.-Z., Zhong, J.-D., Zhang, H.-D., & Guo, X.-Y. (2021). On Multi-Scalar Multiplication Algorithms for Register-Constrained Environments. Electronics, 10(5), 605. https://doi.org/10.3390/electronics10050605







