Robust Spectrum Sensing Detector Based on MIMO Cognitive Radios with Non-Perfect Channel Gain
Abstract
1. Introduction
- (1)
- Observed data vectors in CR with multicell multiple groups at the secondary users are generated while maintaining the SNR levels with range values at the primary users. Then, the Bayesian method is used to assume priors for the unknown probabilistic parameters to extract a posterior probability distribution vector for the observation data samples of the CR system.
- (2)
- We involve the MAP method to determine the posterior probability distribution expression for the unknown probabilistic parameter of the observation data to extract unknown matrices for the distribution parameters.
- (3)
- We present two approaches to address the channel uncertainty and the noise covariance matrix that complicate the resultant optimization problem. The solution for this problem is examined under different approaches; this problem is solved by a sub-optimal solution in the first approach while a robust solution is used in the second approach.
- (4)
- We prove that our approaches in the spectrum sensing problem based on the assumptions are effective methods to address this the uncertainty.
2. Spectrum Sensing Detector
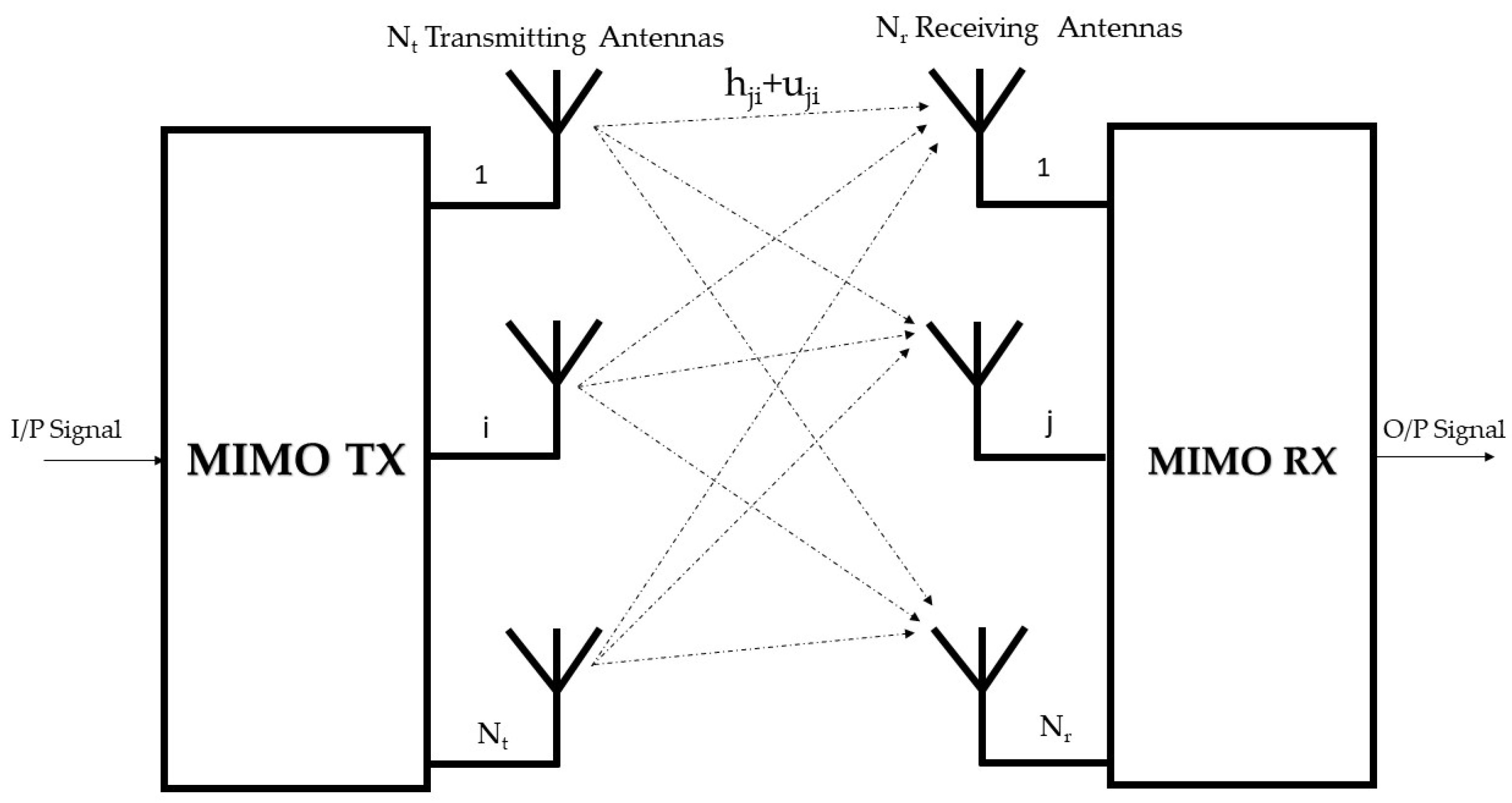
3. System Descriptions
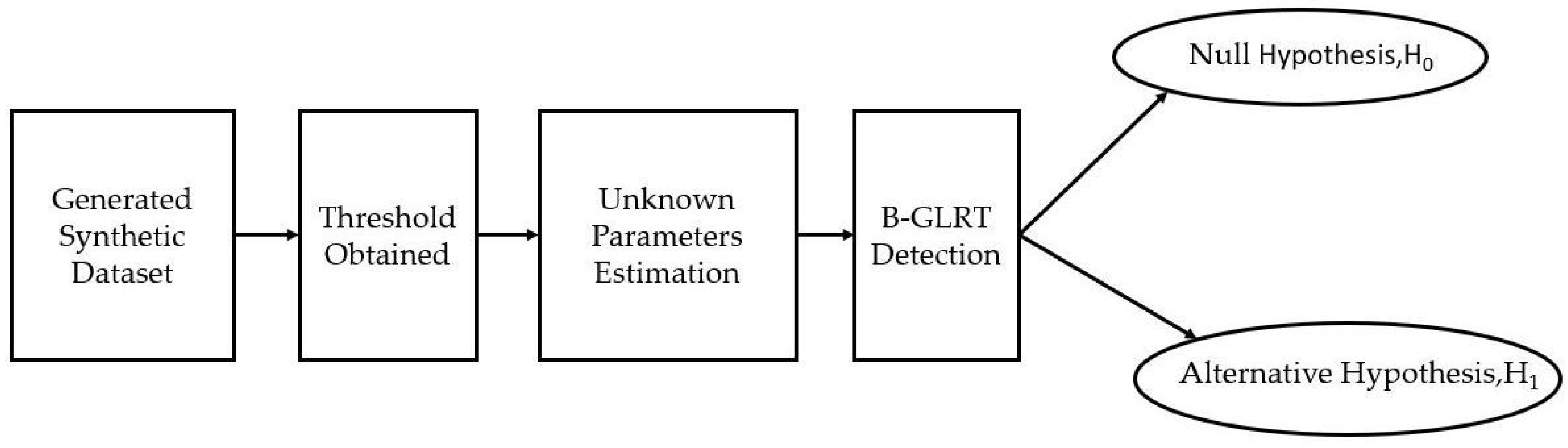
4. Methodology
4.1. B-GLRT Detector for Unknown Noise Covariance Matrix with Perfect CSI (B-GLRT1)
4.2. B-GLRT Detector for Unknown Noise Covariance Matrix with Non-Perfect CSI
4.2.1. Sub-Optimal Solution, B-GLT2
4.2.2. Robust Solution, B-GLT3
- Solving for : in this case, we assume that is unknown and is known and then solve for as shown in .subject toFor additional details see Appendix A.2.
- Solving for : now we can assume that is known and solve for . We also define that , then the problem becomes:subject toAppendix A.2 provides more detail on this derivation.
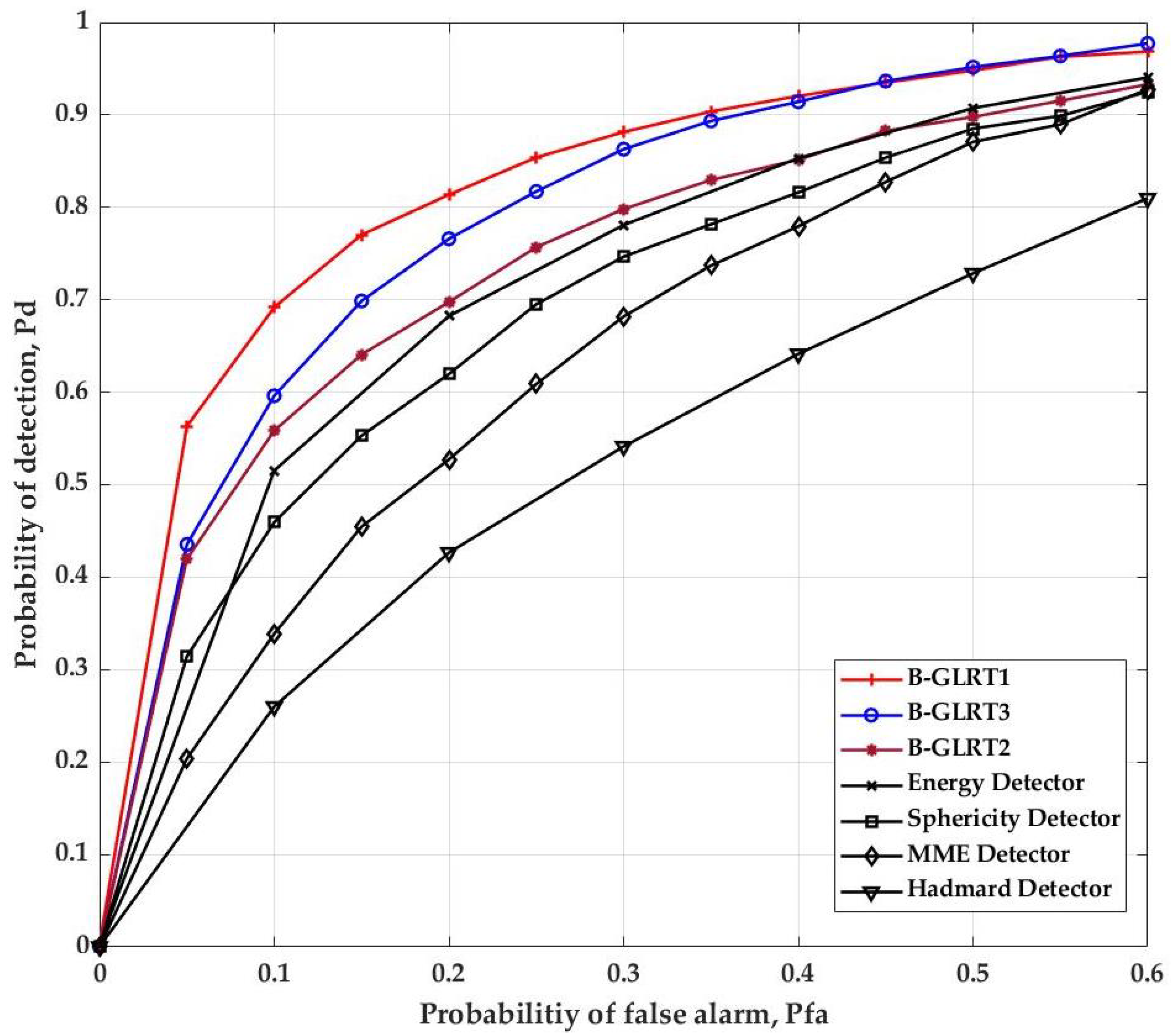
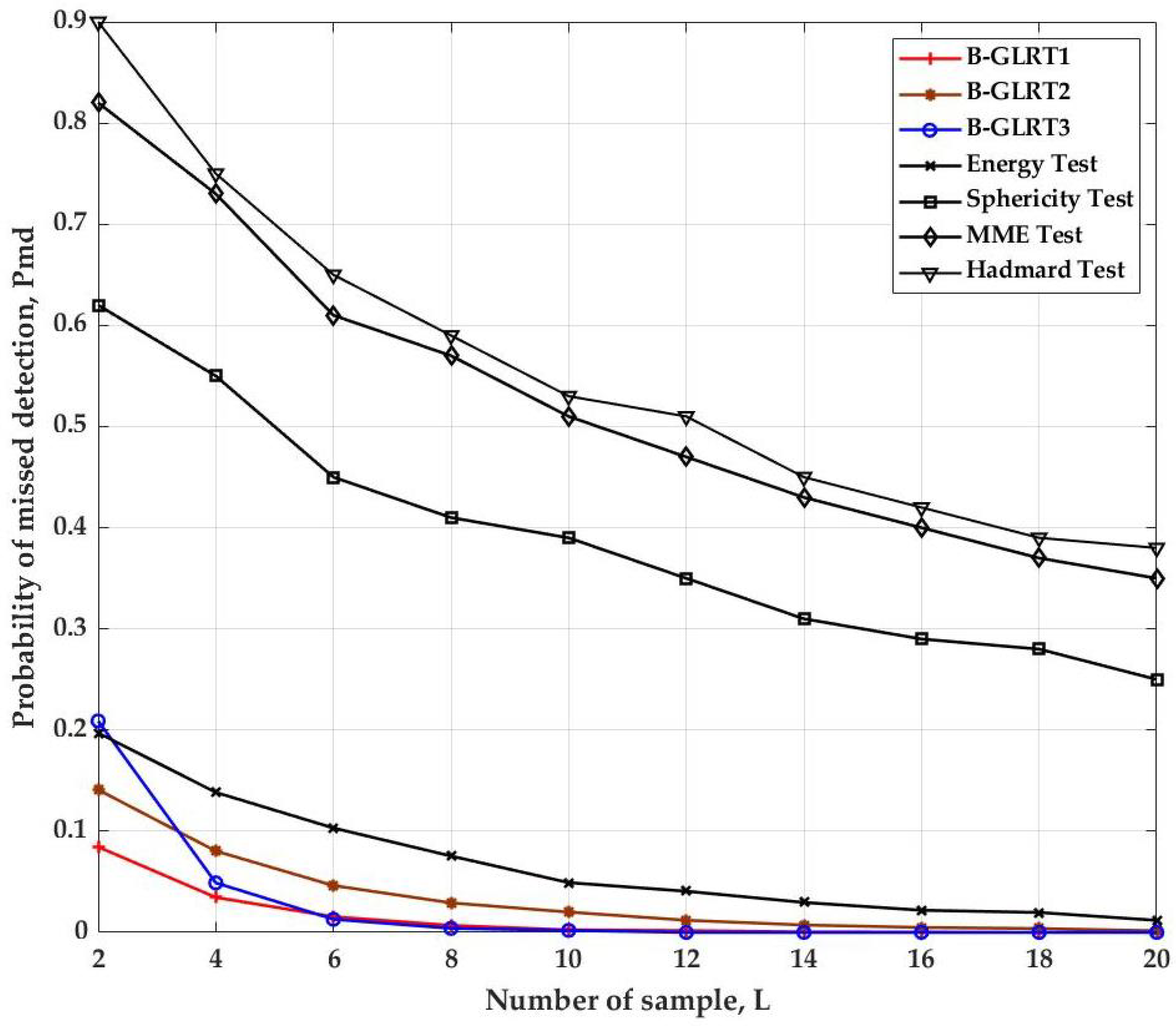
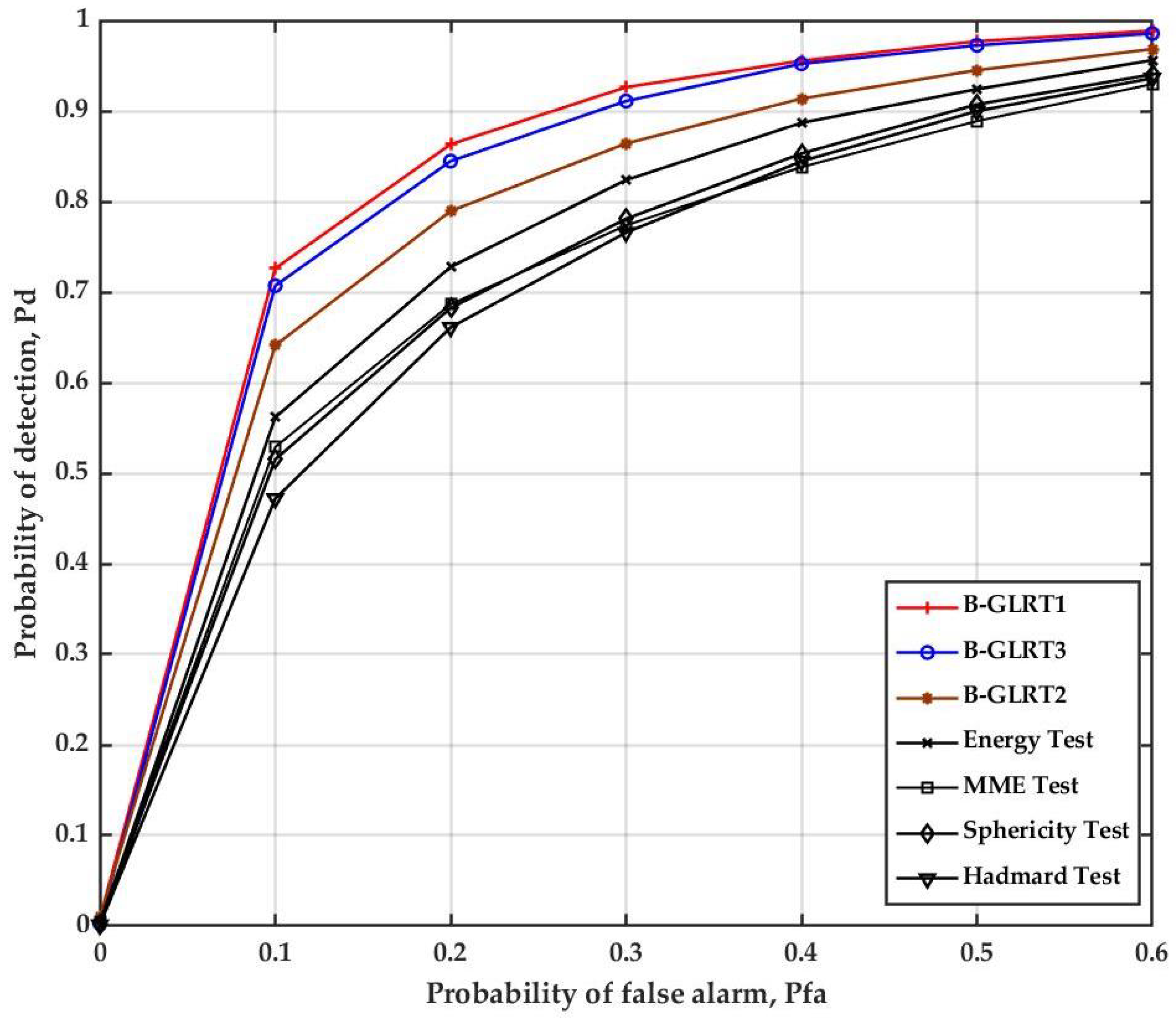
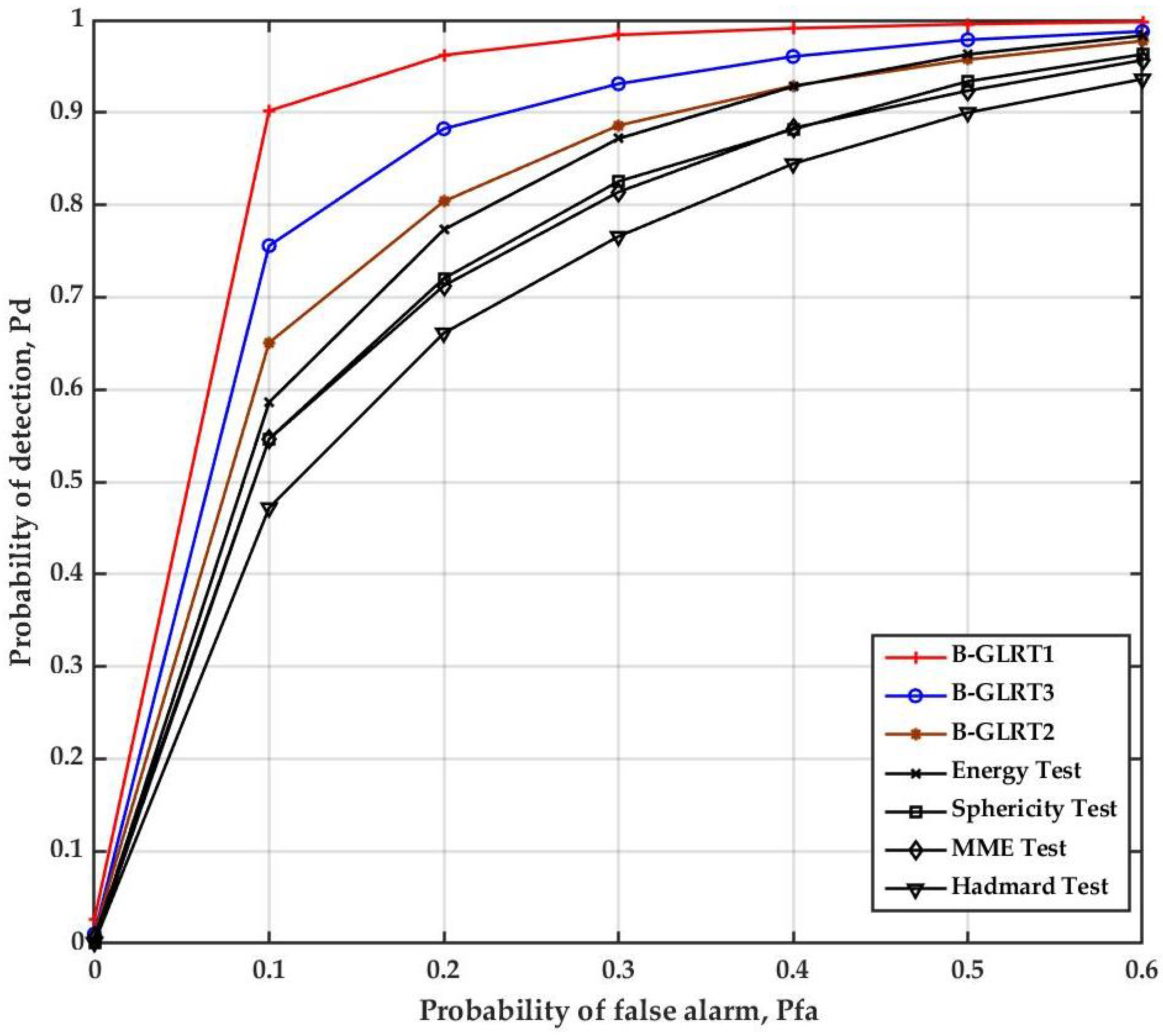
5. Numerical Evaluation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1
- This problem can be solved by using Schur complement as shown in our previous work in [32]:Similarly,
- In sub-optimal method (B-GLRT2), is equal to then problem reduces tosubject to
Appendix A.2
- This problem can be solved according to the solution that is mentioned in Appendix A.1.
- This equation can also be solved using Schur complement; the problem will becomes:
References
- Guo, C.; He, W.; Li, G.Y. Optimal Fairness-Aware Resource Supply and Demand Management for Mobile Edge Computing. IEEE Wirel. Commun. Lett. 2020. [Google Scholar] [CrossRef]
- Mehrabian, A.; Zaimbashi, A. Robust and blind eigenvalue-based multiantenna spectrum sensing under IQ imbalance. IEEE Trans. Wirel. Commun. 2018, 17, 5581–5591. [Google Scholar] [CrossRef]
- Miridakis, N.I.; Tsiftsis, T.A.; Alexandropoulos, G.C. MIMO underlay cognitive radio: Optimized power allocation, effective number of transmit antennas and harvest-transmit tradeoff. IEEE Trans. Green Commun. Netw. 2018, 2, 1101–1114. [Google Scholar] [CrossRef]
- Wang, N.; Han, S.; Lu, Y.; Zhu, J.; Xu, W. Distributed Energy Efficiency Optimization for Multi-User Cognitive Radio Networks Over MIMO Interference Channels: A Non-Cooperative Game Approach. IEEE Access 2020, 8, 26701–26714. [Google Scholar] [CrossRef]
- Shi, Z.; Xie, X.; Lu, H. Deep reinforcement learning based intelligent user selection in massive mimo underlay cognitive radios. IEEE Access 2019, 7, 110884–110894. [Google Scholar] [CrossRef]
- Zhao, X.; Riaz, S.; Geng, S. A reconfigurable MIMO/UWB MIMO antenna for cognitive radio applications. IEEE Access 2019, 7, 46739–46747. [Google Scholar] [CrossRef]
- Rao, P.R.M.; Sangeetha, M. Calculation of Capacity, Spectral Efficiency, Bit Error Rate in Chaotic Cognitive Radio System with Subcarrier Shifting in OFDM-MIMO. In Proceedings of the 2018 International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 3–5 April 2018; pp. 0504–0507. [Google Scholar]
- Haykin, S. Cognitive radar networks. In Proceedings of the 1st IEEE International Workshop on Computational Advances in Multi-Sensor Adaptive Processing, Puerto Vallarta, Mexico, 13–15 December 2005; pp. 1–20. [Google Scholar]
- Chen, A.Z.; Shi, Z.P.; Sun, H.; He, Z.Q.; Bu, F.; Yang, D. A low-complexity spectrum sensing method for noncircular signal in cognitive radio networks with multiple receive antennas. IEEE Commun. Lett. 2019, 23, 1190–1193. [Google Scholar] [CrossRef]
- Badawy, A.; El Shafie, A.; Khattab, T. On the performance of quickest detection spectrum sensing: The case of cumulative sum. IEEE Commun. Lett. 2020, 24, 739–743. [Google Scholar] [CrossRef]
- Hu, L.; Shi, R.; Mao, M.; Chen, Z.; Zhou, H.; Li, W. Optimal energy-efficient transmission for hybrid spectrum sharing in cooperative cognitive radio networks. China Commun. 2019, 16, 150–161. [Google Scholar] [CrossRef]
- Yin, W.; Chen, H. Decision-Driven Time-Adaptive Spectrum Sensing in Cognitive Radio Networks. IEEE Trans. Wirel. Commun. 2020, 19, 2756–2769. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, L.; Liu, M.; Yi, Y.; Yang, Q.; Gong, F. Mimo spectrum sensing for cognitive radio-based internet of things. IEEE Internet Things J. 2020, 7, 8874–8885. [Google Scholar] [CrossRef]
- Li, X.; Zhu, Q.; Wang, X. Privacy-Aware Crowdsourced Spectrum Sensing and Multi-User Sharing Mechanism in Dynamic Spectrum Access Networks. IEEE Access 2019, 7, 32971–32988. [Google Scholar] [CrossRef]
- Cai, P.; Zhang, Y. Intelligent cognitive spectrum collaboration: Convergence of spectrum sensing, spectrum access, and coding technology. Intell. Converg. Netw. 2020, 1, 79–98. [Google Scholar] [CrossRef]
- Xiong, T.; Yao, Y.D.; Ren, Y.; Li, Z. Multiband spectrum sensing in cognitive radio networks with secondary user hardware limitation: Random and adaptive spectrum sensing strategies. IEEE Trans. Wirel. Commun. 2018, 17, 3018–3029. [Google Scholar] [CrossRef]
- Alhamad, R.I. Optimal Power Allocation for Cooperative Spectrum Sensing. In Proceedings of the 2019 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Newark, NJ, USA, 11–14 November 2019; pp. 1–5. [Google Scholar]
- Xing, H.; Zheng, D.; Wang, S. Mobility Improves the Performance of Collaborated Spectrum Sensing. In Proceedings of the 2020 IEEE/CIC International Conference on Communications in China (ICCC), Chongqing, China, 9–11 August 2020; pp. 864–868. [Google Scholar]
- Zhang, X.; Ma, Y.; Gao, Y.; Zhang, W. Autonomous compressive-sensing-augmented spectrum sensing. IEEE Trans. Veh. Technol. 2018, 67, 6970–6980. [Google Scholar] [CrossRef]
- Axell, E.; Leus, G.; Larsson, E.G.; Poor, H.V. Spectrum sensing for cognitive radio: State-of-the-art and recent advances. IEEE Signal Process. Mag. 2012, 29, 101–116. [Google Scholar] [CrossRef]
- Stöckle, C.; Munir, J.; Mezghani, A.; Nossek, J.A. Channel estimation in massive MIMO systems using 1-bit quantization. In Proceedings of the 2016 IEEE 17th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC), Edinburgh, UK, 3–6 July 2016; pp. 1–6. [Google Scholar]
- Kaur, R.; Kumar, D. Multiple-Input Multiple-Output (MIMO) Cognitive Radio User Selection Using Channel State Information at Transmitter (CSIT). In Proceedings of the 2018 International Conference on Inventive Research in Computing Applications (ICIRCA), Coimbatore, India, 11–12 July 2018; pp. 25–30. [Google Scholar]
- Chaudhary, R.K.; Thummaluru, S.R. Reconfigurable MIMO Filtenna for Spectrum Underlay Cognitive Radio. In Proceedings of the 2019 PhotonIcs & Electromagnetics Research Symposium-Spring (PIERS-Spring), Rome, Italy, 17–20 June 2019; pp. 582–586. [Google Scholar]
- Shehata, H.; Khattab, T. Energy detection spectrum sensing in full-duplex cognitive radio: The practical case of rician RSI. IEEE Trans. Commun. 2019, 67, 6544–6555. [Google Scholar] [CrossRef]
- López-Valcarce, R.; Vazquez-Vilar, G.; Sala, J. Multiantenna spectrum sensing for cognitive radio: Overcoming noise uncertainty. In Proceedings of the 2010 2nd International Workshop on Cognitive Information Processing, Elba, Italy, 14–16 June 2010; pp. 310–315. [Google Scholar]
- Yang, X.; Peng, S.; Zhu, P.; Hongyang, C.; Cao, X. Effect of correlations on the performance of GLRT detector in cognitive radios. IEICE Trans. Commun. 2011, 94, 1089–1093. [Google Scholar] [CrossRef]
- Ciuonzo, D.; De Maio, A.; Orlando, D. A unifying framework for adaptive radar detection in homogeneous plus structured interference—Part I: On the maximal invariant statistic. IEEE Trans. Signal Process. 2016, 64, 2894–2906. [Google Scholar] [CrossRef]
- Sedighi, S.; Taherpour, A.; Sala Álvarez, J.; Khattab, T. On the performance of Hadamard ratio detector-based spectrum sensing for cognitive radios. IEEE Trans. Signal Process. 2015, 63, 3809–3824. [Google Scholar] [CrossRef]
- Stoica, P.; Babu, P. On the exponentially embedded family (EEF) rule for model order selection. IEEE Signal Process. Lett. 2012, 19, 551–554. [Google Scholar] [CrossRef]
- Kallummil, S.; Kalyani, S. High SNR consistent linear model order selection and subset selection. IEEE Trans. Signal Process. 2016, 64, 4307–4322. [Google Scholar] [CrossRef]
- Ge, D.; Zeng, X.J. Functional Fuzzy System: A Nonlinear Regression Model and Its Learning Algorithm for Function-on-Function Regression. IEEE Trans. Fuzzy Syst. 2021. [Google Scholar] [CrossRef]
- Sedighi, S.; Taherpour, A.; Monfared, S.S. Bayesian generalised likelihood ratio test-based multiple antenna spectrum sensing for cognitive radios. IET Commun. 2013, 7, 2151–2165. [Google Scholar] [CrossRef]
- Al-Amidie, M.; Al-Asadi, A.; Micheas, A.C.; Islam, N.E. Spectrum sensing based on Bayesian generalised likelihood ratio for cognitive radio systems with multiple antennas. IET Commun. 2018, 13, 305–311. [Google Scholar] [CrossRef]
- Kim, J.; Choi, J.P. Sensing coverage-based cooperative spectrum detection in cognitive radio networks. IEEE Sens. J. 2019, 19, 5325–5332. [Google Scholar] [CrossRef]
- Foschini, G.J.; Gans, M.J. On limits of wireless communications in a fading environment when using multiple antennas. Wirel. Pers. Commun. 1998, 6, 311–335. [Google Scholar] [CrossRef]
- Vishwanath, S.; Jindal, N.; Goldsmith, A. Duality, achievable rates, and sum-rate capacity of Gaussian MIMO broadcast channels. IEEE Trans. Inf. Theory 2003, 49, 2658–2668. [Google Scholar] [CrossRef]
- Gazestani, A.H.; Ghorashi, S.A. Distributed diffusion-based spectrum sensing for cognitive radio sensor networks considering link failure. IEEE Sen. J. 2018, 18, 8617–8625. [Google Scholar]
- Jin, Z.; Yao, K.; Lee, B.; Cho, J.; Zhang, L. Channel status learning for cooperative spectrum sensing in energy-restricted cognitive radio networks. IEEE Access 2019, 7, 64946–64954. [Google Scholar] [CrossRef]
- Vaze, C.S.; Varanasi, M.K. On the achievable rate of the fading dirty paper channel with imperfect CSIT. In Proceedings of the 2009 43rd Annual Conference on Information Sciences and Systems, Baltimore, MD, USA, 18–20 March 2009; pp. 346–351. [Google Scholar]
- Vaze, C.S.; Varanasi, M.K. Dirty paper coding for fading channels with partial transmitter side information. In Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 26–29 October 2008; pp. 341–345. [Google Scholar]
- Vaze, C.S.; Varanasi, M.K. Dirty paper coding for the MIMO cognitive radio channel with imperfect CSIT. In Proceedings of the 2009 IEEE International Symposium on Information Theory, Seoul, Korea, 28 June–3 July 2009; pp. 2532–2536. [Google Scholar]
- Tran, L.N.; Juntti, M.; Bengtsson, M.; Ottersten, B. Weighted sum rate maximization for MIMO broadcast channels using dirty paper coding and zero-forcing methods. IEEE Trans. Commun. 2013, 61, 2362–2373. [Google Scholar] [CrossRef]
- Na, W.; Yoon, J.; Cho, S.; Griffith, D.; Golmie, N. Centralized cooperative directional spectrum sensing for cognitive radio networks. IEEE Trans. Mob. Comput. 2017, 17, 1260–1274. [Google Scholar] [CrossRef]
- Patel, A.; Tripathi, B.; Jagannatham, A.K. Robust Estimator-Correlator for Spectrum Sensing in MIMO CR Networks with CSI Uncertainty. IEEE Wirel. Commun. Lett. 2014, 3, 253–256. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Practical Algorithm Development; Pearson Education: London, UK, 2013; Volume 3. [Google Scholar]
- Enderlein, G.; Wilks, S.S. Mathematical Statistics. Biom. Z. 1964, 6, 214–215. [Google Scholar] [CrossRef]
- Moustakides, G.V. Finite sample size optimality of GLR tests. arXiv 2009, arXiv:0903.3795. [Google Scholar]
- Taherpour, A.; Nasiri-Kenari, M.; Gazor, S. Multiple antenna spectrum sensing in cognitive radios. IEEE Trans. Wirel. Commun. 2010, 9, 814–823. [Google Scholar] [CrossRef]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Grant, M.; Boyd, S.; Ye, Y. CVX: Matlab Software for Disciplined Convex Programming. 2008. Available online: http://stanford.edu/boyd/cvx (accessed on 12 August 2020).
- Schad, A.; Pesavento, M. Max-min fair transmit beamforming for multi-group multicasting. In Proceedings of the 2012 International ITG Workshop on Smart Antennas (WSA), Dresden, Germany, 7–8 March 2012; pp. 115–118. [Google Scholar]
- Liu, L.; Fan, L. The complexity analysis of an efficient interior-point algorithm for linear optimization. In Proceedings of the 2010 Third International Joint Conference on Computational Science and Optimization, Huangshan, China, 28–31 May 2010; Volume 2, pp. 21–24. [Google Scholar]
- Al-Asadi, A.; Al-Amidie, M.; Micheas, A.C.; McGarvey, R.G.; Islam, N.E. Worst case fair beamforming for multiple multicast groups in multicell networks. IET Commun. 2018, 13, 664–671. [Google Scholar] [CrossRef]
- Al-Ali, M.; Ho, K. Transmit Precoding in Underlay MIMO Cognitive Radio with Unavailable or Imperfect Knowledge of Primary Interference Channel. IEEE Trans. Wirel. Commun. 2016. [Google Scholar] [CrossRef]
- Sharma, S.K.; Chatzinotas, S.; Ottersten, B. SNR estimation for multi-dimensional cognitive receiver under correlated channel/noise. IEEE Trans. Wirel. Commun. 2013, 12, 6392–6405. [Google Scholar] [CrossRef]
- Zhou, F.; Beaulieu, N.C. An improved and more accurate expression for a PDF related to eigenvalue-based spectrum sensing. IEEE Syst. J. 2018, 13, 1320–1323. [Google Scholar] [CrossRef]
- Ramírez, D.; Vazquez-Vilar, G.; López-Valcarce, R.; Vía, J.; Santamaría, I. Detection of rank-P signals in cognitive radio networks with uncalibrated multiple antennas. IEEE Trans. Signal Process. 2011, 59, 3764–3774. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Amidie, M.; Al-Asadi, A.; Humaidi, A.J.; Al-Dujaili, A.; Alzubaidi, L.; Farhan, L.; Fadhel, M.A.; McGarvey, R.G.; Islam, N.E. Robust Spectrum Sensing Detector Based on MIMO Cognitive Radios with Non-Perfect Channel Gain. Electronics 2021, 10, 529. https://doi.org/10.3390/electronics10050529
Al-Amidie M, Al-Asadi A, Humaidi AJ, Al-Dujaili A, Alzubaidi L, Farhan L, Fadhel MA, McGarvey RG, Islam NE. Robust Spectrum Sensing Detector Based on MIMO Cognitive Radios with Non-Perfect Channel Gain. Electronics. 2021; 10(5):529. https://doi.org/10.3390/electronics10050529
Chicago/Turabian StyleAl-Amidie, Muthana, Ahmed Al-Asadi, Amjad J. Humaidi, Ayad Al-Dujaili, Laith Alzubaidi, Laith Farhan, Mohammed A. Fadhel, Ronald G. McGarvey, and Naz E. Islam. 2021. "Robust Spectrum Sensing Detector Based on MIMO Cognitive Radios with Non-Perfect Channel Gain" Electronics 10, no. 5: 529. https://doi.org/10.3390/electronics10050529
APA StyleAl-Amidie, M., Al-Asadi, A., Humaidi, A. J., Al-Dujaili, A., Alzubaidi, L., Farhan, L., Fadhel, M. A., McGarvey, R. G., & Islam, N. E. (2021). Robust Spectrum Sensing Detector Based on MIMO Cognitive Radios with Non-Perfect Channel Gain. Electronics, 10(5), 529. https://doi.org/10.3390/electronics10050529










