Cylindrical Waveguide on Ferrite Substrate Controlled by Externally Applied Magnetic Field

Abstract

This paper presents an extension of the formulation of wave propagation in transverse electric (TE) and transverse magnetic (TM) modes for the case of metallic cylindrical waveguides filled with longitudinally magnetized ferrite. The higher order modes were exploited. We externally controlled the cut-off frequency through the application of DC magnetic fields. The numerical results of dispersion diagrams for TE and TM modes were obtained and analyzed. We analyzed a waveguide antenna filled with partially magnetized ferrite using the mode matching (MM) technique based on the TE and TM modes. By using modal analysis, our approach considerably reduced the computation time compared to HFSS. Ferrites are important for various industrial applications, such as circulators, isolators, antennas and filters.

1. Introduction

Recently, many researchers have been interested in guiding devices that use ferrite in some frequency range for their potential applications in microwave circuits. However, there is a lack of research into the dispersion of ferrite cylindrical waveguides. Among the essential research pertaining to this topic, we can cite the work in [1,2,3,4,5,6,7,8,9,10,11,12]. Guided modes in waveguides consisting of anisotropic media [4,13,14,15] have been studied in the literature.

In this paper, we present an extension of the transverse electric (TE) and transverse magnetic (TM) modes to cylindrical waveguides filled with lossless longitudinally magnetized ferrite (LMF) which takes account of the spatial distribution of the permeability of the medium that is applied to the transverse fields. We exploited the propagation modes in this structure. We show how the dispersion diagrams were obtained and we discuss the effects of anisotropic parameters on dispersion characteristics and cutoff frequencies. We also show how the numerical results for the TE and TM modes were obtained. These modes were used in the numerical method applied to the design of our antenna. Our simulations of a cylindrical metallic waveguide antenna filled with partially magnetized ferrite using mode matching (MM) [16,17] were in good agreement with those obtained with HFSS. However, our method was noticeably faster.

Our objective was to analyze the physical discontinuities in a cylindrical metallic waveguide filled with partially magnetized ferrite using the mode matching technique based on the TE and TM modes. An antenna formed by this type of waveguide is presented and analyzed. The magnetization of the ferrite using an external control can be achieved by enveloping the waveguide with Helmholtz coils connected to a variable voltage generator. Each voltage corresponds to a constant magnetic field applied to the ferrite longitudinally which creates the magnetization of this medium. As a result, the magnetic properties of the ferrite change. The permeability of the ferrite becomes tensorial. Our antenna was tuned to the desired operating frequency for the ferrite magnetization circuit by adjusting the voltage applied externally, which in turn affected the variation of the static magnetic field applied to the ferrite. The operating frequency range could vary. Our interest in this study was in the tuning of the operating frequency of the antenna.

This formulation is a useful tool for microwave engineers. This type of material is extensively applied by information technology industries, particularly in microwaves and RF devices, such as patch antennas, waveguide antennas, resonators, circulators, insulators, phase converters and filters.

2. Formulation

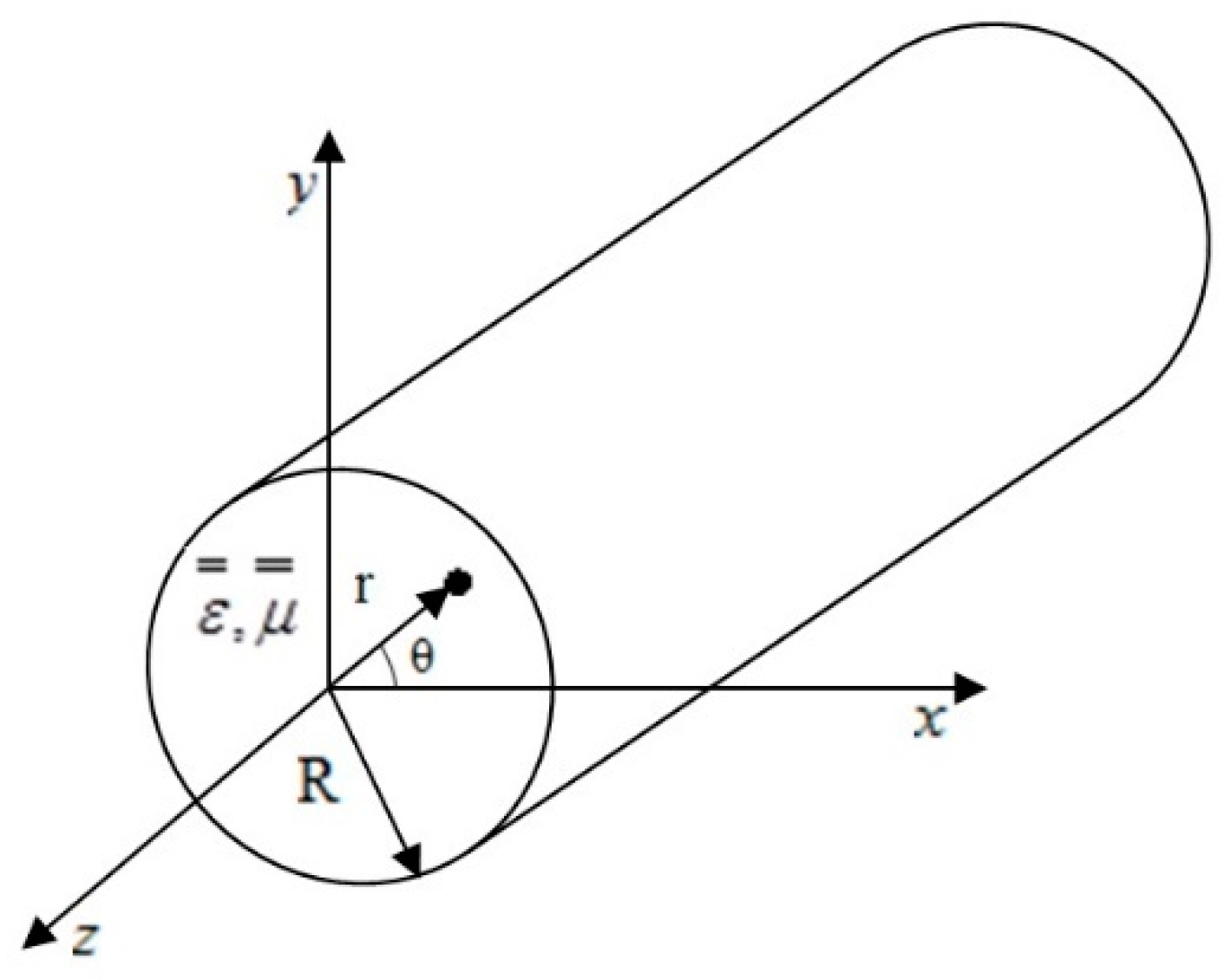
For lossless longitudinally magnetized ferrite, as is shown in Figure 1, the Maxwell equations can be written as:

$$\overrightarrow{\nabla }\times \overrightarrow{E}=-j\omega {\overline{\mu }}_f \overrightarrow{H}$$

(1)

$$\overrightarrow{\nabla }\times \overrightarrow{H}=j\omega {\epsilon }_f \overrightarrow{E}$$

(2)

At the microwave’s frequencies, the ferrites are characterized by a tensor permeability that represents their induced anisotropy under a magnetic field. The permeability of the LMF is tensorial and can be written in a system of cylindrical coordinates, as is given by D. Polder [8], with

$${\overline{\mu }}_f= {\mu }_0 {\overline{\mu }}_{rf}={\mu }_0\left(\begin{array}{ccc}\mu & -j\kappa & 0\\ j\kappa & \mu & 0\\ 0& 0& {\mu }_{rz}\end{array}\right)={\mu }_0\left(\begin{array}{cc}{\mu }_{rT}& 0\\ 0& {\mu }_{rz}\end{array}\right)$$

(3)

where $\mu$, $\kappa$, ${\mu }_{rz}$ and ${\epsilon }_f$ are real quantities.

For a partial magnetization of ferrite, J. J. Green et al. [5] and E. Schloemann [9] give the empirical expressions of $\mu$, $\kappa$, ${\mu }_{rz}$ [11]:

$$\mu ={\mu }_d+\left(1-{\mu }_d\right){\left(\frac{4\pi M}{4\pi M_S}\right)}^{3/2}$$

(4)

$$\kappa =\frac{\gamma \left(4\pi M\right)}{\omega }$$

(5)

$${\mu }_{rz}={\mu }_d{}^{\left(1-{\left(\frac{4\pi M}{4\pi M_S}\right)}^{5/2}\right)}$$

(6)

where

$${\mu }_d=\frac{1}{3}\left\{1+2\sqrt{1-{\left(\frac{\gamma \left(4\pi M_S\right)}{\omega }\right)}^2}\right\}$$

(7)

where $\omega$ is the work pulsation, $\gamma$ is the gyromagnetic constant, $4\pi M_S$ is the magnetization at saturation and $4\pi M$ is the magnetization which is lower than saturation. When the magnetization is equal to zero, $\kappa =0$ and $\mu ={\mu }_{rz}=1$. The ferrite then becomes an isotropic dielectric.

Let us consider a cylindrical waveguide of radius R completely filled with LMF without losses, as represented in the Figure 1. The walls of the guide are perfectly electric conductive. In this study, we rigorously examined the TE and TM modes in a metallic cylindrical waveguide completely full of longitudinally magnetized ferrite.

2.1. Transverse Electric Modes

By considering the propagation in the Oz direction and manipulating Equations (1) and (2), we obtain the expressions of the transverse electromagnetic fields according to the longitudinal fields in the TE modes.

$$E_r^{\left(h\right)}=\frac{-1}{K_c^2}\left(A_1\frac{\partial H_z}{\partial r}+j{A}_2\frac{1}{r}\frac{\partial H_z}{\partial \theta }\right)$$

(8)

$$E_{\theta }^{\left(h\right)}=\frac{1}{K_c^2}\left(j{A}_2\frac{\partial H_z}{\partial r}-A_1\frac{1}{r}\frac{\partial H_z}{\partial \theta }\right)$$

(9)

$$H_r^{\left(h\right)}=\frac{1}{K_c^2}\left(-j{k}_z{K}_{c\mu }^2\frac{\partial H_z}{\partial r}+F{k}_z\frac{1}{r}\frac{\partial E_z}{\partial \theta }\right)$$

(10)

$$H_{\theta }^{\left(h\right)}=\frac{-1}{K_c^2}\left(F{k}_z\frac{\partial H_z}{\partial r}+j{k}_z{K}_{c\mu }^2\frac{1}{r}\frac{\partial H_z}{\partial \theta }\right)$$

(11)

with

$$K_{c\mu }^2=k_0^2{\epsilon }_{rf}\mu -k_z^2$$

(12)

$$F=k_0^2{\epsilon }_{rf}\kappa$$

(13)

$$K_c^2=k_{c\mu }^4-F^2$$

(14)

$$k_0^2={\omega }^2{\epsilon }_0{\mu }_0$$

(15)

$$A_1=\frac{F{k}_z^2}{\omega {\epsilon }_0{\epsilon }_{rf}}$$

(16)

$$A_2=\frac{k_{c\mu }^4-F^2+k_z^2{k}_{c\mu }^2}{\omega {\epsilon }_0{\epsilon }_{rf}}$$

(17)

From Equation (1), the differential equation for z-component can be obtained as follows

$$\frac{{\partial }^2{H}_z}{\partial r^2}+\frac{1}{r}\frac{\partial H_z}{\partial r}+\frac{1}{r^2}\frac{{\partial }^2{H}_z}{\partial {\theta }^2}+{\left(K_{cf}^{\left(h\right)}\right)}^2{H}_z=0$$

(18)

with

$${\left(K_{cf}^{\left(h\right)}\right)}^2=\frac{\omega {\mu }_0{\mu }_{rz}{K}_c^2}{A_2}$$

(19)

The resolution of the differential Equation (18), due to the separation of the two variables, requires the expression of $H_z$ for the $T{E}_{mn}$ modes in the metallic cylindrical waveguide fully filled with LMF. The expression of the longitudinal magnetic field can be written as follows

$$H_z^{\left(h\right)}=H_{0}sin\left(n\theta \right)J_n\left(K_{cf}^{\left(h\right)}r\right)e^{j\left(\omega t-k_z^{\left(h\right)}z\right)}$$

(20)

$J_n$ is the Bessel function of the first kind of order n (n = 0, 1, 2, 3, …).

Equations (8)–(11) become

$$E_r^{\left(h\right)}=\frac{H_0}{K_c^2}\{-A_1{K}_{cf}^{\left(h\right)}sin\left(n\theta \right)J_n^{\prime }\left(K_{cf}^{\left(h\right)}r\right)-j{A}_2\frac{n}{r}cos\left(n\theta \right)J_n\left(K_{cf}^{\left(h\right)}r\right)\}$$

(21)

$$E_{\theta }^{\left(h\right)}=\frac{H_0}{K_c^2}\{j{A}_2{K}_{cf}^{\left(h\right)}sin\left(n\theta \right)J_n^{\prime }\left(K_{cf}^{\left(h\right)}r\right)-A_1\frac{n}{r}cos\left(n\theta \right)J_n\left(K_{cf}^{\left(h\right)}r\right)\}$$

(22)

$$H_r^{\left(h\right)}=\frac{H_0}{K_c^2}\{-j{k}_z^{\left(h\right)}{K}_{c\mu }^2{K}_{cf}^{\left(h\right)}sin\left(n\theta \right)J_n^{\prime }\left(K_{cf}^{\left(h\right)}r\right)+F{k}_z^{\left(h\right)}\frac{n}{r}cos\left(n\theta \right)J_n\left(K_{cf}^{\left(h\right)}r\right)\}$$

(23)

$$H_{\theta }^{\left(h\right)}=\frac{H_0}{K_c^2}\{-F{k}_z^{\left(h\right)}{K}_{cf}^{\left(h\right)}sin\left(n\theta \right)J_n^{\prime }\left(K_{cf}^{\left(h\right)}r\right)-j{k}_z^{\left(h\right)}{K}_{c\mu }^2\frac{n}{r}cos\left(n\theta \right)J_n\left(K_{cf}^{\left(h\right)}r\right)\}$$

(24)

$J_n^{\prime }$ is the derivative of the Bessel function of the first kind of order n (n = 0, 1, 2, 3, …).

The boundary conditions give

$$J_n^{\prime }\left(u_{nm}^{\prime }\right)=0$$

(25)

with

$$u_{nm}^{\prime }=K_{cf}^{\left(h\right)}R$$

(26)

In Equation (26), $u_{nm}^{\prime }$ represents the mth zero (m = 1, 2, 3, …) of the derivative of the Bessel function $J_n^{\prime }$ of the first kind of order n. The determination of constant $H_0$ is done by normalizing the power $P^{TE}$ that crosses the cross-section of the guide, which is in our case a disc of radius R.

$$P^{TE}={{\displaystyle \int }}_0^R{{\displaystyle \int }}_0^{2\pi }\left(E_r^{\left(h\right)}{H}_{\theta }^{*\left(h\right)}-E_{\theta }^{\left(h\right)}{H}_r^{*\left(h\right)}\right)rdrd\theta =1$$

(27)

* indicates the complex conjugate.

Equation (27) gives

$$H_0=\frac{K_c^2{K}_{cf}}{\sqrt{k_z\left(A_2{K}_{c\mu }^2+A_{1}F\right)}}{N}_{nm}^{\left(h\right)}$$

(28)

with

$$N_{nm}^{\left(h\right)}=\frac{1}{\sqrt{\frac{{\sigma }_n}{2}}{\left({\left(u_{nm}^{\prime }\right)}^2-n^2\right)}^{1/2}{J}_n\left(u_{nm}^{\prime }\right)}$$

(29)

$${\sigma }_n=\{\begin{array}{cc}2\pi & if n=0\\ \pi & if n>0\end{array}$$

(30)

From Equation (26), we obtain the propagation equation

$$\begin{gathered} k_z^4+\left(-2{\omega }^2{\epsilon }_0{\mu }_0{\epsilon }_{rf}\mu +\frac{\mu }{{\mu }_{rz}}{\left(\frac{u_{nm}^{\prime }}{R}\right)}^2\right)k_z^2 \\ +{\omega }^2{\epsilon }_0{\mu }_0{\epsilon }_{rf}\left({\mu }^2-{\kappa }^2\right)\left[{\omega }^2{\epsilon }_0{\mu }_0{\epsilon }_{rf}-\frac{1}{{\mu }_{rz}}{\left(\frac{u_{nm}^{\prime }}{R}\right)}^2\right]=0 \end{gathered}$$

(31)

To find cut-off frequencies, the propagation constant should be equated to zero in Equation (31). The cutoff frequency in the TE mode is written

$$f_{c.nm}^{\left(TE\right)}=\frac{c}{2\pi }\frac{1}{\sqrt{{\epsilon }_{rf}{\mu }_{rz}}}\left(\frac{u_{nm}^{\prime }}{R}\right)$$

(32)

If the magnetization 4πM decreases, ${\mu }_{rz}$ increases. Consequently, the cutoff frequency $f_{c.nm}^{\left(TE\right)}$ decreases. We can externally control the cut-off frequency through the application of DC magnetic fields. The magnetization of the ferrite using an external control can be achieved by enveloping the waveguide with Helmholtz coils connected to a variable voltage generator.

2.2. Transverse Magnetic (TM) Modes

By manipulating Equations (1) and (2), we can obtain the expressions of the transverse electromagnetic fields according to the longitudinal fields in the TM modes.

$$E_r^{\left(e\right)}=\frac{k_z}{K_c^2}\left(-j{K}_{c\mu }^2\frac{\partial E_z}{\partial r}+F\frac{1}{r}\frac{\partial E_z}{\partial \theta }\right)$$

(33)

$$E_{\theta }^{\left(e\right)}=\frac{-k_z}{K_c^2}\left(F\frac{\partial E_z}{\partial r}+j{K}_{c\mu }^2\frac{1}{r}\frac{\partial E_z}{\partial \theta }\right)$$

(34)

$$H_r^{\left(e\right)}=\frac{\omega {\epsilon }_0{\epsilon }_{rf}}{K_c^2}\left(F\frac{\partial E_z}{\partial r}+j{K}_{c\mu }^2\frac{1}{r}\frac{\partial E_z}{\partial \theta }\right)$$

(35)

$$H_{\theta }^{\left(e\right)}=\frac{\omega {\epsilon }_0{\epsilon }_{rf}}{K_c^2}\left(-j{K}_{c\mu }^2\frac{\partial E_z}{\partial r}+F\frac{1}{r}\frac{\partial E_z}{\partial \theta }\right)$$

(36)

From Equation (1), the differential equation for the z component can be obtained as follows

$$\frac{{\partial }^2{E}_z}{\partial r^2}+\frac{1}{r}\frac{\partial E_z}{\partial r}+\frac{1}{r^2}\frac{{\partial }^2{E}_z}{\partial {\theta }^2}+{\left(K_{cf}^{\left(e\right)}\right)}^2{E}_z=0$$

(37)

with

$$K_{cf}^{\left(e\right)}=\frac{K_c}{K_{c\mu }}$$

(38)

The resolution of the differential Equation (37), due to the separation of the two variables, requires the expression of $E_z$ for the $T{M}_{nm}$ modes in the metallic cylindrical waveguide fully filled with LMF. The expression of the longitudinal electric field can be written as follows

$$E_z^{\left(e\right)}=E_{0}cos\left(n\theta \right)J_n\left(K_{cf}^{\left(e\right)}r\right)e^{j\left(\omega t-k_z^{\left(e\right)}z\right)}$$

(39)

Equations (33)–(36) become

$$E_r^{\left(e\right)}=\frac{-E_0{k}_z}{K_c^2}\{j{K}_{c\mu }^2{K}_{cf}^{\left(e\right)}cos\left(n\theta \right)J_n^{\prime }\left(K_{cf}^{\left(e\right)}r\right)+F\frac{n}{r}sin\left(n\theta \right)J_n\left(K_{cf}^{\left(e\right)}r\right)\}$$

(40)

$$E_{\theta }^{\left(e\right)}=\frac{E_0{k}_z}{K_c^2}\{-F{K}_{cf}^{\left(e\right)}cos\left(n\theta \right)J_n^{\prime }\left(K_{cf}^{\left(e\right)}r\right)+j{K}_{c\mu }^{\left(2\right)}\frac{n}{r}sin\left(n\theta \right)J_n\left(K_{cf}^{\left(e\right)}r\right)\}$$

(41)

$$H_r^{\left(e\right)}=\frac{\omega {\epsilon }_0{\epsilon }_{rf}{E}_0}{K_c^2}\{F{K}_{cf}^{\left(e\right)}cos\left(n\theta \right)J_n^{\prime }\left(K_{cf}^{\left(e\right)}r\right)-j{K}_{c\mu }^2\frac{n}{r}sin\left(n\theta \right)J_n\left(K_{cf}^{\left(e\right)}r\right)\}$$

(42)

$$H_{\theta }^{\left(e\right)}=\frac{-\omega {\epsilon }_0{\epsilon }_{rf}{E}_0}{K_c^2}\{j{K}_{c\mu }^2{K}_{cf}^{\left(e\right)}cos\left(n\theta \right)J_n^{\prime }\left(K_{cf}^{\left(e\right)}r\right)+F\frac{n}{r}sin\left(n\theta \right)J_n\left(K_{cf}^{\left(e\right)}r\right)\}$$

(43)

The boundary conditions give the following equation

$$J_n^{}\left(u_{nm}\right)=0$$

(44)

with

$$u_{nm}=K_{cf}^{(e)}.R$$

(45)

In Equation (45), $u_{nm}^{}$ represents the mth zero (m = 1, 2, 3, …) of the Bessel function $J_n^{}$ of the first kind of order n. The determination of constant $E_0$ is done by normalizing the power $P^{TM}$ that crosses the cross-section of the guide, which is in our case a disc of radius R.

$$P^{TM}={\displaystyle \underset{0}{\overset{R}{\int }}{\displaystyle \underset{0}{\overset{2\pi }{\int }}\left(E_r^{(e)}{H}_{\theta }^{*(e)}-E_{\theta }^{(e)}{H}_r^{*(e)}\right)rdrd\theta }}=1$$

(46)

Equation (46) gives

$$E_0=\frac{1}{\sqrt{\omega {\epsilon }_0{\epsilon }_{rf}{k}_z}}\frac{K_c^2}{\sqrt{K_{c\mu }^4+F^2}}{N}_{nm}^{(e)}$$

(47)

with

$$N_{nm}^{(e)}=\frac{1}{u_{nm}.J_n^{\prime }\left(u_{nm}\right).\sqrt{\frac{{\sigma }_n}{2}}}$$

(48)

Finally, the propagation constant in the TM mode is given by

$$\begin{array}{l}{k}_z^4+\left(-2{\omega }^2{\epsilon }_0^{}{\mu }_0{\epsilon }_{rf}\mu +{\left(\frac{u_{nm}^{}}{R}\right)}^2\right)k_z^2{\cos }^{-1}\theta \\ +{\omega }^2{\epsilon }_0^{}{\mu }_0{\epsilon }_{rf}\left[{\omega }^2{\epsilon }_0^{}{\mu }_0{\epsilon }_{rf}\left({\mu }^2-{\kappa }^2\right)-\mu {\left(\frac{u_{nm}^{}}{R}\right)}^2\right]=0.\end{array}$$

(49)

Obviously, the cutoff frequency is written

$$f_{c.nm}^{(TM)}=\frac{c}{2\pi }\frac{1}{\sqrt{{\mu }_{reff}{\epsilon }_{rf}}}.\left(\frac{u_{nm}^{}}{R}\right)$$

(50)

with

$${\mu }_{reff}=\frac{{\mu }^2-{\kappa }^2}{\mu }$$

(51)

${\mu }_{reff}$ is the effective permeability.

If the magnetization $4\pi M$ decreases, ${\mu }_{reff}$ increases. Consequently, the cutoff frequency $f_{c.nm}^{(TM)}$ in the TE modes decreases. We can externally control the cut-off frequency through the application of DC magnetic fields.

3. Analysis of Uni-Axial Discontinuities in the Cylindrical Waveguides

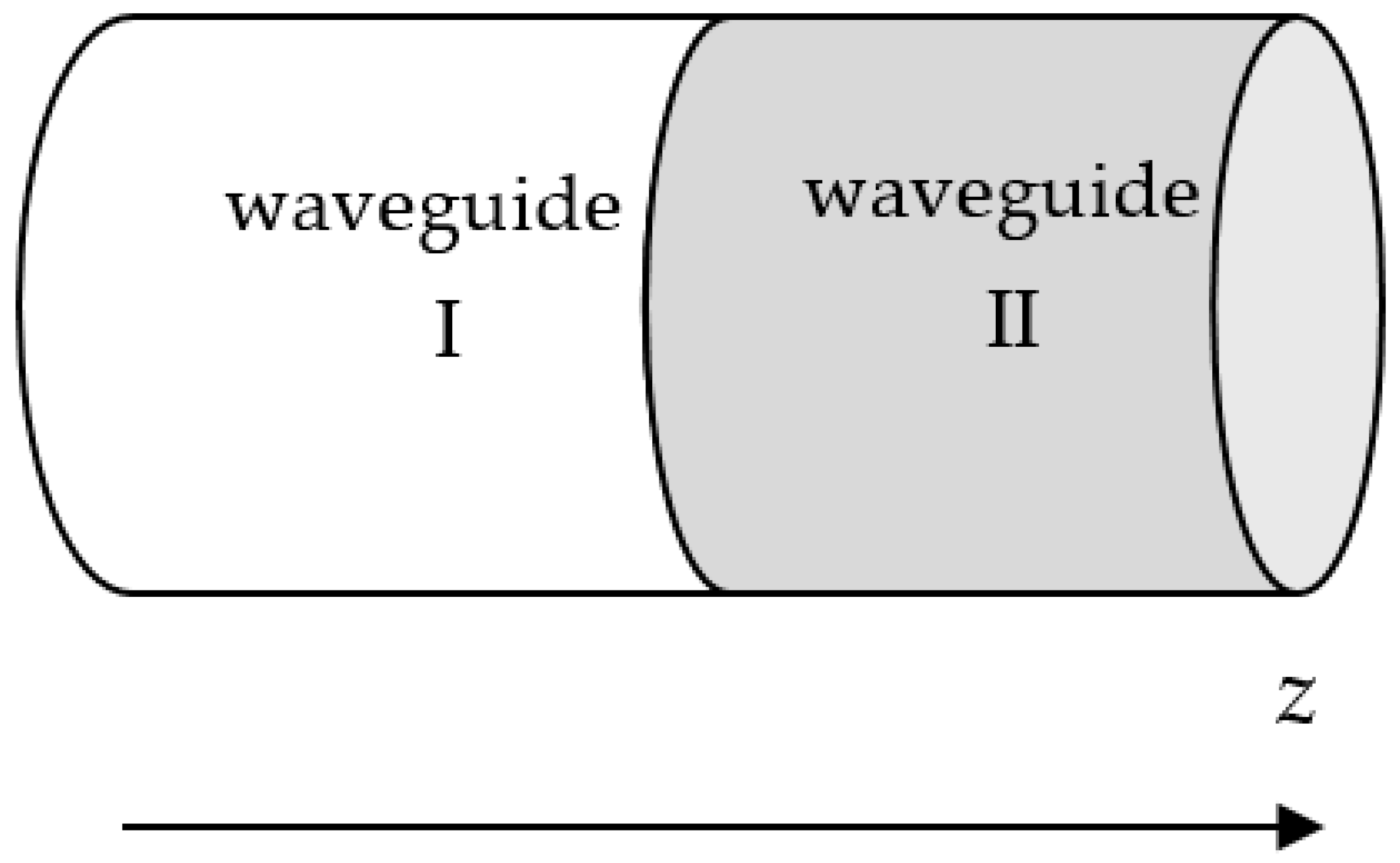
In this section, we describe how the use of MM can be extended to characterize uni-axial discontinuities between metallic cylindrical waveguides filled with the studied medium (LMF). The discontinuities were considered without losses. This method was based on the modal development of the transverse electromagnetic fields.

Figure 2 shows a junction between two cylindrical waveguides filled with two different media with the same cross-sections, where $a^i$ and $b^i$ are the incident and the reflected waves, respectively.

The transverse electric and magnetic fields ($E_T,H_T$) in the waveguides can be written in the modal bases as follows [16,17].

$$E_T={\displaystyle \sum _{m=1}^{\infty }{A}_m^i\left(a_m^i+b_m^i\right)e_m^i}$$

(52)

$$H_T={\displaystyle \sum _{m=1}^{\infty }{B}_m^i\left(a_m^i-b_m^i\right)h_m^i}$$

(53)

where $E_T$ and $H_T$ are the transverse electric and magnetic fields (the sub-index $T$ refers to the components in the transverse plane) and $A_m^i$ and $B_m^i$ are complex coefficients which are determined by normalizing the power flow down the cylindrical guides ($i=I,II$ and m is the index of the mode). $e_m^i$ and $h_m^i$ represent the mth electric and magnetic modal eigenfunction in the guide i, respectively.

At the junction, the continuity of the fields makes it possible to write the following equations:

$$E_T^I=E_T^{II}$$

(54)

$$H_T^I=H_T^{II}$$

(55)

By inserting Equations (52) and (53) into Equations (54) and (55), we obtain:

$${\displaystyle \sum _{m=1}^{N_1}{A}_m^I\left(a_m^I+b_m^I\right)e_m^I}={\displaystyle \sum _{p=1}^{N_2}{A}_p^{II}\left(a_p^{II}+b_p^{II}\right)e_p^{II}}$$

(56)

$${\displaystyle \sum _{m=1}^{N_1}{B}_m^I\left(a_m^I-b_m^I\right)h_m^I}={\displaystyle \sum _{p=1}^{N_2}{B}_p^{II}\left(-a_p^{II}+b_p^{II}\right)h_p^{II}}$$

(57)

N₁ and N₂ are the numbers of considered modes in guides 1 and 2, respectively. By applying Galerkin’s method, Equations (56) and (57) lead to the following systems:

$${\displaystyle \sum _{m=1}^{N_1}{A}_m^I\left(a_m^I+b_m^I\right)\langle e_m^I|e_p^{II}\rangle }=A_p^{II}\left(a_p^{II}+b_p^{II}\right)$$

(58)

$$B_m^I\left(a_m^I-b_m^I\right)={\displaystyle \sum _{p=1}^{N_2}{B}_p^{II}\left(-a_p^{II}+b_p^{II}\right)\langle h_p^{II}|h_m^I\rangle }$$

(59)

The inner product can be defined as:

$$\langle e_m^{}|e_p^{}\rangle ={\displaystyle \underset{S}{\int }{e}_m^{*}{e}_p^{} dS}$$

(60)

Equations (58) and (59) give:

$$-a_p^{II}+{\displaystyle \sum _{m=1}^{N_1}\frac{A_m^I}{A_p^{II}}{a}_m^I\langle e_m^I|e_p^{II}\rangle }=b_p^{II}-{\displaystyle \sum _{m=1}^{N_1}\frac{A_m^I}{A_p^{II}}{b}_m^I\langle e_m^I|e_p^{II}\rangle }$$

(61)

$$a_m^I+{\displaystyle \sum _{p=1}^{N_2}\frac{B_p^{II}}{B_m^I}{a}_p^{II}\langle h_p^{II}|h_m^I\rangle }=b_m^I+{\displaystyle \sum _{p=1}^{N_2}\frac{B_p^{II}}{B_m^I}{b}_p^{II}\langle h_p^{II}|h_m^I\rangle }$$

(62)

which can be written in matrix form:

$$\left[\begin{array}{cc}U& M_1\\ M_2& -U\end{array}\right]\left[\begin{array}{l}{a}_1^I\\ .\\ a_{N_1}^I\\ a_1^{II}\\ .\\ a_{N_2}^{II}\end{array}\right]=\left[\begin{array}{cc}U& M_1\\ -M_2& U\end{array}\right]\left[\begin{array}{l}{b}_1^I\\ .\\ b_{N_1}^I\\ b_1^{II}\\ .\\ b_{N_2}^{II}\end{array}\right]$$

(63)

where U is the identity matrix. $M_1$ and $M_2$ (of dimensions ($N_1\times N_2$) and ($N_2\times N_1$) respectively) are matrixes of the following general terms:

$$M_{1ij}=\frac{B_j^{II}}{B_i^I}\langle h_j^{II}|h_i^I\rangle$$

(64)

$$M_{2ij}=\frac{A_i^I}{A_j^{II}}\langle e_i^I|e_j^{II}\rangle$$

(65)

The scattering matrix of the discontinuity is:

$$S={\left[\begin{array}{cc}U& M_1\\ -M_2& U\end{array}\right]}^{-1}\left[\begin{array}{cc}U& M_1\\ M_2& -U\end{array}\right]$$

(66)

of dimensions $\left(\left(N_1+N_2\right)\times \left(N_1+N_2\right)\right)$.

In the numerical calculations we have to invert a complex matrix of dimensions equal to the sum of the modes taken into account on each side of the discontinuity.

For a structure with multiple uni-axial discontinuities in cascade, the total matrix can be obtained by separating the chaining of S matrixes of discontinuities with waveguides of lengths equal to the distances between the discontinuities.

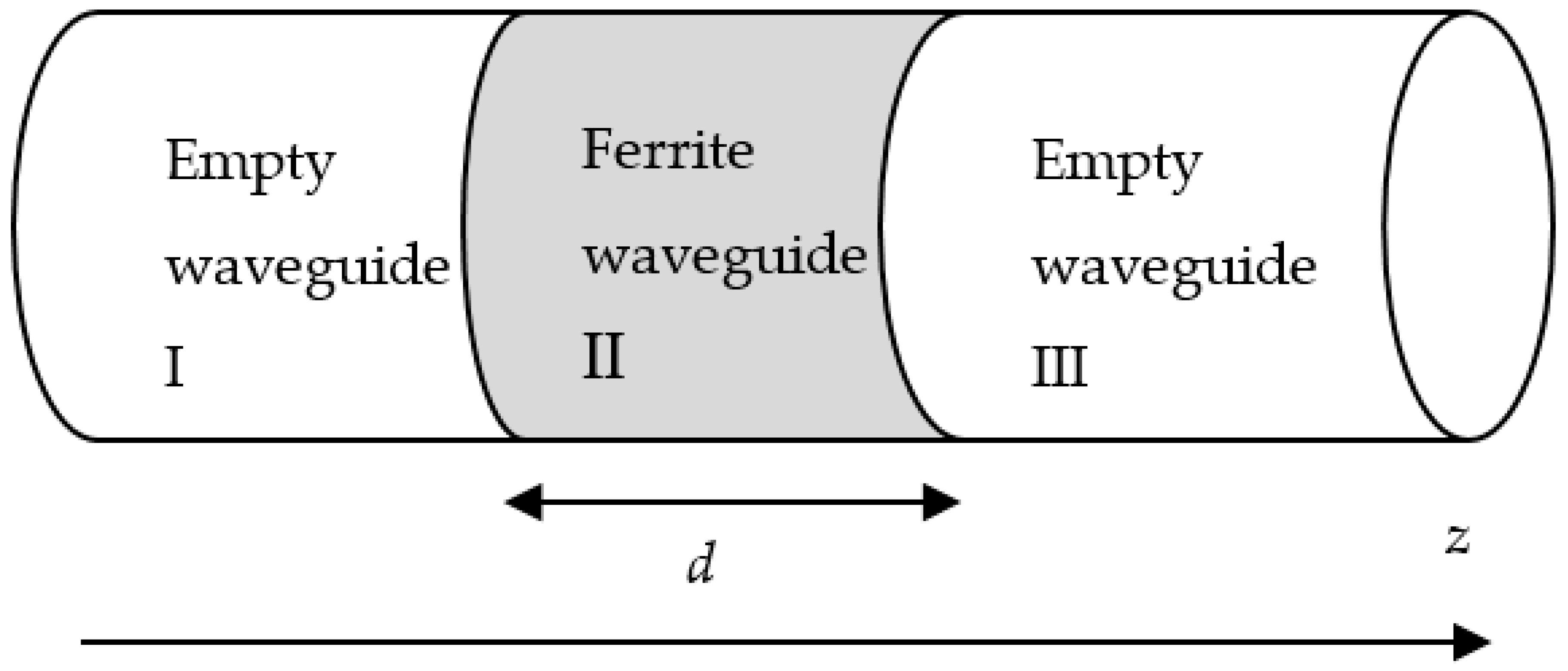
Figure 3 represents a double discontinuity. From the incident and reflected waves, we can write the following equations

$$\left(\begin{array}{l}\left[b_1^I\right]\\ \left[b_2^I\right]\end{array}\right)=S^I\left(\begin{array}{l}\left[a_1^I\right]\\ \left[a_2^I\right]\end{array}\right)$$

(67)

$$\left(\begin{array}{l}\left[b_1^{II}\right]\\ \left[b_2^{II}\right]\end{array}\right)=S^{II}\left(\begin{array}{l}\left[a_1^{II}\right]\\ \left[a_2^{II}\right]\end{array}\right)$$

(68)

$$\left[b_1^I\right]=S_{11}^I\left[a_1^I\right]+S_{12}^I\left[a_2^I\right]$$

(69)

$$\left[b_2^I\right]=S_{21}^I\left[a_1^I\right]+S_{22}^I\left[a_2^I\right]$$

(70)

$$\left[b_1^{II}\right]=S_{11}^{II}\left[a_1^{II}\right]+S_{12}^{II}\left[a_2^{II}\right]$$

(71)

$$\left[b_2^{II}\right]=S_{21}^{II}\left[a_1^{II}\right]+S_{22}^{II}\left[a_2^{II}\right]$$

(72)

There are

$$\left[a_2^I\right]=D\left[b_2^{II}\right]$$

(73)

$$\left[a_2^{II}\right]=D\left[b_2^I\right]$$

(74)

with

$$D=\left[\begin{array}{lll}{e}^{-{\gamma }_1.d}& 0& 0\\ 0& \dots & 0\\ 0& 0& e^{-{\gamma }_N.d}\end{array}\right]$$

(75)

${\gamma }_i$ is the propagation constant of the ith mode of the central guide and N is the number of modes in the same guide.

Using Equations (73) and (74), we get

$$\left[b_1^I\right]=S_{11}^I\left[a_1^I\right]+S_{12}^{I}D\left[b_2^{II}\right]$$

(76)

$$\left[b_1^{II}\right]=S_{11}^{II}\left[a_1^{II}\right]+S_{12}^{II}D\left[b_2^I\right]$$

(77)

$$\left[b_2^I\right]=S_{21}^I\left[a_1^I\right]+S_{22}^{I}D\left[b_2^{II}\right]$$

(78)

$$\left[b_2^{II}\right]=S_{21}^{II}\left[a_1^{II}\right]+S_{22}^{II}D\left[b_2^I\right]$$

(79)

Equation (79), in using Equation (78), becomes

$$\left[b_2^{II}\right]=S_{21}^{II}\left[a_1^{II}\right]+S_{22}^{II}D{S}_{21}^I\left[a_1^I\right]+S_{22}^{II}D{S}_{22}^{I}D\left[b_2^{II}\right]$$

(80)

We put

$$E={\left[U-S_{22}^{II}D{S}_{22}^{I}D\right]}^{-1}$$

(81)

U is the identity matrix. As a result

$$\left[b_2^{II}\right]=E{S}_{22}^{II}D{S}_{21}^I\left[a_1^I\right]+E{S}_{21}^{II}\left[a_1^{II}\right]$$

(82)

$$\begin{array}{ll}\left[b_1^I\right]& =\left[S_{11}^I+S_{12}^{I}DE{S}_{22}^{II}D{S}_{21}^I\right]\left[a_1^I\right]\\ & +\left[S_{12}^{I}DE{S}_{21}^{II}\right]\left[a_1^{II}\right]\end{array}$$

(83)

$$\begin{array}{ll}\left[b_1^{II}\right]& =S_{12}^{I}D\left[U+S_{22}^{I}DE{S}_{22}^{II}D\right]S_{21}^I\left[a_1^I\right]\\ & +\left[S_{11}^{II}+S_{12}^{II}D{S}_{22}^{I}DE{S}_{21}^{II}\right]\left[a_1^{II}\right].\end{array}$$

(84)

The matrix S of the double discontinuity is given by

$$S=\left[\begin{array}{ll}{S}_{11}^I+S_{12}^{I}DE{S}_{22}^{II}D{S}_{21}^I& S_{12}^{I}DE{S}_{21}^{II}\\ S_{12}^{I}D\left[U+S_{22}^{I}DE{S}_{22}^{II}D\right]S_{21}^I& S_{11}^{II}+S_{12}^{II}D{S}_{22}^{I}DE{S}_{21}^{II}\end{array}\right]$$

(85)

Thus, the matrix S of several discontinuities in cascade can be determined from Equation (85) by chaining two matrixes $S_i^{}$ to two other matrixes.

This classic formulation allowed us to analyze several microwave devices [18,19,20].

4. Numerical Results and Discussion

4.1. Propagation Modes

Consider TE mode waves in a metallic cylindrical waveguide of radius $R=13.4 \mathrm{mm}$, fully filled with LMF (see Figure 1) with a partial magnetization $4\pi M$. The waveguide has a resonant frequency of 6.57 GHz for the fundamental mode if it is empty. For the case of ferrite magnetized longitudinally with $\frac{M}{M_S}=0.8$, $4\pi M_S=750 \mathrm{G}$ and a permittivity ${\epsilon }_{rf}=11.3$ (ferrite TT1-414 from Trans-Tech), the resonant frequency is $f_{c.11}^{TE}=3 \mathrm{GHz}$ for the $T{E}_{11}$ mode. When the ferrite is demagnetized, the resonant frequency is $f_{c.11}^{TE}=1.96 \mathrm{GHz}$.

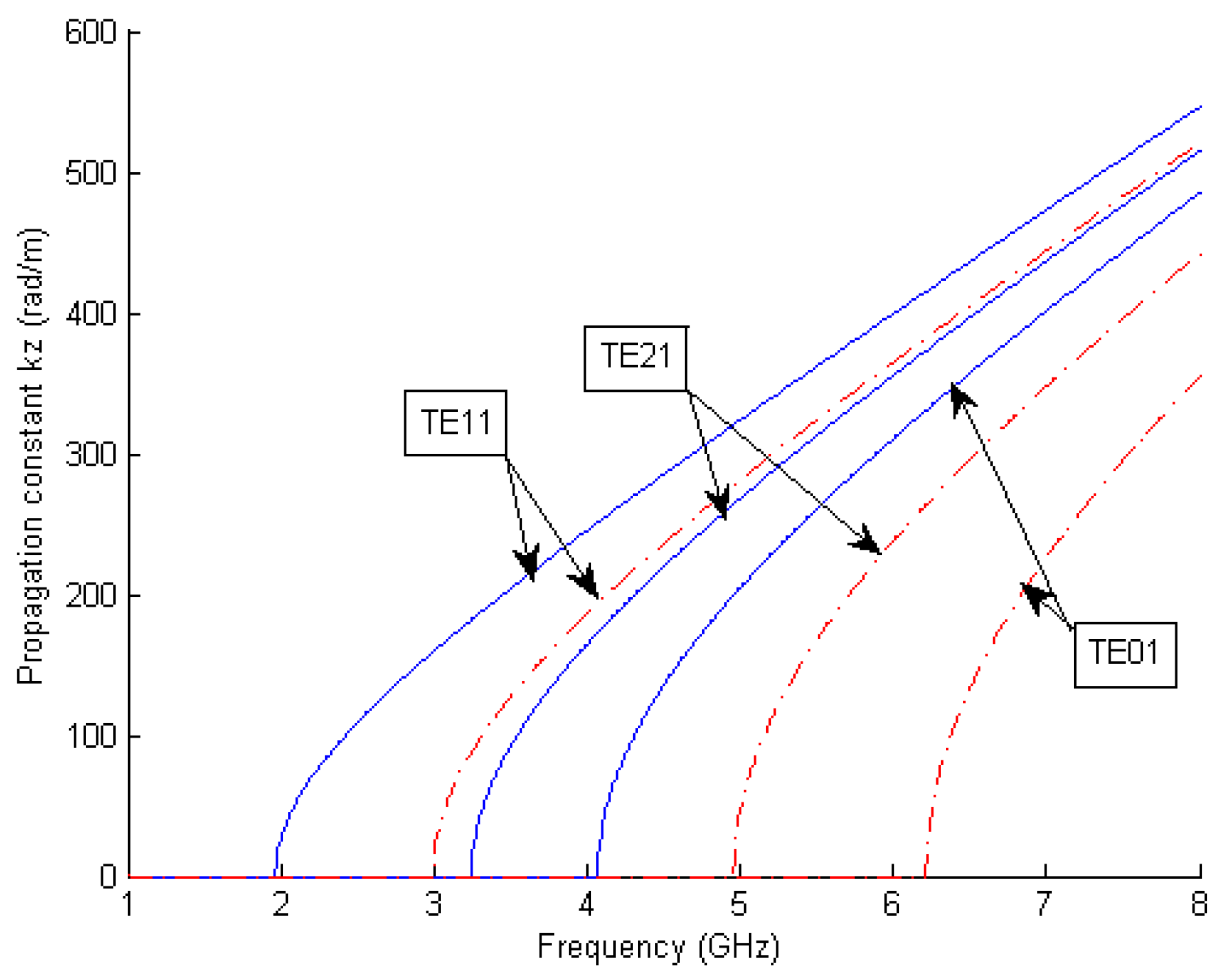
Figure 4 represents calculated curves of the propagation constant for the first three TE modes in the frequency range 1–8 GHz and for the cases where the ferrite is magnetized with $\frac{M}{M_S}=0.8$ or demagnetized. All modes propagate. The propagation constant decreases when the magnetization increases.

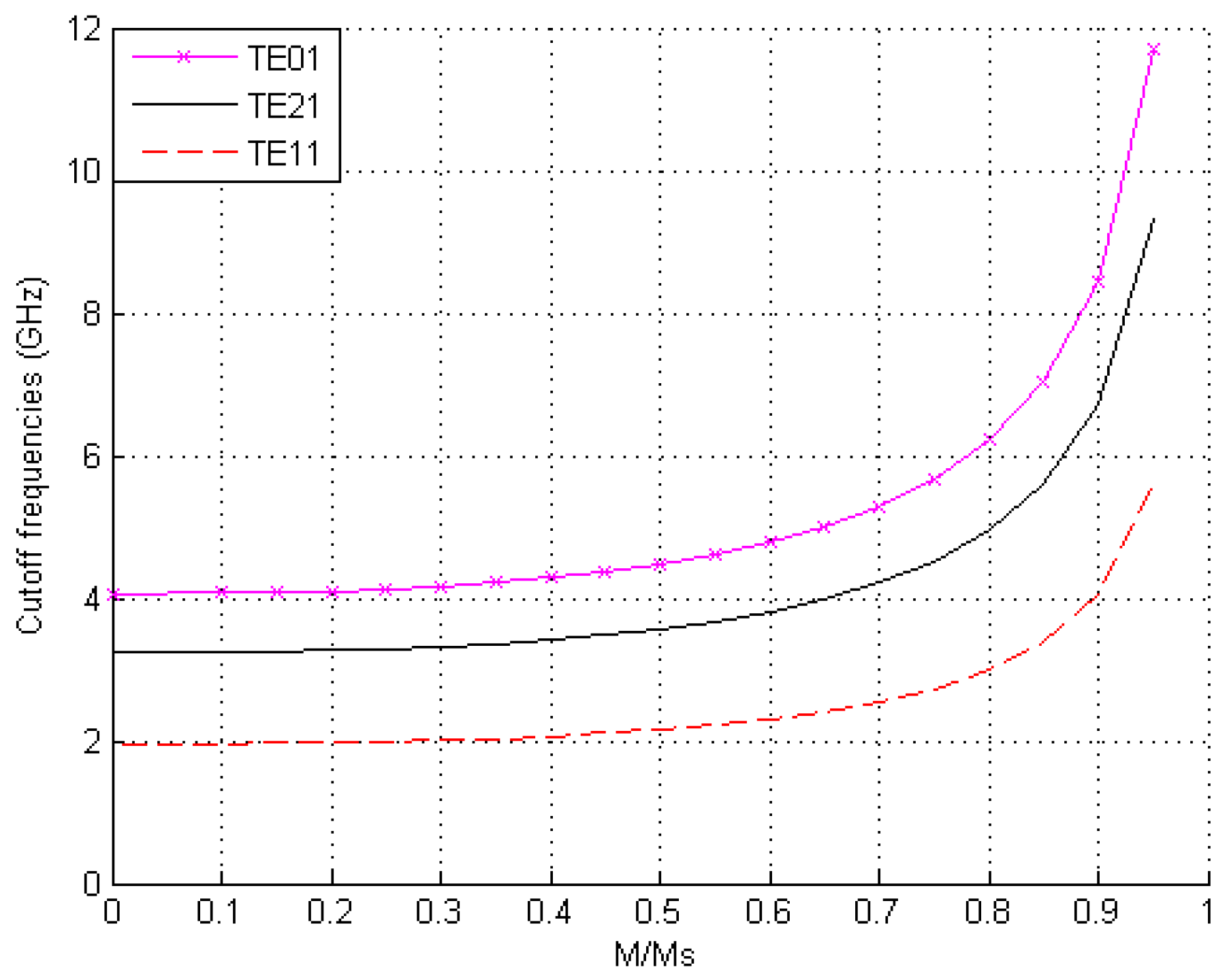
In Figure 5, the cutoff frequencies of the lowest TE modes are shown as $\frac{M}{M_S}$ increases from 0 to 0.99. It can be seen that the cutoff frequencies of the TE modes monotonically decrease as $\frac{M}{M_S}$ decreases. We can notice the same behavior for the TM modes. The numerical results show that the cutoff frequencies can be controlled by external magnetization.

4.2. Ferrite Antenna Design

In this section, we describe how the use of MM can be extended to characterize uni-axial discontinuities between cylindrical waveguides filled with the studied media. The discontinuities were considered without losses. This method was based on the modal development of the transverse electromagnetic fields.

We considered two discontinuities (see Figure 3) constituted by juxtaposing three cylindrical waveguides with the same dimensions (R = 13.4 mm). The central waveguide of width d = 5 mm was filled by LMF, as was studied in the previous section. The other guides were empty.

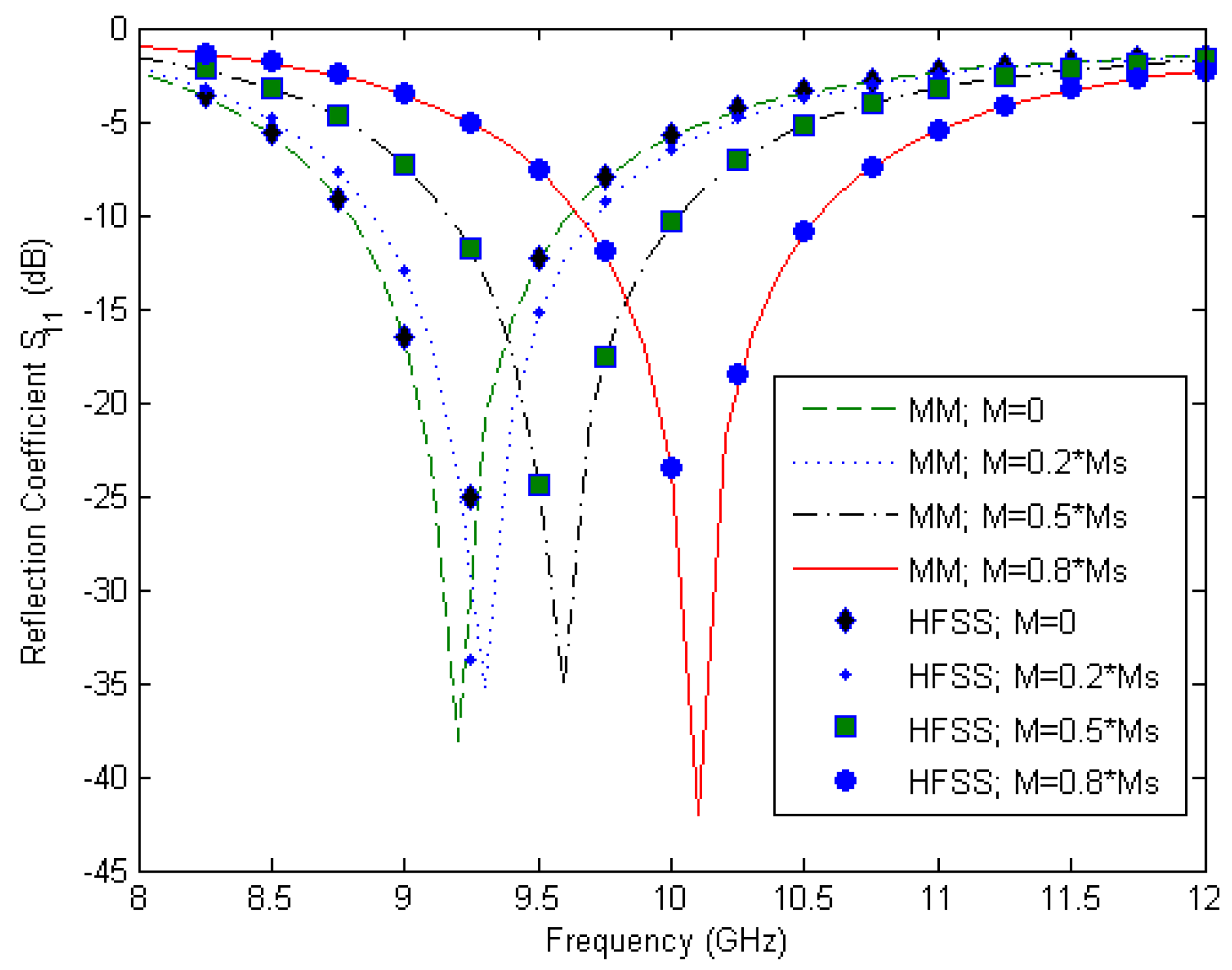
Figure 6 represents the reflection coefficient as a function of the frequency using our approach and HFSS. For the modal method, we used eight modes in the whole circuit. We note that both simulations were in perfect agreement. However, our method was significantly faster than HFSS (7.12 s vs. 9.43 min) because it is a modal method. Thus, by using our approach, it is easy to design antenna according to given specifications.

The magnetization of the ferrite using an external control can be achieved by enveloping the waveguide with Helmholtz coils and connecting them to a variable voltage generator. Each voltage corresponds to a constant magnetic field applied to the ferrite longitudinally that creates the magnetization of this medium. Our interest in this study was in the tuning of the operating frequency of the antenna.

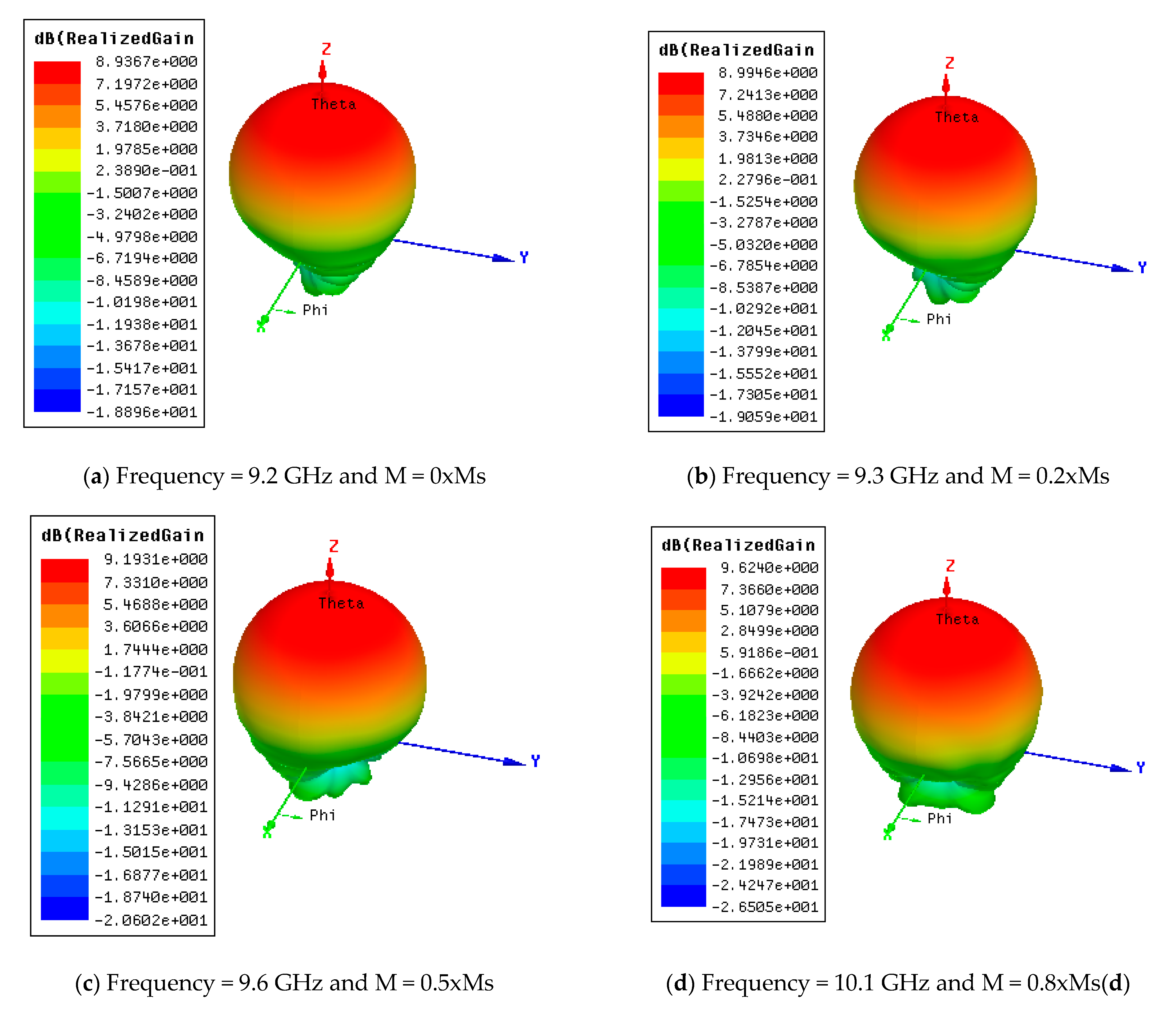
Figure 7 represents the results of the simulation of the radiation pattern and the gain of antenna with HFSS for various values of magnetized ferrite at the resonance frequency. For demagnetized ferrite the gain and resonance frequency of this antenna are 8.93 dB and 9.2 GHz, respectively. It is the geometric discontinuity between the empty cylinder and the free air which radiates. However, the physical discontinuities between the guides and between the materials (ferrite–air) have an effect on the radiation of the antenna. The gain of the antenna depends on the electrical and magnetic characteristics of the ferrite medium.

When the magnetization increases, the gain and the resonant frequency increase. At a magnetization equaling 0.8 Ms, the gain reaches 9.62 dB and the resonant frequency passes to 10.1 GHz.

If magnetization M increases, then the cutoff increases due to the decrease in intermodal interference. So, the gain increases.

We can externally control the resonant frequency with the tensor permeability, which is a function of the magnetization of ferrite. The resonant frequency increases with an increase of the magnetization. The antenna has become multiband.

5. Conclusions

A rigorous TE and TM modes analysis of cylindrical waveguides completely filled with longitudinally magnetized ferrite was developed in this study. It was demonstrated that the electromagnetic characteristics of the waveguide are closely dependent on magnetization. The curves of the dispersion diagram of the fundamental mode and the first two higher order modes of the ferrite waveguide were obtained. The cutoff frequencies could be controlled by external magnetization. These results for the propagation constant can be used in the design of cylindrical ferrite waveguide antennas. Our results were in good agreement with the theoretical prediction. Moreover, in this paper, we applied the mode matching technique to analyze multiple uni-axial discontinuities in metallic cylindrical waveguides filled with anisotropic materials. The results of the simulations of the cylindrical waveguides antenna filled with partially magnetized ferrite using the mode matching technique and those obtained with HFSS were in perfect agreement. However, our method was noticeably faster. The proposed formulation is a useful tool for microwave engineers.