Abstract
An effective way of improving decoding performance of an LDPC code is to extend the single-decoder decoding method to a parallel decoding method with multiple sub-decoders. To this end, this paper proposes a parallel decoding method for the LDPC codes constructed by m-sequence. In this method, the sub-decoders have two types. The first one contains only one decoding module using the original parity-check constraints to implement a belief propagation (BP) algorithm. The second one consists of a pre-decode module and a decoding module. The parity-check matrices for pre-decode modules are generated by the parity-check constraints of the sub-sequences sampled from an m-sequence. Then, the number of iterations of the BP process in each pre-decode module is set as half of the girth of the parity-check matrix, resulting in the elimination of the impact of short cycles. Using maximum a posterior (MAP), the least metric selector (LMS) finally picks out a codeword from the outputs of sub-decoders. Our simulation results show that the performance gain of the proposed parallel decoding method with five sub-decoders is about 0.4 dB, compared to the single-decoder decoding method at the bit error rate (BER) of .
1. Introduction
The m-sequence code, which generates via primitive polynomial, is an LDPC code [1]. The generator of the code is a linear feedback shift register (LFSR), which is suitable for scenarios with limited resources for encoders. Moreover, the m-sequence code is designed with extremely low code rate because it is supposed to work in scenarios with extremely low signal to noise ratio (SNR), such as deep-space communication [2] and wireless sensor network [3]. And It has been proven [1] that the m-sequence code with moderate code length has a better BER performance than the LDPC code constructed by progressive edge growth (PEG) algorithm [4]. Therefore, in such scenarios, improving the bit error ratio (BER) performance of m-sequence code is valuable. And developing decoding method is an effective approach to improve the BER performance, as decoding processes can be done at resource-rich nodes.
The Parallel decoding methods, such as multiple-based belief propagation (MBBP) algorithm [5,6,7] and modified random redundant decoding (mRRD) algorithm [8,9], have been proven that they can achieve better performance than the single-decoder system for decoding block codes. In this paper, we then apply the parallel decoding method to m-sequence codes.
In MBBP algorithm, candidate codewords are outputted by BP decoding module of multiple sub-decoders with different parity-check matrices. Then, they are selected by a least metric selector (LMS) through maximum a posterior (MAP) rule. Therefore, the construction of parity-check matrices is essential for MBBP. Literature [7] had proposed a method that combining the cycles of parity-check matrix of LDPC codes constructed by progressive edge-growth [4] to generate new parity-check matrices. But for m-sequence code, there is no discussion about the construction of parity-check matrices for sub-decoders.
In mRRD, an automorphic group of code is employed to construct parity-check matrix of sub-decoder. Each sub-decoder uses RRD algorithm to output the candidate codeword. Therefore, the essential point of applying mRRD is finding the automorphic group of an LDPC code. Literature [10] proposed an LDPC code constructed by a cyclic code and the automorphic group of this code is easy to be found. This code had achieved great performance improvement by employing mRRD algorithm. However, it is hard to find automorphic group for m-sequence code. The existing parallel decoding methods cannot be employed by m-sequence code.
To solve this problem, we first propose a method to construct parity-check matrix for m-sequence code. Then, we design a new parallel decoding method for m-sequence code. To construct parity-check matrices, the first step is to generate an m-sequence by an order-k primitive polynomial. Then, the sampling sequences are obtained by sampling the m-sequence with multiple sampling intervals which are relatively prime with. The second step is to find new primitive polynomials which can generate the sampling sequences. The final step is to use the parity-check constraints of these new primitive polynomials to construct parity-check matrix by cyclic shift. The constructed parity-check matrices have many short cycles due to the cyclic shift procedure. Therefore, they cannot be employed by the sub-decoders of MBBP algorithm.
To tackle this problem, we propose a new parallel decoding method which can eliminate the affection of short cycles in parity-check matrices. In our method, the sub-decoders are designed to two types. The first type contains only one decoding module, which uses the basic parity-check matrix constructed in [1] to perform BP algorithm and output candidate codeword. The second type is constructed by a pre-decode module and a decoding module. The pre-decode module use a parity-check matrix to perform the BP process and outputs extrinsic information to the decoding module. At this point, the number of iterations in pre-decode module is set as half of girth of parity-check matrix. Therefore, the outputted extrinsic information will not be affected by short cycles. Then the cascaded decoding module output candidate codeword with the help of extrinsic information. At last, all outputted codewords of sub-decoders are sent into the same LMS and the final codeword is selected by MAP rule.
In this paper, the m sequence codes with code length 3000, 1100 are constructed by primitive polynomial and , respectively. Then the bit error rate simulation experiments of these codes are carried out. In the experiment, 6 and 4 parity-check matrices are constructed by the proposed construction method, respectively. In addition, when the numbers of sub-decoders are 5 and 4, the bit error rate (BER) curves have converged. Simulation results show that the proposed parallel decoding method is about 0.4 dB better than the single decoder method in [1].
This paper is organized as follows. Section 2 gives a brief introduction of LDPC code generated via primitive polynomial and presents the problem statement. The construction method of parity-check matrices and new parallel decoding method are specified in Section 3. Section 4 shows and analyzes the numerical results. Finally, some conclusions are drawn in Section 5.
2. Motivation
For an m-sequence generated by an LFSR which employs a primitive polynomial as connected polynomial, the segment of the m-sequence can be an LDPC codeword. This LDPC code is called m-sequence code [1]. In this section, we briefly introduce the basis of the code and refer readers to [1] for more details. Then, we discuss the problem of designing parallel decoding method for m-sequence codes.
2.1. LDPC Codes Generated via Primitive Polynomial
Consider an LFSR with connected primitive polynomial , where are positive integers such that . Denote trace function as a mapping from field to field [11]. Let be a root of and be the initial phase of the LFSR. Then, the m-sequence generated by the register can be described as
For the m-sequence, further gives the following parity-check constraints
With (2), it has been proven that given integer , we can construct an LDPC matrix for all segments truncated from [1]. That is, is a codeword of an LDPC code.
The parity-check matrix of an m-sequence code has two types of check rows. One is obtained from parity-check constraints in (2). The other is derived from the conjugate primitive elements of , where M is the maximum integer such that . Consider the m-sequence generated by conjugate primitive element , it can be written as
Finally, the parity-check matrix can be 4-cycle free if the factors satisfy the conditions derived in [1], i.e.,
2.2. Problem Statement
The code rates of the m-sequence codes are extremely low, as they are supposed to work in extremely low SNR cases. In such cases, it is desirable to design a decoding algorithm with better BER performance.
In [5,6,7], authors show that the performance of a parallel decoding method with multiple sub-decoders can overcome the single-decoder decoding method. For instance, Figure 1 shows the structure of MBBP, in which each sub-decoder uses a different parity-check matrix [5].
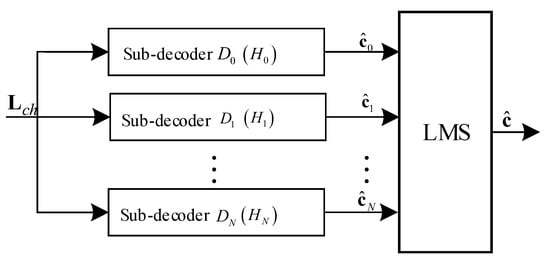
Figure 1.
The structure of multiple-based belief propagation (MBBP) algorithm.
LLR of channel observation value is simultaneously entered into the sub-decoders, resulting in candidate codewords . The value of each element of the codewords is “1” or “−1”. The decoding method is BP decoding algorithm. These candidate codewords are then fed into the LMS, in which the final output codeword is selected by means of the MAP rule or the equivalent minimum distance rule, i.e.,
where is the Euclidean distance between vectors and .
For the parallel decoding architecture shown in Figure 1, it requires for sub-decoders that parity-check matrices contain different parity-check constraints with each other. It is due to the fact that errors cannot be fixed by one parity-check matrix are uncorrectable for other parity-check matrices being of the same parity-check constraints. In order to apply such method on m-sequence codes, we need to construct parity-check matrices through different parity-check constraints. However, the construction methods in [5,6,7] are not design for m-sequence code, while [1] did not give the method to construct different parity-check matrices for m-sequence code.
To solve this problem, we investigate the algebraic properties of sampling sequence of m-sequence to obtain different parity-check constraints. Then, these constraints are utilized to build parity-check matrices for sub-decoders.
3. Parallel Decoding Method for m-Sequence Codes
In this section, we first construct parity-check matrices by using the parity-check constraints of sampling sequence of m-sequence. Then, we analyze the deterioration mechanism of decoding performance caused by short cycles and present a way to eliminate the affection of short cycles. At the last of the section, we develop a new parallel decoding method with sub-decoder consisting of a pre-decode module and a decoding module.
3.1. Construction of Parity-Check Matrices
Finite field can be represented by the powers of a primitive element , i.e.,
Consequently, is the primitive elements of this finite field if and only if [11], where is the greatest common divisor of a and b. The new primitive element can regenerate as follows.
Let be the primitive polynomial of which is a root,
Polynomial is then used to generate a new m-sequence with the same initial phase . Thus, sequence meets the following constraints
In addition, using the trace function, we have
Now, it is clearly shown from (12) that the parity-check constraints of can be used to check the codeword
Based on the above analysis, we design a construction method of parity-check matrices as Algorithm 1 shown, where is the function that using Berlekamp-Messey (BM) algorithm [12] to get the minimum generating polynomial of . is the function to use to construct a parity-check matrix with code length n by cyclic shift as (13).
In Algorithm 1, we first find all the candidate sampling intervals that are relatively prime with . Then we generate a segment of m-sequence with length to get the sampling segment by the sampling interval q. The BM algorithm can be employed to find the maximum generating polynomial of . Finally, we use to construct a parity-check matrix through the way of (13).
| Algorithm 1: Construction of parity-check matrices for m-sequence code |
| Input: A primitive polynomial ; |
| A code length n. |
| Output: The parity-check matrices . |
| 1: Begin procedure |
| 2: Initialize: Let Q be the set of sampling interval, k is the order of , counter . |
| 3: for do |
| 4: if then |
| 5: . |
| 6: end if |
| 7: end for |
| 8: Generate an m-sequence via . |
| 9: for do |
| 10: Sample with sampling interval q to get . |
| 11: . |
| 12: . |
| 13: . |
| 14: end for |
| 15: return . |
The parity-check matrix generated by this method is the result of cyclic shift of one parity-check constraint. Therefore, it has too many short cycles to be equipped into the sub-decoders of the MBBP algorithm. To take full advantage of the parity-check matrices, we thus design a new parallel decoding method in the next subsection.
3.2. Parallel Decoding Method with Multiple Sub-Decoders
Now let us discuss the affection of short cycles on decoding first. In BP algorithm, the information of each node is transferred and iterated according to the connection relation of Tanner graph. If there exist short cycles in the Tanner graph, the information of nodes in the cycles cannot receive enough extrinsic information, resulting in overestimation of node information and errors in decoding results.
Figure 2 shows information flows of short cycles in a Tanner graph, where Figure 2a,b are 4-cycle and 6-cycle cases respectively. The solid line represents the information transfer in the first iteration, while the segment line and dotted line represent the information flow in the second and third iteration, respectively.
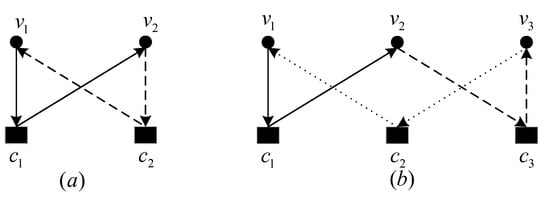
Figure 2.
Information flows of short cycles in a Tanner graph. (a) 4-cycle. (b) 6-cycle.
In Figure 2a, information is first passed to variable node through the check node . In the second iteration, passes the information back to through . This is an information loop. Similarly, the 6-cycle case in Figure 2b completes a loop through 3 iterations.
It can be seen from Figure 2, if the number of iterations is half of the girth, then the information flowing in a short cycle will not back to the original node. As a consequence, the overestimation problem caused by the short cycle will never happen.
However, if the iteration times of BP algorithm is set as half of the girth of parity-check matrix, the BP decoding algorithm is hardly to output a codeword. To tackle this difficult, this paper proposes a new parallel decoding method whose decoding structure is shown in Figure 3.
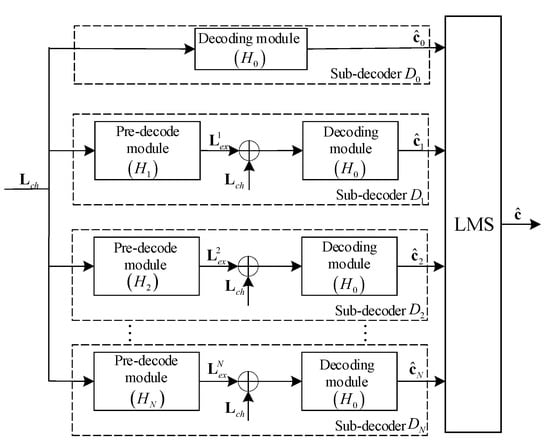
Figure 3.
The structure of parallel decoding method.
The sub-decoders of the designed parallel decoding method are of two types. The first type of sub-decoder only contains the decoding module that directly outputs the codeword . The parity-check matrix employed by decoding module is the basic parity-check matrix . The second type of sub-decoders , are composed by a pre-decode module and a decoding module. In these sub-decoders, after receiving LLR of channel received value , the pre-decode module uses the BP algorithm to output extrinsic information . The employed parity-check matrix is generated by Algorithm 1. The number of iterations in the pre-decode module is set as half of the girth of . Therefore, is not affected by the cycle structure of . Then, plus is sent into the decoding module to get candidate codeword by BP decoding with .
The pre-decode modules employ different parity-check matrices, resulting in different outputted extrinsic information. It enables the decoding modules to output different candidate codewords, which are valuable for the LMS to choose the best final codeword.
The parallel decoding method is summarized in Algorithm 2, where and represents that using BP algorithm with parity-check matrix H to decode the input LLR . The maximum iteration number ist. The output is hard decision sequence for and soft extrinsic information for , respectively.
In Algorithm 2, the LLR value of channel output is simultaneously entered into sub-decoders. Then these sub-decoders , output the candidate codewords respectively. Let S be the set of candidates which satisfy . If , then let be the set of all candidates. The decoding result is selected from S by an LMS with MAP rule.
| Algorithm 2: Parallel decoding method |
| Input: The LLR value of channel output; |
| Maximum iteration number ; |
| Basic parity-check matrix ; |
| Parity-check matrices . |
| Output: The decoding result . |
| 1: Begin procedure |
| 2: Initialize: Let S be the set of candidate codewords, is the half of the girth of . |
| 3: In sub-decoder , . |
| 4: if then |
| 5: |
| 6: end if |
| 7: for do |
| 8: In sub-decoder , . |
| 9: . |
| 10: if then |
| 11: . |
| 12: end if |
| 13: end for |
| 14: if then |
| 15: . |
| 16: end if |
| 17: |
| 18: return. |
4. Numerical Results
In this section, we simulate the BER of m sequence codes generated via primitive polynomials and . The code rates of these two codes are the same 0.03 and the code lengths are 3000 and 1100, respectively. There are two decoding methods employed in the simulation, one is the proposed parallel decoding method with multiple sub-decoders, the other one is the single-decoder decoding method which employed in [1]. The channel is additive white Gaussian noise (AWGN) channel.
Firstly, we simulate the BER performance of the proposed decoding method with different number of sub-decoders. According to the construction method of parity-check matrix proposed in Section 3.1, we have found the sampling intervals to sample the m-sequence generated by and obtain the primitive polynomials of the sampling sequences.
For the m-sequence generated by , we also use sampling intervals to get the sampling sequences and corresponding primitive polynomials.
Then we have simulated the BER performance of the proposed decoding method with different number of sub-decoders for these two codes, the results are shown in Figure 4.
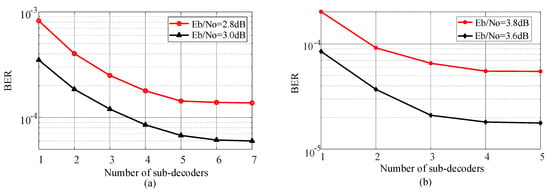
Figure 4.
The bit error rate (BER) performance of the proposed decoding method with different number of sub-decoders. (a) code length 3000. (b) code length 1100.
Figure 4 presents the relation between BER performance and the number of sub-decoders. With the increase of employed sub-decoders, the BER performance is better but the computation complexity is increased. In our method, all the sub-decoders have nearly the same computation complexity. Therefore, the parallel decoding method with N sub-decoders is N times complex than the original single-decoder system. To get the tradeoff of BER performance and complexity, we employ 5 sub-decoders for the code with length 3000 as Figure 4a has shown that the BER curve is converged when employing 5 sub-decoders. Similarly, we employ 4 sub-decoders for the code with length 1100.
In the end, we have simulated the BER performance of these two codes with different decoding methods, the results are shown in Figure 5.
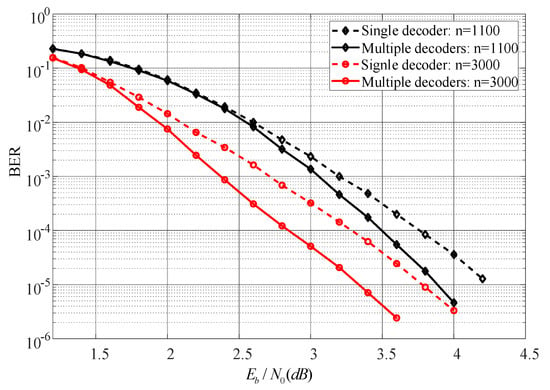
Figure 5.
The BER performance of different decoding methods.
From Figure 5 we can see that, the proposed decoding method outperforms the single-decoder decoding method in terms of BER when the value of is fixed. The range of the simulation is from 1.4 dB to 4.2 dB while the corresponding SNR range is from −13.82 dB to −11.02 dB. In the BER region of , our decoding method has a BER gain of 0.3 dB and 0.4 dB compared to the single-decoder decoding method for these two codes, respectively.
5. Conclusions
In this paper, we had improved the BER performance of m-sequences code by applying parallel decoding method. Firstly, to construct parity-check matrices for sub-decoders, we investigated the parity-check constraints from sampling sequence of m-sequence and used them to construct the parity-check matrices by cyclic shift. Then, to overcome the influence of short cycles of parity-check matrices, we had proposed a new parallel decoding method with two types of sub-decoders. Simulation results show that the proposed decoding method improved about 0.4 dB compared with the original single-decoder decoding method at a BER of .
Author Contributions
Conceptualization, Z.Z. and L.Z.; methodology, Z.Z. and Z.H.Z.; software, Z.Z. and Z.H.Z.; validation, Z.Z., L.Z. and Z.H.Z.; formal analysis, Z.Z. and Z.H.Z.; investigation, Z.Z.; resources, L.Z.; data curation, Z.H.Z.; writing—original draft preparation, Z.Z.; writing—review and editing, Z.Z., L.Z., Z.H.Z.; visualization, Z.Z. and Z.H.Z.; supervision, L.Z.; project administration, L.Z.; funding acquisition, L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| LDPC | Low Density Parity Check |
| BP | Belief Propagation |
| MAP | Maximum A Posterior |
| LMS | Least Metric Selector |
| BER | Bit Error Rate |
| SNR | signal-to-noise-ratio |
| LFSR | Linear Feedback Shift Register |
| MBBP | Multiple-Based Belief Propagation |
| RRD | Random Redundant Decoding |
| LLR | Log-Likelihood Ratio |
| BM | Berlekamp-Messey |
| AWGN | Additive White Gaussian Noise |
References
- Zhang, Z.; Zhou, L.; Du, J.; Peng, S. An algebraic approach to design low rate low density parity check code. In Proceedings of the 2017 9th International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 11–13 October 2017. [Google Scholar]
- De Cola, T.; Paolini, E.; Liva, G.; Calzolari, G.P. Reliability Options for Data Communications in the Future Deep-Space Missions. Proc. IEEE 2011, 99, 2056–2074. [Google Scholar] [CrossRef]
- Abughalieh, N.; Steenhaut, K.; Nowé, A. Low power channel coding for Wireless Sensor Networks. In Proceedings of the 2010 17th IEEE Symposium on Communications and Vehicular Technology in the Benelux (SCVT2010), Enschede, The Netherlands, 24–25 November 2010. [Google Scholar]
- Hu, X.-Y.; Eleftheriou, E.; Arnold, D.M. Regular and irregular progressive edge-growth tanner graphs. IEEE Trans. Inf. Theory 2005, 51, 386–398. [Google Scholar] [CrossRef]
- Hehn, T.; Huber, J.B.; Laendner, S.; Milenkovic, O. Multiple-Bases Belief-Propagation for Decoding of Short Block Codes. In Proceedings of the 2007 IEEE International Symposium on Information Theory, Nice, France, 24–29 June 2007. [Google Scholar]
- Hehn, T.; Huber, J.B.; Milenkovic, O.; Laendner, S. Multiple-bases belief-propagation decoding of high-density cyclic codes. IEEE Trans. Commun. 2010, 58, 1–8. [Google Scholar] [CrossRef]
- Hehn, T.; Huber, J.B.; He, P.; Laendner, S. Multiple-Bases Belief-Propagation with Leaking for Decoding of Moderate-Length Block Codes. In Proceedings of the International ITG Conference on Source and Channel Coding, Ulm, Germany, 14–16 January 2008. [Google Scholar]
- Halford, T.R.; Chugg, K.M. Transactions Letters—Random Redundant Iterative Soft-in Soft-out Decoding. IEEE Trans. Commun. 2008, 56, 513–517. [Google Scholar] [CrossRef]
- Dimnik, I.; Berery, Y. Improved random redundant iterative HDPC decoding. IEEE Trans. Commun. 2009, 57, 1982–1985. [Google Scholar] [CrossRef]
- Chen, C.; Bai, B.; Yang, X.; Li, L.; Yang, Y. Enhancing Iterative Decoding of Cyclic LDPC Codes Using Their Automorphism Groups. IEEE Trans. Commun. 2013, 61, 2128–2137. [Google Scholar] [CrossRef]
- Zhang, K.Q.T. Channel Coding. In Wireless Communications: Principles, Theory and Methodology; Wiley: Hoboken, NJ, USA, 2015; pp. 121–170. [Google Scholar]
- Robert Redinbo, G. Correcting DFT Codes with a Modified Berlekamp-Massey Algorithm and Kalman Recursive Syndrome Extension. IEEE Trans. Comput. 2014, 63, 196–203. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).