Broadband RF Phased Array Design with MEEP: Comparisons to Array Theory in Two and Three Dimensions
Abstract
1. Introduction
2. Phased Array Antenna Theory
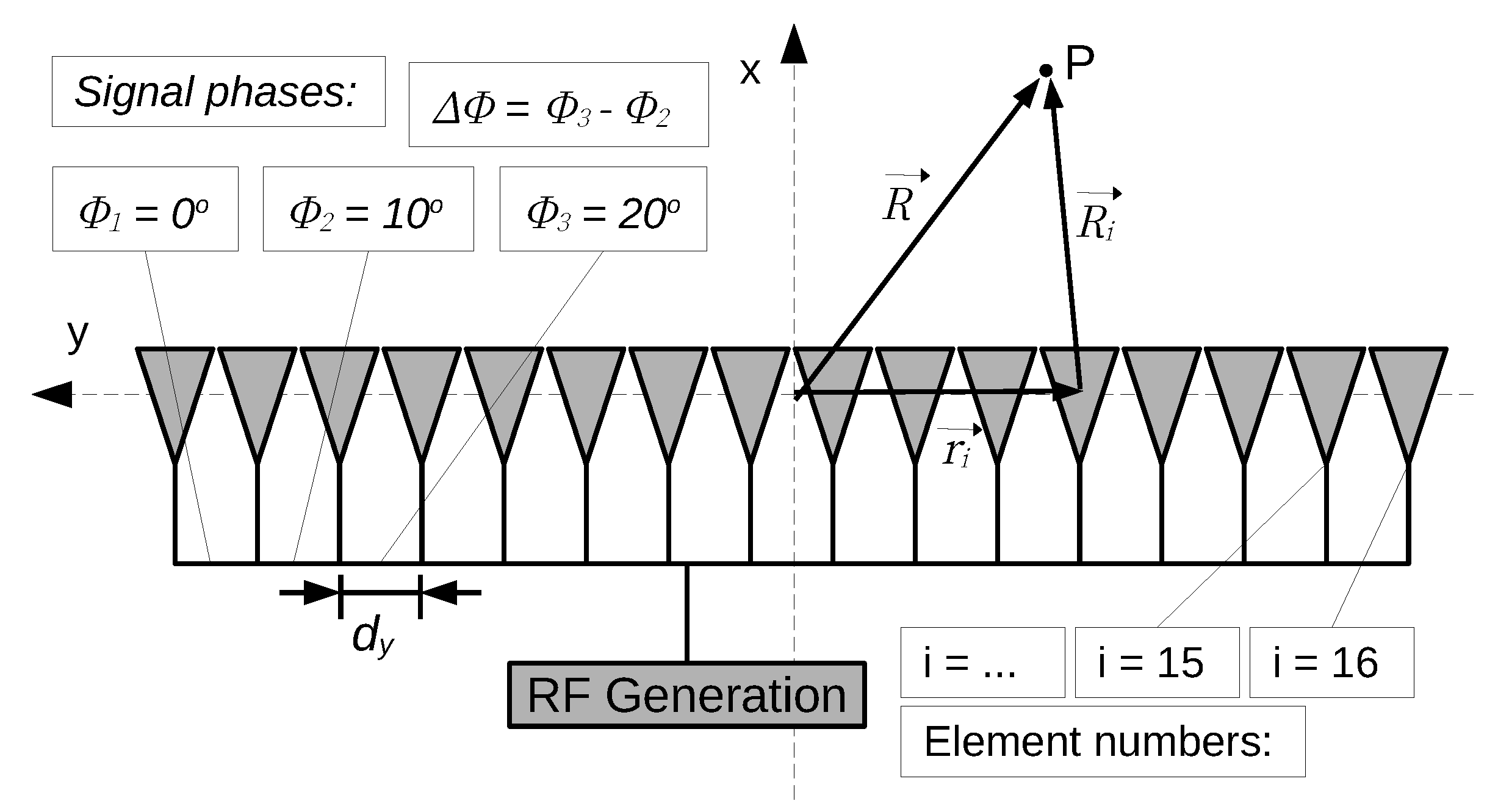
2.1. Phase Steering and Beam Angle
2.2. Radiation Patterns and Beam Width
2.3. Regarding Array Radiation Patterns
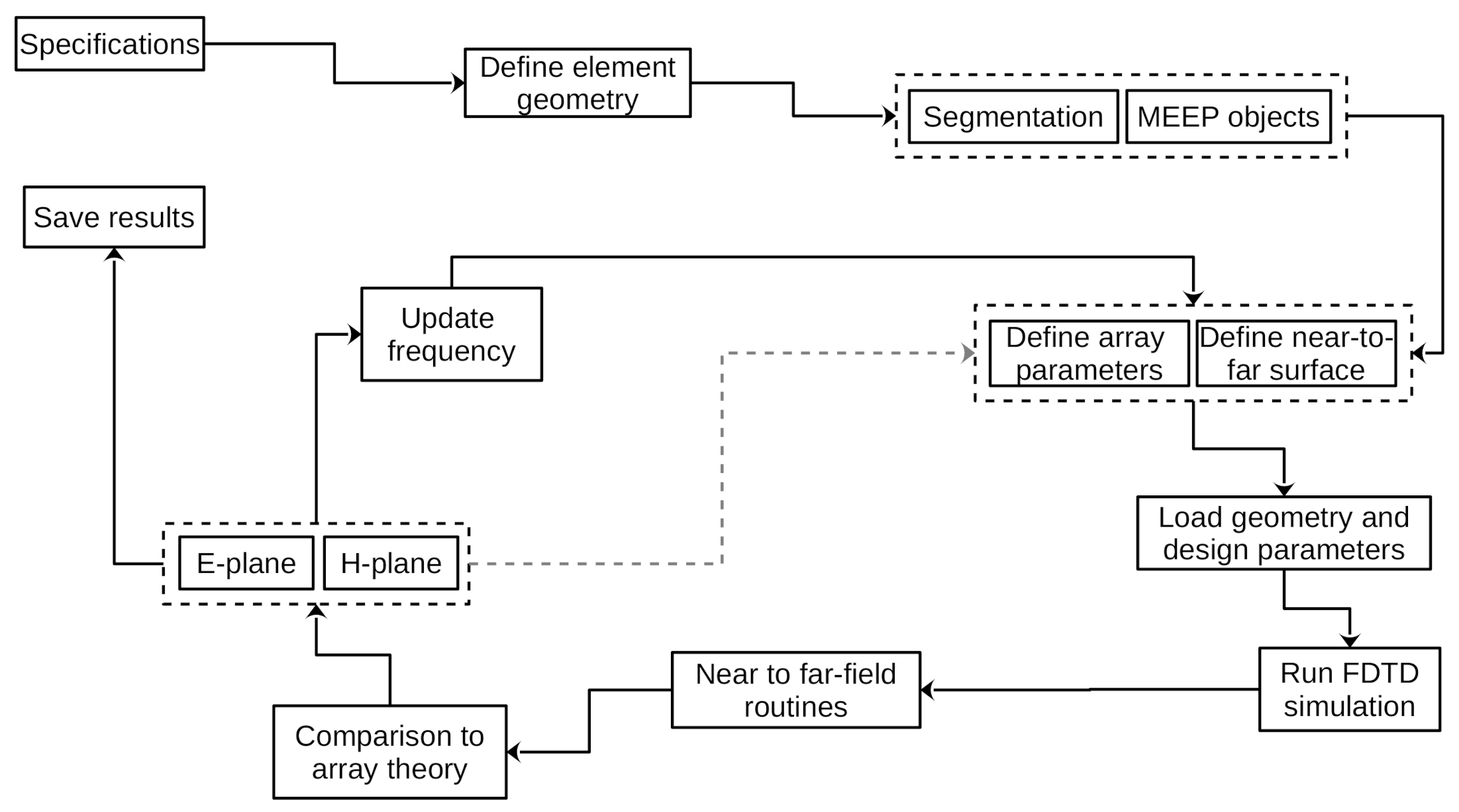
3. Phased Array Designs in One Dimension: Two-Dimensional Fields
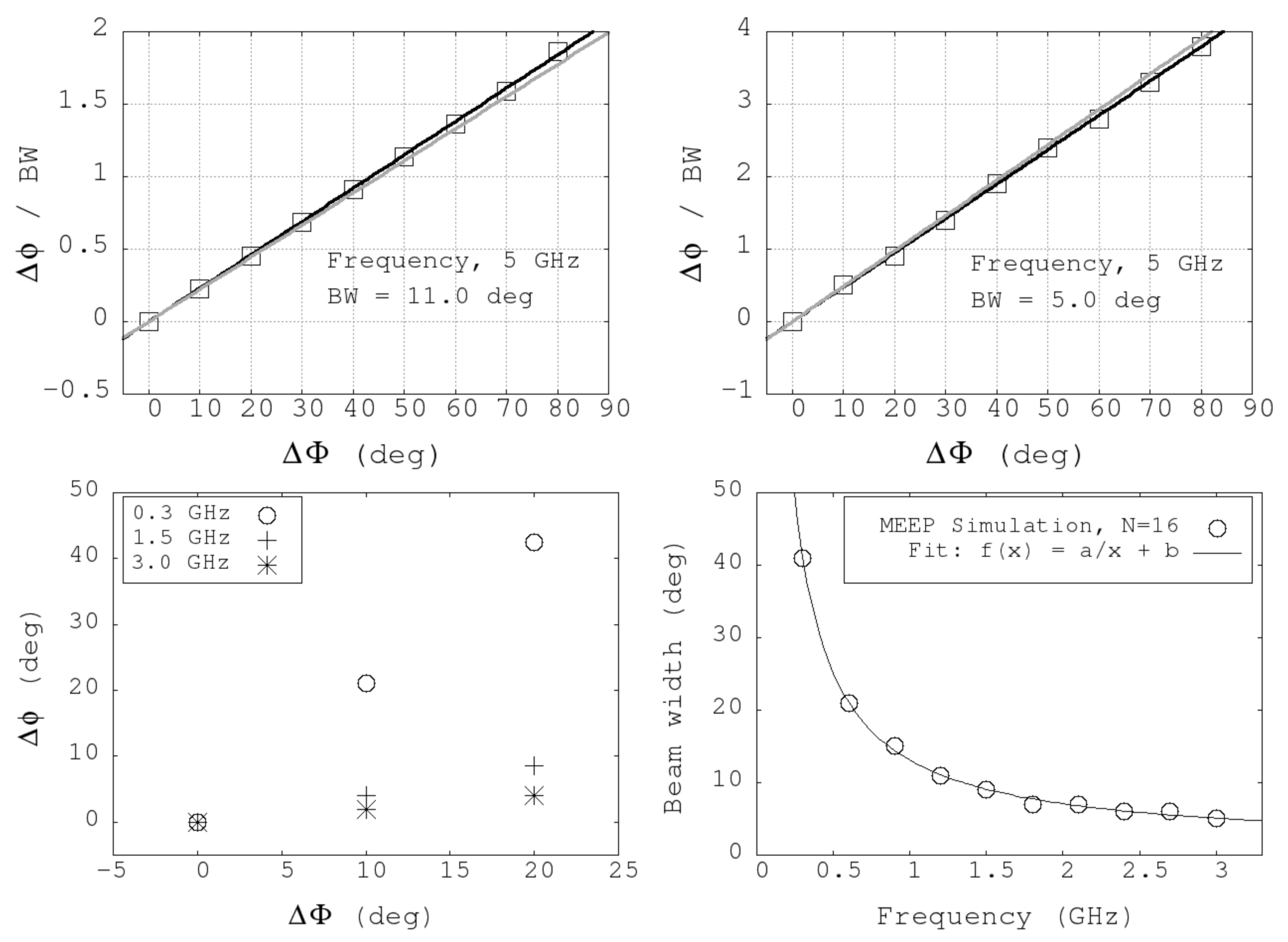
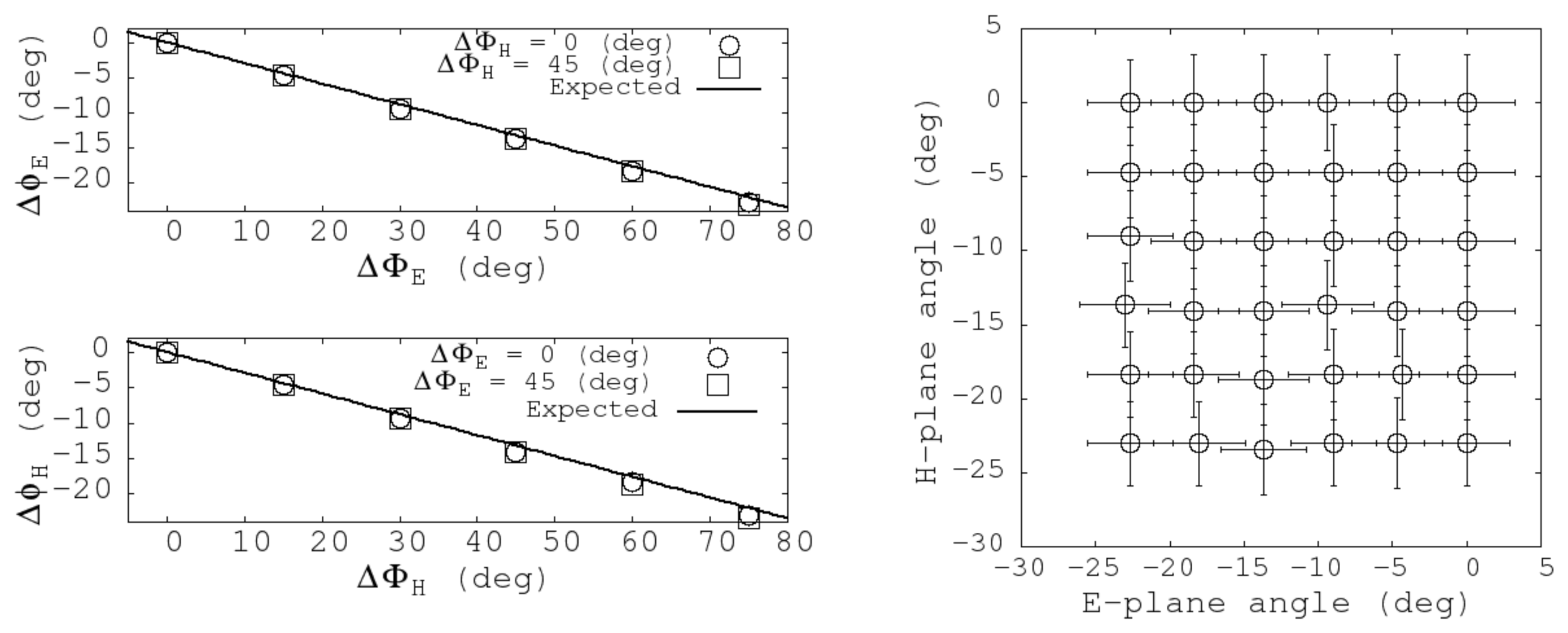
3.1. Phase Steering, Beam Angle, and Beamwidth
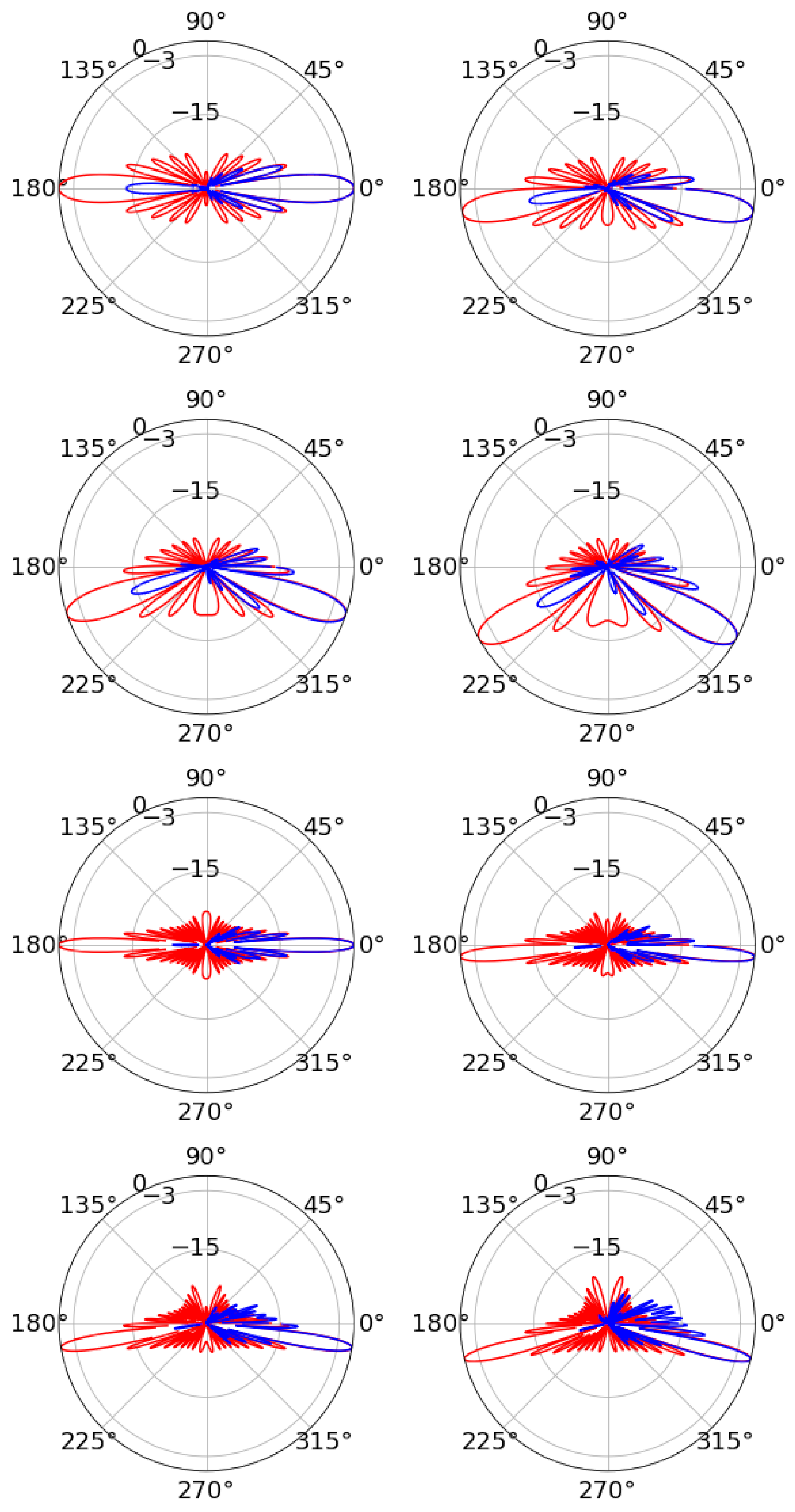
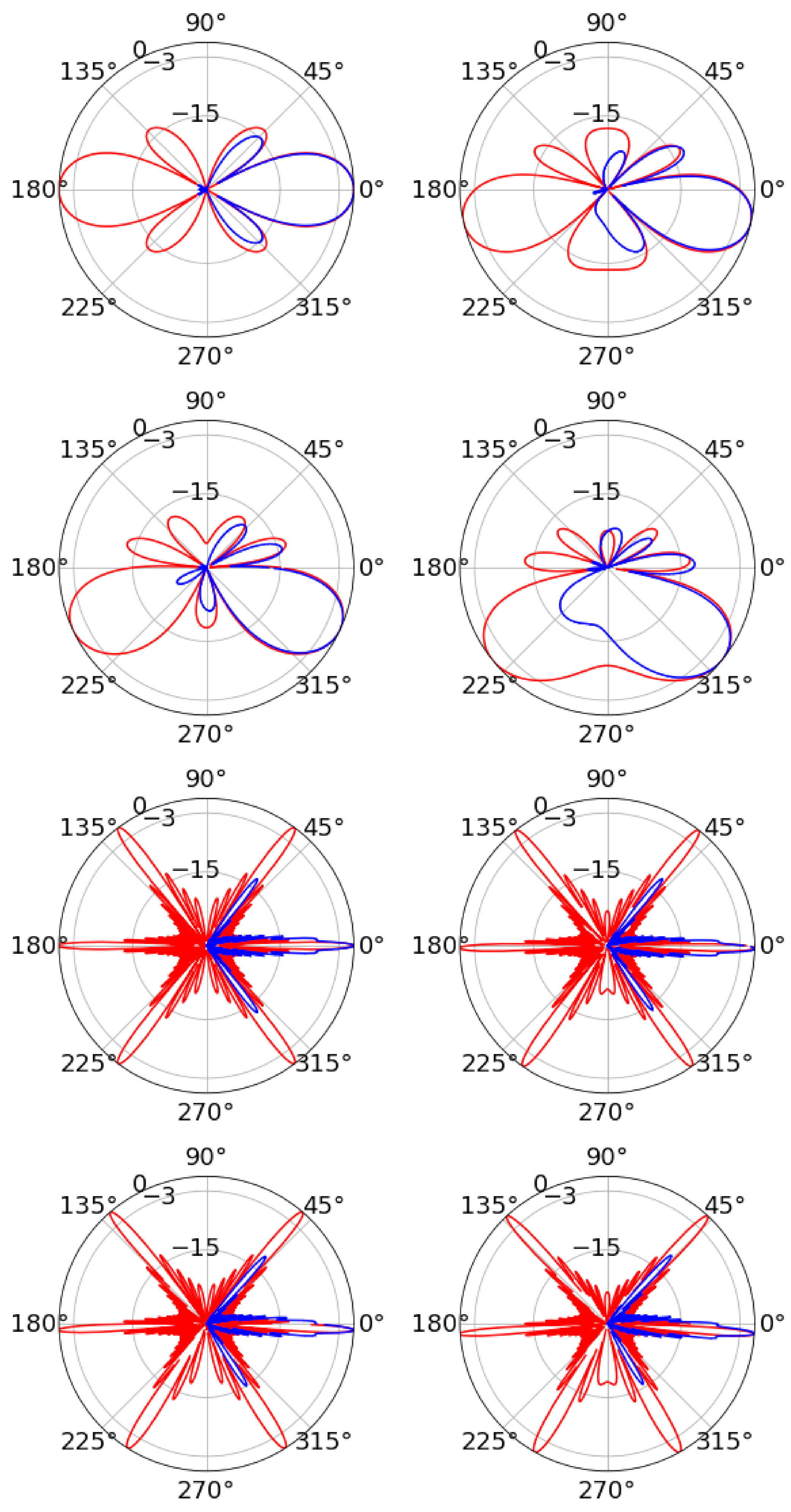
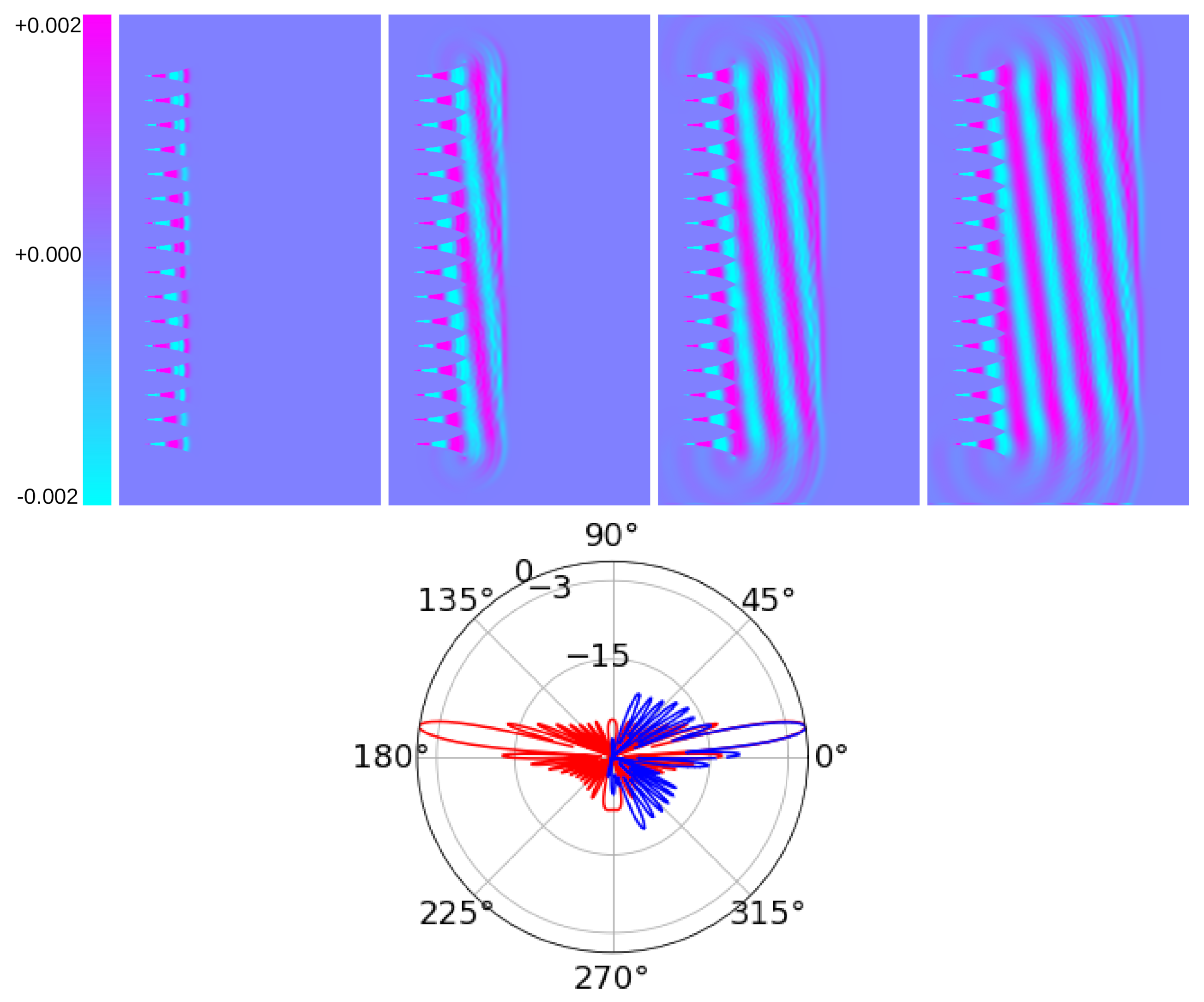
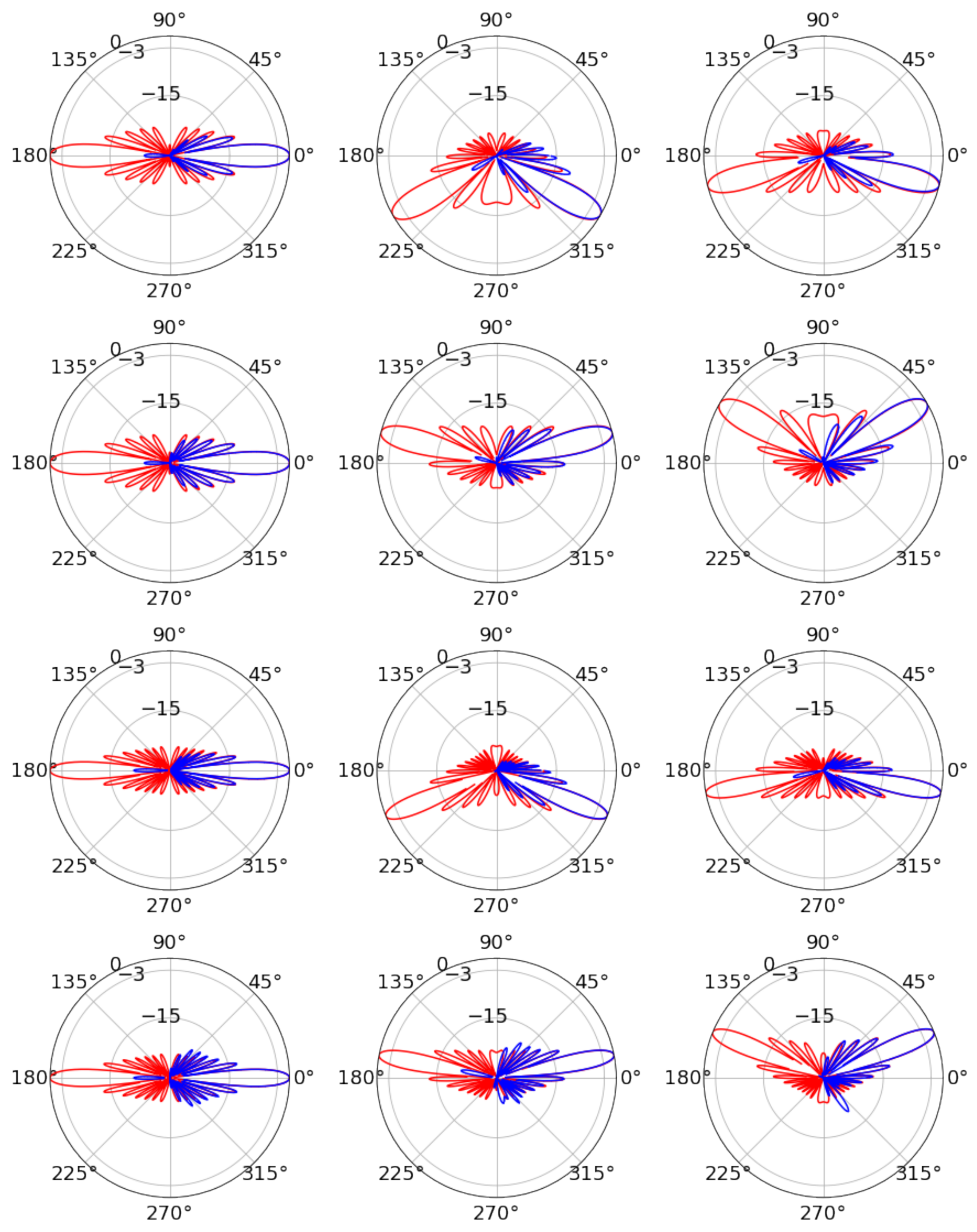
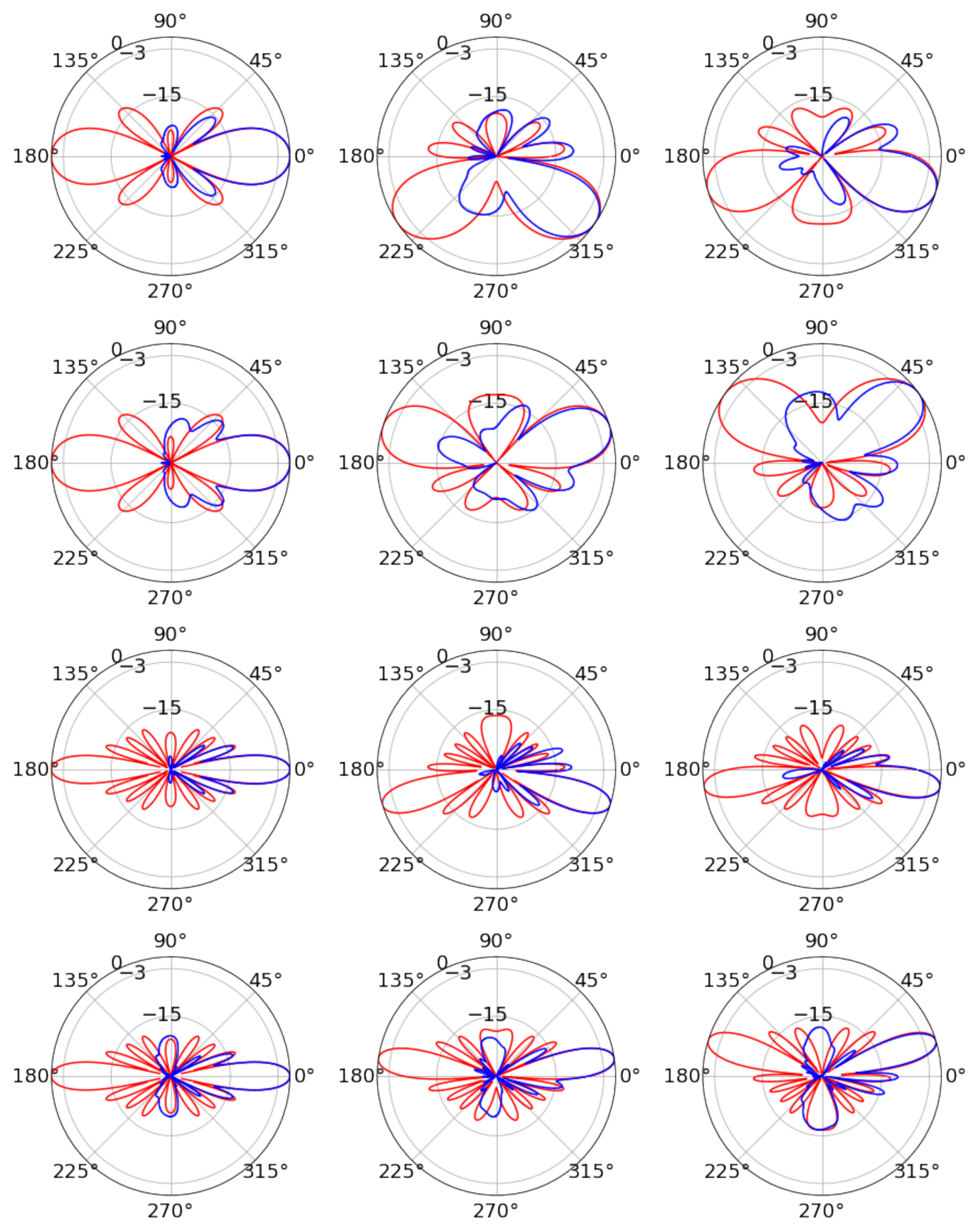
3.2. Radiation Patterns
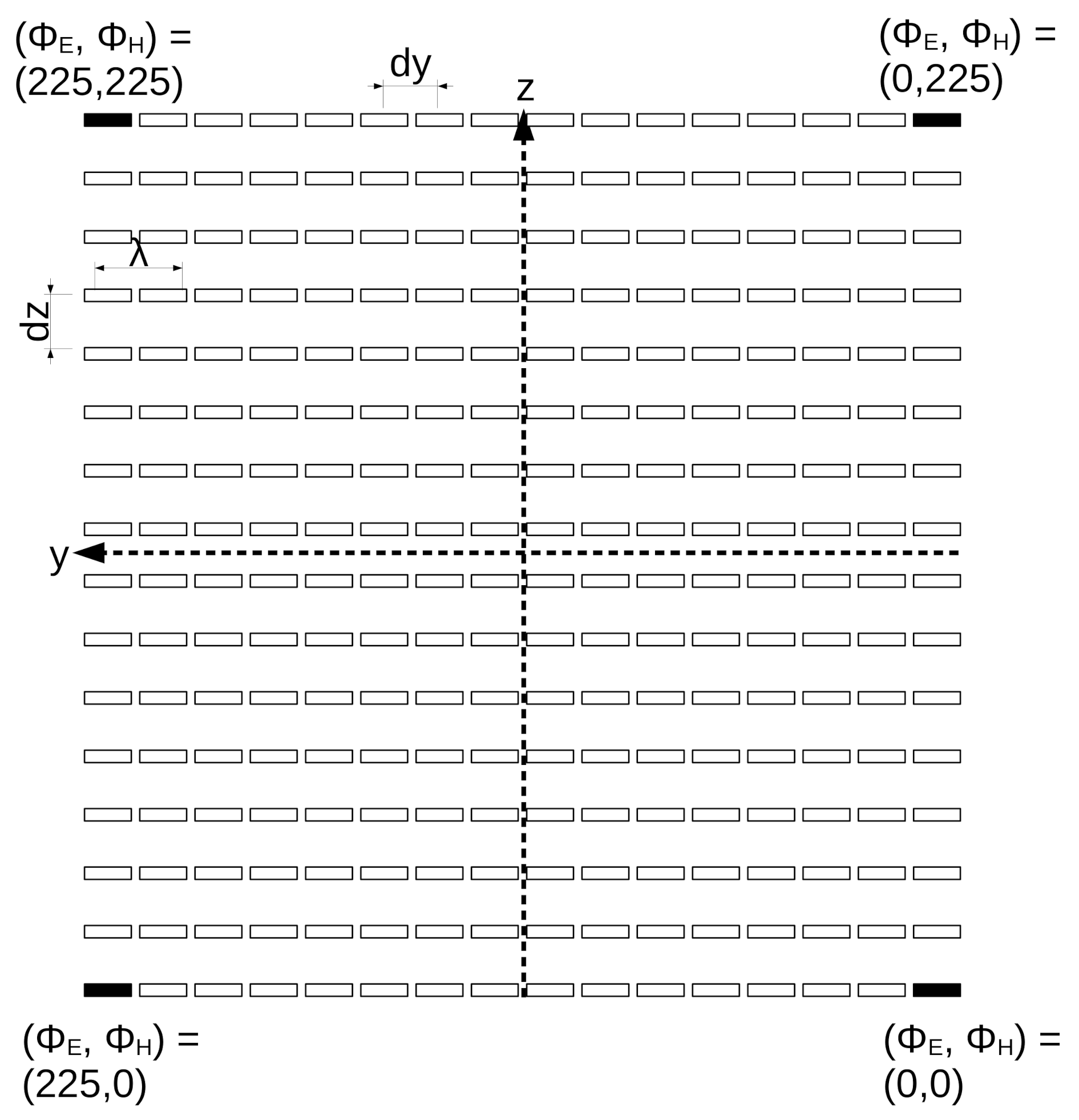
4. Phased Array Designs in Two Dimensions: Three-Dimensional Fields
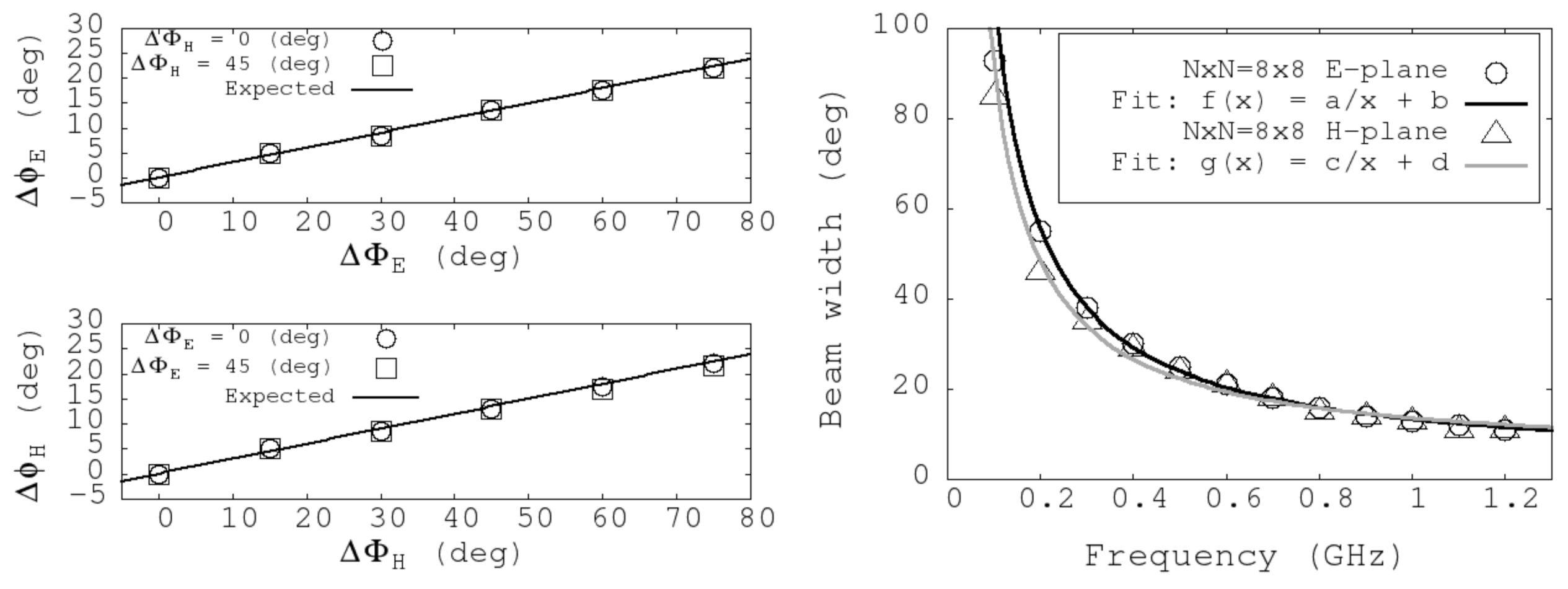
4.1. Phase Steering, Beam Angle, and Beamwidth
4.2. Radiation Patterns
5. Variation of the Index of Refraction
6. Summary and Future Analysis
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Syrytsin, I.; Zhang, S.; Pedersen, G.F. Circularly Polarized Planar Helix Phased Antenna Array for 5G Mobile Terminals. In Proceedings of the 2017 International Conference on Electromagnetics in Advanced Applications (ICEAA), Verona, Italy, 11–15 September 2017; pp. 1105–1108. [Google Scholar] [CrossRef]
- Kikuchi, K.; Mikada, H.; Takekawa, J. Improved Imaging Capability of Phased Array Antenna in Ground Penetrating Radar Survey. In Proceedings of the Conference Proceedings, 79th EAGE Conference and Exhibition, Paris, France, 12–15 June 2017. [Google Scholar] [CrossRef]
- Vieregg, A.; Bechtol, K.; Romero-Wolf, A. A technique for detection of PeV neutrinos using a phased radio array. J. Cosmol. Astropart. Phys. 2016, 2016, 005. [Google Scholar] [CrossRef]
- Munekata, T.; Yamamoto, M.; Nojima, T. A Wideband 16-Element Antenna Array Using Leaf-Shaped Bowtie Antenna and Series-Parallel Feed Networks. In Proceedings of the 2014 IEEE International Workshop on Electromagnetics (iWEM), Sapporo Hokkaido, Japan, 4–6 August 2014; pp. 80–81. [Google Scholar] [CrossRef]
- Avva, J.; Bechtol, K.; Chesebro, T.; Cremonisi, L.; Deaconu, C.; Gupta, A.; Ludwig, A.; Messino, W.; Miki, C.; Nichol, R.; et al. Development Toward a Ground-Based Interferometric Phased Array for Radio Detection of High Energy Neutrinos. In Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment; Elsvier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Ansys, Inc. 3D Electromagnetic Field Simulator for RF and Wireless Design; Ansys, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Feng, N.; Zhang, Y.; Tian, X.; Zhu, J.; Joines, W.T.; Wang, G.P. System-Combined ADI-FDTD Method and Its Electromagnetic Applications in Microwave Circuits and Antennas. IEEE Trans. Microw. Theory Tech. 2019, 67, 3260–3270. [Google Scholar] [CrossRef]
- Zhu, L.; Hwang, H.S.; Ren, E.; Yang, G. High Performance MIMO Antenna for 5G Wearable Devices. In Proceedings of the 2017 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, San Diego, CA, USA, 9–15 July 2017; pp. 1869–1870. [Google Scholar] [CrossRef]
- Ho, T.Q.; Hunt, L.N.; Hewett, C.A.; Ready, T.G.; Mittra, R.; Yu, W.; Zolnick, D.A.; Kragalott, M. Analysis of Electrically Large Patch Phased Arrays via CFDTD. In Proceedings of the 2006 IEEE Antennas and Propagation Society International Symposium, Albuquerque, New Mexico, 9–14 July 2006; pp. 1571–1574. [Google Scholar] [CrossRef]
- Burke, G.J.; Miller, E.K.; Poggio, A.J. The Numerical Electromagnetics Code (NEC)—A Brief History. IEEE Antennas Propag. Soc. Symp. 2004, 3, 2871–2874. [Google Scholar] [CrossRef]
- Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bermel, P.; Joannopoulos, J.; Johnson, S.G. Meep: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 687–702. [Google Scholar] [CrossRef]
- Fedeli, A.; Montecucco, C.; Gragnani, G.L. Open-Source Software for Electromagnetic Scattering Simulation: The Case of Antenna Design. Electronics 2019, 8, 1506. [Google Scholar] [CrossRef]
- Liebig, T.; Rennings, A.; Held, S.; Erni, D. openEMS—A free and open source equivalent-circuit (EC) FDTD simulation platform supporting cylindrical coordinates suitable for the analysis of traveling wave MRI applications. Int. J. Numer. Model. Electron. Networks Dev. Fields 2013, 26, 680–696. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Giannakis, I. gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef]
- Richie, J.E.; Ababei, C. Optimization of patch antennas via multithreaded simulated annealing based design exploration. J. Comput. Des. Eng. 2017, 4, 249–255. [Google Scholar] [CrossRef]
- Mailloux, R. The Phased Array Antenna Handbook; Artech House: Norwood, MA, USA, 2018. [Google Scholar]
- Wahl, P.; Gagnon, D.S.L.; Debaes, C.; Erps, J.V.; Vermeulen, N.; Miller, D.A.B.; Thienpont, H. B-CALM: An Open-Source Multi-GPU-based 3D-FDTD with Mutli-pole dispersion for Plasmonics. Prog. Electromagn. Res. 2013, 138, 467–478. [Google Scholar] [CrossRef][Green Version]
- Gorham, P.; Allison, P.; Barwick, S.; Beatty, J.; Besson, D.; Binns, W.; Chen, C.; Chen, P.; Clem, J.; Connolly, A.; et al. The Antarctic Impulsive Transient Antenna ultra-high energy neutrino detector: Design, performance, and sensitivity for the 2006–2007 balloon flight. Astropart. Phys. 2009, 32, 10–41. [Google Scholar] [CrossRef]
- Gorham, P.; Barwick, S.; Beatty, J.; Besson, D.; Binns, W.; Chen, C.; Chen, P.; Clem, J.; Connolly, A.; Dowkontt, P. Observations of the Askaryan effect in ice. Phys. Rev. Lett. 2007, 99, 171101. [Google Scholar] [CrossRef] [PubMed]
- Barwick, S.; Berg, E.; Besson, D.; Duffin, T.; Hanson, J.; Klein, S.; Kleinfelder, S.; Piasecki, M.; Ratzlaff, K.; Reed, C.; et al. Time-domain response of the ARIANNA detector. Astropart. Phys. 2015, 62, 139–151. [Google Scholar] [CrossRef]
- Hanson, J.C. Ross Ice Shelf Thickness, Radio-frequency Attenuation and Reflectivity: Implications for the Arianna Uhe Neutrino Detector. In Proceedings of the 32nd International Cosmic Ray Conference, Beijing, China, 11–18 August 2011. [Google Scholar] [CrossRef]
- Hanson, J.C.; Barwick, S.W.; Berg, E.C.; Besson, D.Z.; Duffin, T.J.; Klein, S.R.; Kleinfelder, S.A.; Reed, C.; Roumi, M.; Stezelberger, T.; et al. Radar absorption, basal reflection, thickness and polarization measurements from the Ross Ice Shelf, Antarctica. J. Glaciol. 2015, 61, 438–446. [Google Scholar] [CrossRef]
- Avva, J.; Kovac, J.; Miki, C.; Saltzberg, D.; Vieregg, A. An in situ measurement of the radio-frequency attenuation in ice at Summit Station, Greenland. J. Glaciol. 2014. [Google Scholar] [CrossRef]
- Adamidis, G.A.; Vardiambasis, I.O.; Ioannidou, M.P.; Kapetanakis, T.N. Design and implementation of an adaptive beamformer for phased array antenna applications. Microw. Opt. Technol. Lett. 2020, 62, 1780–1784. [Google Scholar] [CrossRef]
- Ahn, B.; Hwang, I.J.; Kim, K.S.; Chae, S.C.; Yu, J.W.; Lee, H.L. Wide-Angle Scanning Phased Array Antenna using High Gain Pattern Reconfigurable Antenna Elements. Sci. Rep. 2019, 9, 18391. [Google Scholar] [CrossRef] [PubMed]
- Gampala, G.; Reddy, C.J. Advanced Computational Tools for Phased Array Antenna Applications. In Proceedings of the 2016 IEEE International Symposium on Phased Array Systems and Technology (PAST), Waltham, MA, USA, 18–21 October 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Dookayka, K. Characterizing the Search for Ultra-High Energy Neutrinos with the ARIANNA Detector. Ph.D. Thesis, Univeristy of California at Irvine, Irvine, CA, USA, 2011. [Google Scholar]
- Barwick, S.W.; Berg, E.C.; Besson, D.Z.; Gaswint, G.; Glaser, C.; Hallgren, A.; Hanson, J.C.; Klein, S.R.; Kleinfelder, S.; Köpke, L.; et al. Observation of classically “forbidden” electromagnetic wave propagation and implications for neutrino detection. J. Cosmol. Astropart. Phys. 2018, 2018, 055. [Google Scholar] [CrossRef]
- Deaconu, C.; Vieregg, A.G.; Wissel, S.A.; Bowen, J.; Chipman, S.; Gupta, A.; Miki, C.; Nichol, R.J.; Saltzberg, D. Measurements and Modeling of Near-Surface Radio Propagation in Glacial Ice and Implications for Neutrino Experiments. Physic. Rev. D 2018, 98, 043010. [Google Scholar] [CrossRef]
- Aguilar, J.A.; Allison, P.; Beatty, J.J.; Bernhoff, H.; Besson, D.; Bingefors, N.; Botner, O.; Buitink, S.; Carter, K.; Clark, B.A.; et al. Design and Sensitivity of the Radio Neutrino Observatory in Greenland (RNO-G). arXiv 2020, arXiv:2010.12279. [Google Scholar]
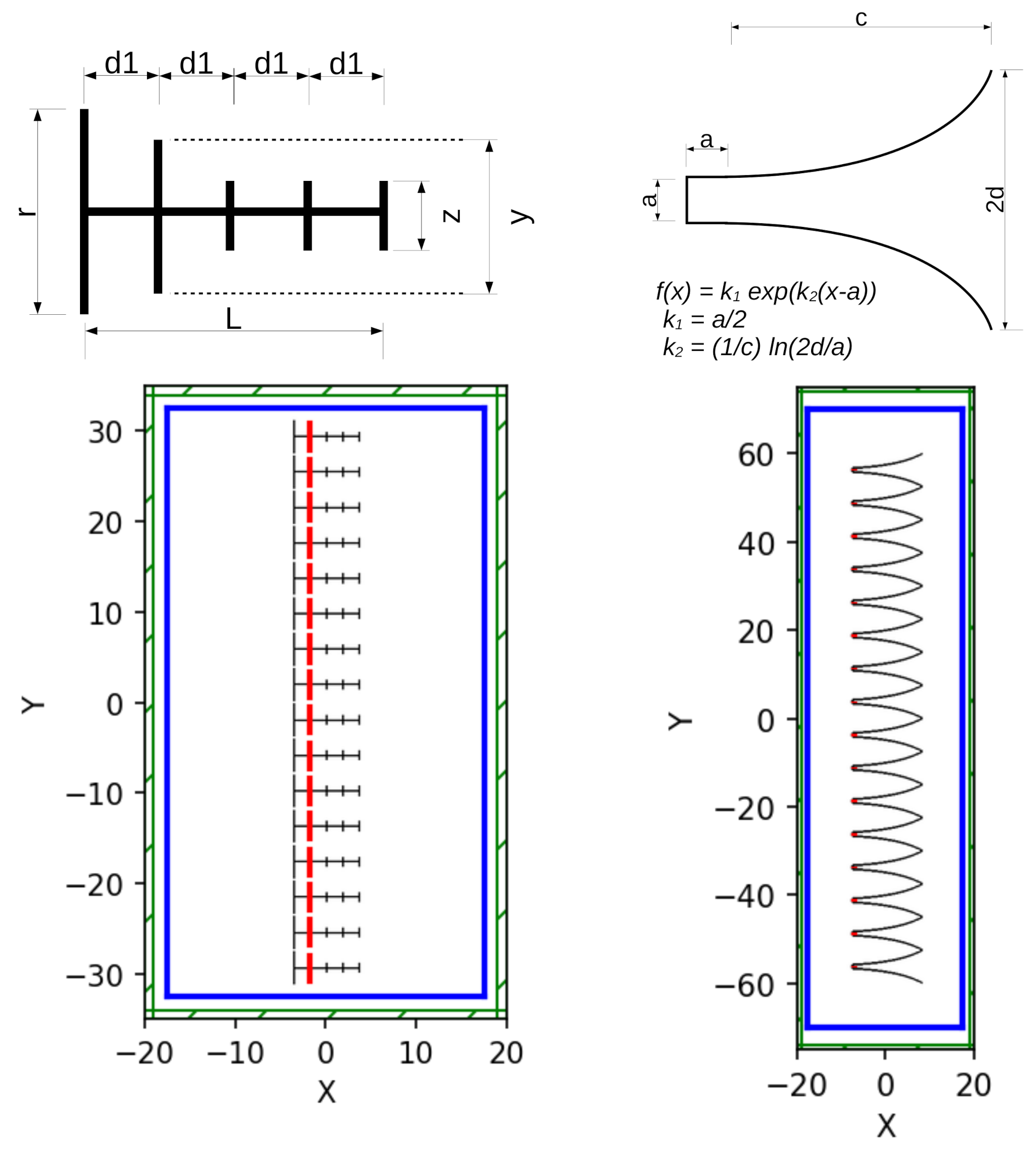

| Yagi-Uda | Horn | SLdb | |||||
|---|---|---|---|---|---|---|---|
| Parameter | Value | Parameter | Value | f (GHz) | (degrees) | ||
| N | 8.16 | N | 8.16 | 0.5 | 80 | 0.125 | −11.6 |
| L | 7.20 | a | 0.95 | 1.0 | 80 | 0.25 | −1.2 |
| 1.80 | c | 15.0 | 2.0 | 80 | 0.5 | −1.0 | |
| r | 3.75 | d | 3.8 | 4.0 | 80 | 1.0 | −0.9 |
| y | 2.81 | 0.1 | |||||
| z | 1.24 | 150 | |||||
| 3.92 | 2d | ||||||
| resolution | 6 | resolution | 6 |
| Horn | ||
|---|---|---|
| Parameter | Value | System Information |
| Memory Consumption | ||
| a | 2.0 | 11.7 GB out of 15.5 GB |
| c | 15.0 | |
| d | 8.0 | CPU cores |
| 0.5 | Intel i7 1.80 GHz (8) | |
| 30 | ||
| 16 | MEEP installation | |
| resolution | 4 | Python3 interface (conda) |
| backplane location | ||
| backplane thickness | 0.5 | |
| backplane dim. | 142 × 142 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hanson, J.C. Broadband RF Phased Array Design with MEEP: Comparisons to Array Theory in Two and Three Dimensions. Electronics 2021, 10, 415. https://doi.org/10.3390/electronics10040415
Hanson JC. Broadband RF Phased Array Design with MEEP: Comparisons to Array Theory in Two and Three Dimensions. Electronics. 2021; 10(4):415. https://doi.org/10.3390/electronics10040415
Chicago/Turabian StyleHanson, Jordan C. 2021. "Broadband RF Phased Array Design with MEEP: Comparisons to Array Theory in Two and Three Dimensions" Electronics 10, no. 4: 415. https://doi.org/10.3390/electronics10040415
APA StyleHanson, J. C. (2021). Broadband RF Phased Array Design with MEEP: Comparisons to Array Theory in Two and Three Dimensions. Electronics, 10(4), 415. https://doi.org/10.3390/electronics10040415






