Microgrids Power Quality Enhancement Using Model Predictive Control
Abstract
1. Introduction
1.1. Literature Review
1.2. Main Contributions
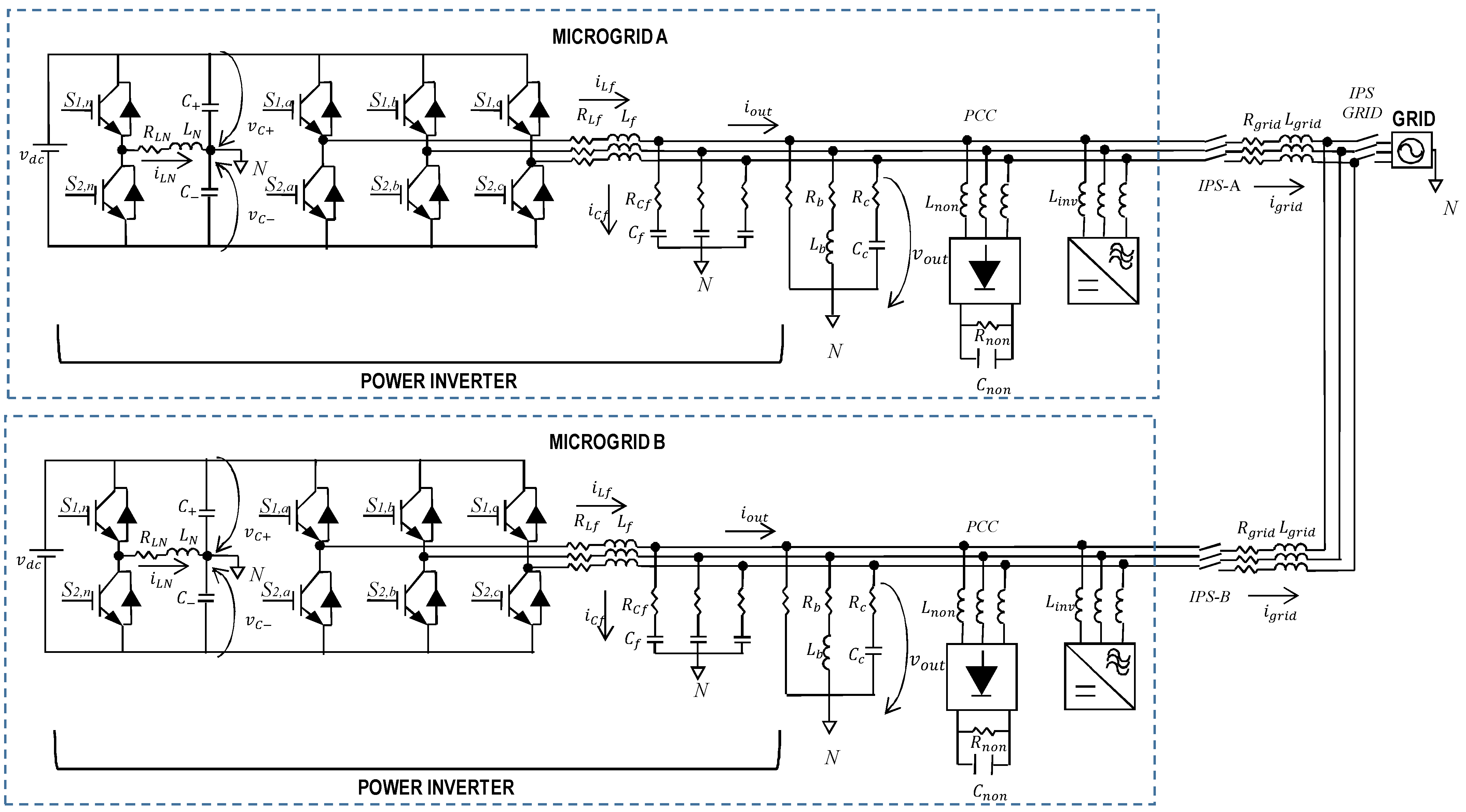
2. Controller Design
2.1. Fourier Expressions
2.2. Predictive Model of the VSI
2.3. Cost Function for the Islanded Mode
2.4. Cost Function for the Grid-Connected Mode
2.5. Cost Function for the Interconnected Mode
3. Simulation Results
3.1. Comparison between MPC and PI-PWM Controllers for Single Microgrids
3.2. Power Quality Management Results for Interconnected Microgrids Working without Presence of Grid
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CCS | Continuous Control Set |
| DER | Distributed Energy Resources |
| DMPC | Distributed Model Predictive Control |
| ESS | Energy Storage System |
| FCS | Finite Control State |
| GPC | Generalized Predictive Control |
| MPC | Model Predictive Control |
| PQR | Power Quality and Realibility |
| RES | Renewable Energy System |
| SHE | Selective Harmonic Elimination |
| SP | Smith Predictor |
| VSI | Voltage Source Inverter |
References
- Bollen, M.; Zhong, J.; Zavoda, F.; Meyer, J.; McEachern, A.; Lopez, F.C. Power quality aspects of smart grids. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’10), Granada, Spain, 23–25 March 2010. [Google Scholar]
- Vasquez, J.C.; Guerrero, J.M.; Miret, J.; Castilla, M.; De Vicuna, L.G. Hierarchical control of intelligent microgrids. IEEE Ind. Electron. Mag. 2010, 4, 23–29. [Google Scholar] [CrossRef]
- Olivares, D.E.; Mehrizi-Sani, A.; Etemadi, A.H.; Cañizares, C.A.; Iravani, R.; Kazerani, M.; Hajimiragha, A.H.; Gomis-Bellmunt, O.; Saeedifard, M.; Palma-Behnke, R.; et al. Trends in microgrid control. IEEE Trans. Smart Grid 2014, 5, 1905–1919. [Google Scholar] [CrossRef]
- Han, Y.; Li, H.; Shen, P.; Coelho, E.A.A.; Guerrero, J.M. Review of active and reactive power sharing strategies in hierarchical controlled microgrids. IEEE Trans. Power Electron. 2016, 32, 2427–2451. [Google Scholar] [CrossRef]
- Rajesh, K.; Dash, S.; Rajagopal, R.; Sridhar, R. A review on control of ac microgrid. Renew. Sustain. Energy Rev. 2017, 71, 814–819. [Google Scholar] [CrossRef]
- Yu, X.; Khambadkone, A.M.; Wang, H.; Terence, S.T.S. Control of parallel-connected power converters for low-voltage microgrid—Part I: A hybrid control architecture. IEEE Trans. Power Electron. 2010, 25, 2962–2970. [Google Scholar] [CrossRef]
- Vandoorn, T.L.; De Kooning, J.D.; Meersman, B.; Guerrero, J.M.; Vandevelde, L. Automatic power-sharing modification of P/V droop controllers in low-voltage resistive microgrids. IEEE Trans. Power Deliv. 2012, 27, 2318–2325. [Google Scholar] [CrossRef]
- Guerrero, J.M.; De Vicuña, L.G.; Matas, J.; Castilla, M.; Miret, J. Output impedance design of parallel-connected UPS inverters with wireless load-sharing control. IEEE Trans. Ind. Electron. 2005, 52, 1126–1135. [Google Scholar] [CrossRef]
- Micallef, A.; Apap, M.; Spiteri-Staines, C.; Guerrero, J.M.; Vasquez, J.C. Reactive power sharing and voltage harmonic distortion compensation of droop controlled single phase islanded microgrids. IEEE Trans. Smart Grid 2014, 5, 1149–1158. [Google Scholar] [CrossRef]
- Savaghebi, M.; Jalilian, A.; Vasquez, J.C.; Guerrero, J.M. Secondary control for voltage quality enhancement in microgrids. IEEE Trans. Smart Grid 2012, 3, 1893–1902. [Google Scholar] [CrossRef]
- Vazquez, S.; Rodriguez, J.; Rivera, M.; Franquelo, L.G.; Norambuena, M. Model predictive control for power converters and drives: Advances and trends. IEEE Trans. Ind. Electron. 2016, 64, 935–947. [Google Scholar] [CrossRef]
- Vazquez, S.; Montero, C.; Bordons, C.; Franquelo, L.G. Design and experimental validation of a model predictive control strategy for a VSI with long prediction horizon. In Proceedings of the IECON 2013-39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 5788–5793. [Google Scholar]
- Vazquez, S.; Acuna, P.; Aguilera, R.P.; Pou, J.; Leon, J.I.; Franquelo, L.G. DC-Link Voltage-Balancing Strategy Based on Optimal Switching Sequence Model Predictive Control for Single-Phase H-NPC Converters. IEEE Trans. Ind. Electron. 2019, 67, 7410–7420. [Google Scholar] [CrossRef]
- Acuna, P.; Moran, L.; Rivera, M.; Dixon, J.; Rodriguez, J. Improved active power filter performance for renewable power generation systems. IEEE Trans. Power Electron. 2013, 29, 687–694. [Google Scholar] [CrossRef]
- Antoniewicz, K.; Jasinski, M.; Kazmierkowski, M.P.; Malinowski, M. Model predictive control for three-level four-leg flying capacitor converter operating as shunt active power filter. IEEE Trans. Ind. Electron. 2016, 63, 5255–5262. [Google Scholar]
- Liu, X.; Wang, D.; Peng, Z. Cascade-free fuzzy finite-control-set model predictive control for nested neutral point-clamped converters with low switching frequency. IEEE Trans. Control Syst. Technol. 2018, 27, 2237–2244. [Google Scholar] [CrossRef]
- Mohapatra, S.R.; Agarwal, V. Model Predictive Control for Flexible Reduction of Active Power Oscillation in Grid-tied Multilevel Inverters under Unbalanced and Distorted Microgrid Conditions. IEEE Trans. Ind. Appl. 2019, 56, 1107–1115. [Google Scholar] [CrossRef]
- Wu, M.; Tian, H.; Li, Y.W.; Konstantinou, G.; Yang, K. A composite selective harmonic elimination model predictive control for seven-level hybrid-clamped inverters with optimal switching patterns. IEEE Trans. Power Electron. 2020, 36, 274–284. [Google Scholar] [CrossRef]
- Aguilera, R.P.; Acuna, P.; Lezana, P.; Konstantinou, G.; Wu, B.; Bernet, S.; Agelidis, V.G. Selective harmonic elimination model predictive control for multilevel power converters. IEEE Trans. Power Electron. 2016, 32, 2416–2426. [Google Scholar] [CrossRef]
- Shan, Y.; Hu, J.; Li, Z.; Guerrero, J.M. A model predictive control for renewable energy based ac microgrids without any pid regulators. IEEE Trans. Power Electron. 2018, 33, 9122–9126. [Google Scholar] [CrossRef]
- Prodanovic, M.; Green, T.C. High-quality power generation through distributed control of a power park microgrid. IEEE Trans. Ind. Electron. 2006, 53, 1471–1482. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Power management of an isolated hybrid AC/DC micro-grid with fuzzy control of battery banks. IET Renew. Power Gener. 2015, 9, 484–493. [Google Scholar] [CrossRef]
- Ahumada, C.; Cárdenas, R.; Saez, D.; Guerrero, J.M. Secondary control strategies for frequency restoration in islanded microgrids with consideration of communication delays. IEEE Trans. Smart Grid 2015, 7, 1430–1441. [Google Scholar] [CrossRef]
- Kayalvizhi, S.; Kumar, D.V. Load frequency control of an isolated micro grid using fuzzy adaptive model predictive control. IEEE Access 2017, 5, 16241–16251. [Google Scholar] [CrossRef]
- Lou, G.; Gu, W.; Xu, Y.; Cheng, M.; Liu, W. Distributed MPC-based secondary voltage control scheme for autonomous droop-controlled microgrids. IEEE Trans. Sustain. Energy 2016, 8, 792–804. [Google Scholar] [CrossRef]
- Kerdphol, T.; Rahman, F.S.; Mitani, Y.; Hongesombut, K.; Küfeoğlu, S. Virtual inertia control-based model predictive control for microgrid frequency stabilization considering high renewable energy integration. Sustainability 2017, 9, 773. [Google Scholar] [CrossRef]
- Gómez, J.S.; Sáez, D.; Simpson-Porco, J.W.; Cárdenas, R. Distributed predictive control for frequency and voltage regulation in microgrids. IEEE Trans. Smart Grid 2019, 11, 1319–1329. [Google Scholar] [CrossRef]
- Garcia-Torres, F.; Bordons, C.; Vazquez, S. Voltage predictive control for microgrids in islanded mode based on fourier transform. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 2358–2363. [Google Scholar]
- Kouro, S.; Perez, M.A.; Rodriguez, J.; Llor, A.M.; Young, H.A. Model predictive control: MPC’s role in the evolution of power electronics. IEEE Ind. Electron. Mag. 2015, 9, 8–21. [Google Scholar] [CrossRef]












| Parameter | Value |
|---|---|
| Filter inductance | 1 [mH] |
| Filter inductance resistance | 0.1 [] |
| Filter capacitor | 0.5 [mF] |
| Filter capacitor resistance | 0.1 [] |
| DC link voltage | 950 [V] |
| Neutral inductance | 2.5 [μF] |
| Neutral inductance resistance | 0.1 [] |
| Neutral balancing capacitors | 6600 [μF] |
| Grid connection line inductance | 0.1 [mH] |
| Grid connection line resistance | 0.1 [] |
| Slave inverter line inductance | 0.1 [mH] |
| Slave inverter line resistance | 0.1 [] |
| Non-linear load line inductance | 0.1 [mH] |
| Non-linear load line resistance | 0.1 [] |
| Non-linear load dc resistance | 60 [] |
| Non-linear load dc capacitor | 6.6 [mF] |
| Unbalanced load phase a resistance | 1 [M] |
| Unbalanced load phase b resistance | 10 [] |
| Unbalanced load phase c resistance | 10 [] |
| Unbalanced load phase b inductance | 1 [mH] |
| Unbalanced load phase c capacitor | 0.1 [mF] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garcia-Torres, F.; Vazquez, S.; Moreno-Garcia, I.M.; Gil-de-Castro, A.; Roncero-Sanchez, P.; Moreno-Munoz, A. Microgrids Power Quality Enhancement Using Model Predictive Control. Electronics 2021, 10, 328. https://doi.org/10.3390/electronics10030328
Garcia-Torres F, Vazquez S, Moreno-Garcia IM, Gil-de-Castro A, Roncero-Sanchez P, Moreno-Munoz A. Microgrids Power Quality Enhancement Using Model Predictive Control. Electronics. 2021; 10(3):328. https://doi.org/10.3390/electronics10030328
Chicago/Turabian StyleGarcia-Torres, Felix, Sergio Vazquez, Isabel M. Moreno-Garcia, Aurora Gil-de-Castro, Pedro Roncero-Sanchez, and Antonio Moreno-Munoz. 2021. "Microgrids Power Quality Enhancement Using Model Predictive Control" Electronics 10, no. 3: 328. https://doi.org/10.3390/electronics10030328
APA StyleGarcia-Torres, F., Vazquez, S., Moreno-Garcia, I. M., Gil-de-Castro, A., Roncero-Sanchez, P., & Moreno-Munoz, A. (2021). Microgrids Power Quality Enhancement Using Model Predictive Control. Electronics, 10(3), 328. https://doi.org/10.3390/electronics10030328











