An Ensemble Learning Approach Based on Diffusion Tensor Imaging Measures for Alzheimer’s Disease Classification
Abstract
1. Introduction
2. Diffusion Tensor Imaging
3. Materials and Methods
3.1. Data Collection
3.2. Image Processing and Feature Extraction
- 1.
- Application of a nonlinear registration for the alignment of all fractional anisotropy maps to a common registration template: in the present analysis, we used the mean FMRIB58_FA standard target, available with the software, obtained as the average of 58 FA images in the MNI152 standard space. This step was performed for MD, RD and LD maps too.
- 2.
- Affine transformation of the entire aligned dataset to a mm standard space: the aligned maps were transformed into the standard space template MNI152.
- 3.
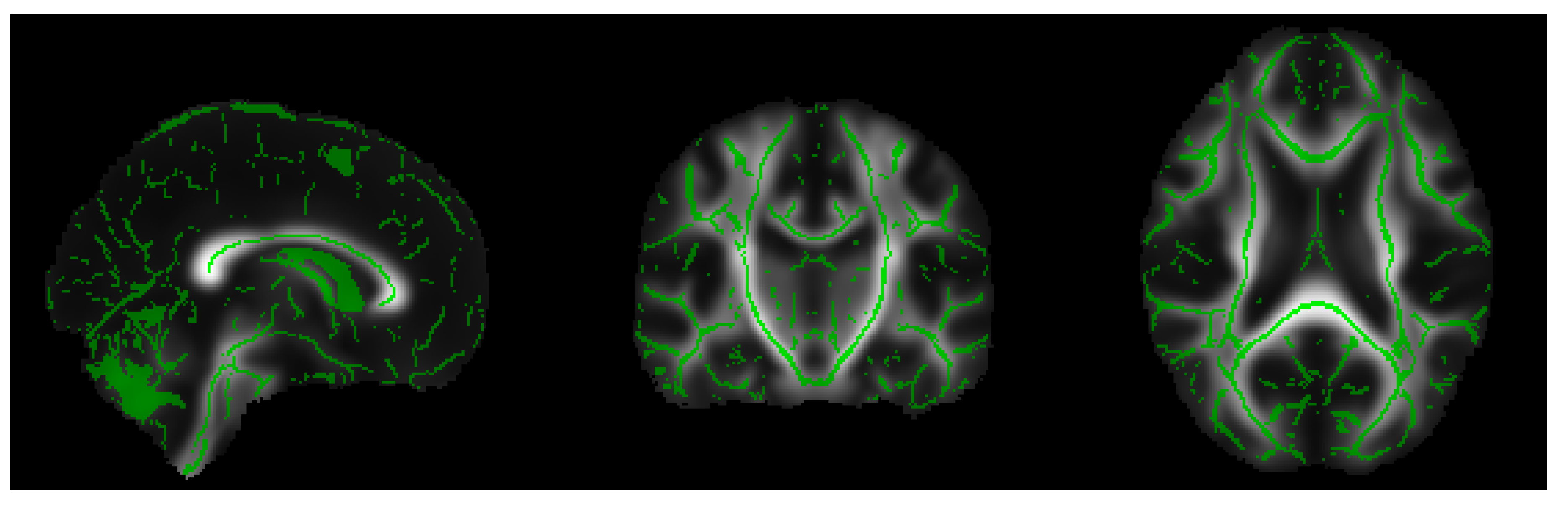
- Extraction of the white matter skeleton: by averaging all the FA maps of the dataset, a mean FA image was obtained, and this result was used to create a mean FA skeleton of WM fiber tracts that were common to all subjects (see Figure 1). A threshold was applied to the mean FA skeleton in order to exclude gray matter and cerebrospinal fluid voxels, and the voxels of the zones characterized by greater inter-subject variability belonging to the outermost part of the cortex.
- 4.
- Projection of all FA maps onto the mean FA skeleton: this allowed us to achieve an alignment among all subjects in the direction orthogonal to the fiber bundle orientation. The same elaboration steps were applied to RD, MD and LD maps.
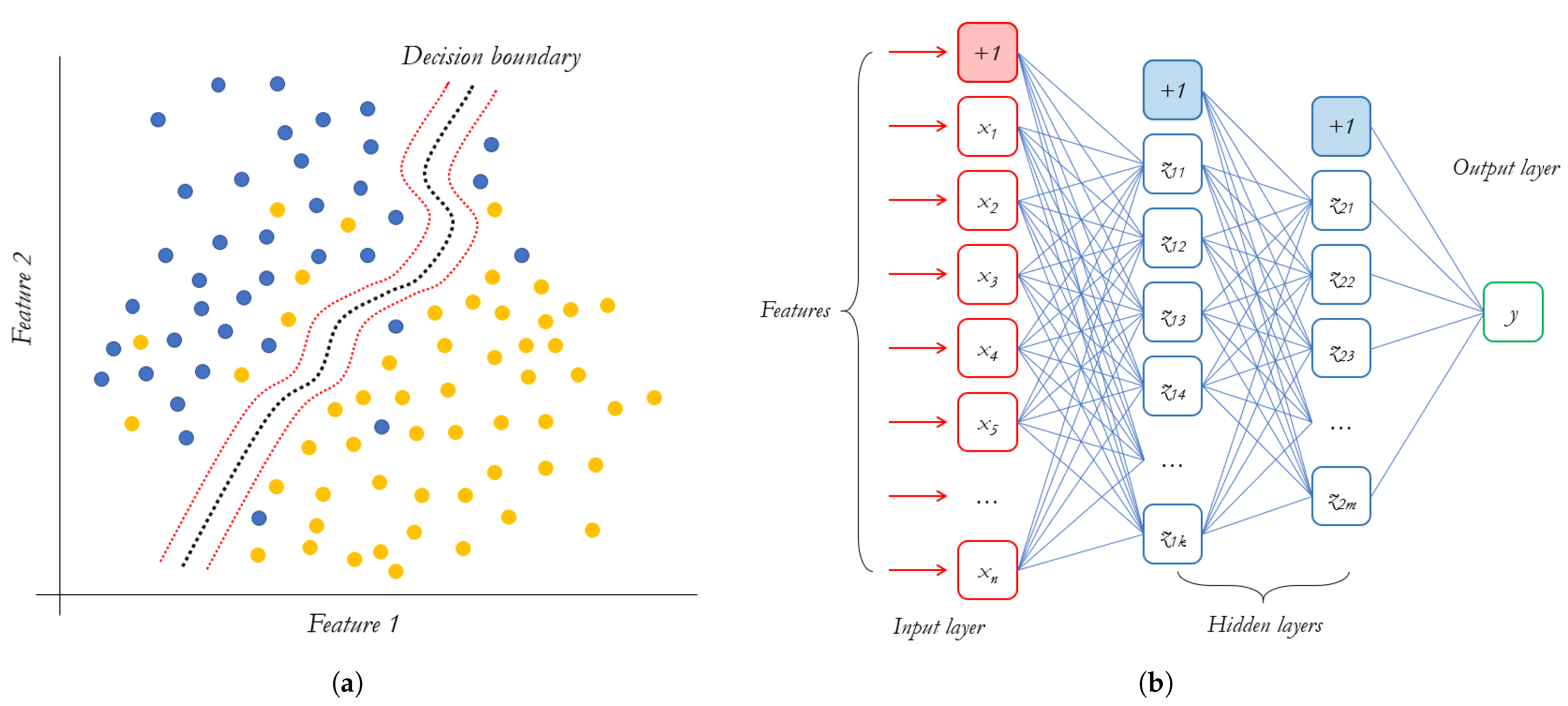
3.3. Classification Methods
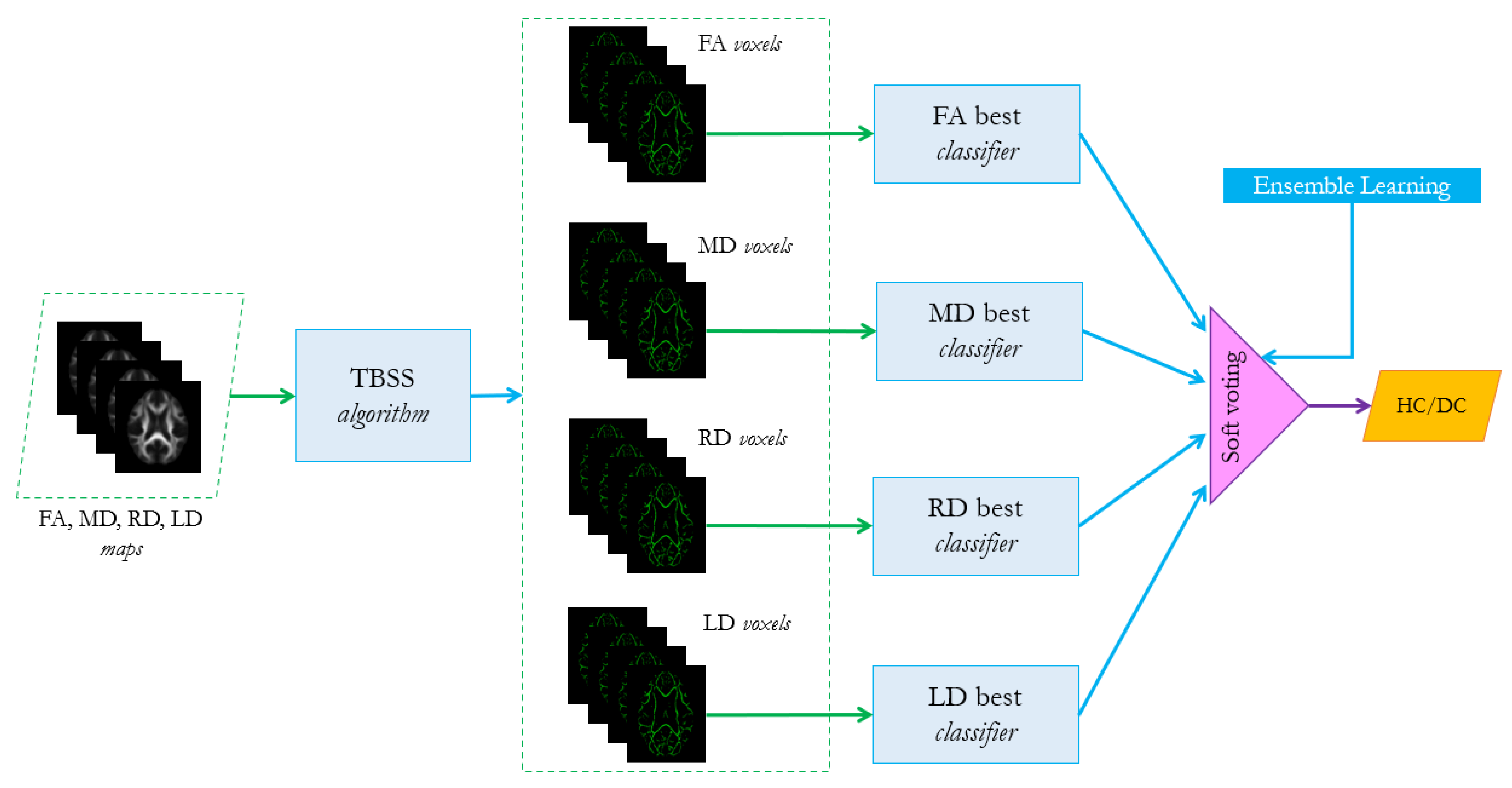
3.4. Learning Experiment
- 1.
- For each group of features in (FA, MD, RD, LD) and their combined feature vector, find the best associated classifier among the three algorithms SVM, RF and MLP, as described in Section 3.3. A 5-fold cross validation grid search procedure should be performed to tune the hyperparameters and evaluate the best performer for each configuration, as shown in Table 2.For instance, for configuration 1-1 the model is chosen among SVM, RF and MLP.
- 2.
- For each possible configuration listed in Table 1, evaluate the performance of the ensemble learning algorithm, based on the combination of the best classifier selected in step 1. The voting scheme is a soft-voting procedure which is based on averaging the probability scores given by the individual classifiers according to the following equation:where is the ensemble predicted label, n is the number of classifiers, is the weight that can be assigned to the jth classifier (in the present analysis we consider uniform weights) and is the probability score assigned to the ith class from the jth classifier. In the case of binary classification . The ensemble algorithm analyzed in the present work refers to the ensemble.VotingClassifier method of Python scikit-learn library [44]. The choice of this scheme is due to the fact that it is more flexible than the hard one, since it takes into account the classifiers’ uncertainty about the final decision, which is more informative than the simple binary prediction.
- 3.
- Repeat steps 1 and 2 on a balanced dataset obtained from the original one (43 AD vs. 49 HC), removing 6 healthy controls using the instance hardness threshold method (IHT) of Smith et al. [45]. IHT is an under-sampling method for reducing class imbalance based on the removal of the “hard” instances (where instance hardness is the likelihood of being misclassified), while focusing on the majority class samples that overlap the minority class sample space. The balanced dataset is then composed of 43 diseased cases and 43 healthy controls.
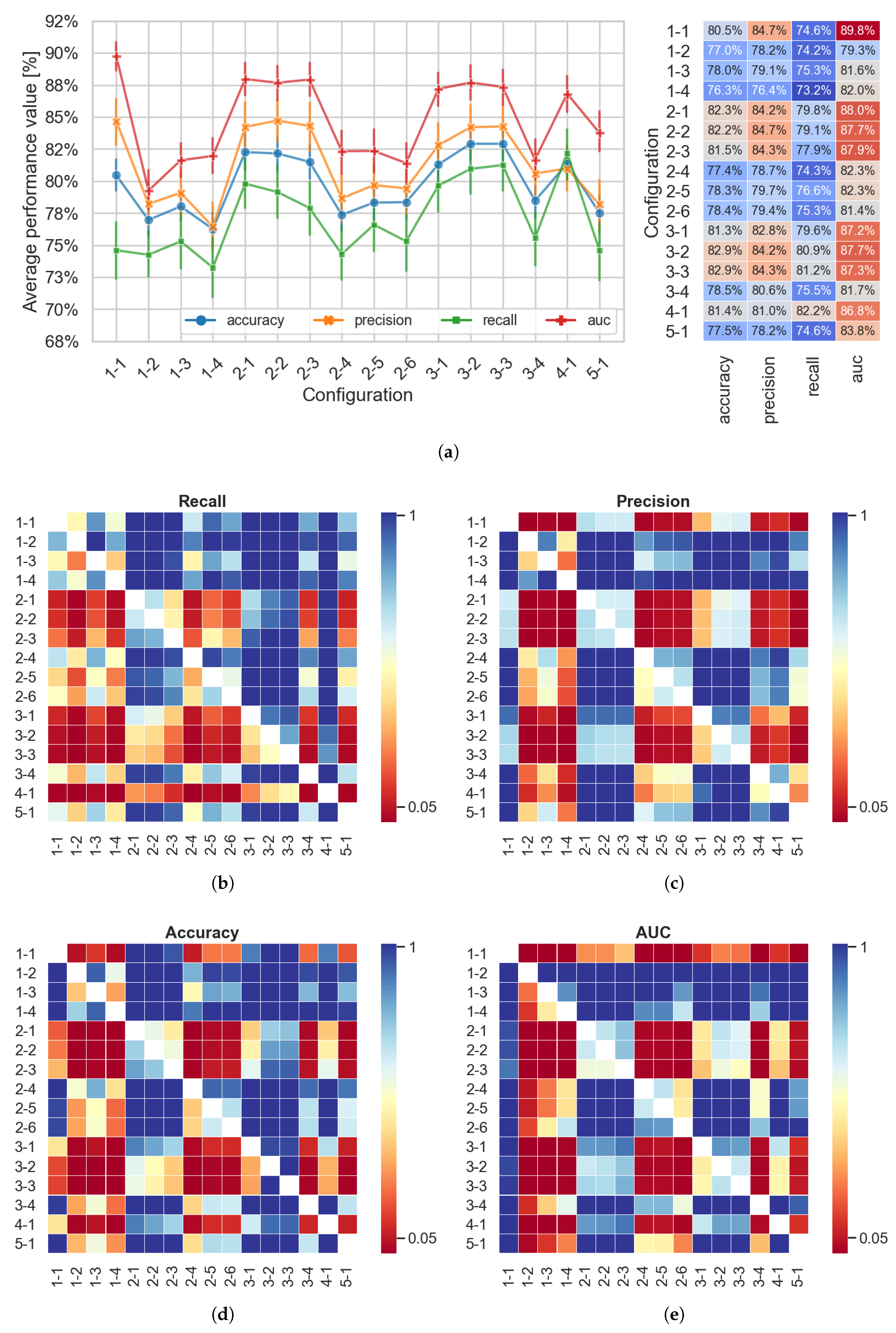
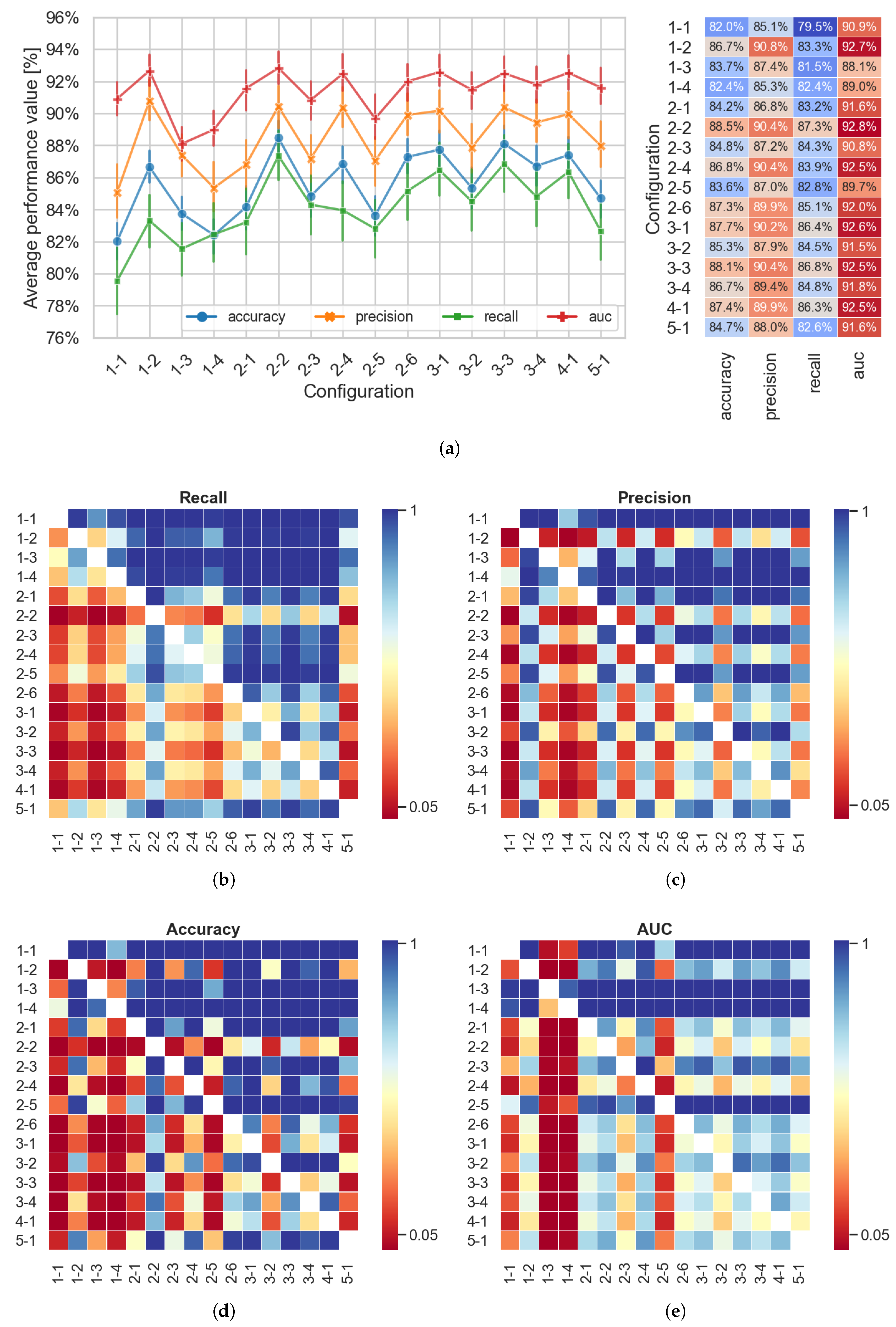
4. Results
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Prince, M.J. World Alzheimer Report 2015: The Global Impact of Dementia: An Analysis of Prevalence, Incidence, Cost and Trends; Alzheimer’s Disease International: London, UK, 2015. [Google Scholar]
- Rombouts, S.A.; Barkhof, F.; Goekoop, R.; Stam, C.J.; Scheltens, P. Altered resting state networks in mild cognitive impairment and mild Alzheimer’s disease: An fMRI study. Hum. Brain Mapp. 2005, 26, 231–239. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Y.; Wang, X.; Liu, B.; Xi, Q.; Guo, Q.; Jiang, H.; Jiang, T.; Wang, P. Disrupted small-world brain networks in moderate Alzheimer’s disease: A resting-state FMRI study. PLoS ONE 2012, 7, e33540. [Google Scholar] [CrossRef]
- Lella, E.; Amoroso, N.; Lombardi, A.; Maggipinto, T.; Tangaro, S.; Bellotti, R.; Initiative, A.D.N. Communicability disruption in Alzheimer’s disease connectivity networks. J. Complex Netw. 2019, 7, 83–100. [Google Scholar] [CrossRef]
- Sidey-Gibbons, J.A.; Sidey-Gibbons, C.J. Machine learning in medicine: A practical introduction. BMC Med. Res. Methodol. 2019, 19, 64. [Google Scholar] [CrossRef] [PubMed]
- Al-Turjman, F.; Nawaz, M.H.; Ulusar, U.D. Intelligence in the Internet of medical things era: A systematic review of current and future trends. Comput. Commun. 2020, 150, 644–660. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef]
- Casalino, G.; Castellano, G.; Consiglio, A.; Liguori, M.; Nuzziello, N.; Primiceri, D. A Predictive Model for MicroRNA Expressions in Pediatric Multiple Sclerosis Detection. In International Conference on Modeling Decisions for Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2019; pp. 177–188. [Google Scholar]
- Angelillo, M.T.; Balducci, F.; Impedovo, D.; Pirlo, G.; Vessio, G. Attentional pattern classification for automatic dementia detection. IEEE Access 2019, 7, 57706–57716. [Google Scholar] [CrossRef]
- Dyrba, M.; Ewers, M.; Wegrzyn, M.; Kilimann, I.; Plant, C.; Oswald, A.; Meindl, T.; Pievani, M.; Bokde, A.L.; Fellgiebel, A.; et al. Robust automated detection of microstructural white matter degeneration in Alzheimer’s disease using machine learning classification of multicenter DTI data. PLoS ONE 2013, 8, e64925. [Google Scholar] [CrossRef]
- Lella, E.; Amoroso, N.; Bellotti, R.; Diacono, D.; La Rocca, M.; Maggipinto, T.; Monaco, A.; Tangaro, S. Machine learning for the assessment of Alzheimer’s disease through DTI. SPIE Proc. 2017, 10396, 1039619. Available online: https://www.spiedigitallibrary.org/conference-proceedings-of-spie/10396/2293188/Front-Matter-Volume-10396/10.1117/12.2293188.full?SSO=1 (accessed on 21 January 2021).
- Lian, C.; Liu, M.; Zhang, J.; Shen, D. Hierarchical fully convolutional network for joint atrophy localization and Alzheimer’s Disease diagnosis using structural MRI. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 42, 880–893. [Google Scholar] [CrossRef]
- Wee, C.Y.; Yap, P.T.; Li, W.; Denny, K.; Browndyke, J.N.; Potter, G.G.; Welsh-Bohmer, K.A.; Wang, L.; Shen, D. Enriched white matter connectivity networks for accurate identification of MCI patients. Neuroimage 2011, 54, 1812–1822. [Google Scholar] [CrossRef] [PubMed]
- Rose, S.E.; Chen, F.; Chalk, J.B.; Zelaya, F.O.; Strugnell, W.E.; Benson, M.; Semple, J.; Doddrell, D.M. Loss of connectivity in Alzheimer’s disease: An evaluation of white matter tract integrity with colour coded MR diffusion tensor imaging. J. Neurol. Neurosurg. Psychiatry 2000, 69, 528–530. [Google Scholar] [CrossRef] [PubMed]
- Head, D.; Buckner, R.L.; Shimony, J.S.; Williams, L.E.; Akbudak, E.; Conturo, T.E.; McAvoy, M.; Morris, J.C.; Snyder, A.Z. Differential vulnerability of anterior white matter in nondemented aging with minimal acceleration in dementia of the Alzheimer type: Evidence from diffusion tensor imaging. Cereb. Cortex 2004, 14, 410–423. [Google Scholar] [CrossRef] [PubMed]
- Basser, P.J.; Mattiello, J.; LeBihan, D. MR diffusion tensor spectroscopy and imaging. Biophys. J. 1994, 66, 259–267. [Google Scholar] [CrossRef]
- Le Bihan, D.; Mangin, J.F.; Poupon, C.; Clark, C.A.; Pappata, S.; Molko, N.; Chabriat, H. Diffusion tensor imaging: Concepts and applications. J. Magn. Reson. Imaging 2001, 13, 534–546. [Google Scholar] [CrossRef] [PubMed]
- O’Dwyer, L.; Lamberton, F.; Bokde, A.L.; Ewers, M.; Faluyi, Y.O.; Tanner, C.; Mazoyer, B.; O’Neill, D.; Bartley, M.; Collins, D.R.; et al. Using support vector machines with multiple indices of diffusion for automated classification of mild cognitive impairment. PLoS ONE 2012, 7, e32441. [Google Scholar] [CrossRef] [PubMed]
- Mesrob, L.; Sarazin, M.; Hahn-Barma, V.; Souza, L.C.D.; Dubois, B.; Gallinari, P.; Kinkingnéhun, S. DTI and structural MRI classification in Alzheimer’s disease. Adv. Mol. Imaging 2012, 2, 12–20. [Google Scholar] [CrossRef]
- Dyrba, M.; Barkhof, F.; Fellgiebel, A.; Filippi, M.; Hausner, L.; Hauenstein, K.; Kirste, T.; Teipel, S.J. Predicting Prodromal Alzheimer’s Disease in Subjects with Mild Cognitive Impairment Using Machine Learning Classification of Multimodal Multicenter Diffusion-Tensor and Magnetic Resonance Imaging Data. J. Neuroimaging 2015, 25, 738–747. [Google Scholar] [CrossRef]
- Dyrba, M.; Grothe, M.; Kirste, T.; Teipel, S.J. Multimodal analysis of functional and structural disconnection in Alzheimer’s disease using multiple kernel SVM. Hum. Brain Mapp. 2015, 36, 2118–2131. [Google Scholar] [CrossRef]
- Lella, E.; Estrada, E. Communicability distance reveals hidden patterns of Alzheimer’s disease. Netw. Neurosci. 2020, 4, 1–23. [Google Scholar] [CrossRef]
- Rasero, J.; Alonso-Montes, C.; Diez, I.; Olabarrieta-Landa, L.; Remaki, L.; Escudero, I.; Mateos, B.; Bonifazi, P.; Fernandez, M.; Arango-Lasprilla, J.C.; et al. Group-level progressive alterations in brain connectivity patterns revealed by diffusion-tensor brain networks across severity stages in Alzheimer’s disease. Front. Aging Neurosci. 2017, 9, 215. [Google Scholar] [CrossRef] [PubMed]
- Daianu, M.; Jahanshad, N.; Nir, T.M.; Toga, A.W.; Jack, C.R., Jr.; Weiner, M.W.; Thompson, P.M. Breakdown of brain connectivity between normal aging and Alzheimer’s disease: A structural k-core network analysis. Brain Connect. 2013, 3, 407–422. [Google Scholar] [CrossRef] [PubMed]
- Ebadi, A.; Dalboni da Rocha, J.L.; Nagaraju, D.B.; Tovar-Moll, F.; Bramati, I.; Coutinho, G.; Sitaram, R.; Rashidi, P. Ensemble classification of Alzheimer’s disease and mild cognitive impairment based on complex graph measures from diffusion tensor images. Front. Neurosci. 2017, 11, 56. [Google Scholar] [CrossRef] [PubMed]
- Prasad, G.; Joshi, S.H.; Nir, T.M.; Toga, A.W.; Thompson, P.M.; Alzheimer’s Disease Neuroimaging Initiative (ADNI). Brain connectivity and novel network measures for Alzheimer’s disease classification. Neurobiol. Aging 2015, 36, S121–S131. [Google Scholar] [CrossRef] [PubMed]
- Lella, E.; Lombardi, A.; Amoroso, N.; Diacono, D.; Maggipinto, T.; Monaco, A.; Bellotti, R.; Tangaro, S. Machine learning and dwi brain communicability networks for alzheimer’s disease detection. Appl. Sci. 2020, 10, 934. [Google Scholar] [CrossRef]
- Maggipinto, T.; Bellotti, R.; Amoroso, N.; Diacono, D.; Donvito, G.; Lella, E.; Monaco, A.; Scelsi, M.A.; Tangaro, S. DTI measurements for Alzheimer’s classification. Phys. Med. Biol. 2017, 62, 2361. [Google Scholar] [CrossRef]
- Dou, X.; Yao, H.; Feng, F.; Wang, P.; Zhou, B.; Jin, D.; Yang, Z.; Li, J.; Zhao, C.; Wang, L.; et al. Characterizing white matter connectivity in Alzheimer’s disease and mild cognitive impairment: An automated fiber quantification analysis with two independent datasets. Cortex 2020, 129, 390–405. [Google Scholar] [CrossRef]
- Da Rocha, J.L.D.; Bramati, I.; Coutinho, G.; Moll, F.T.; Sitaram, R. Fractional Anisotropy changes in parahippocampal cingulum due to Alzheimer’s Disease. Sci. Rep. 2020, 10, 1–8. [Google Scholar]
- Islam, J.; Zhang, Y. Brain MRI analysis for Alzheimer’s disease diagnosis using an ensemble system of deep convolutional neural networks. Brain Inform. 2018, 5, 2. [Google Scholar] [CrossRef]
- Suk, H.I.; Lee, S.W.; Shen, D.; Alzheimer’s Disease Neuroimaging Initiative. Deep ensemble learning of sparse regression models for brain disease diagnosis. Med. Image Anal. 2017, 37, 101–113. [Google Scholar] [CrossRef]
- Zheng, X.; Shi, J.; Zhang, Q.; Ying, S.; Li, Y. Improving MRI-based diagnosis of Alzheimer’s disease via an ensemble privileged information learning algorithm. In Proceedings of the 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017), Melbourne, Australia, 18–21 April 2017; pp. 456–459. [Google Scholar]
- Rokach, L. Ensemble-based classifiers. Artif. Intell. Rev. 2010, 33, 1–39. [Google Scholar] [CrossRef]
- Petersen, R.C.; Aisen, P.; Beckett, L.A.; Donohue, M.; Gamst, A.; Harvey, D.J.; Jack, C.; Jagust, W.; Shaw, L.; Toga, A.; et al. Alzheimer’s disease neuroimaging initiative (ADNI): Clinical characterization. Neurology 2010, 74, 201–209. [Google Scholar] [CrossRef] [PubMed]
- Maintz, J.A.; Viergever, M.A. A survey of medical image registration. Med. Image Anal. 1998, 2, 1–36. [Google Scholar] [CrossRef]
- Jenkinson, M.; Beckmann, C.F.; Behrens, T.E.; Woolrich, M.W.; Smith, S.M. FSL. Neuroimage 2012, 62, 782–790. [Google Scholar] [CrossRef]
- Smith, S.M.; Jenkinson, M.; Johansen-Berg, H.; Rueckert, D.; Nichols, T.E.; Mackay, C.E.; Watkins, K.E.; Ciccarelli, O.; Cader, M.Z.; Matthews, P.M.; et al. Tract-based spatial statistics: Voxelwise analysis of multi-subject diffusion data. Neuroimage 2006, 31, 1487–1505. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Ho, T.K. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Murtagh, F. Multilayer perceptrons for classification and regression. Neurocomputing 1991, 2, 183–197. [Google Scholar] [CrossRef]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Smith, M.R.; Martinez, T.; Giraud-Carrier, C. An instance level analysis of data complexity. Mach. Learn. 2014, 95, 225–256. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a test of whether one of two random variables is stochastically larger than the other. Ann. Math. Stat. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Hollander, M. Nonparametric Statistical Methods; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
- Benjamini, Y.; Hochberg, Y. Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B Methodol. 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Wei, Q.; Dunbrack, R.L., Jr. The role of balanced training and testing data sets for binary classifiers in bioinformatics. PLoS ONE 2013, 8, e67863. [Google Scholar] [CrossRef] [PubMed]
- Haller, S.; Nguyen, D.; Rodriguez, C.; Emch, J.; Gold, G.; Bartsch, A.; Lovblad, K.O.; Giannakopoulos, P. Individual prediction of cognitive decline in mild cognitive impairment using support vector machine-based analysis of diffusion tensor imaging data. J. Alzheimer’s Dis. 2010, 22, 315–327. [Google Scholar] [CrossRef]
- Lella, E.; Vessio, G. Ensembling complex network ‘perspectives’ for mild cognitive impairment detection with artificial neural networks. Pattern Recognit. Lett. 2020, 136, 168–174. [Google Scholar] [CrossRef]
- Pierpaoli, C.; Jezzard, P.; Basser, P.J.; Barnett, A.; Di Chiro, G. Diffusion tensor MR imaging of the human brain. Radiology 1996, 201, 637–648. [Google Scholar] [CrossRef]
- Schouten, T.M.; Koini, M.; de Vos, F.; Seiler, S.; de Rooij, M.; Lechner, A.; Schmidt, R.; van den Heuvel, M.; van der Grond, J.; Rombouts, S.A. Individual classification of Alzheimer’s disease with diffusion magnetic resonance imaging. Neuroimage 2017, 152, 476–481. [Google Scholar] [CrossRef]
- Patil, R.B.; Ramakrishnan, S. Analysis of sub-anatomic diffusion tensor imaging indices in white matter regions of Alzheimer with MMSE score. Comput. Methods Programs Biomed. 2014, 117, 13–19. [Google Scholar] [CrossRef]
- Douaud, G.; Menke, R.A.; Gass, A.; Monsch, A.U.; Rao, A.; Whitcher, B.; Zamboni, G.; Matthews, P.M.; Sollberger, M.; Smith, S. Brain microstructure reveals early abnormalities more than two years prior to clinical progression from mild cognitive impairment to Alzheimer’s disease. J. Neurosci. 2013, 33, 2147–2155. [Google Scholar] [CrossRef]
- Nir, T.M.; Villalon-Reina, J.E.; Prasad, G.; Jahanshad, N.; Joshi, S.H.; Toga, A.W.; Bernstein, M.A.; Jack, C.R., Jr.; Weiner, M.W.; Thompson, P.M.; et al. Diffusion weighted imaging-based maximum density path analysis and classification of Alzheimer’s disease. Neurobiol. Aging 2015, 36, S132–S140. [Google Scholar] [CrossRef]
- Billeci, L.; Badolato, A.; Bachi, L.; Tonacci, A. Machine Learning for the Classification of Alzheimer’s Disease and Its Prodromal Stage Using Brain Diffusion Tensor Imaging Data: A Systematic Review. Processes 2020, 8, 1071. [Google Scholar] [CrossRef]
- Tu, M.C.; Lo, C.P.; Huang, C.F.; Hsu, Y.H.; Huang, W.H.; Deng, J.F.; Lee, Y.C. Effectiveness of diffusion tensor imaging in differentiating early-stage subcortical ischemic vascular disease, Alzheimer’s disease and normal ageing. PLoS ONE 2017, 12, e0175143. [Google Scholar] [CrossRef] [PubMed]
- Shao, J.; Myers, N.; Yang, Q.; Feng, J.; Plant, C.; Böhm, C.; Förstl, H.; Kurz, A.; Zimmer, C.; Meng, C.; et al. Prediction of Alzheimer’s disease using individual structural connectivity networks. Neurobiol. Aging 2012, 33, 2756–2765. [Google Scholar] [CrossRef][Green Version]
- Graña, M.; Termenon, M.; Savio, A.; Gonzalez-Pinto, A.; Echeveste, J.; Pérez, J.; Besga, A. Computer aided diagnosis system for Alzheimer disease using brain diffusion tensor imaging features selected by Pearson’s correlation. Neurosci. Lett. 2011, 502, 225–229. [Google Scholar] [CrossRef] [PubMed]
- Parmar, C.; Grossmann, P.; Bussink, J.; Lambin, P.; Aerts, H.J. Machine learning methods for quantitative radiomic biomarkers. Sci. Rep. 2015, 5, 13087. [Google Scholar] [CrossRef]
- Basaia, S.; Agosta, F.; Wagner, L.; Canu, E.; Magnani, G.; Santangelo, R.; Filippi, M.; Alzheimer’s Disease Neuroimaging Initiative. Automated classification of Alzheimer’s disease and mild cognitive impairment using a single MRI and deep neural networks. NeuroImage Clin. 2019, 21, 101645. [Google Scholar] [CrossRef]
- Vieira, S.; Pinaya, W.H.; Mechelli, A. Using deep learning to investigate the neuroimaging correlates of psychiatric and neurological disorders: Methods and applications. Neurosci. Biobehav. Rev. 2017, 74, 58–75. [Google Scholar] [CrossRef]
- Alberdi, A.; Aztiria, A.; Basarab, A. On the early diagnosis of Alzheimer’s Disease from multimodal signals: A survey. Artif. Intell. Med. 2016, 71, 1–29. [Google Scholar] [CrossRef]
- Chételat, G. Multimodal neuroimaging in Alzheimer’s disease: Early diagnosis, physiopathological mechanisms, and impact of lifestyle. J. Alzheimer’s Dis. 2018, 64, S199–S211. [Google Scholar] [CrossRef]
- Ten Kate, M.; Redolfi, A.; Peira, E.; Bos, I.; Vos, S.J.; Vandenberghe, R.; Gabel, S.; Schaeverbeke, J.; Scheltens, P.; Blin, O.; et al. MRI predictors of amyloid pathology: Results from the EMIF-AD Multimodal Biomarker Discovery study. Alzheimer’s Res. Ther. 2018, 10, 100. [Google Scholar] [CrossRef] [PubMed]
| Label | Configuration | Label | Configuration |
|---|---|---|---|
| 1-1 | 2-5 | , | |
| 1-2 | 2-6 | , | |
| 1-3 | 3-1 | , , | |
| 1-4 | 3-2 | , , | |
| 2-1 | , | 3-3 | , , |
| 2-2 | , | 3-4 | , , |
| 2-3 | , | 4-1 | , , , |
| 2-4 | , | 5-1 |
| 1-1 | 1-2 | 1-3 | 1-4 | 5-1 | |
|---|---|---|---|---|---|
| 5-fold SVM best | SVM | SVM | SVM | SVM | SVM |
| 5-fold RF best | RF | RF | RF | RF | RF |
| 5-fold MLP best | MLP | MLP | MLP | MLP | MLP |
| Best Classifier |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lella, E.; Pazienza, A.; Lofù, D.; Anglani, R.; Vitulano, F. An Ensemble Learning Approach Based on Diffusion Tensor Imaging Measures for Alzheimer’s Disease Classification. Electronics 2021, 10, 249. https://doi.org/10.3390/electronics10030249
Lella E, Pazienza A, Lofù D, Anglani R, Vitulano F. An Ensemble Learning Approach Based on Diffusion Tensor Imaging Measures for Alzheimer’s Disease Classification. Electronics. 2021; 10(3):249. https://doi.org/10.3390/electronics10030249
Chicago/Turabian StyleLella, Eufemia, Andrea Pazienza, Domenico Lofù, Roberto Anglani, and Felice Vitulano. 2021. "An Ensemble Learning Approach Based on Diffusion Tensor Imaging Measures for Alzheimer’s Disease Classification" Electronics 10, no. 3: 249. https://doi.org/10.3390/electronics10030249
APA StyleLella, E., Pazienza, A., Lofù, D., Anglani, R., & Vitulano, F. (2021). An Ensemble Learning Approach Based on Diffusion Tensor Imaging Measures for Alzheimer’s Disease Classification. Electronics, 10(3), 249. https://doi.org/10.3390/electronics10030249






