Two-Stage Hybrid Network Clustering Using Multi-Agent Reinforcement Learning

Abstract

In the Internet-of-Things (IoT) environments, the publish (pub)/subscribe (sub)-operated communication is widely employed. The use of pub/sub operation as a lightweight communication protocol facilitates communication among IoTs. The protocol consists of network nodes functioning as publishers, subscribers, and brokers, wherein brokers transfer messages from publishers to subscribers. Thus, the communication capability of the broker is a critical factor in the overall communication performance. In this study, multi-agent reinforcement learning (MARL) is applied to find the best combination of broker nodes. MARL goes through various combinations of broker nodes to find the best combination. However, MARL is inefficient to perform with an excessive number of broker nodes. Delaunay triangulation selects candidate broker nodes among the pool of broker nodes. The selection process operates as a preprocessing of the MARL. The suggested Delaunay triangulation is improved by the custom deletion method. Consequently, the two-stage hybrid approach outperforms any methods employing single-agent reinforcement learning (SARL). The MARL eliminates the performance fluctuation of the SARL caused by the iterative selection of broker nodes. Furthermore, the proposed approach requires a fewer number of candidate broker nodes and converges faster.

1. Introduction

The publish (pub)/subscribe (sub)-operated communication protocol is commonly used in the Internet-of-Things (IoT) environment. The protocol consists of network nodes functioning as publishers, subscribers, and brokers. The broker transfers messages from publishers to subscribers according to the topic of each message [1]. Although the broker is the essence of the overall communication, it is also a potential hindrance in the pub/sub-operated communication system. The distribution (i.e., number and position) of brokers affects the overall performance of communication networks. A well-organized distribution of brokers affords significant advantages to network operations, i.e., it requires a relatively small amount of transmission energy and the round-trip delay of messages is low. The objective of this research is to develop an effective management scheme for broker distributions in the pub/sub-operated communication among IoT environments.

Effective clustering methods can assign acceptable broker nodes in the IoT environment using the pub/sub communication protocol. The clusters group the communicating nodes, and the centroid nodes of each cluster are acceptable candidate broker nodes. The k-means clustering algorithm is a commonly used clustering method that can be employed for broker assignment [2]. Although k-means clustering can group network nodes and determine the centroid of each cluster, it requires prior knowledge of the number of expected clusters (k).

It is proposed that multi-agent reinforcement learning (MARL) finds the best positions and the suitable number of brokers in the IoT communication network. With regard to the network nodes as agents in typical reinforcement learning, each agent learns whether or not it is to be assigned as a broker. The suggested reinforcement learning explores all candidate broker nodes. An agent generates a reward value at each iteration of the reinforcement learning. This reward value estimates the benefit of the broker assignment for the agent. At the end of learning, the best broker assignment among the candidate broker nodes can be found. The MARL expands reinforcement learning to find multiple brokers among multiple clusters. It estimates the individuals and aggregated reward values for available broker node combinations (Figure 1).

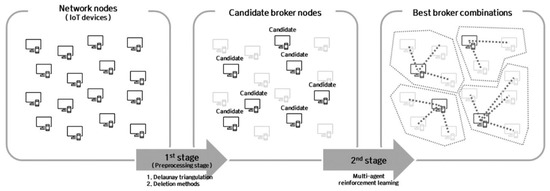
Figure 1. Overall process of two-stage hybrid clustering.

The number of available combinations to learn in MARL is $2^n$, where n is the number of candidate broker nodes. A successful MARL explores all available combinations; however, further explorations require excessive resources. In addition, all agents must learn to find the best broker node combination based on experience. The exponential increase in available combinations makes it considerably problematic to explore all combinations. A small number of available combinations reduces the burden of reward calculation and guarantees a complete feasibility check of all combinations. An effective method to reduce the number of available combinations while maintaining the MARL performance is to use a separate preprocessing stage to reduce the number of candidate broker nodes. Accordingly, the Delaunay triangulation and deletion methods are applied.

Delaunay triangulation reduces the solution space. Delaunay triangulation finds the center heads from the given candidate broker nodes. The center heads save the required resources to activate MARL. The suggested deletion method extends the selection process of Delaunay triangulation by deleting the unnecessary components and recovering the possible information loss. The consecutive and repeated use of the foregoing methods makes it possible to select the best candidate broker nodes from a given set of IoT network nodes.

In this research, the first stage includes the consecutive implementation of the Delaunay triangulation and deletion methods. In the second stage, the MARL is applied to find the best broker assignment in the IoT environment. Using the suggested two-stage hybrid method, effective IoT node clusters for the given pub/sub-operated communication environment can be built. As one of the advanced artificial intelligence (AI) techniques, the MARL performs practical broker assignments without manual computations; this proposed method outperforms typical k-means clustering. Note that single-agent reinforcement learning (SARL) is added to the typical k-means clustering for comparison with the proposed two-stage hybrid clustering method. Moreover, the SARL is employed with k-means clustering because the latter cannot determine the appropriate number of brokers alone [3,4].

Our main contributions are summarized as follows:

• We propose a network clustering algorithm that consists of a preprocessing stage and learning stage to find the best combination of brokers in pub/sub-operated communication protocol.
• We design a custom deletion method to implement Delaunay triangulation prior to MARL.
• We compare the proposed algorithm with three different algorithms: swarm intelligence-based algorithm, k-means clustering implemented SARL with and without preprocessing stage. The results show the superiority of the proposed two-stage hybrid network clustering algorithm compared with other algorithms.

2. Related Works

The proposed two-stage hybrid network clustering algorithm is mainly divided into two stages with different tasks: preprocessing and learning. The main method of the preprocessing stage is Delaunay triangulation which aligns with the Voronoi diagram. The proposed algorithm uses MARL in the learning stage. We use the clustering method to find the best broker combination. The clustering method is applied in various fields and the effective clustering algorithms differ on the task in each field.

2.1. Delaunay Triangulation and Voronoi Diagram

The Voronoi diagram is a set of dataspace partitions; each partition is called a Voronoi cell, which contains points. Each point in the cell is closest to the seed point than the points in other cells [5]. The Delaunay triangulation is an approach used to find the Voronoi diagram in the dataspace as well as superior seed points.

One of the applications of the Voronoi diagram is the location assignment of facilities, such as police stations or fire stations. These facilities should be located considering the shortest path to anywhere that the facility covers [6]. Thus, the seed points of Voronoi cells are potentially the best locations of facilities. Similarly, the brokers in pub/sub-operated communication should be located at the seed points of Voronoi cells to facilitate message transmission between publishers and subscribers.

2.2. Multi-Agent Reinforcement Learning (MARL)

The SARL can be effectively applied to the IoT environment [7,8]. When an independent pub/sub-operated communication within a single cluster is assumed, the single broker in a single cluster acts as a single agent. However, this simplification underestimates the effect of dynamic interactions among network nodes. The SARL has insufficient capability to model the states, actions, and rewards of the actual IoT environment; it requires a long time to converge and necessitates in-depth explorations of candidate broker nodes. Many network nodes cooperate and compete in IoT environments. The multiple network nodes in these environments act as multiple agents, which exert a complex influence on the evaluation of the IoT communication environment [9]. The MARL learns under the cooperative or competitive relationships among IoT network nodes. Each agent repeatedly updates its state and action to enhance the overall communication performance [10,11,12]. Wang et al. [13] used deep reinforcement learning to learn pattern formations for multi-robot systems. Pattern-RL uses an autoencoder to preprocess the large observation space. The deep reinforcement learning in Pattern-RL learns the strategy model to adapt to the pattern changes with the feedback of multiple agents. Yang et al. [14] used k-means clustering to classify the states into different clusters and solved the curse of the dimensionality problem in MARL.

The MARL is implemented in this study to find the best combination of the given candidate broker nodes. The candidate broker nodes act as agents in the MARL, learning whether they are to be fixed as the actual broker nodes. The initial candidate broker nodes are chosen randomly or based on experience. The reward function in the MARL evaluates the expected performance of the selected broker node combination.

2.3. Clustering Applications in Wireless Sensor Networks

The scaling network is an important research topic in the pub/sub-operated communication system, and message dissemination is a general method for solving network scaling problems. Longo et al. [15] introduced the message queuing telemetry transport-spanning tree (MQTT-ST) protocol for interconnecting distributed pub/sub-operated brokers. They aimed at horizontal clustering, focusing on network load balancing. Each broker belongs to different network clusters to minimize the network load difference among them. Moreover, Jutadhamakorn et al. [16] studied load balancing and dynamically allocated brokers in terms of network load status. Koziolek et al. [17] evaluated the usability of message queuing telemetry transport (MQTT) brokers for distributed IoT edge computing. The number of network nodes determined the arrangement of MQTT brokers in the clusters.

Considering only the network loads is not sufficient for practical network management. In this regard, geometric scalability is another important factor for effective network clustering. In particular, the pub/sub-operated communication framework necessitates effective geometrical clustering over a relatively big area. Clustering algorithms use distance data to determine the distribution (i.e., number and position) of brokers; cluster heads obtained by the clustering algorithm can be potential brokers. In wireless sensor networks, the clustering algorithms focus on enhancing reliability, reducing energy consumption, or strengthening security, aiming to group the network nodes. The network nodes are clustered in terms of the distance between adjacent network nodes, data similarity, or performance metrics, such as energy consumption. Lin et al. [18] studied clustering vehicles according to the data correlation of vehicles. Khediri et al. [19] proposed a k-means clustering application to find cluster heads in multiple network node clusters. The cluster heads served as brokers for the pub/sub-operated communication system. They also used energy consumption to evaluate the performance of the proposed clustering method. Ally et al. [20] employed the k-means clustering method to group devices for data offloading; data offloading contributed to the reduction in energy consumption. Nasser et al. [21] used a spectral clustering technique to detect and delete insecure sensors in a communication system. Yang et al. [22] used deep reinforcement learning to cluster in dynamic characteristics of the network in time. Yang et al. proposes a deep reinforcement learning algorithm based on device business priorities maximizing uplink throughput in a smart grid.

2.4. Clustering Applications in Other Studies

The clustering approach is adopted in various fields. Narayanan et al. [23] studied a clustering approach for computer-aided detection of lung nodules. The approach combines the sequential forward selection (SFS) and the Fisher linear discriminant (FLD) classifiers. SFS and FLD are applied with k-means clustering to select and cluster features from a large number of potential nodule candidates. Messay-Kebede et al. [24] implemented PCA (Principal Component Analysis) to process three-dimensional input. Fine k-nearest neighbor classifiers are used to train a deep learning algorithm. The deep learning algorithm detects malware from the given input data. Chang et al. [25] designed a deep k-means cluster in spatial autoencoder and temporal autoencoder in video frames to get motion information from the video.

2.5. Clustering with Swarm Intelligence-Based Algorithms

Swarm intelligence (SI)-based computation is a bio-inspired computation used to solve real-world problems [26,27]. The inspirations derive from the collective behavior of some birds, amphibious, animals, or insects. The SI-based computations expand behaviors of interaction between individuals into group-level behavior. SI algorithms based on insects such as ants, bees, or fireflies adopt behaviors on how the insects build colonies or are attracted into groups. The colony-building SI algorithms are ways of clustering.

The Firefly Optimization algorithm and Glow Worm Optimization algorithm of the SI-based algorithms are applied for clustering problems. We adopt the idea of the Firefly Optimization algorithm and modify the algorithm to use in the network clustering problem. More specific ideas of the modified Firefly algorithm are described in Section 4.

2.6. Broker Assignment

Broker assignment is essential in the pub/sub-operated environments. Cheung et al. [28] and Zhao et al. [29] focus on assigning clients to the brokers. They studied the best mapping of clients and brokers. Cheung et al. studied the client placement in a fixed environment. Zhao et al. proposed the similarity-based client placement that considers the dynamics of the clients’ subscriptions and broker loads. The proposed two-stage hybrid network clustering algorithm focuses more on broker positioning. The best broker positions can minimize the energy consumption between brokers and clients. The minimized energy consumption between the clients and brokers gains more importance where the network nodes are widely distributed. The basic assumption is that all messages are possibly delivered to any of the nodes in the network. Thus, we focus on delivering the published messages fast to the brokers without considering other factors such as topics in pub/sub-operated communication.

A successful broker assignment helps to fairly allocate messages to brokers. Jiang et al. [30] proposed a heuristic and a min-heap-based optimal algorithm to increase fairness in assigning transactions to different blocks in a blockchain network. The relationship between blocks and transactions is identical to the relationship between brokers and network nodes. Jiang et al. focused on distributing transactions to different blocks. The two-stage hybrid algorithm focuses on finding blocks to allocate network nodes.

3. Design of the Two-Stage Hybrid Network Clustering Model

In this study, a two-stage hybrid network clustering method is proposed. A naive approach to implementing a k-means clustering combined with SARL, which finds the value of k, is insufficient for large-scale IoT networks with frequent message publications and multiple brokers. A large-scale IoT network has complex factors; hence, it is difficult for the SARL to find the appropriate k value quickly. The MARL in the proposed clustering technique can overcome the complexities of large-scale IoT networks.

The proposed clustering method consists of two stages:

• First Stage: apply the Delaunay triangulation and deleting methods to fix the candidate broker nodes;
• Second Stage: employ the MARL to find the best combination of broker nodes.

Figure 2 depicts the conceptual model of the two-stage hybrid network clustering. The first stage consists of Delaunay triangulation and deletion methods. The proposed clustering method repeats the candidate broker node selection in the first stage and iterates the MARL to find the best broker node combination in the second stage.

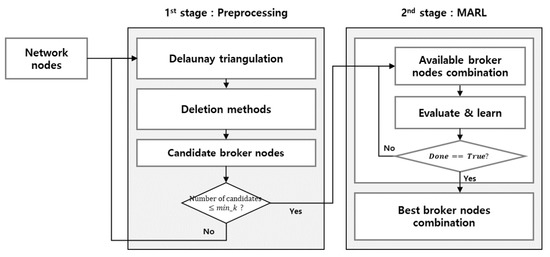
Figure 2. Conceptual model of two-stage hybrid network clustering.

3.1. Delaunay Triangulation and Deletion Methods for Fixing Candidate Broker Nodes

The objective of the first stage is to find candidate broker nodes from the given network nodes using the position data and number of message publications of each network node. Although typical clustering only considers positions, our proposed method also uses the number of message publications. The broker must be located close to talkative network nodes (i.e., nodes with frequent message publications).

The first stage is divided into two successive modules of iterative processes: the Delaunay triangulation and deletion methods (Figure 3). The Delaunay triangulation produces candidate broker nodes from network nodes. Considering the number of message publications, three-dimensional or four-dimensional vectors are employed as input data to find the candidate brokers nodes. Assuming that the network node is located in a plane, the position data and final input data for selecting candidate broker nodes have two and three dimensions, respectively. When we expand the data from plane to space, a four-dimensional vector form represents the input data for selecting candidate broker nodes. The centers of Delaunay triangles, which are constructed using the vertices of circum-hyperspheres, indicate the nearest points of candidate brokers. The typical Delaunay triangulation with two-dimensional input data (i.e., two-dimensional position data are used) produces a relatively small number of centers from the network nodes. However, three-dimensional or four-dimensional input data are used in this work, and the number of centers produced exceeds that of the network nodes [31,32]; the use of deletion methods is necessary to find the candidate broker nodes.

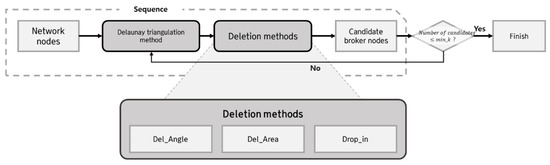
Figure 3. First stage: Delaunay triangulation and deleting methods.

The deleting methods include three parts: Del_Angle, Del_Area, and Drop_in (Figure 3).

• Del_Angle is the part where all obtuse triangles are discarded. The centers of these triangles are outside the triangles and cannot be used as candidate brokers.
• Del_Area is the part where p% of the largest triangles is discarded. After applying Del_Angle, all the remaining triangles are acute. However, when a candidate broker node is assigned near the center of a large triangle, the candidate broker node must have broad coverage, which is inefficient for network clustering. The network nodes must be included with the nearest broker node.
• Drop_in recovers the centers obtained from Delaunay triangulation. After applying Del_Angle and Del_Area, the triangles may have been reduced more than necessary. Drop_in also recovers some of the initial center points of Delaunay triangles and prevents excessive information loss in the repeated sequence of Delaunay triangulation and deleting methods.

3.2. Best Broker Node Combination by MARL

The candidate broker nodes produced in the first stage are not unique in the clusters. The Delaunay triangulation and deletion methods only filter out sufficient network nodes that may be employed as brokers. The proposed MARL evaluates all candidate brokers and creates the best broker combination for the entire communication network. It accepts the output of the first stage as input data, and each candidate broker acts as a MARL agent. Each agent has two states, 1 and 0, which indicate that the candidate broker node is included and not included in the broker node combination, respectively. In each of the MARL steps, each agent chooses to be a member of the broker node combination; then, the combination is evaluated by the reward function of MARL. This reward function measures the communication performance of the combination with the network nodes and other broker node combinations. The network nodes are assigned to the closest brokers which are a member of the broker node combination. The iterative process of MARL yields the best broker combination through the efficient exploration of available broker node combinations (Figure 4).

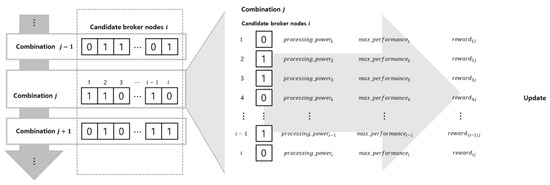
Figure 4. Description of multi-agent reinforcement learning (MARL)-level iteration.

4. Design of Experiments

Experiments are designed to evaluate the performance of the proposed two-stage hybrid clustering. The proposed two-stage hybrid algorithm is compared with two algorithms; k-means clustering with SARL and k-Firefly algorithm with SARL. For comparison, k-means clustering, which is unable to determine the value of k alone, is combined with SARL. To find the value of k, the network nodes perform k-means clustering through the iteration process of SARL; then, the results are evaluated to find the best value of k. Similarly, the k-Firefly algorithm, which adopts the idea of the Firefly Optimization algorithm, has SARL to determine the value of k. The experiments are performed on Jupyter notebook using python language. Jupyter notebook is implemented on a computer using Intel^® Core™ i7-9700F CPU (Intel Corporation, Santa Clara, CA, USA) and 32 GB RAM. Figure 5 depicts the flow of the three clustering methods.

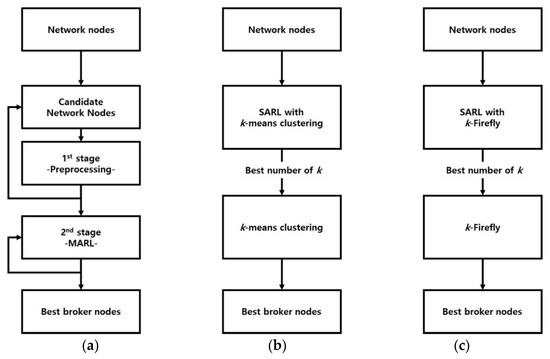
Figure 5. Learning flow: (a) Algorithm 1: two-stage hybrid network clustering using MARL; (b) Algorithm 2: naive k-means clustering algorithm with single-agent reinforcement learning (SARL); (c) Algorithm 3: k-Firefly algorithm with SARL.

4.1. Algorithm 1: Two-Stage Hybrid Network Clustering Using MARL

The parameters of the proposed two-stage hybrid clustering method are defined as follows:

• min_k: stopping threshold of the first stage. The introduction of Delaunay triangulation and deletion methods generates at least $min\_k$ candidate broker nodes;
• area_ratio: discarding ratio of large triangles in Del_Area;
• dropin_ratio: reinstatement ratio of initial center points in Drop_in;
• angle_crit: determinant for obtuse triangles in Del_Angle. To control the discarding ratio of obtuse triangles, angle_crit can be increased or decreased.

The first stage repeats the consecutive processes of the Delaunay triangulation and deletion methods. The iterations stop when the number of candidate broker nodes is less than min_k, which is determined by Equation (1).

$$min\_k=roundup\left(3\times {\displaystyle \sum }_{\forall i}messag{e}_i/processing\_power\right)$$

(1)

where i is the index of message publishers (i.e., network nodes); $messag{e}_i$ is the number of messages published by message publisher i within an hour; $processing\_power$ is the average number of messages that the broker can process within an hour. The Delaunay triangulation and deletion methods generate candidate broker nodes numbering at least three times more than the minimum number of brokers required in the network.

Note that in the actual experiments, the area_ratio is set as 0.1, which indicates that the top 10% of large triangles are to be deleted. The dropin_ratio is set as 0.5, which indicates that 50% of the center points in the Delaunay triangulation are to be reinstated. The magnitude of angle_crit is determined to be 90°; all obtuse triangles are deleted in the first stage.

The performance of each agent i determines the best broker node combination, which is presumed to exhaust the combination’s power for message pub/sub processing. It is observed that extra processing power remains in the broker node combination. In view of this, it is assumed that the combination does not reach the optimal status. The performance of candidate broker i that is achieved in the available broker node combination j is given by Equation (2):

$$performanc{e}_{ij}= -\alpha \times {\left(\frac{processed messag{e}_{ij}}{total processable message{s}_i}-1\right)}^2+1$$

(2)

The ratio of the processed messages to the total processable messages of agent $i$ determines the current performance of this agent in the available broker node combination j. Equation (2) implies that the foregoing ratio should approach 1. Moreover, $\alpha$ indicates the strictness of processing the power evaluation: if $\alpha$ is large, then the difference between the number of processed messages and the maximum number of processable messages is evaluated more strictly. In Equation (2), 1 is added to the equation for it to yield a performance value, i.e., $performanc{e}_{ij}$, of less than 1; the highest expected performance is 1. Note that $\alpha =8$ in the experiment.

Algorithm 1 Two-Stage Hybrid Network Clustering using MARL

Input:  initial network nodes, ${\mathrm{N}}_0$ 01: initialize candidate broker nodes, $\mathrm{CN}\leftarrow {\mathrm{N}}_0$ 02:  while $\mathrm{number}\mathrm{of}\mathrm{CN}>min\_k$ 03:    apply Delaunay triangulation to $\mathrm{CN}$ and obtain seed point (${\mathrm{S}}_{\mathrm{CN}}$), vertices of Delaunay triangles$\left({\mathrm{V}}_{\mathrm{CN}}\right)$ 04:    delete elements of ${\mathrm{S}}_{\mathrm{CN}}$ that are centers of p% of the largest triangles made of ${\mathrm{V}}_{\mathrm{CN}}$ 05:    delete elements of ${\mathrm{S}}_{\mathrm{CN}}$ that are centers of obtuse triangles made of ${\mathrm{V}}_{\mathrm{CN}}$ 06:    use $\mathrm{Drop}\_\mathrm{in}$ with ${\mathrm{S}}_{\mathrm{CN}}$ and $\mathrm{CN}$ to obtain ${\mathrm{CN}}^{\prime }$ 07:      $\mathrm{CN}\leftarrow {\mathrm{CN}}^{\prime }$ 08:  end while 09: let each element of $\mathrm{CN}$ be agent i of MARL 10: initialize action—value function $({\mathrm{Q}}_{ij}$), combination (${\mathrm{S}}_j$), and $max\_rewar{d}_i=0$ for all agent $i$ 11:  for all episodes do 12:    for combination j = 1, M do 13:      for all agent $i$ do 14:        choose action ${\mathrm{a}}_i$ with ${\mathrm{Q}}_{ij}$ or randomly by exploration policy 15:        execute action ${\mathrm{a}}_i$ and obtain ${{\mathrm{S}}_j}^{\prime }$ 16:        obtain $performanc{e}_{ij}$ 17:        $max\_rewar{d}_i\leftarrow \max \left(max\_rewar{d}_i, performanc{e}_{ij}\right)$ 18:        ${\mathrm{S}}_j\leftarrow {{\mathrm{S}}_j}^{\prime }$ 19:      end for 20:      obtain $rewar{d}_{ij}$ 21:      update ${\mathrm{Q}}_{ij}$ with $rewar{d}_{ij}$ for all agent $i$ 22:    end for 23:  end for 24:  obtain best broker node combination and its positions with ${\mathrm{Q}}_{ij}$ for $\mathrm{all}$ agent $i$

For the iterative MARL process (the updating of available broker combinations is shown in Algorithm 1), agent $i$ remembers the best performance, $max\_performanc{e}_i,\mathrm{it}\mathrm{experienced}$. The reward of agent $i$ in broker node combination $j$ is the sum of the average broker performance for combination $j$ (i.e.,$\frac{{\sum }_{i}performanc{e}_{ij}}{\# of candidate broker nodes}$) and the maximum performance (i.e.,$max\_performanc{e}_i$) of each individual. The agent is likely to be selected in the best broker node combination if it has exhibited acceptable performance in any of the explored combinations. The reward of agent $i$ of broker node combination$j$ is shown in Equation (3):

$$rewar{d}_{ij}=\frac{{\sum }_{i}performanc{e}_{ij}}{\# of candidate broker nodes}+max\_performanc{e}_i.$$

(3)

Then, the reward of broker combination$j$ is calculated as the sum of individual broker rewards (Equation (4)):

$$combination\_rewar{d}_j={\displaystyle \sum }_{i}rewar{d}_{ij}$$

(4)

In Algorithm 1, ${\mathrm{Q}}_{ij}$ is the action-value function of agent $i$ in combination $j$; action ${\mathrm{a}}_i$ is the randomly selected or directional action of agent $i$ determined by ${\mathrm{Q}}_{ij}$. If ${\mathrm{a}}_i=0$, then the action chooses to maintain the state of agent $i$ in combination $j$; if ${\mathrm{a}}_i=1$, the action chooses to change the state.

4.2. Algorithm 2: Naive k-Means Clustering Algorithm with SARL

Moreover, to compare with the proposed two-stage hybrid approach, an algorithm that uses k-means clustering with SARL is introduced. The SARL explores the value of k from 0 to $min\_k$ and finds the optimum number of k, which is also the optimum number of brokers in the given IoT environment. Except for the number of k, k-means clustering requires no prior knowledge of SARL. In each iteration of SARL, k-means clustering is performed with the given network nodes, and the centers of k clusters are obtained as brokers. Then, the SARL evaluates each explored value of k. By applying k-means clustering to the network nodes using the best number of brokers derived from SARL, the best positions of brokers for k network clusters are obtained (Algorithm 2).

Algorithm 2k-means clustering with SARL to find k value

Input:  initial network nodes, ${\mathrm{N}}_0$ 01:  initialize action-value function $(Q$) and state ($S)$ 02:  $S\leftarrow 2$ 03:  for all episodes do 04:    for all steps do 05:      choose action $a$ with $Q$ or randomly by exploration policy 06:      execute action $a$ and obtain $S^{\prime }$ 07:      perform k-means clustering using value of $S^{\prime }$ as k 08:      obtain reward $r$ 09:      update $Q$ with reward $r$ 10:    end for 11:  end for 12:  obtain best k with $Q$ 13:  obtain best broker positions by performing k-means clustering with best k

The action-value function in SARL is denoted as$Q$; action $a$ is the randomly selected action or the argmax action of $Q$ at state $S$. The state, $S$, indicates the number of clusters in k-means clustering. If $a=0$, then the number of clusters is increased by 1; if $a=1$, then the current number of clusters is maintained. If $a=2$, then the number of clusters is reduced by 1.

The basic process involved in the clustering algorithm is to group network nodes into different clusters. The k-means clustering algorithm computes the distances among the network nodes (${\mathrm{N}}_0$) and builds k number of clusters. The hybrid algorithm computes the distance between network nodes and selected candidate brokers in the combination. The two-stage hybrid clustering algorithm has the same time complexity when the number of selected candidate brokers is k. The k-means clustering algorithm is an iterative process; thus, k-means clustering with SARL requires additional iterations to find the optimal value of k and compared with the proposed two-stage hybrid method, it requires extra computational time to build clusters.

4.3. Algorithm 3: k-Firefly Algorithm with SARL

In Algorithm 3, the process of the k-Firefly algorithm with SARL is introduced. We adopt the idea of luminosity from the original firefly algorithm. The k number of fireflies is located in randomly selected clients. The k-Firefly algorithm assumes that the brokers should be allocated close to talkative network nodes (i.e., nodes with frequent message publications). The fireflies try to find the most talkative network node within their reachable bounds. $messag{e}_i$, where i is the index of message publishers (i.e., network nodes), is considered luminosity in the k-Firefly algorithm. The firefly flies from the starting node to the most talkative network node it can seek.

Algorithm 3k-Firefly Algorithm with SARL to find k value

Input:  initial network nodes, ${\mathrm{N}}_0$ 01:  initialize action-value function $(Q$) and state ($S)$ 02:  $S\leftarrow 2$ 03:  for all agent $i$ do 04:        $luminosit{y}_i\leftarrow messag{e}_i$ 05:  for all episodes do 06:    for all steps do 07:      choose action $a$ with $Q$ or randomly by exploration policy 08:      execute action $a$ and obtain $S^{\prime }$ 09:      perform k-Firefly using value of $S^{\prime }$ as k 10:      obtain reward $r$ 11:      update $Q$ with reward $r$ 12:    end for 13:  end for 14:  obtain best k with $Q$ 15:  obtain best broker positions by performing k-Firefly with best k

5. Results

The three clustering methods with 50, 100, 200, and 300 candidate broker nodes are compared. The number of published messages and the position information for each candidate broker node are randomly generated. We added reproducibility for comparison between algorithms. Table 1 summarizes the values of min_k for the number of network nodes; min_k is set as approximately 1/4 of the number of network nodes.

Table 1. Values of min_k for each number of network nodes.

Number of Network Nodes	50	100	200	300
min_k	13	22	49	76

The reinforcement learning of the algorithms has 200 episodes, each of which has 50 steps. The states are reset at the beginning of each episode, while the previously learned experience is maintained. In each step, the two-stage hybrid clustering generates a broker combination and evaluates the combination. In addition, the SARL algorithm yields the value of k; then, k-means clustering, or k-Firefly algorithm is activated with the provided k. The simple and effective action-value function of SARL (i.e., the SARL has only two actions: increase k$\leftarrow$k + 1 and decrease k$\leftarrow$k − 1). The action space of single agent is restricted on single axis (i.e., k-value). The search action over the single axis converges relatively fast. There are 50 steps in every episode, and the probability of exploring reinforcement learning decays throughout the episode; the learning rate is set as 0.3.

The processing times of the two-stage hybrid clustering, naive k-means clustering method and k-Firefly method with the same number of selected brokers are compared (Figure 6). The processing time is the overall running time of each algorithm. The two-stage hybrid clustering requires a considerably shorter time to converge. With 300 network nodes, the two-stage hybrid clustering algorithm only requires 11.6% and 5.9% of the processing time compared with k-means clustering with SARL and k-Firefly with SARL, respectively. The processing time of k-Firefly increases more rapidly. The processing time of k-Firefly is greater than that of the naive k-means clustering due to the weak stopping condition. The k-means clustering has a strong stopping condition (i.e., it stop the calculation when it reaches the stable status). The fireflies in k-Firefly normally results in flying between two network nodes. The fireflies themselves cannot determine which of the network nodes will be a better one. Note that, all candidate broker nodes are agents in two-stage hybrid clustering. Each candidate broker node needs to learn to change or maintain the current state: to be the broker or not. The candidate broker nodes are sufficiently evaluated by the two-stage hybrid clustering.

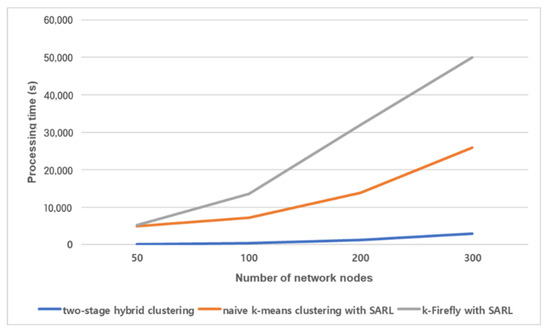
Figure 6. Processing times of algorithms for different numbers of network nodes.

The number of selected brokers presents the performance of each algorithm. We conducted experiments on each algorithm for comparison (see the Table 2). The proposed two-stage hybrid algorithm (Algorithm 1) shows better results in the conducted experiment. The smaller number of brokers guarantees the higher utilization of brokers. Algorithm 1 and Algorithm 2 show similar results with sufficient exploration. However, Algorithm 1 shows higher performance in terms of processing time (see the Figure 6).

Table 2. Number of selected brokers for each number of network nodes.

Number of Network Nodes	50	100	200	300
Algorithm 1	3	10	23	35
Algorithm 2	5	11	21	41
Algorithm 3	9	24	43	53

Table 3 summarizes the results of the proposed two-stage hybrid clustering including the first stage. Without the first stage, it is necessary to apply the MARL to all network nodes and extra processing time is required. We conducted an experiment on k-means clustering with SARL to show the effectiveness of the preprocessing stage. The number of inputs for the clustering decreases with the preprocessing stage. The preprocessing stage shows more effectiveness in the experiment with k-means clustering. The processing time reduced by 15~20% with preprocessing stage. We found that the processing time decreases regardless of the clustering algorithm of the second stage.

Table 3. Two-stage hybrid clustering with and without preprocessing stage (first stage).

	Number of Network Nodes	Number of Candidate Broker Nodes	min_k	Number of Selected Brokers	Processing Time (s)
Two-stage hybrid clustering	50	16	13	3	72
	100	42	22	10	353
	200	70	49	23	1303
	300	121	76	35	2927
Two-stage hybrid clustering without first stage	50	-	13	13	111
	100	-	22	31	417
	200	-	49	56	1680
	300	-	76	73	3918

Figure 7 shows a visual example of the two-stage hybrid clustering within a 200 m × 200 m square area. A total of 30 network nodes are located in the test area. The green bars denote the message publishing for each network node. The yellow points denote the best broker positions identified by the proposed two-stage hybrid clustering algorithm. The network nodes nearest to the yellow points are assigned as actual brokers.

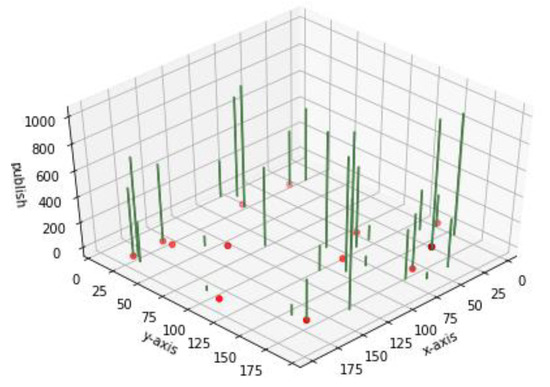
Figure 7. Diagram of two-stage hybrid clustering with 30 network nodes.

6. Conclusions

In this paper, we introduce a two-stage hybrid network clustering algorithm. The proposed two-stage hybrid algorithm consists of preprocessing stage and MARL stage. Leveraging the proposed algorithm, the best broker node combination can be found in the pub/sub-operated communication network.

6.1. Contribution of the Proposed Work

A two-stage hybrid clustering method determines the optimal distribution (i.e., number and position) of brokers in a pub/sub-operated communications system. The proposed MARL for each network node is designed so that the node learns whether or not to be a broker. The two-stage hybrid clustering employing MARL uses three-dimensional data (i.e., number of message publications and positions). The MARL combines three-dimensional Delaunay triangles and generates dynamic network clustering. We expand the Delaunay triangulation to utilize higher-dimensional data, and the position data of network nodes can be expanded from a plane to space.

The robustness of the proposed clustering method is proved in the dynamic IoT environments. It continuously configures communication clusters while the information in the communication networks (i.e., number of message publications and positions of network nodes) highly fluctuates. The two-stage hybrid clustering generates proper clusters using rapid performance estimation and applies the fast-converging action-value function of multiple agents. Even under highly unstable conditions, IoT networks can achieve optimum resilience using the proposed fast-converging MARL. The typical SARL is observed to be unable to find the optimal number of brokers within a limited period of time and number of explorations. Compared with a naive k-means clustering and k-Firefly implemented SARL, the two-stage hybrid clustering has a great advantage in clustering performance with fast converging time.

6.2. Threats of Validity

The dynamic communication environment may limit the practical applicability of the two-stage hybrid clustering. The IoT nodes move place to place and the message publication rate changes in real-time fashion. The proposed algorithm has a limitation to the real-time learning. The two-stage hybrid clustering assumes a fixed message publication rate and a static node distribution. The learning mechanism should be enhanced to be applicable to the dynamic communication environment. One planned future enhancement is to apply a knowledge transfer method. The a priori learned knowledge can be useful for the dynamic network environment. To extend the previously learned knowledge, a higher-level time-series learning method can be suggested. The proposed two-stage hybrid algorithm only uses distribution (i.e., number and position) data and the volume of message publications. However, general communication environments can use more information to provide an improved communication experience: resource availability, connection failure, encryptions, etc. Methods such as Principal Component Analysis (PCA) and k-nearest neighbor classifiers can be applied in the preprocessing steps of our proposed two-stage hybrid clustering. The added preprocessing with the selected additional information can expand our approach to general communication environments.

In reality, the proposed MARL cannot guarantee the finding of optimal broker combinations for every communication environment. To provide the strict guarantee of optimal combination, we must build a mathematical model for broker positioning. All communication behaviors of network nodes should be modeled to a static form. The complete understanding and abstracted presentations are the basic requirement for the mathematical modeling. However, we cannot find an effective model to describe node behaviors such as pub/sub operations and node position data. The complexity of representing the node behaviors limits the development of a mathematical model and the application to obtain the optimal combination. The proposed learning-based approaches have the flexibility to describe the network environment and node behaviors. We expect that a future advanced learning structure may achieve the completeness of mathematical modeling.