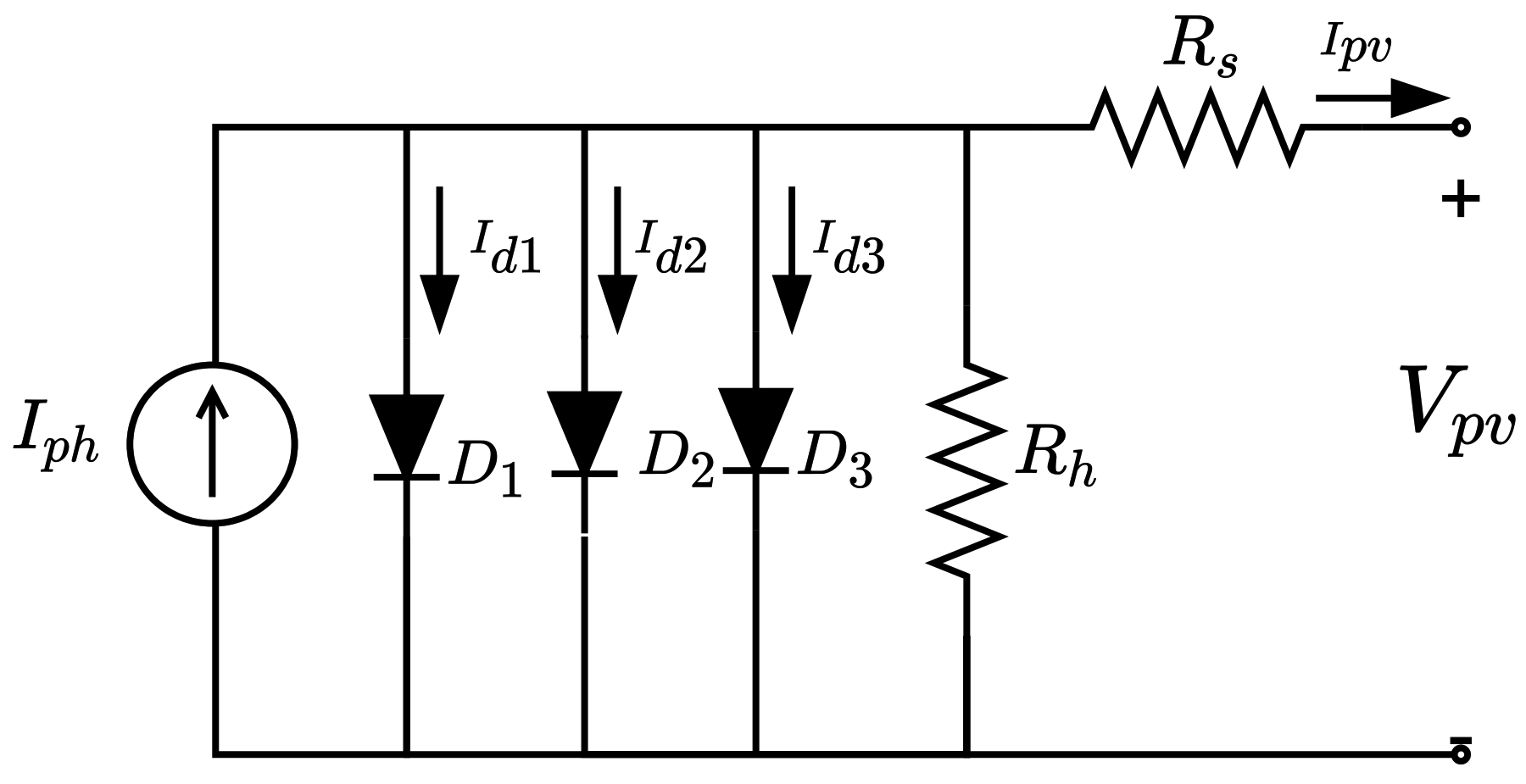
5.1.1. PV Panel
The PV profiles and V-P curves of the panel under the two previously mentioned irradiance levels (i.e., 1000 W/m and 500 W/m) were used to validate the methodology proposed here and represent different power levels in the PV profiles of the panel.
Table 5 and
Table 6 show the results obtained by the different methodologies implemented here to solve the parameter estimation problem of the TDM of the
PV panel under irradiance levels of 500 W/m
and 1000 W/m
, respectively. These tables detail, from left to right, the solution method that was used, the best solution found for the objective function (
), the worst solution found for the
, the mean value of the
, and the standard deviation obtained by each technique after 1000 executions. Additionally,
Figure 2 and
Figure 3 are charts that compare the results obtained by the three other methodologies employed here to solve the parameter estimation problem of the TDM of the
PV panel.
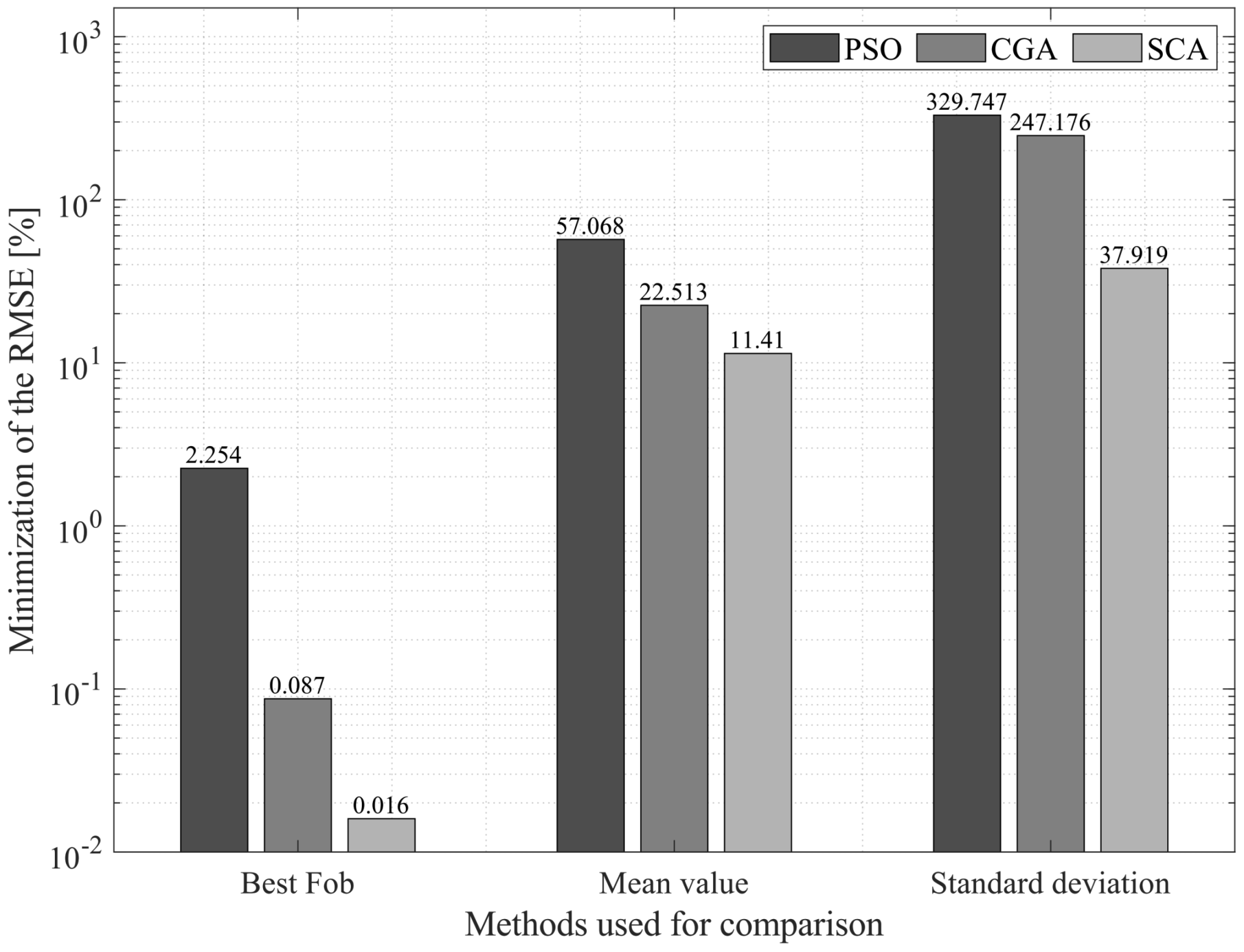
In
Figure 2, which presents the results obtained for the
PV panel under a 500 W/m
irradiance level, the method proposed in this paper outperforms the other three optimization algorithms in all the results. Regarding the best solution in the objective function, the SSA outperformed PSO by
, the CGA by
, and the SCA by
. Likewise, the SSA presented a high-quality standard deviation, outperforming the other solution methodologies by
on average. The outstanding standard deviation of the SSA resulted in a mean value of
, outperforming the SCA by
, the CGA by
, and PSO by
.
The above shows the superiority of the technique proposed here in finding a high-quality solution for the minimization of the objective function (i.e., the RMSE of the TDM of a PV panel under a 500 W/m irradiance level). Likewise, thanks to its excellent standard deviation, the SSA can be used to find a high-quality solution every time it is executed.
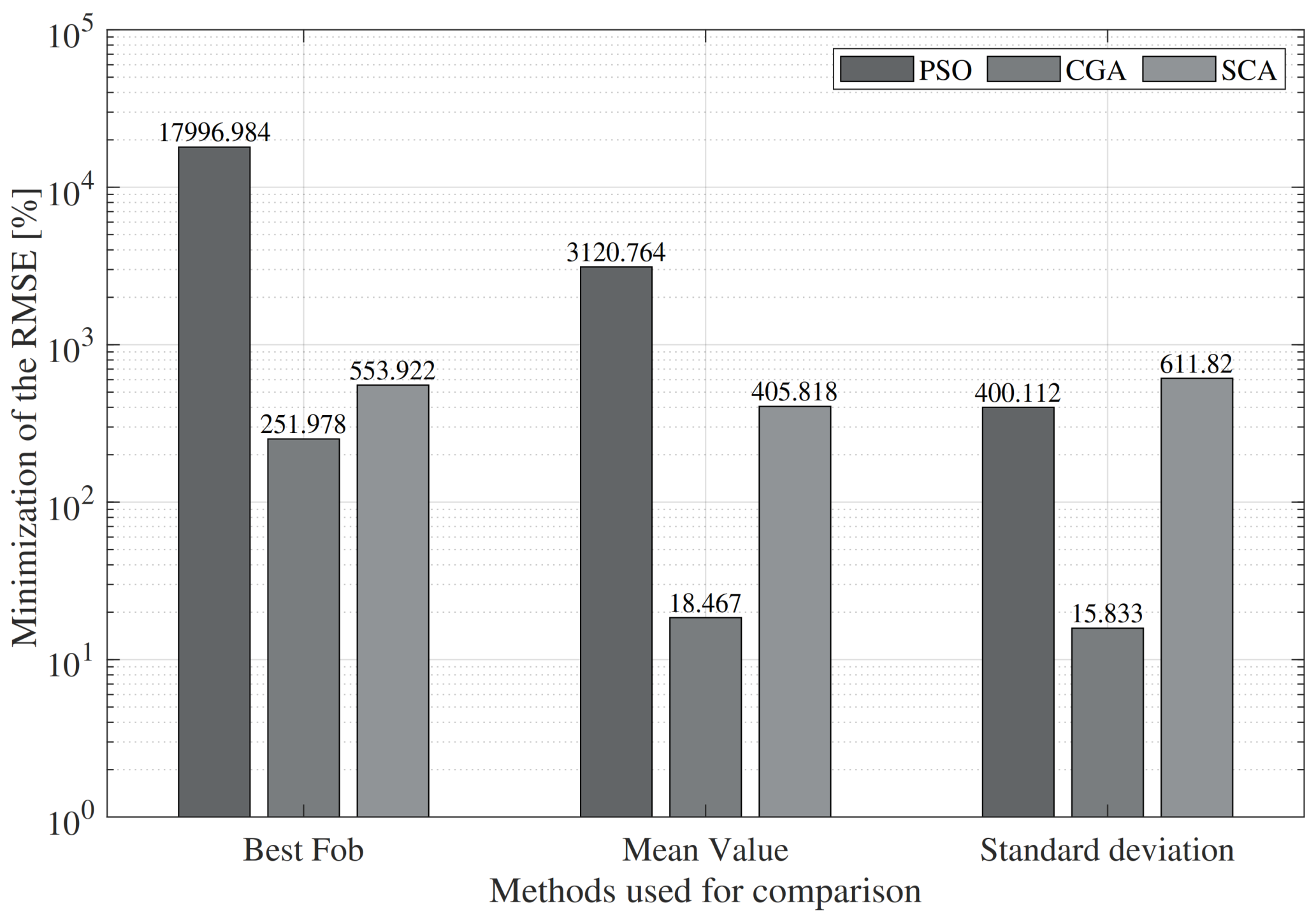
Figure 3 presents the results of the analysis of the
PV panel under a 1000 W/m
irradiance level. Regarding the best solution for the minimization of the RMSE, the SSA outperformed the CGA, the SCA, and PSO by
,
, and
, respectively. In relation to the standard deviation, the SSA fell short against the CGA by
, but outperformed PSO and the SCA by
and
, respectively. Despite producing a standard deviation worse than that of one of the techniques, the SSA was better than all of them in the mean value, outperforming the CGA by
, the SCA by
, and PSO by
. Although the CGA obtained a better standard deviation, the SSA found the best solution for the minimization of the objective function of the problem analyzed in this paper, as well as the best mean solution for the analysis of the
PV panel under a 1000 W/m
irradiance level. Therefore, the SSA will generate a high-quality solution every time it is executed.
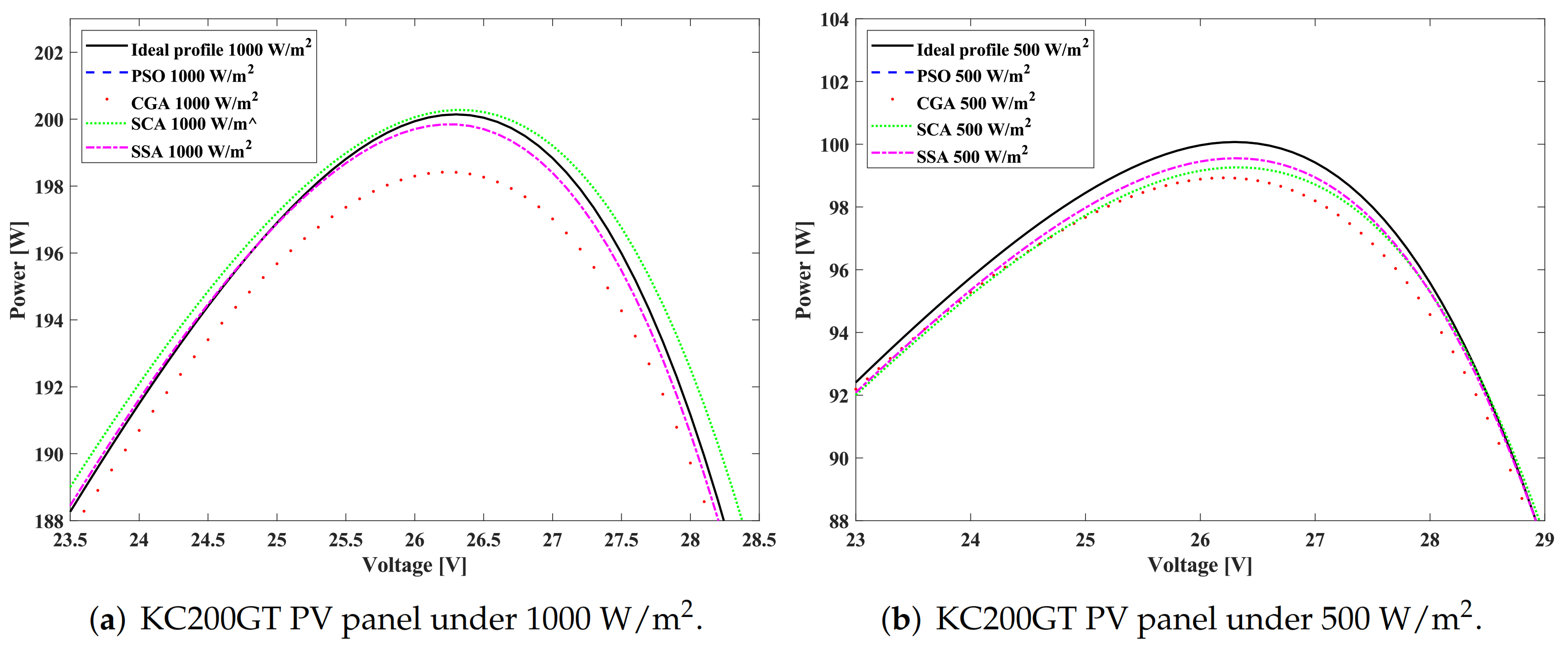
The previous analysis showed that the SSA obtained the best solution for the parameter estimation problem of the TDM of a PV panel (the
panel in this case), demonstrating its superiority, especially in finding the best minimization of the objective function. Additionally,
Figure 4 is a graph that represents the best solutions found for the minimization of the objective function reported in
Table 5 and
Table 6. For more clarity,
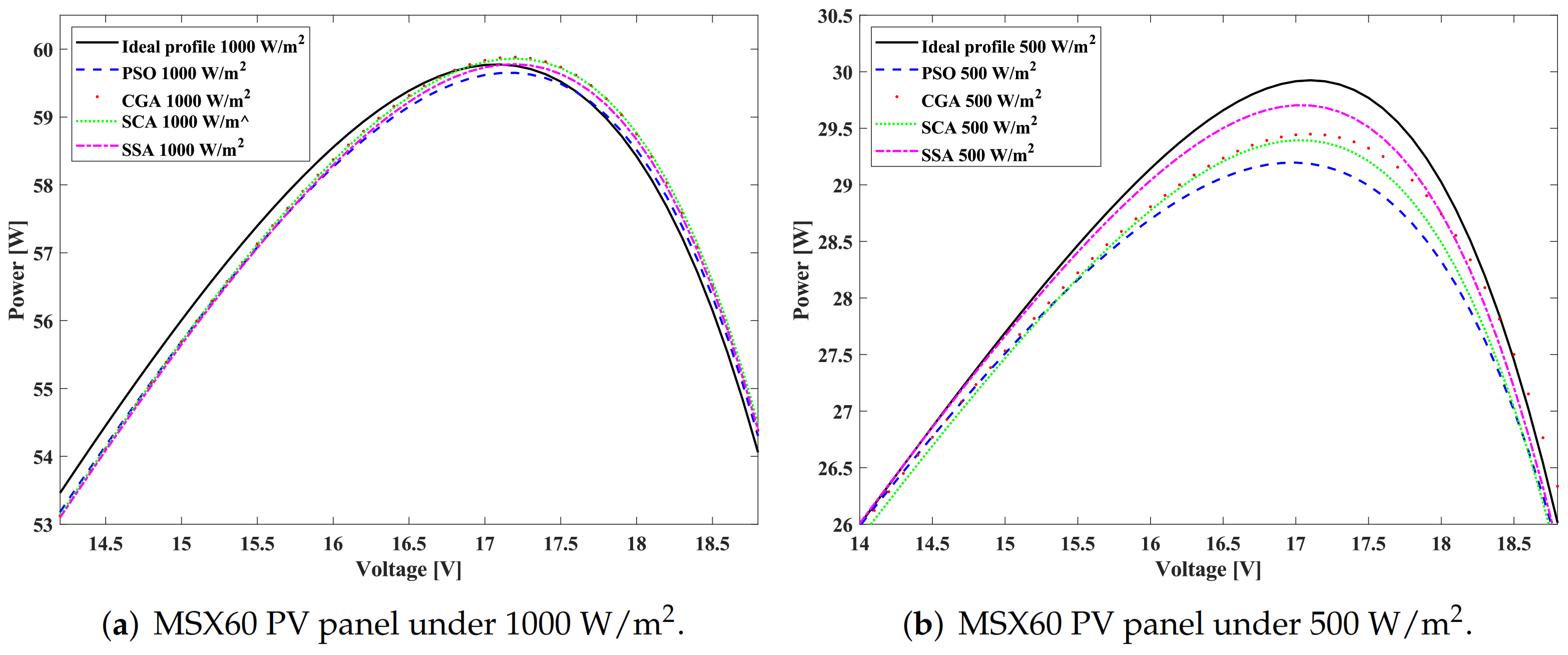
Figure 5 shows two zoom-ins on the power produced under the two irradiance levels. These zoom-ins detail the difference between the ideal PV profile under 500 W/m
and 1000 W/m
and those determined by each optimization technique.
5.1.2. PV Panel
The next validation stage of the methodology proposed in this paper was to analyze a less powerful PV panel, i.e., the
panel, under two irradiance levels (i.e., 500 W/m
and 1000 W/m
) in order to observe the behavior of the optimization techniques under different power scenarios.
Table 7 and
Table 8 present the results of the analysis of this panel under the two irradiance levels, which are organized as those in
Table 5.
Table 7 presents the results obtained by each methodology implemented here to solve the parameter estimation problem of the TDM of the
panel under 500 W/m
.
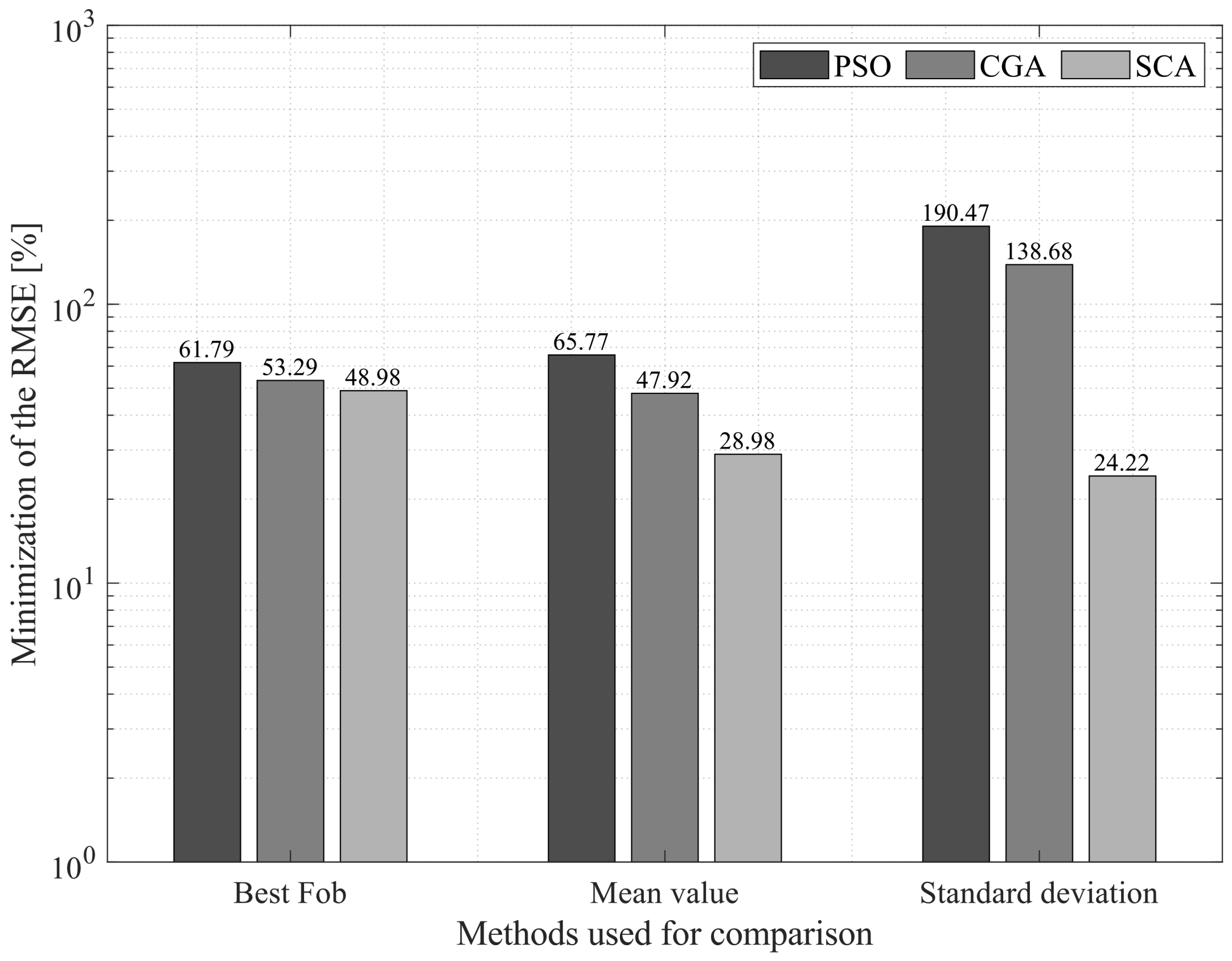
Figure 6, which compares the results obtained for the
panel under a 500 W/m
irradiance level, indicates that the SSA outperformed the rest of the solution algorithms proposed to solve the problem studied in this paper. Regarding the best solution, the SSA outperformed the SCA by
, the CGA by
, and PSO by
. In relation to the mean value, the SSA presented an average improvement of
over the other solution methodologies. In terms of the standard deviation, the SSA outperformed the SCA, the CGA, and PSO by
,
, and
, respectively. These results showed that the SSA produced the best solution for this panel under 500 W/m
.
Table 8 presents the results obtained by the methodologies implemented here to solve the parameter estimation problem of the TDM of the
panel under a 1000 W/m
irradiance level.
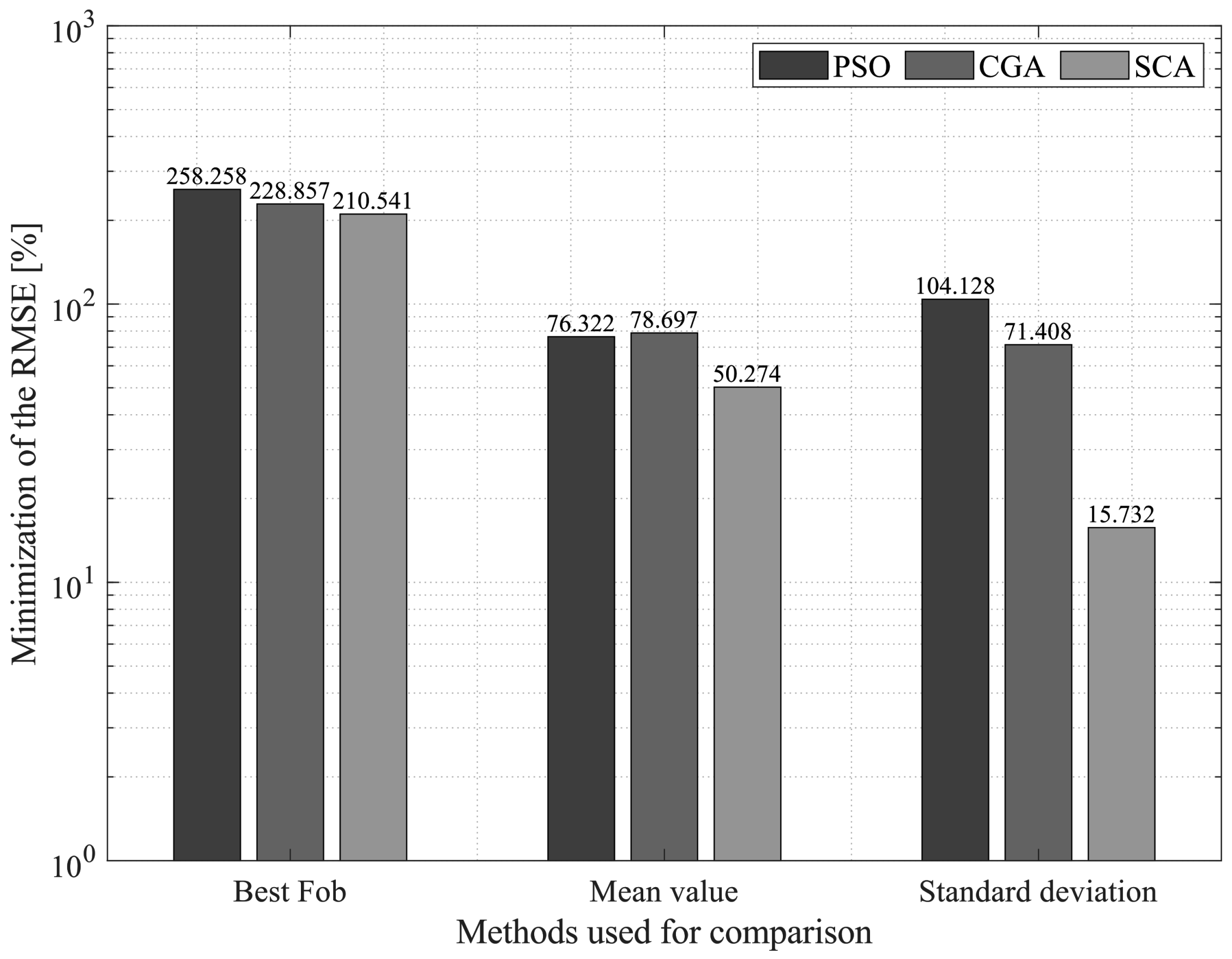
Figure 7 shows the improvements achieved by the SSA compared to the other solution methodologies suggested to solve the parameter estimation problem of the TDM of a
PV panel under a 1000 W/m
irradiance level. In said figure, the SSA obtained the highest percentage of minimization of the objective function, with a value of
, thus outperforming the SCA by
, the CGA by
, and PSO by
. Regarding the mean solution, the SSA presented an improvement of
over the SCA,
over the CGA, and
over PSO. In terms of the standard deviation, the SSA offered the best repeatability to find the solution, outperforming the other techniques by an average of
. These results demonstrate the superiority of the technique proposed in this paper to solve the parameter estimation problem for the
PV panel with a 1000 W/m
irradiance level.
After analyzing the
PV panel, it can be concluded that the methodology proposed here was the technique that found the best solution to the problem of the TDM in this scenario. Additionally, in terms of the repeatability of the solution, the SSA outperformed all the other techniques, which guarantees a high-quality solution every time the algorithm is executed for any power level of said panel.
Figure 8 is a graph that represents the best solutions found for the minimization of the objective function reported in
Table 7 and
Table 8. For more clarity,
Figure 9 shows two zoom-ins on the power produced under the two irradiance levels. These zoom-ins detail the difference between the ideal PV profile under 500 W/m
and 1000 W/m
and those determined by each optimization technique.
Table 9 and
Table 10 are included here to conduct an in-depth analysis to find the most optimal technique to solve the parameter estimation problem of the TDM of a PV panel. These tables present the robustness of the solutions obtained by each one of the algorithms implemented in this paper.
In order to obtain the values shown in
Table 9, the data of the minimization of the objective function for the 500 W/m
and 1000 W/m
irradiance levels were averaged. The same procedure was repeated for the mean value and the standard deviation. Likewise, the previously described procedure was applied to obtain the values in
Table 10 for the case of the
PV panel.
In addition,
Figure 10 and
Figure 11 present the results of
Table 9 and
Table 10, respectively.
Figure 10 shows that the solution methodology proposed in this paper produces the most adequate solution for the minimization of the objective function, outperforming the CGA by
, the SCA by
, and PSO by
. Regarding the mean deviation, the SSA outperformed the CGA, the SCA, and PSO by
,
, and
, respectively. In terms of the standard deviation, the SSA outperformed the other solution methodologies by an average of
. In terms of processing time,
Table 9 presents the average times of each optimization technique with values equal to
s to solve the parameter estimation problem in the SSA, while PSO, the CGA, and the SCA required an average time equal to
s,
s, and
s, respectively. These results demonstrate that the SSA offered the best solutions for the
panel under any irradiance level and scenario.
Figure 11 shows that the SSA outperformed the other techniques in the different solution scenarios evaluated here. Regarding the minimization of the objective function, the SSA outperformed the SCA by
, the CGA by
, and PSO by
. In relation to the mean value for the objective function, the SSA outperformed the SCA by
, the CGA by
, and PSO by
. In terms of the standard deviation obtained by the solution methodologies, the SSA outperformed the SCA by
, the CGA by
, and PSO by
.Analyzing the average processing time required for each method, presented in
Table 10, it can be seen that the SSA required
s, the PSO
s, the CGA
s, and the SCA
s of average time to solve the parameter estimation problem for the MXS60. This analysis demonstrates the superiority of the SSA algorithm in obtaining high-quality solutions for the
panel, outperforming all the other optimization techniques.
The results presented in the previous graphs were compared against the results obtained by the optimization algorithm proposed in this document. This allows optimally visualizing the results obtained by the comparison methods, since all the data presented in the graphs are faced with their counterpart, which was determined by the SSA.