A Carrier-Based Discontinuous PWM Strategy of NPC Three-Level Inverter for Common-Mode Voltage and Switching Loss Reduction

Abstract

For the conventional carrier-based pulse width modulation (CBPWM) strategies of neutral point clamped (NPC) three-level inverters, the higher common-mode voltage (CMV) is a major drawback. However, with CMV suppression strategies, the switching loss is relatively high. In order to solve the above issue, a carrier-based discontinuous PWM (DPWM) strategy for NPC three-level inverter is proposed in this paper. Firstly, the reference voltage is modified by the twice injection of zero-sequence voltage. Switching states of the three-phase are clamped alternatively to reduce both the CMV and the switching loss. Secondly, the carriers are also modified by the phase opposite disposition of the upper and lower carriers. The extra switching at the border of two adjacent regions in the space vector diagram is reduced. Meanwhile, a neutral-point voltage (NPV) control method is also presented. The duty cycle of the switching state that affects the NPV is adjusted to obtain the balance control of the NPV. Still, the switching sequence in each carrier period remains the same. Finally, the feasibility and effectiveness of the proposed DPWM strategy are tested on a rapid control prototype platform based on RT-Lab.

1. Introduction

Compared with two-level inverters, NPC three-level inverters have advantages of lower output harmonics distortion and lower dv/dt of the power device. Thus, it is widely used in medium-voltage high-power traction applications, such as locomotive traction and ship propulsion [1,2,3].

The common-mode voltage emerges between neutral points of DC-link capacitors and stator windings in NPC three-level inverter fed motor system. Numerous hazards are associated with the common-mode voltage. First, the shaft voltage is brought out on the motor bearing, and the life of the motor will be shortened by the shaft current [4]. Secondly, there are high-frequency components in the common-mode voltage. They would cause electromagnetic interference to the power supply [5]. Thirdly, the insulation stress of stator windings is also increased by the CMV. Thus, the aging process of the motor is accelerated [6]. These problems will get worse if the inverter is applied to the medium-voltage high-power traction application.

For three-level inverters, there are two ways commonly used to reduce the CMV. The first is the improvement of topology, and the second is the improvement of modulation strategy. For the former, the CMV can be reduced by several methods, such as the addition of the fourth bridge [7,8], the modification of the DC-link structure [9], the addition of the common-mode inductance [10] and the addition of the filter [11,12]. All the above methods impose extra hardware on the system, resulting in an increase in cost, volume and loss. For the latter, there is no need for any additional hardware so that it attracts more attention all over the world.

The common feature of CMV suppression PWM strategies is that switching states with the lower CMV are adopted to synthesize the switching sequence. In [13], five switching states with the lowest CMV are used to synthesize the switching sequence in each carrier period. Although the CMV can be reduced effectively, the switching loss is inevitably increased. In [14], only the switching state with zero amplitude of CMV can be used, and the output harmonic distortion of the inverter is improved by the proper arrangement of these switching states in each carrier period. However, there are seven switching states in each switching sequence, and the inverter suffers from lower DC-link voltage utilization and higher switching loss. A double modulation wave carrier-based PWM strategy (DMW-CBPWM) is proposed in [15], the reference voltage is modified to reduce the CMV and the NPV ripple simultaneously. In [16,17], four switching states with lower CMV are used to synthesize the switching sequence in each carrier period, and the NPV balance control is achieved by adjusting the duty cycle of the switching states. In [18], carriers are phase opposition arranged, the CMV and the NPV ripple are both suppressed by injecting the DC component into the reference voltage.

With the promotion of power and voltage levels, the switching loss becomes the main component of the overall loss of the system [19,20,21]. Thus, the CMV and the switching loss should be both taken into consideration. Conventional CMV suppression PWM strategies only focus on the performance of CMV and are not suitable for medium-voltage high-power traction applications. DPWM methods are well known to reduce the switching loss and harmonic distortion at a given average switching frequency. Thus, DPWM strategies are extremely suitable for high-power medium-voltage three-level inverters. The conventional DPWMs for a three-level inverter are proposed in [22]. In [23], an improved DPWM is presented to reduce the switching loss and the harmonic distortion. However, the CMV is still larger under higher modulation index conditions.

For the purpose of suppressing CMV and switching loss simultaneously, a carrier-based DPWM strategy is proposed in this paper. By the modification of the reference voltage, switching states with higher CMV are eliminated in the synthesis of the switching sequence. One of the three phases is clamped to a certain switching state in each switching sequence. Thus, the CMV and the switching loss are both reduced. By the modification of the carriers, the extra switches during the transient process of two adjacent regions are decreased to further reduce the switching loss. The proposed DPWM strategy is validated through experimental results. The experimental setup comprises an OPAL-RT OP5700 rapid control prototype and an NPC three-level inverter fed R-L load.

2. NPC Three-Level Inverter and CBPWM

2.1. Topology of the NPC Three-Level Inverter

The topology of the NPC three-level inverter is shown in Figure 1. The DC-link voltage V_dc is equally divided into the upper-capacitor voltage v_C1 and the lower-capacitor voltage v_C2. i_A, i_B and i_C are the three-phase load currents, respectively.

The switching states of the three-level inverter are defined in

Table 1. The definition of switching state for NPC three-level inverter.

Status of Switches				Switching State	Output Voltage
Sx1	Sx2	Sx3	Sx4
1	1	0	0	P	Vdc/2
0	1	1	0	O	0
0	0	1	1	N	−Vdc/2

.

The space vector diagram for the three-level inverter is shown in Figure 2, with 3³ = 27 basic vectors. According to the amplitude, the basic vectors can be divided into four categories: large vector V₁–V₆, medium vector V₇–V₁₂, small vector V_13U–V_18U, V_13L–V_18L and zero vector V_0U, V_0M, V_0L. As can be seen, there are two small vectors that occupy the same position, and they are defined as redundant vectors. The definition is also suitable for zero vectors.

2.2. CBPWM of the Three-Level Inverter

For conventional CBPWM of the three-level inverter, the pulse signal for each power device is produced by the comparison of the carriers and the reference voltage v_x, (x ∈ {A, B, C}). The reference voltages of the three phases are defined as:

$$\{\begin{array}{l}{v}_{\mathrm{A}}=m\frac{V_{\mathrm{dc}}}{\sqrt{3}}\cos \theta \\ v_{\mathrm{B}}=m\frac{V_{\mathrm{dc}}}{\sqrt{3}}\cos \left(\theta -2\mathsf{\pi }/3\right)\\ v_{\mathrm{C}}=m\frac{V_{\mathrm{dc}}}{\sqrt{3}}\cos \left(\theta +2\mathsf{\pi }/3\right)\end{array}$$

(1)

where θ is the phase angle of the reference voltage and m is the modulation index. The modulation index is defined as:

$$m=\sqrt{3}{V}_{\mathrm{m}}/V_{\mathrm{dc}}$$

(2)

where V_m is the amplitude of the reference voltage within the linear modulation range, m ∈ [0, 1]. For sinusoidal PWM (SPWM), the DC-link voltage is not fully utilized compared with space vector PWM (SVPWM). This problem can be solved by the injection of the zero-sequence voltage v_Z1:

$$v_{\mathrm{Z}1}=-\left(v_{\max }+v_{\min }\right)/2$$

(3)

where v_max = max (v_A, v_B, v_C) and v_min = min (v_A, v_B, v_C) are the maximum and minimum values of the three-phase reference voltage at any arbitrary instant. After the injection of v_Z1, the reference voltage is modified to:

$$v_x^{\prime }=v_x+v_{\mathrm{Z}1}$$

(4)

The waveform of reference voltage v′_x is illustrated in Figure 3.

The switching sequence of each phase can be obtained by the comparison of the reference voltage and the two-phase disposition carriers. The switching sequence of a unit carrier period is shown in Figure 4.

3. Analysis of CMV and Switching Frequency of the Three-Level Inverter

3.1. Common-Mode Voltage

The CMV of a three-level inverter refers to the voltage between the neutral point of the DC-link capacitors and the neutral point of the three-phase loads, which is defined as:

$$v_{\mathrm{CM}}=\left(v_{\mathrm{AO}}+v_{\mathrm{BO}}+v_{\mathrm{CO}}\right)/3$$

(5)

where v_CM is the common-mode voltage. v_AO, v_BO and v_CO are the three-phase voltages, respectively. From (5) and Table 1, the CMV of each basic vector can be obtained, as shown in

Table 2. Common-mode voltage of each basic vector.

Basic Vector			Amplitude of CMV
V1: PNN	V3: NPN	V5: NNP	−Vdc/6
V2: PPN	V4: NPP	V16: PNP	Vdc/6
V7: PON	V8: OPN	V9: NPO	0
V10: NOP	V11: ONP	V12: PNO
V13U: ONN	V15U: NON	V17U: NNO	−Vdc/3
V14U: PPO	V16U: OPP	V18U: POP	Vdc/3
V13L: POO	V15L: OPO	V17L: OOP	Vdc/6
V14L: OON	V16L: NOO	V18L: ONO	−Vdc/6
V0U: PPP			Vdc/2
V0M: OOO			0
V0L: NNN			−Vdc/2

.

The amplitude of CMV for a certain switching sequence is determined by the basic vector with the largest amplitude of CMV. Taking switching sequence V_13U–V_14L–V_0M–V_13L (ONN–OON–OOO–POO) as an example (as shown in Figure 4), the amplitude of CMV is V_dc/3. Obviously, the small and zero vectors with the lower amplitude of CMV need to be adopted during the synthesis of the switching sequence in order to reduce the amplitude of CMV.

3.2. Switching Frequency

As shown in Figure 4, small vectors V_13U and V_13L are both used to synthesize the switching sequence. The switching state of these phases is all changed so that the switching sequence belongs to continuous PWM (CPWM). If only the small vector V_13U is adopted, the switching sequence will become V_13U–V_14L–V_0M (ONN–OON–OOO). While if only the small vector V_13L is adopted, the switching sequence will become V_14L–V_0M–V_13L (OON–OOO–POO). For the above two sequences, the switching states of phase A and C are both changed, but the switching state of phase B remains the same. Thus, these switching sequences belong to DPWM. By the use of DPWM, Only one of the redundant vectors appears in each carrier period. As a result, the switching loss can be reduced.

4. Proposed Carrier-Based Discontinuous PWM Strategy

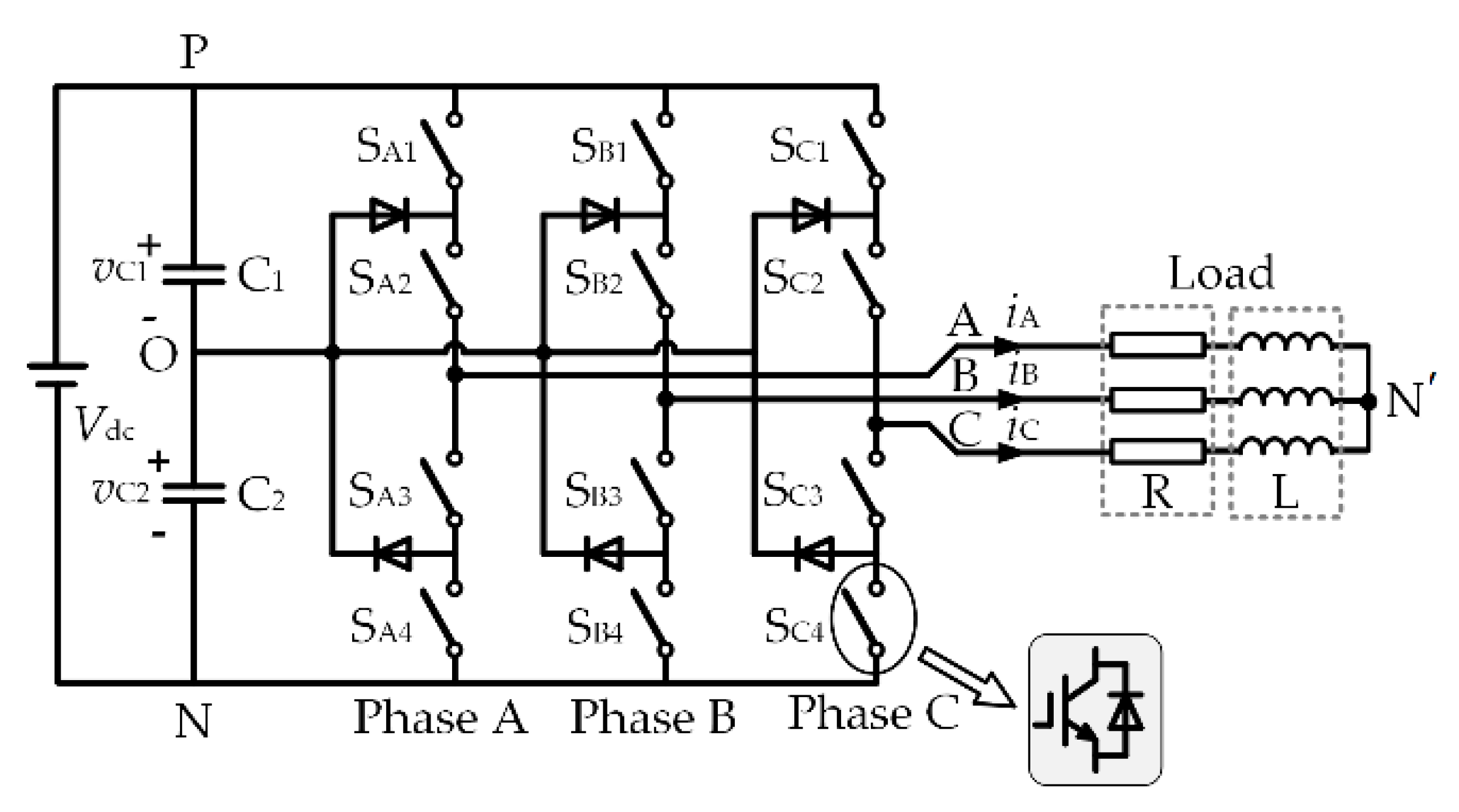
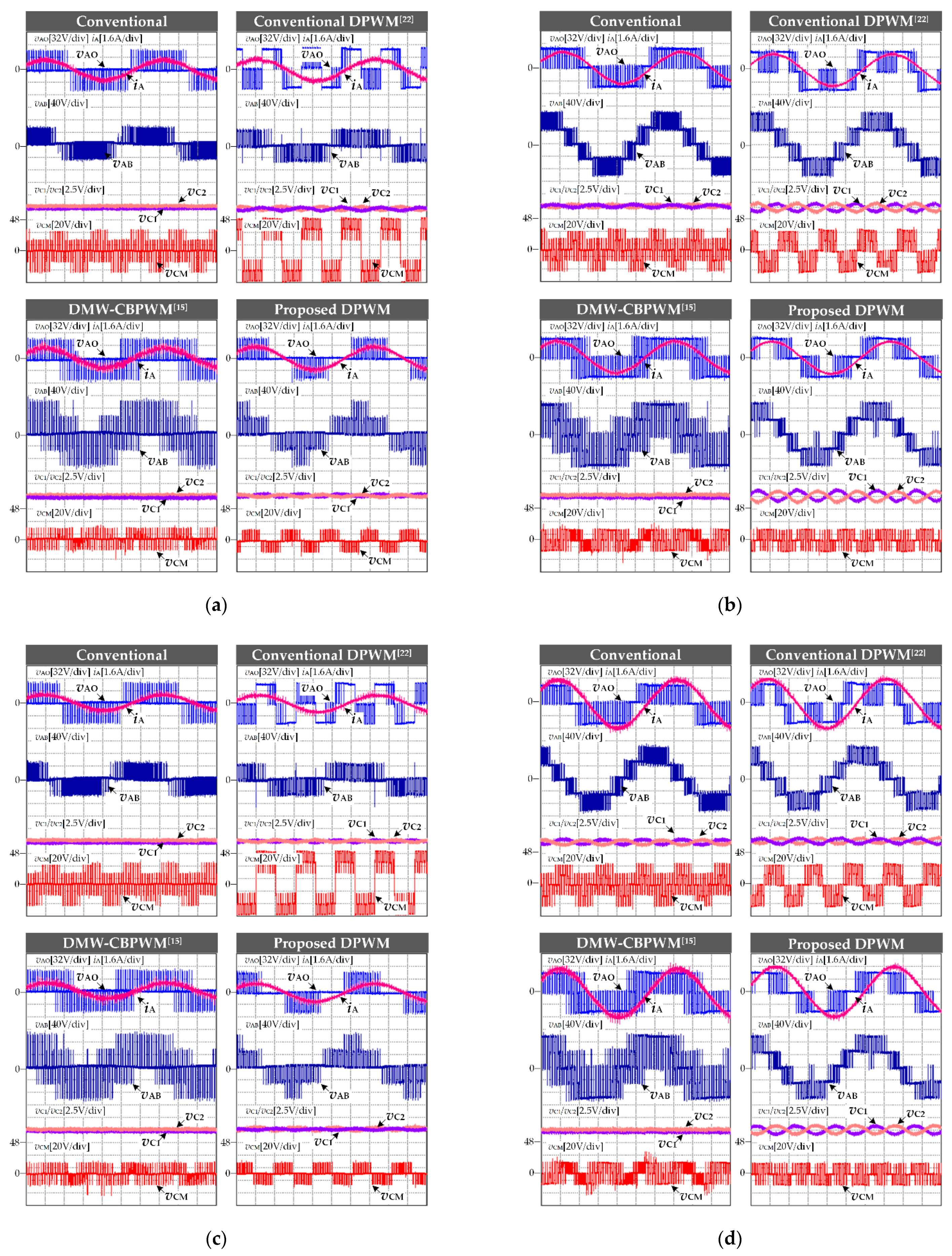
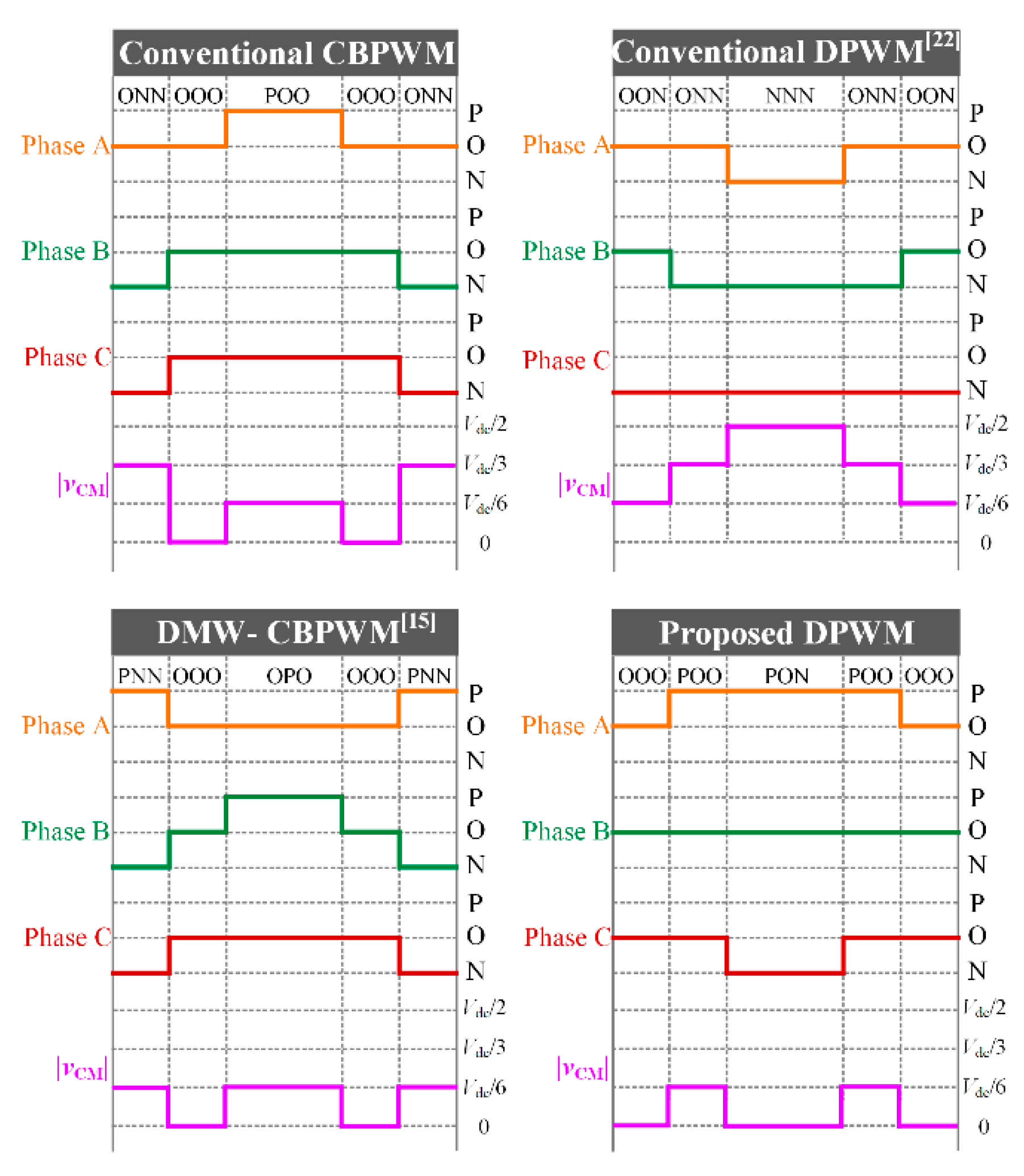
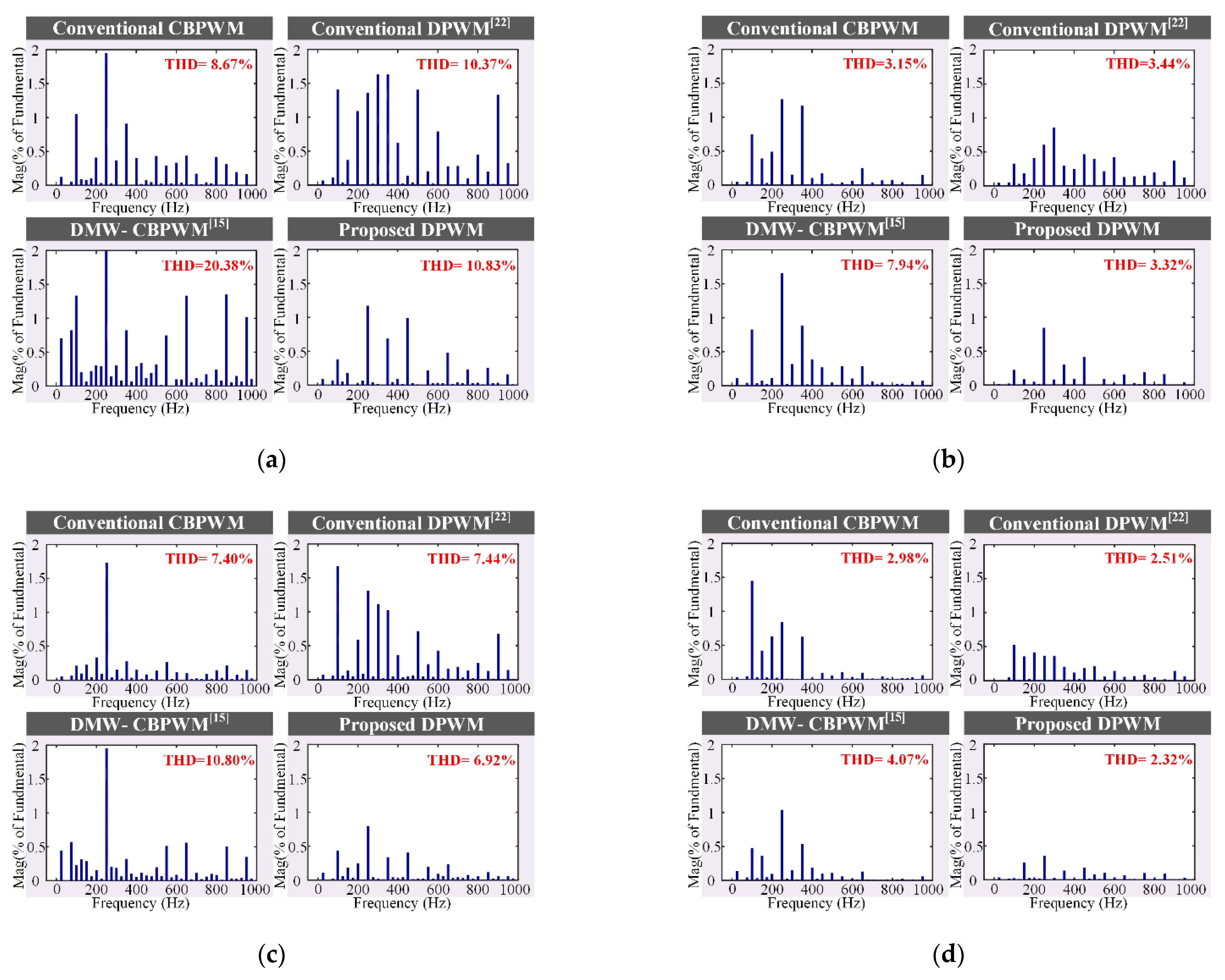
4.1. Switching Sequence Design

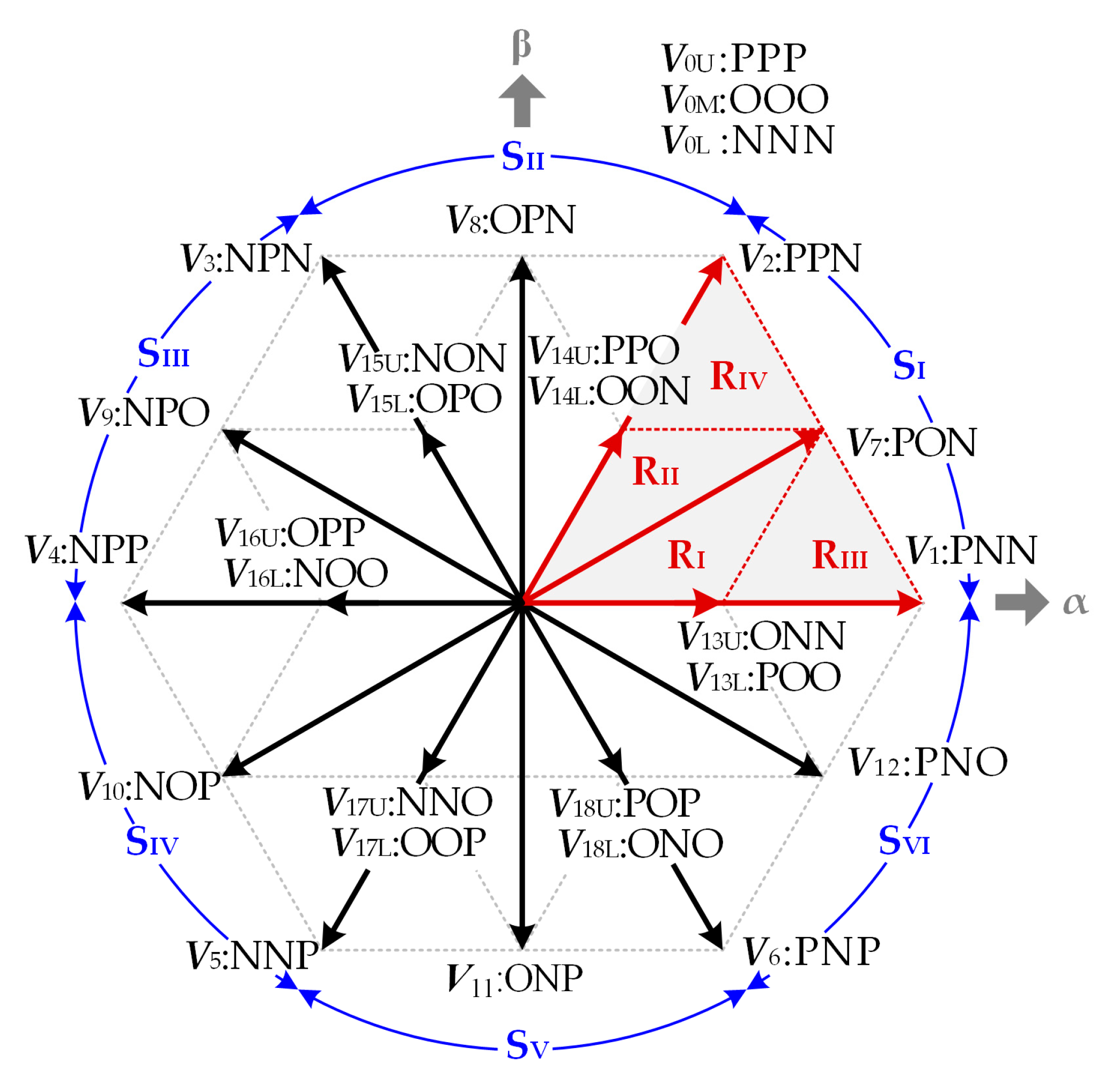
The space vector diagram can be divided into six sectors S_I–S_VI, with the large vector V₁–V₆ as the boundary. Each sector can be further divided into four regions R_I–R_IV. In order to reduce the CMV, small vectors V_13U–V_18U and zero vectors V_0U and V_0L are abandoned. While large vectors, medium vectors, small vectors V_13L–V_18L and zero vector V_0M are adopted to synthesize the switching sequence. Thus, the amplitude of CMV can be limited to V_dc/6. Taking sector S_I as an example:

• In region R_I, V_0M: OOO, V₇: PON and V_13L: POO are used to synthesize the switching sequence;
• In region R_II, V_0M: OOO, V₇: PON and V_14L: OON are used to synthesize the switching sequence;
• In region R_III, V₁: PNN, V₇: PON and V_13L: POO are used to synthesize the switching sequence;
• In region R_IV, V₂: PPN, V₇: PON and V_14L: OON are used to synthesize the switching sequence.

From the aforementioned analysis, phase B is clamped to the switching state O in regions R_I and R_II. It can be defined as clamping state B0. Similarly, phase A is clamped to the switching state P in region R_III, and it can be defined as clamping state A+; phase C is clamped to the switching state N in region R_IV, and it can be defined as clamping state C−. The clamping state of other sectors can be obtained by replacing the vector in S_I by the corresponding vector that occupies the identical position in a given sector, as shown in Figure 5.

4.2. Carrier-Based Implementation

The aforementioned switching sequences can be obtained by the modification of both the reference voltage and the carrier. For the reference voltage, the specific zero-sequence voltage needs to be injected into the reference voltage to realize the clamping state in each region. The CMV and the switching loss are reduced simultaneously. For the carrier, the upper and lower carriers are changed from phase disposition to phase opposition disposition. The extra switches at the boundary of two adjacent regions are reduced. The detailed process is shown as follow:

Reference Vector Modification: The maximum, medium and minimum value of three-phase reference voltages v′_x at any arbitrary instant can be obtained as follows:

$$\{\begin{array}{l}{v}_{\max }^{\prime }=\max \left(v_{\mathrm{A}}^{\prime },v_{\mathrm{B}}^{\prime },v_{\mathrm{C}}^{\prime }\right)\\ v_{\mathrm{mid}}^{\prime }=\mathrm{mid}\left(v_{\mathrm{A}}^{\prime },v_{\mathrm{B}}^{\prime },v_{\mathrm{C}}^{\prime }\right)\\ v_{\min }^{\prime }=\min \left(v_{\mathrm{A}}^{\prime },v_{\mathrm{B}}^{\prime },v_{\mathrm{C}}^{\prime }\right)\end{array}$$

(6)

where max (·), mid (·) and min (·) return the maximum, medium and minimum value of v′_A, v′_B and v′_C. The relationship between v′_max, v′_mid, v′_min and v_x in each sector is shown in

Table 3. Relationship between v′_max, v′_mid, v′_min and v′_x.

Sector	v′max	v′mid	v′min
SI	v′A	v′B	v′C
SII	v′B	v′A	v′C
SIII	v′B	v′C	v′A
SVI	v′C	v′B	v′A
SV	v′C	v′A	v′B
SVI	v′A	v′C	v′B

.

Taking sector S_I as an example:

In region R_I and R_II, phase B needs to maintain clamping state 0. From Table 3, the reference voltage of phase B is v′_mid. Thus, −v′_mid needs to be injected into v′_B to keep the switching state of phase B at O.

In region R_III, phase A needs to maintain clamping state +. The reference voltage of phase A is v′_max. Thus, −v′_max + V_dc needs to be injected into v′_A to keep the switching state of phase A at P.

In region R_IV, phase C needs to maintain clamping state -. The reference voltage of phase C is v′_min. Thus, −v′_max − V_dc needs to be injected into v′_C to keep the switching state of phase C at N.

In conclusion, in order to realize the clamping state in Figure 5, zero-sequence voltage v_Z2 needs to be injected into the reference voltage v′_x. v_Z2 can be expressed as:

$$v_{\mathrm{Z}2}=\{\begin{array}{ll}-v_{\mathrm{mid}}^{\prime }& \mathrm{region}{\mathrm{R}}_{\mathrm{I}}\&{\mathrm{R}}_{\mathrm{II}}\\ -v_{\max }^{\prime }+V_{\mathrm{dc}}/2& \mathrm{region}{\mathrm{R}}_{\mathrm{III}}\\ -v_{\min }^{\prime }-V_{\mathrm{dc}}/2& \mathrm{region}{\mathrm{R}}_{\mathrm{IV}}\end{array}$$

(7)

The three-phase reference voltage after the injection of v_Z2 is v″_x:

$$v_x^{″}=v_x^{\prime }+v_{\mathrm{Z}2}=v_x+v_{\mathrm{Z}1}+v_{\mathrm{Z}2}$$

(8)

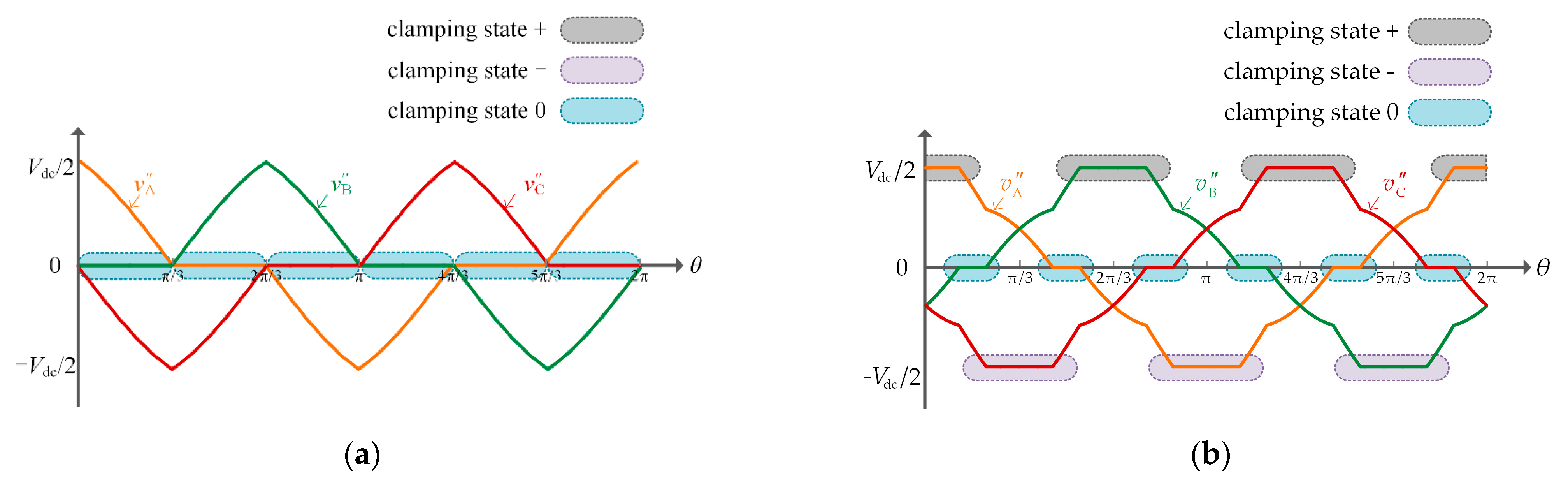
The three-phase reference voltages v″_x in a unit fundamental period are shown in Figure 6. The switching states of the three phases are clamped to the positive bus, the negative bus and the neutral point of the DC-link alternatively, and the discontinuous modulation is realized.

Carrier Modification: For conventional CBPWM of the three-level inverter, the upper and lower-triangular carriers are in phase with each other. The PWM signals of each phase can be obtained by the comparison of the reference voltage v″_x and two carriers. In sector S_I, when the reference voltage travels from region R_III to R_I, the reference voltage and the corresponding switching sequence are shown in Figure 7a.

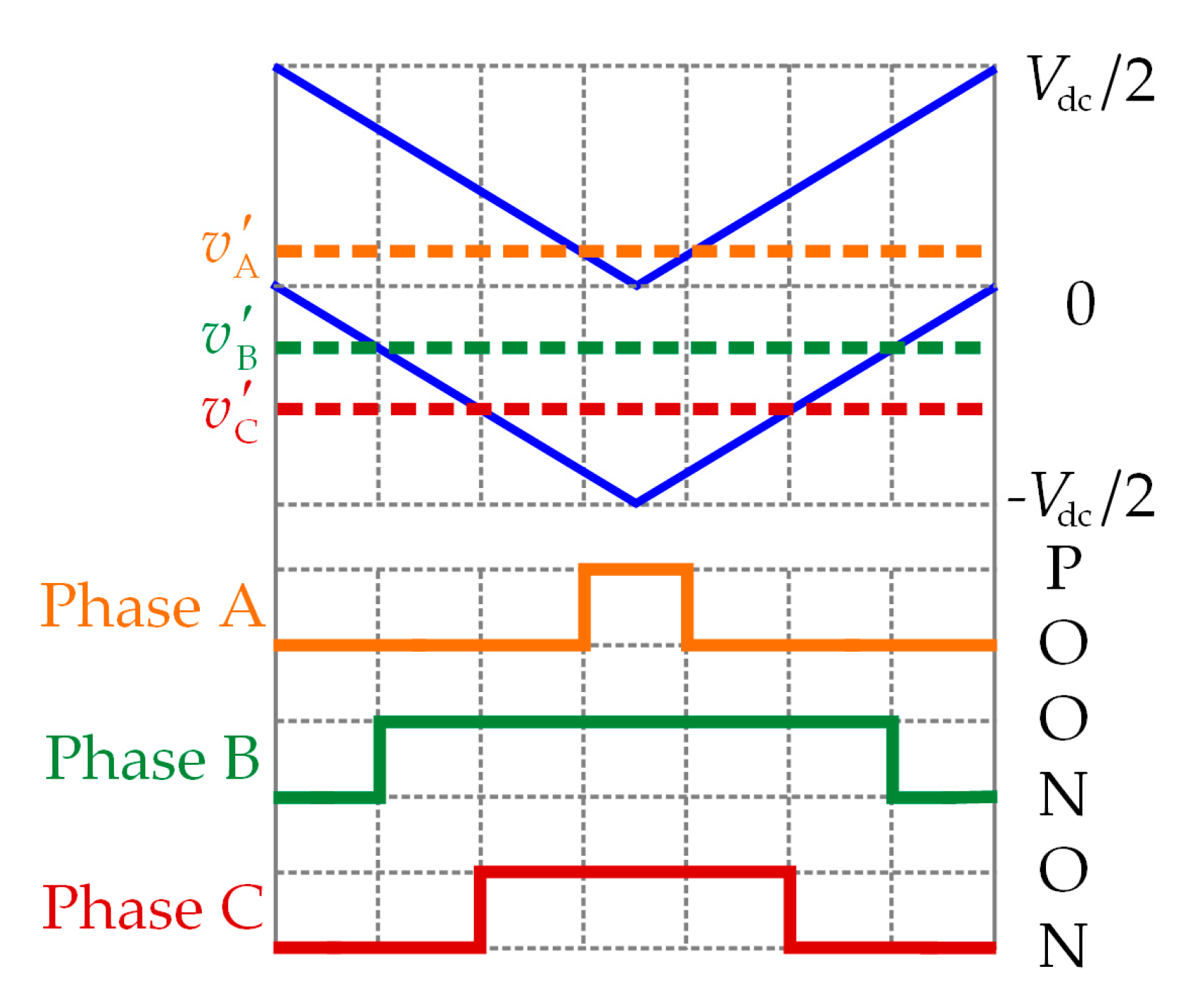
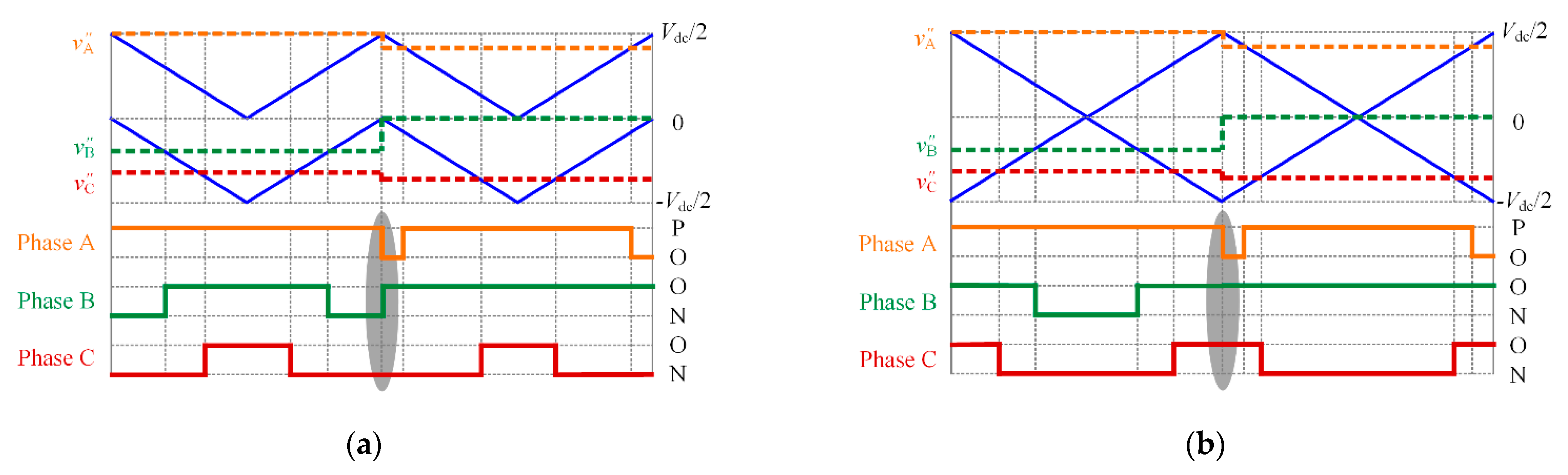
As can be seen, the switching sequence is PNN–PON–POO–PON–PNN in region R_III, and the amplitude of CMV is V_dc/6. The switching sequence is OON–PON→POO–PON–OON in region R_I, and the amplitude of CMV is also V_dc/6. Comparing Figure 7a with Figure 4, the amplitude of CMV is reduced from V_dc/3 to V_dc/6 by the injection of v_Z2. Moreover, the number of switches in each carrier period is reduced from 3 to 2. However, it is worth mentioning that there are extra switches during the transition of two adjacent regions. As shown in Figure 7a, the last switching state of region R_III is PNN, and the first switching state of region R_I is OON. The switching states of phase A and phase B are both changed so that the switching loss is increased. To solve the above issue, the two triangle carriers need to be changed from phase disposition to phase opposition disposition, as shown in Figure 7b. After that, the switching sequence in region R_III becomes POO–PON–PNN–PON–POO, and the switching sequence in region R_I becomes OOO–POO–PON–POO–OOO. The amplitude of CMV is still V_dc/6. Meanwhile, only the switching state of phase A is changed during the transition of two adjacent regions.

In conclusion, the extra switches can be reduced by the phase opposition disposition of the carriers. Then the switching loss can be further suppressed.

4.3. NPV Balance Control

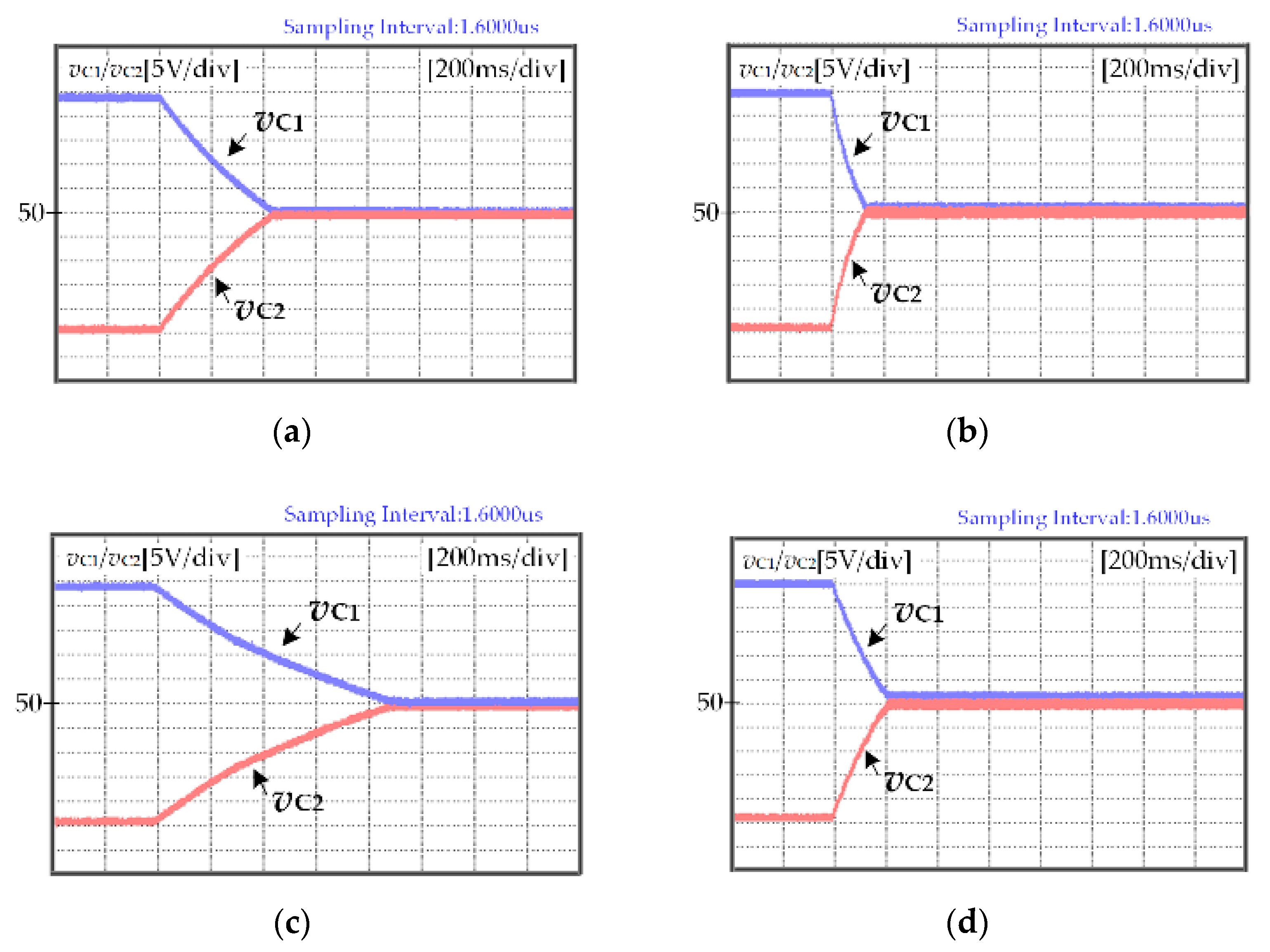
In high-power medium-voltage applications, the NPV balance also needs to be considered, besides the CMV and the switching loss. The NPV is defined as Δv = v_C1 − v_C2, v_th is the threshold value of Δv. When |Δv| < v_th, the NPV does not need to be controlled. When |Δv| > v_th, the NPV ripple must be suppressed. The voltages of the upper capacitor v_C1 and lower capacitor v_C2 are affected by the neutral point current i_O. The neutral point currents are generated by small vectors and medium vectors. Thus, the NPV balance can be realized by adjusting the duty cycle of small and medium vectors in each region of different sectors.

Taking sector S_I as an example, the duty cycle of V_13L: POO (i_O = −i_A) can be adjusted to balance the NPV in region R_I. While the duty cycle of V₇: PON (i_O = i_B) can be adjusted to balance the NPV in region R_III. In region R_I, the neutral point current i_O generated by V_13L: POO is less than zero. When |Δv| > 0, the duty cycle of V_13L: POO needs to be increased. When |Δv| < 0, the duty cycle of V_13L: POO needs to be reduced. In region R_III, the neutral point current i_O generated by V₇: PON is greater than zero. When |Δv| > 0, the duty cycle of V₇: PON needs to be reduced. When |Δv| < 0, the duty cycle of V_13L: POO needs to be increased. Similarly, the duty cycle adjustment rules of small and medium vectors in other sectors are listed in

Table 4. Master vector in each region.

Sector	Region
	RI	RII	RIII & RIV
SI	V13L: PPO (−iA)	V14L: OON (−iC)	V7: PON (iB)
SII	V14L: OON (−iC)	V15L: OPO (−iB)	V8: ONP (iA)
SIII	V15L: OPO (−iB)	V16L: PPO (−iA)	V9: NPO (iC)
SIV	V16L: NOO (−iA)	V17L: OOP (−iC)	V10: NOP (iB)
SV	V17L: OOP (−iC)	V18L: ONO (−iB)	V11: ONP (iA)
SVI	V18L: ONO (−iB)	V13L: PPO (−iA)	V12: PNO (iC)

. The vectors in Table 4 are defined as master vectors, and the other vectors in the same switching sequence are defined as slave vectors.

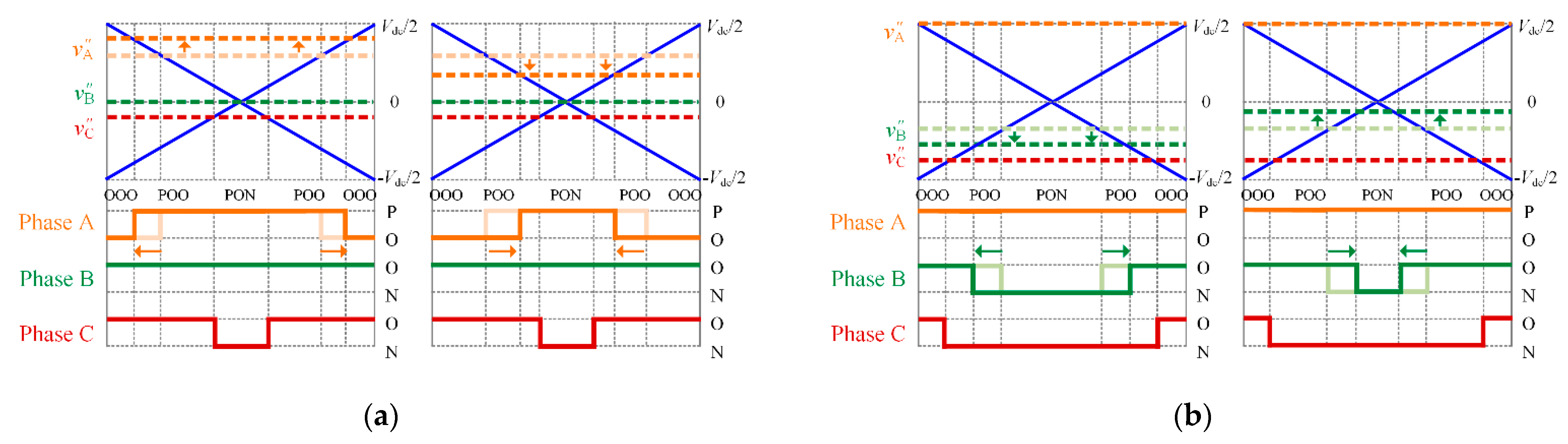
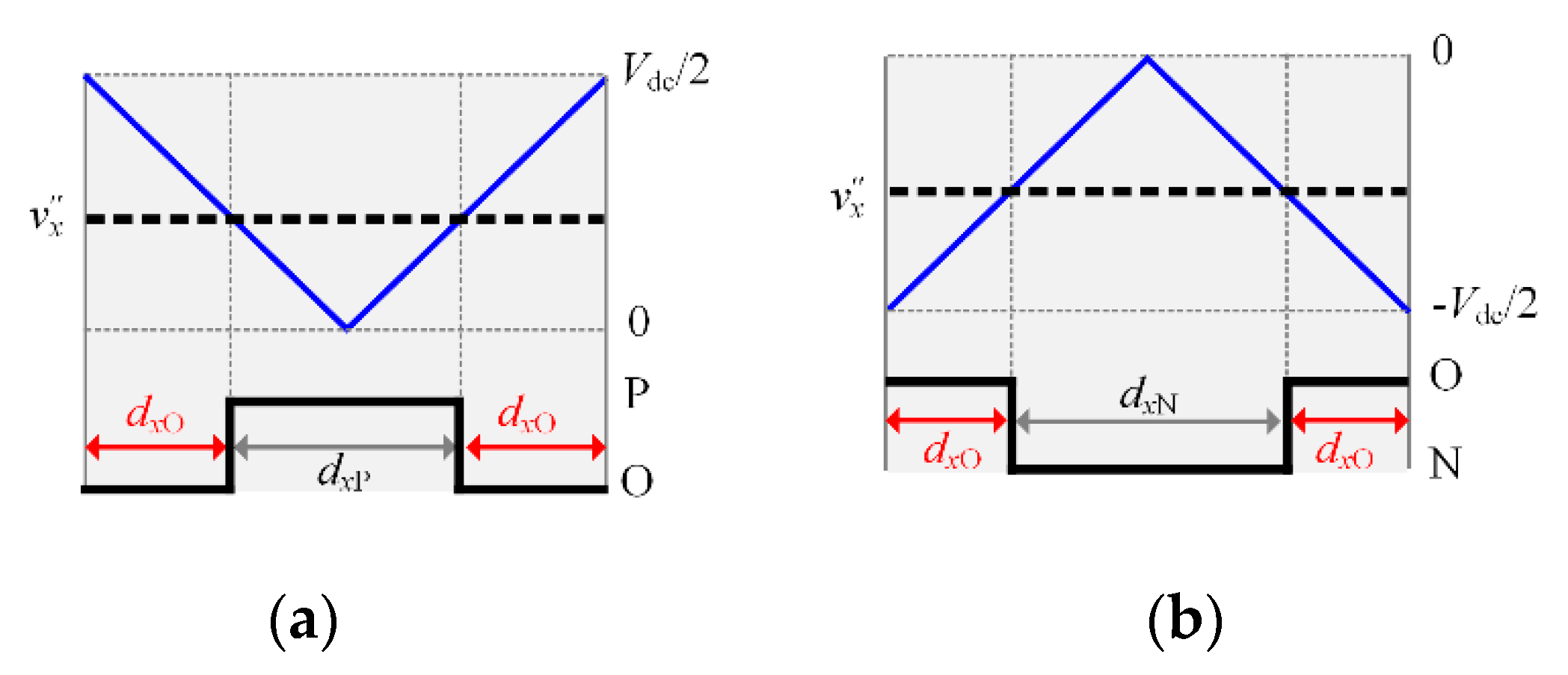
The duty cycle of the master vector can be adjusted by injecting the compensation voltage v_os into the reference voltage v″_x to move the reference voltage up or down. Taking sector S_I as an example, in region R_I, the duty cycle of V_13L: POO will be increased if the reference voltage v″_A is moved up. While the duty cycle of V_13L: POO will be reduced if the reference voltage v″_A is moved down, as illustrated in Figure 8a. In region R_III, the duty cycle of V₇: PON will be increased if the reference voltage v″_B is moved down. While the duty cycle of V₇: PON will be reduced if the reference voltage v″_B is moved up, as illustrated in Figure 8b. It is worth mentioning that the shift of the reference voltage only changes the duty cycle of the master vector and vectors without affecting the NPV. Therefore, the NPV balance can be realized by the shift of the reference voltage.

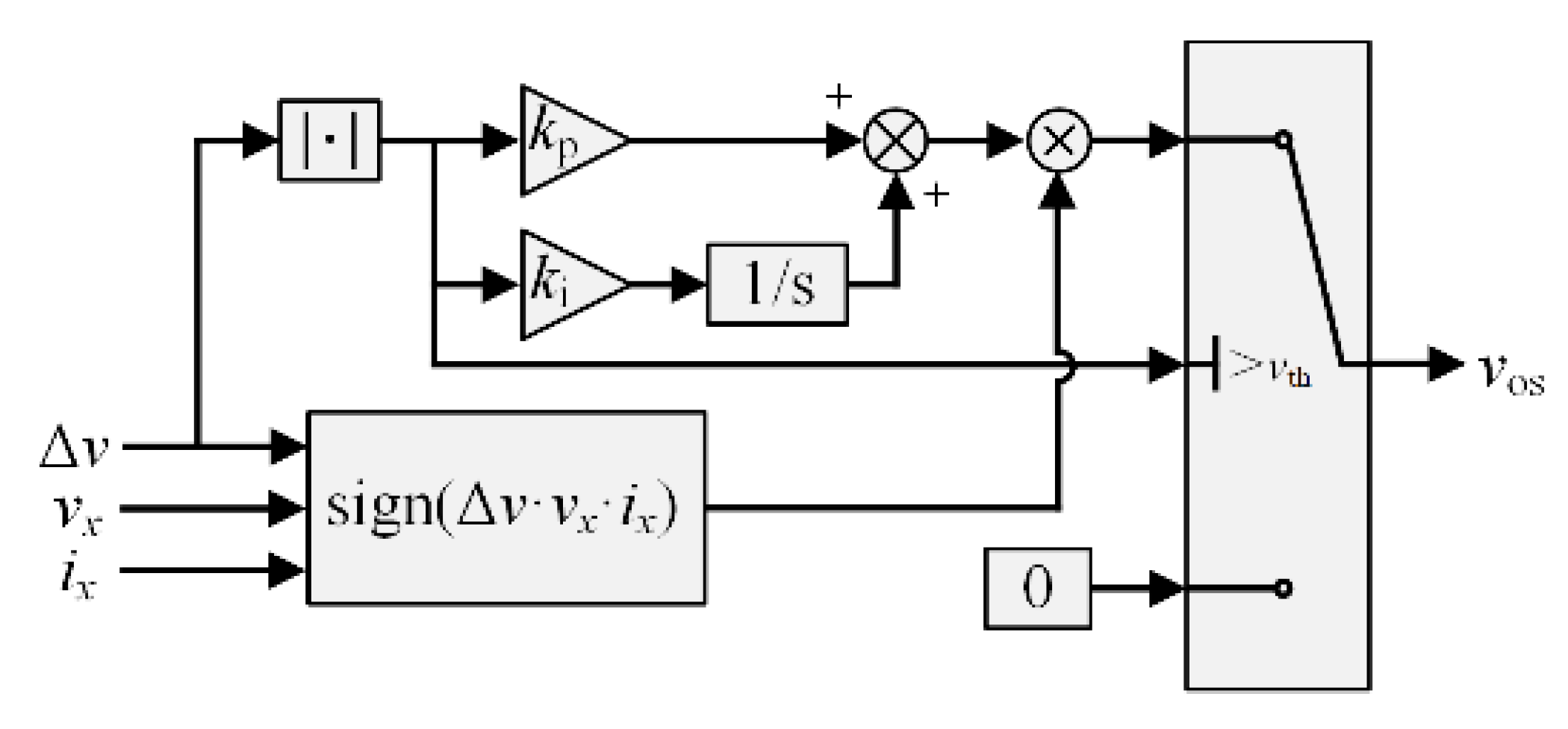
The calculation process of the compensation voltage v_os is shown in Figure 9. When |Δv| < v_th, v_os is set to 0 and three-phase reference voltage v″_x remains the same. When |Δv| > v_th, the compensation voltage v_os is obtained by multiplying the output of the PI controller by sign(Δv·i_x·v_x). Then, v_os is injected into v″_x, according to

Table 5. Compensation voltage injection rules.

Sector	Region
	RI	RII	RIII & RIV
SI & SIV	v*A = v″A + vos	v*A = v″A	v*A = v″A
	v*B = v″B	v*B = v″B	v*B = v″B + vos
	v*C = v″C	v*C = v″C + vos	v*C = v″C
SII & SV	v*A = v″A	v*A = v″A	v*A = v″A + vos
	v*B = v″B	v*B = v″B + vos	v*B = v″B
	v*C = v″C + vos	v*C = v″C	v*C = v″C
SIII & SVI	v*A = v″A	v*A = v″A + vos	v*A = v″A
	v*B = v″B + vos	v*B = v″B	v*B = v″B
	v*C = v″C	v*C = v″C	v*C = v″C + vos

. The reference voltage v*_x = v″_x + v_os after the compensation.

For the NPV balance control, it is necessary to limit the amplitude of v*_x to ensure that the switching sequence is not changed. When v″_x > 0, v*_x will be set to zero if v*_x < 0, while v*_x will be set to v″_max if v*_x > v″_max. When v*_x < 0, v*_x will be set to zero if v*_x > 0, while v*_x will be set to v″_min if v*_x < v″_min, where v″_max and v″_min are the maximum and minimum value of v″_x.

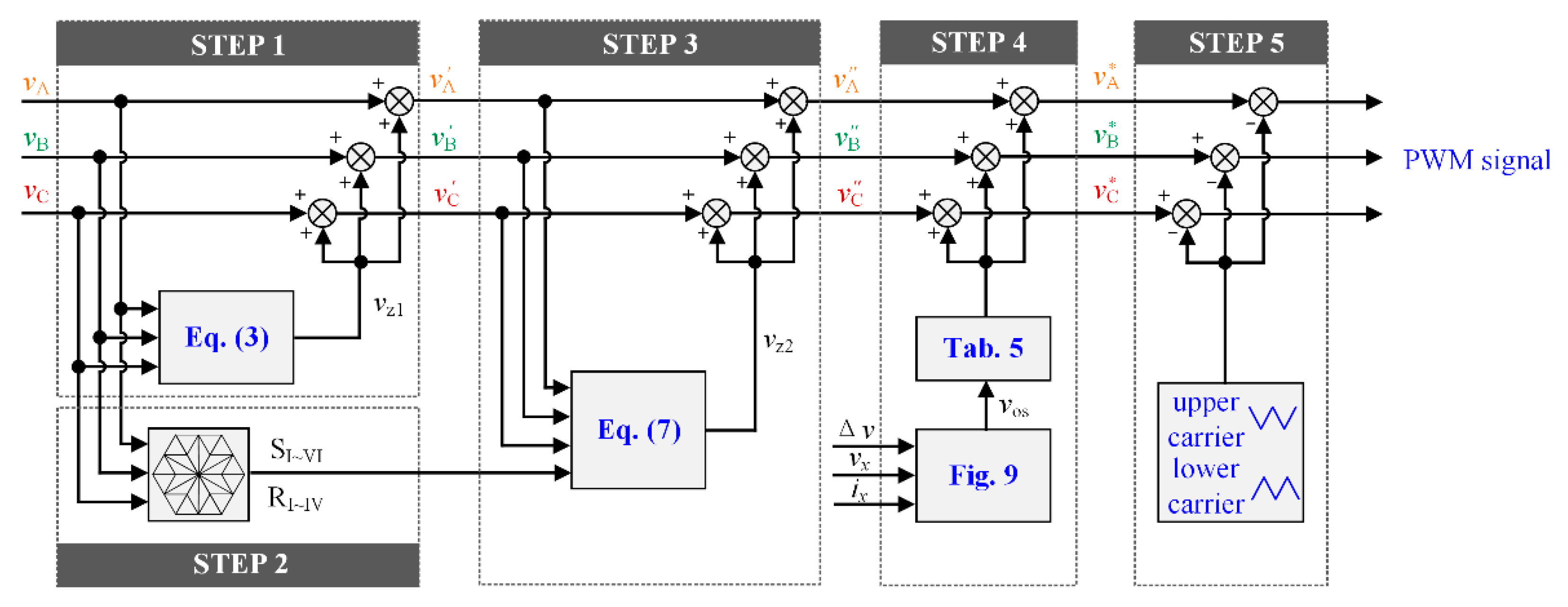
In conclusion, the CMV and the switching loss can be reduced by the modification of the reference voltage and the carriers. Meanwhile, the NPV balance can also be realized by the shift of the reference voltage without changing the switching sequence. The block diagram of the proposed DPWM is shown in Figure 10. The detailed steps are listed as follows:

• STEP 1: the zero-sequence voltage v_Z1 is injected into the reference voltage v_x;
• STEP 2: the sector and region are determined by the three-phase reference voltage;
• STEP 3: the zero-sequence voltage v_Z2 is injected into the reference voltage v′_x;
• STEP 4: the compensation voltage v_os is generated and injected into the reference voltage v″_x;
• STEP 5: the pulse signal of each power switch is generated by the comparison of the reference voltage v*_x and the carriers.

5. Experimental Verification

In order to verify the feasibility and effectiveness of the proposed DPWM strategy, the rapid control prototype OP5700 (OPAL-RT Co. Ltd.,Richardson, Canada) and the NPC three-level power model PEN8018 (Imperix Co. Ltd., Sion, Switzerland) are adopted to establish the experimental setup, as shown in Figure 11.

The proposed DPWM strategy is compared with the conventional CBPWM, the conventional DPWM [22] and the DMW-CBPWM [15]. Parameters of the experimental setup are listed in

Table 6. Experimental parameters of the prototype.

Parameter	Unit	Value
DC-link capacitor C1, C2	μF	1551
DC-link voltage Vdc	V	100
Load Resistance R	Ω	10
Load inductance L	mH	10, 30
Fundamental frequency f	Hz	50
Carrier frequency fc	kHz	2.5

. When R = 10 Ω and L = 10 mH, the power factor cos φ is 0.954. When R = 10 Ω and L = 30 mH, the power factor cos φ is 0.732.

The phase voltage v_AO, line voltage v_AB, phase current i_A, common-mode voltage v_CM and the upper and lower-capacitor voltages v_C1/v_C2 are shown in Figure 12.

5.1. Common-Mode Voltage

The switching sequences and the corresponding CMV of the four tested strategies in a unit carrier period are shown in Figure 13. For the conventional CBPWM, small vectors V_iU (i ∈ {13, 14, …, 18}) are used to synthesize the switching sequence. For the conventional DPWM, zero vector V_0U and V_0L are used to synthesize the switching sequence. Thus, the amplitude of the CMV is higher for these two strategies. For the DMW-CBPWM and the proposed DPWM, small vector V_iU, zero vector V_0U and V_0L are abandoned so that the amplitude of the CMV is lower. As can be seen in Figure 12, the amplitude of the CMV is 33.33 V (V_dc/3) for the conventional CBPWM. The amplitude of CMV is 50 V (V_dc/2) for the conventional DPWM. The amplitude of the CMV is 16.67 V (V_dc/6) for the DMW-CBPWM and the proposed DPWM.

5.2. Switching Loss

In each carrier period, the switch time of the conventional DPWM and the proposed DPWM strategy is two, the switch time of the conventional CBPWM is three and the switch time of the DMW-CBPWM is four, as shown in Figure 13. The efficiency of the inverter with the above four strategies is recorded by Yokogawa WT5000 power analyzer, as listed in

Table 7. The efficiency of the inverter under different strategies.

Modulation Strategy	Efficiency
	R = 10 Ω, L = 10 mH		R = 10 Ω, L = 30 mH
	m = 0.3	m = 0.8	m = 0.3	m = 0.8
Conventional CBPWM	82.920%	93.320%	79.429%	91.978%
Conventional DPWM [22]	84.488%	93.432%	81.085%	92.116%
DMW-CBPWM [15]	82.943%	92.919%	79.203%	91.600%
Proposed DPWM	85.168%	93.482%	81.957%	92.180%

. The efficiency of the proposed DPWM is higher than the other three strategies, which verifies that the switching loss of the inverter can be suppressed by the proposed DPWM.

5.3. Harmonic Distortion

As shown in Figure 12, the output current ripple of DMW-CBPWM is the highest. The output current ripple of the other three strategies is not very different from each other. By the FFT analysis of the experimental results, the harmonics spectra of the output current waveforms under m = 0.3 and m = 0.8 are shown in Figure 14. Under lower modulation index and higher power factor conditions, the THD of the proposed DPWM is greater than Conventional CBPWM and Conventional DPWM but less than DMW-CBPWM. Under lower power factor conditions, regardless of the modulation index, the THD of the proposed DPWM is smaller than the other three strategies. Therefore, the output waveform quality of the inverter can be improved by the proposed DPWM strategy under certain load conditions.

5.4. Neutral Point Voltage

If |Δv| < v_th, the NPV will not be controlled. As shown in Figure 12, the upper and lower-capacitor voltages are approximately the same for all four strategies under lower-modulation index conditions. Under higher-modulation index conditions, there are low-frequency components, which are 150 Hz (three times the fundamental frequency of output current), in both the upper and lower-capacitor voltages for the conventional CBPWM, the conventional DPWM and the proposed DPWM. However, the neutral point voltage is still self-balanced on the fundamental period level. Taking the proposed DPWM as an example, the detailed analysis is as follows. After the injection of v_Z2, the dwell time of switching state O for each phase can be expressed as:

$$d_{xO}=1-\frac{2v_x^{″}}{V_{\mathrm{dc}}}$$

(9)

As shown in Figure 15, in a unit carrier period, the neutral point current i_O is:

$$i_{\mathrm{O}}=i_{\mathrm{A}}\cdot d_{\mathrm{AO}}+i_{\mathrm{B}}\cdot d_{\mathrm{BO}}+i_{\mathrm{C}}\cdot d_{\mathrm{CO}}$$

(10)

The reference voltage, output current and the neutral point current can be regarded as the function of the phase angle θ. Taking sector S_I as an example, when the reference voltage is in region R_I, phase B is clamped to switching state O and d_BO = 1. Substituting (7), (8) and (9) into (10), yields:

$$i_{\mathrm{O}}\left(\theta \right)=i_{\mathrm{A}}\left(\theta \right)\left(1-2\frac{v_{\mathrm{A}}^{\prime }\left(\theta \right)-v_{\mathrm{B}}^{\prime }\left(\theta \right)}{V_{\mathrm{dc}}}\right)+i_{\mathrm{B}}\left(\theta \right)+i_{\mathrm{C}}\left(\theta \right)\left(1-2\frac{v_{\mathrm{C}}^{\prime }\left(\theta \right)-v_{\mathrm{B}}^{\prime }\left(\theta \right)}{V_{\mathrm{dc}}}\right)$$

(11)

When the phase angle is θ + π/3, phase A is clamped to the switching state O and d_AO = 1. The neutral point current is:

$$\begin{array}{c}{i}_{\mathrm{O}}\left(\theta +\mathsf{\pi }/3\right)=i_{\mathrm{A}}\left(\theta +\mathsf{\pi }/3\right)+i_{\mathrm{B}}\left(\theta +\mathsf{\pi }/3\right)\left(1-2\frac{v_{\mathrm{B}}^{\prime }\left(\theta +\mathsf{\pi }/3\right)-v_{\mathrm{A}}^{\prime }\left(\theta +\mathsf{\pi }/3\right)}{V_{\mathrm{dc}}}\right)\\ +i_{\mathrm{C}}\left(\theta +\mathsf{\pi }/3\right)\left(1-2\frac{v_{\mathrm{C}}^{\prime }\left(\theta +\mathsf{\pi }/3\right)-v_{\mathrm{A}}^{\prime }\left(\theta +\mathsf{\pi }/3\right)}{V_{\mathrm{dc}}}\right)\end{array}$$

(12)

The reference voltage and the output current are three-phase symmetrized.

$$\{\begin{array}{l}{v}_{\mathrm{A}}^{\prime }\left(\theta +\mathsf{\pi }/3\right)=-v_{\mathrm{B}}^{\prime }\left(\theta \right),i_{\mathrm{A}}^{\prime }\left(\theta +\mathsf{\pi }/3\right)=-i_{\mathrm{B}}^{\prime }\left(\theta \right)\\ v_{\mathrm{B}}^{\prime }\left(\theta +\mathsf{\pi }/3\right)=-v_{\mathrm{C}}^{\prime }\left(\theta \right),i_{\mathrm{B}}^{\prime }\left(\theta +\mathsf{\pi }/3\right)=-i_{\mathrm{C}}^{\prime }\left(\theta \right)\\ v_{\mathrm{C}}^{\prime }\left(\theta +\mathsf{\pi }/3\right)=-v_{\mathrm{A}}^{\prime }\left(\theta \right),i_{\mathrm{C}}^{\prime }\left(\theta +\mathsf{\pi }/3\right)=-i_{\mathrm{A}}^{\prime }\left(\theta \right)\end{array}$$

(13)

Substituting (13) into (12), yields that i_O(θ) = −i_O(θ + π/3). It indicates that the NPV generated by the neutral point current at any arbitrary instant will be offset by the neutral point current lagging π/3. Thus, there is always a triple fundamental frequency component in the neutral point voltage. However, the neutral point can still be considered balanced on a fundamental period level; as shown in Figure 12a,b.

If |Δv| > v_th, the proposed NPV balance control method will be adopted. Figure 16 shows experimental results for modulation indices of m = 0.3 and m = 0.8, respectively, which illustrates the NPV balance scenario described earlier. The upper and lower capacitor voltages are intentionally unbalanced by 100 V. As can be seen, the voltage difference can be eliminated by the injection of v_os under both higher and lower-modulation index conditions. The settling time is significantly smaller under the higher-modulation index and high-power factor conditions because a larger value of v_os can be added.

6. Conclusions

A carrier-based DPWM strategy of the NPC three-level inverter is proposed in this paper. This strategy can be used in NPC three-level inverters for industrial applications, such as traction inverters in rail transit systems and mine hoist systems, where lower common-mode voltage and lower switching loss are required.

Firstly, the reference voltage is modified by two injections of the zero-sequence voltage. The DC-link voltage utilization of the inverter is enhanced by the first injection of the zero-sequence voltage. Then, the three phases are clamped alternatively to reduce the CMV and the switching loss by the second injection of the zero-sequence voltage. Secondly, the carrier is modified by phase opposition disposition to reduce the extra switches during the transition of two adjacent regions. Finally, without the change of switching sequence in each carrier period, the NPV balance is achieved by the injection of compensation voltage into the reference voltage. In addition, the output harmonic distortion is also improved by the proposed strategy.