Exploiting the S-Iteration Process for Solving Power Flow Problems: Novel Algorithms and Comprehensive Analysis

Abstract

In recent studies, the competitiveness of the Newton-S-Iteration-Process (Newton-SIP) techniques to efficiently solve the Power Flow (PF) problems in both well and ill-conditioned systems has been highlighted, concluding that these methods may be suitable for industrial applications. This paper aims to tackle some of the open topics brought for this kind of techniques. Different PF techniques are proposed based on the most recently developed Newton-SIP methods. In addition, convergence analysis and a comparative study of four different Newton-SIP methods PF techniques are presented. To check the features of considered PF techniques, several numerical experiments are carried out. Results show that the considered Newton-SIP techniques can achieve up to an eighth order of convergence and typically are more efficient and robust than the Newton–Raphson (NR) technique. Finally, it is shown that the overall performance of the considered PF techniques is strongly influenced by the values of parameters involved in the iterative procedure.

1. Introduction

Power Flow (PF) is the backbone of power system analysis. From a mathematical point of view, PF is a nonlinear problem in which the operational steady state of a power system is obtained. Traditional methods for tackling this problem are the iterative NR [1] and decoupled techniques [2,3,4].

Although PF is customarily solved in polar coordinates form, other formulations have been studied. A PF formulation based on current injections instead of power injections has been proposed by da Costa et al. [5] and posteriorly embellished by Garcia et al. in [6]. Saleh has developed a formulation of the PF problem in the well-known d-q framework in [7,8]. More recently, PF formulation in complex variables has been exploited in [9], using Witinger Calculus.

Ill-conditioned systems bring some issues for traditional PF solution techniques. This topic has been profusely studied for decades. For example, the reader can be referred to the works of Iwamoto and Tamura [10], Tripathy et al. [11] or Braz et al. [12]. More recently, these kinds of problems have been tackled using the Continuous Newton’s paradigm by Milano in [13] or by some of the authors in several recent papers [14,15,16]. The works of Pourbagher and Derakhshandeh have been focused on the solution of ill-conditioned power systems using the Levenberg–Marquardt technique [17,18]. Alternatively, a novel paradigm has been proposed by the authors in [19], which studies the application of the Gauss–Newton method for PF analysis.

High-order Newton-like methods have also been studied for PF analysis. In [20], Pourbagher and Derakhshandeh studied the application of Newton-like techniques of 3rd, 4th, and 5th order to PF analysis. On the other hand, a Newton-like technique with a superquadratic convergence rate has been proposed to solve the PF problem in well-conditioned systems by some of the authors in [21].

Regarding continuation, Homotopic and Holomorphic techniques have also been exploited for PF analysis. The well-known Continuation Power Flow [22] may be the greatest exponent of this kind of methodology. This approach is traditionally used to determine the stability margin of a power system by calculating its Maximum Loadability Point. Some recent efforts have been made for adapting Continuation Power Flow to distribution systems [23,24]. The Homotopic principle has been applied to PF analysis by Yang and Zhou in [25]. Posteriorly, a family of robust and efficient PF solution techniques based on a combined Newton–Homotopic approach has been developed by some of the authors in [26]. The PF solution by the Holomorphic Embedding method was firstly studied in [27]. Recently, the PF solution by this principle has been further studied in [28,29].

The application of the S-iteration process (SIP) [30] to PF analysis has been recently tackled by the authors in [31]. In this regard, an iterative algorithm based on a combined Newton-SIP approach developed in [32] was adapted for solving either well or ill-conditioned systems. The developed solver turned out to be very efficient, since only an LU decomposition is required in the whole iterative process. This was reflected in very promising results, frequently outperforming NR or the decoupled methods. In addition, it turned out to be quite robust, efficiently handling some large and very large ill-conditioned systems. However, due to the linear convergence characteristic of this method, it suffers from slow convergence in heavy loading cases. In order to overcome this drawback, a Jacobian updated mechanism has also been proposed. Definitely, the PF solution technique proposed in [31] and its variant can be widely used in industry tools due to its capacity for managing well and ill-conditioned equations and its simplicity and efficiency. However, the application of SIP for PF analysis is still far from being fully studied. For example, several topics still need to be further analyzed:

• The reference [31] is limited to studying only one of the algorithms developed in [32]. In the latter reference, along with [33], three other Newton-SIP methods were developed. The applicability of these techniques to PF analysis has not been studied yet.
• Although the Jacobian updated mechanism proposed in [31] allows overcoming the slow-convergence issues in heavy loading systems, the whole iterative procedure remains linear. Consequently, many iterations are normally employed to achieve a feasible solution.
• The overall performance of the Newton-SIP technique studied in [31] strongly depends on the value of the parameters involved in the iterative procedure (s-parameters).

In order to respond to the issues above, the authors strongly believe that further analysis of the SIP applied to PF analysis is still required. This paper aims to fill this gap by profusely studying the Newton-like methods developed in [32,33]. Two schemes are considered. Firstly, we take the constant Jacobian matrix, which corresponds with the standard form of the techniques developed in [32,33]. This mechanism brings linear algorithms; hence, the Newton-SIP methods are also studied for a fully updated scheme in which the Jacobian matrix involved is updated each iteration. The developed methods are compared in terms of efficiency and convergence rate. Finally, we study several numerical experiments in order to analyze the performance of the different Newton-SIP methods in well and ill-conditioned systems, comparing their results with those obtained by NR and analyzing the influence of the s-parameters in the overall performance of the Newton-SIP approaches.

The remainder of the paper is organized as follows. Firstly, the Newton-SIP methods developed in [32,33] are presented and adapted to the PF problem in Section 2. A convergence study of the considered PF solution techniques is provided in Section 3. Section 4 compares the studied methodologies in terms of efficiency. Section 5 describes the different numerical experiments considered, and the results obtained are interpreted and discussed. Finally, Section 6 concludes the paper.

2. Newton-SIP Methods Applied to PF Analysis

2.1. Background

The PF problem in polar coordinates can be established as a set of $n$ nonlinear equations given by [34]:

$$g\left(\mathit{x}\right)=\left\{\begin{array}{c}{P}_i^{sch}-\sum \left|V_i\right|\left|V_j\right|\left|Y_{ij}\right|\cos \left({\theta }_{ij}-{\delta }_i+{\delta }_j\right)=0\hfill \\ Q_i^{sch}-\sum \left|V_i\right|\left|V_j\right|\left|Y_{ij}\right|\sin \left({\theta }_{ij}-{\delta }_i+{\delta }_j\right)=0\hfill \end{array}\right.$$

(1)

where $P_i^{sch}$ and $Q_i^{sch}$ are the scheduled active and reactive power at $i^{th}$ bus, respectively; $V_i\angle {\delta }_i$ is the complex voltage at the $i^{th}$ bus; $Y_{ij}\angle {\theta }_{ij}$ is the $i{j}^{th}$ element of the admittance matrix; and $\mathit{x}\in {ℝ}^n$ is the PF vector of unknowns, which is defined in polar coordinates as follows:

$$\mathit{x}={\left[\left.{\mathit{\delta }}_{PV}\right|\left.{\mathit{\delta }}_{PQ}\right|{\mathit{V}}_{PQ}\right]}^{\mathit{T}}$$

(2)

where ${\mathit{\delta }}_{PV}\in {ℝ}^{n_g}$ is the vector of voltage angles at PV buses, ${\mathit{\delta }}_{PQ}\in {ℝ}^{n_l}$ is the vector of voltage angles at PQ buses, $V_{PQ}\in {ℝ}^{n_l}$ is the vector of voltage magnitudes at PQ buses, and $n_l$ and $n_g$ are the total number of PQ and PV buses, respectively.

In the formulation above, only the well-known constant power loads have been considered, nevertheless, other type of consumers could be considered following the formulation described in the Appendix A. Explicit solutions of the system of nonlinear equations (1) cannot be directly obtained. In this regard, iterative methods are undoubtedly the most popular techniques for solving this kind of problem. Among them, the NR method has been the most widely used in PF analysis. The generic $k^{th}$ iteration of the NR for solving (1) is given by:

$${\mathit{x}}^{\left(k+1\right)}={\mathit{x}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(k\right)}\right)\right]}^{-1}g\left({\mathit{x}}^{\left(k\right)}\right)$$

(3)

where $\mathit{J}\in {ℝ}^{n\times n}$ is the Jacobian matrix, which is formed by the first partial derivatives of (1) with respect to (2). It is well known that the NR method has local quadratic convergence.

Alternatively, other robust and high-order Newton-like methods have been proposed to solve the PF and overcome the drawbacks posed by NR (See Section 1). This paper is focused on the family of Newton-SIP methods, which are described in the following subsections.

2.2. Newton-SIP Methods (Type 1)

In [32], two Newton-SIP methods have been developed. Firstly, we denote SIP1-J₀ to the methodology whose generic $k^{th}$ iteration for solving the PF is carried out as follows:

$$\left\{\begin{array}{c}\hfill {\mathit{y}}^{\left(k\right)}=\left(1-\alpha \right){\mathit{x}}^{\left(k\right)}+\alpha \left({\mathit{x}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(0\right)}\right)\right]}^{-1}g\left({\mathit{x}}^{\left(k\right)}\right)\right)\hfill \\ \hfill {\mathit{x}}^{\left(k+1\right)}={\mathit{y}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(0\right)}\right)\right]}^{-1}g\left({\mathit{y}}^{\left(k\right)}\right) \hfill \end{array}\right.$$

(4)

where $\alpha$. On the other hand, another Newton-SIP method, namely SIP2-J₀ has been proposed in [32]. In this case, the generic $k^{th}$ iteration of SIP2-J₀ for solving the PF is given by:

$$\left\{\begin{array}{c}\hfill {\mathit{y}}^{\left(k\right)}=\left(1-\alpha \right){\mathit{x}}^{\left(k\right)}+\alpha \left({\mathit{x}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(0\right)}\right)\right]}^{-1}g\left({\mathit{x}}^{\left(k\right)}\right)\right)\hfill \\ \hfill {\mathit{x}}^{\left(k+1\right)}={\mathit{y}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{y}}^{\left(0\right)}\right)\right]}^{-1}g\left({\mathit{y}}^{\left(k\right)}\right) \hfill \end{array}\right..$$

(5)

Both SIP1-J₀ and SIP2-J₀ are defined by only one s-parameter (namely $\alpha$). The main difference between SIP1-J₀ and SIP2-J₀ lies in the latter requiring two Jacobian evaluations. It is noteworthy that the iterative algorithms defined by (4) and (5) only evaluate the Jacobian at ${\mathit{x}}^{\left(0\right)}$ and ${\mathit{y}}^{\left(0\right)}$; hence, they are a priori more efficient than NR.

2.3. Newton-SIP Methods (Type 2)

In [33], two other Newton-SIP algorithms are proposed. Firstly, let us denote SIP3-J₀ to that method whose generic $k^{th}$ iteration for solving the PF is carried out as follows:

$$\left\{\begin{array}{c}{\mathit{z}}^{\left(k\right)}=\left(1-\theta \right){\mathit{x}}^{\left(k\right)}+\theta \left({\mathit{x}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(0\right)}\right)\right]}^{-1}g\left({\mathit{x}}^{\left(k\right)}\right)\right) \\ {\mathit{y}}^{\left(k\right)}=\left(1-\alpha \right)\left({\mathit{x}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(0\right)}\right)\right]}^{-1}g\left({\mathit{x}}^{\left(k\right)}\right)\right)+\alpha \left({\mathit{z}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(0\right)}\right)\right]}^{-1}g\left({\mathit{z}}^{\left(k\right)}\right)\right)\\ {\mathit{x}}^{\left(k+1\right)}={\mathit{y}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(0\right)}\right)\right]}^{-1}g\left({\mathit{y}}^{\left(k\right)}\right) \end{array}\right.$$

(6)

where $\theta$. Finally, the methodology denoted SIP4-J₀ proposed in [33] is carried out at its generic $k^{th}$ iteration for solving the PF problem as follows:

$$\left\{\begin{array}{c}{\mathit{z}}^{\left(k\right)}=\left(1-\theta \right){\mathit{x}}^{\left(k\right)}+\theta \left({\mathit{x}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(0\right)}\right)\right]}^{-1}g\left({\mathit{x}}^{\left(k\right)}\right)\right) \\ {\mathit{y}}^{\left(k\right)}=\left(1-\alpha \right)\left({\mathit{x}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(0\right)}\right)\right]}^{-1}g\left({\mathit{x}}^{\left(k\right)}\right)\right)+\alpha \left({\mathit{z}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{z}}^{\left(0\right)}\right)\right]}^{-1}g\left({\mathit{z}}^{\left(k\right)}\right)\right)\\ {\mathit{x}}^{\left(k+1\right)}={\mathit{y}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{y}}^{\left(0\right)}\right)\right]}^{-1}g\left({\mathit{y}}^{\left(k\right)}\right) \end{array}\right..$$

(7)

As in the previous subsection, the main difference between SIP3-J₀ and SIP4-J₀ lies in the total number of Jacobian evaluations. While the latter requires three Jacobian evaluations, SIP3-J₀ only requires one Jacobian evaluation. An important difference between the methodologies proposed in [32] and those developed in [33] is the number of s-parameters involved. While SIP1-J₀ and SIP2-J₀ are defined by only one s-parameter ($\alpha$), SIP3-J₀ and SIP4-J₀ are characterized by a pair of s-parameters ($\alpha$, $\theta$). Finally, all studied Newton-SIP methods only evaluate the Jacobian matrix at the first iteration (in just one or various points); in this paper, we have considered alternative procedures in which the Jacobian matrices are updated each iteration (as in the standard NR). These alternative techniques have been called SIP1-J, SIP2-J, SIP3-J, and SIP4-J for the SIP1-J₀, SIP2-J₀, SIP3-J₀, and SIP4-J₀, respectively. With the aim to summarize,

Table 1. Main features of the studied PF solution methods.

Method	Jacobian Evaluations	Function Evaluations	S-Parameters
NR	$K$	$K$	--
SIP1-J0	1	$2\times K$	$\alpha$
SIP1-J	$K$	$2\times K$	$\alpha$
SIP2-J0	2	$2\times K$	$\alpha$
SIP2-J	$2\times K$	$2\times K$	$\alpha$
SIP3-J0	1	$3\times K$	$\alpha , \theta$
SIP3-J	$K$	$3\times K$	$\alpha , \theta$
SIP4-J0	3	$3\times K$	$\alpha , \theta$
SIP4-J	$3\times K$	$3\times K$	$\alpha , \theta$

$K\to$ Total number of iterations.

collects the main characteristics of the studied PF solution techniques.

It is also worth commenting that the s-parameters were only defined in the range [0,1] in [32,33]. However, we have not limited their analysis to this range. Therefore, we have avoided this definition in order to avoid misleading.

3. Convergence Analysis of Studied Newton-SIP Methods

In this section, the convergence rate of the studied Newton-SIP methods is derived. In this case, we consider that the Jacobian matrix is updated each iteration, since the convergence features for iterative procedures (4)–(7) can be derived from this analysis. For this study, the Taylor Expansion technique has been used (see [35] for details).

Theorem 1.

Let $g$ be sufficiently differentiable at each point of an open neighborhood $\mathrm{D}$ of $\mathit{r}\in {ℝ}^n$, this is a solution of the system $g\left(\mathit{x}\right)=\mathbf{0}$. Let us suppose that $g\left(\mathit{x}\right)$ is continuous and nonsingular in $\mathit{x}$. Then, the SIP1-J converges to $\mathit{r}$ with the following error function.

$${\mathit{e}}^{\left(k+1\right)}=\left(1-{\alpha }^2\right){\mathit{C}}_{\mathbf{2}}{\mathit{e}}^{{\left(k\right)}^2}+\left(\left({\alpha }^3-3{\alpha }^2+2\right){\mathit{C}}_{\mathbf{3}}+\left(4{\alpha }^2-2\right){\mathit{C}}_{\mathbf{2}}^2\right){\mathit{e}}^{{\left(k\right)}^3}+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^4}\right)$$

(8)

where ${\mathit{C}}_{\mathit{j}}=\left(1/j!\right){\left[g^{\prime }\left(\mathit{r}\right)\right]}^{-1}{g}^{\left(j\right)}\left(\mathit{r}\right)$, $j=2,3,\dots ,$ and ${\mathit{e}}^{\left(k\right)}={\mathit{x}}^{\left(k\right)}-\mathit{r}$.

Proof.

Taylor expansion of $g\left(\mathit{x}\right)$ and $\mathit{J}\left(\mathit{x}\right)$ about $\mathit{r}$ yields:

$$g\left({\mathit{x}}^{\left(k\right)}\right)=\mathit{J}\left(\mathit{r}\right)\left[{\mathit{e}}^{\left(k\right)}+{\mathit{C}}_{\mathbf{2}}{\mathit{e}}^{{\left(k\right)}^2}+{\mathit{C}}_{\mathbf{3}}{\mathit{e}}^{{\left(k\right)}^3}\right]+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^4}\right)$$

(9)

$$\mathit{J}\left({\mathit{x}}^{\left(k\right)}\right)=\mathit{J}\left(\mathit{r}\right)\left[\mathit{I}+2{\mathit{C}}_{\mathbf{2}}{\mathit{e}}^{\left(k\right)}+3{\mathit{C}}_{\mathbf{3}}{\mathit{e}}^{{\left(k\right)}^2}\right]+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^3}\right)$$

(10)

where $\mathit{I}\in {ℝ}^{n\times n}$ is the identity matrix. Now, let us assume that:

$${\left[\mathit{J}\left({\mathit{x}}^{\left(k\right)}\right)\right]}^{-1}=\left[c_1\mathit{I}+c_2{\mathit{e}}^{\left(k\right)}+c_3{\mathit{e}}^{{\left(k\right)}^2}\right]{\left[\mathit{J}\left(\mathit{r}\right)\right]}^{-1}+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^3}\right)$$

(11)

where $c^{\prime }$s$\in ℝ$. Considering the following inverse definition:

$${\left[\mathit{J}\left({\mathit{x}}^{\left(k\right)}\right)\right]}^{-1}{g}^{\prime }\left({\mathit{x}}^{\left(k\right)}\right)=\mathit{J}\left({\mathit{x}}^{\left(k\right)}\right){\left[g^{\prime }\left({\mathit{x}}^{\left(k\right)}\right)\right]}^{-1}=\mathit{I}.$$

(12)

By solving the resulting linear system, one can obtain:

$${\left[\mathit{J}\left({\mathit{x}}^{\left(k\right)}\right)\right]}^{-1}=\left[\mathit{I}-2{\mathit{C}}_{\mathbf{2}}{\mathit{e}}^{\left(k\right)}+\left(4{\mathit{C}}_{\mathbf{2}}^2-3{\mathit{C}}_{\mathbf{3}}\right){\mathit{e}}^{{\left(k\right)}^2}\right]{\left[\mathit{J}\left(\mathit{r}\right)\right]}^{-1}+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^4}\right).$$

(13)

Now, let us define ${\tilde{\mathit{e}}}^{\left(k\right)}=\left({\mathit{x}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(k\right)}\right)\right]}^{-1}g\left({\mathit{x}}^{\left(k\right)}\right)\right)-\mathit{r}$ and ${\mathit{e}}_{\mathit{y}}^{\left(k\right)}={\mathit{y}}^{\left(k\right)}-\mathit{r}$; thus, one can obtain:

$${\mathit{e}}_{\mathit{y}}^{\left(k\right)}=\left(1-\alpha \right){\mathit{e}}^{\left(k\right)}+\alpha {\tilde{\mathit{e}}}^{\left(k\right)}=\left(1-\alpha \right){\mathit{e}}^{\left(k\right)}+\alpha {\mathit{C}}_{\mathbf{2}}{\mathit{e}}^{{\left(k\right)}^2}+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^3}\right).$$

(14)

The Taylor expansion of $\mathbf{g}\left(\mathit{y}\right)$ about $\mathit{r}$ yields:

$$g\left({\mathit{y}}^{\left(k\right)}\right)=\mathit{J}\left(\mathit{r}\right)\left[{\mathit{e}}_{\mathit{y}}^{\left(k\right)}+{\mathit{C}}_{\mathbf{2}}{\mathit{e}}_{\mathit{y}}^{{\left(k\right)}^2}+{\mathit{C}}_{\mathbf{3}}{\mathit{e}}_{\mathit{y}}^{{\left(k\right)}^3}\right]+\mathit{O}\left({\mathit{e}}_{\mathit{y}}^{{\left(k\right)}^4}\right).$$

(15)

Now, we can calculate the error vector at $k+1$ as follows:

$${\mathit{e}}^{\left(k+1\right)}=\left({\mathit{y}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(k\right)}\right)\right]}^{-1}g\left({\mathit{y}}^{\left(k\right)}\right)\right)-\mathit{r}.$$

(16)

After some manipulations, one obtains:

$${\mathit{e}}^{\left(k+1\right)}=\left(1-{\alpha }^2\right){\mathit{C}}_{\mathbf{2}}{\mathit{e}}^{{\left(k\right)}^2}+\left(\left({\alpha }^3-3{\alpha }^2+2\right){\mathit{C}}_{\mathbf{3}}+\left(4{\alpha }^2-2\right){\mathit{C}}_{\mathbf{2}}^2\right){\mathit{e}}^{{\left(k\right)}^3}+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^4}\right).$$

(17)

The proof is complete. □

Theorem 2.

Let $g$ be sufficiently differentiable at each point of an open neighborhood $\mathrm{D}$ of $\mathit{r}\in {ℝ}^n$; this is a solution of the system $g\left(\mathit{x}\right)=\mathbf{0}$. Let us suppose that $g\left(\mathit{x}\right)$ is continuous and nonsingular in $\mathit{x}$. Then, the SIP2-J converges to $\mathit{r}$ with the following error function.

$$\begin{array}{cc}{\mathit{e}}^{\left(k+1\right)}=\hfill & \left({\alpha }^2-2\alpha +1\right){\mathit{C}}_{\mathbf{2}}{\mathit{e}}^{{\left(k\right)}^2}+\left(\left(6{\alpha }^2-2{\alpha }^3-6\alpha +2\right){\mathit{C}}_{\mathbf{3}}+\left(2{\alpha }^3-8{\alpha }^2+8\alpha -2\right){\mathit{C}}_{\mathbf{2}}^2\right){\mathit{e}}^{{\left(k\right)}^3}\hfill \\ & +\left(\left(34{\alpha }^3-7{\alpha }^4-54{\alpha }^2+34\alpha -7\right){\mathit{C}}_{\mathbf{2}}{\mathit{C}}_{\mathbf{3}}+\left(4{\alpha }^4-22{\alpha }^3+37{\alpha }^2-22\alpha +4\right){\mathit{C}}_{\mathbf{2}}^{\mathbf{3}}\right){\mathit{e}}^{{\left(k\right)}^4}\hfill \\ & +\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^5}\right)\hfill \end{array}$$

(18)

Proof.

Taking ${\mathit{e}}_{\mathit{y}}^{\left(k\right)}$ and the Taylor expansion of $g\left(\mathit{y}\right)$ about $\mathit{r}$ from (14) and (15), respectively, let us calculate the Taylor expansion of ${\left[\mathit{J}\left(\mathit{y}\right)\right]}^{-1}$ as (12). Thus, one can obtain:

$${\left[\mathit{J}\left({\mathit{y}}^{\left(k\right)}\right)\right]}^{-1}=\left[\mathit{I}-2{\mathit{C}}_{\mathbf{2}}{\mathit{e}}_{\mathit{y}}^{\left(k\right)}+\left(4{\mathit{C}}_{\mathbf{2}}^2-3{\mathit{C}}_{\mathbf{3}}\right){\mathit{e}}_{\mathit{y}}^{{\left(k\right)}^2}\right]{\left[\mathit{J}\left(\mathit{r}\right)\right]}^{-1}+\mathit{O}\left({\mathit{e}}_{\mathit{y}}^{{\left(k\right)}^3}\right).$$

(19)

Now, we can calculate the error vector at $k+1$ as follows:

$${\mathit{e}}^{\left(k+1\right)}=\left({\mathit{y}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{y}}^{\left(k\right)}\right)\right]}^{-1}g\left({\mathit{y}}^{\left(k\right)}\right)\right)-\mathit{r}.$$

(20)

After some manipulations, one obtains:

$$\begin{gathered} {\mathit{e}}^{\left(k+1\right)}=\left({\alpha }^2-2\alpha +1\right){\mathit{C}}_{\mathbf{2}}{\mathit{e}}^{{\left(k\right)}^2}+\left(\left(6{\alpha }^2-2{\alpha }^3-6\alpha +2\right){\mathit{C}}_{\mathbf{3}}+\left(2{\alpha }^3-8{\alpha }^2+8\alpha -2\right){\mathit{C}}_{\mathbf{2}}^2\right){\mathit{e}}^{{\left(k\right)}^3}+ \\ \left(\left(34{\alpha }^3-7{\alpha }^4-54{\alpha }^2+34\alpha -7\right){\mathit{C}}_{\mathbf{2}}{\mathit{C}}_{\mathbf{3}}+\left(4{\alpha }^4-22{\alpha }^3+37{\alpha }^2-22\alpha +4\right){\mathit{C}}_{\mathbf{2}}^3\right){\mathit{e}}^{{\left(k\right)}^4}+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^5}\right). \end{gathered}$$

(21)

The proof is complete. □

Theorem 3.

Let $g$ be sufficiently differentiable at each point of an open neighborhood $\mathrm{D}$ of $\mathit{r}\in {ℝ}^n$; this is a solution of the system $g\left(\mathit{x}\right)=\mathbf{0}$. Let us suppose that $g\left(\mathit{x}\right)$ is continuous and nonsingular in $\mathit{x}$. Then, the SIP3-J converges to $\mathit{r}$ with the following error function.

$${\mathit{e}}^{\left(k+1\right)}=\left(2-2\alpha {\theta }^2\right){\mathit{C}}_{\mathbf{2}}^2{\mathit{e}}^{{\left(k\right)}^3}+\left(\left(3+2\alpha {\theta }^3-9\alpha {\theta }^2+4\alpha \right){\mathit{C}}_{\mathbf{2}}{\mathit{C}}_{\mathbf{3}}+\left(-{\alpha }^2{\theta }^4+14\alpha {\theta }^2-4\alpha -5\right){\mathit{C}}_{\mathbf{2}}^3\right){\mathit{e}}^{{\left(k\right)}^4}+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^5}\right)$$

(22)

Proof.

Let us define ${\tilde{\mathit{e}}}^{\left(k\right)}=\left({\mathit{x}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(k\right)}\right)\right]}^{-1}g\left({\mathit{x}}^{\left(k\right)}\right)\right)-\mathit{r}$ and ${\mathit{e}}_{\mathit{z}}^{\left(k\right)}={\mathit{z}}^{\left(k\right)}-\mathit{r}$; then, one can obtain:

$${\mathit{e}}_{\mathit{z}}^{\left(k\right)}=\left(1-\theta \right){\mathit{e}}^{\left(k\right)}+\theta {\tilde{\mathit{e}}}^{\left(k\right)}=\left(1-\theta \right){\mathit{e}}^{\left(k\right)}+\theta {\mathit{C}}_{\mathbf{2}}{\mathit{e}}^{{\left(k\right)}^2}+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^3}\right).$$

(23)

The Taylor expansion of $g\left(\mathit{z}\right)$ about $\mathit{r}$ yields:

$$g\left({\mathit{z}}^{\left(k\right)}\right)=\mathit{J}\left(\mathit{r}\right)\left[{\mathit{e}}_{\mathit{z}}^{\left(k\right)}+{\mathit{C}}_{\mathbf{2}}{\mathit{e}}_{\mathit{z}}^{{\left(k\right)}^2}+{\mathit{C}}_{\mathbf{3}}{\mathit{e}}_{\mathit{z}}^{{\left(k\right)}^3}\right]+\mathit{O}\left({\mathit{e}}_{\mathit{z}}^{{\left(k\right)}^4}\right).$$

(24)

Now, let us define ${\widehat{\mathit{e}}}^{\left(k\right)}=\left({\mathit{z}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(k\right)}\right)\right]}^{-1}g\left({\mathit{z}}^{\left(k\right)}\right)\right)-\mathit{r}$ and ${\mathit{e}}_{\mathit{y}}^{\left(k\right)}={\mathit{y}}^{\left(k\right)}-\mathit{r}$; then, we can calculate:

$$\begin{gathered} {\mathit{e}}_{\mathit{y}}^{\left(k\right)}=\left(1-\alpha \right){\tilde{\mathit{e}}}^{\left(k\right)}+\alpha {\widehat{\mathit{e}}}^{\left(k\right)}=\left(1-\alpha {\theta }^2\right){\mathit{C}}_{\mathbf{2}}{\mathit{e}}^{{\left(k\right)}^2}+\left(\left(4\alpha {\theta }^2-2\alpha \right){\mathit{C}}_{\mathbf{2}}^2+\left(\alpha {\theta }^3-3\alpha {\theta }^2+2\alpha \right){\mathit{C}}_{\mathbf{3}}\right){\mathit{e}}^{{\left(k\right)}^3}+ \\ \left(\left(4\alpha -9\alpha {\theta }^2\right){\mathit{C}}_{\mathbf{2}}^3+\left(15\alpha {\theta }^2-5\alpha {\theta }^3-7\alpha \right){\mathit{C}}_{\mathbf{2}}{\mathit{C}}_{\mathbf{3}}\right){\mathit{e}}^{{\left(k\right)}^4}+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^5}\right). \end{gathered}$$

(25)

The Taylor expansion of $g\left(\mathit{y}\right)$ about $\mathit{r}$ yields:

$$g\left({\mathit{y}}^{\left(k\right)}\right)=\mathit{J}\left(\mathit{r}\right)\left[{\mathit{e}}_{\mathit{y}}^{\left(k\right)}+{\mathit{C}}_{\mathbf{2}}{\mathit{e}}_{\mathit{y}}^{{\left(k\right)}^2}+{\mathit{C}}_{\mathbf{3}}{\mathit{e}}_{\mathit{y}}^{{\left(k\right)}^3}\right]+\mathit{O}\left({\mathit{e}}_{\mathit{y}}^{{\left(k\right)}^4}\right).$$

(26)

Now, we can calculate the error vector at $k+1$ as follows:

$${\mathit{e}}^{\left(k+1\right)}=\left({\mathit{y}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(k\right)}\right)\right]}^{-1}g\left({\mathit{y}}^{\left(k\right)}\right)\right)-\mathit{r}.$$

(27)

After some manipulations, one can obtain:

$${\mathit{e}}^{\left(k+1\right)}=\left(2-2\alpha {\theta }^2\right){\mathit{C}}_{\mathbf{2}}^2{\mathit{e}}^{{\left(k\right)}^3}+\left(\left(3+2\alpha {\theta }^3-9\alpha {\theta }^2+4\alpha \right){\mathit{C}}_{\mathbf{2}}{\mathit{C}}_{\mathbf{3}}+\left(-{\alpha }^2{\theta }^4+14\alpha {\theta }^2-4\alpha -5\right){\mathit{C}}_{\mathbf{2}}^3\right){\mathit{e}}^{{\left(k\right)}^4}+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^5}\right).$$

(28)

The proof is complete. □

Theorem 4.

Let $g$ be sufficiently differentiable at each point of an open neighborhood $\mathrm{D}$ of $\mathit{r}\in {ℝ}^n$; this is a solution of the system $g\left(\mathit{x}\right)=0$. Let us suppose that $g\left(\mathit{x}\right)$ is continuous and nonsingular in $\mathit{x}$. Then, the SIP4-J converges to $\mathit{r}$ with the following error function.

$${\mathit{e}}^{\left(k+1\right)}={\mathit{X}}_{\mathbf{4}}{\mathit{e}}^{{\left(k\right)}^4}+{\mathit{X}}_{\mathbf{5}}{\mathit{e}}^{{\left(k\right)}^5}+{\mathit{X}}_{\mathbf{6}}{\mathit{e}}^{{\left(k\right)}^6}+{\mathit{X}}_{\mathbf{7}}{\mathit{e}}^{{\left(k\right)}^7}+{\mathit{X}}_{\mathbf{8}}{\mathit{e}}^{{\left(k\right)}^8}+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^9}\right)$$

(29)

where:

$${\mathit{X}}_{\mathbf{4}}=\left({\alpha }^2{\theta }^4-4{\alpha }^2{\theta }^3+4{\alpha }^2{\theta }^2+2\alpha {\theta }^2-4\alpha \theta \right){\mathit{C}}_2^3$$

(30)

$$\begin{array}{cc}{\mathit{X}}_{\mathbf{5}}=(20{\alpha }^2{\theta }^4\hfill & -4{\alpha }^2{\theta }^5-36{\alpha }^2{\theta }^3+28{\alpha }^2{\theta }^2-4\alpha {\theta }^3-8{\alpha }^2\theta +12\alpha {\theta }^2-12\alpha \theta +4\alpha ){\mathit{C}}_{\mathbf{2}}^2{\mathit{C}}_{\mathbf{3}}\hfill \\ & +\left(4{\alpha }^2{\theta }^5-24{\alpha }^2{\theta }^4+48{\alpha }^2{\theta }^3-36{\alpha }^2{\theta }^2+4\alpha {\theta }^3+8{\alpha }^2\theta -16\alpha {\theta }^2+16\alpha \theta -4\alpha \right){\mathit{C}}_{\mathbf{2}}^4\hfill \end{array}$$

(31)

$$\begin{array}{cc}{\mathit{X}}_{\mathbf{6}}=(4{\alpha }^2{\theta }^6\hfill & -24{\alpha }^2{\theta }^5+60{\alpha }^2{\theta }^4-80{\alpha }^2{\theta }^3+60{\alpha }^2{\theta }^2-24{\alpha }^2\theta +4{\alpha }^2){\mathit{C}}_{\mathbf{2}}{\mathit{C}}_{\mathbf{3}}^2\hfill \\ & +(+2{\alpha }^3{\theta }^6-12{\alpha }^3{\theta }^5-8{\alpha }^2{\theta }^6+24{\alpha }^3{\theta }^4+56{\alpha }^2{\theta }^5-16{\alpha }^3{\theta }^3-146{\alpha }^2{\theta }^4+184{\alpha }^2{\theta }^3\hfill \\ & -128{\alpha }^2{\theta }^2+56{\alpha }^2\theta +6\alpha {\theta }^2-8{\alpha }^2-12\alpha \theta +2){\mathit{C}}_{\mathbf{2}}^3{\mathit{C}}_{\mathbf{3}}\hfill \\ & +(12{\alpha }^3{\theta }^5-2{\alpha }^3{\theta }^6+4{\alpha }^2{\theta }^6-24{\alpha }^3{\theta }^4-32{\alpha }^2{\theta }^5+16{\alpha }^3{\theta }^3+90{\alpha }^2{\theta }^4-112{\alpha }^2{\theta }^3\hfill \\ & +72{\alpha }^2{\theta }^2-32{\alpha }^2\theta -6\alpha {\theta }^2+4{\alpha }^2+12\alpha \theta -2){\mathit{C}}_{\mathbf{2}}^5\hfill \end{array}$$

(32)

$$\begin{array}{cc}{\mathit{X}}_{\mathbf{7}}=(96{\alpha }^3{\theta }^6\hfill & -12{\alpha }^3{\theta }^7-288{\alpha }^3{\theta }^5+396{\alpha }^3{\theta }^4-24{\alpha }^2{\theta }^5-240{\alpha }^3{\theta }^3+144{\alpha }^2{\theta }^4+48{\alpha }^3{\theta }^2-288{\alpha }^2{\theta }^3\hfill \\ & +216{\alpha }^2{\theta }^2-12\alpha {\theta }^3-48{\alpha }^2\theta +48\alpha {\theta }^2-48\alpha \theta +12\alpha ){\mathit{C}}_{\mathbf{2}}^6\hfill \\ & +(24{\alpha }^3{\theta }^7-180{\alpha }^3{\theta }^6+516{\alpha }^3{\theta }^5-696{\alpha }^3{\theta }^4+48{\alpha }^2{\theta }^5+432{\alpha }^3{\theta }^3-264{\alpha }^2{\theta }^4-96{\alpha }^3{\theta }^2\hfill \\ & +504{\alpha }^2{\theta }^3-384{\alpha }^2{\theta }^2+24\alpha {\theta }^3+96{\alpha }^2\theta -84\alpha {\theta }^2+84\alpha \theta -24\alpha ){\mathit{C}}_{\mathbf{2}}^4{\mathit{C}}_{\mathbf{3}}\hfill \\ & +(-12{\alpha }^3{\theta }^7+84{\alpha }^3{\theta }^6-228{\alpha }^3{\theta }^5+300{\alpha }^3{\theta }^4-24{\alpha }^2{\theta }^5-192{\alpha }^3{\theta }^3+120{\alpha }^2{\theta }^4+48{\alpha }^3{\theta }^2\hfill \\ & -216{\alpha }^2{\theta }^3+168{\alpha }^2{\theta }^2-12\alpha {\theta }^3-48{\alpha }^2\theta +36\alpha {\theta }^2-36\alpha \theta +12\alpha ){\mathit{C}}_{\mathbf{2}}^2{\mathit{C}}_{\mathbf{3}}^2\hfill \end{array}$$

(33)

$$\begin{array}{c}{\mathit{X}}_{\mathbf{8}}=(4{\alpha }^4{\theta }^8-32{\alpha }^4{\theta }^7-24{\alpha }^3{\theta }^8+96{\alpha }^4{\theta }^6+240{\alpha }^3{\theta }^7-16{\alpha }^2{\theta }^8-128{\alpha }^4{\theta }^5-944{\alpha }^3{\theta }^6+176{\alpha }^2{\theta }^7+\\ 64{\alpha }^4{\theta }^4+1872{\alpha }^3{\theta }^5-804{\alpha }^2{\theta }^6-2016{\alpha }^3{\theta }^4+1996{\alpha }^2{\theta }^5+1216{\alpha }^3{\theta }^3-2921{\alpha }^2{\theta }^4-408{\alpha }^3{\theta }^2+\\ 2524{\alpha }^2{\theta }^3+48{\alpha }^3\theta -1260{\alpha }^2{\theta }^2+368{\alpha }^2\theta +16\alpha {\theta }^2-40{\alpha }^2-32\theta \alpha +4){\mathit{C}}_{\mathbf{2}}^7+(-7{\alpha }^4{\theta }^8+56{\alpha }^4{\theta }^6+\\ 72{\alpha }^3{\theta }^8-168{\alpha }^4{\theta }^6-672{\alpha }^3{\theta }^7+56{\alpha }^2{\theta }^8+224{\alpha }^4{\theta }^5+2516{\alpha }^3{\theta }^6-580{\alpha }^2{\theta }^7-112{\alpha }^4{\theta }^4-4872{\alpha }^3{\theta }^5+\\ 2518{\alpha }^2{\theta }^6+5280{\alpha }^3{\theta }^4-6000{\alpha }^2{\theta }^5-3280{\alpha }^3{\theta }^3+8546{\alpha }^2{\theta }^4+1128{\alpha }^3{\theta }^2-7368{\alpha }^2{\theta }^3-144{\alpha }^3\theta +\\ 3766{\alpha }^2{\theta }^2-1108{\alpha }^2\theta -28\alpha {\theta }^2+128{\alpha }^2+56\alpha \theta -7){\mathit{C}}_{\mathbf{2}}^5{\mathit{C}}_{\mathbf{3}}+(624{\alpha }^3{\theta }^7-49{\alpha }^2{\theta }^8-2232{\alpha }^3{\theta }^6+476{\alpha }^2{\theta }^7+\\ 4272{\alpha }^3{\theta }^5-1984{\alpha }^2{\theta }^6-4728{\alpha }^3{\theta }^4+4628{\alpha }^2{\theta }^5-72{\alpha }^3{\theta }^8+3024{\alpha }^3{\theta }^3-6598{\alpha }^2{\theta }^4-1032{\alpha }^3{\theta }^2+\\ 5876{\alpha }^2{\theta }^3+144{\alpha }^3\theta -3184{\alpha }^2{\theta }^2+956{\alpha }^2\theta -121{\alpha }^2){\mathit{C}}_{\mathbf{2}}^3{\mathit{C}}_{\mathbf{3}}^2+(24{\alpha }^3{\theta }^8-192{\alpha }^3{\theta }^7+648{\alpha }^3{\theta }^6-\\ 1200{\alpha }^3{\theta }^5+24{\alpha }^2{\theta }^6+1320{\alpha }^3{\theta }^4-144{\alpha }^2{\theta }^5-864{\alpha }^3{\theta }^3+360{\alpha }^2{\theta }^4+312{\alpha }^3\theta -480{\alpha }^2{\theta }^3-48{\alpha }^3\theta +\\ 360{\alpha }^2{\theta }^2-144{\alpha }^2\theta +24{\alpha }^2){\mathit{C}}_{\mathbf{2}}{\mathit{C}}_{\mathbf{3}}^3\end{array}$$

(34)

Proof.

In this case, one can calculate the Taylor expansion of ${\left[\mathit{J}\left(\mathit{y}\right)\right]}^{-1}$ about $\mathit{r}$ as (12). Thus, one can obtain:

$${\left[\mathit{J}\left({\mathit{z}}^{\left(k\right)}\right)\right]}^{-1}=\left[I-2{\mathit{C}}_{\mathbf{2}}{\mathit{e}}_{\mathit{z}}^{\left(k\right)}+\left(4{\mathit{C}}_{\mathbf{2}}^2-3{\mathit{C}}_{\mathbf{3}}\right){\mathit{e}}_{\mathit{z}}^{{\left(k\right)}^2}\right]{\left[\mathit{J}\left(\mathit{r}\right)\right]}^{-1}+\mathit{O}\left({\mathit{e}}_{\mathit{z}}^{{\left(k\right)}^3}\right)$$

(35)

where ${\mathit{e}}_{\mathit{z}}^{\left(k\right)}$ is already calculated in (23). Now, taking the Taylor expansion of $g\left(\mathit{z}\right)$ about $\mathit{r}$ from (24), let us define ${\widehat{\mathit{e}}}^{\left(k\right)}=\left({\mathit{z}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{z}}^{\left(k\right)}\right)\right]}^{-1}g\left({\mathit{z}}^{\left(k\right)}\right)\right)-\mathit{r}$ and ${\mathit{e}}_{\mathit{y}}^{\left(k\right)}={\mathit{y}}^{\left(k\right)}-\mathit{r}$; then, we can calculate:

$${\mathit{e}}_{\mathit{y}}^{\left(k\right)}=\left(1-\alpha \right){\tilde{\mathit{e}}}^{\left(k\right)}+\alpha {\widehat{\mathit{e}}}^{\left(k\right)}$$

(36)

where ${\tilde{\mathit{e}}}^{\left(k\right)}=\left({\mathit{x}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(k\right)}\right)\right]}^{-1}g\left({\mathit{x}}^{\left(k\right)}\right)\right)-\mathit{r}$. Now, manipulating (31), one obtains:

$${\mathit{e}}_{\mathit{y}}^{\left(k\right)}=\left(\alpha {\theta }^2-2\alpha \theta +1\right){\mathit{C}}_{\mathbf{2}}{\mathit{e}}^{{\left(k\right)}^2}+\left(\left(2\alpha {\theta }^3-8\alpha {\theta }^2+8\alpha \theta -2\alpha \right){\mathit{C}}_{\mathbf{2}}^2+\left(6\alpha {\theta }^2-2\alpha {\theta }^3-6\alpha \theta +2\alpha \right){\mathit{C}}_{\mathbf{3}}\right){\mathit{e}}^{{\left(k\right)}^3}+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^4}\right).$$

(37)

The Taylor expansion of $g\left(\mathit{y}\right)$ and of ${\left[\mathit{J}\left(\mathit{y}\right)\right]}^{-1}$ about $\mathit{r}$ yields:

$$g\left({\mathit{y}}^{\left(k\right)}\right)=\mathit{J}\left(\mathit{r}\right)\left[{\mathit{e}}_{\mathit{y}}^{\left(k\right)}+{\mathit{C}}_{\mathbf{2}}{\mathit{e}}_{\mathit{y}}^{{\left(k\right)}^2}+{\mathit{C}}_{\mathbf{3}}{\mathit{e}}_{\mathit{y}}^{{\left(k\right)}^3}\right]+\mathit{O}\left({\mathit{e}}_{\mathit{y}}^{{\left(k\right)}^4}\right)$$

(38)

$${\left[\mathit{J}\left({\mathit{y}}^{\left(k\right)}\right)\right]}^{-1}=\left[I-2{\mathit{C}}_{\mathbf{2}}{\mathit{e}}_{\mathit{y}}^{\left(k\right)}+\left(4{\mathit{C}}_{\mathbf{2}}^2-3{\mathit{C}}_{\mathbf{3}}\right){\mathit{e}}_{\mathit{y}}^{{\left(k\right)}^2}\right]{\left[\mathit{J}\left(\mathit{r}\right)\right]}^{-1}+\mathit{O}\left({\mathit{e}}_{\mathit{y}}^{{\left(k\right)}^3}\right).$$

(39)

At this point, we can calculate the error vector at $k+1$ as follows:

$${\mathit{e}}^{\left(k+1\right)}=\left({\mathit{y}}^{\left(k\right)}-{\left[\mathit{J}\left({\mathit{x}}^{\left(k\right)}\right)\right]}^{-1}g\left({\mathit{y}}^{\left(k\right)}\right)\right)-\mathit{r}.$$

(40)

After some manipulations, one can obtain:

$${\mathit{e}}^{\left(k+1\right)}={\mathit{X}}_{\mathbf{4}}{\mathit{e}}^{{\left(k\right)}^4}+{\mathit{X}}_{\mathbf{5}}{\mathit{e}}^{{\left(k\right)}^5}+{\mathit{X}}_{\mathbf{6}}{\mathit{e}}^{{\left(k\right)}^6}+{\mathit{X}}_{\mathbf{7}}{\mathit{e}}^{{\left(k\right)}^7}+{\mathit{X}}_{\mathbf{8}}{\mathit{e}}^{{\left(k\right)}^8}+\mathit{O}\left({\mathit{e}}^{{\left(k\right)}^9}\right)$$

(41)

where the $\mathit{X}$s are defined in (30)–(34); hence, the proof is complete. □

At this point, one can easily check that the studied techniques achieve their highest convergence rates when the s-parameters are equal to 1. Thus, SIP1-J, SIP2-J, SIP3-J, and SIP4-J can show third, fourth, fourth, and eighth convergence rates, respectively. In this regard, it is important to note that the mentioned techniques present a higher convergence rate compared with NR, which presents quadratic convergence. On the other hand, it is worth mentioning that the studied Newton-SIP methods have the characteristic lowest convergence rate even when $\alpha , \theta \ne 1$. By observing the error functions of these techniques, one can deduce that the order of convergence of SIP1-J and SIP2-J is at least two, while it is three in the case of SIP3-J and four for SIP4-J.

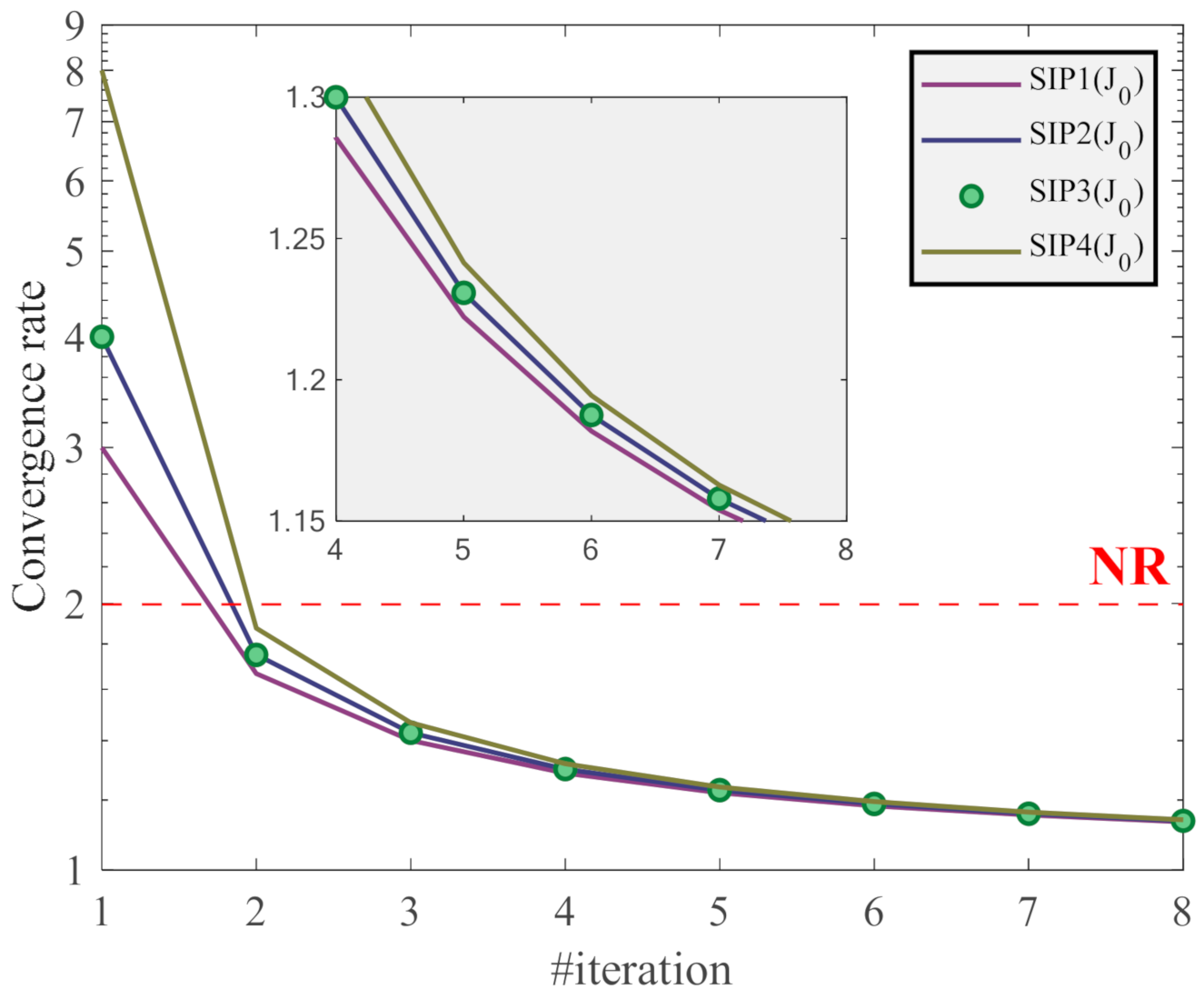
In the case of the standard forms of studied Newton-SIP methods (Equations (4)–(7)), since their convergence rates do not remain constant during the iterative procedure, it is more suitable to study them by successive substitution and Taylor expansion in their respective algorithms (details of this technique can be found in [36]). Figure 1 shows the convergence rates of the algorithms SIP1-J₀, SIP2-J₀, SIP3-J₀, and SIP4-J₀ as a function of the iteration number. In this figure, the convergence rate of the conventional NR has been also included for comparison. From this figure, it can be deduced that SIP4-J₀ and SIP1-J₀ show the highest and the lowest convergence rate, respectively, while both SIP2-J₀ and SIP3-J₀ have the same convergence order. Anyway, for these techniques, the convergence rate is linear after the first iteration. Therefore, their convergence orders are always less than two, being so overcome by NR.

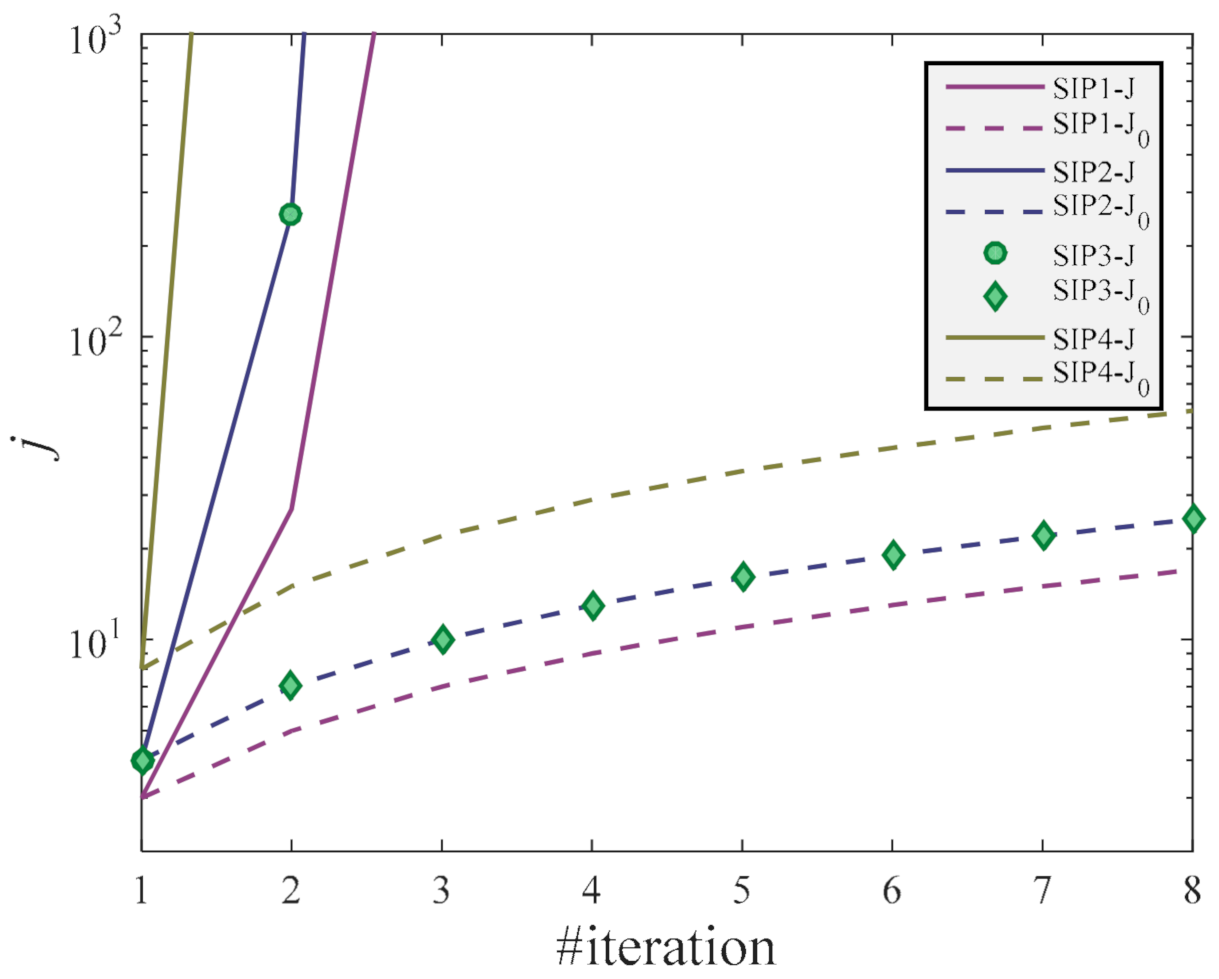
To compare the algorithms (4)–(7) and their respective counterparts (in which the Jacobian is updated each iteration), let us refer to the convergence rate of the initial error vector. It means, let us suppose that the error vector evolves as ${\mathit{e}}^{{\left(0\right)}^{\mathit{J}}}$. Thus, as $j$ grows, the solution is assumed to be more closely approached. Therefore, it is assumed that an algorithm will converge faster as $j$ grows rapidly. Figure 2 plots the value of $j$ of the studied Newton-SIP methods at different iterations. From this figure, it can be seen that $j$ exponentially grows in the case of SIP1-J, SIP2-J, SIP3-J, and SIP4-J, while it grows linearly with SIP1-J₀ SIP2-J₀, SIP3-J₀, and SIP4-J₀. To complete the section,

Table 2. Comparison of the convergence rates of studied PF solution techniques.

Method	Convergence Rate
	Minimum	Maximum
NR	2	2
SIP1-J0	Linear	Linear
SIP1-J	2	3
SIP2-J0	Linear	Linear
SIP2-J	3	4
SIP3-J0	Linear	Linear
SIP3-J	3	4
SIP4-J0	Linear	Linear
SIP4-J	4	8

summarizes the convergence analysis of the considered techniques and the NR. As commented, the studied techniques achieve their maximum convergence rate when the s-parameters are equal to 1.

4. Comparison of the Efficiency of Different Iterative Algorithms

In this section, we compare the efficiency of the studied PF solution methods. To do that, let us consider the following efficiency index [37].

$$FEI=p^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$CO$}\right.}$$

(42)

where $p\in {ℝ}^{+}$ is the order of convergence, and $CO$ stands for the total computational cost of an iteration. In this sense, the following theorem is generally used to estimate the cost of a LU decomposition [35].

Theorem 5.

The number of products and quotients required for solving $q$ linear systems of equations with the same matrix of coefficients, using LU factorization, is:

$$o\left(n,q\right)=\frac{1}{3}{n}^3+q{n}^2-\frac{1}{3}n.$$

(43)

It is also suitable to consider the computational cost of each function evaluation $o\left(g\right)$ and Jacobian evaluation $o\left(g^{\prime }\right)$; hence, the total computational cost of an iteration can be estimated as follows:

$$CO=o\left(g\right)+o\left(g^{\prime }\right)+o\left(n,q\right).$$

(44)

The value of the index (42) for studied Newton-SIP methods and NR is depicted in Figure 3 for different sizes of the PF state vector ($n$). From this figure, it can be appreciated that Newton-SIP techniques are more efficient than NR. In addition, the following relations hold:

$$FE{I}_{\mathrm{NR}}<FE{I}_{\mathrm{SIP}2-\mathrm{J}}=FE{I}_{\mathrm{SIP}4-\mathrm{J}}<FE{I}_{\mathrm{SIP}1-\mathrm{J}}<FE{I}_{\mathrm{SIP}3-\mathrm{J}}.$$

(45)

5. Numerical Experiments

In this section, several numerical experiments are carried out, and their results are analyzed. The studied Newton-SIP PF techniques are compared with NR in several test systems. All simulations have been done using Matpower v7.0 [38]. The studied systems have been taken from MATPOWER’s database [39,40,41].

In all simulations, $g{\left(\mathit{x}\right)}_{\infty }\le {10}^{-6}$ has been taken as a convergence criterion, and a flat start has been considered for initializing the PF analysis. The reported execution times have been obtained under Windows 10 on a 3.4 GHz Intel Core i7-8750H CPU 2.2 GHz personal laptop (16.00 GB RAM) and calculated as the average value of 1000 simulations.

5.1. Well-Conditioned Cases

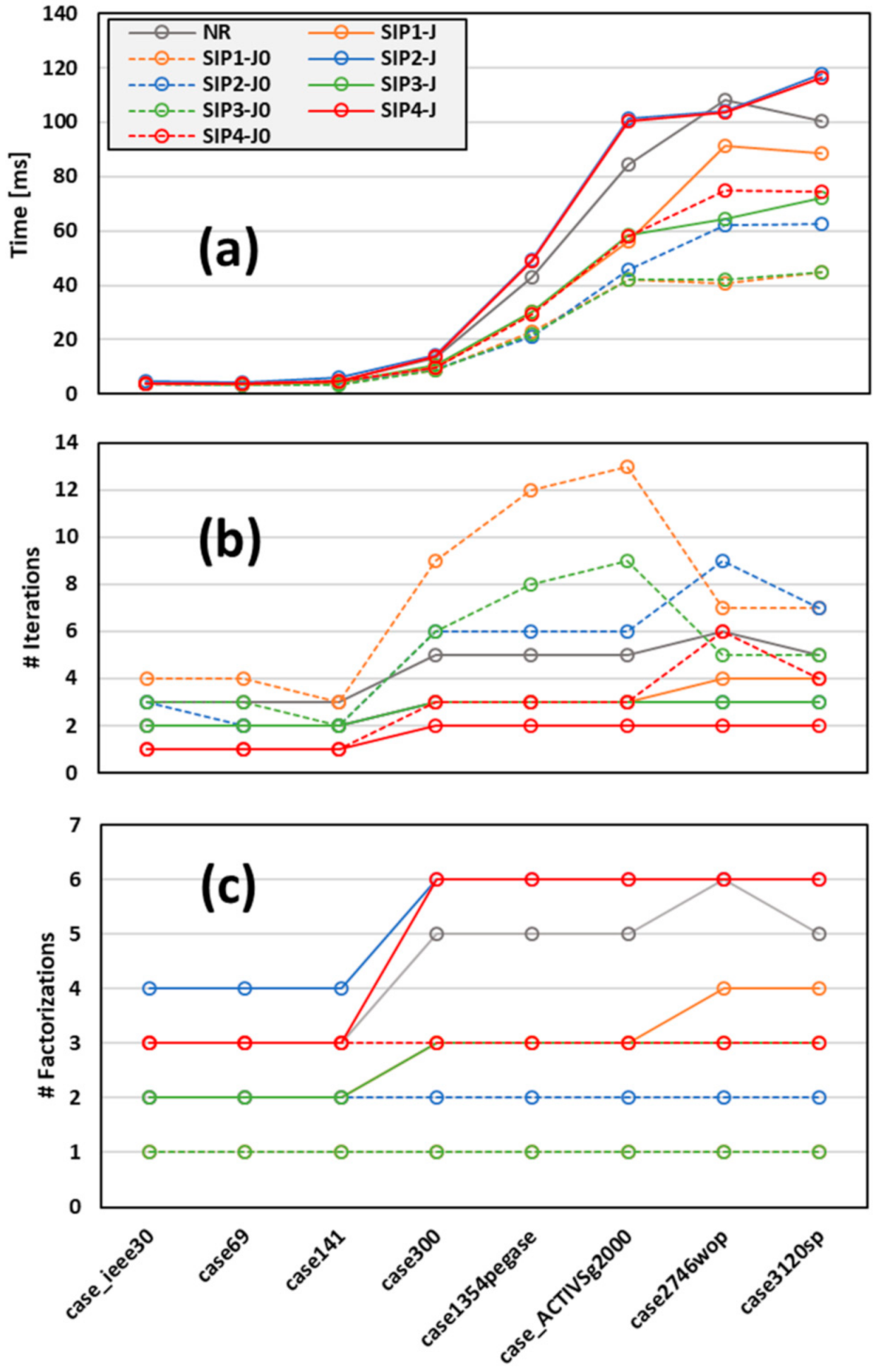
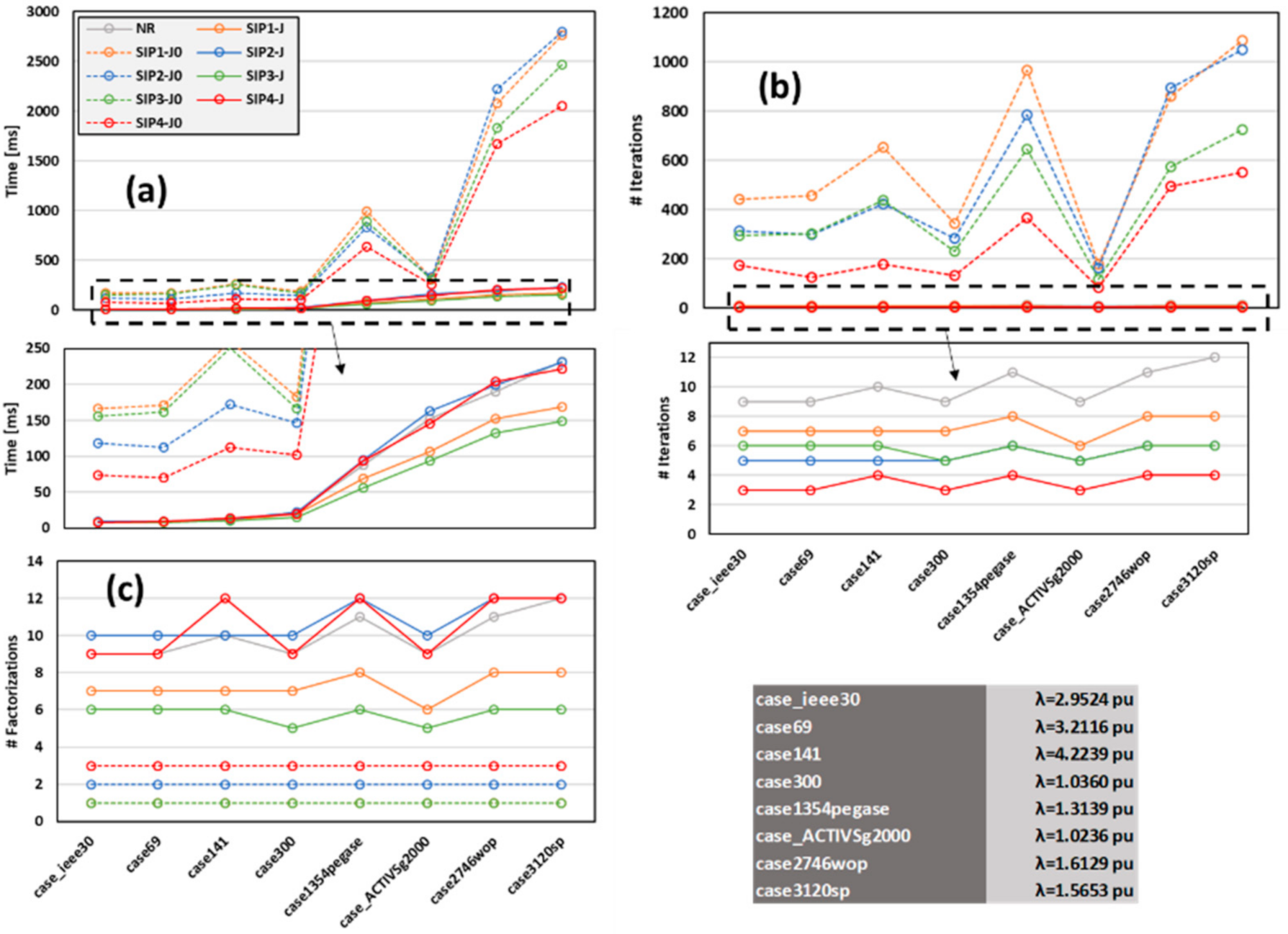
Firstly, we have analyzed the performance of studied PF techniques in several well-conditioned systems, which range from 30 to 3120 buses. Figure 4 shows the obtained results of these systems. These results have been obtained for the maximum convergence rate of the studied Newton-SIP PF techniques, i.e., when the s-parameters are 1.

As expected, SIP1-J₀ and SIP3-J₀ are the fastest methods, which is strongly linked with the number of factorizations required (one should note that the LU decomposition is the heaviest part of any PF calculation [13]). Among all the studied Newton-SIP techniques, only SIP2-J and SIP4-J are occasionally slower than NR. These results may look not coherent with the analysis performed in Section 4; however, Figure 4c provides a clear explanation about this issue. In this figure, it can be appreciated that these two techniques frequently required more factorizations than NR, which is reflected in a higher computational burden and therefore less competitive execution times. Regarding the total iterations required to attain the solution, the results are expected since the highest convergence rate has the lowest number of total iterations required for achieving the solution. Regarding those algorithms with linear convergence (Equations (4)–(7)), the following relations normally hold:

$$i{t}_{\mathrm{SIP}4-{\mathrm{J}}_0}<i{t}_{\mathrm{SIP}2-{\mathrm{J}}_0}<i{t}_{\mathrm{SIP}3-{\mathrm{J}}_0}<i{t}_{\mathrm{SIP}1-{\mathrm{J}}_0}$$

(46)

where $i{t}_{\mathrm{a}}$ indicates the total number of iterations of the method “a”. One should note that relations (46) are coherent with the theoretical analysis performed in Section 3 (see Figure 2); nevertheless, there are exceptions such as case2746wop.

Now, let us consider the influence of the loading level. To do that, the active and reactive powers injected at PQ buses along the active powers injected at PV buses have been progressively increased in steps of $\lambda =0.0001 \mathrm{pu}$ until all studied techniques have diverged. Figure 5 is analogous to Figure 4 for limit-loading cases. In this case, all techniques diverged for the same loading level; hence, all of them have been tested for the same conditions.

While similar conclusions can be extracted for SIP1-J, SIP2-J, SIP3-J, and SIP4-J, linear algorithms are not competitive in this scenario due to the huge amount of iterations required to reach the solution. Hence, although they frequently employed very few factorizations, their execution times are not competitive at all. In addition, relations (46) are not held in this situation for SIP2-J₀ and SIP3-J₀, since it can be observed in Figure 5 that clearly $i{t}_{\mathrm{SIP}3-{\mathrm{J}}_0}<i{t}_{\mathrm{SIP}2-{\mathrm{J}}_0}$.

In order to overcome the important drawbacks shown by linear techniques when the loading level is high, s-parameters can be occasionally set greater than one. In this case, these parameters have an accelerating effect on the convergence performance of the studied Newton-SIP techniques. Figure 6 shows the total number of iterations of different linear Newton-SIP techniques when their s-parameters are fixed greater than one and therefore achieve the fastest convergence. Under these settings, the results are compared with those results depicted in Figure 5. In this case, s-parameters have been obtained empirically. As can be seen, the total number of iterations can be drastically reduced; however, the criteria for determining the best values of s-parameters do not follow any specific pattern, as shown in Figure 6b. In light of the results obtained, this topic looks strongly case-dependent.

5.2. Ill-Conditioned Cases

Now, we have considered case3012wp, case3375wp, and case13659pegase, which are available in MATPOWER’s database. These cases correspond with snapshots of real cases, which demonstrates that ill-conditioned solvers may appear in real applications and they are even more frequent nowadays [42]. NR fails to solve these systems when a flat start is used, so that they can be categorized as ill-conditioned [13]. In previous simulations, we have taken the s-parameters to be equal to one, since the studied methods achieve their maximum convergence rate for these values. However, in ill-conditioned systems, this strategy may lead to divergence. Therefore, it is more suitable to study which values of the s-parameters in the considered Newton-SIP methods are reliable. 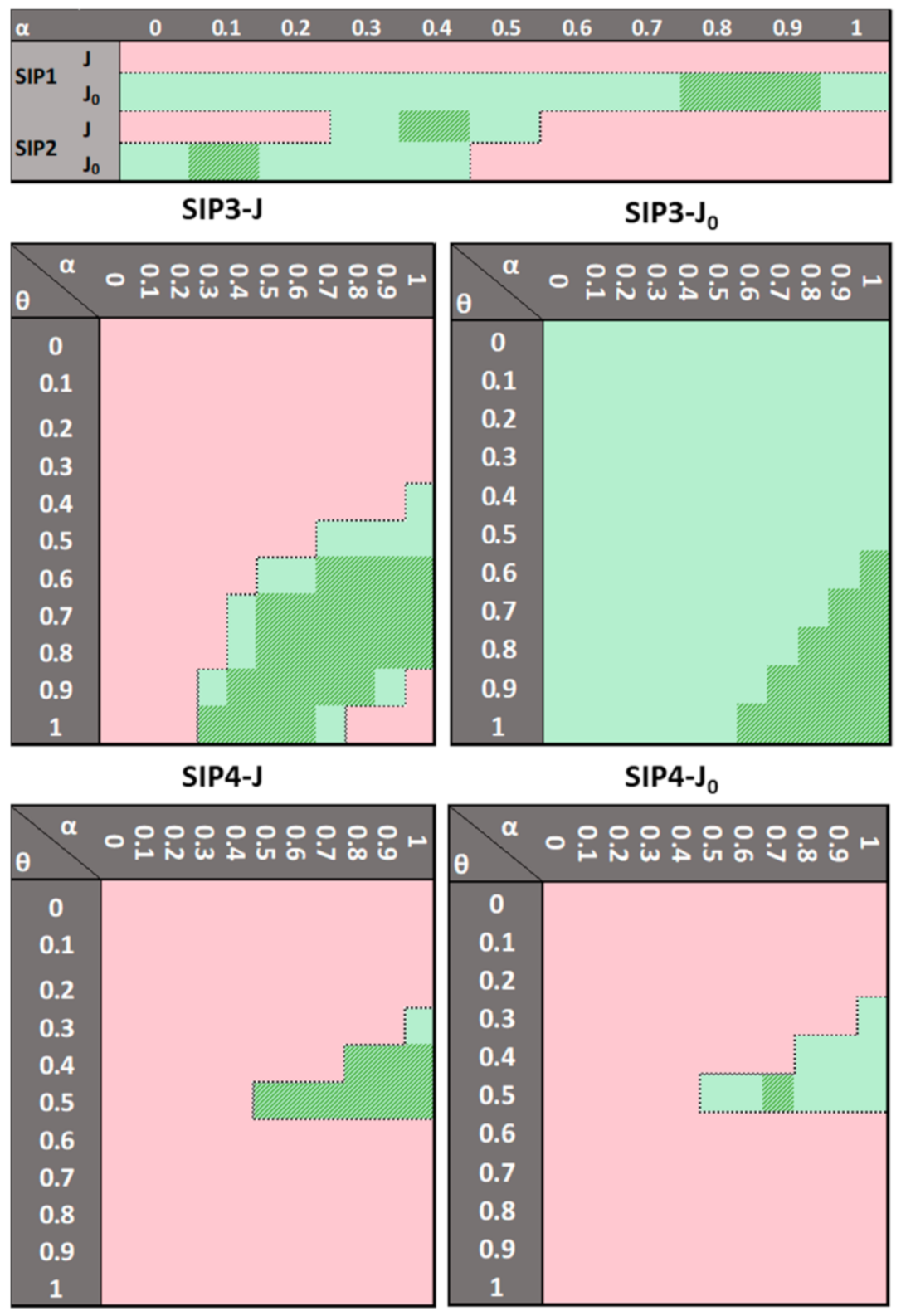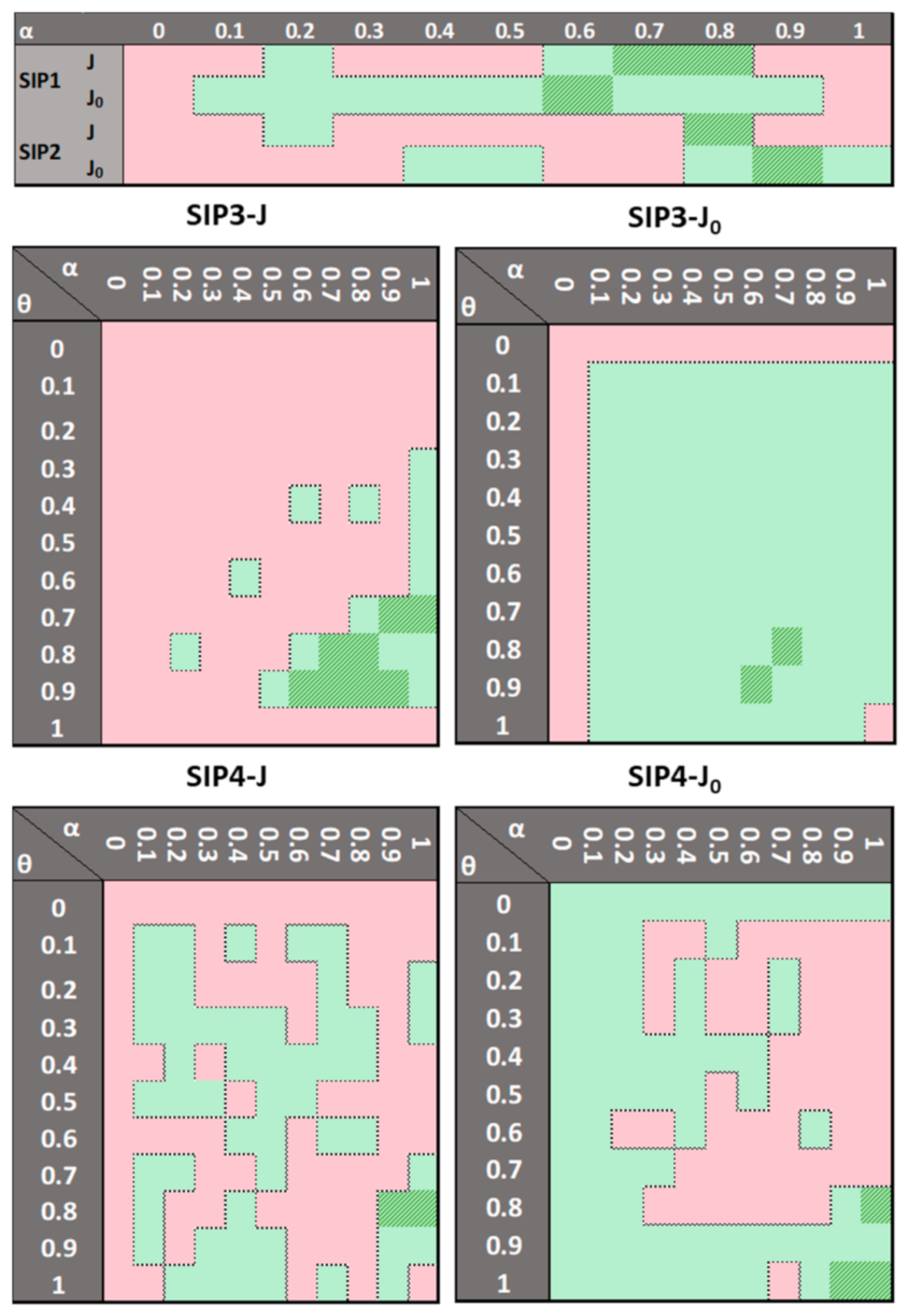Figure 7, Figure 8 and Figure 9 show the areas of successful convergence for the studied ill-conditioned cases. Hence, it is considered to have failed since both divergence and convergence lead to inaccurate solutions.

Firstly, it can be easily appreciated that SIP1-J, SIP2-J, SIP3-J, and SIP4-J are typically less reliable than SIP1-J₀, SIP2-J₀, SIP3-J₀, and SIP4-J_0, since the latter normally showed wider convergence areas. There are some remarkable cases; for example, SIP1-J did not converge in the case3012wp and case3375wp; on the other hand, SIP1-J₀ and SIP3-J₀ frequently converged, regardless of the value of parameters. Finally, SIP4-J and SIP4-J₀ look very sensitive to the values of s-parameters. Their convergence rate precisely explains the superior robustness features of linear methods. In [43], it is said that the methods with high convergence rates normally show narrow Regions of Attraction; in other words, the highest convergence rate has the most sensitivity with respect to the initial guess. This fact can also be appreciated for other PF techniques such as [10,14], which introduce a discrete step size to reduce the convergence rate and obtain robust techniques properly.

From Figure 7, Figure 8 and Figure 9, it can also be seen that tuning the s-parameters is a strongly case-dependent topic. For example, while the considered techniques performed very similar in case3012wp and case3375wp, the behavior of the techniques became erratic in the case13659pegase. In addition, the least number of iterations is not always achieved for the same s-parameters.

In order to properly compare the studied Newton-SIP techniques in these ill-conditioned cases, let us consider only those cases in which the considered techniques required the least number of iterations for successfully converging. Figure 10 shows the execution time along with the total number of iterations and factorizations employed by the Newton-SIP PF techniques in the studied ill-conditioned systems. As commented, NR failed in these cases.

As in well-conditioned systems, SIP1-J₀, SIP2-J₀, and SIP3-J₀ are the fastest techniques, while SIP1-J, SIP2-J, SIP3-J, and SIP4-J typically reached the solution employing less iterations. It is worth mentioning that SIP3-J is occasionally faster than SIP4-J₀ in the case13659pegase. This is because these two methods require the same number of factorizations in this system; however, SIP4-J₀ computes more calculations per iteration. SIP1-J only converged in the case13659pegase.

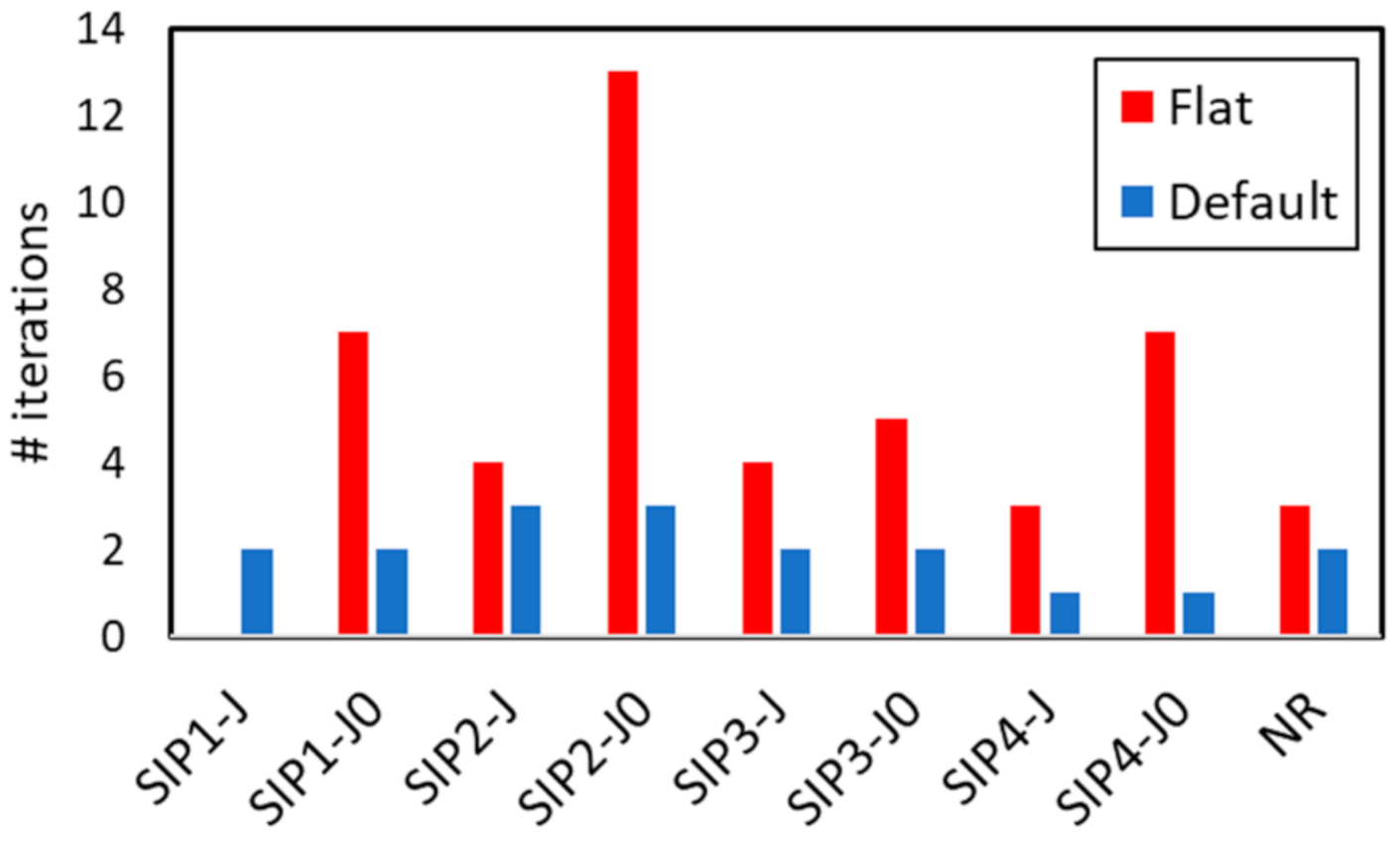
To conclude this analysis, the influence of the initial guess ${\mathit{x}}_0$ on the convergence features of each studied technique has been analyzed. To this end, two cases have been compared. On the one hand, we assume a flat start as in previous simulations, taking the best value of the s-parameters for each case. On the other hand, we took the default starter provided in Matpower, which is normally closer to the solution than the flat initialization. Figure 11 shows the number of iterations for these two cases in the case3012wp. As observed, the quality of the initialization directly affects the convergence of the studied methods, normally employing more iterations when a flat start is used. These results are coherent, since the closer the solution is to the start point, the faster the convergence. This same conclusion was attained in other recent papers such as [44].

It is also worth noting how the starter point affects the robustness of the solvers. Particularly, in the case of SIP1-J, the solution is successfully achieves starting from the default point, while this solver failed from the flat starter. This is coherent with the definition of ill-conditioned systems provided in [13], which is strongly related with the quality of the starting point.

5.3. Influence of the R/X Ratio

It is well-known that the R/X ratio may negatively impact on the convergence features of PF solvers [21]. In this section, we analyze how the studied techniques are affected by this parameter. To this end, we have considered the small-scale case_ieee30, since high R/X ratios are more frequently in this kind of network. To properly analyze this aspect, we have considered that the branch resistances are multiplied by a real factor $\mu$, and the number of iterations for various values of $\mu$ is compared in Figure 12. 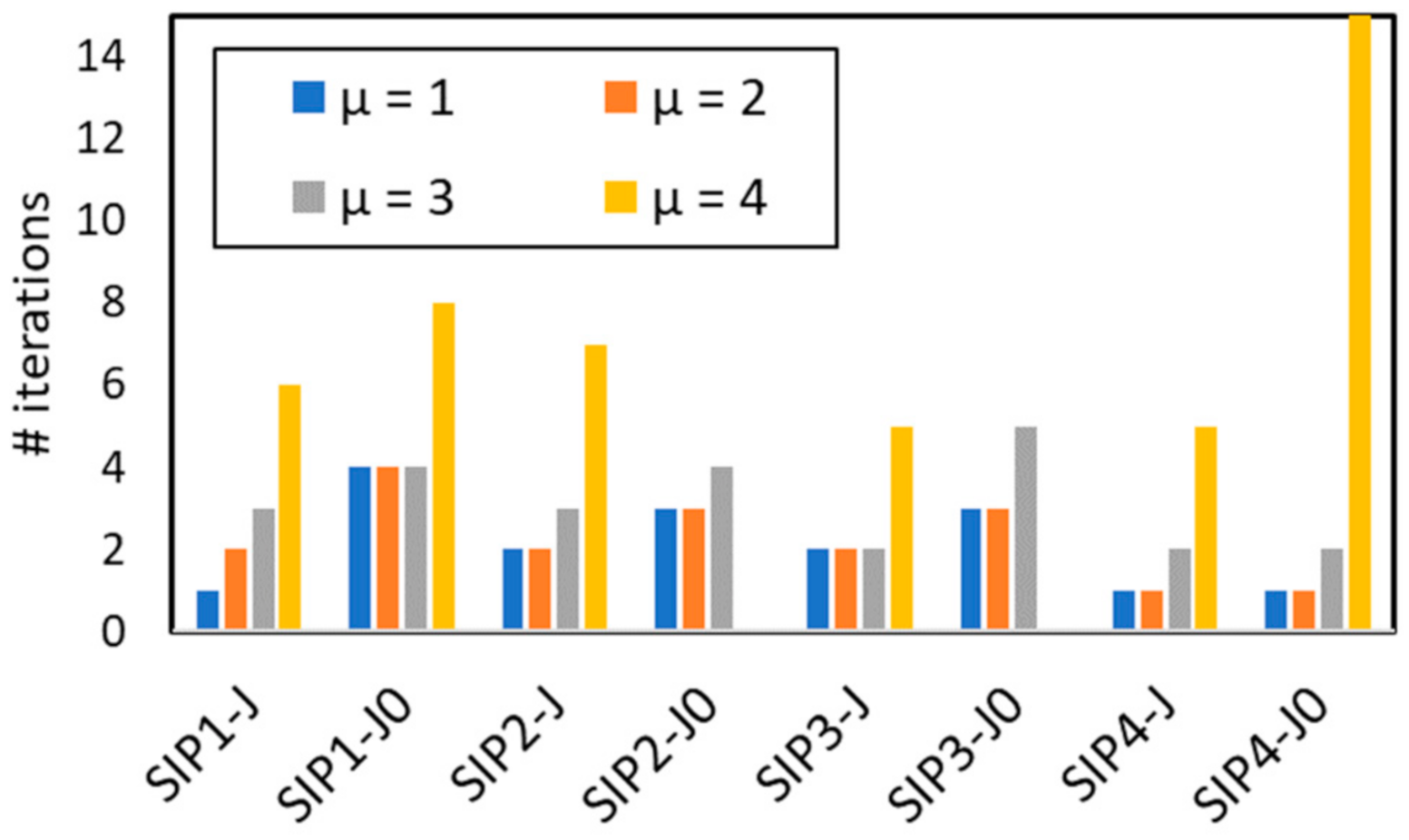In this case, the s-parameters were fixed equal to 1 in order to attain the highest convergence rate. As expected, the higher the R/X ratio, the higher the number of iterations employed to converge. This fact is especially remarkable in those solvers with fixed Jacobian, provoking divergence in some cases.

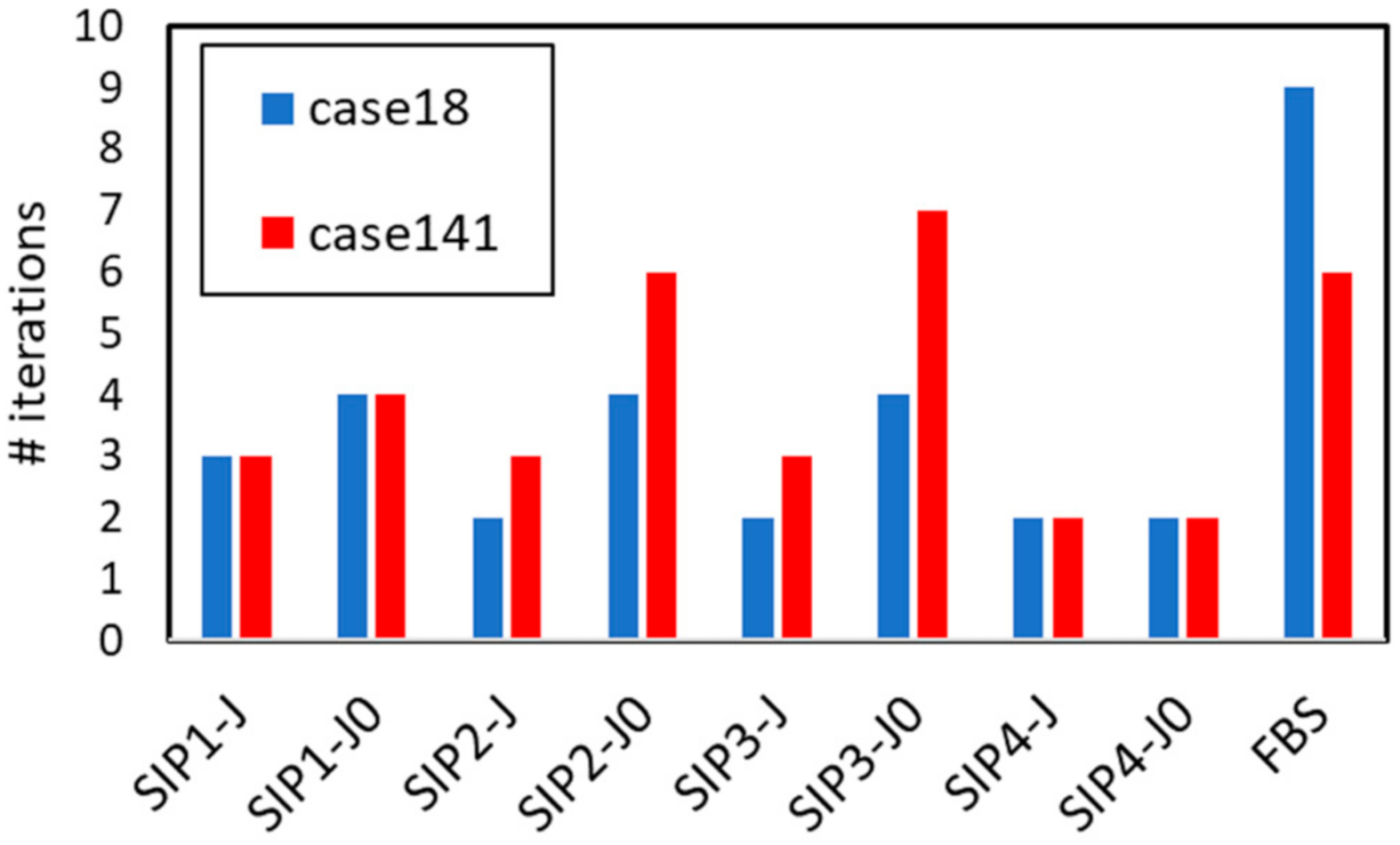
Lastly, we analyze the performance of the developed solvers on a real radial distribution system. To this end, we have considered case18 (18-bus radial distribution system from Grady, Samotyj, and Noyola) and case141 (141-bus radial distribution system from Khodr, Olsina, De Jesus, and Yusta) from Matpower’s database. In this case, the results obtained by the studied solvers have been compared with the Forward–Backward sweep algorithm (FBS) [45], which is frequently considered the most conventional solver for radial distribution systems. Figure 13 shows the total number of iterations in the studied radial systems. As observed, the Newton-SIP methods normally outperformed FBS, thus proving their efficacy to handle a wide variety of networks with different features and topologies.

6. Conclusions and Future Works

In this paper, the applicability of different Newton-SIP methods for solving the PF problems has been comprehensively studied. Four techniques [32,33] have been considered, and two different iterative schemes have been analyzed. Firstly, we have considered the standard form of Newton-SIP techniques, i.e., those algorithms in which the Jacobian matrix is only updated at the first iteration. Secondly, a fully updated iterative scheme has been considered, in which the Jacobian matrix is updated each iteration as NR.

The convergence characteristics of the considered PF techniques have been studied. In case a fully updated iterative scheme is considered, the techniques can achieve up to the eighth order of convergence. It has been also demonstrated that the highest convergence rate is achieved when the s-parameters are set equal to one. On the other hand, the convergence rate of the standard form of Newton-SIP methods is always linear.

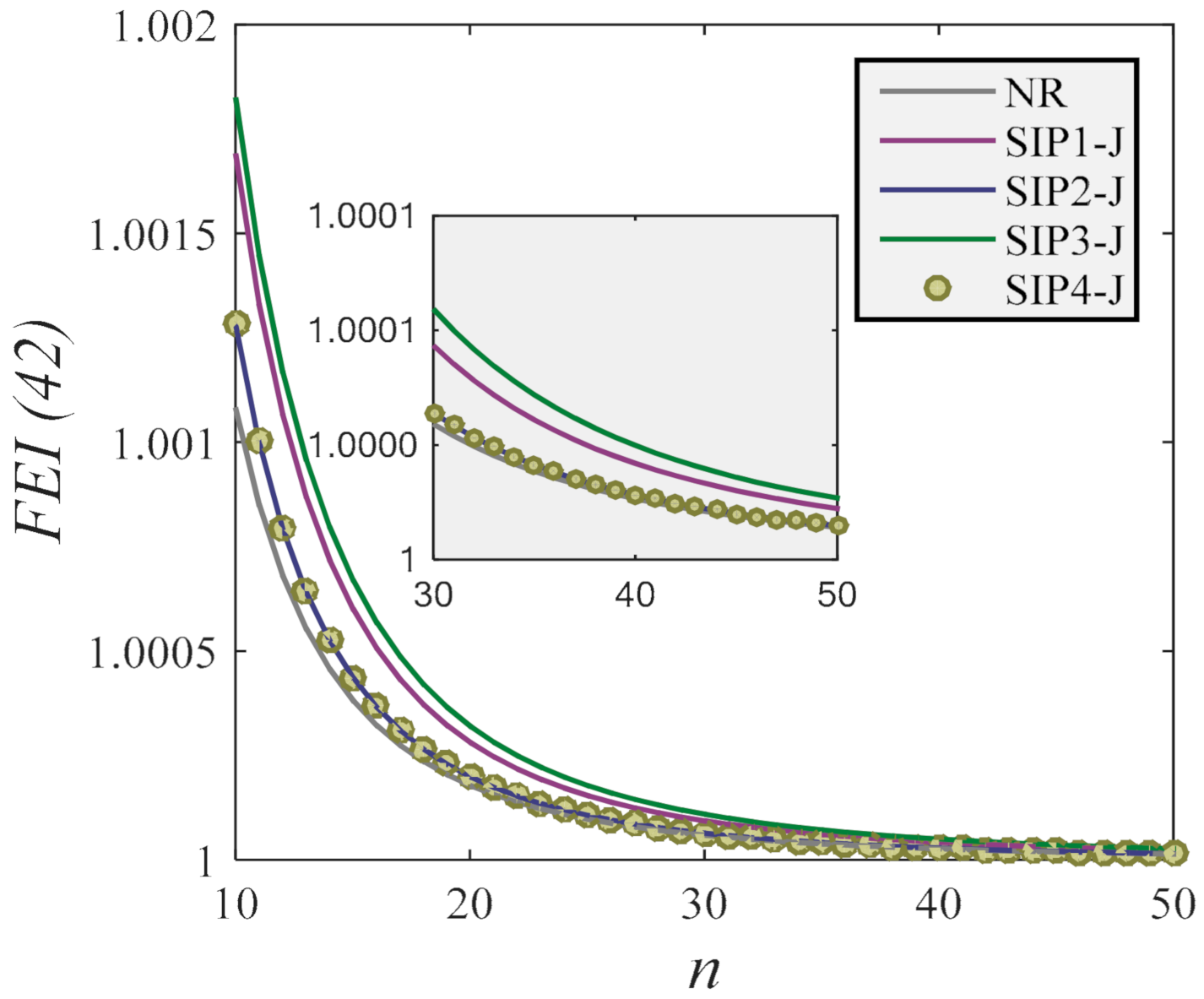
The efficiency of the studied techniques has been compared using a well-known efficiency index. The results indicate that the SIP3-J is the most efficient Newton-SIP technique, since it is able to achieve the 4th order of convergence by only factorizing one Jacobian matrix for each iteration. Nevertheless, all the studied techniques showed higher efficiency indices than NR.

Various numerical experiments have been carried out for several well and ill-conditioned systems with different sizes and topologies. The most remarkable conclusion is the Newton-SIP techniques’ ability to manage both well and ill-conditioned systems efficiently. They typically outperformed NR in well-conditioned systems. In addition, they are more robust than NR in ill-conditioned cases. These features make Newton-SIP techniques very suitable for widespread industrial applications, as it was pointed out in [31]. Drawbacks showed by the linear Newton-SIP techniques in heavy loading cases can be overcome using their fully updated schemes. Comparing the studied Newton-SIP techniques, the best trade-off between robustness and efficiency is normally obtained with SIP3-J.

However, the performance of Newton-SIP techniques is notably influenced by the values of the involved s-parameters. For example, in heavy loading systems, it has been shown that the convergence characteristics can be notably improved by taking advantage of the accelerating effect of s-parameters. On the other hand, the robustness properties of the Newton-SIP techniques are strongly affected by the parameters involved. However, the analysis carried out in this work shows that tuning the s-parameters is a strong case-dependent topic. It also looks very difficult to be tackled, since any common pattern has been observed.

In radial distribution systems, the studied techniques outperformed FBS, thus demonstrating their ability to handle a wide variety of networks. These results along those obtained in large-scale well and ill-conditioned cases manifest the suitability of the Newton-SIP methods to be applied in real industry tools and even for voltage stability analysis and optimization problems. Further results will be obtained in future works to confirm that point.

Consequently, future works should be focused on further tackling alternative schemes for optimally tuning the s-parameters in order to get a good trade-off between efficiency and robustness and avoid the necessity to be initially set by the user. In this sense, optimal conditions should be derived, thus allowing implementing auxiliary routines to properly set those parameters.