Abstract
Due to the global growth in popularity of Fifth Generation (5G) cellular communications, the demand for shielding against it has risen for a variety of applications, mainly related to cybersecurity but also to isolation, calm areas and so on. This research paper aims to provide a suitable dual-band fractal FSS (Frequency Selective Surface) for the 5G lower band frequencies: 750 MHz and GHz. The unit cell is in the shape of a bow tie, where each of the triangular parts are Sierpiński triangles. One major addition to the unit cell is a central metal strip to make the manufacturing of the FSS more feasible and to tune the operation frequencies and bandwidths. As with each different stage of a fractal antenna, the different stages of the fractal FSS design behave differently. For this application, stage 2 is sufficient, as we are able to cover frequency bands among those included in the FR1 5G spectrum. Some equations were derived using linear regression in order to provide specific design tools for building an FSS. These equations have high accuracy and can be used to adapt the proposed design to other frequencies. Some other parameters, which are not represented in the aforementioned equations, can also be adjusted for minor tweaking of the final design. This design performs well except under large incidence angles. This should be taken into account when proposing the installation of a structure based on it. A good agreement between simulation and measurement results is observed.
1. Introduction
Fifth Generation (5G) cellular communications system is all the rage at the moment; it is planned to be implemented by every country and major telecommunication operator. Frequency allocation to such a system was carried out, grouping all available bands into two groups: FR1 involving all sub-6 GHz bands, and FR2 for millimeter-wave bands [1,2,3,4,5]. The technology used for this deployment is mature, and auctions have been organized all around the world in order to assign spectrum usage to different 5G operators [6,7]. This expected-to-be-fast development of the new technology and subsequent rollout seem to have slowed down due to the economic effects of the COVID-19 pandemic on both society and businesses. However, the lockdown confinement periods due to this same reason boosted the social valuation of communication networks and increased the importance of accessing fast and trustworthy services. In such dichotomy, 5G was born as a support for the new ‘online way of living’ but limited by face-to-face restrictions: operators have to install new facilities with equipment that someone had to manufacture, and commercials have limited access to their future clients.
As with previous transitions between successive communication standards, the move from 4G (Fourth Generation) to 5G will not be easy. The spectrum requirements of the new technology are large, and the refarming of spectrum (re)allocation had been carried out, removing obsolete analogue systems and liberating the bands occupied to be used by new deployments [8]. This harmonization seems to be a must for the operators, as having access to low frequency bands (i.e., sub-1 GHz) would be used as capital to provide widespread coverage in urban and rural areas. Mid-bands ( GHz, but also refarmed spectra by operators at 1800 MHz or 2 and some GHz) would maintain a good balance between capacity and coverage for many end user applications. Both are within the FR1 spectrum portion.
The use of these new bands carries the transmission of some old issues to frequencies not previously considered. Solutions to those bands should be adopted by tuning the forgoing proposals or by designing new ones. This is the case with isolation or site shielding applications: they are needed for several situations, from mitigating the interference between adjacent access points or providing cybersecurity protection, to allowing calm and peaceful spaces (in hospitals, commercial centers or mindfulness places such as churches or meditation areas). For such requirements, frequency selective surfaces (FSS) arise as a possible solution [9,10].
Such an FSS performs as a distributed electromagnetic filter, providing a frequency response that can be tuned, and then adapted to the frequency allocation of the wireless system wanted to be impacted [9,10]. It can act as a band-pass or band-stop filter for radio waves propagating across the surface itself.
As the FR1 spectrum is the one which will be used by operators in the first 5G deployments, this paper focuses its design efforts on these lower 5G frequency bands, particularly at 700 MHz and GHz. The proposal is to design an FSS suitable for mitigating and even blocking radio signals at both bands, taking into account that the bandwidth for both frequencies needs to be at least 400 MHz and of use in real-life applications. Then, this paper aims to provide an appropriate, less blunt, approach towards shielding devices from 5G.
An attempt has been made to find a fitting solution using a self-similar design. Earlier research such as [11] showed promising results for a single-layer FSS dual-band design. The self-similar structures and fractal antennas are handled in Section 2, and the unit cell is described in Section 3. Section 4 details a couple of equations to apply this design to other frequencies with simple parameter adjustments, which extend the usability of the proposal, and provides a tool for radio network designers. All simulations were carried out in CST Microwave Studio 2019 [12], following the guidance of Numan and Sharawi [13] and the CST product manual [14]. The real-life cases with different angles of incidence are simulated in Section 5. Measurements are described in Section 6. Finally, Section 7 extracts the conclusions.
2. Self-Similar Structures and Fractal Antennas
The first time fractals were looked at as something useful to improve real-life applications was by the mathematician Mandelbrot in his book ‘The fractal geometry of nature’ [15], where the occurrence of fractals in nature and their relation to roughness are explained. A couple of years later, Kim and Jaggard published the first paper on fractal antenna theory [16]. After that, Cohen made the first real-life fractal antenna [17]. Werner and Gangul compiled Much’s research on fractal antenna design [18]. More general fractal antenna design rules were also compiled in a book by Ghohs et al. [19].
Among these fractal proposals, a well-known self-similar geometric shape is the Sierpiński triangle, of which the first four different stages are shown in Figure 1. This shape was used in previous antenna and FSS designs. Romeu and Rahmat-Samii [11] used the triangle to create a bow tie FSS that works for two frequencies. This dual-band design forms the base of the design used in this research.
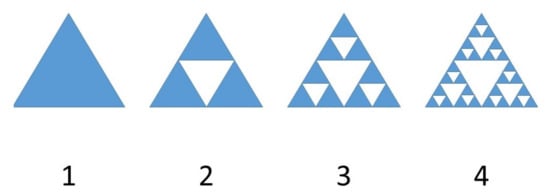
Figure 1.
Different stages for the Sierpiński triangle [18].
3. The Unit Cell
Many FSS designs consist of the repetition of a unit cell element replicated in an organized manner, typically following a bidimensional square matrix structure. Then, when the objective is to analyze the performance of the surfaces composed by a squared matrix of replicated unit cells, the design of such a unit cell is the first step to reach a valid design. The design of the unit cell is described in this section, with its geometrical parameters shown in Figure 2. The unit cell is made out of a combination of a pair of Sierpiński triangles organized as a bow tie, connected by a central metal strip. Both triangles in the bow tie are stage 2 fractal Sierpiński triangles, horizontally mirroring each other. In Table 1, all the required design parameters are defined. Moreover, it contains the final sizes reached after the design process explained further in this paper. The distances between the bow ties are defined as followed:
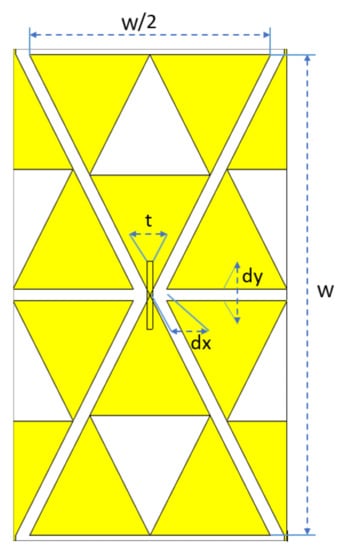
Figure 2.
Unit cell design.

Table 1.
The parameters of the unit cell and the values of them in the final design.
- is the distance from the center of the metal strip and the corners of Sierpiński triangles to the side;
- is the distance in between the bottom and the top of two neighboring Sierpiński triangles.
The main difference between the bow tie from [11] and the one proposed here is the possibility to vary the width t of the added central metal strip. This element is an excellent granular tuning parameter, which helps in fine tuning both band-stop central frequencies and bandwidths around them. The simulation results of the tuning can be found in Section 4.2. Another benefit of adding this metal strip is the effect it has on the production of the physical FSS. The connection point of the two triangles is essential, and the contact area is very small. If the two are not connected as expected, the resonance could be completely different. Then, the presence of the metal strip makes it easier for prototyping: one can simulate almost everything, but prototyping implies taking into account construction tolerances, and the vortex of the triangle is not easy to build perfectly.
Regarding the two triangular elements, these are fractal objects that must be developed by iteratively growing an initial shape in multiple stages. In order to decide the fractal stage required to reach the objective, initial simulations were performed with unit cells composed by pairs of stage 1, 2, 3 or 4 Sierpiński triangles, described in Figure 3. Frequency responses of these unit cells can be observed in Figure 4. The number of resonances is directly related to the iteration on the Sierpinski triangle. When the design does not iterate on itself (in stage 1), there is only one notch at the lower frequency band in the attenuation frequency response, around 800 MHz. When the stage 2 design is implemented, a second notch at the higher frequency band of GHz also appears. This means that, at least, a stage 2 unit cell is needed to obtain the dual-band characteristic. When the design iterates more upon itself to stages 3 and 4, no further improvements can be noted within the bandwidth of interest. These higher iterations increase complexity, and thus make it more challenging to produce prototypes or final products. This is why the final design sticks with the stage 2. Another notable effect of increasing the number of iterations is the shift of the two notches. The fourth iteration has a complete shift to the lower frequencies, but also brings the two notches closer towards each other. Considering the frequency performance of the FSS unit cell and its design complexity, stage 2 of the fractal elements is selected for further development.
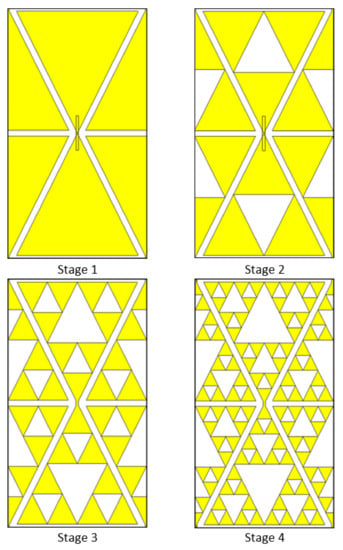
Figure 3.
Unit cell designs at different fractal stages.
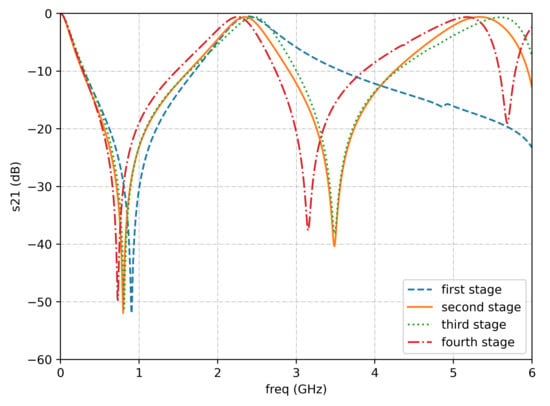
Figure 4.
Frequency responses (by CST Microwave Studio) at different fractal stages.
4. Design Parameters and Guidelines
This section provides a guide to adjust the unit cell to be used with other frequencies. The four adjustable parameters in order of frequency tuning importance are w, t, and , and are listed in Table 1 with their explanation. Designing a unit cell, such as the one purposed in this paper, starts with the general size of the element [9,20]. This size is directly related to the resonance wavelength. Even more specific, in this design, the placement of the first resonance frequency. This can be concluded from the iteration results discussed in Section 3. On Figure 3 stage 1 only resonates at the lower of the two frequencies: it only has a valley around 800 MHz (and not the predetermined 700 MHz) and not around GHz. All parameters have some influence in both low and high frequencies, and in the related bandwidths. Then, it is not possible to control both bands independently, i.e., there are no separate sets of parameters for each frequency band. However, the weights and thus the influence of those parameters vary significantly from one band to the other.
The and parameters depict the distance between the individual bow ties, and are fixed at 3 and 2 mm, respectively. When these values are too low, the different bow ties will touch each other and the known response of the FSS will be lost. This also eases the way the simulations can be carried out in CST Microwave Studio.
4.1. Simulating in CST Microwave Studio
Simulations were carried out using the frequency domain solver of the periodic structure workflow in CST. The simulations started with the FSS unit cell template and this ensured a correct basic adjustment of key simulation settings such as the boundaries and background. All simulations were carried out using unit cell boundaries, ensuring the three-by-three unit cell surface was considered. This allows us to include the effect of mutual coupling among adjacent cells, avoiding important mismatches when neglected. Ports Zmin and Zmax are automatically created by CST and their distance to the reference plane was not modified. The unit cell boundary settings enabled the Floquet boundary simulation mode, , to be selected as the Floquet port [14]. The source type was plane wave. The frequency solver was set up so that frequencies from 0 to 6 GHz were taken into account. The frequency response plots in this paper represent plots (in CST the , result) and plots (in CST the , result) [13].
Initial dimensions for just one unit cell were obtained adjusting the results in [11] for the desired resonant frequencies. Initial simulations were run for this single unit cell and then corrected by incorporating mutual coupling, as indicated previously. These initial dimensions were mm, mm, mm, mm. To obtain the later-explained Equations (1)–(4), parameter sweeps with varying values for t, w, and were performed. With each sweep, only one of the earlier mentioned parameters wass varied in an interval. After this process, the final unit cell design was closed with the dimensions given in Table 1.
Once the final design was obtained, a larger structure (50 cm by 50 cm) was also simulated in order to obtain additional insight on the impact of each element on the complete FSS. Figure 5 depicts the analyzed structure, whereas Figure 6a,b represent the electric fields induced on the surfaces at 800 MHz and GHz, respectively. It can be observed that the lower frequency resonates with the larger overall bow tie structure and the higher frequency resonates with the smaller triangle cut-outs of the second iteration.

Figure 5.
A 50 by 50 cm FSS structure.
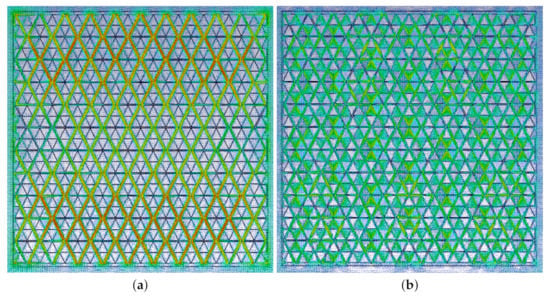
Figure 6.
E-field comparison. (a) Electric field distribution at 800 MHz. (b) Electric field distribution at GHz.
The frequency response with the geometrical parameters provided in Table 1 is depicted in Figure 7. Both deep attenuation valleys are observed at target bands in this figure, which means that the design is able to fit the requirements for being used to mitigate (and almost block) 5G FR1 signals.
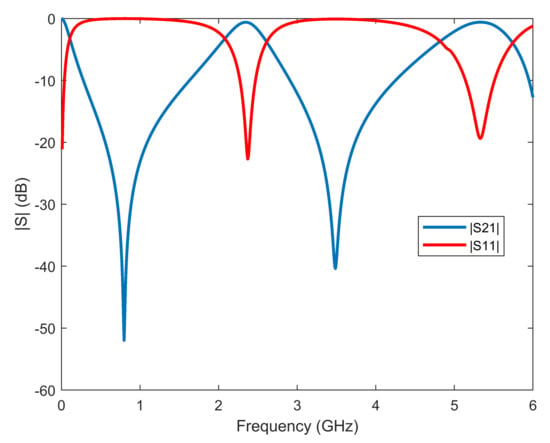
Figure 7.
Frequency response of the final design.
4.2. Unit Cell Size w and Central Element Width t
As explained in the first part of this section, the two parameters that allow the most consistent flexibility in adjusting for frequency and bandwidth, are w, and to a lesser extent, t. w stands for the size of the element and is measured from the top of the bow tie to the bottom. t is defined as the width of the central metal strip and has a limited range. The size parameter w is investigated from 70 to 100 mm. In this interval, the frequency shifts follow a linear relationship. The range for t goes from to mm. Its lower limit is due to the physical design limitations of a copper trace width. The upper limit is in place so that the different bow ties will not end up touching each other.
These two intervals were used to carry out a parameter sweep in the CST Microwave Studio. The results from these simulations were then analyzed to derive equations for the frequency and bandwidths of the two attenuation bands. Using Python, the results were plotted on four different graphs as point clouds, as can be seen in Figure 8.
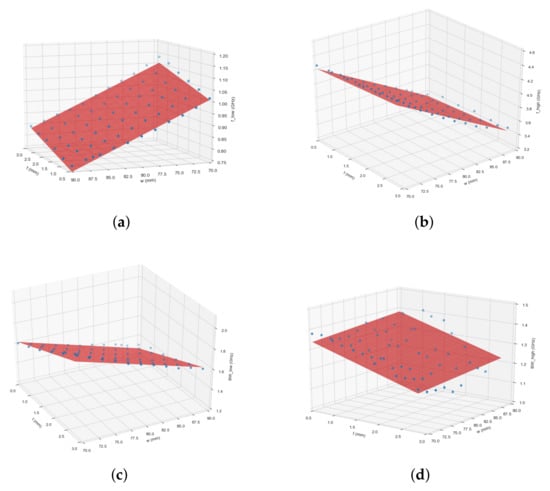
Figure 8.
The effects of w [mm] and t [mm]. (a) Frequency shift around 800 MHz. (b) Frequency shift around GHz. (c) Bandwidth shift around 800 MHz. (d) Bandwidth shift around GHz.
From the previously mentioned plots in Figure 8, it is clear that there is some linear relationship for the center frequencies as well as the bandwidths. These linear relationships lead to the following four equations (Equations (1)–(4)), derived using linear regression. The precision (p), as calculated by the algorithm, for these equations is also given. These numbers are only valid in the simulation intervals. Outside these intervals, the curves start to diverge from the planes with increasing and decreasing w values.
Equation (1) is a good starting point to adjust the first notch. It is valid from 750 MHz to 1150 MHz. It can be noted that an increase in overall size w has a large effect on the resonance: although t weights more, it denotes the width of the central metal strip, and it is not possible to vary by a lot.
The second equation has a wider useful interval, from GHz to GHz. This means that the same change in w yields a more drastic frequency shift in the second resonance band than in the first lower one. t in comparison seems to have less effect when the equations are looked at more closely; t has about 50% less effect on the low band center frequency position than the high-frequency center band position. The precision of both Equations (1) and (2) is both high and similar. This means that both can be a good starting point for designing a similar design around 800 MHz and GHz.
When the design requirements are taken into account, the frequency response needs to have at least a bandwidth of 400 MHz around the center frequencies at the dB level. The center frequency for the lower band varies around 800 MHz, and not the predetermined 700 MHz. Because of the larger bandwidth, the suppression of reflectivity is still dB at 700 MHz, and the total width around 700 MHz is more than sufficiently damped. In Figure 8c, the bandwidth variation interval is visible on the z-axis and ranges from GHz to 2 GHz. This is wide enough and can be effectively tweaked with Equation (3). The influence of t on the bandwidth is this time higher than the influence of w. This can be interesting for some applications. For example, one can achieve a high bandwidth and low first frequency band by using a high w value and high t value. The precision of this equation is again relatively high, with more than 98% accuracy.
The last equation is an interesting one. The first and maybe most important of the differences with the other equations is clearly visible in Figure 8d. The fitted plane decreases in bandwidth with higher t values. This is the opposite of the lower band response. This means that trying to achieve a wider bandwidth at the lower frequency yields a smaller bandwidth around the higher center frequency. It must be said that the precision of this equation is a lot lower than the precision of the other equations. The variability with this one is high. Using this equation for the bandwidth might result in a good approximation of the real-life response, but it is advisable to first look at the other equations before the fourth one.
4.3. Distance between Bow Ties dx and dy
The distance between the bow ties is represented by the parameters and . The exact depiction of and is visible in Figure 2. When adjusting the FSS design for other frequencies, it is best to start with fixed values for and ; all previous equations were derived for and values of 3 and 2 mm, respectively. Afterwards, when w and t are set, minor adjustments of and towards the center frequency can be performed.
The results for parameter sweeps of and can be seen in Figure 9. The other two parameters w and t were fixed at 87 mm and mm, respectively. Both and were again limited so that the neighboring unit cells would not touch each other. This would, as mentioned earlier, result in unexpected behavior. In Figure 9a, the low band center frequency shift differs a lot from to . The curve follows a logarithmic path, but the variation is more akin to a quadratic function. This means that one needs to take a lot of care when adjusting one of the parameters; the results could be surprising. One should not expect linear behavior. Figure 9b shows that the responses for and are more similar to each other; both follow a logarithmic function. The equations for the trend lines and the trend lines themselves are not depicted here, because they will change together when w and t are modified. One could even expect linear behavior near the previously achieved frequency (using the equations from Section 4.2). If all previously mentioned equations and small and adjustments were correctly implemented, then one should now have the intended design.
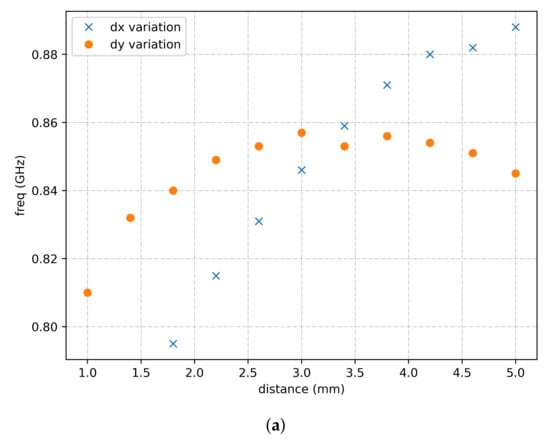
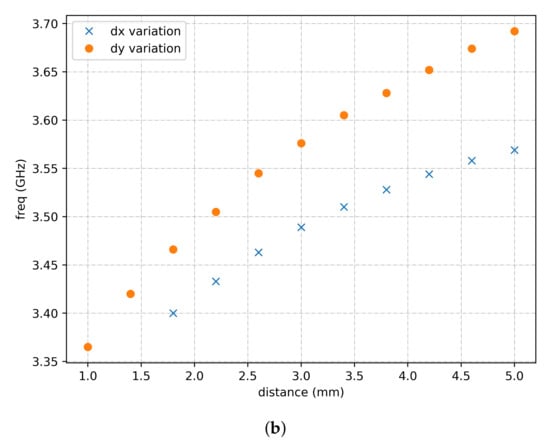
Figure 9.
The effects of and variation. (a) Around 800 MHz. (b) Around GHz.
5. Angle of Incidence
All previous simulations use incident waves perpendicular to the FSS surface. This section checks the design robustness under different angles of incidence. Figure 10 shows the simulation results for different angles, where and are angles in the and directions. When changes, the angle of incidence changes, but the incident electric field is still parallel to the FSS. When changes, the angle of incidence changes, and the incident electric field is no longer parallel to the FSS. The bow tie has a decent invariance against changes in the direction. This means that the resistance against changing angles in this direction is strong. Some extra variations above GHz are introduced, but the behavior around 700 MHz and GHz stays more or less the same as long as the size of does not exceed 45°. The situation for is entirely different; the slightest change (more than 10°) in angle and the lower frequency behavior will begin to disappear, which means that the design is not strong against polarization of the incident wave. The FSS might still be usable because the notch is still wide at dB. If a wave is tilted in both directions, a similar result is visible as only changes. This is likely since the unit cell is not uniformly symmetric and presents better behavior with waves impinging in one of the directions.
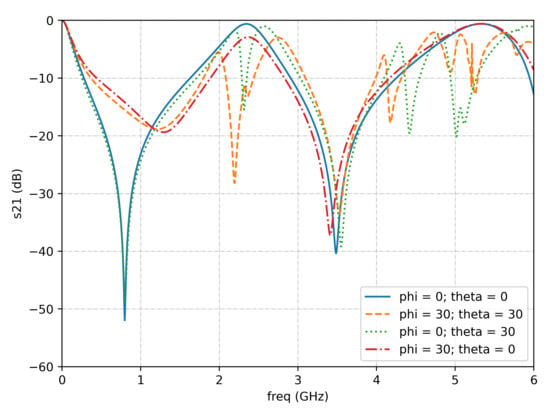
Figure 10.
Frequency response for different incidence angles.
6. Measurements
Practical validation of the proposed dual-band single-layer FSS was obtained from specific measurements carried out inside an anechoic chamber. The FSS prototype used for the measurements is shown in Figure 11. The measurement geometry is depicted in Figure 12, in which the FSS under test is placed on a mechanical test fixture (sample holder) whose dimensions are by 2 m (height × width), and its center was cut in a square shape (window) with 41 by 41 cm². The sample holder is covered with pyramidal RF absorbers and aluminum foil on one side, as depicted in Figure 13. The purpose of this fixture is to minimize the contamination of measurement results due to diffraction and transmission, mainly occurring through the center square window.

Figure 11.
FSS prototype used for the measurements.
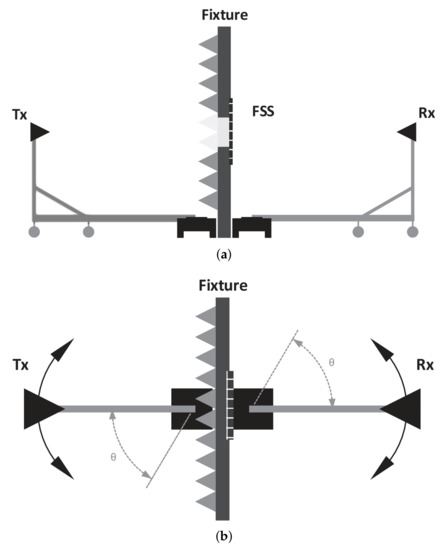
Figure 12.
Measurement setup inside the anechoic chamber for FSS characterization. (a) Side view. (b) Top view.

Figure 13.
Measurement setup with FSS under test, set for vertical polarization.
Wideband directional log-periodic antennas used in measurements were placed at a 2 and m distance from the test fixture, respectively, for the transmitter and receiver. In the former, an Aaronia Hyperlog 30,100 antenna, covering the 300 MHz to 10 GHz frequency band was used, whereas in the latter, an Aaronia Hyperlog 60,100 antenna (600 MHz–10 GHz) was employed. The two antennas were connected to a Vector Network Analyzer (VNA) and placed on top of support masts.
In particular, the complex frequency response was obtained from 10 MHz to 6 GHz, with 1601 points and averaged out from 20 complete frequency sweeps, for both vertical and horizontal polarizations. Although the discrimination of both antennas for frequencies below MHz falls within the available dynamic range of the measurement system, significant noise in the measurement results up to 600 MHz was observed, and thus measurement results are presented only for frequencies above 600 MHz.
An initial reference measurement was obtained without any sample (open window), which was used for normalization purposes. The normalized response of the FSS structure for both vertical and horizontal polarizations, assuming normal incidence, is depicted in Figure 14. A relatively good agreement is observed between simulation and measurement results, in which the two resonant frequencies appear around 800 and GHz, with similar reject levels to that of the simulations. The insertion loss in the pass-band was measured to be below 2 dB, which is also in good agreement with the simulations.
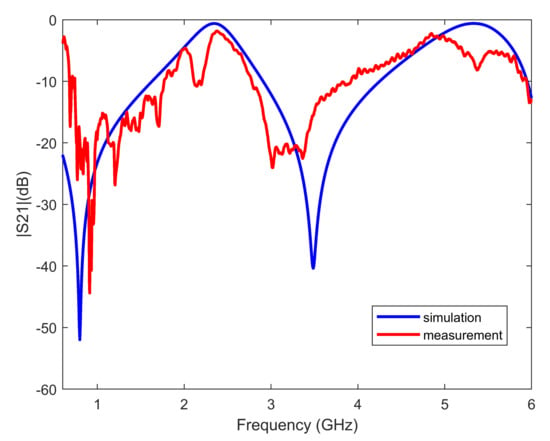
Figure 14.
Measurements with vertical polarization, compared with simulations.
7. Conclusions
This paper proposes a bow tie FSS design to block lower-band 5G frequencies (FR1). Multiple simulation results proved that this is a decent attempt, with wide and deep attenuation valleys around the desired center frequencies of 700 MHz and GHz. Through the equations derived in this work, other researchers could adapt the design to be used for their purposes. For instance, adjusting the design to new frequencies in the specified low and high frequency bands would only require solving a 2 × 2 linear system determined by Equations (1) and (2) to obtain t and w. The other important parameters were shown to be less reliable in adjusting, but they can be used for minor tweaking of the center frequencies. Different angles of incidence show that the design is limited in real-life applications due to its poor performance in changes. It does not mean that it will not be usable, just that this fact needs to be considered before going through with its implementation. As an overall conclusion, this design, supported by measurements, is versatile and provides clear FSS behavior that could make it useful for specific applications.
Author Contributions
Conceptualization, I.C., M.G.S. and J.V.; methodology, M.G.S. and I.C.; software, B.D. and S.M.; validation, M.G.S. and R.C.; formal analysis, I.C., M.G.S. and J.V.; investigation, B.D. and S.M.; writing—original draft preparation, B.D. and S.M.; writing—review and editing, I.C., R.C. and J.V.; project administration, M.G.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Spanish Government, Ministerio de Ciencia e Innovación, Secretaría General de Investigación, grant number PID2020-112545RB-C52; Xunta de Galicia, project ED431C 2019/26; atlantTTic Research Center and the European Regional Development Fund (ERDF); FCT/MCTES through national funds and when applicable co-funded EU funds under the projects UIDB/EEA/50008/2021.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Shafi, M.; Molisch, A.F.; Smith, P.J.; Haustein, T.; Zhu, P.; De Silva, P.; Tufvesson, F.; Benjebbour, A.; Wunder, G. 5G: A Tutorial Overview of Standards, Trials, Challenges, Deployment, and Practice. IEEE J. Sel. Areas Commun. 2017, 35, 1201–1221. [Google Scholar] [CrossRef]
- Ghosh, A.; Maeder, A.; Baker, M.; Chandramouli, D. 5G Evolution: A View on 5G Cellular Technology Beyond 3GPP Release 15. IEEE Access 2019, 7, 127639–127651. [Google Scholar] [CrossRef]
- Henry, S.; Alsohaily, A.; Sousa, E.S. 5G is Real: Evaluating the Compliance of the 3GPP 5G New Radio System With the ITU IMT-2020 Requirements. IEEE Access 2020, 8, 42828–42840. [Google Scholar] [CrossRef]
- Tullberg, H.; Popovski, P.; Li, Z.; Uusitalo, M.A.; Hoglund, A.; Bulakci, O.; Fallgren, M.; Monserrat, J.F. The METIS 5G System Concept: Meeting the 5G Requirements. IEEE Commun. Mag. 2016, 54, 132–139. [Google Scholar] [CrossRef]
- Imran, A.; Zoha, A.; Abu-Dayya, A. Challenges in 5G: How to Empower SON with Big Data for Enabling 5G. IEEE Netw. 2014, 28, 27–33. [Google Scholar] [CrossRef]
- South Korea Wraps 5G Auction for 3.5, 28 GHz. Available online: https://www.fiercewireless.com/wireless/south-korea-wraps-5g-auction-for-3-5-28-ghz (accessed on 17 November 2021).
- A Guide to 5G Spectrum Auctions in Western Europe: Nordic Edition. Available online: https://blog.telegeography.com/a-guide-to-5g-spectrum-auctions-in-western-europe-nordic-edition (accessed on 17 November 2021).
- 5G Spectrum. GSMA Public Policy Position; GSMA Head Office: London, UK, March 2020. [Google Scholar]
- Munk, B.A. Frequency Selective Surfaces: Theory and Design; Wiley: New York, NY, USA, 2000. [Google Scholar]
- Ferreira, D.; Caldeirinha, R.F.S.; Cuinas, I.; Fernandes, T.R. A Review of Manufacturing Materials and Production Methods for Frequency-Selective Structures [Wireless Corner]. IEEE Antennas Propag. Mag. 2018, 60, 110–119. [Google Scholar] [CrossRef]
- Romeu, J.; Rahmat-Samii, Y. Fractal FSS: A Novel Dual-Band Frequency Selective Surface. IEEE Trans. Antennas Propag. 2000, 48, 1097–1105. [Google Scholar] [CrossRef] [Green Version]
- CST Microwave Studio. Dassault Système, Vélizy-Villacoublay Cedex. Available online: https://www.3ds.com/products-services/simulia/products/cst-studio-suite/ (accessed on 17 November 2021).
- Numan, A.B.; Sharawi, M.S. Extraction of Material Parameters for Metamaterials Using a Full-Wave Simulator [Education Column]. IEEE Antennas Propag. Mag. 2013, 55, 202–211. [Google Scholar] [CrossRef]
- Dassault Systèmes. CST Studio Suite Help; Dassault Systèmes: Waltham, MA, USA, 2019. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H.Freeman & Co Ltd.: San Francisco, CA, USA, 1982. [Google Scholar]
- Kim, Y.; Jaggard, D.L. The Fractal Random Array. Proc. IEEE 1986, 74, 1278–1280. [Google Scholar] [CrossRef]
- Felber, P. Fractal Antennas; Technical Report; Illinois Institute of Technology: Chicago, IL, USA, 2000. [Google Scholar]
- Werner, D.H.; Ganguly, S. An Overview of Fractal Antenna Engineering Research. IEEE Antennas Propag. Mag. 2003, 45, 38–57. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, B.; Sinha, S.N.; Kartikeyan, M.V. Fractal Apertures in Waveguides, Conducting Screens and Cavities; Springer Series in Optical Sciences; Springer International Publishing: Cham, Switzerland, 2014; Volume 187. [Google Scholar] [CrossRef]
- Munk, B.A. Finite Antenna Arrays and FSS; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).