A Comparative Study on Power Flow Methods Applied to AC Distribution Networks with Single-Phase Representation
Abstract
:1. Introduction
- ✓
- A complete comparison between recently developed power flow methods comprising four derivative-free and two derivative-based methods. These comparisons present convergence properties that are linear for derivative-free methods and quadratic for derivative-based approaches.
- ✓
- A new iterative method for power flow solution from the family of non-derivative approaches that present linear convergence and use the information of the nodal admittance matrix to obtain its recursive formula.
2. Power Flow Formulations
2.1. Formulation of the General Power Flow Problem
2.2. Successive Approximation Power Flow Method
2.3. Matricial Backward/Forward Power Flow Method
- ✓
- , if the current of the line j is leaving from the node k.
- ✓
- , if the current of the line j is arriving at the node k.
- ✓
- , if the line j is not connected to the node k.
2.4. Triangular-Based Power Flow Method
- ✓
- , if the current of the line j support the current consumption at node k.
- ✓
- , if the current of the line j does not support the current consumption at node k.
2.5. Power Flow Approach Based on Voltage Product Linearization
2.6. Power Flow Approach Based on Hyperbolic Voltage Relation Linearization
2.7. Diagonal Approximation Power Flow Approach
3. Test Feeders
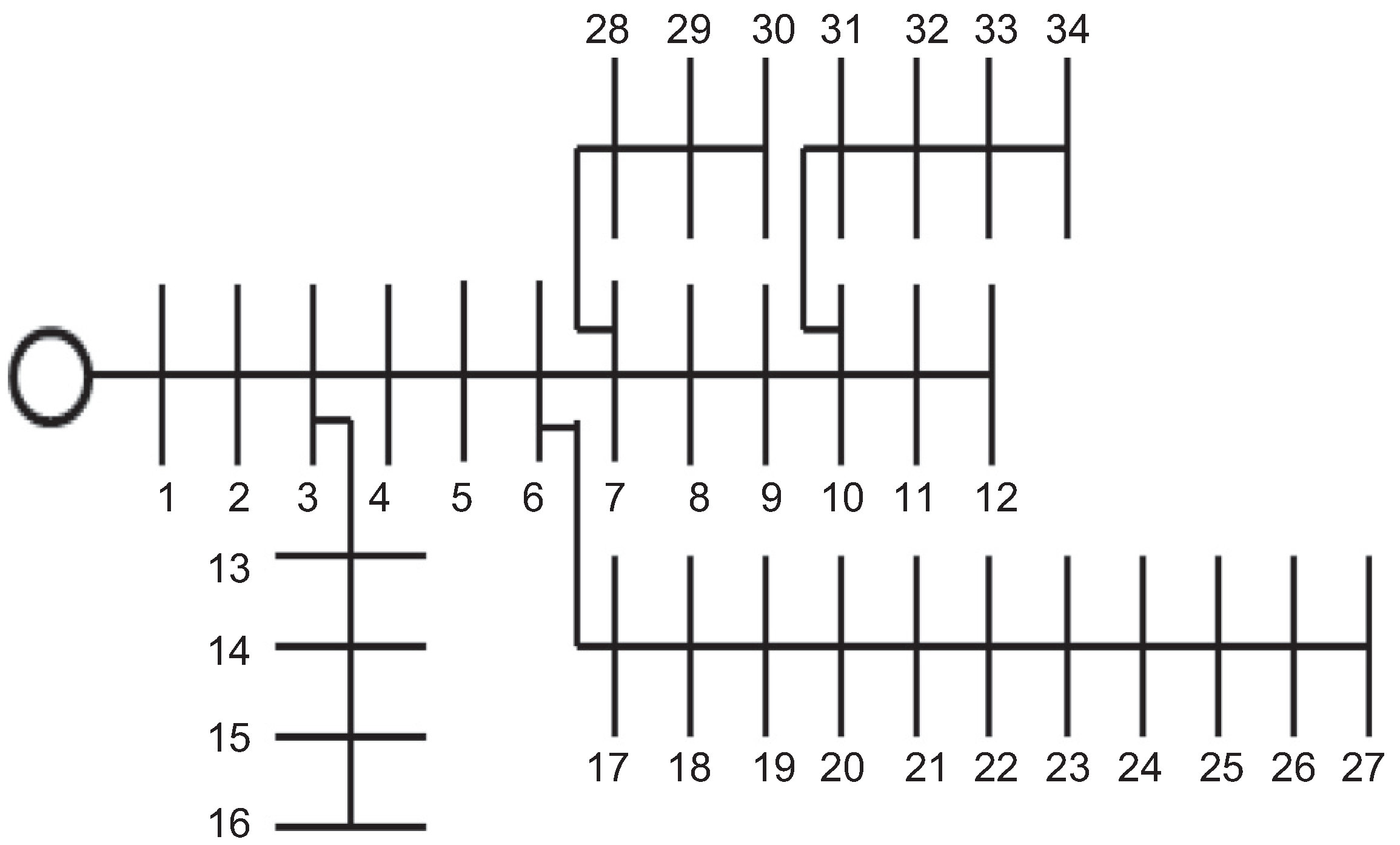
3.1. IEEE 34-Bus System
3.2. IEEE 85-Bus System
4. Computational Implementation
4.1. Power Flow Results in the IEEE 34-Bus System
4.2. Power Flow Results in the IEEE 85-Bus System
4.3. Additional Comments
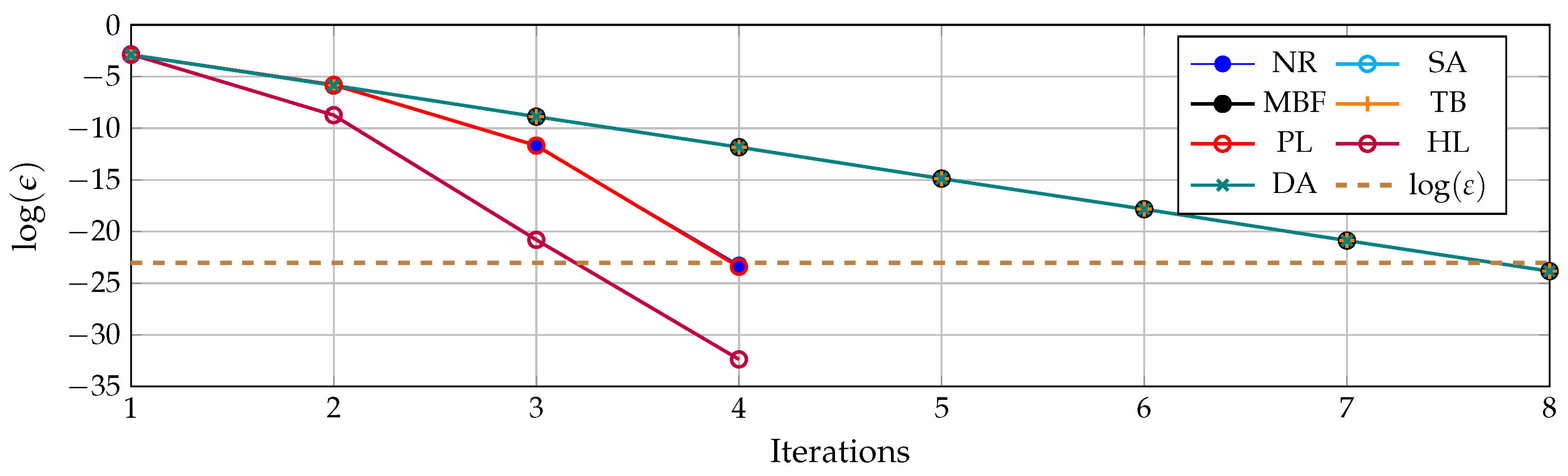
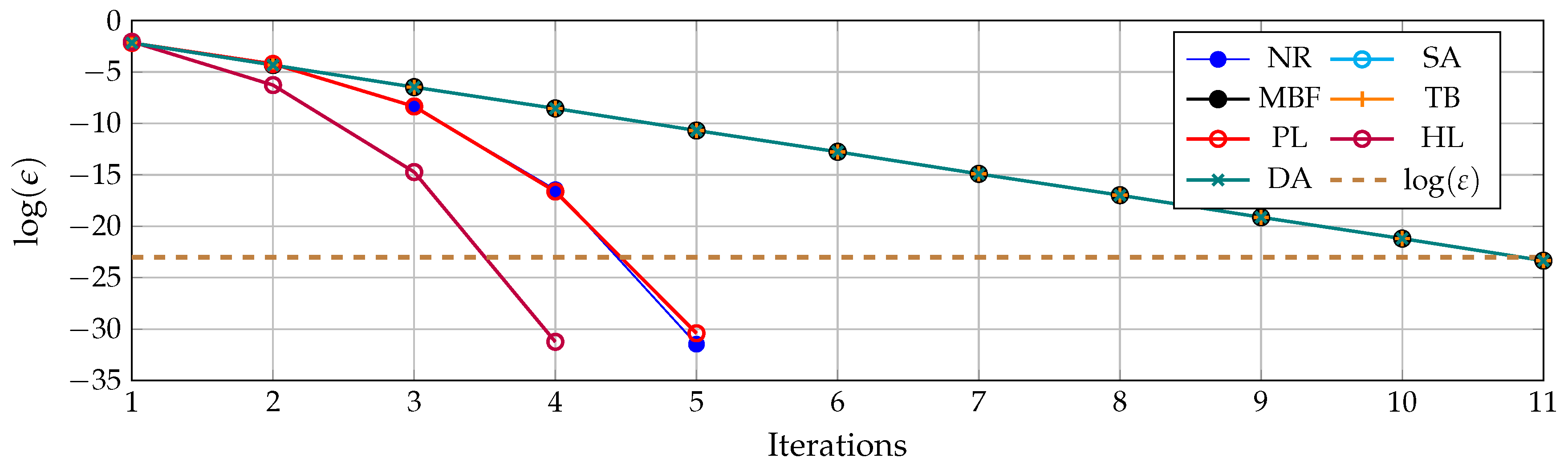
- All derivative-free methods exhibit a linear convergence since their formulation is merely based on the reorganization of the power flow equations in an iterative manner, which implies that information regarding the gradient direction is not included to accelerate their performance regarding the number of iterations, while the derivative-based methods (including the Newton–Raphson approach) have in their formulation variable gains (marices) that help with the reduction of the voltage error after each iteration, which causes these methods to have a quadratic convergence rate.
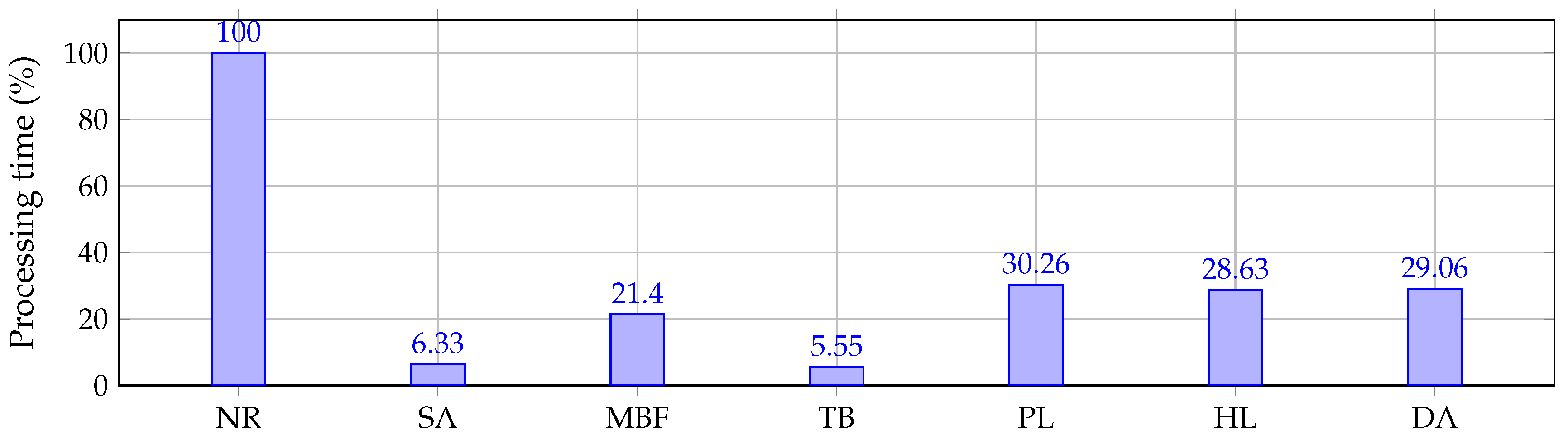
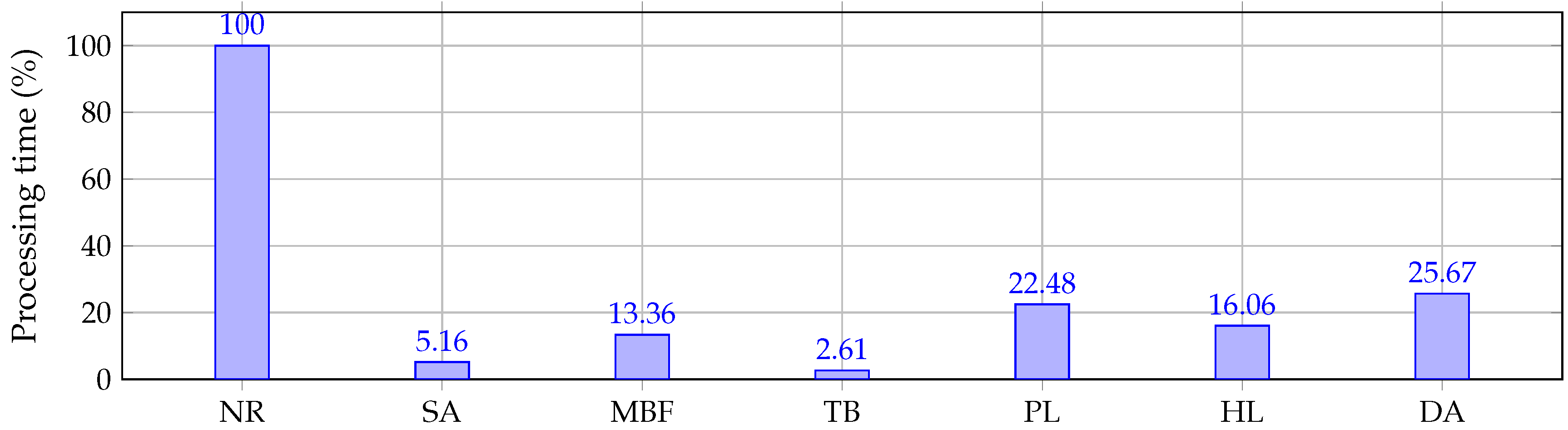
- The diagonal approximation method, as well as the successive approximation method, is derived from the same power flow formula (see the second row of (4)); therefore, their numerical performance is very similar regarding the number of iterations and the convergence rate. However, the main advantage of the successive approximation method (6) over the diagonal approximation method (27) is the lesser total processing time required to solve the power flow problem since the former method uses a constant matrix that is once time inverted and stored, while the latter method requires inverse calculation at each time, leading to an additional computational effort.
- All the studied methods provide the power flow solution regarding the final power losses estimation and voltage calculations; in fact, any one of them can be selected as a power flow tool for specialized optimization algorithms; however, the importance of knowing the total processing times deals with the selection of the most adequate method for specialized algorithms that evaluate thousands of power flows since, in these recursive optimization algorithms, small differences in the processing times of the power flow can produce important differences in the total execution time of the complete optimization algorithm.
5. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Murty, P. Load Flow Analysis. In Electrical Power Systems; Elsevier: Amsterdam, The Netherlands, 2017; pp. 527–587. [Google Scholar] [CrossRef]
- Albadi, M. Power Flow Analysis. In Computational Models in Engineering; IntechOpen: London, UK, 2020. [Google Scholar] [CrossRef] [Green Version]
- Tyagi, A.; Kumar, K.; Ansari, M.A.; Kumar, B. An efficient load flow solution for distribution system with addition of distributed generation using improved harmony search algorithms. J. Electr. Syst. Inf. Technol. 2020, 7, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Milano, F. Analogy and Convergence of Levenberg’s and Lyapunov-Based Methods for Power Flow Analysis. IEEE Trans. Power Syst. 2016, 31, 1663–1664. [Google Scholar] [CrossRef]
- Acosta, C.; Hincapié, R.A.; Granada, M.; Escobar, A.H.; Gallego, R.A. An Efficient Three Phase Four Wire Radial Power Flow Including Neutral-Earth Effect. J. Control Autom. Electr. Syst. 2013, 24, 690–701. [Google Scholar] [CrossRef]
- Herrera-Briñez, M.C.; Montoya, O.D.; Alvarado-Barrios, L.; Chamorro, H.R. The Equivalence between Successive Approximations and Matricial Load Flow Formulations. Appl. Sci. 2021, 11, 2905. [Google Scholar] [CrossRef]
- Shirmohammadi, D.; Hong, H.; Semlyen, A.; Luo, G. A compensation-based power flow method for weakly meshed distribution and transmission networks. IEEE Trans. Power Syst. 1988, 3, 753–762. [Google Scholar] [CrossRef]
- Cheng, C.; Shirmohammadi, D. A three-phase power flow method for real-time distribution system analysis. IEEE Trans. Power Syst. 1995, 10, 671–679. [Google Scholar] [CrossRef]
- Haque, M. Efficient load flow method for distribution systems with radial or mesh configuration. IEE Proc. Gener. Transm. Distrib. 1996, 143, 33. [Google Scholar] [CrossRef]
- Teng, J.H. A modified Gauss–Seidel algorithm of three-phase power flow analysis in distribution networks. Int. J. Electr. Power Energy Syst. 2002, 24, 97–102. [Google Scholar] [CrossRef]
- Teng, J.H. A direct approach for distribution system load flow solutions. IEEE Trans. Power Deliv. 2003, 18, 882–887. [Google Scholar] [CrossRef]
- Yang, H.; Wen, F.; Wang, L. Newton-Raphson on Power Flow Algorithm and Broyden Method in the Distribution System. In Proceedings of the 2008 IEEE 2nd International Power and Energy Conference, Johor Bahru, Malaysia, 1–3 December 2008. [Google Scholar] [CrossRef]
- Lagace, P.J.; Vuong, M.H.; Kamwa, I. Improving Power Flow Convergence by Newton Raphson with a Levenberg-Marquardt Method. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA, USA, 20–24 July 2008. [Google Scholar] [CrossRef]
- Augugliaro, A.; Dusonchet, L.; Favuzza, S.; Ippolito, M.; Sanseverino, E.R. A backward sweep method for power flow solution in distribution networks. Int. J. Electr. Power Energy Syst. 2010, 32, 271–280. [Google Scholar] [CrossRef]
- Lourenco, E.M.; Loddi, T.; Tortelli, O.L. Unified Load Flow Analysis for Emerging Distribution Systems. In Proceedings of the 2010 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenburg, Sweden, 11–13 October 2010. [Google Scholar] [CrossRef]
- Jesus, P.D.O.D.; Alvarez, M.; Yusta, J. Distribution power flow method based on a real quasi-symmetric matrix. Electr. Power Syst. Res. 2013, 95, 148–159. [Google Scholar] [CrossRef]
- Tortelli, O.L.; Lourenco, E.M.; Garcia, A.V.; Pal, B.C. Fast Decoupled Power Flow to Emerging Distribution Systems via Complex pu Normalization. IEEE Trans. Power Syst. 2015, 30, 1351–1358. [Google Scholar] [CrossRef]
- Sianipar, G.H.M.; Setia, G.A.; Santosa, M.F. Implementation of Axis Rotation Fast Decoupled Load Flow on Distribution Systems. In Proceedings of the 2016 3rd Conference on Power Engineering and Renewable Energy (ICPERE), Yogyakarta, Indonesia, 29–30 November 2016. [Google Scholar] [CrossRef]
- Garces, A. A Linear Three-Phase Load Flow for Power Distribution Systems. IEEE Trans. Power Syst. 2016, 31, 827–828. [Google Scholar] [CrossRef]
- Bolognani, S.; Zampieri, S. On the Existence and Linear Approximation of the Power Flow Solution in Power Distribution Networks. IEEE Trans. Power Syst. 2016, 31, 163–172. [Google Scholar] [CrossRef] [Green Version]
- Shen, T.; Li, Y.; Xiang, J. A Graph-Based Power Flow Method for Balanced Distribution Systems. Energies 2018, 11, 511. [Google Scholar] [CrossRef] [Green Version]
- Marini, A.; Mortazavi, S.; Piegari, L.; Ghazizadeh, M.S. An efficient graph-based power flow algorithm for electrical distribution systems with a comprehensive modeling of distributed generations. Electr. Power Syst. Res. 2019, 170, 229–243. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W. On the numerical analysis based on successive approximations for power flow problems in AC distribution systems. Electr. Power Syst. Res. 2020, 187, 106454. [Google Scholar] [CrossRef]
- Bocanegra, S.Y.; Gil-Gonzalez, W.; Montoya, O.D. A New Iterative Power Flow Method for AC Distribution Grids with Radial and Mesh Topologies. In Proceedings of the 2020 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 4–6 November 2020. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Giral, D.A. On the Matricial Formulation of Iterative Sweep Power Flow for Radial and Meshed Distribution Networks with Guarantee of Convergence. Appl. Sci. 2020, 10, 5802. [Google Scholar] [CrossRef]
- Herrera-Briñez, M.C.; Montoya, O.D.; Molina-Cabrera, A.; Grisales-Noreña, L.F.; Giral-Ramirez, D.A. Convergence analysis of the triangular-based power flow method for AC distribution grids. Int. J. Electr. Comput. Eng. (IJECE) 2021, 12. [Google Scholar] [CrossRef]
- Montoya, O.D.; Giraldo, J.S.; Grisales-Noreña, L.F.; Chamorro, H.R.; Alvarado-Barrios, L. Accurate and Efficient Derivative-Free Three-Phase Power Flow Method for Unbalanced Distribution Networks. Computation 2021, 9, 61. [Google Scholar] [CrossRef]
- Montoya, O.D.; Rueda, L.E.; Gil-Gonzalez, W.; Molina-Cabrera, A.; Chamorro, H.R.; Soleimani, M. On the Power Flow Solution in AC Distribution Networks Using the Laurent’s Series Expansion. In Proceedings of the 2021 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 2–5 February 2021. [Google Scholar] [CrossRef]
- Sereeter, B.; Markensteijn, A.; Kootte, M.; Vuik, C. A novel linearized power flow approach for transmission and distribution networks. J. Comput. Appl. Math. 2021, 394, 113572. [Google Scholar] [CrossRef]
- Kawambwa, S.; Mwifunyi, R.; Mnyanghwalo, D.; Hamisi, N.; Kalinga, E.; Mvungi, N. An improved backward/forward sweep power flow method based on network tree depth for radial distribution systems. J. Electr. Syst. Inf. Technol. 2021, 8, 1–18. [Google Scholar] [CrossRef]
- Deng, J.J.; Chiang, H.D. Convergence Region of Newton Iterative Power Flow Method: Numerical Studies. J. Appl. Math. 2013, 2013, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Kulworawanichpong, T. Simplified Newton–Raphson power-flow solution method. Int. J. Electr. Power Energy Syst. 2010, 32, 551–558. [Google Scholar] [CrossRef]
- Prakash, D.; Lakshminarayana, C. Optimal siting of capacitors in radial distribution network using Whale Optimization Algorithm. Alex. Eng. J. 2017, 56, 499–509. [Google Scholar] [CrossRef] [Green Version]
- Molzahn, D.K.; Hiskens, I.A. Convex Relaxations of Optimal Power Flow Problems: An Illustrative Example. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 650–660. [Google Scholar] [CrossRef] [Green Version]
- Garces, A. A quadratic approximation for the optimal power flow in power distribution systems. Electr. Power Syst. Res. 2016, 130, 222–229. [Google Scholar] [CrossRef] [Green Version]
- Bahrami, S.; Therrien, F.; Wong, V.W.; Jatskevich, J. Semidefinite Relaxation of Optimal Power Flow for AC–DC Grids. IEEE Trans. Power Syst. 2017, 32, 289–304. [Google Scholar] [CrossRef]
- Molzahn, D.K.; Holzer, J.T.; Lesieutre, B.C.; DeMarco, C.L. Implementation of a Large-Scale Optimal Power Flow Solver Based on Semidefinite Programming. IEEE Trans. Power Syst. 2013, 28, 3987–3998. [Google Scholar] [CrossRef]
- Yuan, Z.; Hesamzadeh, M.R. Second-order cone AC optimal power flow: Convex relaxations and feasible solutions. J. Mod. Power Syst. Clean Energy 2018, 7, 268–280. [Google Scholar] [CrossRef] [Green Version]
- Chowdhury, T.; Kamalasadan, S. A New Second-Order Cone Programming Model for Voltage Control of Power Distribution System with Inverter Based Distributed Generation. IEEE Trans. Ind. Appl. 2021, in press. [Google Scholar] [CrossRef]
- Ferreira, L. Tellegen’s theorem and power systems-new load flow equations, new solution methods. IEEE Trans. Circuits Syst. 1990, 37, 519–526. [Google Scholar] [CrossRef]
- Issicaba, D.; Coelho, J. Evaluation of the Forward-Backward Sweep Load Flow Method using the Contraction Mapping Principle. Int. J. Electr. Comput. Eng. (IJECE) 2016, 6, 3229. [Google Scholar] [CrossRef]
- Wang, X.F.; Song, Y.; Irving, M. Modern Power Systems Analysis; Springer: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Zhang, D.; Fu, Z.; Zhang, L. An improved TS algorithm for loss-minimum reconfiguration in large-scale distribution systems. Electr. Power Syst. Res. 2007, 77, 685–694. [Google Scholar] [CrossRef]
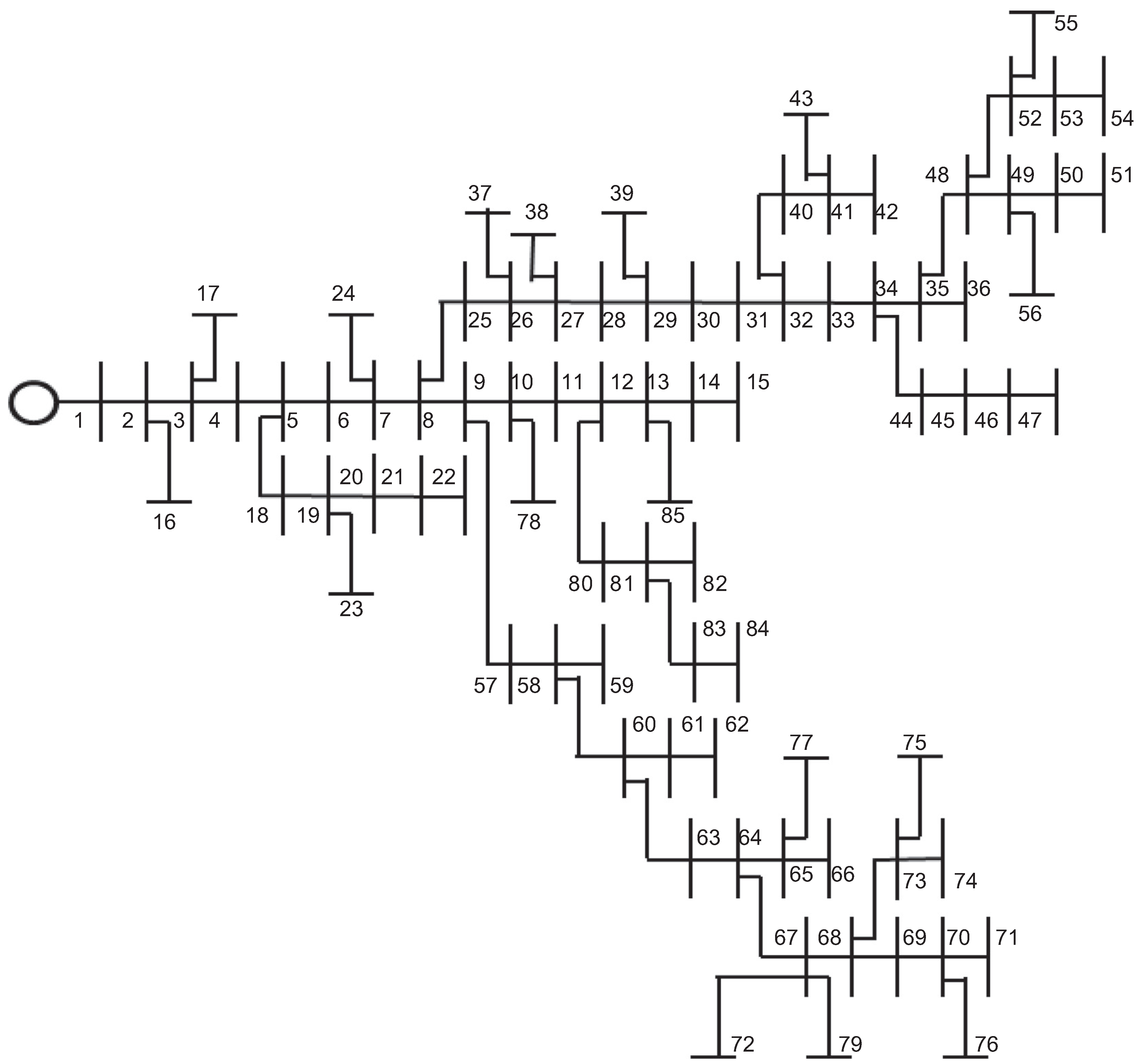
| Solution Methodology | Year | Type | Refs. |
|---|---|---|---|
| Power flow solution using multi-port compensation technique for radial and meshed grids | 1988 | DF | [7] |
| Backward/forward power flow method considering voltage-controlled nodes | 1995 | DF | [8] |
| Current injection power flow method for radial and meshed distribution networks | 1996 | DF | [9] |
| Improved Gauss–Seidel power flow method for distribution systems | 2002 | DF | [10] |
| Direct power flow solution using LU matrix decomposition | 2003 | DF | [11] |
| Improved Newton–Raphson method with Broyden’s method for distribution grids | 2008 | DB | [12] |
| Improved Newton–Raphson method with Levenberg–Marquardt method for distribution grids | 2008 | DB | [13] |
| Backward/forward power flow solution for radial and weakly meshed distribution grids | 2010 | DF | [14] |
| Fast decoupled power flow method for emerging distribution grids | 2010 | DB | [15] |
| Triangular formulation based on a real quasi-symmetry matrix | 2013 | DF | [16] |
| Fast decoupled power flow method for distribution grids | 2015 | DB | [17] |
| Axis rotation fast decoupled load flow on distribution systems | 2016 | DB | [18] |
| Linear power flow approximation with hyperbolic linearization | 2016 | DB | [19] |
| Linear power flow approximation based on the admittance matrix | 2016 | DB | [20] |
| Graph-based power flow using an incidence matrix | 2018 | DF | [21] |
| Graph-based power flow using an upper-triangular matrix | 2019 | DF | [22] |
| Successive approximations power flow method that guarantees convergence | 2020 | DF | [23] |
| Hyperbolic recursive linearization power flow method | 2020 | DB | [24] |
| Matricial backward/forward power flow method that guarantees convergence and includes voltage-controlled nodes | 2020 | DF | [25] |
| Triangular-based power flow method that guarantees convergence | 2021 | DF | [26,27] |
| Product linearization power flow method | 2021 | DB | [28] |
| Linearized power flow approach for transmission and distribution networks | 2021 | DB | [29] |
| k | m | () | () | (kW) | (kW) | k | m | () | () | (kW) | (kW) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0.1170 | 0.0480 | 230 | 142.5 | 18 | 19 | 0.2079 | 0.0473 | 230 | 142.5 |
| 2 | 3 | 0.1073 | 0.0440 | 0 | 0 | 19 | 20 | 0.1890 | 0.0430 | 230 | 142.5 |
| 3 | 4 | 0.1645 | 0.0457 | 230 | 142.5 | 20 | 21 | 0.1890 | 0.0430 | 230 | 142.5 |
| 4 | 5 | 0.1495 | 0.0415 | 230 | 142.5 | 21 | 22 | 0.2620 | 0.0450 | 230 | 142.5 |
| 5 | 6 | 0.1495 | 0.0415 | 0 | 0 | 22 | 23 | 0.2620 | 0.0450 | 230 | 142.5 |
| 6 | 7 | 0.3144 | 0.0540 | 0 | 0 | 23 | 24 | 0.3144 | 0.0540 | 230 | 142.5 |
| 7 | 8 | 0.2096 | 0.0360 | 230 | 142.5 | 24 | 25 | 0.2096 | 0.0360 | 230 | 142.5 |
| 8 | 9 | 0.3144 | 0.0540 | 230 | 142.5 | 25 | 26 | 0.1310 | 0.0225 | 230 | 142.5 |
| 9 | 10 | 0.2096 | 0.0360 | 0 | 0 | 26 | 27 | 0.1048 | 0.0180 | 137 | 85 |
| 10 | 11 | 0.1310 | 0.0225 | 230 | 142.5 | 7 | 28 | 0.1572 | 0.0270 | 75 | 48 |
| 11 | 12 | 0.1048 | 0.0180 | 137 | 84 | 28 | 29 | 0.1572 | 0.0270 | 75 | 48 |
| 3 | 13 | 0.1572 | 0.0270 | 72 | 45 | 29 | 30 | 0.1572 | 0.0270 | 75 | 48 |
| 13 | 14 | 0.2096 | 0.0360 | 72 | 45 | 10 | 31 | 0.1572 | 0.0270 | 57 | 34.5 |
| 14 | 15 | 0.1048 | 0.0180 | 72 | 45 | 31 | 32 | 0.2096 | 0.0360 | 57 | 34.5 |
| 15 | 16 | 0.0524 | 0.0090 | 13.5 | 7.5 | 32 | 33 | 0.1572 | 0.0270 | 57 | 34.5 |
| 6 | 17 | 0.1794 | 0.0498 | 230 | 142.5 | 33 | 34 | 0.1048 | 0.0180 | 57 | 34.5 |
| 17 | 18 | 0.1645 | 0.0457 | 230 | 142.5 | — | — | — | — | — | — |
| k | m | () | () | (kW) | (kW) | k | m | () | () | (kW) | (kW) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0.108 | 0.075 | 0 | 0 | 34 | 44 | 1.002 | 0.416 | 35.28 | 35.99 |
| 2 | 3 | 0.163 | 0.112 | 0 | 0 | 44 | 45 | 0.911 | 0.378 | 35.28 | 35.99 |
| 3 | 4 | 0.217 | 0.149 | 56 | 57.13 | 45 | 46 | 0.911 | 0.378 | 35.28 | 35.99 |
| 4 | 5 | 0.108 | 0.074 | 0 | 0 | 46 | 47 | 0.546 | 0.226 | 14 | 14.28 |
| 5 | 6 | 0.435 | 0.298 | 35.28 | 35.99 | 35 | 48 | 0.637 | 0.264 | 0 | 0 |
| 6 | 7 | 0.272 | 0.186 | 0 | 0 | 48 | 49 | 0.182 | 0.075 | 0 | 0 |
| 7 | 8 | 1.197 | 0.820 | 35.28 | 35.99 | 49 | 50 | 0.364 | 0.151 | 36.28 | 37.01 |
| 8 | 9 | 0.108 | 0.074 | 0 | 0 | 50 | 51 | 0.455 | 0.189 | 56 | 57.13 |
| 9 | 10 | 0.598 | 0.410 | 0 | 0 | 48 | 52 | 1.366 | 0.567 | 0 | 0 |
| 10 | 11 | 0.544 | 0.373 | 56 | 57.13 | 52 | 53 | 0.455 | 0.189 | 35.28 | 35.99 |
| 11 | 12 | 0.544 | 0.373 | 0 | 0 | 53 | 54 | 0.546 | 0.226 | 56 | 57.13 |
| 12 | 13 | 0.598 | 0.410 | 0 | 0 | 52 | 55 | 0.546 | 0.226 | 56 | 57.13 |
| 13 | 14 | 0.272 | 0.186 | 35.28 | 35.99 | 49 | 56 | 0.546 | 0.226 | 14 | 14.28 |
| 14 | 15 | 0.326 | 0.223 | 35.28 | 35.99 | 9 | 57 | 0.273 | 0.113 | 56 | 57.13 |
| 2 | 16 | 0.728 | 0.302 | 35.28 | 35.99 | 57 | 58 | 0.819 | 0.340 | 0 | 0 |
| 3 | 17 | 0.455 | 0.189 | 112 | 114.26 | 58 | 59 | 0.182 | 0.075 | 56 | 57.13 |
| 5 | 18 | 0.820 | 0.340 | 56 | 57.13 | 58 | 60 | 0.546 | 0.226 | 56 | 57.13 |
| 18 | 19 | 0.637 | 0.264 | 56 | 57.13 | 60 | 61 | 0.728 | 0.302 | 56 | 57.13 |
| 19 | 20 | 0.455 | 0.189 | 35.28 | 35.99 | 61 | 62 | 1.002 | 0.415 | 56 | 57.13 |
| 20 | 21 | 0.819 | 0.340 | 35.28 | 35.99 | 60 | 63 | 0.182 | 0.075 | 14 | 14.28 |
| 21 | 22 | 1.548 | 0.642 | 35.28 | 35.99 | 63 | 64 | 0.728 | 0.302 | 0 | 0 |
| 19 | 23 | 0.182 | 0.075 | 56 | 57.13 | 64 | 65 | 0.182 | 0.075 | 0 | 0 |
| 7 | 24 | 0.910 | 0.378 | 35.28 | 35.99 | 65 | 66 | 0.182 | 0.075 | 56 | 57.13 |
| 8 | 25 | 0.455 | 0.189 | 35.28 | 35.99 | 64 | 67 | 0.455 | 0.189 | 0 | 0 |
| 25 | 26 | 0.364 | 0.151 | 56 | 57.13 | 67 | 68 | 0.910 | 0.378 | 0 | 0 |
| 26 | 27 | 0.546 | 0.226 | 0 | 0 | 68 | 69 | 1.092 | 0.453 | 56 | 57.13 |
| 27 | 28 | 0.273 | 0.113 | 56 | 57.13 | 69 | 70 | 0.455 | 0.189 | 0 | 0 |
| 28 | 29 | 0.546 | 0.226 | 0 | 0 | 70 | 71 | 0.546 | 0.226 | 35.28 | 35.99 |
| 29 | 30 | 0.546 | 0.226 | 35.28 | 35.99 | 67 | 72 | 0.182 | 0.075 | 56 | 57.13 |
| 30 | 31 | 0.273 | 0.113 | 35.28 | 35.99 | 68 | 73 | 1.184 | 0.491 | 0 | 0 |
| 31 | 32 | 0.182 | 0.075 | 0 | 0 | 73 | 74 | 0.273 | 0.113 | 56 | 57.13 |
| 32 | 33 | 0.182 | 0.075 | 14 | 14.28 | 73 | 75 | 1.002 | 0.416 | 35.28 | 35.99 |
| 33 | 34 | 0.819 | 0.340 | 0 | 0 | 70 | 76 | 0.546 | 0.226 | 56 | 57.13 |
| 34 | 35 | 0.637 | 0.264 | 0 | 0 | 65 | 77 | 0.091 | 0.037 | 14 | 14.28 |
| 35 | 36 | 0.182 | 0.075 | 35.28 | 35.99 | 10 | 78 | 0.637 | 0.264 | 56 | 57.13 |
| 26 | 37 | 0.364 | 0.151 | 56 | 57.13 | 67 | 79 | 0.546 | 0.226 | 35.28 | 35.99 |
| 27 | 38 | 1.002 | 0.416 | 56 | 57.13 | 12 | 80 | 0.728 | 0.302 | 56 | 57.13 |
| 29 | 39 | 0.546 | 0.226 | 56 | 57.13 | 80 | 81 | 0.364 | 0.151 | 0 | 0 |
| 32 | 40 | 0.455 | 0.189 | 35.28 | 35.99 | 81 | 82 | 0.091 | 0.037 | 56 | 57.13 |
| 40 | 41 | 1.002 | 0.416 | 0 | 0 | 81 | 83 | 1.092 | 0.453 | 35.28 | 35.99 |
| 41 | 42 | 0.273 | 0.113 | 35.28 | 35.99 | 83 | 84 | 1.002 | 0.416 | 14 | 14.28 |
| 41 | 43 | 0.455 | 0.189 | 35.28 | 35.99 | 13 | 85 | 0.819 | 0.340 | 35.28 | 35.99 |
| Method | Power Losses (kW) | No. of Iterations | Proc. Time (ms) |
|---|---|---|---|
| Newton–Raphson (NR) | 4 | 2.9929 | |
| Successive approximations (SA) | 8 | 0.1893 | |
| Matricial backward/forward (MBF) | 8 | 0.6405 | |
| Triangular-based (TB) | 221.752357 | 8 | 0.1662 |
| Product linearization (PL) | 4 | 0.9057 | |
| Hyperbolic linearization (HL) | 4 | 0.8568 | |
| Diagonal approximation (DA) | 8 | 0.8696 |
| Method | Power Losses (kW) | No. of Iterations | Proc. Time (ms) |
|---|---|---|---|
| Newton-Raphson (NR) | 5 | 20.8949 | |
| Successive approximations (SA) | 11 | 1.0791 | |
| Matricial backward/forward (MBF) | 11 | 2.7924 | |
| Triangular-based (TB) | 316.117496 | 11 | 0.5450 |
| Product linearization (PL) | 5 | 4.6976 | |
| Hyperbolic linearization (HL) | 4 | 3.3564 | |
| Diagonal approximation (DA) | 11 | 5.3632 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montoya, O.D.; Molina-Cabrera, A.; Hernández, J.C. A Comparative Study on Power Flow Methods Applied to AC Distribution Networks with Single-Phase Representation. Electronics 2021, 10, 2573. https://doi.org/10.3390/electronics10212573
Montoya OD, Molina-Cabrera A, Hernández JC. A Comparative Study on Power Flow Methods Applied to AC Distribution Networks with Single-Phase Representation. Electronics. 2021; 10(21):2573. https://doi.org/10.3390/electronics10212573
Chicago/Turabian StyleMontoya, Oscar Danilo, Alexander Molina-Cabrera, and Jesus C. Hernández. 2021. "A Comparative Study on Power Flow Methods Applied to AC Distribution Networks with Single-Phase Representation" Electronics 10, no. 21: 2573. https://doi.org/10.3390/electronics10212573
APA StyleMontoya, O. D., Molina-Cabrera, A., & Hernández, J. C. (2021). A Comparative Study on Power Flow Methods Applied to AC Distribution Networks with Single-Phase Representation. Electronics, 10(21), 2573. https://doi.org/10.3390/electronics10212573








