Active Contour Model Using Fast Fourier Transformation for Salient Object Detection
Abstract
1. Introduction
- A new hybrid active contour model using FFT comprising efficient features of the local region-based and global region-based fitting energies for salient object detection is proposed.
- Frequency domain has a property that can be used for discovering the salient object.
- Fourier force function is used to distinguish saliency objects from background for the active contour.
- Evaluating the proposed fast Fourier active contour model through a set of experiments using medical and synthetic images.
- The fast Fourier transform (FFT) is an effective process to design the discreate Fourier transform (DFT) time of series. The series takes advantages of the information that DFT coefficients can furnish iteratively to save considerable computational time.
- FFT not only set the computational problem, but also significantly reduces the associated round of errors computations.
- Frequency-based formulation provides simple characterization of the processing kernel.
- Automated smooth fitted curve during initialization time.
- Avoids re-initialization and re-iteration.
- Immediately draws curve on object boundary.
- Calculates accurate salient object with minimum complexity.
- Fast execution offers significant computational savings.
2. Related Work
2.1. Active Contour (Snake) Formulations
2.2. Chan-Vese Model
2.3. Active Contour with Selective Local and Global Segmentation Model
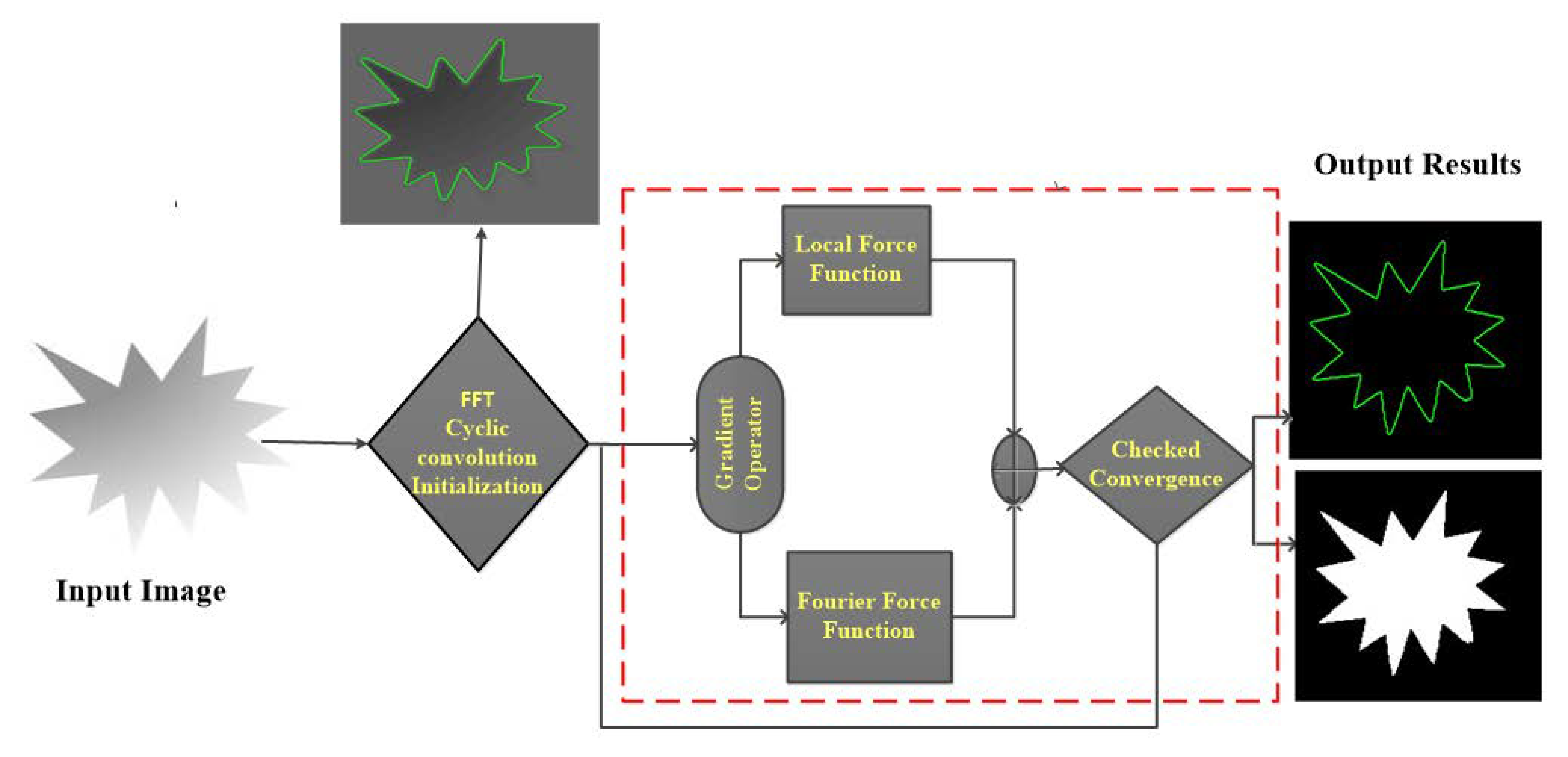
3. Solution Implementing Fast Fourier Transformation
3.1. Fourier Solution for Region Based Model
3.2. The Local Force from the Gradient
3.3. Fourier Force Function
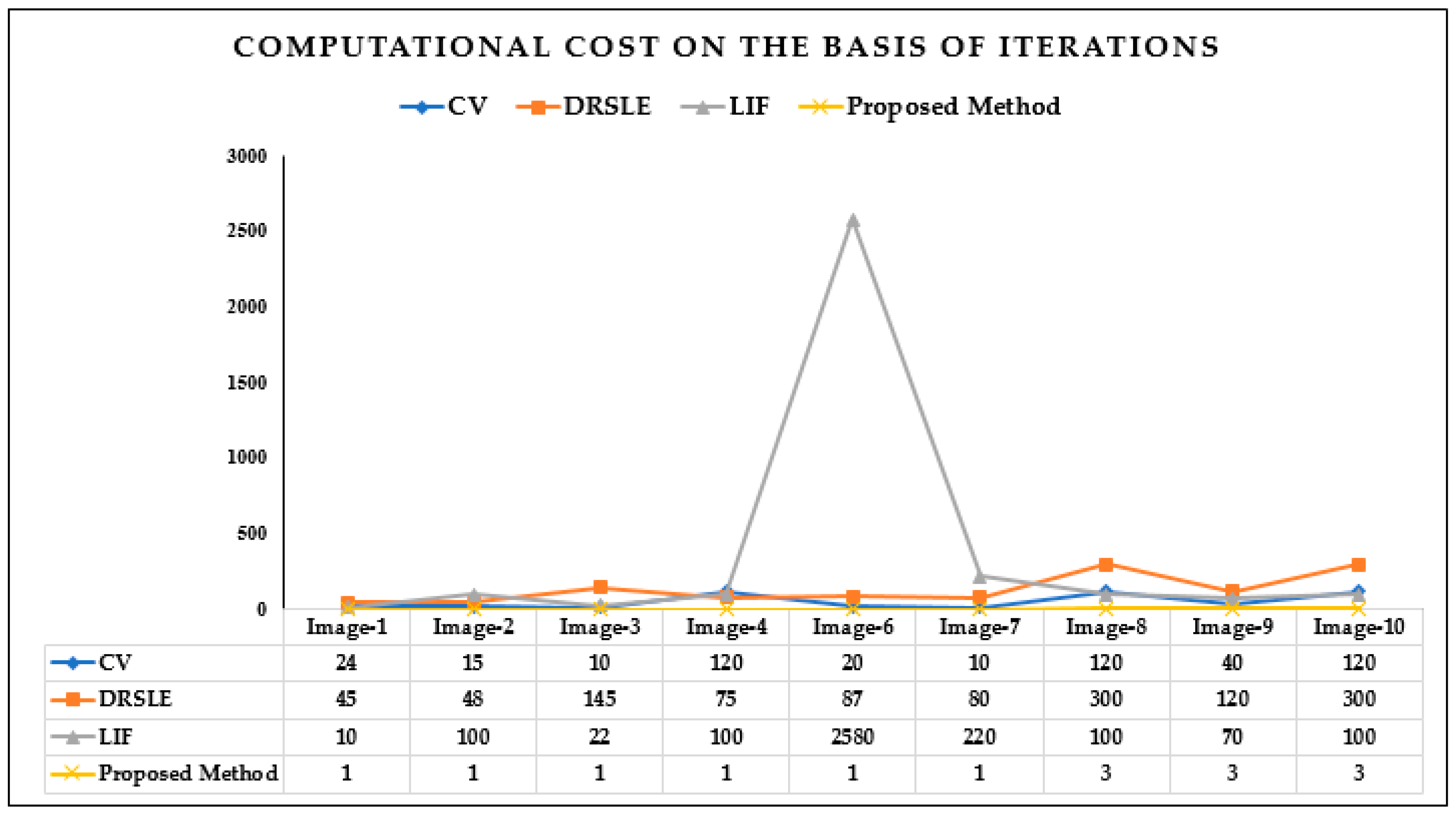
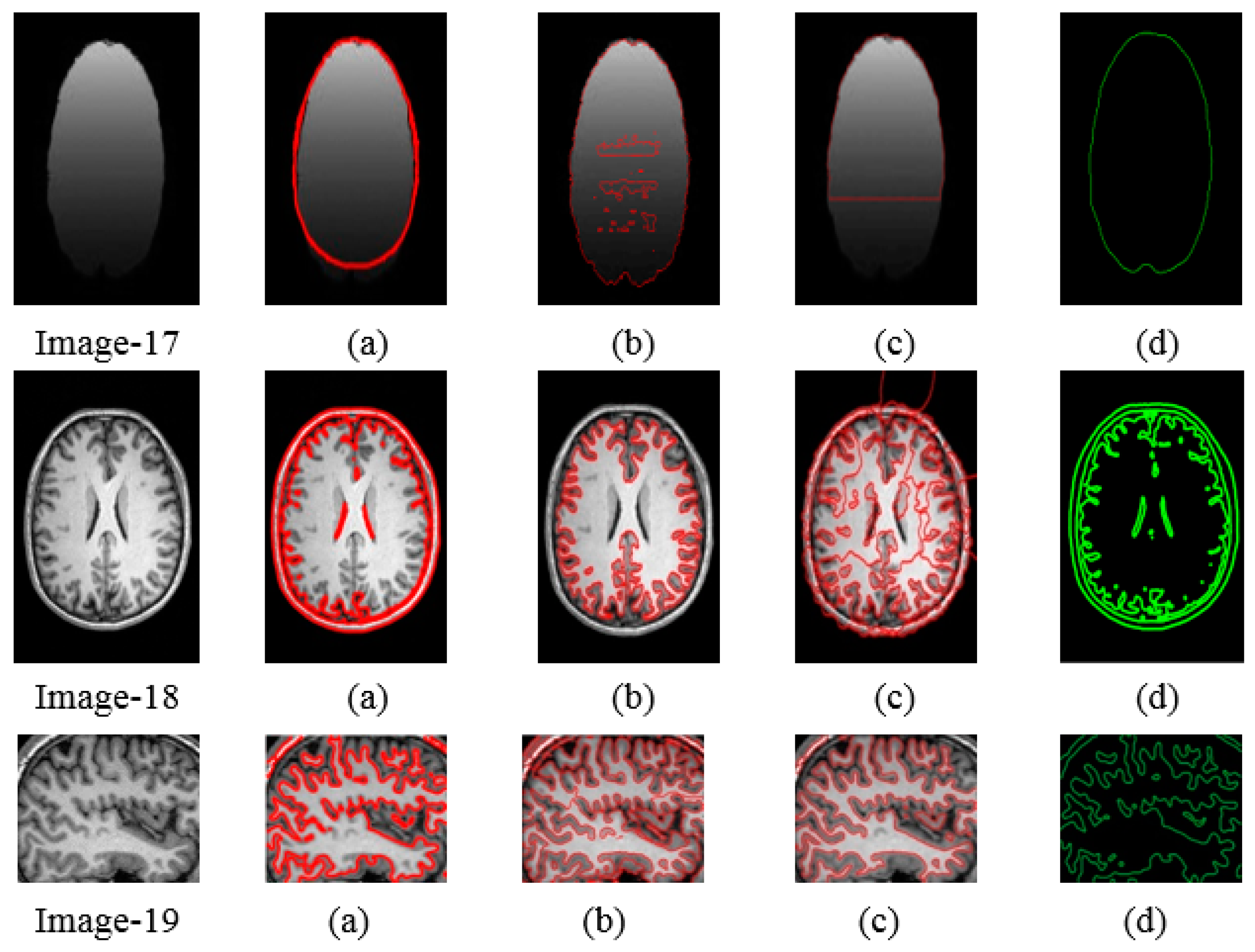
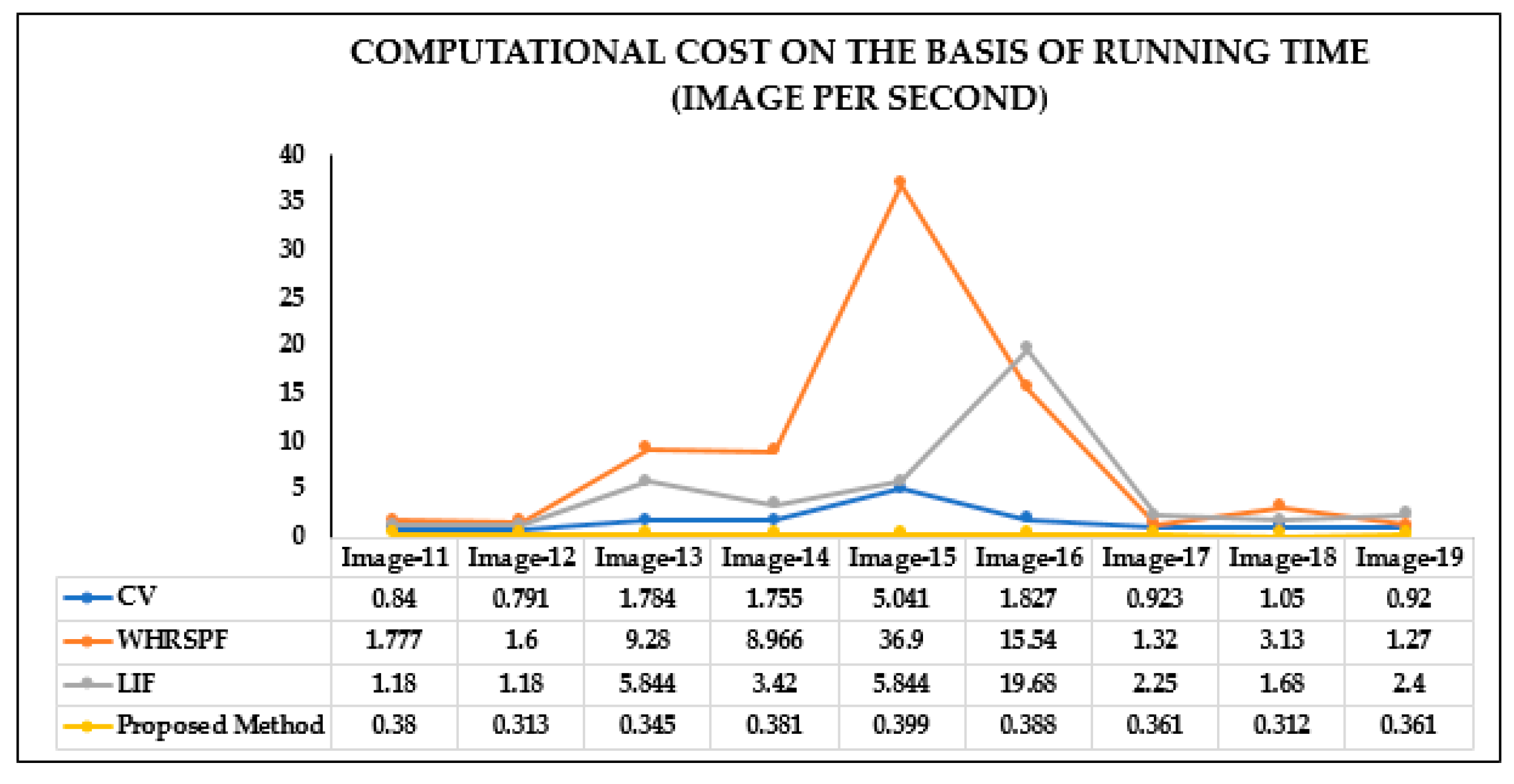
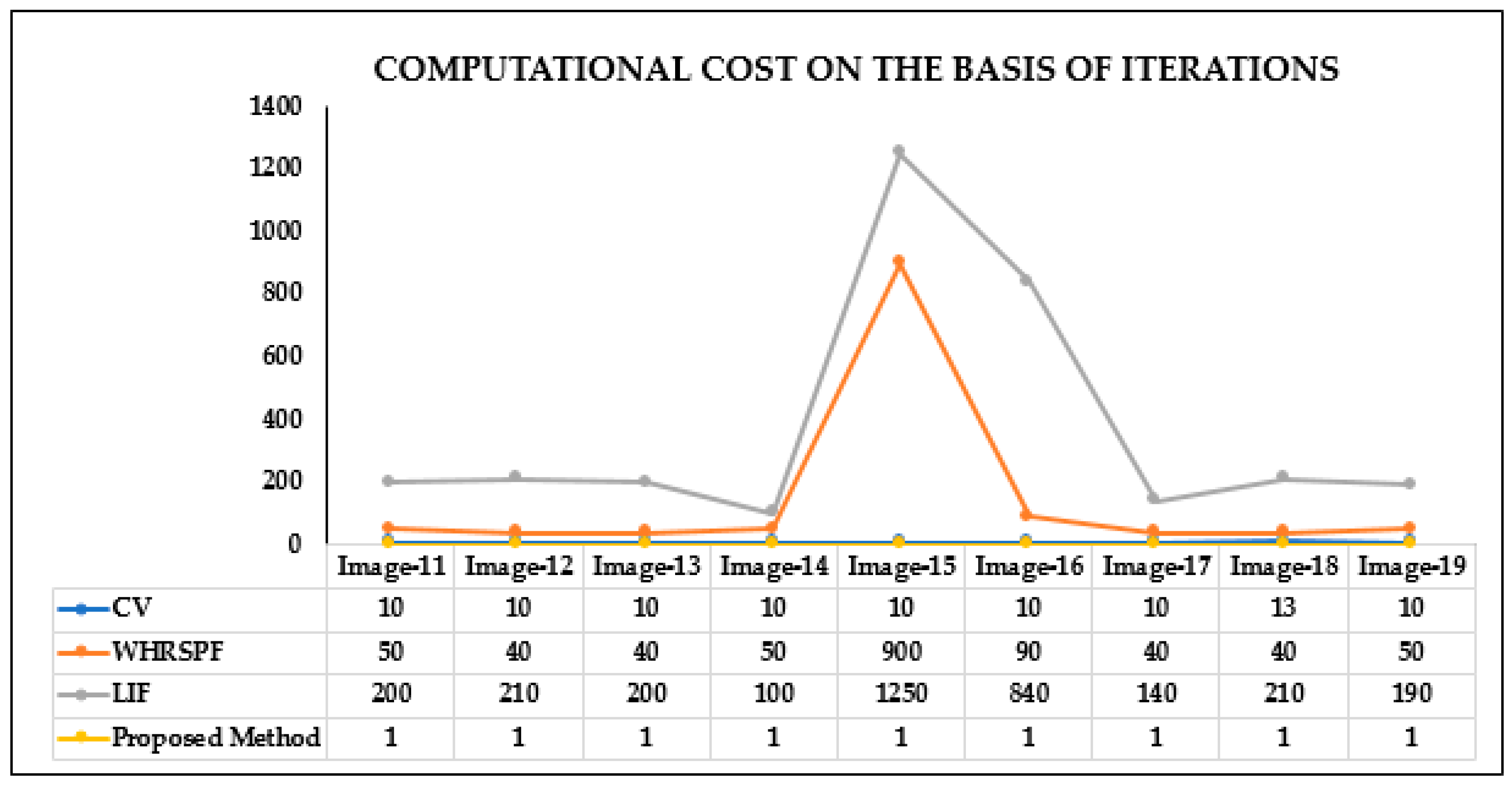
4. Experimental Results and Discussion
| Algorithm 1. The pseudo-code for the proposed algorithm. |
| Input: the input image I, the initial level set function . |
| Initialization: |
| 1: Initialization the Fourier level set function according to Equation (20). |
| 2: Initialize the related parameters: . |
| Repeat: |
| 3: For 1 to T do |
| 4: Compute Magnitude using Fourier external function with Equation (21). |
| 5: Compute Fourier force function on Equation (22). |
| 6: Update the level set function according to Equation (23). |
| 7: end for |
| 8: If converge |
| 9: end |
| 10: Output: The resultant salient object . |
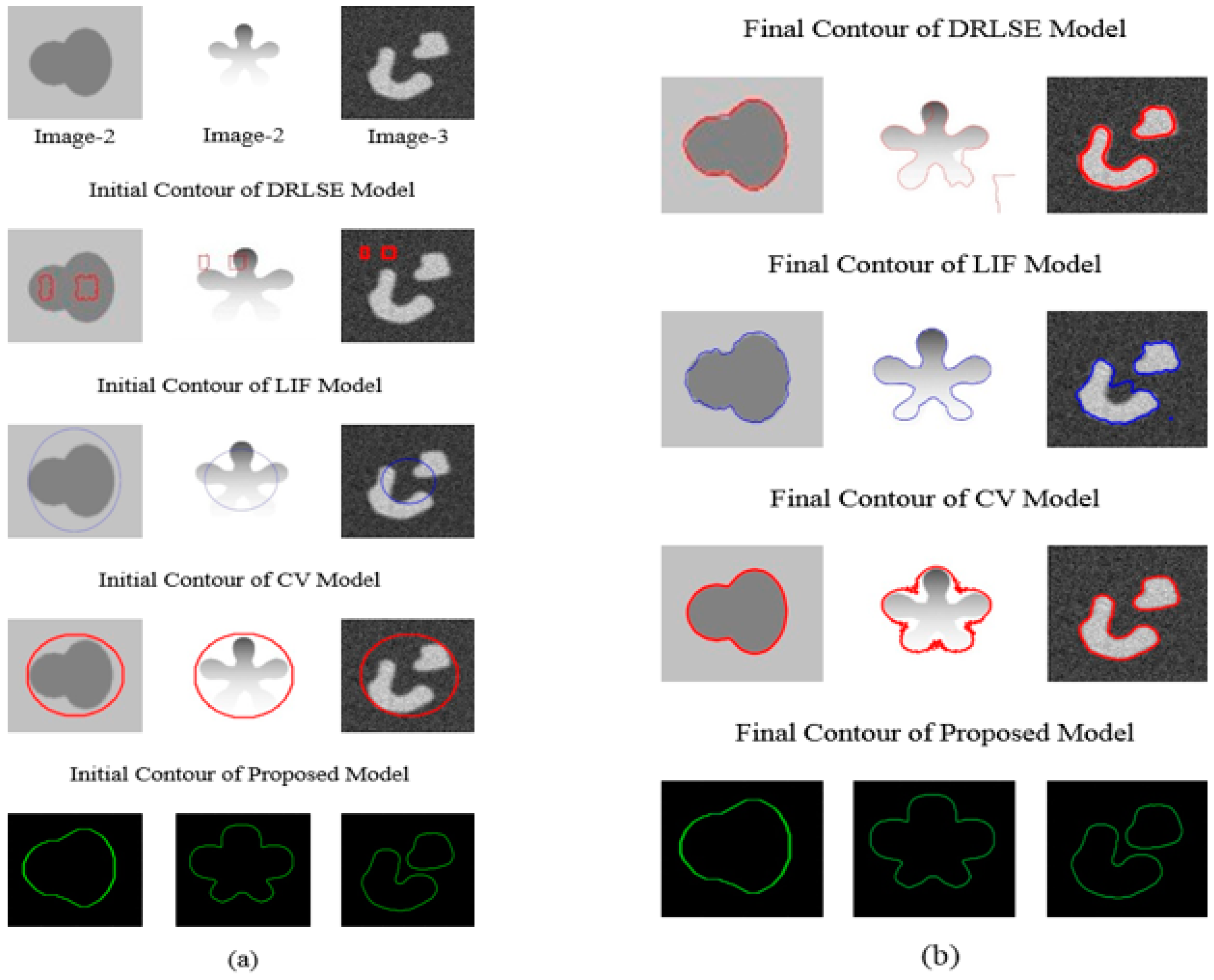
4.1. Robustness to Initial Curves
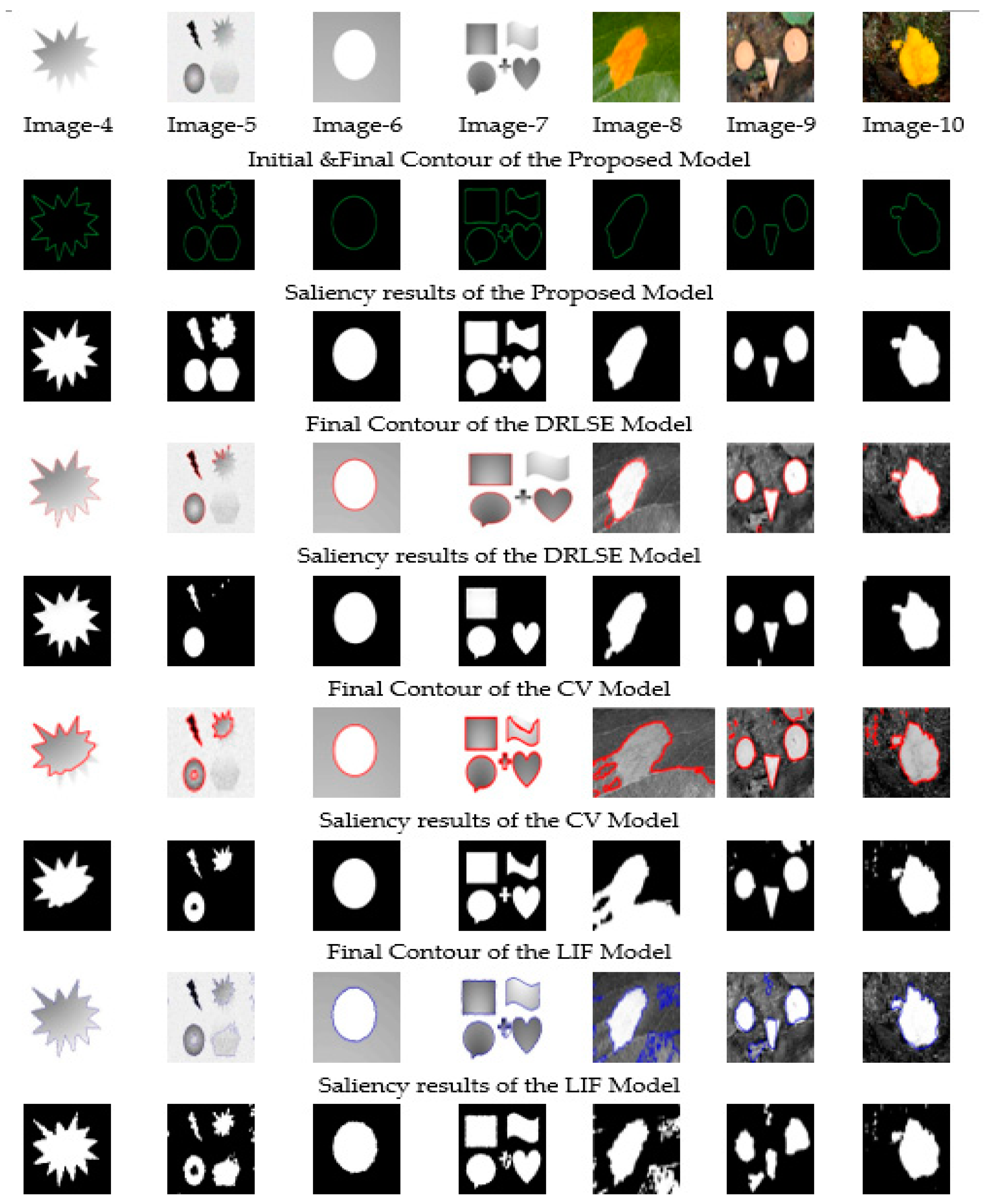
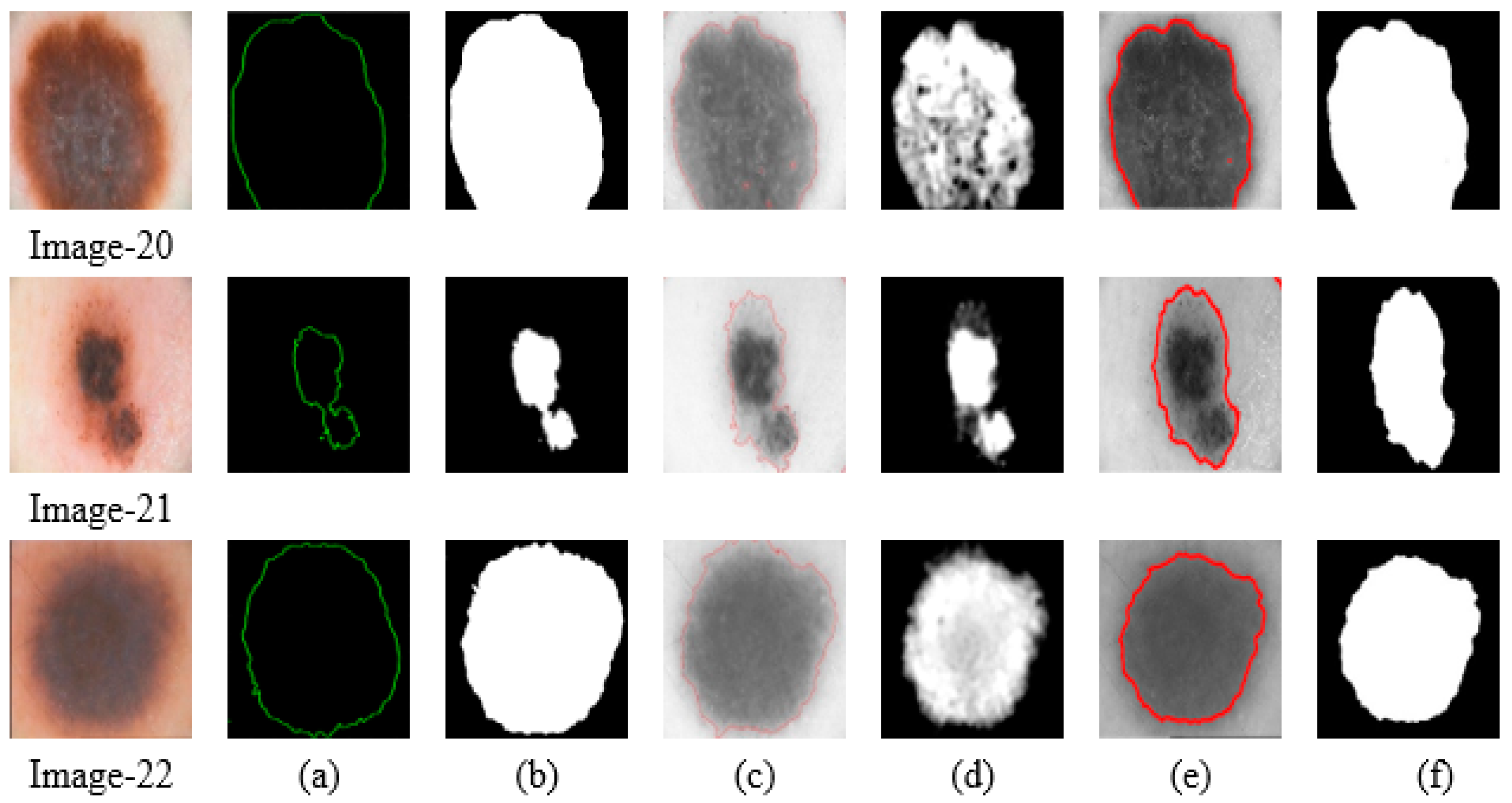
4.2. Qualitative Analysis
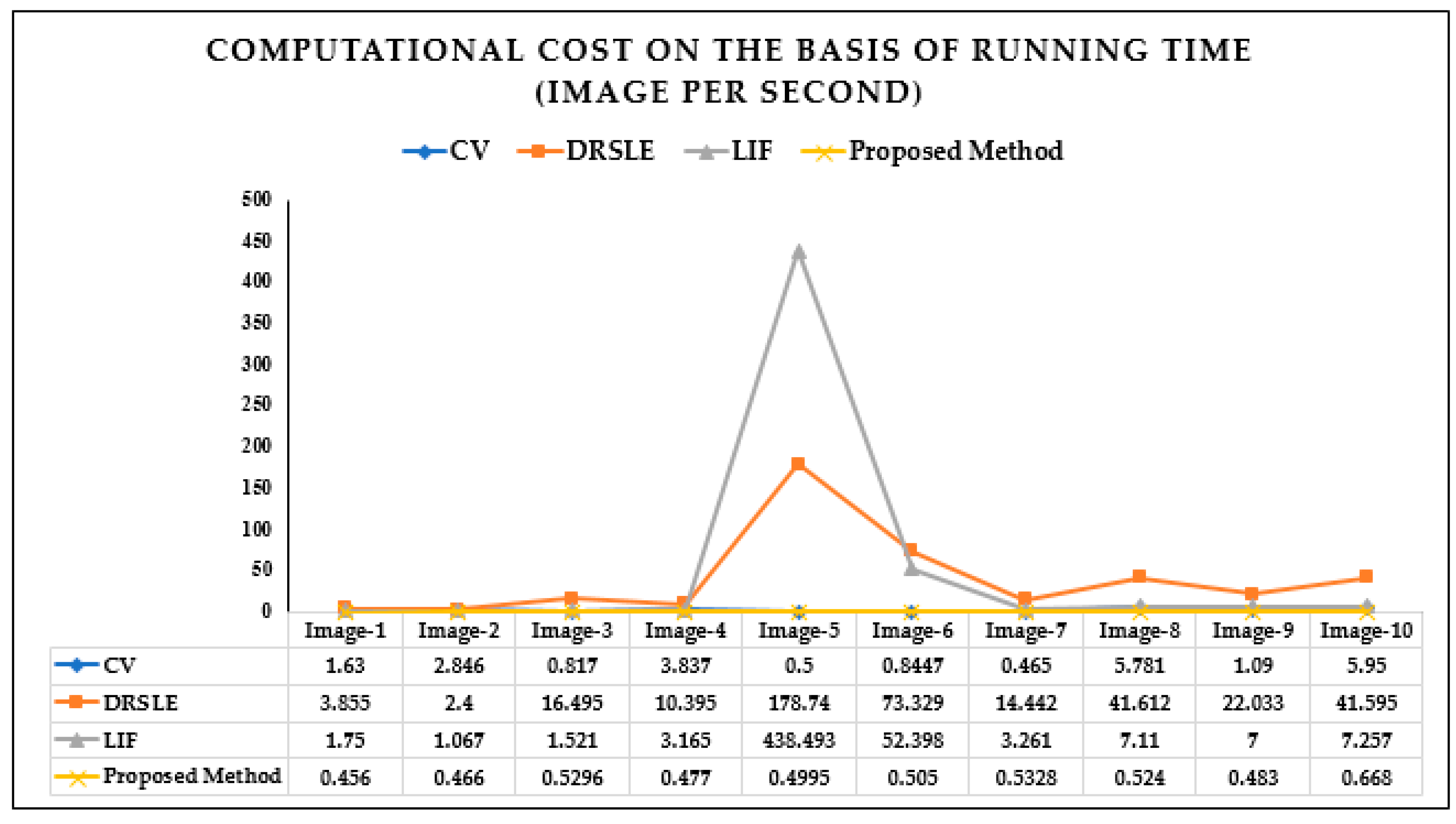
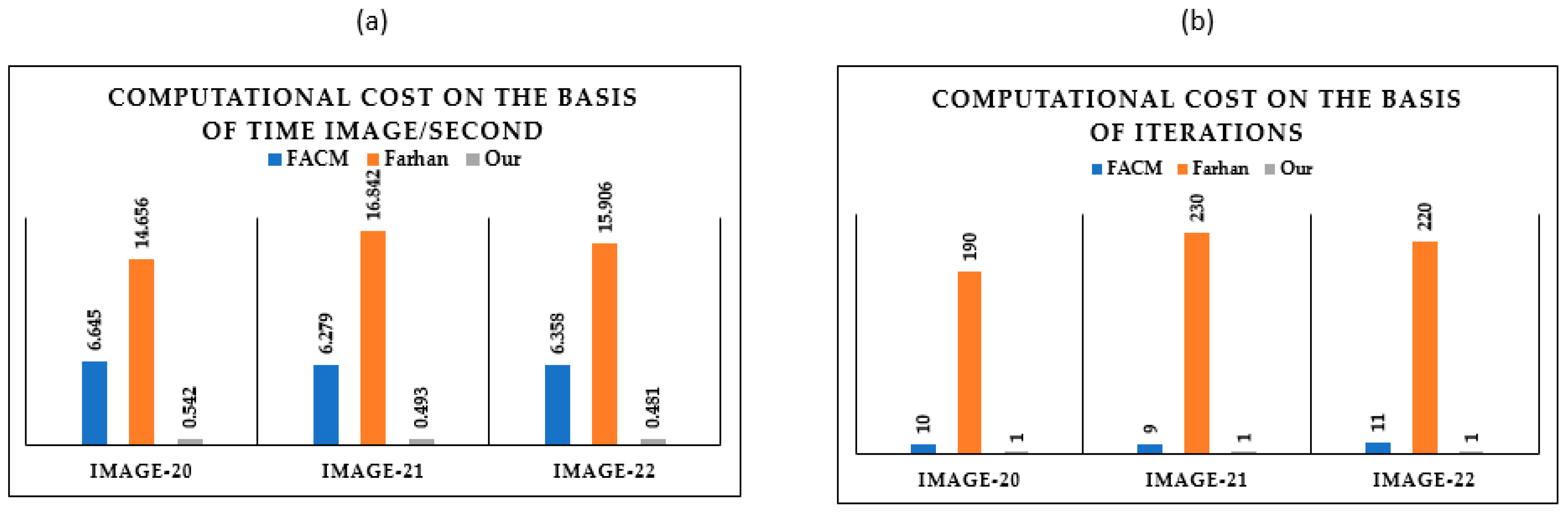
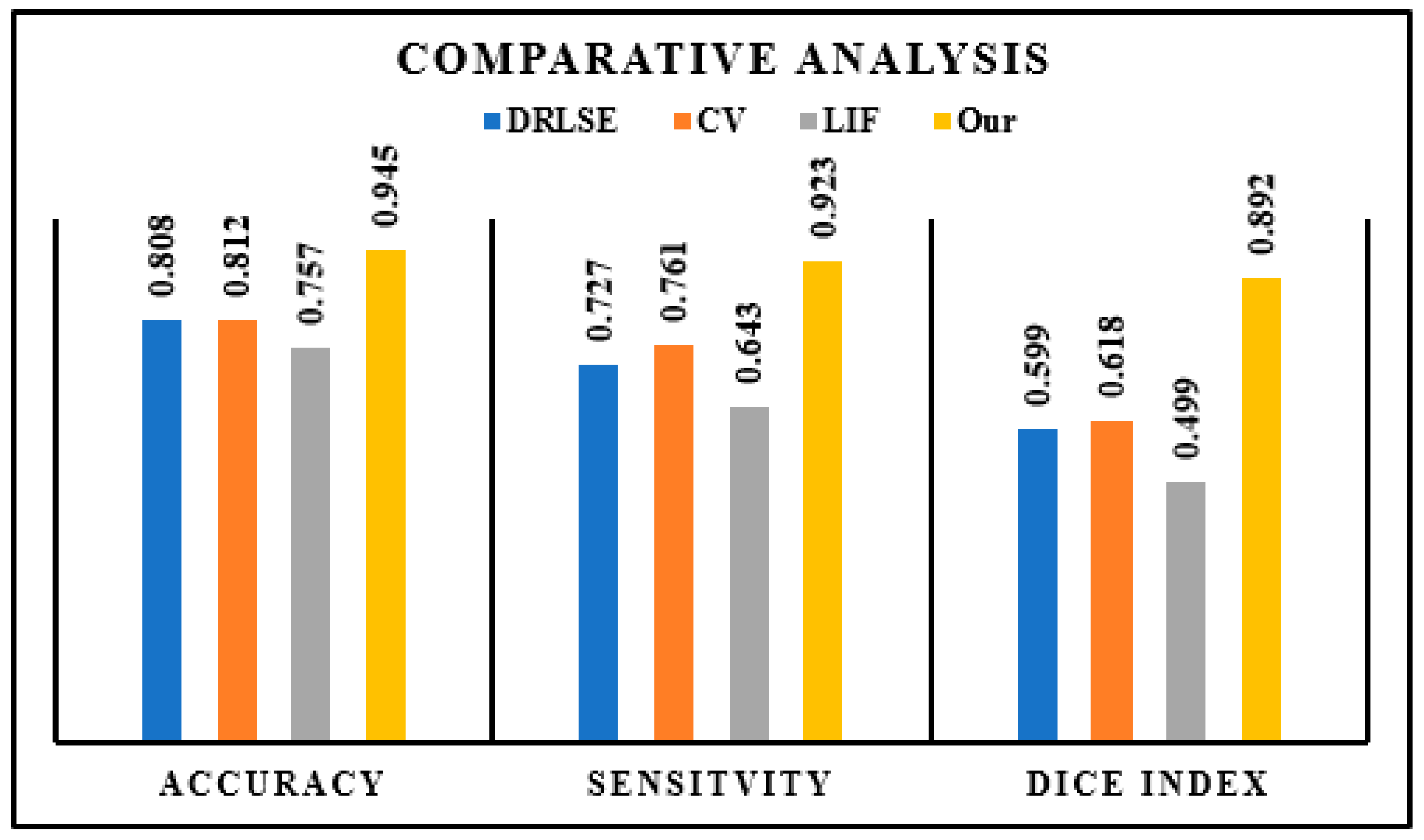
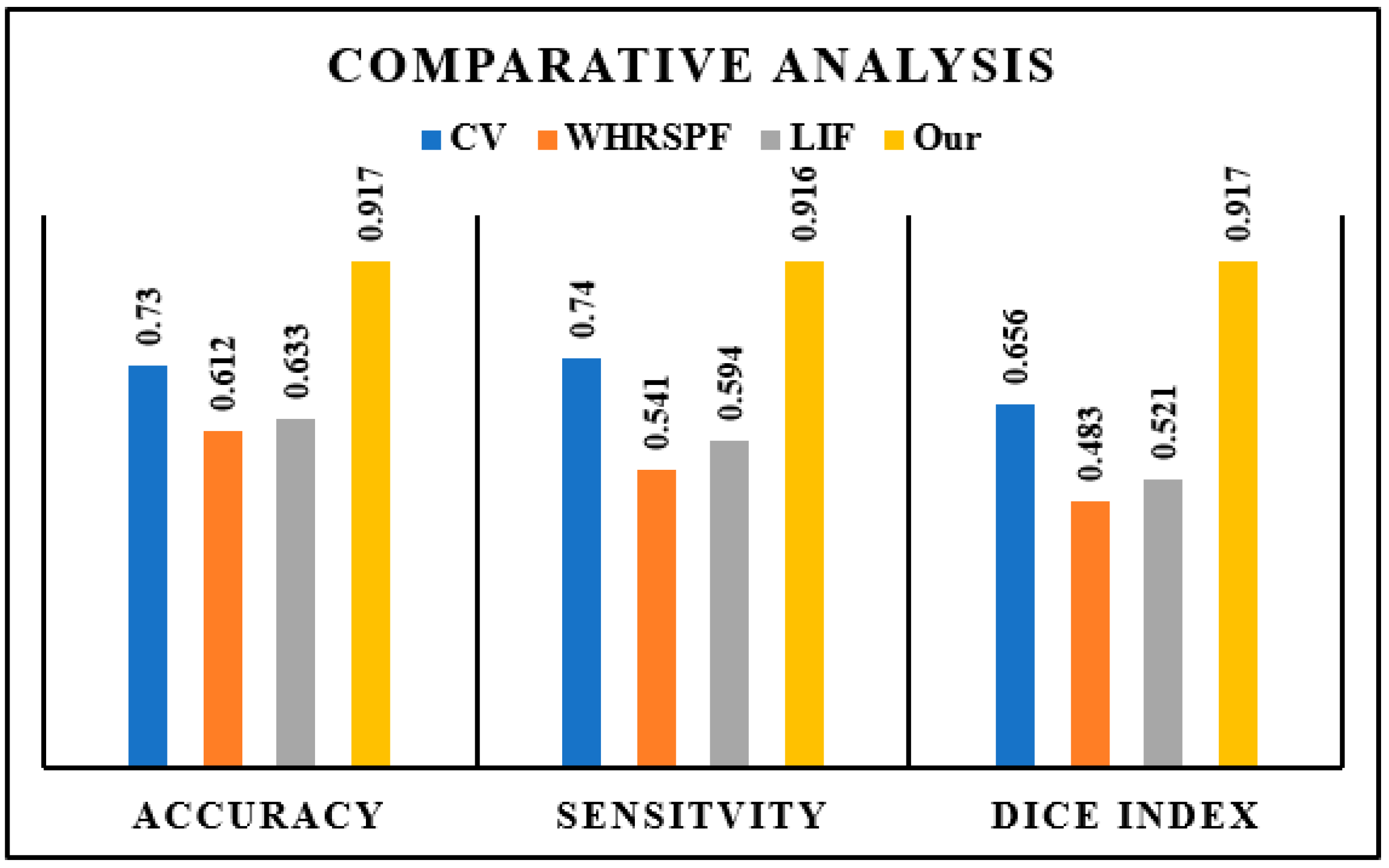
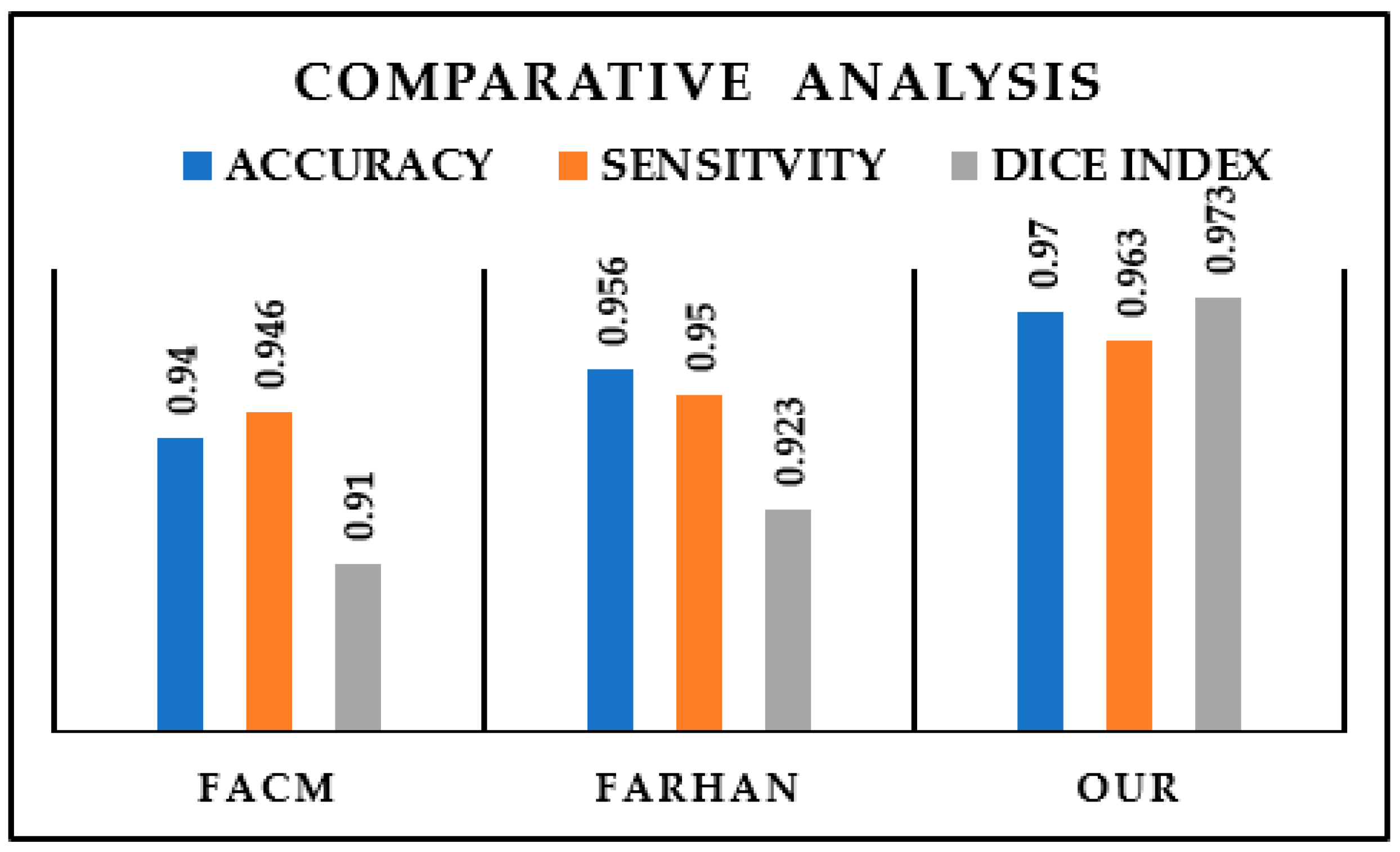
4.3. Quantitative Analysis
4.4. Robustness to Noisy Images
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Miao, J.; Huang, T.-Z.; Zhou, X.; Wang, Y.; Liu, J. Image segmentation based on an active contour model of partial image restoration with local cosine fitting energy. Inf. Sci. 2018, 447, 52–71. [Google Scholar] [CrossRef]
- Yang, X.; Jiang, X. A hybrid active contour model based on new edge-stop functions for image segmentation. Int. J. Ambient Comput. Intell. 2020, 11, 87–98. [Google Scholar] [CrossRef]
- Caselles, V.; Kimmel, R.; Sapiro, G. Geodesic active contours. Int. J. Comput. Vis. 1997, 22, 61–79. [Google Scholar] [CrossRef]
- Baswaraj, D.; Govardhan, A.; Premchand, P. Active Contours and Image Segmentation: The Current State of the Art. Available online: https://globaljournals.org/GJCST_Volume12/1-Active-Contours-and-Image-Segmentation.pdf (accessed on 19 August 2020).
- Kass, M.; Witkin, A.; Terzopoulos, D. Snakes: Active contour models. Int. J. Comput. Vis. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Metaxas, D.N. Physics-Based Deformable Models: Applications to Computer Vision, Graphics and Medical Imaging; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Cohen, L.D.; Cohen, I. Finite-element methods for active contour models and balloons for 2-D and 3-D images. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 1131–1147. [Google Scholar] [CrossRef]
- Han, B.; Wu, Y. Active contours driven by global and local weighted signed pressure force for image segmentation. Pattern Recognit. 2019, 88, 715–728. [Google Scholar] [CrossRef]
- Reddy, G.R.; Ramudu, K.; Yugander, P.; Rao, R.R. Fast global region based minimization of satellite and medical imagery with geometric active contour and level set evolution on noisy images. In Proceedings of the 2011 IEEE Recent Advances in Intelligent Computational Systems, Trivandrum, India, 22–24 September 2011; pp. 696–700. [Google Scholar]
- Xia, X.; Lin, T.; Chen, Z.; Xu, H. Salient object segmentation based on active contouring. PLoS ONE 2017, 12, e0188118. [Google Scholar] [CrossRef]
- Han, B.; Wu, Y. Active contour model for inhomogenous image segmentation based on Jeffreys divergence. Pattern Recognit. 2020, 107, 107520. [Google Scholar] [CrossRef]
- Qi, Y.; Yao, H.; Sun, X.; Sun, X.; Zhang, Y.; Huang, Q. Structure-aware multi-object discovery for weakly supervised tracking. In Proceedings of the 2014 IEEE International Conference on Image Processing (ICIP), Paris, France, 27–30 October 2014; pp. 466–470. [Google Scholar]
- Yi, Y.; Ni, F.; Ma, Y.; Zhu, X.; Qi, Y.; Qiu, R.; Zhao, S.; Li, F.; Wang, Y. High Performance Gesture Recognition via Effective and Efficient Temporal Modeling. In Proceedings of the IJCAI, Macao, China, 10–16 August 2019; pp. 1003–1009. [Google Scholar]
- Hong, Y.; Rodriguez-Opazo, C.; Qi, Y.; Wu, Q.; Gould, S. Language and visual entity relationship graph for agent navigation. Adv. Neural. Inf. Process. Syst. 2020, 33, 2. [Google Scholar]
- Zhang, L.; Zhang, S.; Jiang, F.; Qi, Y.; Zhang, J.; Guo, Y.; Zhou, H. BoMW: Bag of manifold words for one-shot learning gesture recognition from kinect. IEEE Trans. Circuits Syst. Video Technol. 2017, 28, 2562–2573. [Google Scholar] [CrossRef]
- Qi, Y.; Pan, Z.; Zhang, S.; van den Hengel, A.; Wu, Q. Object-and-action aware model for visual language navigation. In Proceedings of the European Conference on Computer Vision (ECCV), Glasgow, UK, 23–28 August 2020; pp. 23–28. [Google Scholar]
- Yang, Y.; Li, G.; Qi, Y.; Huang, Q. Release the Power of Online-Training for Robust Visual Tracking. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 7–12 February 2020; pp. 12645–12652. [Google Scholar]
- Qi, Y.; Wu, Q.; Anderson, P.; Wang, X.; Wang, W.Y.; Shen, C.; Hengel, A. REVERIE: Remote Embodied Visual Referring Expression in Real Indoor Environments. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 9982–9991. [Google Scholar]
- Qi, Y.; Qin, L.; Zhang, S.; Huang, Q.; Yao, H. Robust visual tracking via scale-and-state-awareness. Neurocomputing 2019, 329, 75–85. [Google Scholar] [CrossRef]
- Qi, Y.; Zhang, S.; Jiang, F.; Zhou, H.; Tao, D.; Li, X. Siamese local and global networks for robust face tracking. IEEE Trans. Image Process. 2020, 29, 9152–9164. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Wang, W.; Li, D.; Zou, B.; Yao, H. Object contour tracking via adaptive data-driven kernel. Eurasip J. Adv. Signal. Process. 2020, 2020, 1–13. [Google Scholar] [CrossRef]
- Zhang, K.; Song, H.; Zhang, L. Active contours driven by local image fitting energy. Pattern Recognit. 2010, 43, 1199–1206. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, L.; Song, H.; Zhou, W. Active contours with selective local or global segmentation: A new formulation and level set method. Image Vis. Comput. 2010, 28, 668–676. [Google Scholar] [CrossRef]
- Memon, A.A.; Soomro, S.; Shahid, M.T.; Munir, A.; Niaz, A.; Choi, K.N. Segmentation of Intensity-Corrupted Medical Images Using Adaptive Weight-Based Hybrid Active Contours. Comput. Math. Methods Med. 2020, 1–14, 1–14. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, J.; Zhang, S.; Liang, Y.; Gong, Y. Active contour model based on local and global intensity information for medical image segmentation. Neurocomputing 2016, 186, 107–118. [Google Scholar] [CrossRef]
- Fang, L.; Wang, X.; Wang, L. Multi-modal medical image segmentation based on vector-valued active contour models. Inf. Sci. 2020, 513, 504–518. [Google Scholar] [CrossRef]
- Sun, L.; Meng, X.; Xu, J.; Tian, Y. An image segmentation method using an active contour model based on improved SPF and LIF. Appl. Sci. 2018, 8, 2576. [Google Scholar] [CrossRef]
- Thanh, D.N.; Hien, N.N.; Prasath, V.S.; Hai, N.H. Automatic initial boundary generation methods based on edge detectors for the level set function of the Chan-Vese segmentation model and applications in biomedical image processing. In Frontiers in Intelligent Computing: Theory and Applications; Springer: New York, NY, USA, 2020; pp. 171–181. [Google Scholar]
- Li, Y.; Cao, G.; Wang, T.; Cui, Q.; Wang, B. A novel local region-based active contour model for image segmentation using Bayes theorem. Inf. Sci. 2020, 506, 443–456. [Google Scholar]
- Ksantini, R.; Boufama, B.; Memar, S. A new efficient active contour model without local initializations for salient object detection. Eurasip J. Image Video Process. 2013, 2013, 40. [Google Scholar] [CrossRef]
- Khan, U.S.; Zhang, X.; Su, Y. Active Contours in the Complex Domain for Salient Object Detection. Appl. Sci. 2020, 10, 3845. [Google Scholar] [CrossRef]
- Weruaga, L.; Verdu, R.; Morales, J. Frequency domain formulation of active parametric deformable models. IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 1568–1578. [Google Scholar] [CrossRef] [PubMed]
- Johnson, C.R., Jr.; Sethares, W.A.; Klein, A.G. Software Receiver Design: Build Your Own Digital Communication System in Five Easy Steps; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Takos, G. A Survey on Deep Learning Methods for Semantic Image Segmentation in Real-Time. arXiv 2020, arXiv:2009.12942. [Google Scholar]
- Shafiq, M.A.; Long, Z.; Di, H.; Regib, G.A.; Deriche, M. Fault detection using attention models based on visual saliency. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 1508–1512. [Google Scholar]
- Cui, X.; Liu, Q.; Metaxas, D. Temporal spectral residual: Fast motion saliency detection. In Proceedings of the 17th ACM International Conference on Multimedia, Seattle, WA, USA, 12–16 October 2009; pp. 617–620. [Google Scholar]
- Sumengen, B.; Manjunath, B. Edgeflow-Driven Variational Image Segmentation: Theory and Performance Evaluation. Available online: https://vision.ece.ucsb.edu/sites/default/files/publications/05TechRepBaris_0.pdf (accessed on 19 August 2020).
- Wang, B.; Gao, X.; Tao, D.; Li, X. A nonlinear adaptive level set for image segmentation. IEEE Trans. Cybern. 2014, 44, 418–428. [Google Scholar] [CrossRef]
- Caselles, V.; Catté, F.; Coll, T.; Dibos, F. A geometric model for active contours in image processing. Numer. Math. 1993, 66, 1–31. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, G.; Sun, X.; Zhou, X. Fast edge integration based active contours for color images. Comput. Electr. Eng. 2009, 35, 141–149. [Google Scholar] [CrossRef]
- Chan, T.; Vese, L. An active contour model without edges. In Proceedings of the International Conference on Scale-Space Theories in Computer Vision, Corfu, Greece, 26–27 September 1999; pp. 141–151. [Google Scholar]
- Lie, J.; Lysaker, M.; Tai, X.-C. A binary level set model and some applications to Mumford-Shah image segmentation. IEEE Trans. Image Process. 2006, 15, 1171–1181. [Google Scholar] [CrossRef]
- Cheng, M.-M.; Mitra, N.J.; Huang, X.; Torr, P.H.; Hu, S.-M. Global contrast based salient region detection. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 569–582. [Google Scholar] [CrossRef]
- Kichenassamy, S.; Kumar, A.; Olver, P.; Tannenbaum, A.; Yezzi, A. Conformal curvature flows: From phase transitions to active vision. Arch. Ration. Mech. Anal. 1996, 134, 275–301. [Google Scholar] [CrossRef]
- He, L.; Peng, Z.; Everding, B.; Wang, X.; Han, C.Y.; Weiss, K.L.; Wee, W.G. A comparative study of deformable contour methods on medical image segmentation. Image Vis. Comput. 2008, 26, 141–163. [Google Scholar] [CrossRef]
- Cremers, D.; Rousson, M.; Deriche, R. A review of statistical approaches to level set segmentation: Integrating color, texture, motion and shape. Int. J. Comput. Vis. 2007, 72, 195–215. [Google Scholar] [CrossRef]
- Itti, L.; Koch, C.; Niebur, E. A model of saliency-based visual attention for rapid scene analysis. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 1254–1259. [Google Scholar] [CrossRef]
- Wolfe, J.M. Guided search 2.0 a revised model of visual search. Psychon. Bull. Rev. 1994, 1, 202–238. [Google Scholar] [CrossRef] [PubMed]
- Tsai, A.; Yezzi, A.; Willsky, A.S. Curve evolution implementation of the Mumford-Shah functional for image segmentation, denoising, interpolation, and magnification. IEEE Trans. Image Process. 2001, 10, 1169–1186. [Google Scholar] [CrossRef] [PubMed]
- Vese, L.A.; Chan, T.F. A multiphase level set framework for image segmentation using the Mumford and Shah model. Int. J. Comput. Vis. 2002, 50, 271–293. [Google Scholar] [CrossRef]
- Ihlow, A.; Seiffert, U.; Gatersleben, I. Snakes revisited–speeding up active contour models using the Fast Fourier Transform. In Proceedings of the Eighth IASTED International Conference on Intelligent Systems and Control (ISC 2005), Cambridge, MA, USA, 31 October–2 November 2005; pp. 416–420. [Google Scholar]
- Chan, T.F.; Vese, L.A. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef]
- Mumford, D.; Shah, J. Optimal approximations by piecewise smooth functions and associated variational problems. Commun. Pure Appl. Math. 1989, 42, 577–685. [Google Scholar] [CrossRef]
- Aubert, G.; Kornprobst, P. Mathematical Problems in Image Processing: Partial Differential Equations and the Calculus of Variations; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Fedkiw, S.O.R.; Osher, S. Level set methods and dynamic implicit surfaces. Surfaces 2002, 44, 77. [Google Scholar]
- Hou, X.; Zhang, L. Saliency detection: A spectral residual approach. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–8. [Google Scholar]
- Hussain, S.; Khan, M.S.; Asif, M.R.; Chun, Q. Active contours for image segmentation using complex domain-based approach. IET Image Process. 2016, 10, 121–129. [Google Scholar] [CrossRef]
- Li, C.; Xu, C.; Gui, C.; Fox, M.D. Distance regularized level set evolution and its application to image segmentation. IEEE Trans. Image Process. 2010, 19, 3243–3254. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Zhang, X.; Li, M.; Zhang, Z.; Xu, H. A Level Set Method Combined with Gaussian Mixture Model for Image Segmentation. In Proceedings of the Chinese Conference on Pattern Recognition and Computer Vision (PRCV), Nanjing, China, 16–18 October 2020; pp. 185–196. [Google Scholar]
- Gao, M.; Chen, H.; Zheng, S.; Fang, B. A factorization based active contour model for texture segmentation. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 4309–4313. [Google Scholar]
- Akram, F.; Garcia, M.A.; Puig, D. Active contours driven by local and global fitted image models for image segmentation robust to intensity inhomogeneity. PLoS ONE 2017, 12, e0174813. [Google Scholar]
- Menze, B.H.; Jakab, A.; Bauer, S.; Kalpathy-Cramer, J.; Farahani, K.; Kirby, J.; Burren, Y.; Porz, N.; Slotboom, J.; Wiest, R. The multimodal brain tumor image segmentation benchmark (BRATS). IEEE Trans. Med. Imaging 2014, 34, 1993–2024. [Google Scholar] [CrossRef] [PubMed]
- Mendonça, T.; Ferreira, P.M.; Marques, J.S.; Marcal, A.R.; Rozeira, J. PH 2-A dermoscopic image database for research and benchmarking. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 5437–5440. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, U.S.; Zhang, X.; Su, Y. Active Contour Model Using Fast Fourier Transformation for Salient Object Detection. Electronics 2021, 10, 192. https://doi.org/10.3390/electronics10020192
Khan US, Zhang X, Su Y. Active Contour Model Using Fast Fourier Transformation for Salient Object Detection. Electronics. 2021; 10(2):192. https://doi.org/10.3390/electronics10020192
Chicago/Turabian StyleKhan, Umer Sadiq, Xingjun Zhang, and Yuanqi Su. 2021. "Active Contour Model Using Fast Fourier Transformation for Salient Object Detection" Electronics 10, no. 2: 192. https://doi.org/10.3390/electronics10020192
APA StyleKhan, U. S., Zhang, X., & Su, Y. (2021). Active Contour Model Using Fast Fourier Transformation for Salient Object Detection. Electronics, 10(2), 192. https://doi.org/10.3390/electronics10020192




