A GAN-Based Video Intra Coding

Abstract

Intra prediction is a vital part of the image/video coding framework, which is designed to remove spatial redundancy within a picture. Based on a set of predefined linear combinations, traditional intra prediction cannot cope with coding blocks with irregular textures. To tackle this drawback, in this article, we propose a Generative Adversarial Network (GAN)-based intra prediction approach to enhance intra prediction accuracy. Specifically, with the superior non-linear fitting ability, the well-trained generator of GAN acts as a mapping from the adjacent reconstructed signals to the prediction unit, implemented into both encoder and decoder. Simulation results show that for All-Intra configuration, our proposed algorithm achieves, on average, a 1.6% BD-rate cutback for luminance components compared with video coding reference software HM-16.15 and outperforms previous similar works.

1. Introduction

With the explosive growth of multimedia applications, video traffic accounts for the vast majority of the total network traffic in wired and mobile services [1]. Video coding plays an indispensable role in promoting the video consumption for ultra-high definition videos. Aiming to represent the video signal by eliminating as much as possible, the redundancies in the spatial, temporal, frequency and statistical domains, intra coding, inter coding, transform, quantization, entropy coding and post-processing are all pivotal procedures in mainstream video compression standards. More importantly, intra coding, which exploits the spatial correlations, is not only a key process of video coding, but also is a still image codec.

In H.264/AVC, intra prediction is executed by spreading the adjacent reconstructed samples of a predicted unit. At most, eight directional modes in conjunction with two non-angular modes (Planar, DC) are used to capture angular texture information (e.g., straight edges at various directions) and predict low frequency areas [2]. High Efficiency Video Coding (H.265/HEVC), which inherits the fundamental methodology of intra coding in H.264/AVC, and 33 angular modes in total are adopted [3]. Moreover, in order to represent the arbitrary directional textures that appear in various video content, the number of intra angular modes in Versatile Video Coding (H.266/VVC) is raised from 33 to 65 [4], as deployed in H.265. As for the unit dimension, it varies from 4 × 4 to 16 × 16 in H.264, while the largest size is expanded to 64 × 64 in H.265 and 128 × 128 in H.266. More directional modes and more flexible block sizes can improve intra prediction accuracy in some way by separating the textures into more sets with slight direction divergence.

For further improvement of intra prediction, Matrix-weighted Intra Prediction (MIP) [5] and Multiple Reference Line (MRL) [6] are both techniques that are strongly worth mentioning. Due to the diversity of images and videos, using a set of fixed angular rules to generate predictions often fails when facing coding blocks with irregular textures. In response to above issue, Matrix-weighted Intra Prediction (MIP) [5] is proposed. It is a set of tools that generate the intra predicted pixels out of one single line of reconstructed pixels above and left a prediction unit by a matrix vector multiplication and an offset addition. However, it is noteworthy that all the aforementioned intra prediction methods, which use only the closest reconstructed signals for predicting a unit, ignore abundant context between the prediction unit and corresponding adjacent samples and thus produce inaccurate results especially when weak spatial coherence exists between the prediction unit and the nearest reconstructed signals. To tackle this issue, Multiple Reference Line (MRL) [6] intra prediction is also adopted in VVC. However, MRL is just a simple linear combination based on the hypothesis that the texture information follows a specified direction, which could not cope with blocks with weak directivity, fuzzy edge or intricate texture, such as circle or oval patterns.

To address the drawbacks mentioned above, some copying-based methods have been introduced for video coding, such as Intra Block Copy (IBC), also named Current Picture Referencing (CPR) [7,8] and Template Matching Prediction (TMP) [9,10], of which intra block copy is well known that it greatly enhances the coding performance of screen content and is adopted in H.265/HEVC extensions on Screen Content Coding (SCC). However, the effectiveness of these copying-based methods extremely depends on the similarity between blocks and may fail in natural camera-captured content.

Different from most of the aforementioned approaches based on linear computation, neural networks show their mighty potential in video coding due to their violent non-linear fitting capability. Typically, the neural network-based approaches are implemented into the video compression architecture to strengthen the coding performance of each specific section, such as mode estimation [11,12], partitioning [13,14], intra prediction [15,16,17,18,19,20,21], inter prediction [22] and post-processing [23,24].

A pioneering approach of deep learning-based intra prediction for video compression is [15], the first to tap the potentiality of Fully Connected (FC) neural networks in intra prediction. The works [17,18] introduced Convolutional Neural Networks (CNNs) and Recurrent Neural Networks (RNN) into intra coding, respectively, showing significant BD-rate gains compared to HEVC. With regard to Generative Adversarial Networks (GANs) [25], one of the most essential study topics in the area of artificial intelligence, its excellent image data generation ability has attracted widespread attention. Based on the game theory, GAN has two neural networks, generator and discriminator. The mission of the generator is to produce an as authentic image as possible to fool the discriminator while the task of the discriminator is to identify bogus pictures from genuine ones. Countless practical applications of GAN are deployed in the field of computer vision, including super-resolution [26], image translation [27] and image restoration [28,29], etc. Inspired by the powerful data generation ability of GAN, introducing GAN into the video coding framework to fully exploit the potential of neural networks in video prediction is a work worthy of in-depth exploration.

In this article, we propose an intra prediction technique guided by generative adversarial network, focusing on the prediction of a fixed block size 16 × 16. Compared to previous literature specializing in fixed size block: FC [15], CNN [17] and RNN [18,19], we proposed a GAN-based intra prediction for a larger block size, which is accompanied by greater prediction difficulty. With the superior non-linear fitting ability, the well-trained generator of GAN provides a new scheme for intra prediction of larger blocks, which are more difficult to predict, serving as a mapping from the adjacent reconstructed samples to the prediction unit. Furthermore, in comparison, in terms of the ratio of area size between reference block and prediction block, our proposal utilizes less reference context.

The rest of this article is arranged as follows: The related studies are introduced in Section 2. Section 3 details the GAN-based scheme. Experimental conditions and results are demonstrated in Section 4, followed by the conclusions in Section 5.

2. Related Work

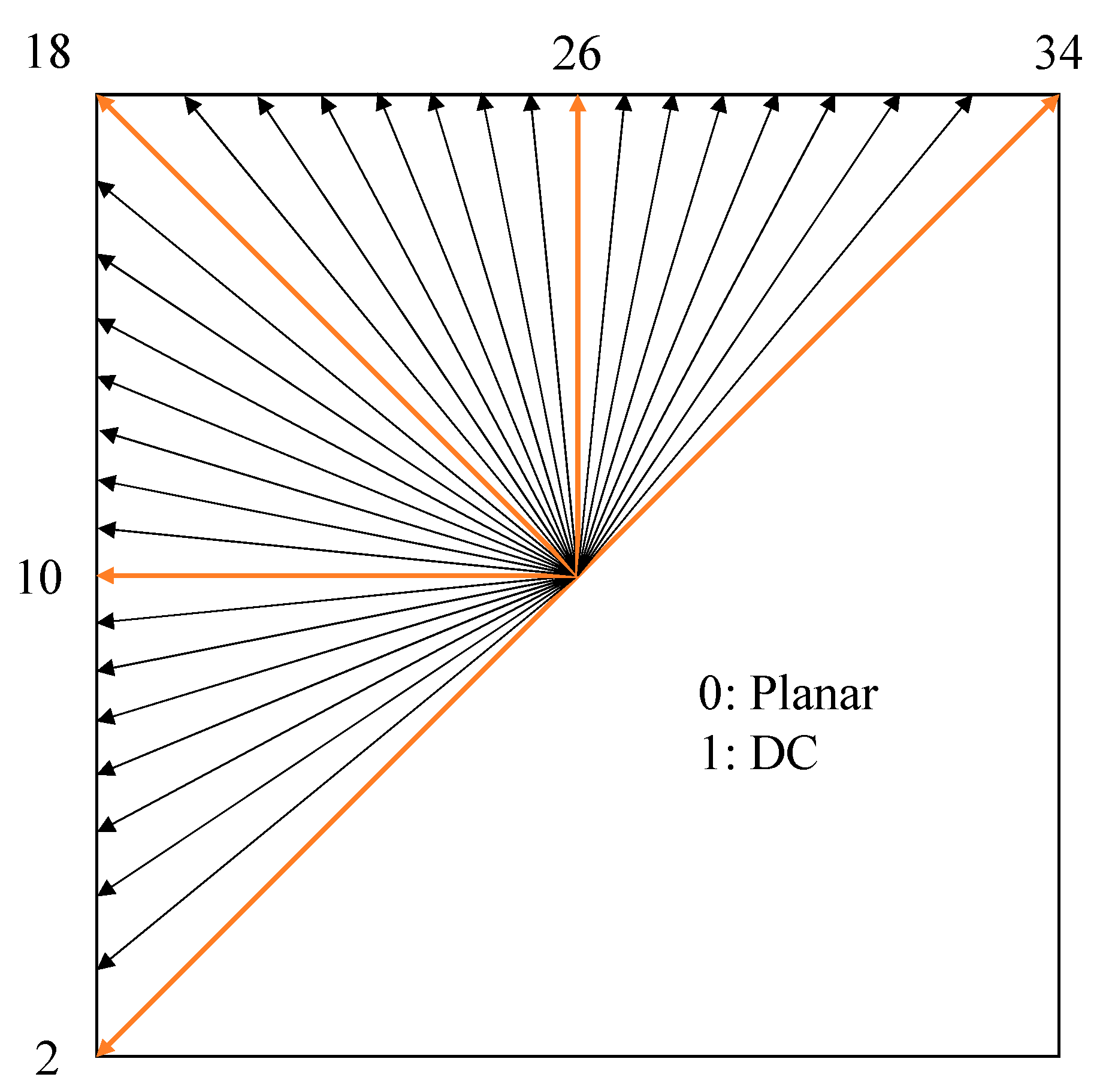
2.1. Intra Coding in Video Compression Framework

For the purpose of representing the image/video signal by eliminating the redundancies in the spatial domain as much as possible, intra prediction is a critical component in mainstream image/video compression framework. The aim of intra prediction is to infer a predicted unit of pixels from the adjacent reconstructed samples. The predicted unit is then subtracted from the raw unit to yield the residual unit followed by transform, quantization and entropy coding. In HEVC intra coding framework, 35 modes in total are adopted, including Planar, DC and 33 directional modes. Each mode has its own index, which indicates its angular direction (2–34), except for the non-directional modes (index 0 for planar and 1 for DC), as shown in Figure 1. In H.266/VVC, the number of directional modes is extended to 65. With denser directional modes, VVC intra coding can further enhance the coding efficiency by capturing more edge directions presented in various images. However, just based on the hypothesis that the texture information follows a specified direction, simply extrapolating the pixel values along explicit directions could not cope with prediction units with weak directivity, fuzzy edge or intricate texture. Considering the strong spatial correlation of the nearest neighbor pixels, HEVC utilizes the closest reconstructed row and column of the current unit to generate predicted pixels, i.e., for a predicted unit with dimension of N × N, a total of 4N + 1 pixels in the nearest reconstructed lines is used for prediction, as shown in Figure 2. However, this approach ignores abundant context between the prediction unit and corresponding adjacent samples, leading to inaccurate results especially when weak spatial coherence exists between the prediction unit and the nearest reconstructed signals.

Compared with its predecessor HEVC, VVC includes various new intra prediction tools, such as Matrix-weighted Intra Prediction (MIP) [5] and Multiple Reference Line (MRL) [6]. MIP, a newly added intra coding method into VVC, employs one line of nearest reconstructed neighboring samples as input and yields prediction pixels based on three steps: averaging, matrix vector multiplication and linear interpolation. Despite the fact that the closest reconstructed signals usually have intense statistical coherence with prediction unit, in some cases, the non-adjacent reconstructed samples can also provide potential better prediction. Based on the above perspective, MRL is adopted in a VVC framework for better prediction accuracy, using multiple reference lines. However, MRL is a simple linear combination based on the hypothesis that the texture information follows a specified direction, which inevitably suppresses the gain of intra coding.

Different from the aforementioned approaches that simply extrapolate the adjacent previously decoded pixels to obtain predicted results, some non-local methods have also been introduced for intra prediction, such as Intra Block Copy (IBC) [7,8] and Template Matching Prediction (TMP) [9,10], with a main focus on dealing with screen content video. These copying-based methods are extremely effective for screen content video, especially computer-generated text, because duplicate patterns appear frequently within the same picture. However, when it comes to more universal camera captured videos, these copying-based methods expose their limitations and achieve little gain.

2.2. Neural Network-Based Video Coding

With the ability of the modelling complex non-linear relationships, neural network-based methods outperform traditional strategies by a great margin in the field of computer vision, including style transfer, object detection, and semantic segmentation, etc. Introducing neural networks into video compression to achieve better coding gain is a new perspective worthy of in-depth study.

There are two categories of neural network-based strategies. The first one is full neural network-based system architecture, such as [30,31], jumping out of the classic hybrid coding framework. In [30], a machine learning-based video codec in low-latency mode is presented and surpasses all commercial video codecs in terms of Multi-Scale Structural Similarity Index (MS-SSIM) [32]. Ref. [31] proposes a DeepCoder, a brand-new deep learning-based framework, basing the hypothesis that any data are a combination of their prediction and residual. The second type is integrating the neural network-based technique as one specific component into the current image/video coding framework, e.g., [13,14,15,16,17,18,19,20,22,23]. In [13], a neural network-based fast HEVC intra coding algorithm is proposed and achieves 75.2% intra encoding computational complexity cutback with negligible quality degradation. In [22], for inter prediction, a neural network-based algorithm using the spatial-temporal information is proposed and achieves an average 1.7% BD-rate cutback compared to HEVC. For in-loop filters, the authors in [23] first presented an in-loop filtering technique guided by CNN for coding gain and subjective quality improvement.

As for intra prediction, in [15], a Fully Connected (FC) neural network-based intra prediction is adopted in HEVC to deal with 8 × 8 block prediction and achieves 1.1% bitrate saving on average. Similar to [15], the authors in [17,18,19] proposed CNN- and RNN-based intra prediction separately to cope with the prediction of a fixed block size 8 × 8, exploring the potential of CNN and RNN in video intra coding. Specifically, in [17], a CNN-based method, called IPCNN, is first directly applied for intra prediction. In [18,19], a CNN-guided spatial RNN is designed to enhance the coding efficiency in HEVC. By learning the statistical characteristics between image signals, the network takes five 8 × 8 available reconstructed blocks as input and then progressively generates the prediction signals to address the asymmetric prediction problem. In [20], an image inpainting based intra prediction is presented. In [20], the neural network-based predictor treats the neighboring reconstructed Coding Tree Units (CTUs) as inputs; however, the prediction units using a neural network-based scheme are much smaller blocks. Although [20] achieves significant coding gain, its computational complexity is extremely high, especially on the decoder side.

3. The Proposed Method

In this section, we will describe and analyze the proposed GAN-based intra prediction in detail, including network architecture, loss function, training strategy and the process of integration of proposed method into HEVC. After obtaining a suitable network architecture with well-trained parameters, we implement the generator of GAN into both encoder and decoder, serving as a mapping from the adjacent reconstructed samples to the prediction unit to provide a more accurate prediction with the help of the excellent non-linear fitting ability of GAN.

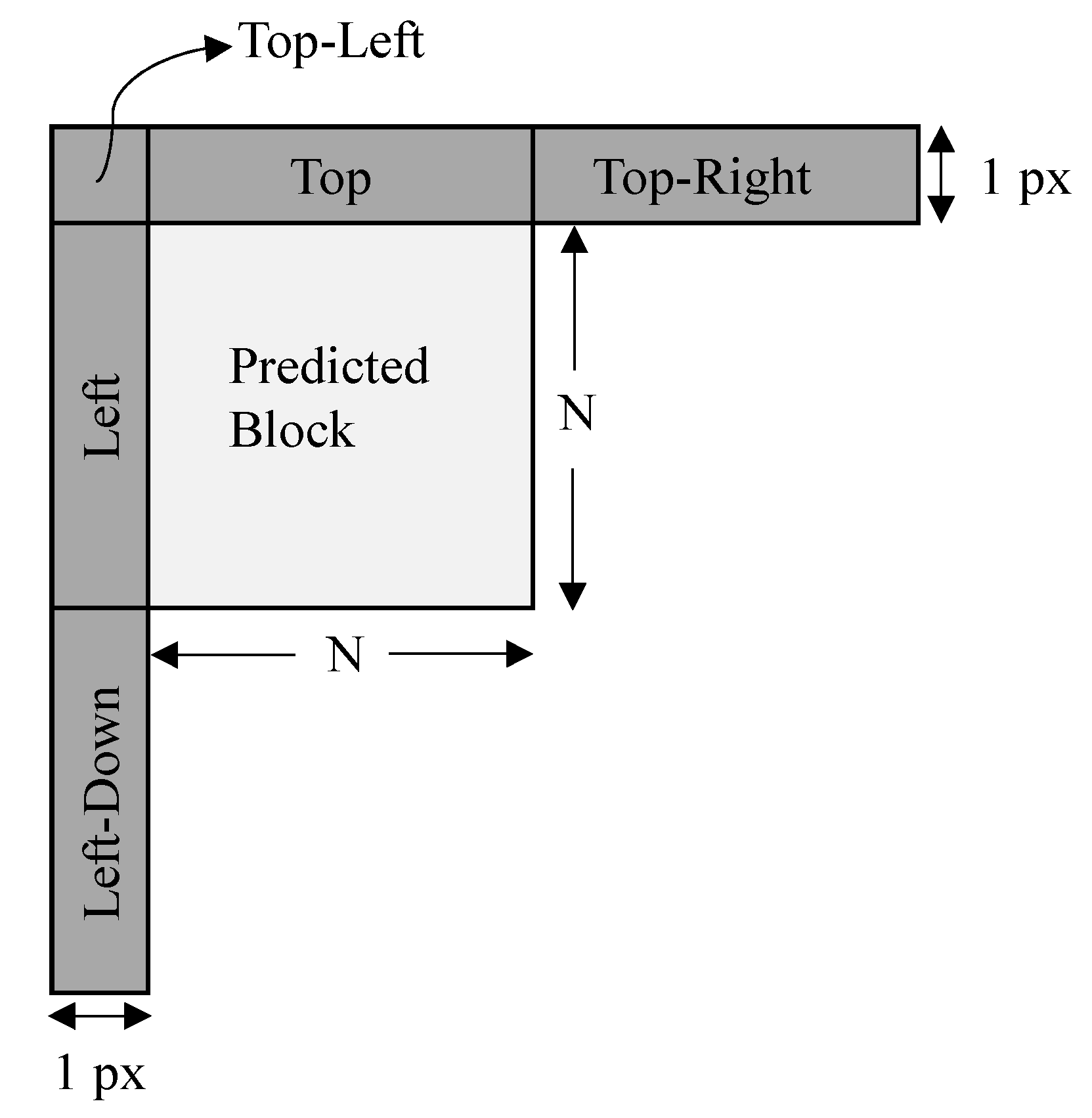
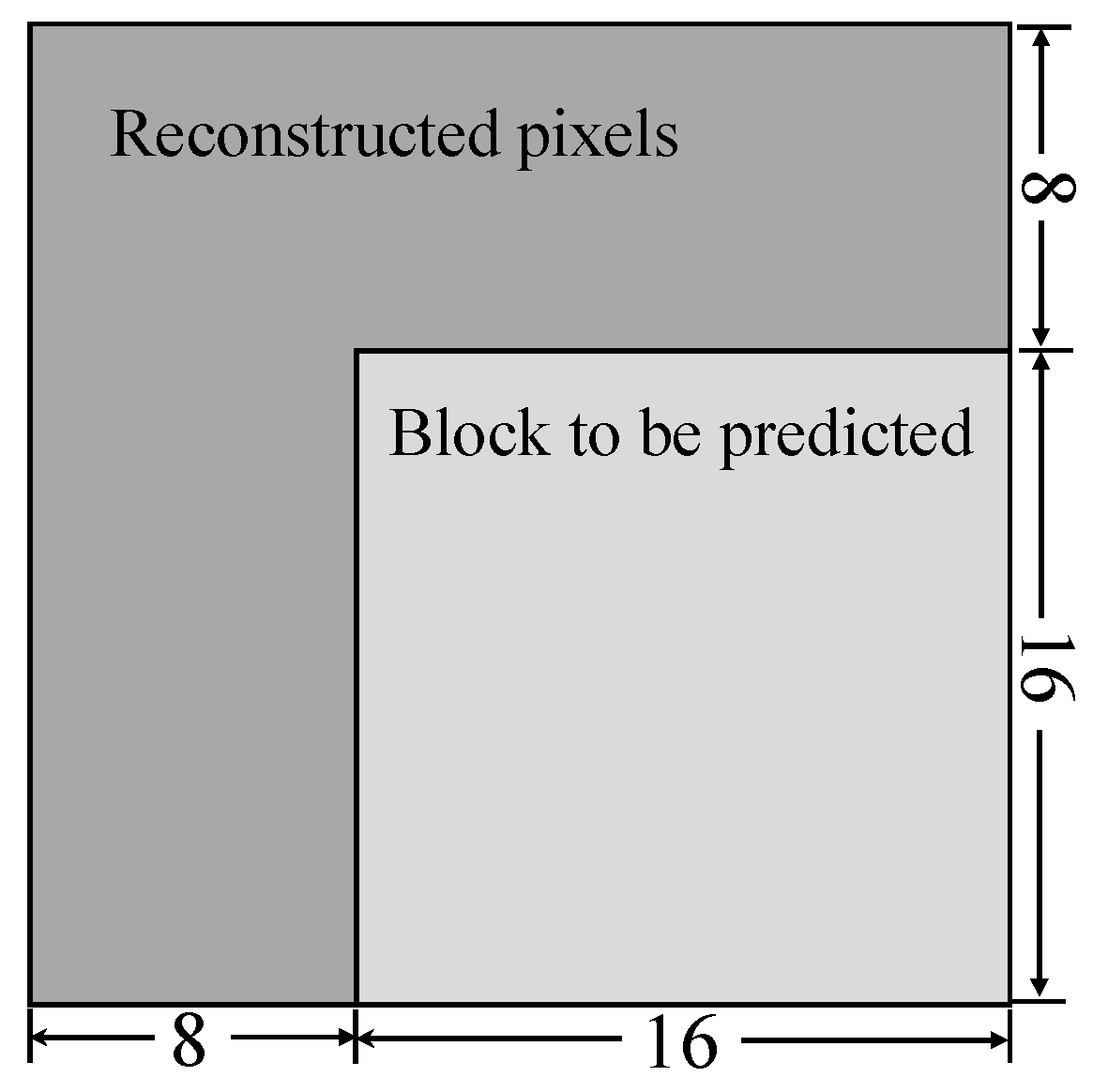
3.1. Network Architecture

For a 16 × 16 block, the network treats the nearest 8 lines of reconstructed pixels in above, left, and above-left area as input, and yields corresponding predicted unit at the bottom-right portion, as shown in Figure 3. The basic idea of our network architecture originated from [29]. In [29], for image restoration, a coarse-to-fine network architecture with contextual attention is proposed and achieves state-of-art visual results. However, applying it directly to our scenario is not appropriate as we now focus on a 16 × 16 block prediction instead of image restoration.

Our proposed network is shown in Figure 4. The whole architecture contains two networks: generator, denoted as the G, and discriminator, denoted as the D. The G is used for predicting the coding block while D is a critic to distinguish whether the generated unit is genuine or artificial. Noted that the discriminator is only used for network training and is not needed in real intra prediction. In order to enhance the coding performance, we adopted a two-stage coarse-to-fine network framework. More specifically, the first generative network produces preliminary rough predictions while the second generative network adopts the rough results, i.e., outputs of the first network, as inputs, and predicts precise results. Intuitively, the refinement generative network “sees” a more exhaustive view than the raw picture with masked areas, thus it learns a more superior feature representation than the rough one. Furthermore, two discriminators are adopted, i.e., global discriminator and local discriminator. The global discriminator adopts the whole 24 × 24 picture as input to determine the overall coherence of the completed image, while the local discriminator takes just the 16 × 16 block to be predicted as input to enhance the regional consistency, as shown in Figure 4. The generator network is trained to deceive both the global and local discriminator networks, which requires a generator to forge pictures that are indistinguishable from genuine ones in terms of both global coherence and local details.

Compared to [29], for our scenario, we exclude some redundant downsampling layers and dilated convolution layers because we are now specializing to 16 × 16 block instead of the whole picture. In the meantime, we also remove the contextual attention layer in [29] as we found it time-consuming and of little gain. The detailed parameters of the neural network are shown in

Table 1. Detailed parameters of the generator. The coarse network shares the same parameters with refinement network.

Type	Kernel	Dilation	Stride	Outputs
Conv.	5 × 5	1	1 × 1	32
Conv.	3 × 3		2 × 2	64
Conv.			1 × 1
Conv.				128
Dilated Conv.		2
Conv.		1
Conv.				64
Conv.				32
Deconv.			1/2 × 1/2	16
Conv.			1 × 1	1

,

Table 2. Detailed parameters of local discriminator.

Type	Outputs
Conv.	64
Conv.	128
Flatten.	2048
FC.	1

and

Table 3. Detailed parameters of global discriminator.

Type	Outputs
Conv.	64
Conv.	128
Conv.	128
Flatten.	1152
FC.	1

. Specifically, for the generator, after each convolution operation, apart from the last layer, there is an Exponential Linear Unit (ELU) activation layer. As for the last output layer, its values are clipped to [−1, 1]. With regard to the discriminators, all convolutional layers employ 5 × 5 kernels with a stride of 2 × 2 pixels. In the tables, “Outputs” denotes specific number of output channels of the convolutional layer, “Deconv” denotes the deconvolutional layer, and “Dilated Conv” refers to dilated convolution, which can effectively “see” a greater receptive field of input pictures than standard convolutional layer, when computing each output pixel.

3.2. Loss Function

In our mission, the goal is to minimize the divergence between predicted results and raw pixels. Different from most previous literatures that specialize in intra prediction, we use pixel-wise $l_1$ loss instead of Mean Square Error (MSE) because we found it conducive to stable network training. Furthermore, considering the fact that closer pixels have stronger spatial correlation, spatially weighted $l_1$ loss is introduced using a weight mask m. The weight of each signal in the mask is calculated as $r^l$, where $l$ denotes the distance of the pixel to the nearest reconstructed pixel and $r$ is a hyperparameter. In addition, we adopted the version of Wasserstein GAN with Gradient Penalty (WGAN-GP) [33,34] in [29] for adversarial supervision. Following [29], specifically, Wasserstein GAN (WGAN) uses the Earth-Mover distance $W\left(p_r,p_g\right)$ for calculating raw and artificial data distributions. Its loss function is formulated using the Kantorovich–Rubinstein duality:

$$\underset{G}{min}\underset{D\in \mathcal{D}}{max}\underset{x~p_r}{E}\left[D\left(x\right)\right]-\underset{\tilde{x}~p_g}{E}\left[D\left(\tilde{x}\right)\right]$$

(1)

where $\mathcal{D}$ is the set of 1-Lipschitz functions and $p_g$ is the model distribution implicitly defined by $\tilde{x}=G\left(z\right)$, z is the input data to the generator.

WGAN-GP is an advanced edition of WGAN with a gradient penalty subitem:

$$\lambda \underset{\widehat{x}~p_{\widehat{x}}}{E}{\left(\parallel {𝛻}_{\widehat{x}}D\left(\widehat{x}\right){\parallel }_2-1\right)}^2$$

(2)

where $\widehat{x}$ is uniformly sampled from straight lines between points sampled from data distribution $p_r$ and generator distribution $p_g$. For our scenario, as we only try to predict the coding block at the bottom-right corner; hence, the gradient penalty item should only be applied to samples within the predicted block. Therefore, the gradient penalty term is changed to:

$$\lambda \underset{\widehat{x}~p_{\widehat{x}}}{E}{\left(\parallel {𝛻}_{\widehat{x}}D\left(\widehat{x}\right)\odot \left(1-m\right){\parallel }_2-1\right)}^2$$

(3)

where m is a binary mask that takes the value 0 inside bottom-right region to be predicted and 1 elsewhere. Additionally, $\odot$ denotes pixel-wise multiplication.

In summary, according to Equations (1) and (3), the overall adversarial loss is redefined as:

$$L=\underset{x~p_r}{E}\left[D\left(x\right)\right]-\underset{\tilde{x}~p_g}{E}\left[D\left(\tilde{x}\right)\right]+\lambda \underset{\widehat{x}~p_{\widehat{x}}}{E}{\left(\parallel {𝛻}_{\widehat{x}}D\left(\widehat{x}\right)\odot \left(1-m\right){\parallel }_2-1\right)}^2$$

(4)

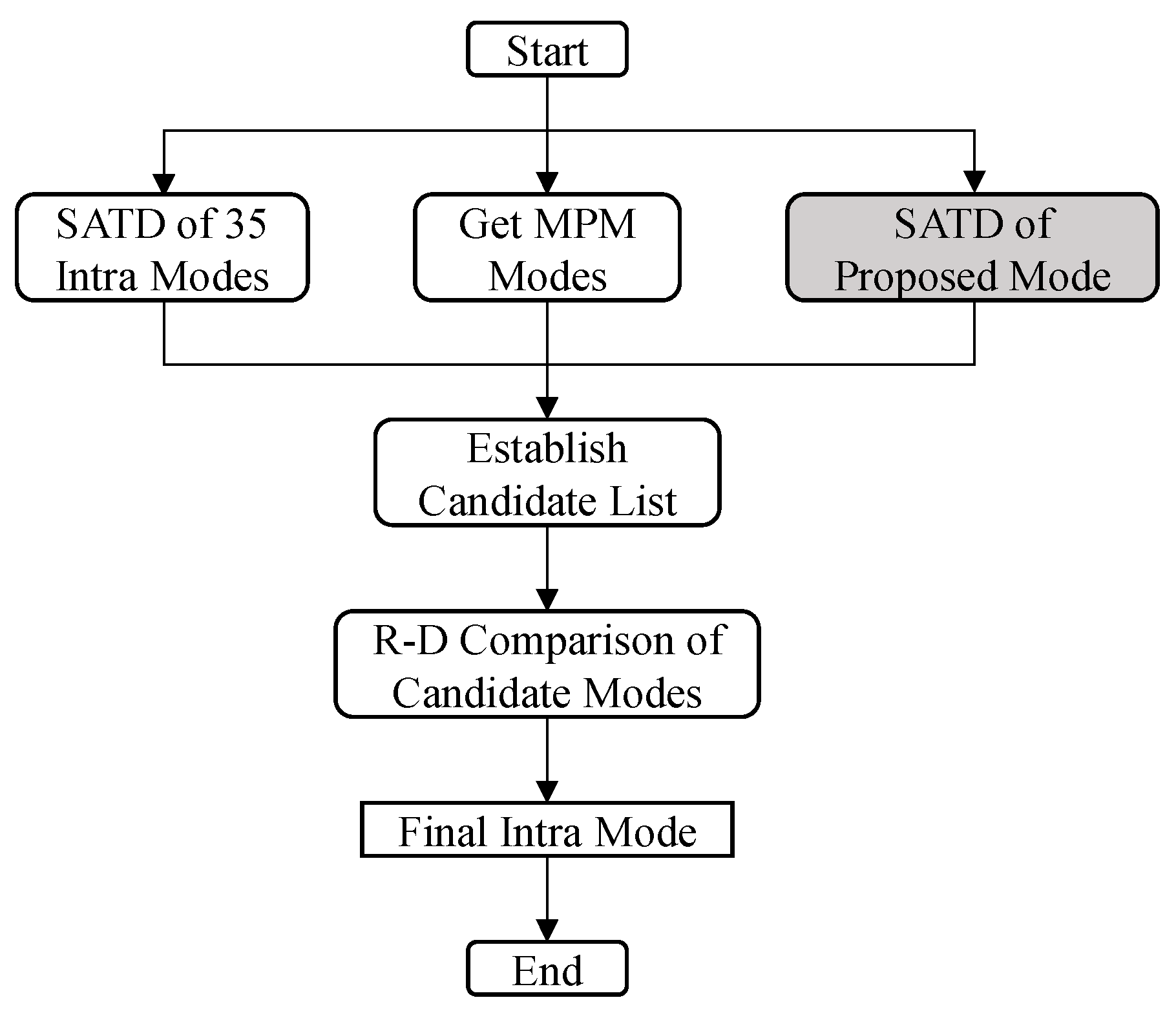
3.3. Training Strategy

We employ the published New York city library [35] for network training. The dataset consists of a total of 2550 pictures with various sizes. By traversing the images in the dataset and randomly cropping them with a 24 × 24 window, a total of 2.4 million images are finally obtained as the training data. In most previous literature, the training images are encoded firstly via HEVC with specific Quantization Parameters (QPs) in the process of data pretreatment; however, [36] had demonstrated that it is not necessary to train neural networks on reference pixels with quantization noise. Therefore, in this paper, we directly use original pixels fetched from the ground truth images. Of note, only luminance elements are extracted for network training.

As shown in Figure 3, for a coding block to be predicted with size of 16 × 16, its nearest 8 lines of reconstructed pixels are extracted as the reference context. As for training, the whole process is similar to [29] and hyperparameters remain the same as [29]. Given a raw image x with size of 24 × 24, a binary mask m is sampled at the bottom-right of x. The binary mask m adopts the value 0 inside area to be predicted at the bottom-right corner and value 1 elsewhere. Input image z is then corrupted from the original picture as $z=x\odot m$. Taking z and m as input, the generator of generative adversarial network then outputs the predicted picture $\tilde{x}=x+G\left(z,m\right)\odot \left(1-m\right)$ with the same dimension of input. The intra prediction result is obtained by cropping the masked region of $\tilde{x}$. Both input and output values of images are linearly scaled to [−1, 1] in all experiments. The specific training process of the proposed networks is presented in Algorithm 1.

Algorithm 1. Training Process of Generative Adversarial Networks.

1: while generator is not converged do

2:   for i = 1, …, k do

3:     Fetch batch data x from raw pictures.

4:     Sample masks m for x.

5:     Corrupt inputs $\mathit{z}\leftarrow \mathit{x} \odot \mathit{m}$.

6:     Get predictions $\tilde{\mathit{x}}\leftarrow \mathit{x}+\mathit{G}\left(\mathit{z}, \mathit{m}\right) \odot \left(1-\mathit{m}\right)$.

7:     Sample $\mathit{t}~\mathit{U}\left[0, 1\right]$ and $\widehat{\mathit{x}}\leftarrow \left(1-\mathit{t}\right)\mathit{x}+\mathit{t}\tilde{\mathit{x}}$.

8:     Update both discriminators with $\mathit{x}$, $\tilde{\mathit{x}}$ and $\widehat{\mathit{x}}$.

9:   end for

10:  Fetch batch data x from raw pictures.

11:  Sample masks m for x.

12:  Update generator with ${\mathit{l}}_1$ loss and adversarial discriminators losses.

13: end while

3.4. Integration of Proposed Method into HEVC

A total of 35 intra modes are supported in HEVC, which could be divided into directional and non-directional modes. The former, i.e., directional modes, can be classified according to their directions and the latter includes two modes: Planar with index 0 and DC with index 1. To select the optimal mode from 35 intra modes for a given prediction unit, two steps are carried out. Firstly, based on the Sum of Absolute Transformed Differences (SATD), a candidate list is established from 35 intra modes. After that, the Most Probable Modes (MPMs), a list of modes that derived from the context of the above and left prediction blocks, are appended in the candidate list. During the second step, based on the Rate–Distortion (R–D) cost, the optimal mode is finally determined from the candidate list.

In order to integrate the proposed method into HEVC, two schemes can be adopted. The first scheme is to replace one original HEVC intra prediction mode with the proposed method. However, it possibly damages the prediction accuracy in some specific images though this method seems natural and easy to implement. The second scheme adds the proposed method to original HEVC modes, thus we have 36 modes in total. As for the selection of the best luma mode, Figure 5 illustrates the detailed process. To binarize overall 36 modes, a mode signaling method is introduced as illustrated in Figure 6. Firstly, one bit is encoded to identify whether the optimal mode is our proposed method. If the optimal mode is the original HEVC intra mode, the signaling procedure remains the same as the original HEVC. Otherwise, no more flag for mode information is encoded. Moreover, we modify the selection procedure for the three Most Probable Modes (MPMs). Specifically, in the case where the proposed method belongs to the MPM list, we replace the corresponding MPM mode with Planar, DC or the horizontal mode in order of priority.

4. Experimental Results

This section describes the experimental settings and simulation results for our generative adversarial network-based intra prediction approach. The proposed scheme is implemented into HEVC reference software, HM16.15 [37].

4.1. Experimental Settings

We implemented the proposed approach into the HEVC test Model (HM 16.15). As our proposal focuses on intra coding, the simulation experiments are based on the test sequences from JCT-VC as test samples, using All-Intra configuration suggested by common test conditions [38]. The Quantization Parameter (QP) values are set as 22, 27, 32 and 37. The coding efficiency is assessed by BD-rate [39]. Negative value represents coding gain.

4.2. Coding Performance of the Proposal

In our proposed approach, a two-stage coarse-to-fine generator network framework is adopted. The first generative network produces preliminary rough predictions, while the second generative network adopts the rough results as inputs and predicts refined results, as shown in Figure 4. To confirm the effectiveness of the two-stage coarse-to-fine network, two strategies are defined. Among them, the first strategy, denoted as stage_1, is to use only coarse network for prediction, while the second strategy, denoted as stage_2, is to use the full two-stage coarse-to-fine network to yield predicted results. The simulation results of two strategies are shown in

Table 4. Experimental result of our proposal compared with the anchor (HM 16.15). The coding efficiency is assessed by BD-rate luma.

Sequence		Stage_1	Stage_2
Class B	Kimono	−1.5%	−2.0%
	ParkScene	−1.1%	−1.3%
	Cactus	−1.4%	−1.6%
	BasketballDrive	−0.9%	−1.8%
	BQTerrace	−1.2%	−1.5%
Class C	BasketballDrill	−1.1%	−1.0%
	BQMall	−1.5%	−2.0%
	PartyScene	−1.1%	−1.4%
	RaceHorses	−1.0%	−1.3%
Class D	BasketballPass	−0.8%	−1.1%
	BQSquare	−0.8%	−0.9%
	BlowingBubbles	−1.0%	−1.6%
	RaceHorses	−1.1%	−1.4%
Class E	FourPeople	−1.6%	−2.1%
	Johnny	−1.6%	−2.3%
	KristenAndSara	−1.1%	−1.9%
Average		−1.2%	−1.6%

. Both the anchor and proposed method are only allowed 16 × 16 intra coding. As can be observed, our proposal can save BD-rate for all test sequences. Furthermore, we found that the proposed stage_2 strategy outperforms stage_1 strategy in all test cases. The proposed stage_2 strategy achieves an average of 1.6% BD-rate reduction while the stage_1 strategy achieves an average of 1.2% BD-rate reduction on the luminance component. It demonstrates the effectiveness of the two-stage coarse-to-fine generator network.

We also compare the coding results with previous literatures [15,17,18,19] that focus on fixed size block intra prediction using neural network-based methods. Considering the fact that they are dedicated to 8 × 8 block prediction, while our network is designed for larger blocks, i.e., 16 × 16, for a justified comparison, we redesigned the experiment platform, i.e., only 8 × 8 intra coding is allowed for both the anchor and proposed method, as these works [15,17,18,19] do. In our proposed method, for the fixed 8 × 8 blocks, as their sizes are smaller than 16 × 16, the predicted signals are copied from corresponding blocks with size of 16 × 16 at the same location. As shown in

Table 5. Coding efficiency comparison with previous works.

Sequence		FC [15]	CNN [17]	RNN [18]	RNN [19]	Stage_1	Stage_2
Class B	Kimono	−3.2%	−0.2%	-	−2.8%	−1.6%	−1.9%
	ParkScene	−1.1%	−0.8%	-	−1.7%	−1.8%	−1.9%
	Cactus	−0.9%	−0.8%	-	−1.2%	−1.7%	−1.9%
	BasketballDrive	−0.9%	−0.6%	-	−1.0%	−2.1%	−2.3%
	BQTerrace	−0.5%	−0.8%	-	−1.0%	−1.3%	−1.4%
Average of Class B		−1.3%	−0.8%	−0.2%	−1.5%	−1.7%	−1.9%
Class C	BasketballDrill	−0.3%	−0.5%	-	−1.0%	−1.0%	−0.9%
	BQMall	−0.3%	−0.6%	-	−0.8%	−1.4%	−1.6%
	PartyScene	−0.4%	−0.5%	-	−1.0%	−1.5%	−1.7%
	RaceHorses	−0.8%	−0.7%	-	−1.1%	−1.5%	−1.8%
Average of Class C		−0.5%	−0.6%	−0.2%	−1.0%	−1.4%	−1.5%
Class D	BasketballPass	−0.4%	−0.4%	-	−0.8%	−1.1%	−1.3%
	BQSquare	−0.2%	−0.1%	-	−0.6%	−0.8%	−0.8%
	BlowingBubbles	−0.6%	−0.7%	-	−1.0%	−1.2%	−1.3%
	RaceHorses	−0.6%	−0.7%	-	−1.1%	−2.0%	−2.3%
Average of Class D		−0.5%	−0.5%	−0.1%	−0.9%	−1.3%	−1.4%
Class E	FourPeople	−0.8%	−0.3%	-	−2.2%	−1.5%	−1.6%
	Johnny	−1.0%	−1.0%	-	−1.5%	−1.7%	−2.3%
	KristenAndSara	−0.8%	−0.8%	-	−1.3%	−1.2%	−1.8%
Average of Class E		−0.9%	−0.7%	−0.8%	−1.7%	−1.4%	−1.9%
Overall Average		−0.8%	−0.7%	−0.3%	−1.3%	−1.4%	−1.7%

, our proposal achieves a better coding gain and outperforms previous similar works, which demonstrates the effectiveness of our proposal. Note that [29] is unnecessary for comparison since it focuses on image restoration while our proposal is dedicated to video intra coding.

We further compare our proposal with [20]. In [20], it treats the neighboring reconstructed CTUs as the inputs of neural networks; however, the prediction units using neural networks based scheme are much smaller blocks. Compared to [20], our proposal utilizes much less context for prediction. Comprehensive comparison of coding efficiency and computational complexity with [20] is shown in

Table 6. Comprehensive comparison with [20] in terms of coding efficiency and computational complexity under the platform of CPU (HEVC anchor is 1).

	Encode Complexity	Decode Complexity	BD-Rate (Y)
[20]	149	5264	−6.6%
Stage_1	39.62	68.24	−1.2%
Stage_2	74.23	150.46	−1.6%

. As can be seen, although [20] achieves better coding gain, its complexity is 77 times higher than our proposed stage_1 and 35 times higher than our proposed stage_2 at the decoder side. In stark contrast, we employ two-stage coarse-to-fine generator network architecture to meet different complexity requirements as a more cost-effective way.

5. Conclusions

In this article, we propose an intra prediction approach guided by generative adversarial network. The proposed GAN-based intra predictor learns a map from the adjacent reconstructed signals to the prediction unit and enhances the intra prediction. Simulation results confirm that, compared with HEVC, the proposed predictor can save an average of 1.6% BD-rate for luminance component. Compared to the previous literature specializing in a fixed size block, our proposal focuses on a larger block size, which is accompanied by greater prediction difficulty. In the meanwhile, we utilize less reference context in terms of the ratio of area size between reference block and prediction block.

As for future work, due to the continuous development of video codec standards, it is worth continuing to explore the optimization of the network and apply the network to the latest standards, such as VVC and AVS3. Since the coding efficiency of the GAN predictor has been proved for a fixed block dimension of 16 × 16, more block sizes with GAN-based predictors also deserve investigation to further enhance the intra coding. Furthermore, acceleration for the neural network-based prediction is also the focus of the study.