An Optimization Model for Energy Community Costs Minimization Considering a Local Electricity Market between Prosumers and Electric Vehicles
Abstract
1. Introduction
- An optimization model that determines the best electricity transactions between prosumers and EVs in a local energy community.
- The implementation of a new P2V market where the EVs can buy electricity at the cheapest prices compared to tariff available on retailers.
- The possibility of prosumers to sell the excess RES generation to EVs in a more profitable way.
- The model includes realistic constraints, prosumers load and generation profiles, PV systems, energy storage systems, EVs and market transactions constraints.
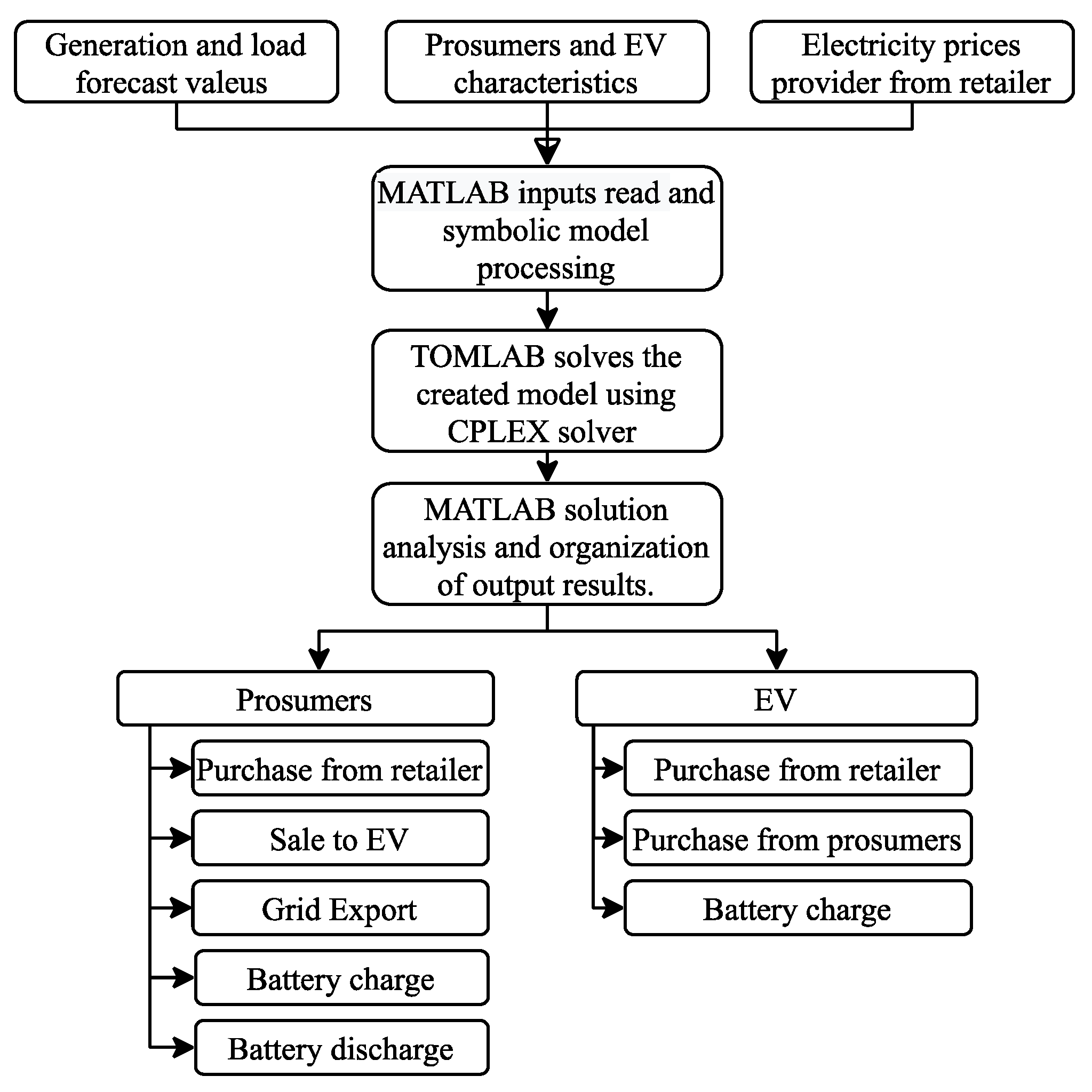
2. Proposed Formulation
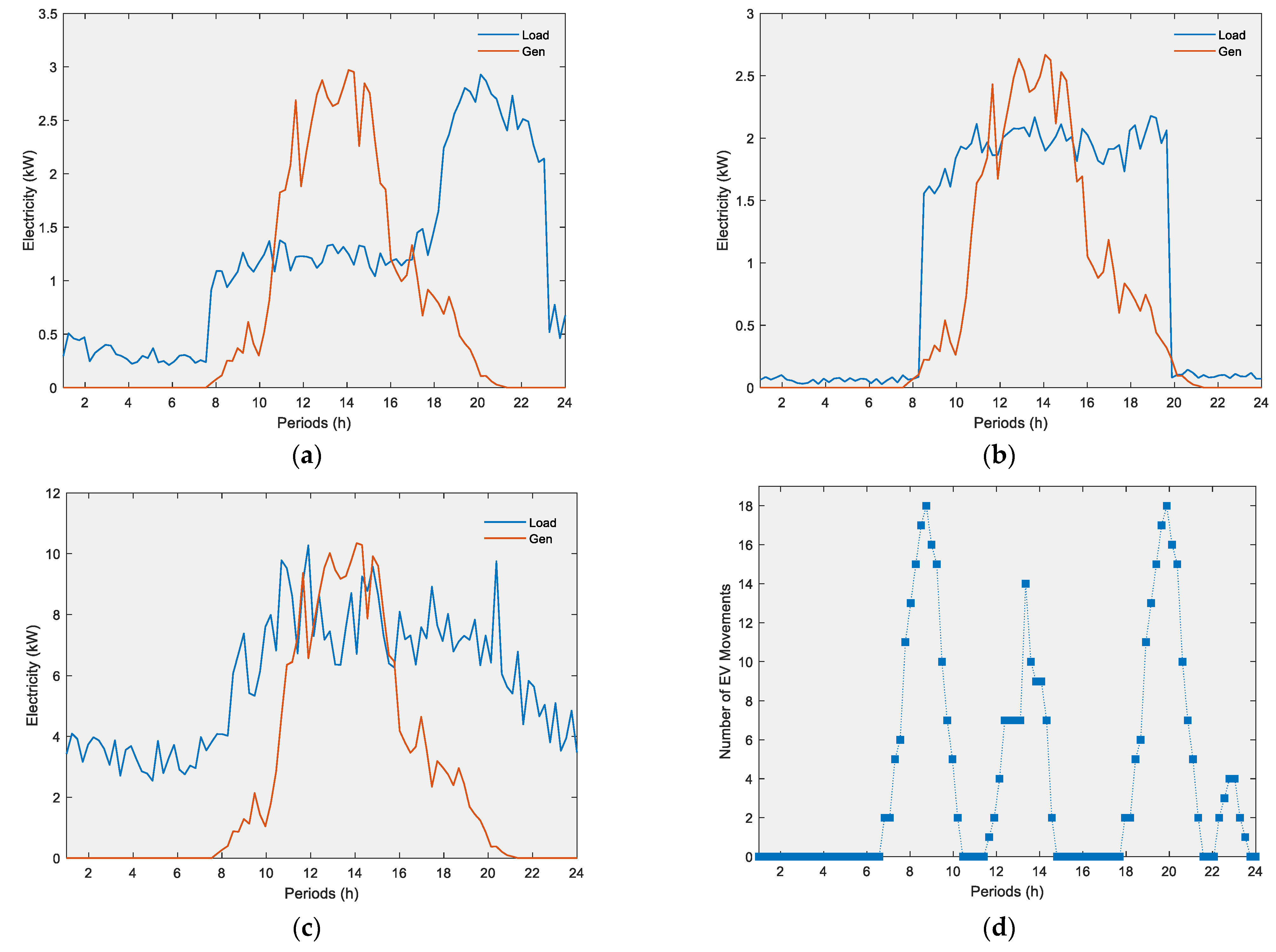
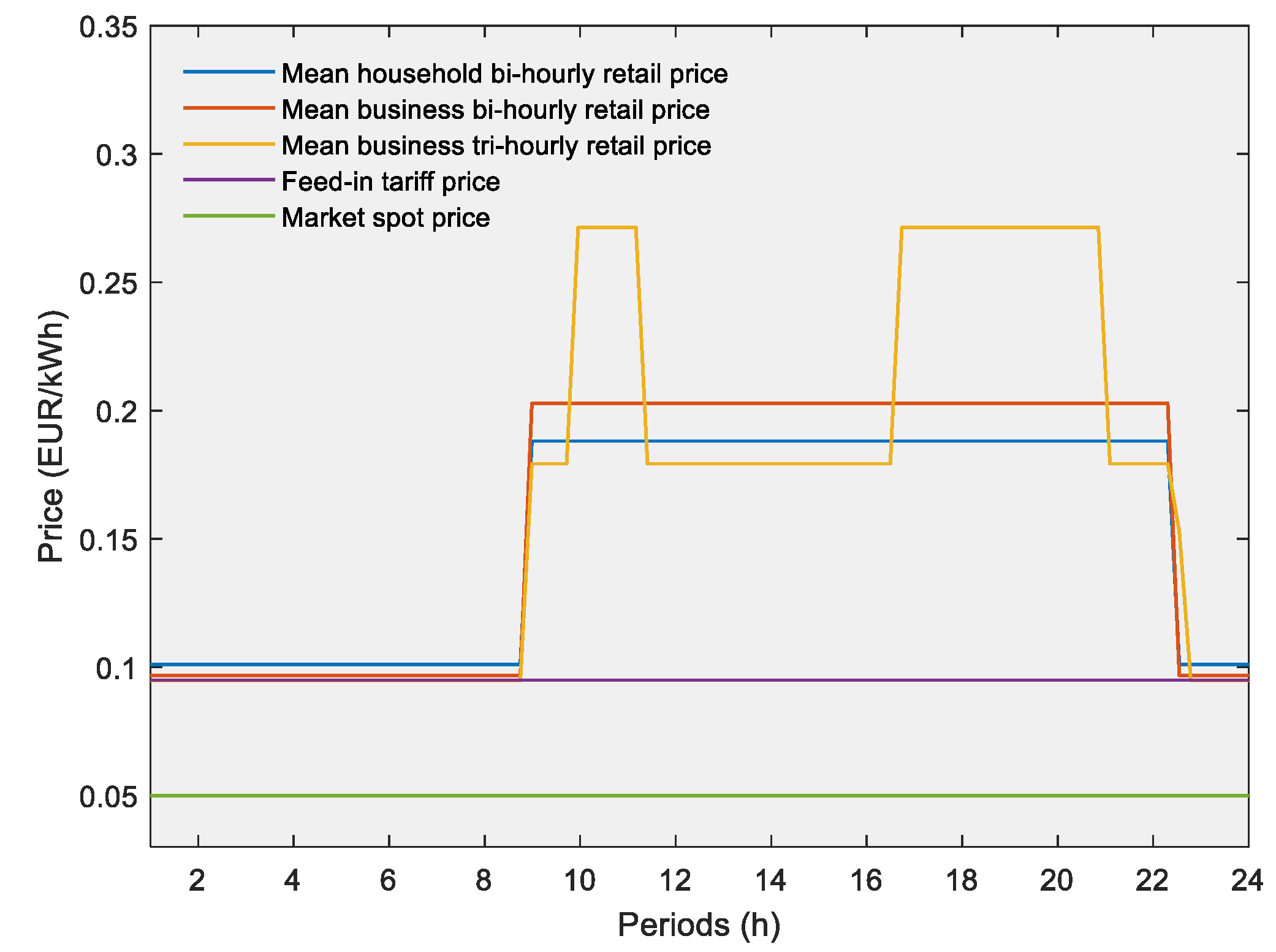
3. Case Study
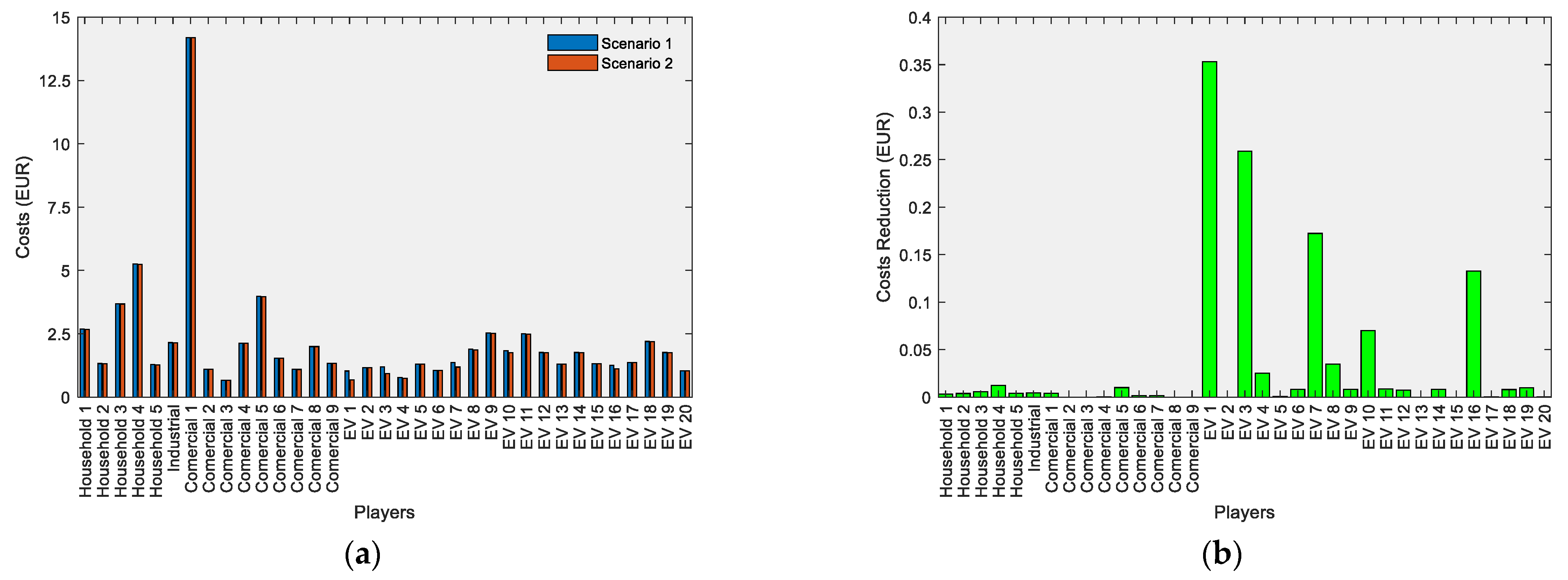
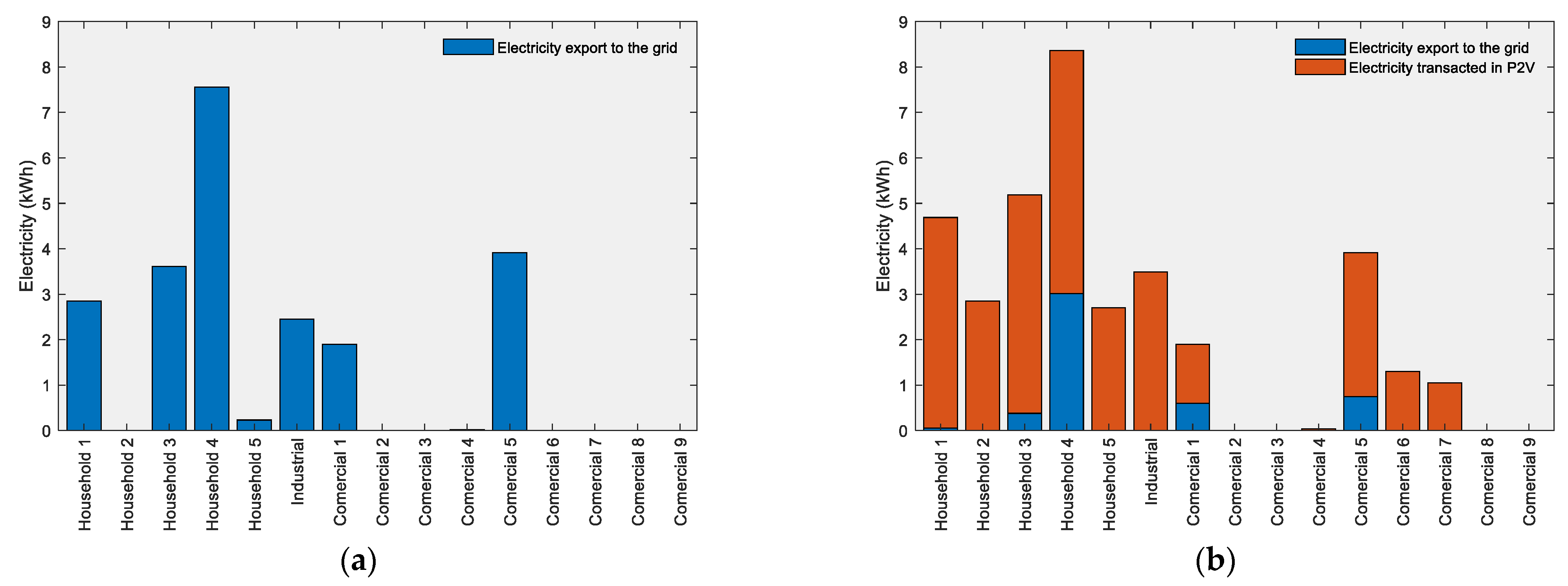
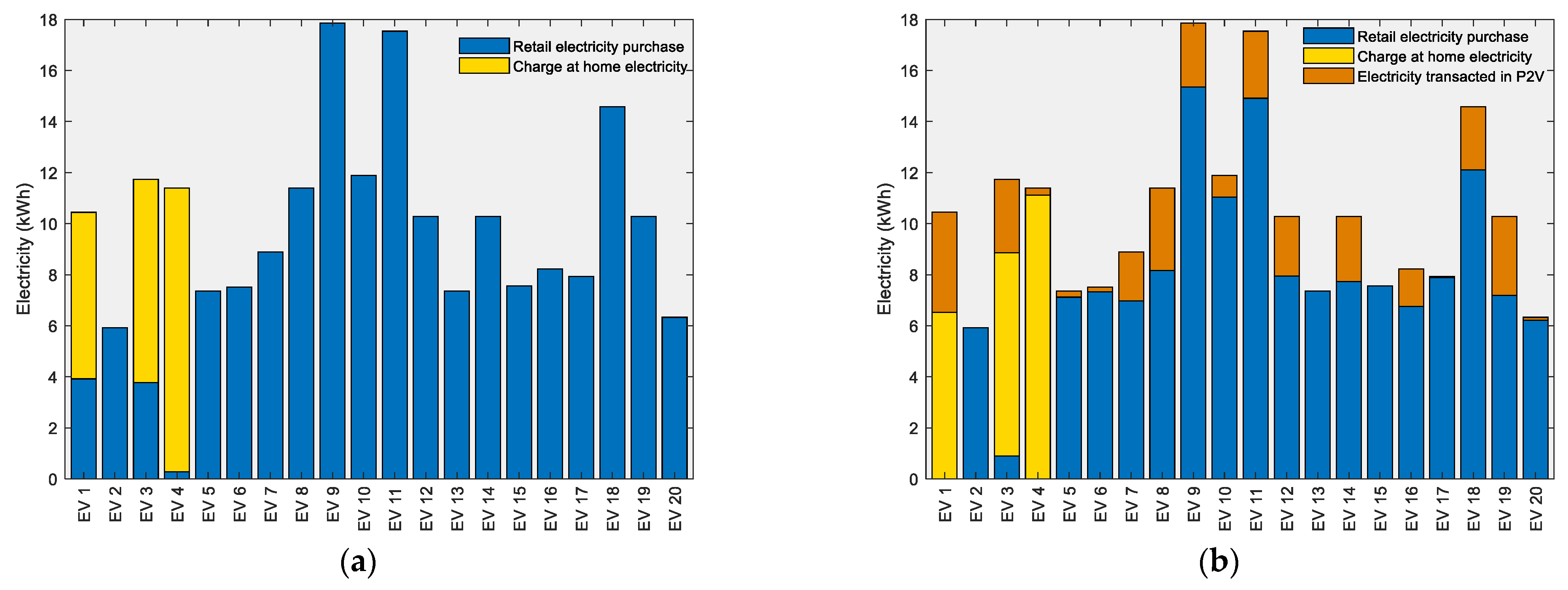
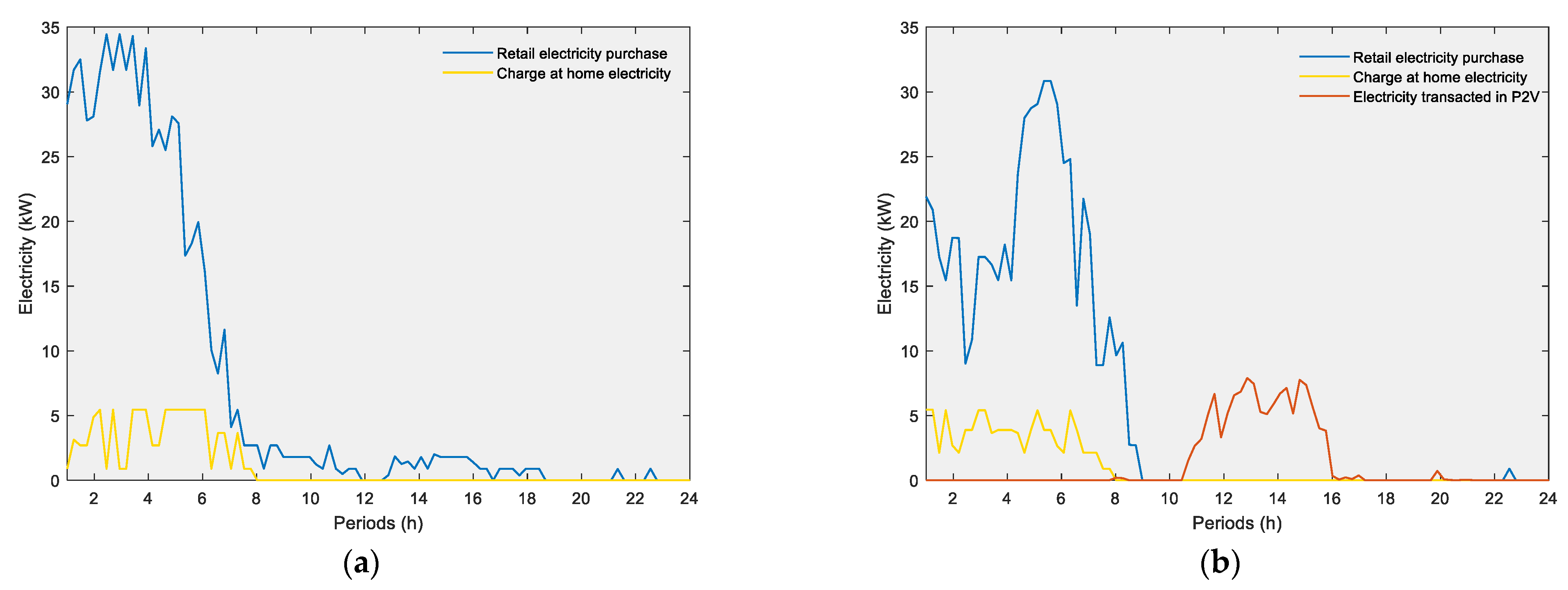
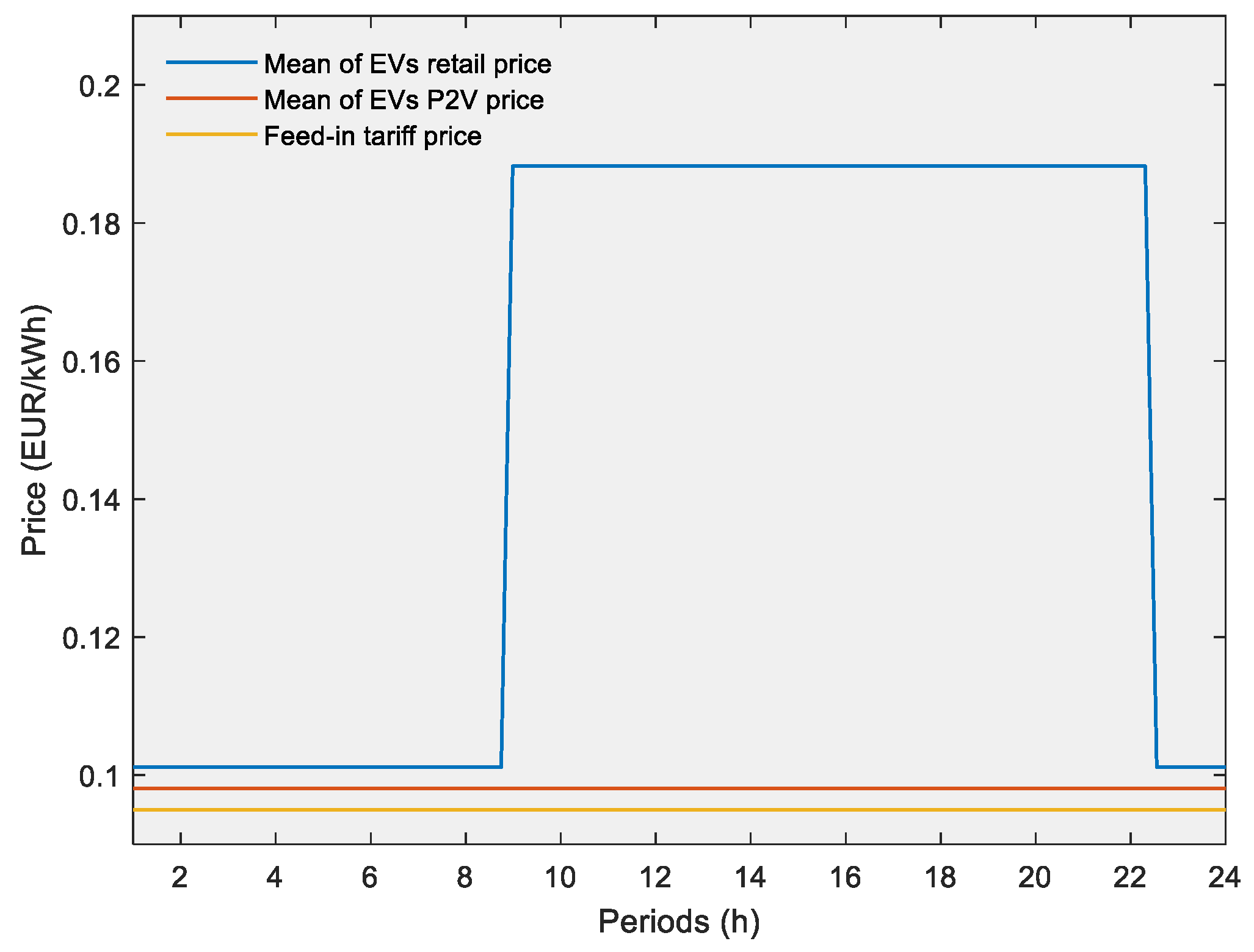
4. Results
- Scenario 1—Without the P2V market and considering the Portuguese feed-in tariff (0.095 EUR/kWh) for electricity export.
- Scenario 2—With P2V market and considering the Portuguese feed-in tariff (0.095 EUR/kWh) for electricity export.
- Scenario 3—Without the P2V market and considering the MIBEL Spot price (0.050 EUR/kWh) for electricity export.
- Scenario 4—With P2V market and considering the MIBEL Spot price (0.050 EUR/kWh) for electricity export.
- Scenario 5—Without P2V market and electricity export to the grid not remunerated.
- Scenario 6—With P2V market and electricity export to the grid not remunerated.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Indices: | |
| Periods | |
| Prosumers | |
| Vehicles | |
| Parameters: | |
| Efficiency of EV battery charge | |
| Efficiency of prosumer battery charge | |
| Efficiency of prosumer battery discharge | |
| Electricity consumption of EV during trips | |
| Electricity generated | |
| Factor adjustment | |
| Fixed costs | |
| Indicates if the EV is at home (1) or not (0) | |
| Indication if the EV is travelling (0) or it is available to charge (1) | |
| Limit of electricity export to the grid | |
| Load of each prosumer | |
| Maximum capacity of the prosumer battery | |
| Maximum limit electricity sale to the EV | |
| Maximum limit for EV electricity purchase to the retailer | |
| Maximum power for prosumer battery charge | |
| Maximum power for the prosumer battery discharge | |
| Maximum power of EV battery charge located at prosumer | |
| Maximum power that prosumer can buy from the grid | |
| Maximum value for the EV battery capacity | |
| Minimum retail price for each EV | |
| Minimum value for the EV battery capacity | |
| Number of periods | |
| Number of prosumers | |
| Number of vehicles | |
| Price of electricity export to the grid | |
| Price of electricity transaction between prosumer and EV | |
| Retail price of electricity | |
| Retail price to charge EV from the grid | |
| Variables: | |
| Binary variable for EV battery that represents the charge action | |
| Binary variable for prosumer buy from grid | |
| Binary variable for prosumer sell to grid | |
| Binary variable for prosumer to EV transaction | |
| Binary variable for the prosumer battery that represents the charge action | |
| Binary variable for the prosumer battery that represents the discharge action | |
| Binary variable to active the transaction of electricity between EV and retailer | |
| Electric vehicles costs | |
| Electricity battery charge | |
| Electricity charged by each EV | |
| Electricity charged by EV from the house | |
| Electricity purchase by each EV to the retailer | |
| Electricity state of the EV battery | |
| Electricity transacted between prosumer and EV | |
| Energy battery discharge | |
| EV electricity purchase from the retailer | |
| Prosumer costs | |
| Prosumers electricity purchase from the retailer | |
| Prosumers electricity sale to the grid | |
| State of charge of the battery | |
References
- European Environment Agency. National emissions reported to the UNFCCC and to the EU Greenhouse Gas Monitoring Mechanism. In National Greenhouse Gas Inventories (IPCC Common Reporting Format Sector Classification); European Environment Agency: Copenhagen, Danmark, 2018. [Google Scholar]
- European Union. White Paper on Transport; European Union: Brussels, Belgium, 2011; pp. 1–32. [Google Scholar] [CrossRef]
- Telles, S.; Reddy, S.K.; Nagendra, H.R. A European Strategy for Low-Emission Mobility. Eur. Comm. 2019, 53, 1689–1699. [Google Scholar] [CrossRef]
- International Energy Agency. Global EV Outlook 2018; OECD: Paris, France, 2018; ISBN 9789264302365. [Google Scholar]
- Fachrizal, R.; Shepero, M.; van der Meer, D.; Munkhammar, J.; Widén, J. Smart charging of electric vehicles considering photovoltaic power production and electricity consumption: A review. eTransportation 2020, 4, 100056. [Google Scholar] [CrossRef]
- Garcia Villalobos, J. Optimized Charging Control Method for Plug-in Electric Vehicles in LV Distribution Networks. Ph.D. Thesis, Universidad del País Vasco (UPV/EHU), Leioa, Spain, 2016; pp. 1–230. [Google Scholar]
- Hoarau, Q.; Perez, Y. Interactions between electric mobility and photovoltaic generation: A review. Renew. Sustain. Energy Rev. 2018, 94, 510–522. [Google Scholar] [CrossRef]
- García-Villalobos, J.; Zamora, I.; San Martín, J.I.; Asensio, F.J.; Aperribay, V. Plug-in electric vehicles in electric distribution networks: A review of smart charging approaches. Renew. Sustain. Energy Rev. 2014, 38, 717–731. [Google Scholar] [CrossRef]
- Aoun, A.; Ibrahim, H.; Ghandour, M.; Ilinca, A. Supply side management vs. Demand side management of a residential microgrid equipped with an electric vehicle in a dual tariff scheme. Energies 2019, 12, 4351. [Google Scholar] [CrossRef]
- Asif, A.; Singh, R. Further Cost Reduction of Battery Manufacturing. Batteries 2017, 3, 17. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.-H.; Baek, J.-W.; Kim, H.-M. Stationary Energy Storage System for Fast EV Charging Stations: Simultaneous Sizing of Battery and Converter. Energies 2019, 12, 4516. [Google Scholar] [CrossRef]
- Lezama, F.; Soares, J.; Hernandez-Leal, P.; Kaisers, M.; Pinto, T.; Vale, Z. Local Energy Markets: Paving the Path toward Fully Transactive Energy Systems. IEEE Trans. Power Syst. 2019, 34, 4081–4088. [Google Scholar] [CrossRef]
- European Union. The Strategic Energy Technology (SET) Plan; European Union: Brussels, Belgium, 2017. [Google Scholar]
- Faia, R.; Pinto, T.; Vale, Z.; Corchado, J.M. A Local Electricity Market Model for DSO Flexibility Trading. In Proceedings of the International Conference on the European Energy Market, Ljubljana, Slovenia, 8–20 September 2019. [Google Scholar]
- Masood, A.; Hu, J.; Xin, A.; Sayed, A.R.; Yang, G. Transactive Energy for Aggregated Electric Vehicles to Reduce System Peak Load Considering Network Constraints. IEEE Access 2020, 8, 31519–31529. [Google Scholar] [CrossRef]
- Abrishambaf, O.; Lezama, F.; Faria, P.; Vale, Z. Towards transactive energy systems: An analysis on current trends. Energy Strateg. Rev. 2019, 26. [Google Scholar] [CrossRef]
- Kikusato, H.; Fujimoto, Y.; Hanada, S.I.; Isogawa, D.; Yoshizawa, S.; Ohashi, H.; Hayashi, Y. Electric Vehicle Charging Management Using Auction Mechanism for Reducing PV Curtailment in Distribution Systems. IEEE Trans. Sustain. Energy 2020, 11, 1394–1403. [Google Scholar] [CrossRef]
- Gomes, L.; Vale, Z.A.; Corchado, J.M. Multi-Agent Microgrid Management System for Single-Board Computers: A Case Study on Peer-to-Peer Energy Trading. IEEE Access 2020, 8, 64169–64183. [Google Scholar] [CrossRef]
- Soares, J.; Canizes, B.; Lobo, C.; Vale, Z.; Morais, H. Electric vehicle scenario simulator tool for smart grid operators. Energies 2012, 5, 1881–1899. [Google Scholar] [CrossRef]
| Brand | Model | Type | Battery Capacity (kWh) | Charge Rate (kW) | Discharge Rate (kW) | Efficiency (%) | No. |
|---|---|---|---|---|---|---|---|
| Sonnen | 9.43 | Stationary | 15.000 | 3.300 | 3.300 | 0.9 | 7 |
| Tesla | Powerwall | Stationary | 13.500 | 5.000 | 5.000 | 0.9 | 6 |
| Alpha | Smile | Stationary | 14.500 | 2.867 | 2.867 | 0.9 | 3 |
| Tesla | Model 3 Sta. Range + | EV | 50.000 | 11.000 | - | 0.9 | 5 |
| VW | e-Golf | EV | 35.800 | 7.200 | - | 0.9 | 4 |
| Nissan | Leaf | EV | 40.000 | 3.600 | - | 0.9 | 4 |
| VW | ID.4 | EV | 82.000 | 11.000 | - | 0.9 | 3 |
| VW | e-Up! | EV | 36.800 | 7.200 | - | 0.9 | 2 |
| Honda | e | EV | 35.500 | 6.600 | - | 0.9 | 1 |
| Peugeot | e-208 | EV | 50.000 | 7.400 | - | 0.9 | 1 |
| Parameter | Designation | Value | Units | |
|---|---|---|---|---|
| Min | Max | |||
| Number of prosumers | 15 | - | ||
| Number of EV | 20 | - | ||
| Retail price (Prosumers) | 0.094 | 0.294 | EUR/kWh | |
| Export price (feed-in, spot market) | 0 | 0.095 | EUR/kWh | |
| Retail price (EVs) | 0.101 | 0.189 | EUR/kWh | |
| P2V prices | 0.051 | 0.098 | EUR/kWh | |
| Fixed costs of prosumers | 0.218 | 1.024 | EUR/day | |
| Fixed costs of EV | 0.292 | 0.719 | EUR/day | |
| Prosumer electricity generation | 0 | 10.349 | kW | |
| Prosumers electricity load | 0 | 10.277 | kW | |
| The maximum power limit (prosumers) | 3.450 | 20.700 | kW | |
| The maximum export power limit | 1.725 | 10.350 | kW | |
| The maximum P2V power transaction limit | 1.725 | 10.350 | kW | |
| The initial level of prosumer battery | 0 | kWh | ||
| Max. charge/discharge power prosumer battery | 2.867 | 5.000 | kW | |
| The maximum level for the prosumer battery | 13.500 | 15.000 | kWh | |
| Consumption related to PV movements | 0 | 13.300 | kWh | |
| The maximum limit for EV charge | 3.600 | 11.000 | kW | |
| The maximum power limit retailer contract | 4.600 | 13.800 | kW | |
| The minimum level for the prosumer battery | 7.100 | 16.400 | kWh | |
| The maximum level for EV battery | 35.500 | 82.000 | kWh | |
| The initial level of EV battery | 7.100 | 16.400 | kWh | |
| Maximum P2V power transaction limit (EVs) | 4.600 | 13.800 | kW | |
| Export Grid Price | Sce. | P2V Market | Total Cost (EUR) | Average Prosumer Cost (EUR) | Average EV Cost (EUR) | P2V Red. (%) | Time (s) |
|---|---|---|---|---|---|---|---|
| Feed-in tariff | 1 | No | 74.76 | 2.959 | 1.52 | - | 2.94 |
| 2 | Yes | 73.60 | 2.956 | 1.46 | 1.56 | 182.84 | |
| Market spot price | 3 | No | 75.66 | 3.019 | 1.52 | - | 2.72 |
| 4 | Yes | 73.79 | 3.014 | 1.43 | 2.47 | 78.16 | |
| Export not remunerated | 5 | No | 76.66 | 3.086 | 1.52 | - | 2.67 |
| 6 | Yes | 73.99 | 3.079 | 1.39 | 3.48 | 117.08 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faia, R.; Soares, J.; Vale, Z.; Corchado, J.M. An Optimization Model for Energy Community Costs Minimization Considering a Local Electricity Market between Prosumers and Electric Vehicles. Electronics 2021, 10, 129. https://doi.org/10.3390/electronics10020129
Faia R, Soares J, Vale Z, Corchado JM. An Optimization Model for Energy Community Costs Minimization Considering a Local Electricity Market between Prosumers and Electric Vehicles. Electronics. 2021; 10(2):129. https://doi.org/10.3390/electronics10020129
Chicago/Turabian StyleFaia, Ricardo, João Soares, Zita Vale, and Juan Manuel Corchado. 2021. "An Optimization Model for Energy Community Costs Minimization Considering a Local Electricity Market between Prosumers and Electric Vehicles" Electronics 10, no. 2: 129. https://doi.org/10.3390/electronics10020129
APA StyleFaia, R., Soares, J., Vale, Z., & Corchado, J. M. (2021). An Optimization Model for Energy Community Costs Minimization Considering a Local Electricity Market between Prosumers and Electric Vehicles. Electronics, 10(2), 129. https://doi.org/10.3390/electronics10020129








