Output Voltage and Resistance Assessment of Load-Independent-Voltage-Output Frequency Operating Inductive Wireless Power Transfer Link Utilizing Input DC-Side Measurements Only

Abstract

The paper puts forward a method for predicting output voltage and resistance of a series-series (SS) compensated inductive wireless power transfer (IWPT) link operating at load-independent-voltage-output (LIVO) frequency. The link is a part of the static system (reported by the authors in earlier works), wirelessly delivering power into an enclosed compartment without any secondary-to-primary feedback. The proposed algorithm employs input DC-side quantities (which are slow-varying and nearly noise-free, thus measured utilizing low-cost, low-bandwidth sensors) only to monitor output DC-side quantities, required for protection and/or control. It is shown that high estimation accuracy is retained as long as system parameter values are known and the phasor-domain equivalent circuit is valid (i.e., upon continuous-conduction mode (CCM) of the diode rectifier, where the proposed methodology utilizes the recently revealed modified diode rectifier equivalent model for enhanced accuracy). Under light loading (i.e., in discontinuous conduction mode (DCM)), a nonlinear correction is combined with the proposed technique to retain accuracy. The proposed methodology is well-verified by application to a 400 V to 400 V, 1 kW static IWPT link by simulations and experiments.

1. Introduction

One of the most conceivable solutions for future power delivery to portable electronics, implanted medical devices, and electric vehicles (EV’s) is the inductive wireless power transfer (IWPT) technique [1,2]. As of today, the most practiced technique for wireless energy transfer is resonant inductive with series–series (SS) compensation, which is also considered in the paper.

IWPT output is typically regulated by the primary-side inverter, employing secondary DC-side voltage and/or current feedback. Due to its contactless nature, it goes without saying that the transfer of output current and/or voltage information to the primary side is realized by wireless communication link [3,4,5,6], typically requiring special high-cost circuits. Another solution is modulating the feedback signal over high-frequency power transfer, causing noisy ripples at IWPT output [7]. An alternative approach is identifying the output variables utilizing electrical information of primary AC-side only [8,9,10] without any feedback from the secondary side, applicable in case the values of all IWPT components except coupling coefficient and load resistance/power are known. The most common methods proposed for estimation based on primary AC-side quantities rely on the phasor-domain theory [11,12], valid for the first harmonic equivalent circuit (FHEC), which is solved as a two-port system. Once magnitudes and phases of primary AC-side variables are detected and IWPT link parameters are known, secondary-side phasors may be calculated using two-port relations. Nevertheless, the first harmonic components of primary AC-side variables are not straightforwardly available from measurements due to non-sinusoidal shape of actual instantaneous voltage and current. Therefore, commonly used RMS-based calculations and peak/zero-crossing detection-based estimations are quite imprecise. To overcome this issue, utilizing a quadrature demodulator has been recently proposed in [13]. However, the high costs and complexity of high-frequency current sensor and phase demodulator comprise the downside of the method.

For SS-compensated IWPT links, two operating frequencies were shown to yield load-independent voltage output, one residing below (capacitive region) and the other above (inductive region) resonant frequency [14,15], both being coupling coefficient dependent. In case the latter is constant and known (such as in case of wireless power delivery system into enclosed compartment, where transmitting and receiving coils reside statically on two sides of the compartment walls [12,16,17]), load-independent voltage output (LIVO) may be ideally achieved at the design stage, and the system may potentially be feedback-free [12]. In practice, LIVO operation is impossible due to primary and secondary nonzero parasitic-resistances and invalidity of the phasor-domain equivalent circuit under light loading. Thus, the output voltage remains affected by the load even if the IWPT is operating at LIVO frequency and must therefore be monitored. On the other hand, since LIVO operation is relevant for systems in which the coupling coefficient is constant and known, the load remains the only unknown quantity. Therefore, the uncertainty degree is reduced two-fold, and thus is the amount of primary-side information required for secondary-side variables prediction. It is shown in the paper that information contained in primary AC-side voltage and current magnitudes and phases (four values in total) is no longer needed, and output voltage and load resistance may be estimated using primary DC-side voltage and current (two values in total) only.

The static SS-compensated IWPT link (IWPTL) considered in the paper is part of an off-grid AC-AC wireless power delivery system into a glass-enclosed compartment, schematically shown in Figure 1 [12,17]. The IWPT link is fed by a standard grid-interfacing boost-type unity power factor AC/DC converter with regulated DC output V_I and terminated by a typical load-interfacing buck-type DC/AC converter supplying regulated AC output v_L to a load. While both AC/DC and DC/AC converters possess individual local closed-loop control schemes, the IWPT link operates without secondary-to-primary feedback. As shown in [17], in order to assure correct operation of DC-AC converter, the allowed range of IWPT link output voltage V_O is restricted. Therefore, it is highly desired to monitor both output voltage and equivalent load resistance of the IWPT for protection purposes employing the proposed methodology without utilizing any receiver-to-transmitter feedback.

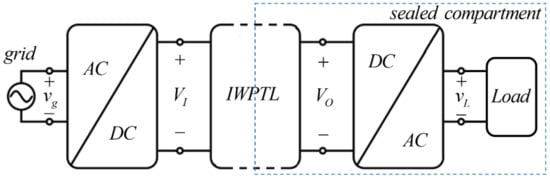
Figure 1. Wireless power delivery system based on SS-compensated IWPTL.

The rest of the paper is organized as follows. Series-series compensated IWPT link is analyzed in Section 2, presenting phasor domain solution and time-domain solution alongside the theory of LIVO operation. Relations between primary DC-side quantities to primary and secondary AC-side phasors are revealed in Section 3. An example of the proposed method application is described in detail in Section 4. The paper is summarized in Section 5.

2. SS-Compensated IWPT Link Essentials

2.1. The Circuitry

Consider an SS-compensated IWPTL, shown in Figure 2, with V_I and V_O denoting input and output dc voltages, L₁ and L₂ symbolizing primary and secondary inductances, C₁ and C₂ representing primary and secondary compensating capacitances, r₁ and r₂ signifying equivalent primary and secondary equivalent series resistances, k indicating coupling coefficient, C_I and C_O standing for input and output filter capacitances and R_O denotes equivalent load resistance, respectively. The inverter is operated with 50% duty cycle at constant frequency ω = 2π∙f, thus that inverter output voltage

$$v_1(t)=\left\{\begin{array}{cc}{V}_I,& 0<\omega t\le \pi \\ -V_I& \pi <\omega t\le 2\pi \end{array}\right\}={\displaystyle \sum _{n=1,odd}^{\infty }{V}_{1n}\sin (n\omega t)}$$

(1)

is a bipolar square-wave signal with V_1n denoting nth harmonic magnitude. Primary-side current is given by

$$i_1(t)={\displaystyle \sum _{n=1,odd}^{\infty }{I}_{1n}}\sin \left(n\omega t+{\phi }_n\right)$$

(2)

with I_1n and φ_n denoting nth harmonic magnitude and phase, respectively. The resonant frequency of the system ω_R is given by

$${\omega }_R=\frac{1}{\sqrt{L_1{C}_1}}=\frac{1}{\sqrt{L_2{C}_2}}$$

(3)

and secondary-side variables are described by

$$v_2(t)={\displaystyle \sum _{n=1,odd}^{\infty }{V}_{2n}}\sin \left(n\omega t+{\theta }_n\right),\hspace{0.33em} i_2(t)={\displaystyle \sum _{n=1,odd}^{\infty }{I}_{2n}}\sin \left(n\omega t+{\delta }_n\right)$$

(4)

with V_2n, I_2n and θ_n, δ_n denoting nth secondary voltage and current harmonic magnitudes and phases, respectively.

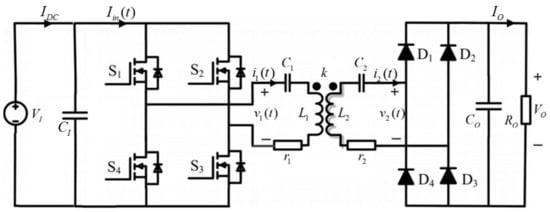
Figure 2. SS-compensated IWPT link.

The IWPT link may be represented in phasor-domain by its first-harmonic equivalent circuit (FHEC) shown in Figure 3 [5] with

$$\begin{array}{cccc}{\overrightarrow{v}}_1=V_{11}\angle 0,& {\overrightarrow{i}}_1=I_{11}\angle {\phi }_1,& {\overrightarrow{v}}_2=V_{21}\angle {\theta }_1,& {\overrightarrow{i}}_2=I_{21}\angle {\delta }_1\end{array}$$

(5)

and equivalent AC-side load [9]

$${\overrightarrow{Z}}_L=\frac{{\overrightarrow{v}}_2}{{\overrightarrow{i}}_2}=R_L+j\omega L_L$$

(6)

Figure 3. Equivalent phasor-domain circuit.

Denoting

$$\begin{array}{c}\begin{array}{ccc}{X}_1=\omega L_1-\frac{1}{\omega C_1},& X_2=\omega L_2-\frac{1}{\omega C_2},& X_M=\omega k\sqrt{L_1{L}_2}\end{array}\\ {\overrightarrow{Z}}_1=r_1+j{X}_1,{\overrightarrow{Z}}_2=r_2+j{X}_2,\end{array}$$

(7)

Figure 3 suggests that phasor domain solution of secondary AC-side variables may be derived as

$$\left(\begin{array}{c}{\overrightarrow{v}}_2\\ {\overrightarrow{i}}_2\end{array}\right)=\left(\begin{array}{cc}-j\frac{{\overrightarrow{Z}}_2}{X_M}& j\frac{{\overrightarrow{Z}}_1{\overrightarrow{Z}}_2+X_M^2}{X_M}\\ j\frac{1}{X_M}& -j\frac{{\overrightarrow{Z}}_1}{X_M}\end{array}\right)\left(\begin{array}{c}{\overrightarrow{v}}_1\\ {\overrightarrow{i}}_1\end{array}\right)$$

(8)

Representing voltage and current phasors as a sum of in-phase (real) and quadrature (imaginary) components

$$\begin{array}{cc}{\overrightarrow{v}}_1=V_{1R}+j{V}_{1I},& {\overrightarrow{v}}_2=\end{array}{V}_{2R}+j{V}_{2I},\begin{array}{cc} {\overrightarrow{i}}_1=I_{1R}+j{I}_{1I},& {\overrightarrow{i}}_2=\end{array}{I}_{2R}+j{I}_{2I},$$

(9)

respectively, and substituting into Equation (8) yields

$$\left(\begin{array}{l}{V}_{2R}\\ V_{2I}\\ I_{2R}\\ I_{2I}\end{array}\right)=\left(\begin{array}{cccc}\frac{X_2}{X_M}& \frac{r_2}{X_M}& -\frac{X_1{r}_2+r_1{X}_2}{X_M}& -\frac{r_1{r}_2-X_1{X}_2-X_M^2}{X_M}\\ \frac{-r_2}{X_M}& \frac{X_2}{X_M}& \frac{r_1{r}_2-X_1{X}_2-X_M^2}{X_M}& -\frac{X_1{r}_2+r_1{X}_2}{X_M}\\ 0& \frac{-1}{X_M}& \frac{X_1}{X_M}& \frac{r_1}{X_M}\\ \frac{1}{X_M}& 0& \frac{-r_1}{X_M}& \frac{X_1}{X_M}\end{array}\right)\cdot \left(\begin{array}{l}{V}_{1R}\\ V_{1I}\\ I_{1R}\\ I_{1I}\end{array}\right)$$

(10)

Considering Equations (6) and (9), AC-side voltage and load impedance components are then given by

$$\begin{array}{l}\begin{array}{cc}{V}_{21}=\sqrt{V_{2R}^2+V_{2I}^2},& {\theta }_1={\tan }^{-1}\left(\frac{V_{2I}}{V_{2R}}\right)\end{array},\\ R_L=\frac{V_{2R}{I}_{2R}+V_{2I}{I}_{2I}}{I_{2R}^2+I_{2I}^2}, X_L=\frac{V_{2I}{I}_{2R}+V_{2R}{I}_{2I}}{I_{2R}^2+I_{2I}^2}\end{array}$$

(11)

2.2. LIVO Operation

AC voltage gain of the circuit in Figure 3 may be derived from Equation (8) as [12]

$$\frac{{\overrightarrow{v}}_2}{{\overrightarrow{v}}_1}=\frac{j{X}_M}{{\overrightarrow{Z}}_1+\frac{{\overrightarrow{Z}}_1{\overrightarrow{Z}}_2+X_M^2}{{\overrightarrow{Z}}_L}}$$

(12)

LIVO frequencies (imposing load-independent voltage gain Equation (12)) can be calculated by forcing the load-related component in Equation (12) to zero, i.e.,

$${\overrightarrow{Z}}_1{\overrightarrow{Z}}_2+X_M^2=0$$

(13)

Neglecting equivalent series resistances $r_1$ and $r_2$ brings Equation (13) to

$$X_1{X}_2=X_M^2.$$

(14)

Two LIVO frequencies ${\omega }_1$ and ${\omega }_2$are identified by solving Equation (14) using Equations (4) and (7) as

$${\omega }_1=\frac{{\omega }_R}{\sqrt{1+k}},\hspace{0.33em}{\omega }_2=\frac{{\omega }_R}{\sqrt{1-k}}$$

(15)

with ${\omega }_1$ residing below resonance (capacitive region) and ${\omega }_2$ belonging to the inductive region above resonance, i.e., ${\omega }_2>{\omega }_R>{\omega }_1$. Inductive region frequency ${\omega }_2$ is typically used for LIVO operation, allowing a lower harmonic distortion of primary and secondary currents and natural zero voltage switching (ZVS) of inverter valves, and is considered in this paper. In order to derive load impedance components in Equation (11), the time-domain solution of the circuit in Figure 2 is necessary, carried out in the following subsection.

2.3. Equivalent Input Impedance of Diode Rectifier Operating in CCM

Operation at $\omega ={\omega }_2$ yields (neglecting equivalent series resistances $r_1$ and $r_2$) θ₁ = 0 (see [12] for details). Time-domain behavior of the IWPTL in Figure 2 is then described by the following system of differential equations,

$$\begin{array}{l}{v}_1(t)=u_{C1}(t)+(1-k)L_1\frac{d{i}_1(t)}{dt}+k{L}_1\frac{d\left(i_1(t)-\sqrt{\frac{L_2}{L_1}}{i}_2(t)\right)}{dt}\\ v_2(t)=-u_{C2}(t)-(1-k)L_2\frac{d{i}_2(t)}{dt}+k\sqrt{L_2{L}_1}\frac{d\left(i_1(t)-\sqrt{\frac{L_2}{L_1}}{i}_2(t)\right)}{dt}\\ i_1(t)=C_1\frac{d{u}_{C1}(t)}{dt}\\ i_2(t)=C_2\frac{d{u}_{C2}(t)}{dt}\end{array}$$

(16)

with u_C1, u_C2 denoting instantaneous voltages across primary and secondary capacitances, respectively, and initial conditions given by

$$i_2(0)=i_2(\frac{{\omega }_2}{\pi })=0$$

(17)

and

$$u_{C1}(0)=-u_{C1}(\frac{{\omega }_2}{\pi }), u_{C2}(0)=-u_{C2}(\frac{{\omega }_2}{\pi })$$

(18)

Solving Equation (17) with (18) yields [14]

$$\begin{array}{l}{i}_1(t)=\sqrt{\frac{L_2}{L_1}}\left(\frac{V_O}{{\omega }_2{L}_2\sqrt{1-k^2}}\sin ({\omega }_{1}t)-\frac{V_O}{{\omega }_2{L}_2\sqrt{1-k^2}}\tan (\frac{\pi }{2}\sqrt{\frac{1-k}{1+k}})\cos ({\omega }_{1}t)\right)+\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\sqrt{\frac{L_2}{L_1}}\left(\frac{\pi }{2}{I}_O\sin ({\omega }_{2}t)-\frac{V_O}{{\omega }_2{L}_2\sqrt{1-k^2}}\tan (\frac{\pi }{2}\sqrt{\frac{1-k}{1+k}})\cos ({\omega }_{2}t)\right),\\ i_2(t)=-\frac{V_O}{{\omega }_2{L}_2\sqrt{1-k^2}}\sin ({\omega }_{1}t)+\frac{V_O}{{\omega }_2{L}_2\sqrt{1-k^2}}\tan (\frac{\pi }{2}\sqrt{\frac{1-k}{1+k}})\cos ({\omega }_{1}t)+\frac{\pi }{2}{I}_O\sin ({\omega }_{2}t)-\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\frac{V_O}{{\omega }_2{L}_2\sqrt{1-k^2}}\tan (\frac{\pi }{2}\sqrt{\frac{1-k}{1+k}})\cos ({\omega }_{2}t)\end{array}$$

(19)

with

$$\hspace{0.17em}\hspace{0.17em}{I}_O=\frac{V_O}{R_O}=\frac{{\omega }_2}{\pi }{\displaystyle \underset{0}{\overset{\frac{\pi }{{\omega }_2}}{\int }}{i}_2(t)dt}$$

(20)

denoting the output DC-side current of the IWPT link. Observing Equation (19), it may be concluded that although IWPT link operation frequency is ${\omega }_2$, both current contains a term at lower LIVO frequency ${\omega }_1$ as well. Since in general ${\omega }_2$ is not a multiple of ${\omega }_1$, the term at lower LIVO frequency ${\omega }_1$ may contribute to both active and reactive components. Hence, when calculating phasor domain components of secondary current, it is necessary to utilize Fourier decomposition of Equation (19) thus that

$$\begin{array}{l}{I}_{2R}=\frac{2\pi }{{\omega }_2}{\displaystyle \underset{0}{\overset{\frac{\pi }{\omega }}{\int }}{i}_2(t)}\sin ({\omega }_{2}t)dt=\frac{\pi }{2}{I}_O,\\ I_{2I}=\frac{2\pi }{{\omega }_2}{\displaystyle \underset{0}{\overset{\frac{\pi }{\omega }}{\int }}{i}_2(t)}\cos ({\omega }_{2}t)dt=\frac{V_O}{{\omega }_2{L}_2}\left(\frac{2}{\pi k}-\frac{1}{\sqrt{1-k^2}}\tan (\frac{\pi }{2}\sqrt{\frac{1-k}{1+k}})\right)\end{array}$$

(21)

On the other hand, secondary side voltage phasor may be expressed as

$${\overrightarrow{v}}_2=V_{2R}+j{V}_{2I}=\frac{4V_O}{\pi }+j0$$

(22)

Equivalent input impedance of the diode rectifier ${\overrightarrow{Z}}_L$ is typically considered as series-connected resistance and reactance (Figure 4a), calculated from Equations (6) and (11). However, it may also be expressed by parallel-connected resistance and reactance (Figure 4b). Noticing that

$${\overrightarrow{i}}_2=I_{2R}+j{I}_{2I}=\frac{\pi }{2}{I}_O+j\frac{V_O}{{\omega }_2{L}_2}\left(\frac{2}{\pi k}-\frac{1}{\sqrt{1-k^2}}\tan (\frac{\pi }{2}\sqrt{\frac{1-k}{1+k}})\right),$$

(23)

there are

$$R_{L\_p}=\frac{V_{2R}}{I_{2R}}=\frac{8}{{\pi }^2}\frac{V_O}{I_O}$$

(24)

and

$$L_{L\_p}=\frac{1}{{\omega }_2}{X}_{L\_p}=\frac{1}{{\omega }_2}\frac{V_{2R}}{I_{2I}}=\frac{\sqrt{1-k^2}}{\frac{\pi }{4}\tan \left(\frac{\pi }{2}\sqrt{\frac{1-k}{1+k}}\right)-\frac{\sqrt{1-k^2}}{2k}}{L}_2$$

(25)

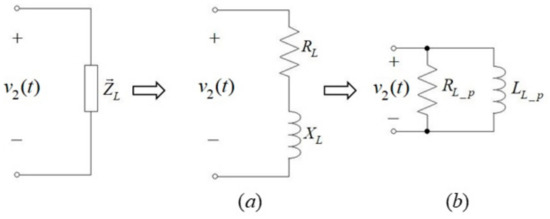
Figure 4. Equivalent load impedance circuit: (a) series form, (b) parallel form.

It may be concluded from Equation (25) that for a known secondary side inductance L₂ and coupling coefficient k, inductance $L_{L\_p}$ is both well defined and load-independent.

3. Input DC-Side Quantities-Based Estimation Method

3.1. Primary AC-Side Variables in-Phase Components Derivation

The first harmonic in-phase component of the inverter output voltage is related to input DC voltage as

$$V_{1R}=\frac{4}{\pi }{V}_I$$

(26)

Moreover, inverter input current i_in(t) is related to inverter output current i₁(t) as (see Figure 5)

$$i_{in}(t)=\left\{\begin{array}{cc}{i}_1(t),& 0<\omega t\le \pi \\ -i_1(t),& \pi <\omega t\le 2\pi \end{array}\right.\hspace{0.17em}$$

(27)

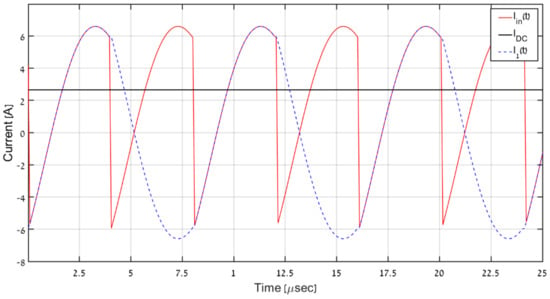
Figure 5. Primary-side current shapes of a LIVO-operating IWPT.

On the other hand, input DC-side current of the IWPT link I_DC is given by

$$I_{DC}=\frac{{\omega }_2}{\pi }{\displaystyle \underset{0}{\overset{\frac{\pi }{{\omega }_2}}{\int }}{i}_{in}(t)dt}$$

(28)

Consequently, the first harmonic in-phase component of primary AC-side current is obtained as

$$I_{1R}=\frac{\pi }{2}{I}_{DC}=I_{11}\cos ({\phi }_1)$$

(29)

3.2. Estimation of Output DC-Side Voltage and Resistance Utilizing Input DC-Side Variables in CCM

Using Equations (10), (26), (28), and (29), secondary AC-side output voltage is given by

$${\overrightarrow{v}}_2=V_{2R}=\frac{X_2{V}_{1R}-(X_2{r}_2+X_1{r}_1)I_{1R}-(r_1{r}_2-X_1{X}_2+X_M^2)I_{1I}}{X_M}$$

(30)

i.e., quadrature component of primary AC-side current can be expressed as

$$I_{1I}=-V_{1R}\frac{X_2+X_{L\_p}}{X_1{X}_{L\_p}-r_1{r}_2+X_1{X}_2-X^2{}_M}+I_{1R}\frac{r_1{X}_{L\_p}+X_2{r}_1+X_1{r}_2}{X_1{X}_{L\_p}-r_1{r}_2+X_1{X}_2-X^2{}_M}$$

(31)

Furthermore, substituting Equations (22), (25), and (31) into (10) yields

$$\left(\begin{array}{c}{V}_{2R}\\ V_{2I}\\ I_{2R}\\ I_{2I}\end{array}\right)=\frac{1}{X_M(X_1{X}_{L\_p}-r_1{r}_2+X_1{X}_2-X^2{}_M)}\left(\begin{array}{cc}\hfill A& \hfill -E\\ \hfill B& \hfill \hspace{0.17em}F\\ \hfill -C& \hfill G\\ \hfill -D& \hfill H\end{array}\right)\left(\begin{array}{l}\frac{4}{\pi }\hspace{0.17em}{V}_I\\ \frac{2}{\pi }\hspace{0.17em}{I}_{DC}\end{array}\right)$$

(32)

with

$$\begin{array}{l}A=X_{L\_p}(r_1{r}_2+X^2{}_M), B=r_1{X}_2(X_{L\_p}+X_2)+r_2(r_1{r}_2+X^2{}_M),\hspace{0.33em}\\ C=r_1(X_2+X_{L\_p}), D=r_1{r}_2+X^2{}_M, E=X_{L\_p}{r}_2(X^2{}_1+r^2{}_1)+r_1{X}_{L\_p}{X}^2{}_M),\hspace{0.33em} \\ F=X_2(-r^2{}_1-X^2{}_1)(X_{L\_p}+X_2)+X^2{}_M(X_1{X}_{L\_p}-2r_1{r}_2+2X_1{X}_2-X^2{}_M)-r^2{}_2(r^2{}_1-X^2{}_1),\\ G=(X^2{}_1+r^2{}_1)(X_{L\_p}+X_2)-X_1{X}^2{}_M, H=r_2(X^2{}_1+r^2{}_1)+r_1{X}^2{}_M\end{array}$$

(33)

It may be concluded that primary and secondary AC-side voltage and current components may be obtained utilizing primary DC-side variables V_I and I_DC only. In case the diode rectifier operates in continuous conduction mode (CCM), combining the solution of Equation (32) with Equation (11) yields [9,18]

$$\begin{array}{cc}{V}_O=\frac{\pi }{4}{V}_{21},& R_O=\frac{{\pi }^2}{8}{R}_L=\frac{V_O^2}{P_O}\end{array}$$

(34)

with P_O denoting DC-side output load power of the system.

3.3. Correction for DCM Regime

Operation at $\omega ={\omega }_2$ in CCM while neglecting equivalent series resistances $r_1$ and $r_2$ yields) cf. (12)–(15)) [17]

$${\overrightarrow{v}}_2=j{\overrightarrow{v}}_1\sqrt{\frac{L_2}{L_1}}\Rightarrow V_O=\sqrt{\frac{L_2}{L_1}}{V}_I$$

(35)

However, parasitic resistances $r_1$ and $r_2$ are nonzero in practice. Moreover, as mentioned above, the linear relation between secondary AC and DC side variables Equation (34) is only valid in case the diode rectifier operates in CCM and does not hold in DCM. As presented in [19], the imaginary part of the diode rectifier input impedance possesses inductive characteristics, which are relatively insignificant in CCM (and may thus be neglected [14]) but rise significantly in DCM. Moreover, IWPT currents possess significant harmonic content in the DCM regime thus that the FHEC (Figure 3) is no longer accurate. Consequently, operation at ${\omega }_1$ or ${\omega }_2$ does not result in LIVO in practice. It was demonstrated in [17] that SS-compensated IWPTL output voltage at LIVO frequency is given by

$$V_O\approx \left\{\begin{array}{cc}\sqrt{\frac{L_2}{L_1}}{V}_I-\frac{{\pi }^2}{8V_I}\left(\sqrt{\frac{L_1}{L_2}}{r}_2+\sqrt{\frac{L_2}{L_1}}{r}_1\right)P_O,& P_O\ge P_{O,B}\\ X_1+X_2\cdot P_O^{-0.5},& P_{O,MIN}<P_O\le P_{O,B}\end{array}\right.$$

(36)

with

$$\begin{array}{cc}{X}_1=V_{O,B}-P_{O,B}^{-0.5}{X}_2,& X_2=\frac{V_{O,MAX}-V_{O,B}}{P_{O,MIN}^{-0.5}-P_{O,B}^{-0.5}}\end{array},$$

(37)

where P_O denotes the load power, P_O,B signifies load power level corresponding to the bound between CCM and DCM, P_O,MIN represents minimum allowed IWPTL load power [20] and V_O,B and V_O,MAX symbolize output DC-side voltages corresponding to P_O,B and P_O,MIN, respectively. It is well-evident that neglecting patristics resistances $r_1$ and $r_2$ reduces the first row of Equation (36) (corresponding to CCM) to Equation (35). On the other hand, the relation between the output voltage and load power relation is highly nonlinear yet well-defined analytically in DCM regime (second row of Equation (36)). Nevertheless, the relation between the rows of Equation (36) is injective (one-to-one), and hence DCM-related output voltage may be estimated from its corresponding CCM counterpart. The relation between the load resistance value and the load power may be obtained by substituting (36) into

$$R_O=\frac{1}{P_O}{V}_O^2$$

(38)

4. Example

Consider the 1 kW SS-compensated IWPT link shown in Figure 2 with parameter values summarized in Table 1, operating at LIVO frequency $\omega ={\omega }_2$. According to Table 1, resonant and operating frequencies of the IWPT link are

$${\omega }_R=2\pi \cdot 67000\frac{rad}{s},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\omega ={\omega }_2=2\pi \cdot 124500\frac{rad}{s}$$

(39)

respectively. The IWPT link is designed to be utilized for delivering power into an enclosed compartment through 10 mm-thick polyvinyl-chloride plate (see Figure 6) with near-unity voltage gain. The transmitter-side inverter is realized by modified Transphorm TDINV1000P100-KIT 1-kW Inverter GaN Evaluation Platform (Transphorm, Goleta, CA, USA) [21] utilizing 650 V, 150 mΩ TPH3206PSB gallium-nitride field-effect transistors (Transphorm, Goleta, CA, USA) driven by silicon labs SI8273AB1 isolated drivers (Skyworksinc, Irvine, CA, USA). Switching signals are generated by Texas Instrument TMS320F28335 digital signal processor (Texas Instruments, Dallas, TX, USA). The diode rectifier is formed by four Microsemi APT40DQ120BG devices. The system is fed from IT61517D ITECH high-voltage DC power supply (ITECH, New Taipei City 23586, Taiwan) and loaded by Maynuo M9715 DC (Maynuo, Nanjing, Jiangsu 20019, China) electronic load, functioning in constant-power mode. IWPT link DC output is terminated by a 20 kΩ resistor to realize the minimum allowed load of P_O,MIN = 9 W [20].

Table 1. System Parameter Values.

Parameter	Value	Units
VI	400	V
L1, L2	180	µH
k	0.71	--
r1, r2	1.5	Ω
C1, C2	31.2	nF
CO	660	µF

Figure 6. Experimental setup.

Output voltage and load resistance versus load power curves were derived experimentally in [18] and are reproduced in Figure 7 and Figure 8, respectively. The output voltage versus load power relation of the system is given by

$$V_O\approx \left\{\begin{array}{cc}395-0.008P_O,& P_O\ge 250W\\ 386+145P_O^{-0.5},& 9W<P_O\le 250W\end{array}\right.$$

(40)

corresponding to (36) with V_O,B = 395 V, V_O,MAX = 428 V, P_O,B = 250 W and P_O,MIN = 9 W. Due to the fact that CCM is assumed for the phasor domain solution Equation (10), IWPT link output voltage would be given by the first row of Equation (40) all load levels. In order to include a nonlinear correction to allow accurate estimation of V_O in DCM,

$$V_O^{est}=\left\{\begin{array}{cc}{V}_O,& V_O\le V_{O,B}=395\\ 386+145{\left(\frac{397-V_O}{0.0095}\right)}^{-0.5},& V_O>V_{O,B}=395\end{array}\right.\hspace{0.17em}$$

(41)

yields the final IWPT link output voltage estimate for all feasible load levels.

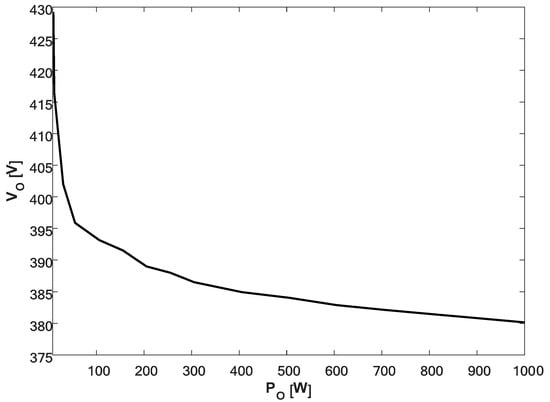
Figure 7. Measured output voltage versus load power [19].

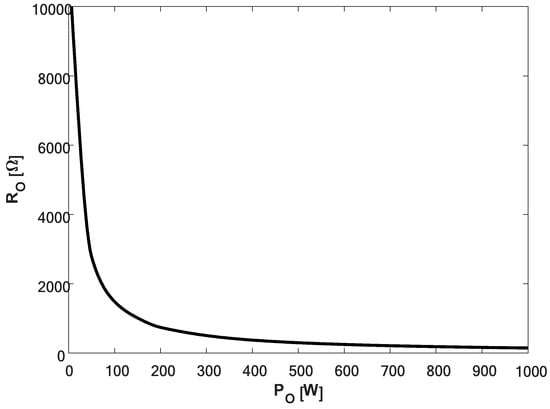
Figure 8. Measured load resistance versus load power [19].

According to Equations (38) and (40), there is

$$R_O\approx \left\{\begin{array}{cc}\frac{1}{P_O}{\left(395-0.008P_O\right)}^2,& P_O\ge 250W\\ \frac{1}{P_O}{\left(386+145P_O^{-0.5}\right)}^2,& 9W\le P_O<250W\end{array}\right.$$

(42)

Again, CCM is assumed for the phasor domain solution Equation (10) and hence IWPT link output resistance would be given by the first row of Equation (42) for all load levels. In order to perform a nonlinear correction to allow accurate estimation of R_O in DCM,

$$R_O^{est}=\left\{\begin{array}{cc}{R}_O,& R_O\le R_{O,B}=624\\ \frac{{\left(386+145{\left(580-0.55R_O\right)}^{-0.5}\right)}^2}{580-0.55R_O},& R_O>R_{O,B}=624\end{array}\right.\hspace{0.17em}$$

(43)

with $R_{O,B}=V_{O,B}^2/P_{O,B}$ signifying load resistance corresponding to diode rectifier operation on the bound between CCM and DCM yields the final IWPT link output resistance for all feasible load levels.

4.1. Simulations

In order to validate the proposed DC-side measurement-based estimation methodology, the system was simulated with input DC-side variables employed as real-time inputs to the proposed secondary AC-side estimator (32). Simulated AC-side variables were compared to estimated ones (recognized by superscript ‘est’ from now on). Time-domain AC-side waveforms for different load levels (1000 W and 600 W corresponding to CCM regime and 200 W, 100 W, and 50 W imposing DCM regime) are shown in Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 where V₁, I₁, V₂, I₂ denote primary and secondary AC-side voltages and currents, respectively; V1_h1, I1_h1, V2_h1, I2_h1 symbolize corresponding first-harmonic components (obtained by band-pass filtering of V₁, I₁, V₂, I₂ around operation frequency), and V₁₁, I₁₁, V₂₁, I₂₁ with α₁, ϕ₁, θ₁, δ₁ signify estimated phasor component values calculated using (32) and (11). It is well-evident that CCM operation imposes continuous secondary currents and the square-wave secondary voltage, as expected. On the other hand, the discontinuous nature of secondary current and distortion of secondary voltage during the non-conduction period is clearly visible in DCM.

Figure 9. Simulation results, P_O = 1000 W.

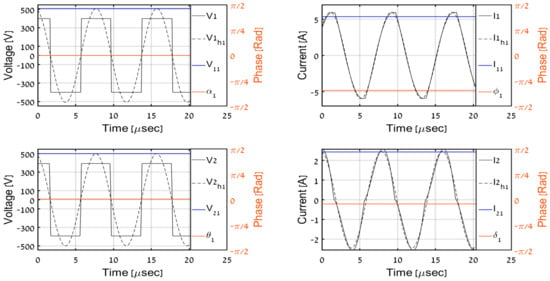
Figure 10. Simulation results, P_O = 600 W.

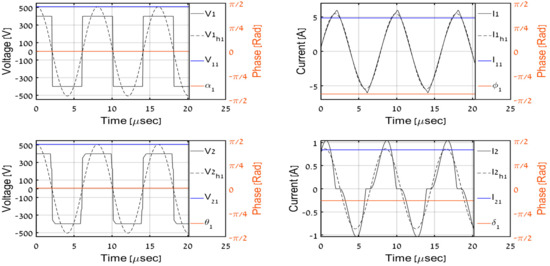
Figure 11. Simulation results, P_O = 200 W.

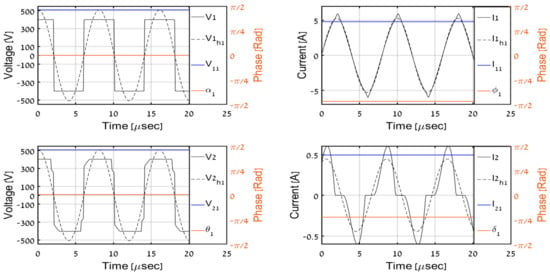
Figure 12. Simulation results, P_O = 100 W.

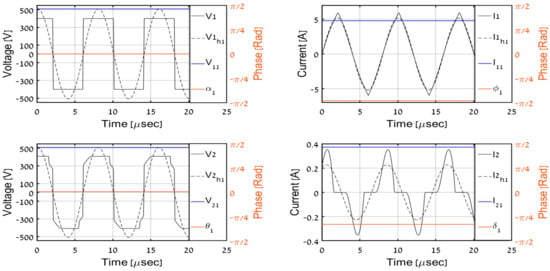
Figure 13. Simulation results, P_O = 50 W.

Observing the results, it may be concluded that the methodology results in accurate prediction of the first harmonic components of primary-side variables and their secondary-side counterparts for all load levels. Then, (34), (41), and (43) are applied to estimate the output DC-side voltage and resistance based on secondary AC-side estimations. Table 2 summarizes the estimation algorithm performance. It may be concluded that estimated values of output voltage and resistance are satisfactory to indicate the correct operation of the system, which is the major goal of the proposed process.

Table 2. Simulation results summary.

Power	${\mathit{V}}_{\mathit{O}}$	${\mathit{V}}_{\mathit{o}}^{\mathit{e}\mathit{s}\mathit{t}}$	${\mathit{R}}_{\mathit{O}}$	${\mathit{R}}_{\mathit{L}}^{\mathit{e}\mathit{s}\mathit{t}}$
1000	387.85	387.82	150.4	149
600	392.78	392.76	257.2	251
200	398.8	399	794	730
100	403.1	403.3	1625	1710
50	408.1	407.4	3330	3375

4.2. Experiments

In order to experimentally validate the proposed methodology, the system in Figure 6 was operated under multiple load levels (including those during simulations). All AC-side and DC-side variables were acquired during experiments. Then, recorded input DC waveforms were applied to (32) in an offline manner to obtain corresponding estimations and compare them to their measured counterparts. Time-domain AC-side waveforms for load levels matching the simulations are shown in Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18, respectively. It is well-evident that estimated phasor components match well with corresponding first harmonic waveforms. Table 3 summarizes the estimation algorithm performance.

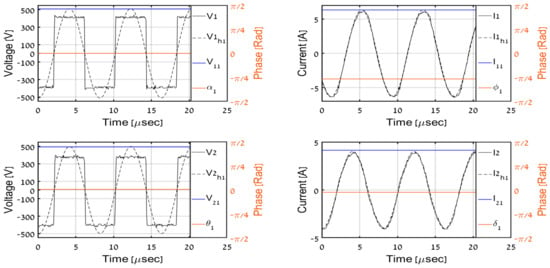
Figure 14. Experimental results, P_O = 1000 W.

Figure 15. Experimental results, P_O = 600 W.

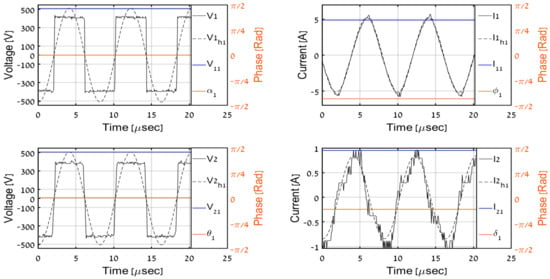
Figure 16. Experimental results, P_O = 200 W.

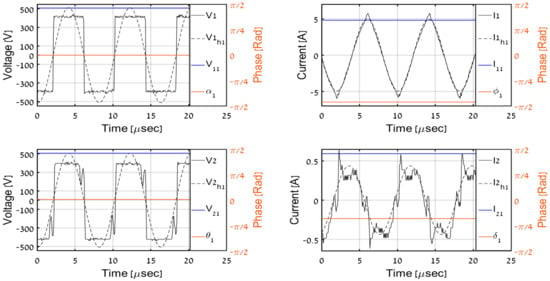
Figure 17. Experimental results, P_O = 100 W.

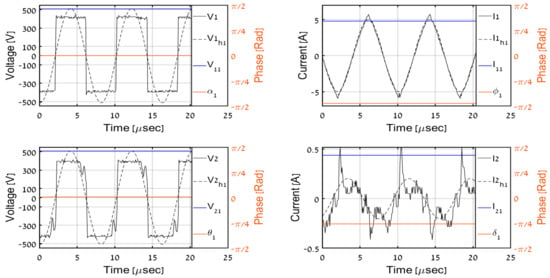
Figure 18. Experimental results, P_O = 50 W.

Table 3. Experimental results summary.

Power	${\mathit{V}}_{\mathit{O}}$	${\mathit{V}}_{\mathit{o}}^{\mathit{e}\mathit{s}\mathit{t}}$	${\mathit{R}}_{\mathit{O}}$	${\mathit{R}}_{\mathit{L}}^{\mathit{e}\mathit{s}\mathit{t}}$
1000	387.1	387.25	149	145
600	389.9	391.1	250	239
200	396	395.4	764	716
100	399.3	400	1710	1765
50	403	404.5	2937	3295

It should be emphasized that DCM secondary current waveforms are somewhat different from their simulation counterparts. This is due to the fact that the simulation model does not include parasitic capacitances of the coils and the diode bridge since they do not affect the first harmonic behavior. In general, if parasitics are brought into the model, the results look much more similar [20]. Here, the first harmonics only are of interest, and it is shown that the first harmonic approximations are quite similar in simulations and experiments.

In order to further validate algorithm performance, Figure 19 and Figure 20 graphically demonstrate estimated values of output load values and load resistance, respectively, versus corresponding measurements for the whole load power levels range. Recalling that the estimation process is used for monitoring and protection rather than for feedback control, the obtained accuracy may be considered satisfactory.

Figure 19. IWPT link measured and estimated output DC voltage versus load power.

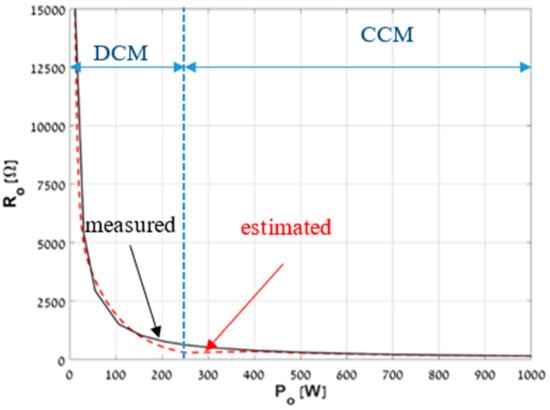
Figure 20. IWPT link measured and estimated output resistance versus load power.

5. Conclusions

Input DC-side variables-based methodology is proposed for estimation of the output voltage and resistance of IWPT link with known coupling coefficient, operating at LIVO frequency. The time-domain solution contributes the necessary additional equation to describe the system in addition to the commonly used phasor domain equation. The proposed approach yields highly accurate results in the CCM regime yet requires a nonlinear correction in DCM region. Compared to other methods used for output voltage and resistance estimation, the proposed approach uses a simpler and lower-cost solution. The outcomes were supported by simulations and experiments. Future work on the subject may focus on accuracy improvement of the method and adoption of different artificial intelligence methods [22,23,24,25,26] to perform the task.