A High-Accuracy Stochastic FIR Filter with Adaptive Scaling Algorithm and Antithetic Variables Method

Abstract

Digital filter is an important fundamental component in digital signal processing (DSP) systems. Among the digital filters, the finite impulse response (FIR) filter is one of the most commonly used schemes. As a low-complexity hardware implementation technique, stochastic computing has been applied to overcome the huge hardware cost problem of high-order FIR filters. However, the stochastic FIR filter (SFIR) scheme suffers from long processing latency and accuracy degradation. In this paper, the bit stream representation noise is theoretically analyzed, and an adaptive scaling algorithm (ASA) is proposed to improve the accuracy of SFIR with the same bit stream length. Furthermore, a novel antithetic variables method is proposed to further improve the accuracy. According to the simulation results on a 64-tap FIR filter, the ASA and AV methods gain 17 dB and 6 dB on the signal-to-noise ratio (SNR), respectively. The hardware implementation results are also presented in this paper, which illustrates that the proposed ASA-AV-SFIR filter increases 4.6 times hardware efficiency with respect to the existing SFIR schemes.

1. Introduction

Digital filter is an important fundamental component in digital signal processing (DSP) systems such as image processing [1], speech signal processing, and communication systems [2]. In particular, the finite impulse response (FIR) filter is one of the basic and most commonly used digital filters due to its linear phase feature. The major challenge of high-throughput FIR filter implementation is the huge hardware cost, especially for high-order filter applications.

Stochastic computing (SC) is a low-complexity hardware implementation technique, which has been widely used in communication systems [3], image processing systems [4], and support vector machines [5]. In the existing schemes, stochastic computing has been applied to the FIR filter to reduce the hardware cost and critical path delay. Different from the conventional 2’s complement system (TCS), the input signal and coefficients are represented with stochastic bit streams in SC-based FIR filters. As a result, the complex arithmetic operations in TCS circuits can be mapped into quite simple logic gates operation [2,6,7,8,9,10,11]. Reference [6] proposes a bipolar mapping scheme and presents a complete stochastic FIR filter architecture, where the XNOR gate can implement the multiplication. To further reduce the hardware cost, a pseudo-random number sharing method is proposed in [12], reducing the total number of random number generators in the SFIR. The SFIR filter shows advantages in the extremely low hardware cost. While it still suffers from the long processing latency and accuracy degradation due to the relatively long stochastic bit streams [4]. To improve the calculation accuracy of SFIR filters, Reference [2] proposed a two-line mapping scheme, where the sign and magnitude are represented with two bit streams, respectively, and demonstrates obvious accuracy gains. In [7], a hybrid scheme is proposed, where the multiplication is implemented with stochastic logic and the addition is still in the TCS manner. In [13,14], it was observed that stochastic computing suffers from low accuracy for small number values. Thus, a scaling method was utilized on the filter coefficient, which scales up the coefficients to achieve higher accuracy. However, the scaling method in [14] is quasi-static and coefficient-only processing, which cannot applied on the real-time input signals directly. Furthermore, there is still a lack of theoretical analysis.

In this paper, a high-accuracy stochastic FIR filter with adaptive scaling algorithm and antithetic variable method is proposed. The main contributions are as follows:

• The relationship between representation noise and represented values of a stochastic bit stream is theoretically analyzed, and it is found that stochastic computing can achieve high accuracy in certain value intervals, providing a potential way to improve the accuracy even with the same stochastic bit stream length.
• An adaptive scaling algorithm (ASA) is proposed for the SFIR to scale both the input signals and coefficients into low-noise regions.
• A novel antithetic variables method (AV) is proposed to further improve the accuracy, and the theoretical proof is also provided.
• The hardware architecture of the proposed ASA–SFIR and ASA–AV–SFIR is designed and implemented, which demonstrates high-accuracy performance advantages with respect to the existing SFIR filters.

The remainder of this paper is organized as follows. Section 2 introduces the theoretical background of FIR filter, stochastic computing, and stochastic filter designs. Afterward, the proposed design with ASA and AV is presented in Section 3. Section 4 demonstrates the performance evaluation and hardware implementation of the proposed design. The last section concludes the performed work and discusses the potential future work.

2. Theoretical Background

In this section, the background of FIR filter, stochastic computing, and the existing SFIR filters are introduced.

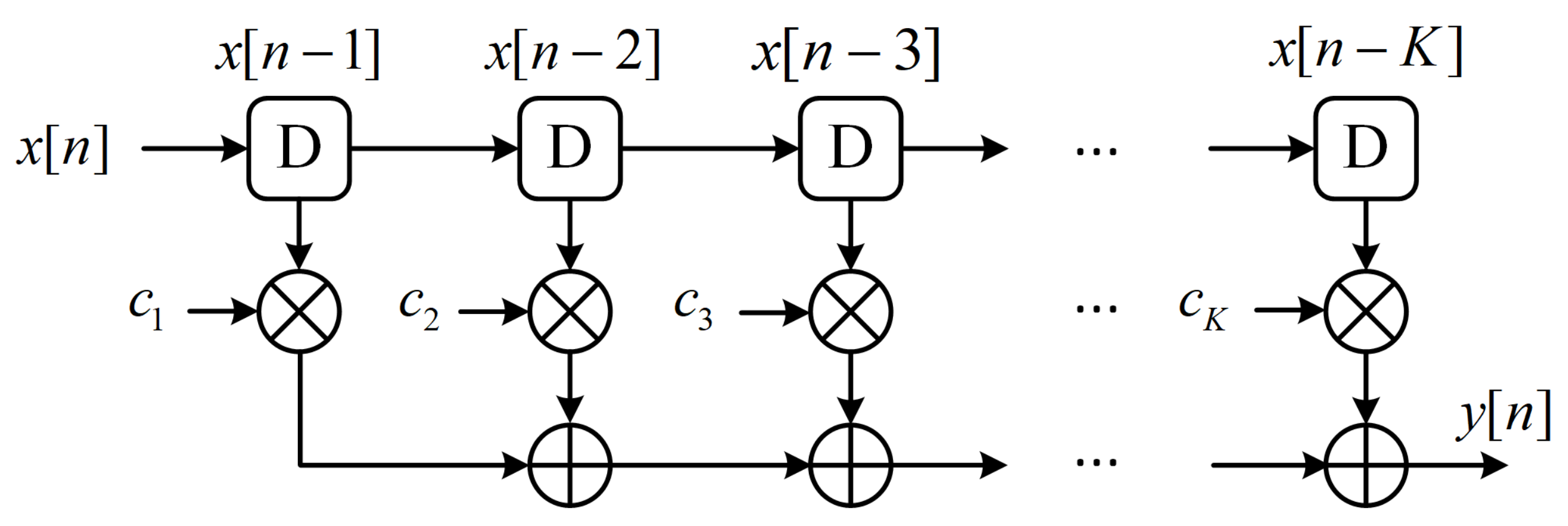
2.1. FIR Filter

The FIR filter is one of the most commonly used digital filters in digital signal processing systems. In general, the output signal $y\left[n\right]$ of a K-tap FIR filter can be calculated in the time domain as (1), where $x\left[n\right]$ is the input discrete-time signal, $c_i$ is the filter coefficient, and K is the tap of the FIR filter.

$$y\left[n\right]=\sum _{i=1}^{K}x[n-i]·c_i$$

(1)

In the practical hardware implementation, the filter coefficient $c_i$ is usually normalized as (2) to keep the dynamic range of output signals the same with input signals and avoid the calculation overflow error. The filter coefficients are all normalized in the following.

$$c_i^{\mathrm{norm}}=c_i/\sum _{j=1}^K\left|c_j\right|$$

(2)

It can be observed that K multipliers and $K-1$ adders are required for a K-tap FIR filter in the conventional hardware implementation schemes, illustrated as Figure 1. It would be a huge complexity for practical DSP systems with high-order FIR filters.

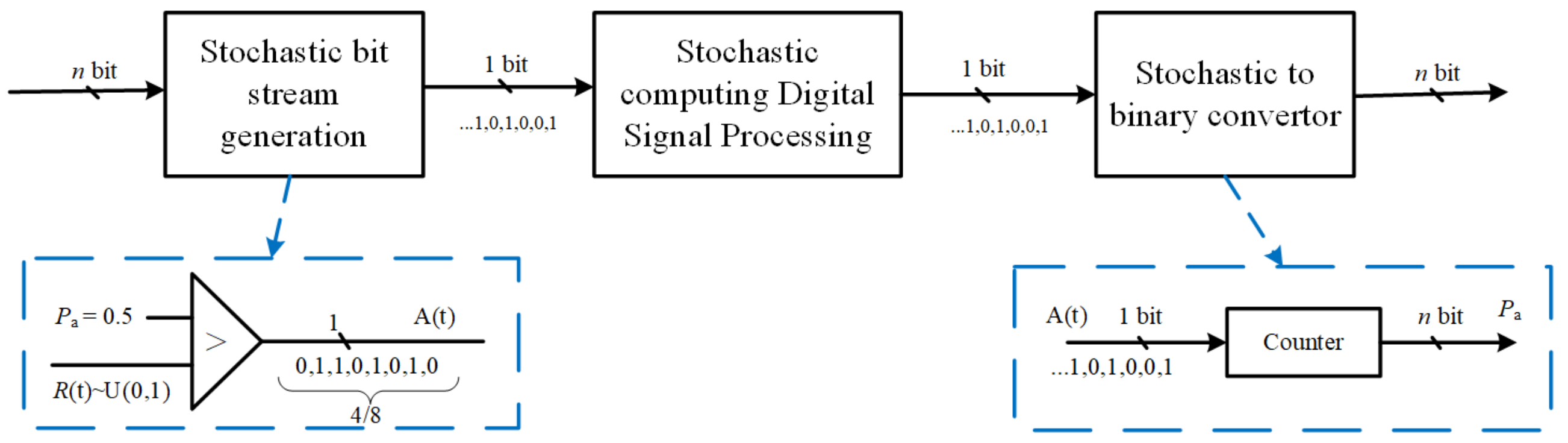
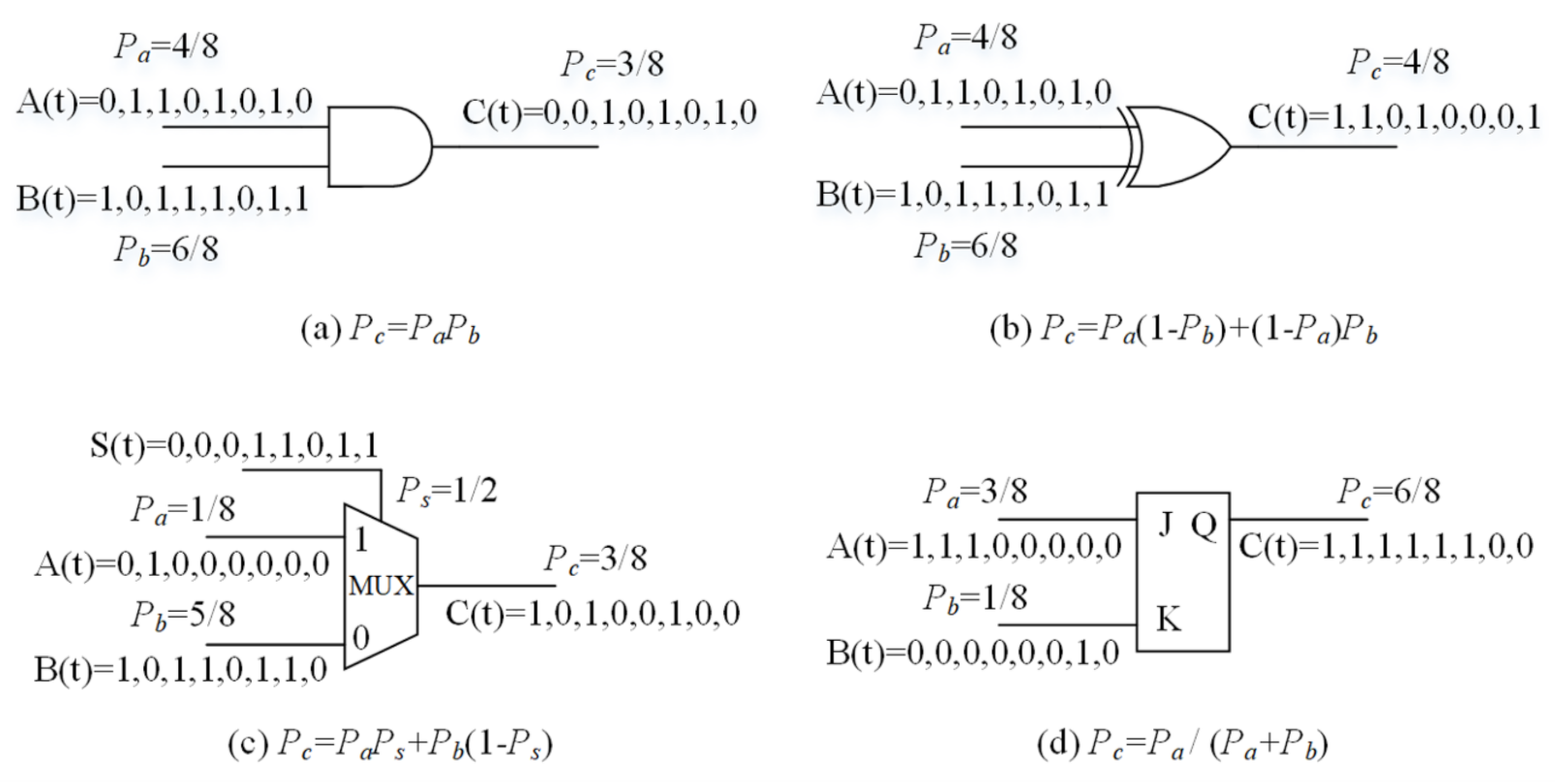
2.2. Stochastic Computing

Stochastic computing is a low complexity algorithm design and hardware implementation technique, where a numerical value a is represented with stochastic bit stream $A_i$, $i=1,2,...,N$. As a result, the complex operations in conventional TCS systems can be mapped into quite simple logic operations. A typical stochastic computing-based DSP system is illustrated in Figure 2.

• For a numerical value $a\in [0,1]$, the unipolar format can be utilized to transform it to bit stream $A_i$ by comparing it with a uniform distributed random number $R\left(t\right)\sim U(0,1)$, where $\mathrm{Pr}\{A_i=1\}=a$. The corresponding hardware architecture of unipolar format stochastic computing is shown as “stochastic bit stream generation” in Figure 2.
• For a numerical value $a\in [-1,1]$, the bipolar format bit stream generation is required [4,11], where $\mathrm{Pr}\{A_i=1\}=(a+1)/2$. The bipolar format bit stream generation could share a similar hardware architecture with unipolar format by comparing $(a+1)/2$ with the random number $R\left(t\right)$.

The stochastic computing-based logic circuits could significantly reduce the hardware cost and critical path delay compared with conventional TCS circuits, illustrated as Figure 3a, where the multiplication $P_c=P_a·P_b$ is implemented by a single “AND” logic [16]. As shown in Figure 3b, a simple “XOR” logic is used to perform $P_c=P_a·(1-P_b+(1-P_a)·P_b)$ calculation. The scaled addition $P_c=P_a·P_s+P_b·(1-P_s)$ can be realized by a multiplexer logic shown as Figure 3c, and the sum is scaled according to $P_s$. Except for the linear computation, addition and multiplication, the division $P_c=P_a/(P_a+P_b)$ can be implemented by a J-K Flip-Flop illustrated as Figure 3d. The backward-transformed numerical value is shown as “Stochastic to binary convertor” in Figure 2.

2.3. Stochastic FIR Filter

To reduce the hardware cost of the FIR filter, a bipolar format SFIR filter is proposed in [6], where input signals and coefficients are normalized into the range [−1,1] and transformed into bit streams. As a result, the multiplication and addition involved in the FIR filter are mapped into “XNOR” logic and multiplexer, respectively. The bipolar-based SFIR filter has an extremely low hardware costs. However, the main drawback is the degradation of accuracy.

To overcome the accuracy degradation problem, a two-line scheme-based SFIR filter is proposed in [2], where each numerical value is represented with two stochastic bit streams: one is sign bit-stream and the other is magnitude bit-stream. The multiplication of two magnitude bit-streams and sign bit-streams are mapped into “AND” logic and “XOR” logic, respectively. The addition is implemented with a novel non-scaled two-line adder. The two-line scheme outperforms the bipolar scheme on accuracy with comparable hardware cost. However, there is still a relatively large gap with the ideal performance.

3. Stochastic FIR Filter with Adaptive Scaling

In this section, the representation noise of a stochastic bit stream is firstly analyzed in Section 3.1. Afterward, an adaptive scaling algorithm (ASA) is proposed in Section 3.2. Furthermore, the antithetic variables (AV) method is introduced in Section 3.3. Finally, ASA–AV–SFIR filter architecture is presented in Section 3.4.

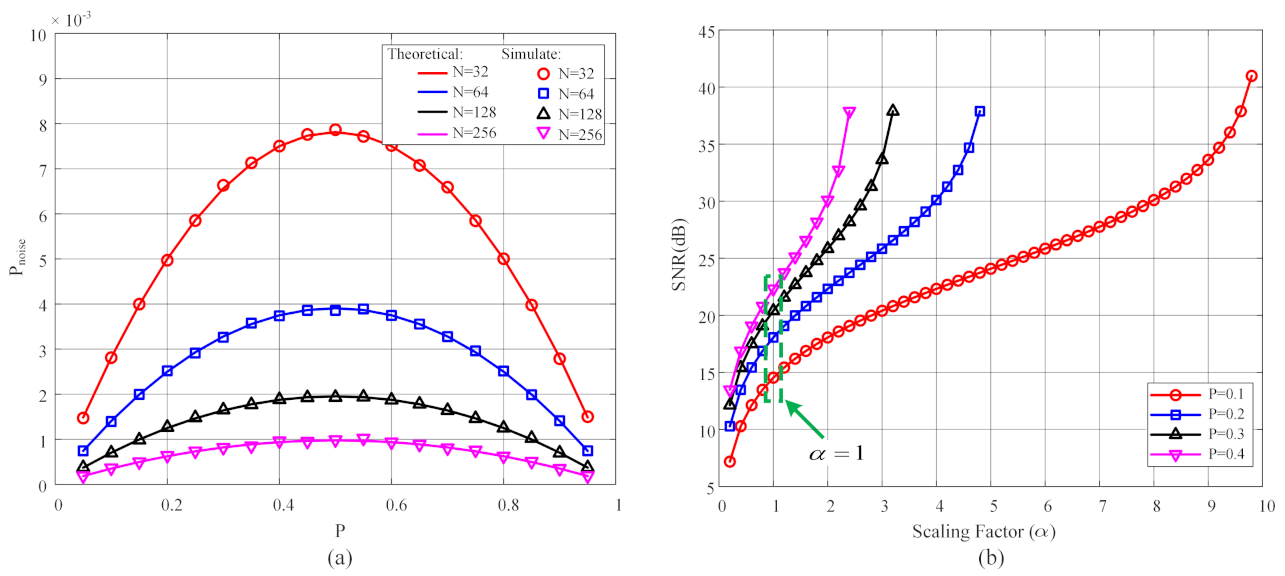
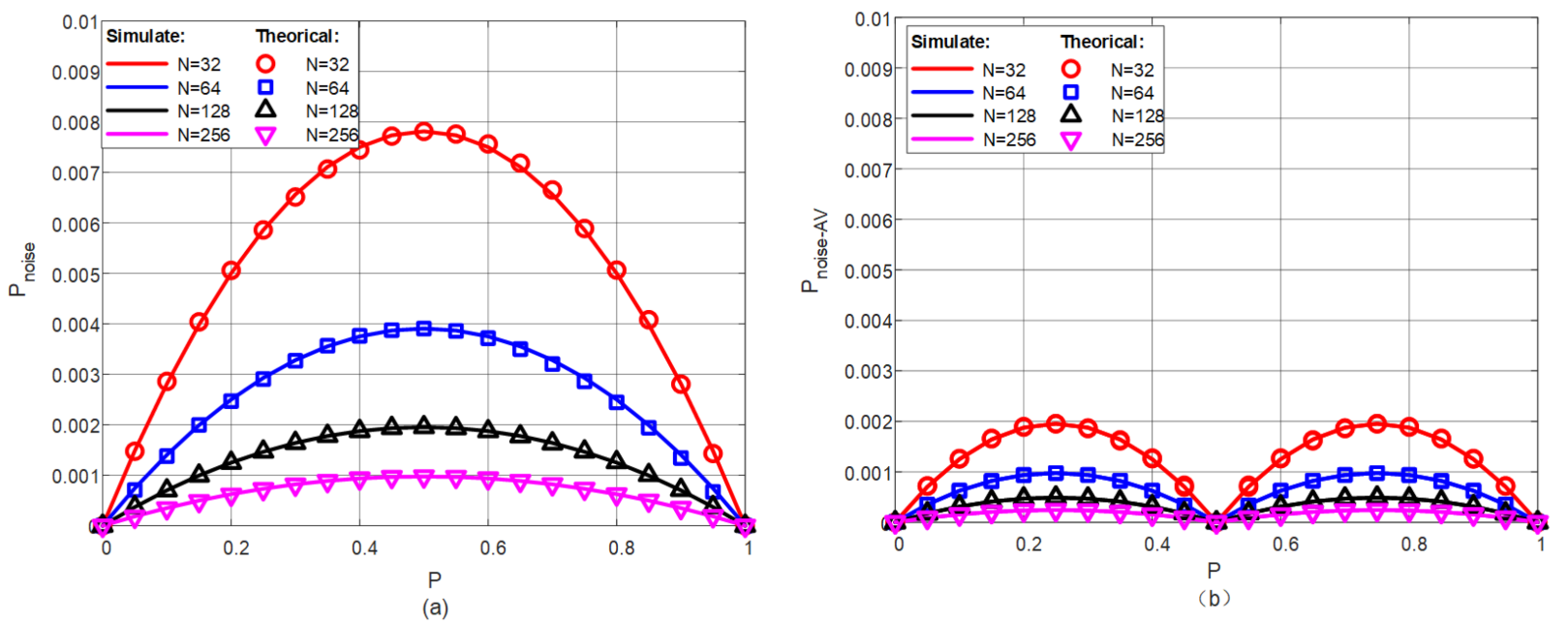
3.1. Noise Analysis of Stochastic Bit Stream

Consider a numerical value $P\in [0,1]$ represented with a stochastic bit stream $X_i$, $i=1,2,...,N$. Each bit in the stochastic bit stream follows Bernoulli distribution, and the variance of each bit can be written as $D\left(X_i\right)=E\left[{(X_i-P)}^2\right]=P·(1-P)$. When transformed back to a binary system, the estimated numerical value $\widehat{P}$ and the corresponding variance can be written as (3) and (4), respectively.

$$\widehat{P}=\frac{1}{N}·\sum _{i=1}^N{X}_i$$

(3)

$$D\left(\widehat{P}\right)=\frac{N·D\left(X_i\right)}{N^2}=\frac{P·(1-P)}{N}$$

(4)

For the stochastic bit stream representation, the representation noise power $P_{noise}$ can be calculated as (5). It can be observed that the noise power $P_{noise}$ decreases with the increasing bit stream length N. In addition, the noise power $P_{noise}$ also relies on the numerical value P. A bit-by-bit stochastic FIR filter simulation is operated using Matlab software, and the theoretical and simulation results are shown as Figure 4a, which demonstrates that the noise power is much lower when the numerical value P approaches 0 or 1.

$$P_{noise}=E\left[{(P-\widehat{P})}^2\right]=D\left(\widehat{P}\right)=\frac{P·(1-P)}{N}$$

(5)

Furthermore, the signal-noise ratio (SNR) can be calculated as (6), where the signal power $P_s=P^2$. It can be observed that the SNR would be affected by the numerical value P. Thus, it would be possible to increase the SNR by scaling the numerical value. In other words, when P is scaled up, the SNR would be increased even with the same bit stream length.

$$\mathrm{SNR}=10·{log}_{10}\frac{P_s}{P_{noise}}=10·{log}_{10}\frac{N·P}{1-P}$$

(6)

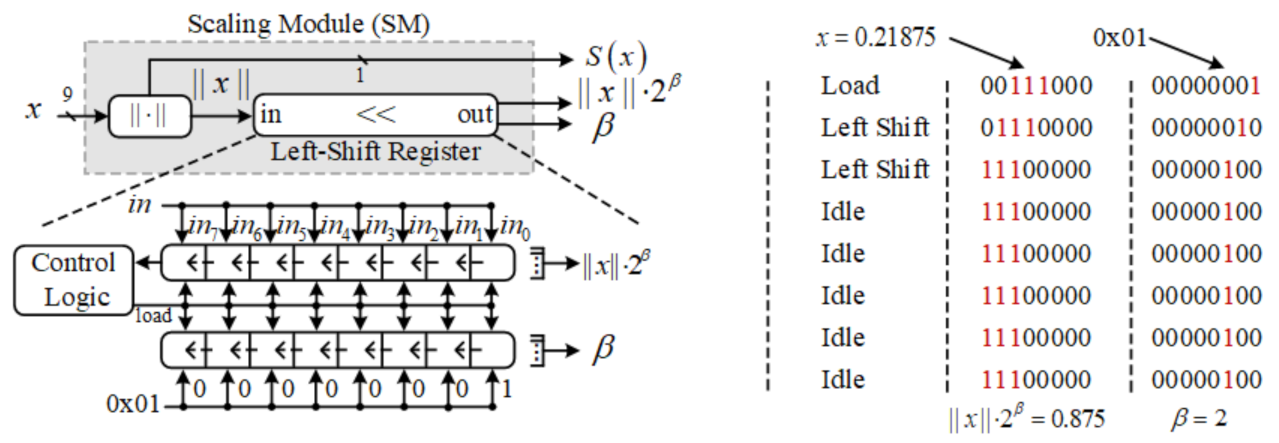
3.2. Adaptive Scaling Algorithm

To improve the calculation accuracy of SFIR filters, a scaling method has been utilized on the filter coefficients [13,14], which demonstrates improvements in accuracy. However, the scaling is quasi-static coefficient-only processing and cannot be applied to the real-time input signals directly. Based on the noise analysis in Section 3.1, a new adaptive scaling algorithm is proposed in this section, where both the input signal and the filter coefficients are adaptively scaled to the high accuracy region of stochastic computing.

As shown in (6), SNR improves with the increasing numerical value P. Thus, a scaling factor $\alpha$ is set to scale up the numerical value $P^{\prime }=\alpha ·P$ before stochastic bit stream generation. The SNR can be re-written as (7). To reduce the hardware complexity of the scaling operation, $\alpha$ is selected in $\alpha =2^{\beta }$ manner, where $\beta$ is shown as (8). As a result, the scaling operation can be implemented with shift registers. After scaling operation, the scaled numerical value $P^{\prime }$ can be transformed into a stochastic bit stream.

$$\mathrm{SNR}=10·{log}_{10}\frac{N·P^{\prime }}{1-P^{\prime }}=10·{log}_{10}\frac{N·\alpha P}{1-\alpha P}$$

(7)

$$P^{\prime }=2^{\beta }·P\le 1\Rightarrow \beta =⌊{log}_2\frac{1}{P}⌋$$

(8)

After the bit-stream generation and stochastic computing-based operation, the output numerical value has to be re-scaled, which can also be implemented with shift registers.

Combing the scaling and re-scaling operation, the adaptive scaling algorithm (ASA) is applied to an “AND” logic to implement multiplication $z=x·c$, shown as Algorithm 1. Note that the “Find scaling factor” step can also be implemented by shift registers, which would be presented in the next section.

Algorithm 1 Adaptive Scaling Algorithm (ASA)

Input:  $x,c\in [0,1]$ Output:  $z=x·c$   1: Find scaling factor: ${\beta }_x=\lfloor {log}_{2}1/x\rfloor$, ${\beta }_c=\lfloor {log}_{2}1/c\rfloor$   2: Scaling: $x<<{\beta }_x,c<<{\beta }_c$   3: Bit Stream Generation: $x,c\Rightarrow X_i,C_i,i=1,2,\dots N$   4: AND Logic: $Z_i^{\prime }=X_i\cap C_i$   5: Bit-wise Re-scaling: $Z_i=Z_i^{\prime }>>({\beta }_x+{\beta }_c)$   6: Transform Back: $\widehat{z^{\prime }}={\sum }_{i=1}^N{Z}_i/N$

3.3. Antithetic Variables Method

The parallelism method is a widely used method for stochastic computing to make a trade-off between processing latency and hardware cost. Consider a numerical value $P\in [0,1]$ represented with a stochastic bit stream $X_i$, $i=1,2,...,N$. It takes N clock cycles to process the N bits in the bit stream. To reduce the processing latency, the bit stream $X_i$ can be separate into two parts: $X_i^1$ and $X_i^2$, $i=1,2,...,N/2$, where $X_i^1=X_i$ and $X_i^2=X_{i+N/2}$. The estimated $\widehat{P}$ can be written as

$$\widehat{P}=\frac{1}{N}·\sum _{i=1}^N\frac{X_i^1+X_i^2}{2}$$

(9)

For the reason that each bit in the stochastic bit stream follows Bernoulli distribution and is individual to the others, $X_i^1$ is individual to $X_i^2$ and $Cov(X_i^1,X_i^2)=0$. Thus, the variance of $(X_i^1+X_i^2)/2$ can be written as

$$\begin{array}{cc}\hfill D(\frac{X_i^1+X_i^2}{2})& =\frac{D\left(X_i^1\right)+D\left(X_i^2\right)+2Cov(X_i^1,X_i^2)}{4}\hfill \\ \hfill & =\frac{D\left(X_i\right)+Cov(X_i^1,X_i^2)}{2}=\frac{D\left(X_i\right)}{2}\hfill \end{array}$$

(10)

It can be observed from (10) that the variance is reduced by 2 times. Combining (10) and (4), it demonstrates that the calculation accuracy can be improved by 2 times using the 2-parallelism method. However, the hardware cost is also 2 times higher, which is required by the parallel processing.

In this paper, an novel antithetic variables method is proposed to further improve the calculation accuracy. The basic idea is generate a certain bit stream $X_i^2$ to make $Cov(X_i^1,X_i^2)<0$:

$$\begin{array}{cc}\hfill X_i^1& =\left\{\begin{array}{cc}1,\hfill & P\ge R\left(t\right);\hfill \\ 0,\hfill & otherswise;\hfill \end{array}\right.\hfill \\ \hfill X_i^2& =\left\{\begin{array}{cc}1,\hfill & P\ge 1-R\left(t\right);\hfill \\ 0,\hfill & otherswise;\hfill \end{array}\right.\hfill \end{array}$$

(11)

where $R\left(t\right)\sim U(0,1)$ and $1-R\left(t\right)\sim U(0,1)$. The expectation of $X_i^1$ and $X_i^2$ can be written as,

$$\begin{array}{cc}\hfill E\left(X_i^1\right)& ={\int }_0^{P}1dr\hfill \\ \hfill E\left(X_i^2\right)& ={\int }_{1-P}^{1}1dr\hfill \end{array}$$

(12)

Based on (12), the covariance $Cov(X_i^1,X_i^2)$ can be written as (13).

$$\begin{array}{cc}\hfill Cov(X_i^1,X_i^2)& =E\left(X_i^1{X}_i^2\right)+E\left(X_i^1\right)E\left(X_i^2\right)\hfill \\ \hfill & =\left\{\begin{array}{cc}0+E\left(X_i^1\right)E\left(X_i^2\right),\hfill & P<0.5;\hfill \\ {\int }_{1-P}^{P}1dr+E\left(X_i^1\right)E\left(X_i^2\right),\hfill & P\ge 0.5;\hfill \end{array}\right.\hfill \\ \hfill & =\left\{\begin{array}{cc}-P^2,\hfill & P<0.5;\hfill \\ -P^2+2P-1,\hfill & P\ge 0.5;\hfill \end{array}\right.\hfill \end{array}$$

(13)

Similar with the analysis in Section 3.1, $X_i^1$ and $X_i^2$ both follow Bernoulli distribution, and the variance of $X_i^1$ and $X_i^2$ can be directly presented as (14). Combining (13) and (14), the variance of $\frac{X_i^1+X_i^2}{2}$ can be written as (15).

$$\begin{array}{c}\hfill D\left(X_i^1\right)=P(1-P)\\ \hfill D\left(X_i^2\right)=P(1-P)\end{array}$$

(14)

$$\begin{array}{cc}\hfill D(\frac{X_i^1+X_i^2}{2})& =\frac{D\left(X_i^1\right)+D\left(X_i^2\right)+2Cov(X_i^1,X_i^2)}{4}\hfill \\ \hfill & =\left\{\begin{array}{cc}(P-2P^2)/2,\hfill & P<0.5;\hfill \\ (-2P^2+3P-1)/2,\hfill & P\ge 0.5;\hfill \end{array}\right.\hfill \end{array}$$

(15)

Finally, the noise power of antithetic variables-method-based bit stream representation can be written as (16), and the corresponding simulation results are shown as Figure 5, which indicates that the simulation results agree with the theoretical analysis as (16).

$$\begin{array}{cc}\hfill P_{noise-AV}& =D\left(\frac{1}{N}·\sum _{i=1}^N\frac{X_i^1+X_i^2}{2}\right)\hfill \\ \hfill & =\frac{1}{N^2}·\sum _{i=1}^{N}D\left(\frac{X_i^1+X_i^2}{2}\right)\hfill \\ \hfill & =\left\{\begin{array}{cc}(P-2P^2)/(2·N),\hfill & P<0.5;\hfill \\ (-2P^2+3P-1)/(2·N),\hfill & P\ge 0.5;\hfill \end{array}\right.\hfill \end{array}$$

(16)

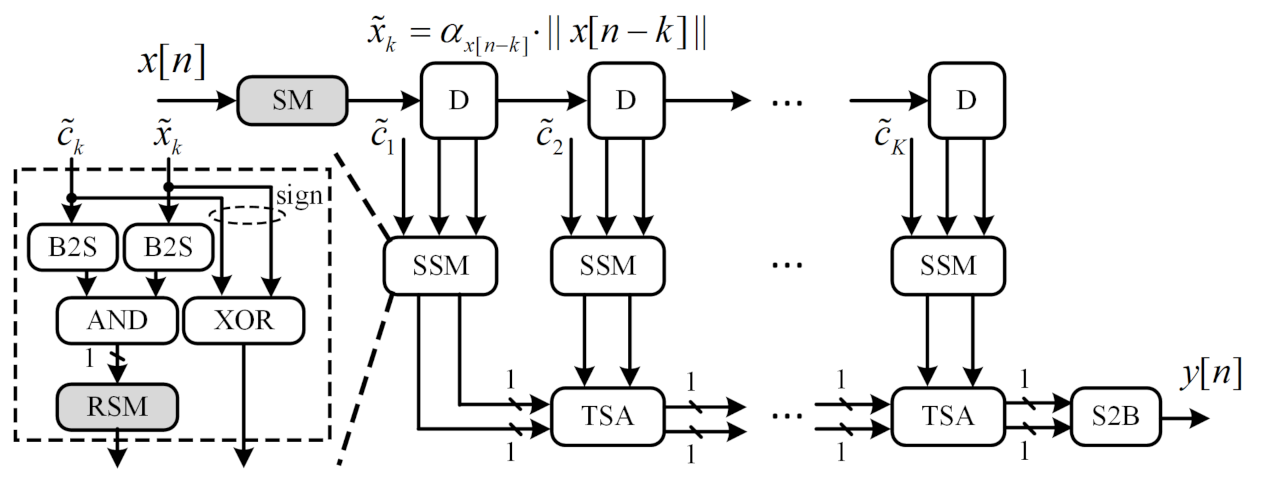
3.4. Stochastic FIR Filter with ASA and AV

Applying the proposed ASA to the SFIR filter would be helpful to improve calculation accuracy and SNR of the output signal. The hardware architecture of the scaling module (SM) is illustrated in Figure 6, which corresponds to “Find scaling factor” and “Scaling” step in Algorithm 1. The scaling factor ${\beta }_x=\lfloor {log}_{2}1/x\rfloor$ is easy to find using the left-shift registers. As a general example, consider a input value $x=0.21875$, whose sign bit $S\left(x\right)=$“$0"$ is extracted firstly. The magnitude value in binary format $\left|x\right|=$ “b’$00111000$” and initial scaling factor value in binary format ${\beta }_x=$ “b’$00000001$” are loaded in the left-shift registers. Afterward, all of the registers begin to left-shift until the first “1” occurs at the most significant bit (MSB), and the rest cycles are in an idle state. Note that the total number of left-shift cycles equals the date width of $\left|x\right|$. Finally, the scaled value $\left|x\right|·2^{\beta }=0.875=$ “b’$11100000$” and scaling factor ${\beta }_x=2$ are output.

After scaling and serials of stochastic-logic-based operations, re-scaling module is required to realize the re-scaling operation, which is corresponding to the “Bit-wise Re-scaling” step in Algorithm 1. The architecture of re-scaling module (RSM) is shown as Figure 7, where the bit stream $X\left(t\right)$ is accumulated by a counter as,

$$cnt\left(t\right)=X\left(t\right)+cnt(t-1).$$

(17)

Afterward, the counter $cnt\left(t\right)$ is compared with scaling factor ${\beta }_x$ with “XNOR” logic. The output re-scaled bit stream can be represented as (18).

$$X^{\prime }\left(t\right)=\left\{\begin{array}{cc}0,\hfill & cnt\left(t\right)\ne {\beta }_x;\hfill \\ 1,\hfill & cnt\left(t\right)={\beta }_x;\hfill \end{array}\right.$$

(18)

As introduced in Section 1, the two-line scheme-based SFIR [2] outperforms the bipolar format-based scheme [6] on accuracy performance. Using the proposed ASA method, the accuracy performance of the two-line scheme-based SFIR can be further improved. The hardware architecture is shown as Figure 8, where ASA is applied in the scaling stochastic multiplication (SSM) module, involving scaling module (SM) and re-scaling module (RSM).

Except for the scaling module and re-scaling module, binary-to-stochastic converter (B2S) and stochastic-to-binary converter (S2B) are required to realize the conversion between binary numbers and stochastic bit streams. The two-line stochastic addition (TSA) module is similar to [2], which is a calculation-error-free addition scheme. The specific steps of the ASA-based SFIR filter are as follows:

Step 1:

The FIR filter coefficient $c_k(k=1,2,...,K)$ is initially scaled up to ${\tilde{c}}_k$, while the input signal $x_k$ is scaled up to ${\tilde{x}}_k$ in real-time using SM module.

Step 2:

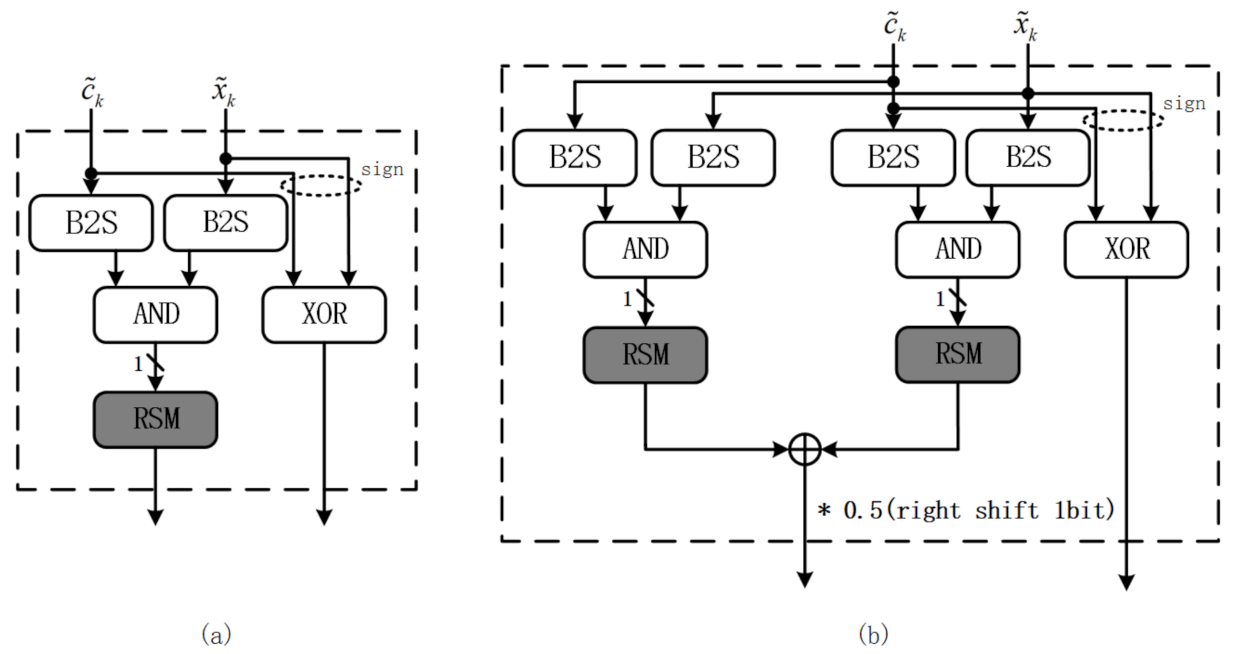
In the scaled stochastic multiplication module (SSM), the sign bit $S\left(x_k\right)$ and $S\left(c_k\right)$ are extracted from ${\tilde{x}}_k$ and ${\tilde{c}}_k$, respectively, while the magnitude bit-streams $M\left(x_k\right)$, $M\left(c_k\right)$ are transformed from ${\tilde{c}}_k$ and ${\tilde{x}}_k$, respectively, using B2S module.

Step 3:

Afterward, The multiplication on sign bit and magnitude bit-streams are mapped into “XOR” logic and ”AND” logic, respectively. The bit-wise re-scaling operation is implemented by the RSM module.

Step 4:

Finally, The outputs of the SSM module are summed up with the TSM module and transformed back to binary format using the S2B module.

Combining the proposed ASA and AV methods can further improve SNR of the output signal. The only difference between ASA based SFIR filter and ASA-AV based SFIR filter is the scaled stochastic multiplication module (SSM). The SSM of SFIR Filter with ASA is shown as Figure 9a and the SSM of SFIR Filter with ASA and AV is shown as Figure 9b.

In the SSM of SFIR filter with ASA and AV, ${\tilde{c}}_k$ can be transformed into magnitude bit-stream M1($c_k$) and M2($c_k$) by comparing it with rand numbers R1(t) and (1-R1(t)), respectively, and ${\tilde{x}}_k$ can be transformed into magnitude bit-stream M1($x_k$) and M2($x_k$) by comparing it with rand numbers R2(t) and (1-R2(t)), respectively. Then the multiplication of M1($c_k$) and M1($x_k$) is mapped into an “AND” logic and the multiplication of M2($c_k$) and M2($x_k$) is mapped into another “AND” logic. The bit-wise re-scaling operation is implemented by two RSM modules, respectively. Finally, the output is half of the sum of outputs of the two RSM modules.

4. Evaluation and Implementation

In this section, the SNR performance simulation results are firstly presented. Afterward, the hardware implementation is compared with the existing works.

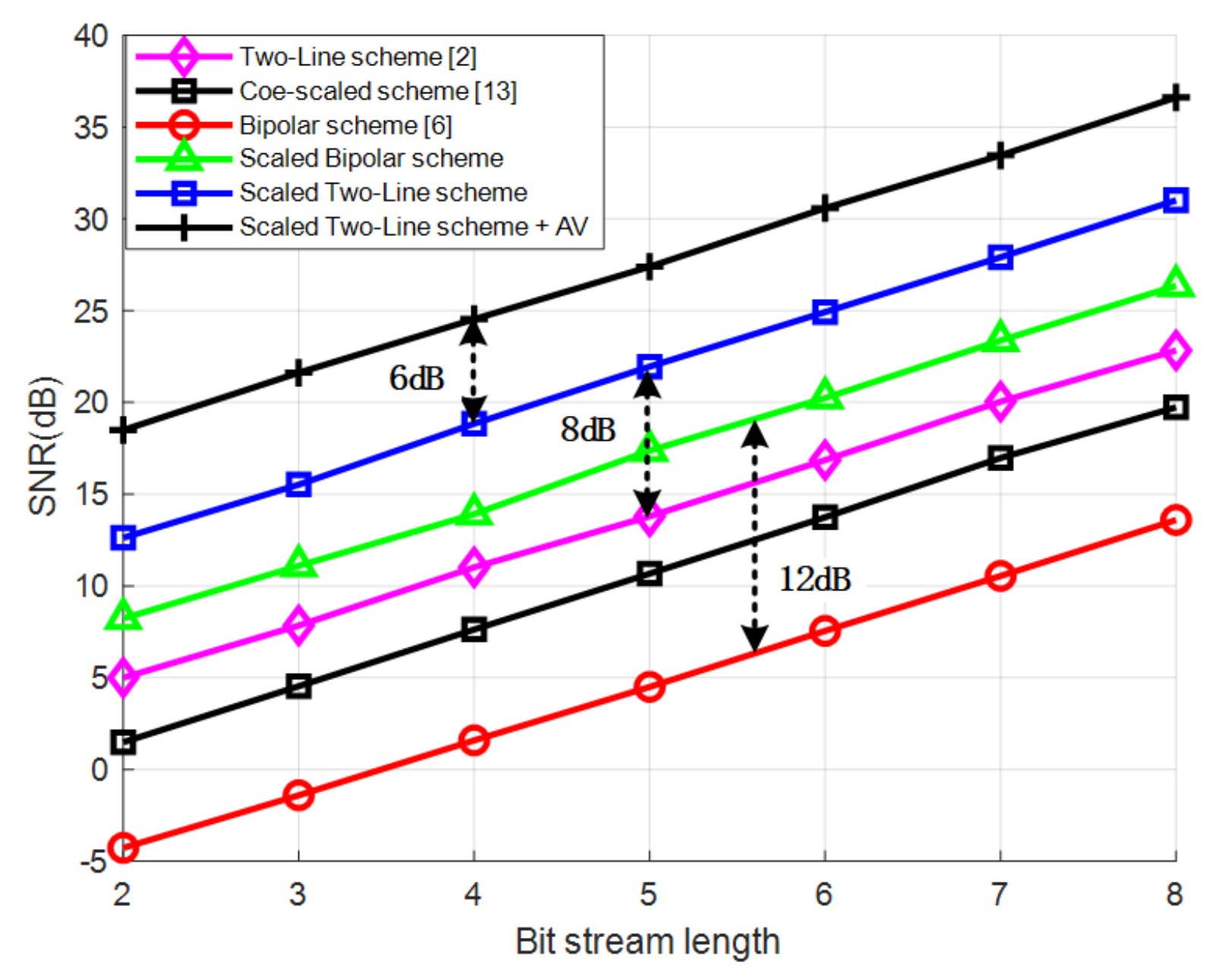
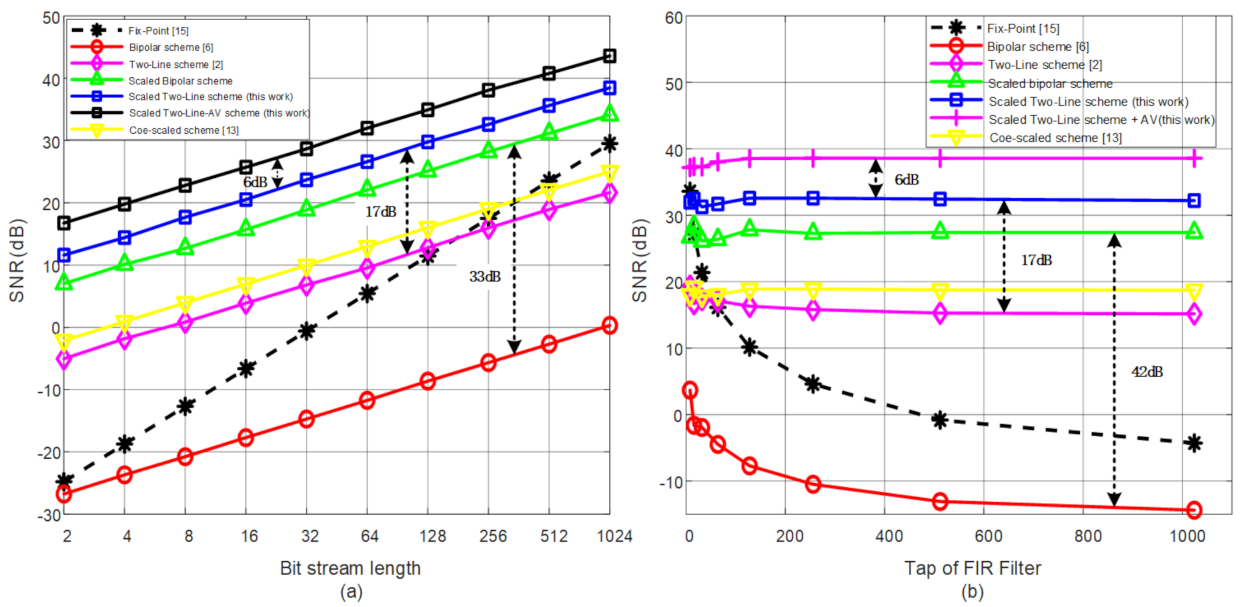
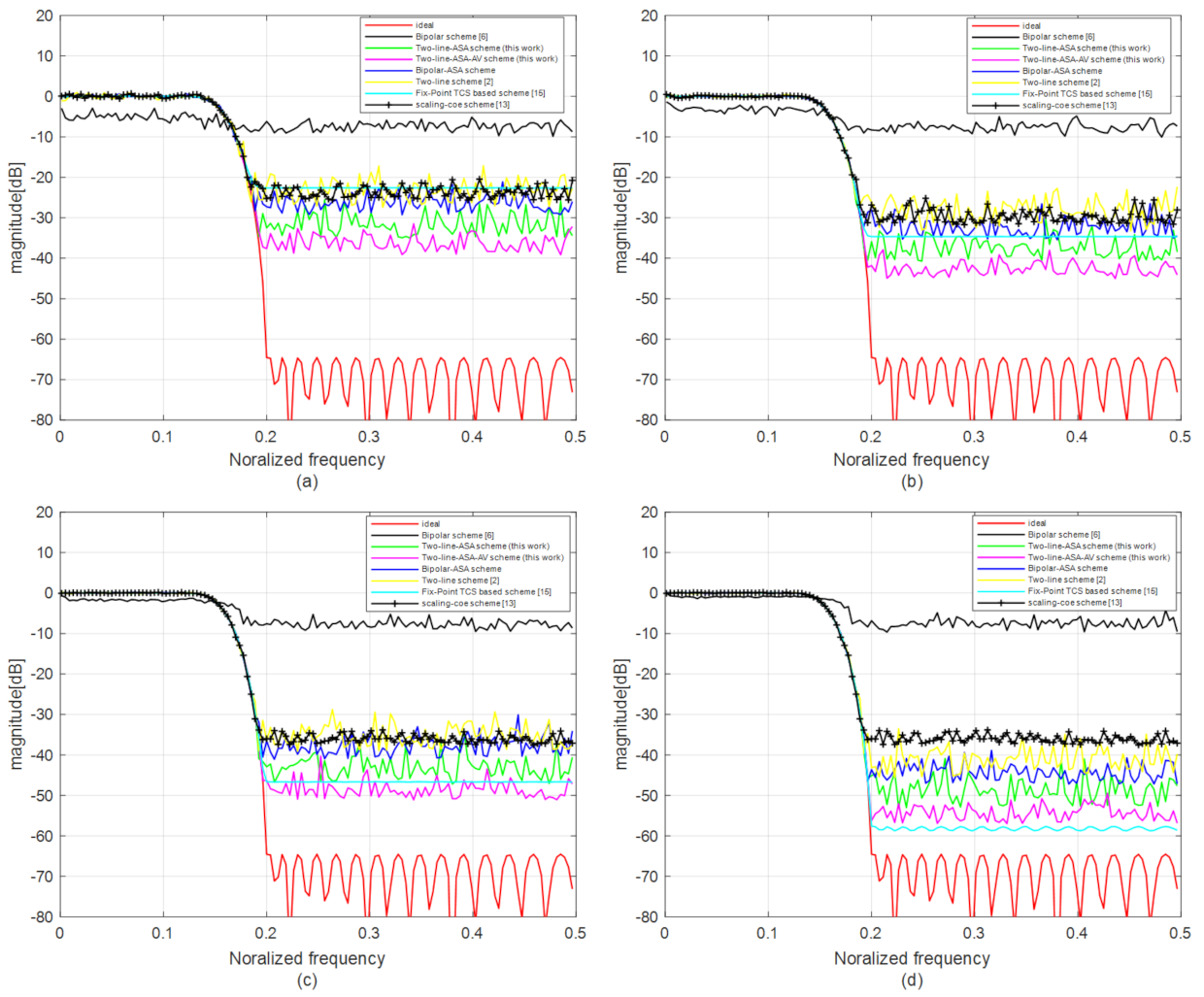
4.1. Performance Simulation

Firstly, the SNR performance of stochastic logic-based multiplication unit under different bit stream length $N=4,8,16,...,256$ is shown as Figure 10. Using the proposed adaptive scaling algorithm, the SNR of bipolar scheme [6] and two-line scheme [2] is significantly improved by 12 dB and 8 dB, respectively. Combining the Antithetic Variables method, the SNR is further improved by 6dB.

Afterward, the ASA based SFIR filter with 48-tap under different bit stream length $N=2,4,8,16,...,1024$ was simulated, and the results are shown in Figure 11a. The SNR performance gains on the bipolar scheme and two-line scheme are 33 dB and 17 dB, respectively. Furthermore, the ASA-AV-based SFIR filter gained 6 dB on SNR performance compared with the ASA-based scheme. The fix-point TCS-based scheme is also presented in Figure 11 as a comparison, which is optimized using state variable analysis method [18].

Furthermore, the SNR performance of SFIR filter with bit stream length $N=256$ under different taps are illustrated as Figure 11b, which indicates that the proposed ASA method and AV method both contribute stable accuracy gains with increasing filter taps.

Finally, the magnitude responses of 47-th order lowpass filer under different bit stream length is shown as Figure 12. The proposed ASA method significantly improves the computational accuracy: on the bipolar scheme and the two-line scheme, 33 dB improvement and 9 dB improvement are achieved, respectively, in the case of $N_{sto}$ = $2^{14}$. In addition, the ASA-AV scheme has 6 dB improvement compared with the ASA scheme.

4.2. Hardware Implementation

The proposed AV–ASA–based SFIR is implemented using VHDL and synthesized with Synopsys design complier (DC) using the SMIC 90 nm library, shown as

Table 1. Implementation results comparison.

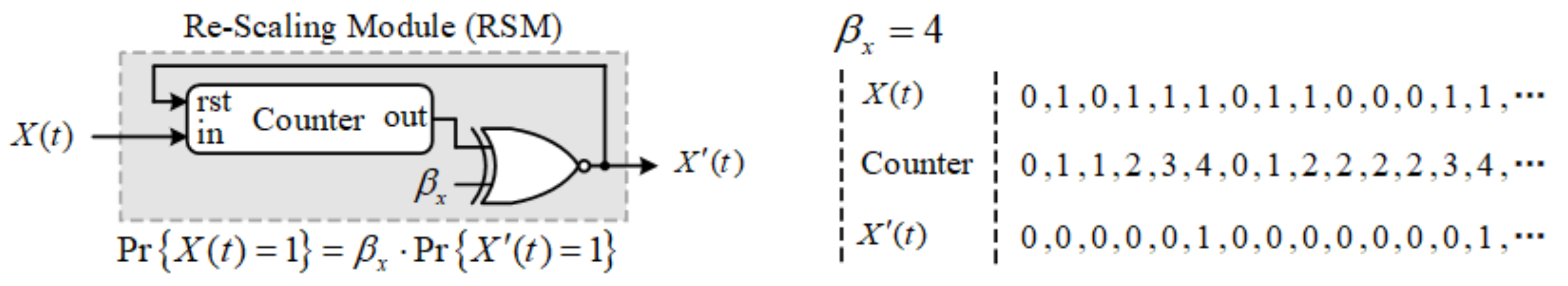
SFIR Schemes	Bipolar SFIR [6]	Two-Line SFIR [2]	MUX SFIR [12]	Binary FIR (Fix-Point)	ASA-SFIR (This Work)	AV-ASA-SFIR (This Work)
CMOS Tech.	90 nm	90 nm	90 nm *	90 nm	90 nm	90 nm	90 nm
Filter Tap	64	64	64	64	64	64	64
Bit Stream Length (bits)	256	256	256	–	256	256	16
Fix-Point Width (bits)	–	–	–	9	–	–	–
SNR (dB)	−4.41	17.21	–	23.51	31.38	37.40	25.64
Error ($\times {10}^{-2}$)	34.42	2.8	2.38	1.5	0.39	0.2	0.85
Clock (MHz)	800	750	–	200	750	750	750
Area (um${}^2$)	18,304	44,800	≈14,000 **	229,452	49,286	59,121	59,121
Power (mW)	–	–	–	2.40	1.913	2.31	2.31
Latency (ns)	320.00	341.32	–	5.00	341.32	341.32	21.33
Throughout (MSample/s)	3.13	2.92	–	200.00	2.92	2.92	46.88
Hardware Efficiency (MS/s/mm${}^2$)	0.17	0.07	–	0.87	–	–	0.79

* Original 45 nm results is converted to 90 nm technology by ×4((90/45)${}^2$) according to [19] for a fair comparison. ** Only 4, 8, 16, 32, 33, 100, 300-tap FIR filters are reported in [12], the area consumption of 64-tap filter is derived approximately.

. The bipolar scheme [6] and two-line scheme [2] are also listed as a comparison with 64 filter taps and 256-length bit stream. Furthermore, the binary fix-point FIR filter is also synthesized with the same CMOS technology and listed in Table 1.

Firstly, all of the stochastic filters take lower area cost compared with the binary filter due to the simple hardware architecture. The Bipolar, Two-Line, MUX, and AV-ASA schemes show 92%, 80%, 94%, and 74% area reduction compared to binary scheme, respectively. However, the processing latency is much higher than that of binary filter, which is caused by the long bit streams. Using the adaptive scaling algorithm and antithetic variable method, the proposed AV-ASA-SFIR scheme (16 bit stream length) achieves comparable hardware efficiency with respect to binary FIR filter, where the hardware efficiency is defined as throughput-to-area ratio as

$$\mathrm{Hardware}\mathrm{Efficiency}(\mathrm{MS}/\mathrm{s}/\mathrm{mm}{}^2)=\frac{\mathrm{Throughput}(\mathrm{MS}/\mathrm{s})}{\mathrm{Area}(\mathrm{mm}{}^2)}.$$

(19)

Among the SFIR schemes, the two-line scheme greatly improves the SNR performance from −4.41 dB to 17.21 dB, with 2.4 times chip area consumption overhead, compared with the bipolar scheme. The main hardware cost lies on the two-line stochastic adder (TSA) module. The proposed ASA–SFIR scheme gains 14.17 dB on SNR performance compared with the two-line scheme, with only 10.01% more hardware cost. Benefitting from the simple architecture of the SM and RSM module, the proposed design does not increase the critical path delay, achieving the same clock frequency as the two-line scheme. Moreover, combining the ASA and AV method, the AV–ASA–SFIR scheme gains 20.19 dB on SNR compared with the two-line scheme, with 32% area consumption overhead. Due to the significant improvement on accuracy, the proposed design require much shorter bit stream length compared with the existing stochastic FIR filters and shows advantages on processing latency. Note that the hardware architecture of the proposed design requires no change when modifying the bit stream length to achieve a trade-off between accuracy and latency.

4.3. Discussion

The representation noise analysis and the proposed adaptive scaling algorithm is based on a general stochastic bit stream and not specialized for the SFIR filter, which makes it possible to extend it to many other stochastic computing-based DSP systems, such as fast Fourier transform (FFT), discrete wavelet transform (DWT), and support vector machine (SVM). The proposed adaptive scaling method shall be considered in these modules in the future.

5. Conclusions

This paper presents a high-accuracy SFIR filter design based on an adaptive scaling algorithm. The relationship between representation noise and represented values of a stochastic bit stream is theoretically analyzed, providing a potential way to improve the accuracy under the same stochastic bit stream length. Afterward, an adaptive scaling algorithm (ASA) is proposed for the SFIR to scale the input signals into low-noise regions adaptively.According to the simulation results on a 64-tap FIR filter, the ASA and AV methods gained 17 dB and 6 dB in terms of signal-to-noise ratio (SNR), respectively. Finally, the hardware architecture of the proposed ASA-based SFIR (ASA-SFIR) is designed and implemented, which demonstrates 4.6 times hardware efficiency improvement with respect to the existing SFIR schemes.