Abstract
Parkinson’s disease (PD) is globally the most common neurodegenerative movement disorder. It is characterized by a loss of dopaminergic neurons in the substantia nigra of the brain. However, current methods to diagnose PD on the basis of clinical features of Parkinsonism may lead to misdiagnoses. Hence, noninvasive methods such as electroencephalographic (EEG) recordings of PD patients can be an alternative biomarker. In this study, a deep-learning model is proposed for automated PD diagnosis. EEG recordings of 16 healthy controls and 15 PD patients were used for analysis. Using Gabor transform, EEG recordings were converted into spectrograms, which were used to train the proposed two-dimensional convolutional neural network (2D-CNN) model. As a result, the proposed model achieved high classification accuracy of 99.46% (±0.73) for 3-class classification (healthy controls, and PD patients with and without medication) using tenfold cross-validation. This indicates the potential of proposed model to simultaneously automatically detect PD patients and their medication status. The proposed model is ready to be validated with a larger database before implementation as a computer-aided diagnostic (CAD) tool for clinical-decision support.
1. Introduction
Parkinson’s was defined in the early 1800s, and further refined in the late 1800s by Jean-Martin Charcot, as a neurological syndrome characterized by slowness of movement (bradykinesia), involuntary tremors, rigidity, and postural instability [1,2]. Patients with PD also have nonmotor symptoms including depression, loss of smell, constipation, and sleep problems [3]. These prodromal symptoms often precede motor symptoms even by 10 years [4].
The two pathological hallmarks of PD are the loss of dopamine-containing (dopaminergic) neurons that arise in the part of the midbrain called the substantia nigra pars compacta and project to the striatum, and the accumulation of misfolded alpha-synuclein proteins in intracytoplasmic inclusions called Lewy bodies. The nigrostriatal pathway is considered to be critical for the control of movement, and the replacement of dopamine is the mainstay of current therapies aimed at improving motor symptoms for PD [5,6,7]. However, dopamine replacement does not tackle the underlying neurodegenerative process.
As shown in Figure 1, the amount of dopamine transmitted across synapses is reduced within the striatum of PD patients as compared to that of healthy individuals [8]. Although no neuroimaging technique is yet specifically recommended for routine use in clinical practice for PD, molecular imaging with positron emission tomography (PET) and single-photon emission compute tomography (SPECT) can detect in vivo changes in presynaptic dopaminergic function within the brains of individuals with PD compared to those of healthy controls [9]. For example, PET and SPECT imaging can demonstrate a marked reduction in the striatum of molecules related to dopamine synthesis and transport, namely, dopamine transporters (DAT); vesicular monoamine transporter 2 (VMAT2), a membrane protein that transports dopamine from the cytosol into synaptic vesicles; and L-aromatic amino acid decarboxylase (L-AAAD), an enzyme important in the conversion of the precursor L-DOPA to dopamine. The reduction in dopamine transporters (DAT) demonstrated by SPECT is schematically depicted in Figure 2.
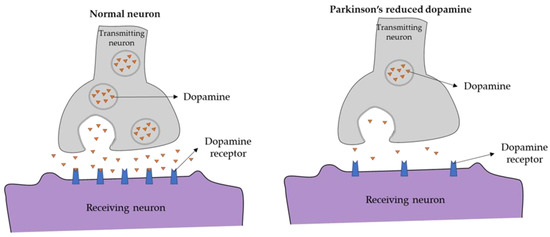
Figure 1.
Synaptic terminal in (left) healthy controls and (right) PD patients.
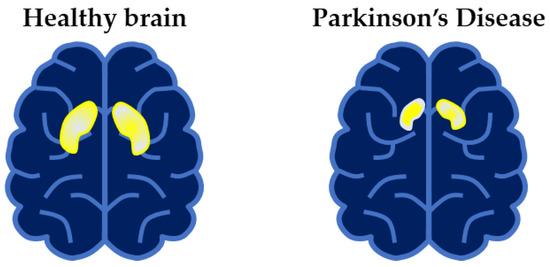
Figure 2.
Schematic drawing of Single-photon emission compute tomography (SPECT) scan of (left) healthy controls and (right) PD patients. Availability of dopamine transporters (DAT) in the striatum represented by the highlighted portion in the brain.
The most important risk factor for PD is advancing age [10]. Men are more likely to be at risk than women are [11]. Some environmental factors, such as certain pesticides and solvents, were linked to the risk of PD [12,13]. In industrialized countries, the estimated prevalence of PD is 0.3% of the general population, rising to 3% for those over 80 years. Between 1990 and 2016, the number of globally affected individuals by PD increased from 2.5 million to 6.1 million [13]. This figure is expected to continue to rise due to aging populations and exposure to harmful chemical pollutants [13]. Hence, PD is one of the fastest growing neurological disorders that require more efficient disease management, including the early precise detection and, ideally, prevention of disease [14].
Currently, PD is clinically diagnosed according to the diagnostic criteria of the Movement Disorders Society, which include the essential criteria of bradykinesia with at least one feature of rest tremor or rigidity, symptoms closely linked to dopaminergic neurons, and the absence of certain exclusion criteria and presence of supportive criteria, the main being a clear and dramatic beneficial response to dopaminergic therapy [15,16]. The set of supportive and exclusion criteria are complex, and misdiagnosis is not uncommon due to an array of differential diagnoses, many of which are not accompanied by a decrease in dopamine levels [4,17].
Moreover, by the time that PD is typically diagnosed, it was estimated that over 60% of dopaminergic neurons are already lost [18]. To exacerbate the matter, waiting lists to see expert neurologists can be long and are set to worsen due to aging populations [19], thus prolonging the time of diagnosis for individuals affected by PD. Some nonmotor symptoms (referred to as prodromal or premotor symptoms) may start even 10 years before diagnosis can be made on the basis of motor symptoms. The earlier accurate diagnosis of this prodromal period might allow for a critical therapeutic window for neuroprotective treatments to halt or even reverse the neurodegenerative process [4].
Therefore, a more efficient diagnostic approach that does not rely on the detection of clinical motor features is critically important to improve outcomes for individuals with PD. An alternative diagnostic approach utilizes electroencephalographic (EEG) recordings of PD patients [20,21]. EEG reflects the electrical activity of the brain, and in the case of a patient with PD, Soikkeli et al. [22] reported that the EEG frequency of PD patients is abnormally slow compared to that of age-matched controls. As EEG signals are naturally nonlinear, the nonlinear time-series method or Fourier transform can be employed for the analysis of EEG signals [20,23]. As a result, several studies observed abnormality in the EEG rhythm of PD patients [22,24,25,26].
In this study, the spectrogram images of EEG recordings are used to train a proposed deep convolutional-neural-network (CNN) model for automated PD detection.
Related Works
To date, several studies explored computer-aided diagnostic (CAD) tools that can learn the EEG characteristic features of PD patients, and automatically distinguish PD patients from healthy controls. These studies are summarized in Table 1.

Table 1.
List of automated Parkinson’s disease (PD)detection studies from 2016 to 2021.
Eight out of ten automated PD detection studies in Table 1 proposed conventional machine-learning models [21,27,29,30,31,32,33,34], and half of these studies employed a support-vector-machine (SVM) classifier. The highest classification accuracy obtained using a machine-learning methodology was by Yuvaraj et al. [34]. They extracted high-order spectra (HOS) bispectral features from EEG signals and fed them into the SVM classifier, obtaining a high classification accuracy of 99.62%. Apart from SVM, another machine-learning study by de Oliveira et al. [30] proposed a random-forest classifier fed with significant features of EEG that was extracted using partial directed coherence, and they obtained a high classification accuracy of 99.22%. However, conventional machine-learning approaches require tedious feature-extraction and -selection procedures that might result in the information loss of EEG signals [35,36]. In addition, feature-extraction and -selection methods can only be carried out manually by experienced experts, such that an accurate judgement can be made [35,36]. Thus, an alternative to machine-learning approaches are deep-learning models that can greatly reduce the burden of machine-learning algorithms by eliminating the need for feature extraction.
So far, only two studies proposed deep-learning models [23,28], and they both proposed CNN models for automated PD detection. The highest classification accuracy was 100%, obtained by Khare et al. [28], who trained their proposed CNN models using the time–frequency representation (TFR) of EEG signals, which were extracted using smoothed pseudo-Wigner Ville distribution. The other deep-learning study, by Oh et al. [23], used entire EEG signals to train their proposed CNN model without prior extraction of features and obtained a relatively high classification accuracy of 88.25%. Thus, this study proposes a CNN model for automated PD detection using spectrogram images of EEG signals to promote the efficacy and ease of PD detection with a deep-learning model.
2. Materials and Methods
2.1. Dataset Acquisition
The publicly available PD dataset used in this study was downloaded from OpenNeuro [37]. This PD dataset contained the EEG recordings of 16 healthy controls and 15 PD patients whose EEG recordings were recorded off and on dopaminergic medications. The healthy control group consisted of 7 males and 9 females (mean age = 63.5 ± 9.6), while the PD group consisted of 7 males and 8 females (mean age = 63.2 ± 8.2) [38,39,40,41,42]. All PD patients were on either Stage 2 or 3 on the Hoehn and Yahr scale. Participants were told to focus on a cross-image presented on the computer screen while their EEG signals were recorded at sampling frequency of 512 Hz for approximately 3 min. For each participant, a total of 32 EEG channels were recorded using Biosemi ActiveTwo EEG system [38,39,40,41,42]. Table 2 summarizes the characteristics of the healthy controls and PD patients in the PD dataset. Scores from the North American Adult Reading Test (NAART) and Mini-Mental Status Exam (MMSE) were utilized to match the PD patients to the healthy controls [38]. The United Parkinson’s Disease Rating Scale for motor section (UPDRS III) reflects greater motion impairment with a higher score [38].

Table 2.
Summary of subjects’ clinical characteristics in the PD dataset used in this study. Values are represented as mean (standard deviation).
2.2. Experimental Setup
The workflow of this study is illustrated in Figure 3. EEG recordings were split in half before applying Gabor transform to obtain respective spectrograms. Hence, each EEG recording generated two spectrogram images, and the summary of the number of spectrogram images in the healthy control group, PD without medication, and PD with medication is shown in Table 3.
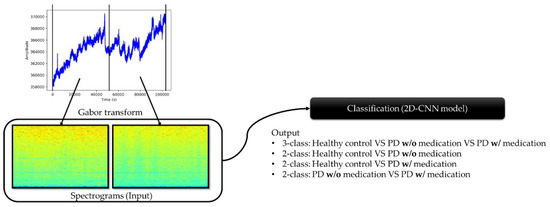
Figure 3.
Workflow process from preprocessing of EEG recordings to classification by the proposed model.

Table 3.
Number of spectrograms generated for the respective groups.
Subsequently, four experiments were conducted with the proposed 2D-CNN model:
- Experiment 1: 3-class classification, namely, healthy control, PD without medication, and PD with medication (total no. of spectrogram images = 2944).
- Experiment 2: healthy control versus PD patients without medication (total no. of spectrogram images = 1984).
- Experiment 3: healthy control versus PD patients with medication (total no. of spectrogram images = 1984).
- Experiment 4: PD patients with and without medication (total no. of spectrogram images = 1920).
For multiclass classification, i.e., Experiment 1, the softmax activation function was used in the last output layer of the proposed 2D-CNN model. In the remaining binary-classification experiments, the sigmoid activation function was used instead of softmax. Tenfold cross-validation was used to evaluate the performance of the proposed model.
2.3. Preprocessing (Gabor Transform)
Gabor transform was developed by Dennis Gabor as an improvement to Fourier transform [43]. The issue concerning Fourier transform is that only the frequency domain of the signal is provided, but the time when the frequencies occur is not included [44]. Hence, Gabor transform is a combination of Fourier transform and Gaussian distribution function that can be used to produce a spectrogram that plots frequency against time. The Gaussian distribution function in Gabor transform plays the role of a kernel that moves along one-dimensional signals and computes the multiplication of Fourier transform and Gaussian function within its window, thereby providing information on time where different frequencies occur. The equation of Fourier transform () and Gaussian distribution function () are shown in Equations (1) and (2), respectively, and their combination that leads to Gabor transform () is shown in Equation (3) [44]. The time and frequency domains are represented by (), while τ and a represent the center and the spread of the window in Gaussian function, respectively.
In this study, EEG signals were split into half, and Gabor transform was applied to each half. The window of the Gabor transform was 1024 timesteps with 128 timestep overlaps. The resulting spectrograms of the healthy controls, and PD patients with and without medication are shown in Figure 4.
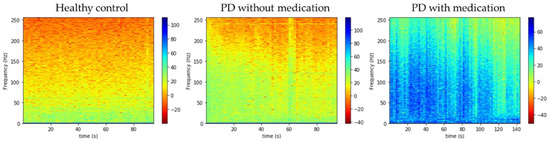
Figure 4.
Spectrograms of three respective groups of subjects.
2.4. Model Architecture
In this study, we propose a deep 2D-CNN model to recognize the EEG characteristics of healthy controls, and PD patients with and without medication from their spectrograms. CNN models became known for their image-recognition ability when Krizhevsky et al. [45] achieved top five in the ImageNet Large Scale Visual Recognition Competition with their proposed CNN model. A typical CNN model comprises three layers: the convolutional, pooling, and fully connected layers. Convolutional layers convolve the input images with multiple kernels to produce different types of feature maps, as shown in Figure 5. Pooling layers follow the convolutional layer to reduce the complexity of the feature maps, so as to prevent CNN models from overfitting. In our proposed model, zero padding was used to prevent information loss at the edges of the image; hence, the dimensions of the feature map were the same as those of the input image, 217 × 334 (Table 2) [46]. The operation of the convolutional and pooling layers () is illustrated in Equations (4) and (5), respectively. The input image () with the dimension of undergoes a discrete convolution operation () with (), which is the convolutional kernel that updates its weight each time the kernel slides across the input image [46,47].
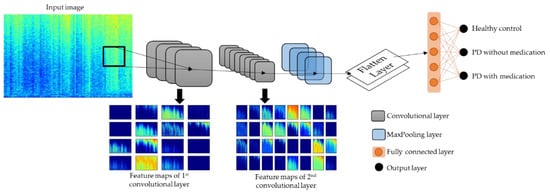
Figure 5.
Model architecture of proposed 2D-CNN model.
After the pooling layers, the feature maps were flattened into single-list vectors that were fed into the fully connected layers. The fully connected and output layers contain nodes that are neurons that are trained to recognize and classify the single-list vectors. The number of nodes at the output layer differed according to the type of experiments conducted in this study. For multiclass classification in Experiment 1, the softmax activation function was used at the output layer, which require 3 nodes, as shown in Figure 5. For binary classification in Experiments 2 to 4, the sigmoid activation function was used, which requires only 1 node. The softmax activation function computes the probability scores for each single-list vector that has a chance of being classified into each of the three classes, and single-list vectors are classified into the class where they achieved the highest probability score. On the other hand, sigmoid activation function output a value between 0 and 1 for each single-list vector. Taking Experiment 2 as an example, single-list vectors with output values nearer to 0 were classified as healthy controls, and values nearer to 1 were classified as PD patients without medication. The operation of the sigmoid and softmax activation functions are shown in Equations (6) and (7), respectively [48].
The complete details on the layer parameters of the proposed model are listed in Table 4. The used optimizer for the proposed model was the Adam optimizer with a learning rate of 0.001 and a decay rate of 0.01. The model was constructed using Keras with the Tensorflow back-end in Python programming.

Table 4.
Complete details of layer parameters of proposed 2D-CNN model.
3. Results
The performance of the model was evaluated with tenfold cross-validation, and results are summarized in Table 5. All experiments achieved promising results. The correctly identified samples from each experiment are visualized with a confusion matrix in Figure 6, where the correctly identified samples are in dark-colored boxes.

Table 5.
Various performance values for each experiment. Standard deviation for all ROC–AUC scores was less than 0.01.
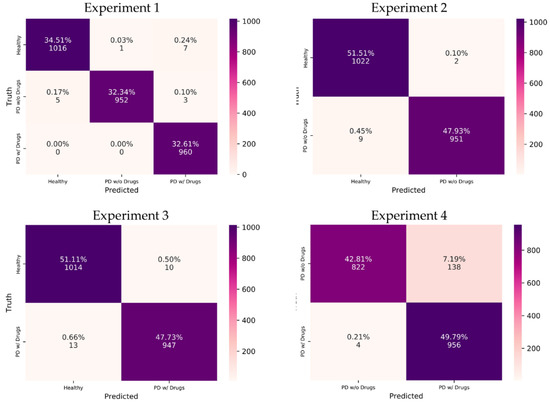
Figure 6.
Confusion matrix of respective experiments. w/o, without; w/, with. Drugs refer to the dopaminergic medications taken by PD patients.
The proposed model achieved the highest classification accuracy of 99.46% in the multiclass classification of Experiment 1 (Table 5). The breakdown of performance metrics for each class in Experiment 1 is shown in Table 6. The highest model precision (99.90%) was observed for PD without medication, indicating that the proposed model could correctly distinguish more cases of PD without medication as compared to other classes (healthy and PD with medication). This can be seen from the confusion matrix of Experiment 1 in Figure 6, where the vertical axis for predicted PD without medication shows 952 correctly predicted cases, while only 1 case from healthy control was wrongly predicted as PD without medication. On the other hand, PD with medication achieved the highest model sensitivity (100%), which means that the proposed model could correctly distinguish all cases of PD with medication. This was also observed from the confusion matrix where the proposed model correctly distinguished all 960 cases of PD with medication (Figure 6).

Table 6.
Multiclass performance values for each class in Experiment 1. Drugs refer to the dopaminergic medications taken by PD patients.
Regarding binary classification in Experiments 2 to 4, high classification accuracies of 99.44% and 98.84% were observed for Experiments 2 and 3, respectively (Table 5). The lowest classification accuracy of 92.60% was observed for Experiment 4 (Table 5). Nonetheless, Experiments 2 to 4 achieved a high receiver operating characteristics—area under the curve (ROC–AUC) score of near 1, which indicates that the proposed model could correctly identify the positive and negative classes for the respective experiments (Table 5). The interpretation of performance values differs slightly for binary classification. For example, the highest model precision of 99.79% was observed in Experiment 2, which indicates that it was highly unlikely for the proposed model to misclassify healthy cases (negative class) as PD without medication (Table 5). As such, only 2 cases of healthy controls in Experiment 2 were wrongly classified as PD without medication (Figure 6). Experiment 4, despite having the lowest classification accuracy of 92.60%, achieved the highest sensitivity score of 99.58% (Table 5). This result shows that the proposed model could correctly detect the majority of PD with medication cases, where 956 out of 960 cases of PD with medication were correctly predicted in Experiment 4 (Figure 6). On the other hand, Experiment 4 had the lowest model precision of 88.37% due to the misclassification of 138 cases of PD without medication (Table 5 and Figure 6). This is also reflected in the performance graph of Experiment 4 in Figure 7, where overfitting and a large deviation in model validation accuracy were observed. Experiments 1, 2, and 3, however, exhibited no signs of overfitting. Nonetheless, all experiments achieved a high F1 score of >90%, which means that the proposed model could successfully balance the trade-off between model sensitivity and precision score in all experiments (Table 5).
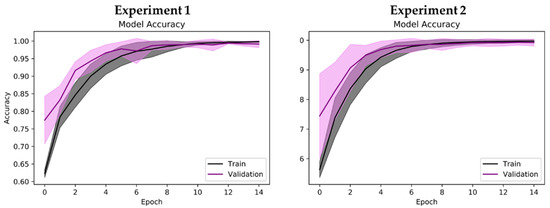
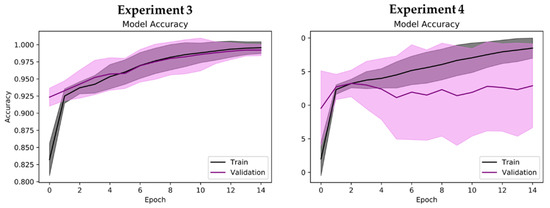
Figure 7.
Performance graph (model accuracy) of proposed 2D-CNN model during tenfold cross-validation. Shaded region represents standard deviation of model accuracy during tenfold cross-validation (mean accuracy ± standard deviation).
4. Discussion
This study utilized the EEG recordings of 16 healthy controls and 15 PD patients with mild to moderate (Hoehn and Yahr Stages 2/3) severity, which are considered to be prodromal PD. As a result, EEG is a good biomarker for automated PD detection with high classification accuracy achieved in all Experiments (1 to 4). Since the EEG recordings of prodromal PD patients were considered, this study also demonstrated that EEG biomarkers can diagnose PD in early stages. This is also supported by a few studies that observed EEG abnormalities in the rapid-eye-movement (REM) sleep of prodromal PD patients [49,50,51,52]. Therefore, EEG is a promising noninvasive method used for the early diagnosis of PD with a low error rate, and is strongly considered to assist medical professionals in clinical decisions.
The automated PD detection model proposed in this study involves the conversion of subject’s EEG recordings into spectrograms via Gabor transform, and the proposed 2D-CNN model automatically classified spectrograms into healthy controls, and PD patients with or without dopaminergic medications. As a result, the proposed 2D-CNN model displayed exemplary classification ability when the task involved distinguishing healthy controls from PD patients (with or without dopaminergic medication). However, the proposed model was weak in differentiating between PD patients on medication versus those who were not on medication. This was within expectations because the effectiveness of dopaminergic medication differs in each PD patient, which was reflected in their EEG recordings. Swann et al. [39], who had developed the dataset, also mentioned that they observed elevated phase-amplitude coupling in PD patients not on medication, and this phenomenon was seen in 14 out of 15 of their PD patients. Hence, some of the spectrograms of the PD patients may have been ambiguous due to different drug responses to the dopaminergic medications. This, in turn, hindered the proposed model from recognizing PD patients who were on or off medications. Fortunately, Experiment 1 (multiclass classification), which involved all three classes of subjects, showed that, with the inclusion of healthy controls, the proposed model could better distinguish the two types of PD patients.
In addition, the dataset used in our study is relatively new, as it was only made publicly available in 2020. Apart from our study, two other studies were used this dataset for automated PD detection (Table 7) [28,29]. Khare et al. [29] proposed a machine-learning approach by using tunable Q wavelet transform to automatically decompose EEG signals into multiple sub-bands for automatic PD detection with a least-square SVM classifier. Their approach achieved classification accuracy of 97.65% for the binary classification between healthy controls and PD patients with medication. Khare et al. [28], in another study, obtained the highest classification accuracy of 100% (healthy control versus PD patients with medication) with a deep-learning model. They employed the smoothed pseudo-Wigner Ville distribution (SPWVD) of EEGs with a deep CNN model. However, their study only utilized this dataset for binary classifications. In their study, they segmented EEG recordings into 2 s epochs, which allowed for them to capture more significant characteristics from time–frequency images to train their proposed CNN model. Having more sample images resulted in higher classification accuracy for their model, but the disadvantage was that the CNN was computationally intensive; hence, the number of images to train the model was limited. Therefore, the study by Khare et al. [28] was restricted to binary classification.

Table 7.
Summary of automated PD detection studies that used the same publicly available PD dataset from OpenNeuro [37].
Our study is the first to explore this dataset for automated PD detection with three-class classification to individually detect healthy controls, and PD patients off and on dopaminergic medications. Multiclass classification is possible with our approach because the number of EEG recordings was split in half instead of segmenting EEGs into 2 s epochs. This helped to generate fewer spectrograms for our model training, but allowed for the model to detect more classes. As a consequence, our proposed model could simultaneously detect PD patients and identify which patients were on medication.
In summary, the notable aspects of this study are:
- Simple workflow.
- A new publicly available PD dataset was used.
- Spectrograms via Gabor transformation of EEG signals were used for analysis.
- Deep-learning model based of 2D-CNN was proposed for automated PD detection.
- High model performance for three-class classification: healthy controls, and PD patients with and without dopaminergic medications.
- The proposed model could automatically detect PD patients and distinguish if each patient was on medication or not.
However, our study comes with a few limitations:
- Two-dimensional CNN models are computationally demanding, which results in long training times.
- Large computer memory is required, as the model may crash when it exceeds the memory load due to the large number of images for model training.
- The small number of participants in the PD dataset used in this study may reduce the generalizability of the proposed model.
In the future, we wish to improve the existing model, such that it can be a practical CAD tool for clinical-decision support. The proposed model must be validated with a huge database that has information on other brain abnormalities, such as sleep disorders, depression, and autism. Hence, the proposed model can learn to detect various brain disorders instead of detecting only one disease. Future work to modify the proposed model into a cloud-compatible device is also under consideration, as deep-learning models require a huge memory space, and this can be provided by the cloud. As such, a software application can easily access data from the cloud, and perform EEG analysis and diagnostic prediction. An illustration of the process from the EEG recordings of patients to the diagnosis of disease by medical professionals with the help of cloud computing is shown in Figure 8.
Figure 8.
Workflow of cloud-based system to assist medical professionals to automatically detect PD using EEG recordings.
In addition to EEG signals, we can also explore different methods of PD diagnosis. For instance, speech impairment and dysgraphia are commonly observed in 90% of PD patients. This opens the possibility of automatic PD diagnosis based on speech and handwriting recognition [53,54,55]. Gait analysis is another alternative for PD detection, as motion impairments are reflected in the gait features of PD patients, such as reduced arm swing, balance, and postural control [56]. As such, inertial measurement units (IMUs) are an indispensable tool for motion capture and data collection for gait analysis and the diagnosis of PD [57]. The availability of various automated diagnostic methods for PD increases the chance of the early diagnosis for individuals suspected to have PD and open the door to potential novel therapies to reduce the severity of PD.
5. Conclusions
This study proposed a deep-learning model based on 2D-CNN architecture for automated PD detection using a new publicly available EEG database. The EEG recordings of healthy controls, and PD patients with and without medication were converted into spectrograms via Gabor transform for analysis. These spectrograms were utilized for the model training of the proposed 2D-CNN model, and four experiments were conducted. Experiment 1, which involved three-class classification, obtained the highest classification accuracy of 99.46%, indicating that our proposed model could detect PD patients and differentiate if patients had taken their medication or not. The limitation of this work is that we used only 31 subjects (16 healthy controls and 15 PD). The high model performance of the proposed model highlighted its potential as a CAD tool for clinical-decision support. The proposed model requires further validation with a larger EEG database containing information on other abnormalities, such that it can be developed into a versatile CAD tool.
Author Contributions
Conceptualization, H.W.L. and U.R.A.; methodology, H.W.L., P.D.B., S.D., T.T. and M.B.; software, H.W.L.; writing—original-draft preparation, H.W.L.; writing—review and editing, H.W.L., C.P.O., E.P., T.T. and U.R.A.; visualization, H.W.L.; supervision, U.R.A.; project administration, H.W.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data available in a publicly accessible repository. The data presented in this study are openly available in OpenNeuro at doi:10.18112/openneuro.ds002778.v1.0.4.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Goetz, C.G. The history of Parkinson’s disease: Early clinical descriptions and neurological therapies. Cold Spring Harb. Perspect. Med. 2011, 1, a008862. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bhat, S.; Acharya, U.R.; Hagiwara, Y.; Dadmehr, N.; Adeli, H. Parkinson’s disease: Cause factors, measurable indicators, and early diagnosis. Comput. Biol. Med. 2018, 102, 234–241. [Google Scholar] [CrossRef] [PubMed]
- Politis, M.; Wu, K.; Molloy, S.; Bain, P.G.; Chaudhuri, K.R.; Piccini, P. Parkinson’s disease symptoms: The patient’s perspective. Mov. Disord. 2010, 25, 1646–1651. [Google Scholar] [CrossRef] [PubMed]
- Balestrino, R.; Schapira, A.H.V. Parkinson disease. Eur. J. Neurol. 2020, 27, 27–42. [Google Scholar] [CrossRef]
- Báez-Mendoza, R.; Schultz, W. The role of the striatum in social behavior. Front. Neurosci. 2013, 7, 233. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Savitt, J.M.; Dawson, V.L.; Dawson, T.M. Diagnosis and treatment of Parkinson disease: Molecules to medicine. J. Clin. Investig. 2006, 116, 1744–1754. [Google Scholar] [CrossRef] [Green Version]
- Yuvaraj, R.; Murugappan, M.; Acharya, U.R.; Adeli, H.; Ibrahim, N.M.; Mesquita, E. Brain functional connectivity patterns for emotional state classification in Parkinson’s disease patients without dementia. Behav. Brain Res. 2016, 298, 248–260. [Google Scholar] [CrossRef] [PubMed]
- Imbriani, P.; Schirinzi, T.; Meringolo, M.; Mercuri, N.B.; Pisani, A. Centrality of Early Synaptopathy in Parkinson’s Disease. Front. Neurol. 2018, 9. [Google Scholar] [CrossRef] [Green Version]
- Pagano, G.; Niccolini, F.; Politis, M. Imaging in Parkinson’s disease. Clin. Med. 2016, 16, 371–375. [Google Scholar] [CrossRef]
- Orozco, J.L.; Valderrama-Chaparro, J.A.; Pinilla-Monsalve, G.D.; Molina-Echeverry, M.I.; Pérez Castaño, A.M.; Ariza-Araújo, Y.; Prada, S.I.; Takeuchi, Y. Parkinson’s disease prevalence, age distribution and staging in Colombia. Neurol. Int. 2020, 12, 8401. [Google Scholar] [CrossRef]
- Miller, I.N.; Cronin-Golomb, A. Gender differences in Parkinson’s disease: Clinical characteristics and cognition. Mov. Disord. 2010, 25, 2695–2703. [Google Scholar] [CrossRef] [Green Version]
- Dick, F.D.; De Palma, G.; Ahmadi, A.; Scott, N.W.; Prescott, G.J.; Bennett, J.; Semple, S.; Dick, S.; Counsell, C.; Mozzoni, P.; et al. Environmental risk factors for Parkinson’s disease and parkinsonism: The Geoparkinson study. Occup. Environ. Med. 2007, 64, 666–672. [Google Scholar] [CrossRef] [Green Version]
- Dorsey, E.R.; Elbaz, A.; Nichols, E.; Abd-Allah, F.; Abdelalim, A.; Adsuar, J.C.; Ansha, M.G.; Brayne, C.; Choi, J.Y.J.; Collado-Mateo, D.; et al. Global, regional, and national burden of Parkinson’s disease, 1990–2016: A systematic analysis for the Global Burden of Disease Study 2016. Lancet Neurol. 2018, 17, 939–953. [Google Scholar] [CrossRef] [Green Version]
- GBD 2015 Neurological Disorders Collaborator Group. Global, regional, and national burden of neurological disorders during 1990–2015: A systematic analysis for the Global Burden of Disease Study 2015. Lancet Neurol. 2017, 16, 877–897. [Google Scholar] [CrossRef] [Green Version]
- Rizek, P.; Kumar, N.; Jog, M.S. An update on the diagnosis and treatment of Parkinson disease. CMAJ 2016, 188, 1157–1165. [Google Scholar] [CrossRef] [Green Version]
- Postuma, R.B.; Berg, D.; Stern, M.; Poewe, W.; Olanow, C.W.; Oertel, W.; Obeso, J.; Marek, K.; Litvan, I.; Lang, A.E.; et al. MDS clinical diagnostic criteria for Parkinson’s disease. Mov. Disord. 2015, 30, 1591–1601. [Google Scholar] [CrossRef] [PubMed]
- Beach, T.G.; Adler, C.H. Importance of low diagnostic Accuracy for early Parkinson’s disease. Mov. Disord. 2018, 33, 1551–1554. [Google Scholar] [CrossRef] [PubMed]
- Marsden, C.D. Parkinson’s disease. Lancet 1990, 335, 948–949. [Google Scholar] [CrossRef]
- Burton, A. How do we fix the shortage of neurologists? Lancet Neurol. 2018, 17, 502–503. [Google Scholar] [CrossRef] [Green Version]
- Han, C.-X.; Wang, J.; Yi, G.-S.; Che, Y.-Q. Investigation of EEG abnormalities in the early stage of Parkinson’s disease. Cogn. Neurodyn. 2013, 7, 351–359. [Google Scholar] [CrossRef]
- Bhurane, A.A.; Dhok, S.; Sharma, M.; Yuvaraj, R.; Murugappan, M.; Acharya, U.R. Diagnosis of Parkinson’s disease from electroencephalography signals using linear and self-similarity features. Expert Syst. 2019, e12472. [Google Scholar] [CrossRef]
- Soikkeli, R.; Partanen, J.; Soininen, H.; Pääkkönen, A.; Riekkinen, P. Slowing of EEG in Parkinson’s disease. Electroencephalogr. Clin. Neurophysiol. 1991, 79, 159–165. [Google Scholar] [CrossRef]
- Oh, S.L.; Hagiwara, Y.; Raghavendra, U.; Yuvaraj, R.; Arunkumar, N.; Murugappan, M.; Acharya, U.R. A deep learning approach for Parkinson’s disease diagnosis from EEG signals. Neural Comput. Appl. 2020, 32, 10927–10933. [Google Scholar] [CrossRef]
- Neufeld, M.Y.; Inzelberg, R.; Korczyn, A.D. EEG in demented and non-demented parkinsonian patients. Acta Neurol. Scand. 1988, 78, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Neufeld, M.Y.; Blumen, S.; Aitkin, I.; Parmet, Y.; Korczyn, A.D. EEG frequency analysis in demented and nondemented parkinsonian patients. Dementia 1994, 5, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Stoffers, D.; Bosboom, J.L.W.; Deijen, J.B.; Wolters, E.C.; Berendse, H.W.; Stam, C.J. Slowing of oscillatory brain activity is a stable characteristic of Parkinson’s disease without dementia. Brain 2007, 130, 1847–1860. [Google Scholar] [CrossRef] [PubMed]
- Gunduz, H. An efficient dimensionality reduction method using filter-based feature selection and variational autoencoders on Parkinson’s disease classification. Biomed. Signal Process. Control 2021, 66, 102452. [Google Scholar] [CrossRef]
- Khare, S.K.; Bajaj, V.; Acharya, U.R. PDCNNet: An automatic framework for the detection of Parkinson’s Disease using EEG signals. IEEE Sens. J. 2021, 1. [Google Scholar] [CrossRef]
- Khare, S.K.; Bajaj, V.; Acharya, U.R. Detection of Parkinson’s disease using automated tunable Q wavelet transform technique with EEG signals. Biocybern. Biomed. Eng. 2021, 41, 679–689. [Google Scholar] [CrossRef]
- de Oliveira, A.P.S.; de Santana, M.A.; Andrade, M.K.S.; Gomes, J.C.; Rodrigues, M.C.A.; dos Santos, W.P. Early diagnosis of Parkinson’s disease using EEG, machine learning and partial directed coherence. Res. Biomed. Eng. 2020, 36, 311–331. [Google Scholar] [CrossRef]
- Khoshnevis, S.A.; Sankar, R. Classification of the stages of Parkinson’s disease using novel higher-order statistical features of EEG signals. Neural Comput. Appl. 2020. [Google Scholar] [CrossRef]
- Anjum, M.F.; Dasgupta, S.; Mudumbai, R.; Singh, A.; Cavanagh, J.F.; Narayanan, N.S. Linear predictive coding distinguishes spectral EEG features of Parkinson’s disease. Parkinsonism Relat. Disord. 2020, 79, 79–85. [Google Scholar] [CrossRef]
- Liu, G.; Zhang, Y.; Hu, Z.; Du, X.; Wu, W.; Xu, C.; Wang, X.; Li, S. Complexity Analysis of Electroencephalogram Dynamics in Patients with Parkinson’s Disease. Parkinsons. Dis. 2017, 2017, 8701061. [Google Scholar] [CrossRef]
- Yuvaraj, R.; Acharya, U.R.; Hagiwara, Y. A novel Parkinson’s Disease Diagnosis Index using higher-order spectra features in EEG signals. Neural Comput. Appl. 2018, 30, 1225–1235. [Google Scholar] [CrossRef]
- Loh, H.W.; Ooi, C.P.; Vicnesh, J.; Oh, S.L.; Faust, O.; Gertych, A.; Acharya, U.R. Automated Detection of Sleep Stages Using Deep Learning Techniques: A Systematic Review of the Last Decade (2010–2020). Appl. Sci. 2020, 10, 8963. [Google Scholar] [CrossRef]
- Faust, O.; Hagiwara, Y.; Hong, T.J.; Lih, O.S.; Acharya, U.R. Deep learning for healthcare applications based on physiological signals: A review. Comput. Methods Programs Biomed. 2018, 161, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Rockhill, A.P.; Jackson, N.; George, J.; Aron, A.; Swann, N.C. UC San Diego Resting State EEG Data from Patients with Parkinson’s Disease. OpenNeuro 2020. [Google Scholar] [CrossRef]
- George, J.S.; Strunk, J.; Mak-McCully, R.; Houser, M.; Poizner, H.; Aron, A.R. Dopaminergic therapy in Parkinson’s disease decreases cortical beta band coherence in the resting state and increases cortical beta band power during executive control. NeuroImage Clin. 2013, 3, 261–270. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swann, N.C.; de Hemptinne, C.; Aron, A.R.; Ostrem, J.L.; Knight, R.T.; Starr, P.A. Elevated synchrony in Parkinson disease detected with electroencephalography. Ann. Neurol. 2015, 78, 742–750. [Google Scholar] [CrossRef] [Green Version]
- Jackson, N.; Cole, S.R.; Voytek, B.; Swann, N.C. Characteristics of Waveform Shape in Parkinson’s Disease Detected with Scalp Electroencephalography. Eneuro 2019, 6. [Google Scholar] [CrossRef] [Green Version]
- Appelhoff, S.; Sanderson, M.; Brooks, T.L.; van Vliet, M.; Quentin, R.; Holdgraf, C.; Chaumon, M.; Mikulan, E.; Tavabi, K.; Höchenberger, R.; et al. MNE-BIDS: Organizing electrophysiological data into the BIDS format and facilitating their analysis. J. Open Source Softw. 1896, 4, 1896. [Google Scholar] [CrossRef] [Green Version]
- Pernet, C.R.; Appelhoff, S.; Gorgolewski, K.J.; Flandin, G.; Phillips, C.; Delorme, A.; Oostenveld, R. EEG-BIDS, an extension to the brain imaging data structure for electroencephalography. Sci. Data 2019, 6, 103. [Google Scholar] [CrossRef] [Green Version]
- Christensen, O.; Feichtinger, H.G.; Paukner, S. Gabor Analysis for Imaging. In Handbook of Mathematical Methods in Imaging; Scherzer, O., Ed.; Springer: New York, NY, USA, 2015; pp. 1717–1757. [Google Scholar] [CrossRef] [Green Version]
- Brunton, S.L.; Kutz, J.N. Data-Driven Science and Engineering; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar] [CrossRef] [Green Version]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Yildirim, O.; Baloglu, U.B.; Acharya, U.R. A Deep Learning Model for Automated Sleep Stages Classification Using PSG Signals. Int. J. Environ. Res. Public Health 2019, 16, 599. [Google Scholar] [CrossRef] [Green Version]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Hafemann, L.G.; Sabourin, R.; Oliveira, L.S. Learning features for offline handwritten signature verification using deep convolutional neural networks. Pattern Recognit. 2017, 70, 163–176. [Google Scholar] [CrossRef] [Green Version]
- Latreille, V.; Carrier, J.; Gaudet-Fex, B.; Rodrigues-Brazete, J.; Panisset, M.; Chouinard, S.; Postuma, R.B.; Gagnon, J.F. Electroencephalographic prodromal markers of dementia across conscious states in Parkinson’s disease. Brain 2016, 139, 1189–1199. [Google Scholar] [CrossRef] [Green Version]
- Amato, N.; Caverzasio, S.; Galati, S. Clinical implication of high-density EEG sleep recordings in Parkinson’s disease. J. Neurosci. Methods 2020, 340, 108746. [Google Scholar] [CrossRef] [PubMed]
- Högl, B.; Stefani, A.; Videnovic, A. Idiopathic REM sleep behaviour disorder and neurodegeneration—An update. Nat. Rev. Neurol. 2018, 14, 40–55. [Google Scholar] [CrossRef]
- Al-Qassabi, A.; Fereshtehnejad, S.-M.; Postuma, R.B. Sleep Disturbances in the Prodromal Stage of Parkinson Disease. Curr. Treat. Options Neurol. 2017, 19, 22. [Google Scholar] [CrossRef] [PubMed]
- Sakar, B.E.; Isenkul, M.E.; Sakar, C.O.; Sertbas, A.; Gurgen, F.; Delil, S.; Apaydin, H.; Kursun, O. Collection and Analysis of a Parkinson Speech Dataset with Multiple Types of Sound Recordings. IEEE J. Biomed. Health Inform. 2013, 17, 828–834. [Google Scholar] [CrossRef] [PubMed]
- Pereira, C.R.; Pereira, D.R.; Da Silva, F.A.; Hook, C.; Weber, S.A.; Pereira, L.A.; Papa, J.P. A Step towards the Automated Diagnosis of Parkinson’s Disease: Analyzing Handwriting Movements. In Proceedings of the 2015 IEEE 28th International Symposium on Computer-Based Medical Systems, São Carlos and Ribeirão Preto, Brazil, 22–25 June 2015; pp. 171–176. [Google Scholar] [CrossRef]
- Tuncer, T.; Dogan, S.; Acharya, U.R. Automated detection of Parkinson’s disease using minimum average maximum tree and singular value decomposition method with vowels. Biocybern. Biomed. Eng. 2020, 40, 211–220. [Google Scholar] [CrossRef]
- di Biase, L.; Di Santo, A.; Caminiti, M.L.; De Liso, A.; Shah, S.A.; Ricci, L.; Di Lazzaro, V. Gait Analysis in Parkinson’s Disease: An Overview of the Most Accurate Markers for Diagnosis and Symptoms Monitoring. Sensors 2020, 20, 3529. [Google Scholar] [CrossRef] [PubMed]
- Caramia, C.; Torricelli, D.; Schmid, M.; Munoz-Gonzalez, A.; Gonzalez-Vargas, J.; Grandas, F.; Pons, J.L. IMU-Based Classification of Parkinson’s Disease From Gait: A Sensitivity Analysis on Sensor Location and Feature Selection. IEEE J. Biomed. Health Inform. 2018, 22, 1765–1774. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).