1. Introduction
Lung cancer is the leading cause of cancer death worldwide [
1,
2]. There are two main histopathological types of lung cancer, non-small cell lung cancer (NSCLC) and small cell lung cancer (SCLC), with their incidence rates representing about 85% and 15% of lung cancer cases, respectively [
3,
4]. Lung cancer has a poor prognosis despite the recent development of various novel treatments: the 5 year survival rate for NSCLC is about 22% and that for SCLC is 6% [
5]. The accurate prediction of a patient’s outcome, such as overall survival following a cancer diagnosis, is essential to guide treatment decision-making. Traditional survival analysis (SA) using the Cox proportional hazards model is based on the assumption that a patient’s risk is a linear combination of covariates. This assumption of linear–proportional hazards is difficult to satisfy with real-world data. Recently, the use of neural network-based survival prediction has been investigated to solve this limitation of SA and to improve the performance of prediction models. In previous studies, deep learning (DL) using various prognostic information was shown to have equal or superior performance compared to traditional SA in predicting survival [
6,
7,
8]. Prognostic information from genomic or medical imaging data is helpful, but these data are not available for all patients. However, clinical factors including age, gender, histology, stage, and smoking are routinely obtained during diagnostic evaluation in lung cancer patients. This study focused on the use of clinical information in the analysis of NSCLC patients’ survival time.
For the NSCLC survival analysis in our study, we observed that the number of samples in NSCLC was small due to challenges in collecting patient information. DL is data-hungry as it relies on data to learn latent information automatically while also providing a good feature. Therefore, a small sample makes the model prone to overfitting. In the field of medicine, it is challenging to collect patient information; therefore, this leads to the problem of a small sample size.
In this work, we propose a network architecture that combines a variational autoencoder (VAE) with a hazard function estimator and individual survival time predictor to enable multiple tasks to be learned simultaneously. This combination solves the problem of the small sample size in the practice of medicine and improves the performance of SA tasks.
2. Materials and Methods
2.1. Subjects
This study was approved by the Independent Institutional Review Board (IRB) of Chonnam National University Hwasun Hospital. Both methods and data collection were carried out in compliance with the applicable rules and regulations. The dataset, named CNUHHC, was collected in Chonnam National University Hwasun Hospital. Clinical variables which were obtained at diagnosis of NSCLC from 2004 to 2017 were collected from electric medical records by five reviewers. Patients were treated according to the multidisciplinary team’s treatment decisions: surgery, radiotherapy, concurrent chemoradiotherapy, and medical treatments including chemotherapy, targeted therapy, and immunotherapy. In the present study, we aimed to predict a patient’s outcome at diagnosis to guide the decision-making regarding their initial treatment. The staging included pathologic examination from specimens obtained by transbronchial or transthoracic biopsies, torso FDG PET/CT, contrast-enhanced chest CT, and brain MRI. The clinical T/N/M stage was assigned according to the seventh edition of the American Joint Committee on Cancer (AJCC) cancer staging manual by a multidisciplinary tumor board for lung cancer consisting of pulmonary oncologists, thoracic surgeons, neurosurgeons, radiation oncologists, pathologists, radiologists, and nuclear medicine physicians. CNUHHC includes the clinical information of 5206 patients. There are four categories and seven continuous fields in our clinical data in addition to the survival time that needs to be predicted.
Table 1 shows some statistical information regarding the selected dataset. The mean age was 66.8 (95% CI 66.6 to 67.0). There were 1241 females (23.8%) and 3965 males (76.2%). For NSCLC, the number of males was triple that of females. The number of patients in the early stages was smaller than in the late stages, with only one-third of patients diagnosed as stage I and II. In raw clinical data, we used three labels: dead, alive, and follow-up loss. Patients that live and patients lost to follow-up are considered as censoring data (right censoring) in traditional medical survival analysis such as the Cox proportional hazard regression model. In this work, 39.4% of the total data comprised censoring data in which we did not exactly know a patient’s outcome. With a 95% confidence interval, the population’s mean survival time was between 916 and 970 days, based on 5206 samples.
Table 2 shows the description of all fields in the dataset. There were two fields in the continuous form, including age in the basic group and amount in the smoking group. Two other fields were in a binary categorical form, including gender and status (smoking). T/N/M stages were also given as numbers 1, 2, 3, 4, but these were regarded as categorical variables (with a start mark). Even though the T/N/M stages were ordered, the spacing between the values may not have been the same across the variables’ levels; this was a kind of ordinal variable. Other fields were in a categorical form, including morphology code (MCODE), MCODE description, histology, and overall stage. There were 28 different values of MCODE and 27 for its description in the CNUHHC dataset. There were four values of histology: adenocarcinoma, large cell, squamous cell carcinoma, and not otherwise specified (NOS). The overall stage was one of nine different values.
2.2. Proposed Method
2.2.1. Multi-Task Network Architecture with Variational Autoencoder
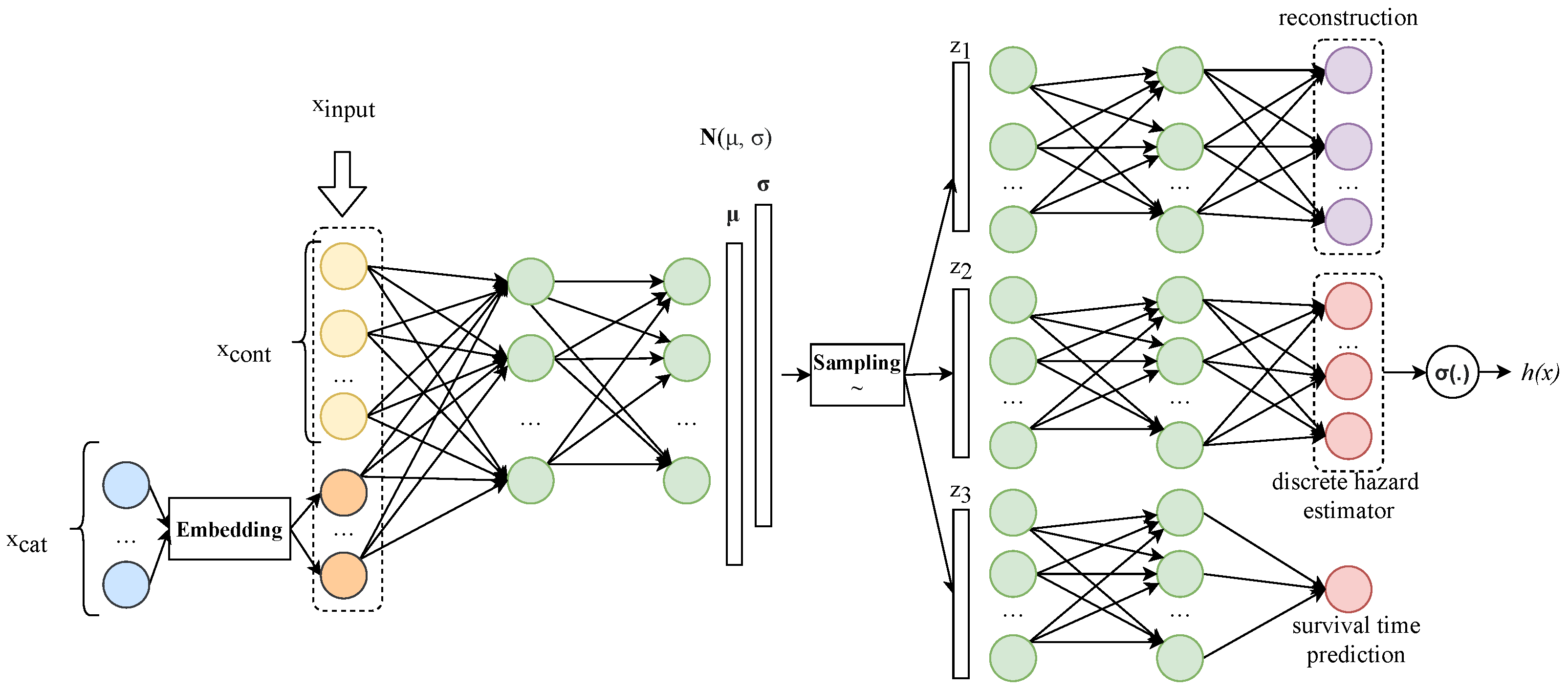
Figure 1 shows the proposed network architecture, named multiple task variational autoencoder survival analysis (MVAESA). As with some other VAE network architectures, two parts are included in MVAESA: an encoder and decoder. The objective of the encoder is to translate the input to the latent space that represents the input with some semantic. The decoder part is used to ground the output on the particular task from the latent space. Our approach combines a variational autoencoder and task-specific approach. Most of the internal data passing through our network are in vector form, and thus a fully connected neuron network—DNN—is used. The left part is an encoder, which receives a real number vector as an input and generates two vectors:
and
. Two vectors are the mean and variance of the encoding of the input in the latent space.
There are three decoders on the right of
Figure 1, which are responsible for reconstruction, hazard estimation, and survival time prediction from the top to the bottom of the figure. The reconstruction module aims to rebuild the original input from the latent vector. This module is basically taken from the vanilla VAE network architecture. The second decoder is used for the discrete hazard estimator. Finally, the individual survival time prediction module generates the estimated survival time for the patient. Each decoder module’s input is separated by sampling from
and
with a Gaussian distribution by using thereparameterization trick [
9]. Details of each block are given as follows.
2.2.2. Input Processing and Encoder Block
In most studies related to clinical datasets, the authors use only numeric fields. Most approaches are based on the linear approach, machine learning, and deep learning only working with numeric data. In practice, there are many fields in which the data are in a categorical form; thus, input processing is needed to convert non-numeric fields to numeric fields before passing them to the deep network. Some studies utilize a one-hot vector to perform encoding, but embedding shows success in many applications [
10,
11]. The embedding approach was introduced by Mikolov et al. [
12]. We formulate the original input clinical information of the patient, including continuous and category fields, as
in Equation (
1).
where
: the original input includes both continuous and categorical data fields;
: numeric fields;
: categorical fields;
concatenation operator.
For all fields in the categorical form, we choose the dimension to perform embedding to the continuous space. The embedding operator converts a discrete domain value to a continuous vector
, where
is the space dimension chosen for
. Because each categorical variable has different properties, the embedding space may have a different
; e.g.,
or
. Then, we concatenate all continuous and embedded vectors to create the input for the encoder block as shown in Equation (
2). The
was also used as the base to be reconstructed during the training process of our VAE.
where
: the input vector to pass through the deep network;
: a function that implement as embedding layers in the network;
: the concatenation operator;
: the concatenation operator for all elements.
Several fully connected (FC) layers are used for the encoder block with some ReLU function. Due to the low dimension of the input
and the small size, we keep the number of hidden nodes for all FC layers less than or equal to 128 to avoid the overfitting problem. At the end of the encoder process, there are two vectors—
—which act as typical encoders of a VAE network (
).
L is the latent space dimension, for which a value of 128 is chosen. Those values represent the input in the latent space, which follows the Gaussian distribution
. For later use in the decoder blocks, the sampling action is needed to make a vector from the distribution
and
. In our approach, each decoder uses separated sampling values. In
Figure 1,
,
, and
represent three sampled values after three different sampling processes.
2.2.3. Decoder Blocks
Typical VAE networks have only one decoder block, where the sampling vector from the latent space is passed through the DNN to reconstruct the original input. In our approach, we combine this kind of block with some other decoder blocks to employ multiple task learning strategies.
The objective of the reconstruction decoder is to make the vector as similar as possible to the input. As mentioned above, our approach tries to deal with both continuous and discrete covariates. The concatenate value is then used after embedding step as the reconstruction objective instead of .
The second decoder block aims to estimate the hazard function of the patient. This function returns the rate of probability of death over time. While some studies try to work with this function in the continuous domain [
13], few researchers have converted it to the discrete domain [
14,
15]. Our approach proceeds from the continuous to the discrete domain. From an outcome ranging from
to
, we divide this into
T equality segments; e.g.,
for
with a unit of years, and thus each segment will be
years. The decoder was designed to represent the objective, including several FC layers, and the output layer has
T nodes. As shown in
Figure 1,
T nodes then pass through the
sigmoid function to obtain the hazard function
of the input (
).
The third decoder was designed to predict the survival time of the patient. The output layer includes a single node, which is a non-negative number that represents the survival time.
2.2.4. Loss Function
Our network was designed for multiple task strategies, including the variational autoencoder part and survival analysis part, and the loss function should be designed so that the network learns both tasks together. Some studies have shown that learning multiple tasks simultaneously gives the network better coverage as it learns general information instead of particular task features [
16,
17,
18].
The loss function is the combination of
and
, which is given in Equation (
3).
As typical VAE loss functions,
is the combination of two partitions, including Kullback–Leibler (KL) divergence and the reconstruction. KL divergence aims to make the latent space, represented by
and
, controllable. Then, the normal distribution
is chosen. KL divergence is shown in Equation (
5). Reconstruction loss is given by the mean squared error and gives the difference between the output and the network input. After the embedding step, the input vector
is used to reference this loss function. In the traditional VAE architecture, the reconstruction module attempts to recover the original input from the latent vector. However, this approach only works with numeric inputs. We extend the network structure in
Figure 1 and adapt it with the categorical inputs; then, the loss function should be modified. As shown in
Figure 1 and Equation (
2), the
is the vector made from
combining
and the embedding of categorical fields. In consequence, the loss function uses this vector (
) instead of
. While each continuous field is seen as a float number, the category field is a vector in which the number of dimensions is usually more than one. The loss function for this part has to be modified to make sure that all fields make equal contributions to the loss function. We used the weighted approach as in Equation (
4).
where:
corresponding weight for element of
if field i embedded to space , then there is continue elements of with same value
The KL divergence score is given by Equation (
5).
is calculated from two sub-loss functions as Equation (
6).
The survival analysis decoders form the main part of our network architecture. This step involves two tasks: the hazard function estimator and individual survival time prediction.
includes the loss for the hazard function estimator and loss for individual survival time prediction. For the hazard function estimator, the negative log-likelihood of the discrete-time hazard loss function given by Havard Kvamme and Ornulf Borgan in [
15] is used. If we have data for
n independent individuals, the loss is given as Equation (
7).
where
: the input for patient i;
: event indicator for patient i;
: observed time for patient i;
: density function at time of the input ;
: survival function at time of the input .
and
are calculated from the estimated hazard function
of the model, as shown in Equation (
8).
Finally, a custom version of the mean squared error (CMSE) is used as the loss function for the regression problem of individual survival time prediction. Censoring data is a problem in most SA tasks. In our case, all censoring is in the form of right censoring. We make an update to the mean squared error (MSE) loss function to support this kind of problem. For right-censoring patients, the loss values are counted only if the predicted value is less than the ground truth value. Then, the CMSE is given as in Equation (
9).
where
2.3. Experimental Setup
The experimental setup used to verify the performance of our approach was compared with the baseline network architecture of DNN. Besides, the sample in the training set was also considered. While CNUHHC includes more than 5000 patients, it was collected for about 14 years, which is difficult in medical practice. We conducted two experiments with two parts of data for training, keeping the testing data separated for comparison. Typically, k-fold cross-validation is used to test datasets in which the number of samples is small; however, we wanted to verify the effect on our approach of a small dataset by comparing it not only other with approaches but also with itself when the training size changed. Consequently, a single independent validation data point was used for a fair comparison. By following the test–retest protocol, we randomly divided our data into two separated parts. About 20% of data was used for testing purposes and 80% formed the training set. The first part was the entire training set, called the large-sized set, with 4107 samples; the small-sized part had only 379 samples randomly selected from the large-sized set. There were 1099 patients in the test set (independent validation), which were kept separate from the training process. The embedding sizes were set as 14, 14, 2, and 5. There were seven fields in the form of numerical values. Therefore, the input size passed to the network was given by
The latent space dimension was set to 128, which means .
In the reconstruction part, the number of output nodes was set as equal to the network input after embedding: 42. We set , and each segment length was half of the year. The number of nodes for the hazard function estimator was 20.
We used popular metrics to evaluate our system and compare it with some previous studies. The concordance index (C-index) is one of the most important metrics for SA tasks. The C-index was introduced by Antolini et al. [
19]. This is an extension of the area under the receiver operating characteristic curve (AUC) in which right-censored data are also taken into account. This metric is given a value in the range [0,1], where 1 shows perfect results and 0 shows that the prediction is in the reverse order to the ground truth. A C-index of 0.5 indicates that the model outputs are random. Three popular survival analysis methods were selected to compare with our approach: CoxTime, CoxCC [
20], and CoxPH [
13]. CoxTime and CoxCC were introduced by Kvamme et al., who used neural networks to expand the Cox proportional hazards model for time-to-event prediction. CoxPH, also know as DeepSurv, is a deep learning approach that extends the Cox proportional hazards model.
2.4. Pre-Processing
The pre-processing step included some smaller steps. First, the data needed to be cleaned. Some categorical fields were in the form of text, which needed to be normalized and converted to an integer number. For survival analysis, censoring data always occurs, and this has an essential role in the analysis model. We had 1263 censoring patients, which were of two types: alive and not followed-up. All right-censoring patients were converted to the non-event type. The next step was data transformation. Some binary categorical fields could easily be converted to a binary number; that is, 0 or 1.
3. Results
Table 3 shows the comparison of our network architecture with the baseline network (DNN) with the same structure. With a large size of training data, our approach obtained a C-index of
, while CoxCC, CoxPH, and CoxTime methods obtained scores of
,
, and
, respectively. When the training size only included 379 samples, our approach achieved a C-index
while the baseline methods obtained
,
, and
, respectively. For all methods, the performance dropped a little when the training size became smaller; as shown, all C-index values with a small amount of training data were lower than with the large dataset. The C-index dropped from 0.713 to 0.689 for CoxCC, 0.703 to 0.688 for CoxPH, and 0.710 to 0.690 for CoxTime. In the same situation, MVAESA exhibited a drop from 0.722 to 0.707. Overall, in MVAESA, the C-index dropped less than all other approaches.
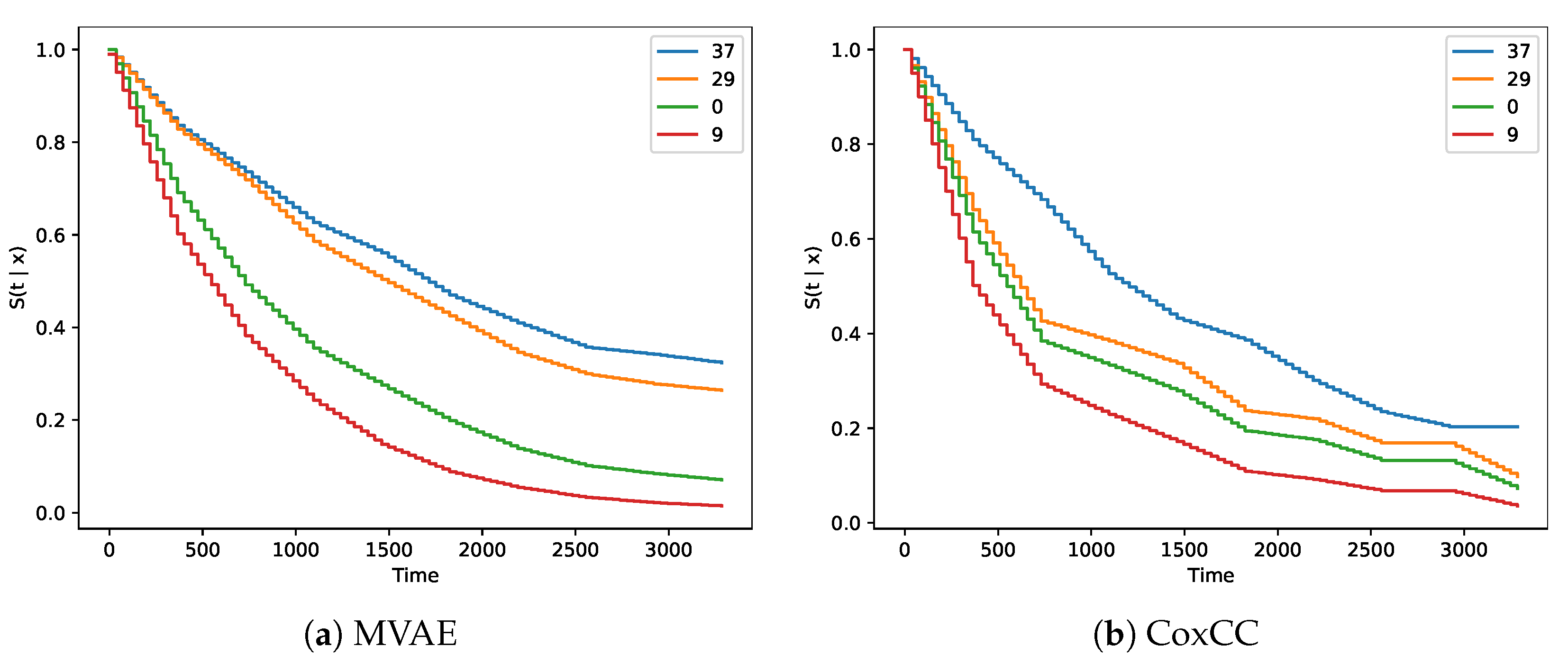
Figure 2a,b show survival curves for four patients in the validation set with patient IDs 37, 29, 0, and 9. Their values were inferred from the discrete hazard that was estimated the decoder.
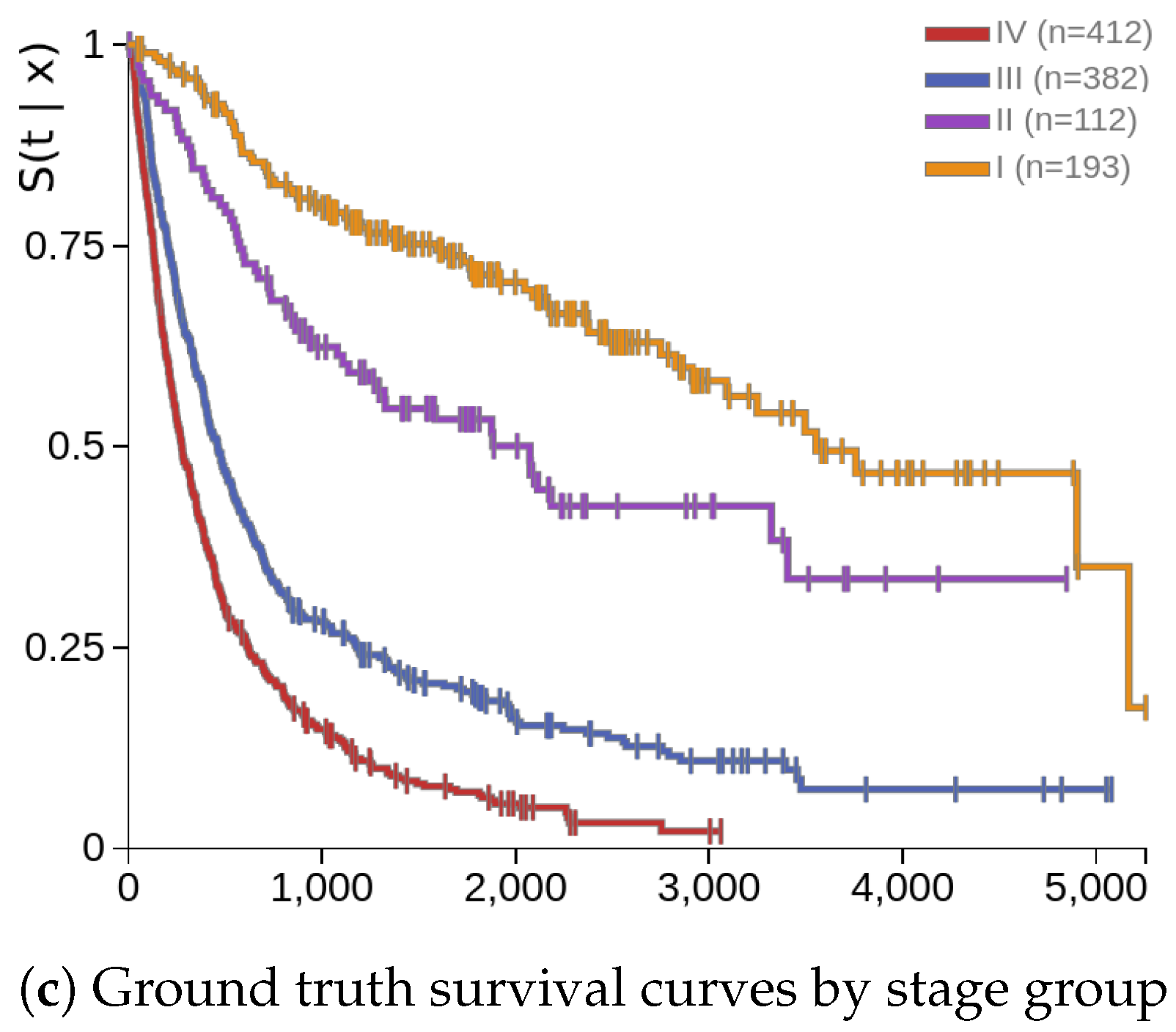
Figure 2c shows the survival curves for the validation by stage groups, which is given for reference. The overall stages and survival times each of four patients were I (222), II (3321), III (1965), and IV (142), in this order. In comparison,
Figure 2a,b shows better separation between early and late stage groups. However, the patient with ID 37 in stage I showed a better survival curve, but the survival time was only 222 days, compared to patient 0 in stage III with a survival time of 1965 days.
4. Discussion
The results show that our approach outperforms other approaches in the common metric in the SA tasks (C-index) for both cases of training sizes. With the entire training set, the relative improved shown by our approach was 1.26%; in particular, the difference was about twice as large (2.46%) in the case of a small-sized dataset. All approaches showed lower accuracy when the number of samples in training was limited, implying that the size of training data matters with DL. For all methods, the C-index dropped while the size of the training data decreased from 4107 to . However, the lower drop in performance shown by our approach implies that this network architecture is more stable with decreasing training data. Data collection in the medical sector is not easy due to privacy concerns and the management process. It is more likely to obtain a few samples instead of hundreds or thousands for certain diseases; in those instances, our solution would be beneficial.
Katzman et al. introduced CoxPH, which is also referred to as DeepSurv—a deep neural network that predicts a patient’s hazard rates based on their covariates [
13]. The network combines some Fully-Connected (FC) layers with some dropout layers and finally outputs the predicted value. Kvamme et al. built time-to-event prediction using neural networks that expands on the Cox proportional hazards model, with methods named CoxTime and CoxCC [
20]. DeepHit was proposed by Lee et al. to solve the problem of survival analysis with competing events [
14]. DeepHit can learn some low-level, common features with the shared sub-network before passing them through each branch for cause-specific prediction. Havard Kvamme and Ornulf Borgan investigated continuous and discrete-time survival prediction [
15]. In lung cancer survival analysis, Wang et al. introduced unsupervised deep learning to learn and extract features before using the Cox proportional hazards model for analysis [
21]. While previous studies focus on modeling and extending the traditional approaches for SA tasks using neural networks, none of them take the small size of training data into account, as has been shown in our work.
Besides clinical information, some data such as imaging [
22] and gene expression profiles [
23] may be included to improve the prediction accuracy. DL has been used to analyze the survival rates of a variety of cancers, including brain cancer [
24], breast cancer [
25], oral cancer [
8], and so on.
There are several limitations to this study. Firstly, while our approach is likely general, this study only focuses on NSCLC with a single dataset. Besides the patient’s current status, the treatment process also plays an essential role in a patient’s outcome. Some studies use data with this information to improve the performance [
26]; however, our dataset does not include this information. Those limitations should be addressed in future.
5. Conclusions
This study aims to solve the NSCLC survival analysis problem using clinical information. Data in medicine are difficult to obtain due to privacy concerns and the management process, resulting in a paucity of samples. To deal with this kind of difficulty, we combined multiple tasks with a VAE and developed a network called MVAESA. The experimental results show that the network architecture obtained a significant improvement when the number of samples was small, as is typical in practice. With a small size of the training set, we achieved a C-index of 0.707 compared to the values of 0.689, 0.688, and 0.690 for CoxCC, CoxPH, and CoxTime, respectively. Our approach also uses a mixture of numeric and categorical data, which was lacking in a recent study about survival analysis.
Author Contributions
Conceptualization, S.-H.K., T.-H.V., G.-S.L. and H.-J.Y.; methodology and investigation T.-H.V.; resources, S.-H.K., S.-R.K. and I.-J.O.; data curation, S.-R.K. and I.-J.O.; writing—original draft preparation, T.-H.V.; writing—review and editing, S.-H.K., S.-R.K., I.-J.O. and T.-H.V.; supervision, S.-H.K.; project administration, S.-H.K. All authors provided critical feedback and helped to shape the research, analysis and manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Bio and Medical Technology Development Program of the National Research Foundation (NRF) and funded by the Korean government (MSIT) grant number NRF-2019M3E5D1A02067961. This research was funded by the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea grant number HR20C0021.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki and approved by the independent institutional review board (IRB) of Chonnam National University Hwasun Hospital (IRB approval number: CNUHH-2019-194 and date: 19 November 2019).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Acknowledgments
This research was supported by the Bio and Medical Technology Development Program of the National Research Foundation (NRF) and funded by the Korean government (MSIT) (NRF-2019M3E5D1A02067961). This research was supported by a grant of the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI), funded by the Ministry of Health & Welfare, Republic of Korea (grant number: HR20C0021).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| SA | Survival analysis |
| NSCLC | Non-small cell lung cancer |
| SCLC | Small cell lung cancer |
| C-index | Concordance index |
| ML | Machine learning |
| DL | Deep learning |
| DNN | Deep neural network |
| FC | Fully connected |
| VAE | Variational Autoencoder |
| KL | Kullback–Leibler |
| PET | Positron Emission Tomography |
| CT | Computed Tomography |
| CI | Confidence interval |
References
- Torre, L.A.; Bray, F.; Siegel, R.L.; Ferlay, J.; Lortet-Tieulent, J.; Jemal, A. Global cancer statistics, 2012. CA Cancer J. Clin. 2015, 65, 87–108. [Google Scholar] [CrossRef] [PubMed]
- Choi, C.M.; Kim, H.C.; Jung, C.Y.; Cho, D.G.; Jeon, J.H.; Lee, J.E.; Ahn, J.S.; Kim, S.J.; Kim, Y.; Choi, Y.D.; et al. Report of the Korean Association of Lung Cancer Registry (KALC-R), 2014. Cancer Res. Treat. 2019, 51, 1400–1410. [Google Scholar] [CrossRef] [PubMed]
- Oser, M.G.; Niederst, M.J.; Sequist, L.V.; Engelman, J.A. Transformation from non-small-cell lung cancer to small-cell lung cancer: Molecular drivers and cells of origin. Lancet Oncol. 2015, 16, e165–e172. [Google Scholar] [CrossRef]
- Lu, T.; Yang, X.; Huang, Y.; Zhao, M.; Li, M.; Ma, K.; Yin, J.; Zhan, C.; Wang, Q. Trends in the incidence, treatment, and survival of patients with lung cancer in the last four decades. Cancer Manag. Res. 2019, 11, 943. [Google Scholar] [CrossRef] [PubMed]
- National Cancer Institute. Surveillance, Epidemiology, and End Results Program (SEER). Available online: http://seer.cancer.gov/csr/1975_2012/browse_csr.php (accessed on 22 March 2021).
- Mobadersany, P.; Yousefi, S.; Amgad, M.; Gutman, D.A.; Barnholtz-Sloan, J.S.; Vega, J.E.V.; Brat, D.J.; Cooper, L.A. Predicting cancer outcomes from histology and genomics using convolutional networks. Proc. Natl. Acad. Sci. USA 2018, 115, E2970–E2979. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.; Chun, S.H.; Hong, J.H.; Woo, I.S.; Kim, S.; Jeong, J.W.; Kim, J.J.; Lee, H.W.; Na, S.J.; Beck, K.S.; et al. DeepBtS: Prediction of Recurrence-free Survival of non-small cell Lung cancer Using a time-binned Deep neural network. Sci. Rep. 2020, 10, 1952. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.W.; Lee, S.; Kwon, S.; Nam, W.; Cha, I.H.; Kim, H.J. Deep learning-based survival prediction of oral cancer patients. Sci. Rep. 2019, 9, 6994. [Google Scholar] [CrossRef] [PubMed]
- Kingma, D.P.; Salimans, T.; Welling, M. Variational dropout and the local reparameterization trick. In Proceedings of the Advances in Neural Information Processing Systems 28 (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Guo, C.; Berkhahn, F. Entity embeddings of categorical variables. arXiv 2016, arXiv:1604.06737. [Google Scholar]
- Wang, P.; Xu, B.; Xu, J.; Tian, G.; Liu, C.L.; Hao, H. Semantic expansion using word embedding clustering and convolutional neural network for improving short text classification. Neurocomputing 2016, 174, 806–814. [Google Scholar] [CrossRef]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient estimation of word representations in vector space. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- Katzman, J.L.; Shaham, U.; Cloninger, A.; Bates, J.; Jiang, T.; Kluger, Y. DeepSurv: Personalized treatment recommender system using a Cox proportional hazards deep neural network. BMC Med. Res. Methodol. 2018, 18, 24. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.; Zame, W.; Yoon, J.; van der Schaar, M. Deephit: A deep learning approach to survival analysis with competing risks. In Proceedings of the 2018 AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Kvamme, H.; Borgan, Ø. Continuous and discrete-time survival prediction with neural networks. arXiv 2019, arXiv:1910.06724. [Google Scholar]
- Collobert, R.; Weston, J. A Unified Architecture for Natural Language Processing: Deep Neural Networks with Multitask Learning. In Proceedings of the 25th International Conference on Machine Learning, Helsinki, Finland, 5–9 July 2008; Association for Computing Machinery: New York, NY, USA, 2008; pp. 160–167. [Google Scholar] [CrossRef]
- Deng, L.; Hinton, G.; Kingsbury, B. New types of deep neural network learning for speech recognition and related applications: An overview. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 8599–8603. [Google Scholar] [CrossRef]
- Girshick, R. Fast R-CNN. In Proceedings of the 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 11–18 December 2015; pp. 1440–1448. [Google Scholar] [CrossRef]
- Antolini, L.; Boracchi, P.; Biganzoli, E. A time-dependent discrimination index for survival data. Stat. Med. 2005, 24, 3927–3944. [Google Scholar] [CrossRef] [PubMed]
- Kvamme, H.; Borgan, Ø.; Scheel, I. Time-to-event prediction with neural networks and Cox regression. arXiv 2019, arXiv:1907.00825. [Google Scholar]
- Wang, S.; Liu, Z.; Chen, X.; Zhu, Y.; Zhou, H.; Tang, Z.; Wei, W.; Dong, D.; Wang, M.; Tian, J. Unsupervised Deep Learning Features for Lung Cancer Overall Survival Analysis. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Honolulu, HI, USA, 18–21 July 2018; pp. 2583–2586. [Google Scholar] [CrossRef]
- Haarburger, C.; Weitz, P.; Rippel, O.; Merhof, D. Image-based survival prediction for lung cancer patients using CNNS. In Proceedings of the 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019), Venice, Italy, 8–11 April 2019; pp. 1197–1201. [Google Scholar]
- Lai, Y.H.; Chen, W.N.; Hsu, T.C.; Lin, C.; Tsao, Y.; Wu, S. Overall survival prediction of non-small cell lung cancer by integrating microarray and clinical data with deep learning. Sci. Rep. 2020, 10, 4679. [Google Scholar] [CrossRef] [PubMed]
- Suter, Y.; Jungo, A.; Rebsamen, M.; Knecht, U.; Herrmann, E.; Wiest, R.; Reyes, M. Deep Learning Versus Classical Regression for Brain Tumor Patient Survival Prediction. In Brainlesion: Glioma, Multiple Sclerosis, Stroke and Traumatic Brain Injuries; Crimi, A., Bakas, S., Kuijf, H., Keyvan, F., Reyes, M., van Walsum, T., Eds.; Springer International Publishing: Cham, Switzerland, 2019; Volume 11384, pp. 429–440. [Google Scholar] [CrossRef]
- Huang, Z.; Zhan, X.; Xiang, S.; Johnson, T.S.; Helm, B.; Yu, C.Y.; Zhang, J.; Salama, P.; Rizkalla, M.; Han, Z.; et al. SALMON: Survival analysis learning with multi-omics neural networks on breast cancer. Front. Genet. 2019, 10, 166. [Google Scholar] [CrossRef] [PubMed]
- She, Y.; Jin, Z.; Wu, J.; Deng, J.; Zhang, L.; Su, H.; Jiang, G.; Liu, H.; Xie, D.; Cao, N.; et al. Development and Validation of a Deep Learning Model for Non–Small Cell Lung Cancer Survival. JAMA Netw. Open 2020, 3, e205842. [Google Scholar] [CrossRef] [PubMed]
Short Biography of Authors
![Electronics 10 01396 i001 Electronics 10 01396 i001]() | VO THANH HUNG is currently working toward a Ph.D. degree in the Pattern Recognition Lab, Department of Artificial Intelligence Convergence, Chonnam National University, Korea. He received B.Eng. and M.Eng. degrees in Computer Science from Ho Chi Minh City University of Technology, Vietnam National University, Vietnam in 2010 and 2013. Since 2011, he has worked at Ho Chi Minh City University of Technology as a lecturer. His research interests include natural language processing, pattern recognition, and medical image processing |
![Electronics 10 01396 i002 Electronics 10 01396 i002]() | GUEE-SANG LEE received a B.S. degree in Electrical Engineering and an M.S. degree in Computer Engineering from Seoul National University, South Korea in 1980 and 1982, respectively, and a Ph.D. degree in Computer Science from Pennsylvania State University in 1991. He is currently a Professor with the Department of Electronics and Computer Engineering, Chonnam National University, South Korea. His primary research interests include image processing, computer vision, and video technology. |
![Electronics 10 01396 i003 Electronics 10 01396 i003]() | HYUNG-JEONG YANG received B.S., M.S., and Ph.D. degrees from Chonbuk National University, South Korea. She is currently a Professor with the Department of Electronics and Computer Engineering, Chonnam National University, Gwangju, South Korea. Her main research interests include multimedia data mining, medical data analysis, social network service data mining, and understanding video data. |
![Electronics 10 01396 i004 Electronics 10 01396 i004]() | In-Jae Oh received M.D., M.S., and Ph.D. degrees from Chonnam National University, South Korea. He is currently a Professor with the Department of Internal Medicine, Chonnam National University Medical School and Hwasun Hospital. His research interests include molecular diagnosis and translational research into lung cancer. |
![Electronics 10 01396 i005 Electronics 10 01396 i005]() | Soo-Hyung Kim received a B.S. degree in Computer Engineering from Seoul National University in 1986, and M.S. and Ph.D. degrees in Computer Science from the Korea Advanced Institute of Science and Technology in 1988 and 1993, respectively. Since 1997, he has been a Professor with the School of Electronics and Computer Engineering, Chonnam National University, South Korea. His research interests include pattern recognition, document image processing, medical image processing, and deep learning. |
![Electronics 10 01396 i006 Electronics 10 01396 i006]() | Sae-Ryung Kang received M.D., M.S., and Ph.D. degrees from Chonnam National University, South Korea. She is currently an Assistant Professor of the Department of Nuclear Medicine, Chonnam National University Hwasun Hospital. Her research interests include nuclear medicine and molecular imaging. |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).