A Novel Fast-Locking ADPLL Based on Bisection Method

Abstract

Based on the idea of bisection method, a new structure of All-Digital Phased-Locked Loop (ADPLL) with fast-locking is proposed. The structure and locking method are different from the traditional ADPLLs. The Control Circuit consists of frequency compare module, mode-adjust module and control module, which is responsible for adjusting the frequency control word of digital-controlled-oscillator (DCO) by Bisection method according to the result of the frequency compare between reference clock and restructure clock. With a high frequency cascade structure, the DCO achieves wide tuning range and high resolution. The proposed ADPLL was designed in SMIC 180 nm CMOS process. The measured results show a lock range of 640-to-1920 MHz with a 40 MHz reference frequency. The ADPLL core occupies 0.04 mm², and the power consumption is 29.48 mW, with a 1.8 V supply. The longest locking time is 23 reference cycles, 575 ns, at 1.92 GHz. When the ADPLL operates at 1.28 GHz–1.6 GHz, the locking time is the shortest, only 9 reference cycles, 225 ns. Compared with the recent high-performance ADPLLs, our design shows advantages of small area, short locking time, and wide tuning range.

1. Introduction

Locking time is one of the key parameters in All-Digital Phased Locked Loop (ADPLL) [1,2,3,4]. Ideally, the locking time should be as small as possible. The traditional structure All-Digital Phased Locked Loop (TS-ADPLL) usually uses the adaptive-bandwidth technique [5] or the Digitally Controlled Oscillator (DCO) tuning word estimating with presetting technique [6,7,8] to reduce the locking time. The adaptive-bandwidth technique changes the bandwidth of filter according to the different state. The DCO tuning word estimating and presetting technique change the initial frequency of Digitally Controlled Oscillator, getting more closer to the target frequency, in order to reduce the locking time. And their frequency resolution is not high enough. The traditional structure’s locking time is related to output frequency range, filter’s bandwidth, target frequency, and frequency resolution. The larger the output frequency range is, the smaller the bandwidth of the filter is, the farther the target frequency is from the initial frequency, and the higher frequency resolution of DCO is, resulting in longer locking time [9,10,11,12,13,14,15].

In order to solve the above problem, this paper proposes a new structure All-Digital Phased Locked Loop (NS-ADPLL), which is based on bisection method. The new structure’s locking time, only related to reference frequency, output frequency range, and frequency resolution, has no relationship with the target frequency and Filter’s bandwidth. And the new structure’s locking time growth rate is far slower than the traditional one when the frequency range and the resolution of DCO is increased. The All-Digital Phased Locked Loop proposed in this paper can effectively reduce the lock-in time by 80–90%.

2. Circuit Design

The block diagram of the proposed ADPLL is shown in Figure 1, consisting of Control circuit, DCO circuit and DIV circuit. Control circuit includes: Frequency Compare module (FC), Mode-Adjust module (MA), and Control module.

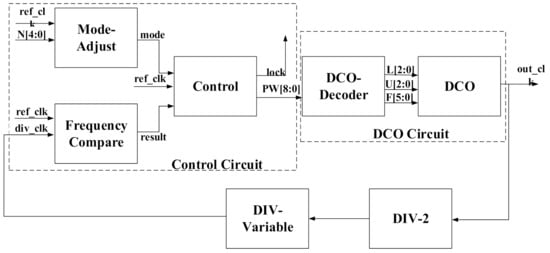
Figure 1. Block diagram of the new structure ADPLL.

DCO is made up of DCO-Decoder and DCO module. The basic workflow of the ADPLL system is as follows: FC module detects the difference between the reference signal ref_clk ($f_{ref}$) and the reconstructed signal div_clk ($f_{div}$), and it delivers the results to the Control module. When the System is in the first 9 reference clock cycles, the MA module output signal, mode signal, is logic “0”, which means that the system is in the Coarse Adjustment Mode (CAM). After the first 9 reference clock cycles, the MA module will adjust mode signal to logic “1”, which means the system changes from CAM to Fine Adjustment Mode (FAM). According to the MA module and FC module output, the control module will change the PresetWord (PW) of DCO, and the DCO Circuit will adjust frequency of output signal ($f_{out}$) based on the PW. After that, the DIV circuit will divide the $f_{out}$ to $f_{div}$, and $f_{div}$ will compare with $f_{ref}$ again. Finally, the ADPLL gradually enters the state of lock, and control module output signal, lock signal, changes to “1”.

The locking method used by the NS-ADPLL is also different from TS-ADPLL. The specific locking process is shown in Figure 2. Figure 2a is the frequency change process of TS-ADPLL, which follows the target frequency step by step. Obviously, the locking time is related to the output frequency range, the bandwidth of the filter and the target frequency, etc. Figure 2b is the locking process of the NS-ADPLL. First, the relationship between $f_{div}$ and $f_{ref}$ must be determined. If $f_{div}$ is smaller than $f_{ref}$, the minimum frequency ($f_{min}$) will be changed to $f_{div}$, and then the $f_{div}$ increases. If $f_{div}$ is larger than $f_{ref}$, the maximum frequency ($f_{max}$) is changed to $f_{div}$, and then $f_{div}$ decreases, which can be calculated as follows:

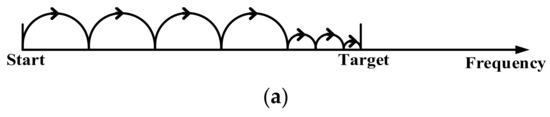
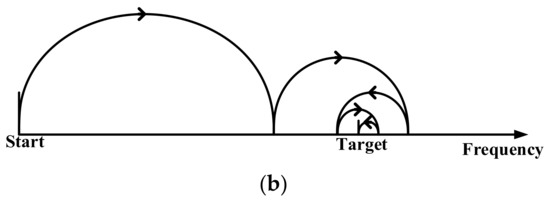
Figure 2. Locking process (a) TS-ADPLL, (b) NS-ADPLL.

$f_{div}<f_{ref}:$

$$f_{min}=f_{div}^{n-1}, f_{div}^n=f_{div}^{n-1}+\frac{\left(f_{max}-f_{div}^{n-1}\right)}{2};$$

(1)

($f_{div}^n$ represents the DCO frequency of next state)

$f_{div}>f_{ref}:$

$$f_{max}=f_{div}^{n-1}, f_{div}^n=f_{div}^{n-1}-\frac{\left(f_{div}^{n-1}-f_{min}\right)}{2};$$

(2)

($f_{div}^{n-1}$ represents the DCO frequency of current state).

Equations (1) and (2) can be implemented using Verilog code as in Equations (3) and (4)

$f_{div}<f_{ref}:ControlWor{d}_{DCO}^n=ControlWor{d}_{DCO}^{n-1}+lengt{h}_{PW}$

$$PresetWor{d}_{min}=ControlWor{d}_{DCO}^{n-1},$$

(3)

$f_{div}>f_{ref}:ControlWor{d}_{DCO}^n=ControlWor{d}_{DCO}^{n-1}-lengt{h}_{PW}$

$$PresetWor{d}_{max}=ControlWor{d}_{DCO}^{n-1}.$$

(4)

2.1. Control Circuit

Control circuit consists of three modules: MA module, FC module, and Control module.

MA module is responsible for changing the NS-ADPLL working mode. NS-ADPLL has three working modes: CAM, FAM, and Locked-in mode. The working mode is changed according to the reference clock and the relationship between $F_{ref}$ and $F_{div}$. At the first 9 reference clock cycles, the NS-ADPLL works at CAM mode. In this working mode, the PW will be adjusted according to the Bisection Method. Because the $f_{ref}$ is 40 MHz, the NS-ADPLL will stay in this mode for 225 ns. Then, the NS-ADPLL will change to FAM. In this mode, the PW will be changed slowly, and the system will enter the next mode after the relationship between $F_{ref}$ and $F_{div}$ changes three times. The next mode is lock mode, where $f_{div}$ will continue to track $f_{ref}$, and the system is locked-in. The flowchart of MA module is shown in Figure 3.

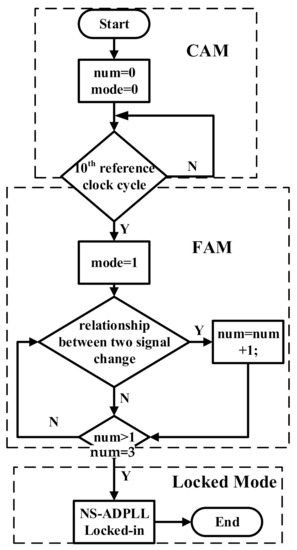
Figure 3. Operating principle of the MA module.

FC module is responsible for comparing the frequency between reference clock and reconstructed signal. It compares the frequency according to the phase. Figure 4 shows the FC module operating principle. Initially, the module will adjust the phase of $F_{div}$, forcing the two signals have the same phase. Then, it senses the first positive edge of $f_{div}$ or $f_{ref}$. If reference signal comes first, it means that $f_{ref}$ is larger than $f_{div}$. If reconstructed signal comes first, it means that $f_{div}$ is larger than $f_{ref}$.

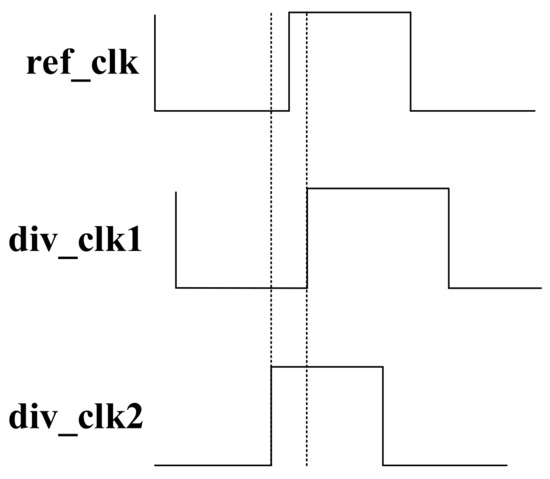
Figure 4. Operating principle of the FC module.

As shown in the Figure 4, the $f_{div\_clk1}$ is smaller than $f_{ref}$, and the $f_{div\_clk2}$ is larger than $f_{ref}$.

The Control module is shown in Figure 5, which is responsible for adjusting the PW according to the result of FC module, based on which the NS-ADPLL will enter different working mode (CAM or FAM).

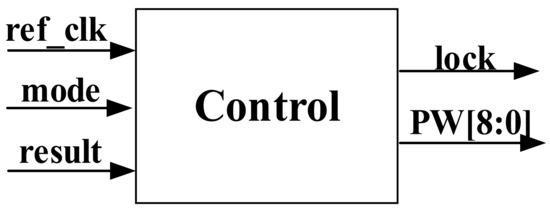
Figure 5. Block diagram of the Control module.

At CAM, the PW will change considerably based on bisection method. The control circuit will cost 9 reference clock cycles in CAM. The number of cycles which the system spends in CAM depends on the number of PW. In NS-ADPLL, DCO has 320 different PW because:

$$2^8<320<2^9.$$

NS-ADPLL will spend 9 reference clock cycles in CAM. When NS-ADPLL is in CAM, the FC module will compare the frequency of $f_{ref}$ and $f_{div}$ every cycle and output the result. If the result is 1, it means $f_{ref}$ is higher than $f_{div}$, and the PW will reduce. Otherwise, when the result is 0, it means $f_{ref}$ is lower than $f_{div}$, and the PW will increase. For example, we suppose the result that FC module output in CAM is 0, 0, 0, 1, 1, 1, 0, 0, 0. According to (1) and (2), PW will increase 3 times, from 0 to 159($\frac{319-0}{2}$), from 159 to 239($159+\frac{319-159}{2}$), and from 239 to 279($239+\frac{319-239}{2}$). Then, it will reduce 3 times, from 279 to 259($279-\frac{279-239}{2}$), from 259 to 249($259-\frac{259-239}{2}$), and from 249 to 244($249-\frac{249-239}{2}$). Finally it will increase 3 times, from 244 to 246($244+\frac{249-244}{2}$), from 246 to 247($246+\frac{249-246}{2}$), and from 247 to 248($247+\frac{249-247}{2}$). After CAM, NS-ADPLL have a PW which is close to the target PW. Then, NS-ADPLL enters the FAM.

At FAM mode, Control module will adjust PW to make the $f_{div}$ closer to the $f_{ref}$. It will cost 100 ns to 300 ns. Because the system always has delay, the DCO output frequency cannot change immediately when PW completes the adjustment. It will lead to the PW which gets in the CAM, not entirely correct, but very close to the right one. Therefore, NS-ADPLL needs FAM to adjust the PW and eliminate the effect of system’s delay. In order to increase the correctness of the PW and reduce the working time of NS-ADPLL in FAM, the system will be locked after the relationship between $f_{div}$ and $f_{ref}$ changes twice or three times.

Finally, NS-ADPLL is locked, the control module will keep fine tune the PW to make $f_{div}$ to continue to track $f_{ref}$. The flowchart of the control module is shown in Figure 6. Although it shows that PW will only be adjusted after NS-ADPLL locked, NS-ADPLL will actually keep adjusting the PW to continue to track $F_{ref}$.

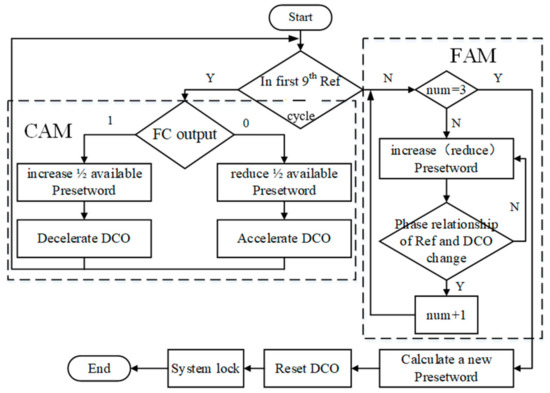
Figure 6. Flowchart of the Control module (num is the number of changes in the relationship between $f_{div}$ and $f_{ref}$).

2.2. DCO Circuit

DCO circuit consists of DCO and DCO-Decoder. DCO is an important block in the ADPLL, it will affect the frequency range of ADPLL’s output clock and the power consumption of ADPLL. A high frequency cascade structure DCO with a wide frequency range and fine resolution was designed [16]. Both wide frequency range (500 MHz–2.4 GHz) and fine resolution (1–8 ps) are obtained using a cascading structure consisting of a coarse delay chain and an interpolator. Figure 7 shows the schematic diagram of the proposed DCO.

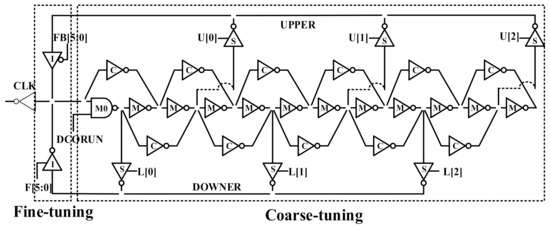
Figure 7. Schematic of the DCO.

The DCO has two submodules: coarse-tuning module and fine-tuning module.

The coarse-tuning module is designed with the delay path selection technique, which can achieve very wide frequency range. It consists of eleven main inverters(M-Inv) and eleven compensated inverters(C-Inv) and six switches. In order to reset the DCO, the first M-Inv is replaced with a NAND gate with the reset signal DCORUN. The coarse-tuning module can only select two adjacent delay path to adjust the frequency of DCO. Therefore, there are five different options. For example, when switches L[2] and U[2] are selected, other switches all closed, DCO has the maximum delay and the lowest frequency. If the switches L[0] and U[0] are selected, DCO will have the minimum delay and the highest frequency. We can see that it is easy to increase the output frequency range with the number of M-Inv, C-Inv, and switches increasing. The minimum adjustment of delay is 224 ps in coarse-tuning module

And the fine-tuning module is designed with the interpolator technique in order to improve the resolution of DCO. The schematic of the fine-tuning module is shown in Figure 8. It consists of two types of tri-state inverters; each type has seven inverters, and there are fourteen inverters in all. The first two tri-state inverters are connected to $V_{DD}$, so the fine-tuning module is controlled by a 6 bits binary control codes F[5:0]. When the control code is in low level, the corresponding tri-state inverter which is connected to the signal UPPER will open, and the one connected to the signal DOWNER will close conversely. The different number of the control code of tri-state inverter represent the different weighted size of tri-state inverter. The binary control code F[5:0] provides 64 options in fine-tuning stage. The total delay rang of the fine-tuning module is equal to one option of coarse-tuning module.

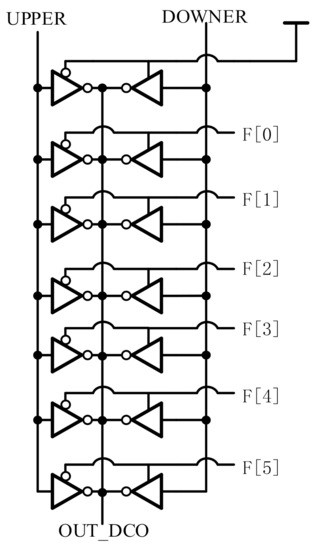
Figure 8. Schematic of the fine-tuning module.

The DCO has five coarse-tuning options, and each option owns 64 fine-tuning options. Therefore, the DCO has 320 different Control words in total. The post-simulation result is shown in Table 1. We can see that the DCO can work within wide frequency range of 500 MHz–2 GHz and has a high resolution of 1–8 ps. And the layout occupies 0.006 ${\mathrm{mm}}^2$. With the current-hungry structure, the DCO dissipates about 24 mW.

Table 1. DCO post-simulation results.

Symbol	Quantity	Data
ps	Coarse-tuning	224
ps	Fine-tuning	Best 1 ps, Worst 8 ps
GHz	Output frequency range	0.5–2
${\mathrm{mm}}^2$	Area	0.006

In order to prevent the dead zone, which may result in the NS-ADPLL unlocked, the control words and output frequency of DCO must be monotonic. Simulated output period time versus digital control-word for the DCO at 1.8 V supply voltage is shown in Figure 9. The output clock period increases with the control-word.

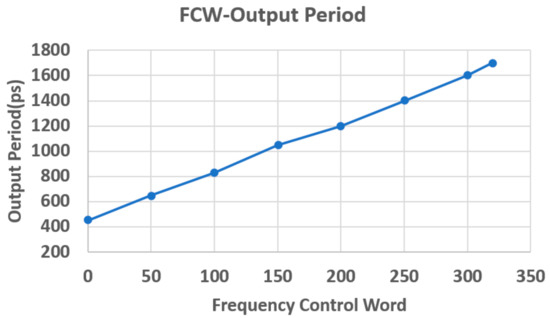
Figure 9. Frequency vs. Control word of the DCO.

3. Experimental Results

The proposed NS-ADPLL was implemented in SMIC 180 nm CMOS process with a 1.8 V supply. The microphotograph of the prototype chip is illustrated in Figure 10, The entire die area of the NS-ADPLL is 0.04 ${\mathrm{mm}}^2$. Figure 11 shows the locking time in different output frequency, which shows that the best locking time (225 ns, 9 reference clock cycles) occurs at 1.28 GHz to 1.6 GHz; however, the worst one (575 ns, 23 reference clock cycles) at 1.92 GHz. Figure 12 shows the power consumption in different output frequency. The power consumption increases with the output frequency increases. With a 1.8 V supply at 1.92 GHz, the NS-ADPLL consumes 29.48 mW, of which 80% comes from DCO circuit.

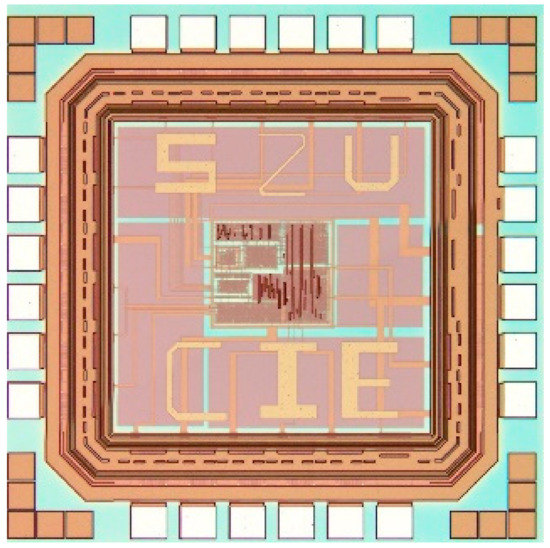
Figure 10. The microphotograph of the proposed NS-ADPLL.

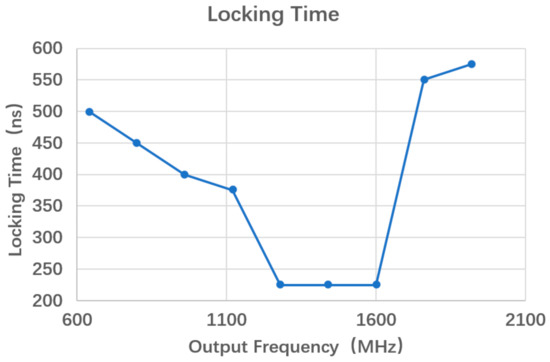
Figure 11. The locking time of the NS-ADPLL.

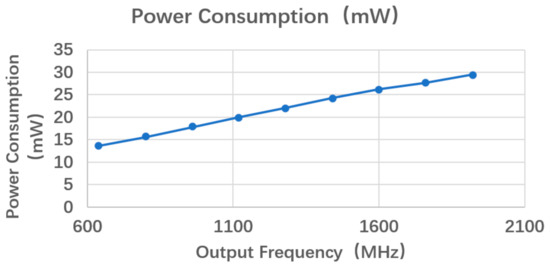
Figure 12. The power consumption of the NS-ADPLL.

To evaluate the performance of the proposed ADPLL, comparisons had been performed with other high-performance designs, including Young’s ADPLL [1], Amr’s ADPLL [3], Chung’s ADPLL [4], and Chou ADPLL [8]. The comparison results shown in Table 2. It can be observed that the NS-ADPLL shows the best performance in the locking time, output range, and core area.

Table 2. NS-ADPLL performance comparison.

	[1]	[3]	[4]	[8]	This Work
Process (nm)	130	65	90	45	180
Supply (v)	1.8	-	1.2		1.8
Area (${\mathrm{mm}}^2$)	-	0.013	0.065	0.013	0.04
Power (mW)	1.37	5.1	0.92	5.6	29.48
Input (MHz)	500	200	20	150	40
Output (GHz)	1.8	2.76–6	0.06–0.6	2.4	0.64–1.92
RMS jitter (ps)	-	1.37	13.7	0.91	15.6@1.6 GHz
Ref cycles (Locked)	150	200	16	270	9@1.6 GHz
Time (ns)	300	1000	800	1800	225@1.6 GHz