Abstract
This paper aims to present carefully selected scientific papers that have pushed the boundaries in the application of advanced computational intelligence–based methods in power engineering, mainly in optimal power system management. Contemporary development of the Smart Grid and detailed framework for power grid digitalization enabled the real and efficient application of advanced optimization algorithms presented in this paper. Papers that are not directly related to Smart Grid management are also considered, since they solve the partial challenges of planning and development with metaheuristic procedures, and according to the authors, they are highly applicable and represent a fundamental starting point for wider application. This paper covers papers and research whose results are reproducible and can be realized in production-grade software. The emphasis of the paper is on the considerate and impartial way of providing a concise overview of the methods for solving technical challenges within the accepted Smart Grid architecture. The paper is the result of many years of research and commitment to this field and represents the foundation for present research and development.
1. Introduction
Smart Grid research is the new, challenging area with great interest of research teams in the EU space [1,2]. Future advanced and smarter power network relies heavily on the possibility of independent permanence and self-sufficiency based on data and informed management [3,4]. The development of the power network at the distribution level and the increasing integration of renewable energy sources (RES) makes the network heterogeneous and more diverse. The laws of network management that were once applicable to the whole system become less valid in the era of changing power system and novel paradigms. Such system requires advanced methods of rapid analysis of a multitude of possible scenarios to achieve optimal power system management. This paper examines the scientific and engineering foundations of using computational intelligence (CI) methods for achieving optimal real-time or quasi-real time management of Active Distribution Network (ADN). ADN is the first stage in the formation of more advanced Smart Grid which involves usual power distribution equipment along with information and communication technologies (ICT) and monitoring systems. The goal of Smart Grid is more reliable power supply and adequate power quality (PQ) in the ever-changing environment. The presented methods are currently oblivious to information technology and are focusing on electrical engineering principles since those are the foundations for every other application. Objectives observed by this paper are energy balancing, losses reduction, reliability increase and policy definitions described in latest scientific achievements. Energy balancing is the most important part of Smart Grid and it can be a topic for itself, especially when market considerations become equally important to technical ones.
Although most scientific papers presented here focused on optimal Distributed Generation (DG) allocation and sizing in distribution network, objectives achieved by papers presented in this work can be used as an engineering foundation for ADN operational management based on advanced CI optimization algorithms. The scope covered by Distribution Network Optimization is much larger than just the allocation of DG units and includes optimization of the topology and timetable planning of existing power plants to achieve optimal power flows [5,6]. Accordingly, this paper includes the papers that in a concise and precise way define the application of CI methods in solving modern challenges in the power system, especially the problem of utilization of a larger number of DG units. Real-time power flow optimization, as described Reference [5], comes only after a real-world software solution is set up at the planning level. This paper defines the principles that such a software solution should meet and describes the leading CI algorithms that can result in such a software solution. Subsequently, a new part of such a solution may be real-time optimization module for optimization of power flows, voltage profile and oscillation damping control, as given in Reference [5]. For such real-time power flow optimization with limited infrastructure for data acquisition in the distribution grid, a robust state estimation engine is crucial [6] to address uncertainties in the distribution network.
Scientific works observed by this paper can lead to the development of ADN management solutions and the current activities of the authors confirm that hypothesis. Assumptions of ADN operational management by CI is unequivocally and unanimously highlighted and validated by papers [7,8,9]. The challenges ahead in the field of Big Data collection and consumption monitoring using advanced metering infrastructure are certainly part of the development of such ADN management solutions [6].
The rest of the paper is structured as follows: Section 2 provides the overview of the used methodology, sources of information, knowledge collection, synthesis and solution assessment criteria. Section 3 analyzes the scope of DG impact in the distribution network and what are physical constraints that need to be respected when evaluating applicability of any CI method. Section 3 presents most important papers that use CI for optimal allocation and optimal scheduling of DG units, while considering the physical and technical limitations of the considered ADN system. Selected papers are the result of described methodology and selection criteria. Moreover, by the opinion of the authors of this paper, selected papers can be utilized in market-oriented planning and scheduling scenarios in real-world systems nowadays. Section 4 describes papers that bring significant breakthroughs in the operational management of the ADN with multiple DG units. Finally, the conclusion outlines observations and knowledge gathered by this paper.
2. Methodology
The papers covered in this paper are partly part of the research during the preparation of the doctoral dissertation, and partly during the research phase of the project mentioned in the acknowledgment. Given the constant changes in technology, the criteria for including and excluding processed papers required fine-tuning throughout the research process. What is common to all the presented works is that the team of development experts, to a greater or lesser extent, managed to replicate the outcomes at the level of the model and the prototype solution. This was also a key criterion for the processing of individual work—high reliability that the proposed solution can be refined and developed for the needs of the actual system.
For the purpose of collecting valid information, journals indexed in the leading databases Web of Science, Scopus and Inspec were consulted. The advanced search considered more than 7000 papers. This huge amount of information has been reduced to a little over 1000 basic papers by thorough processing according to the thematic criteria and observed challenges. Additionally, by the criteria of the number of mentions and the context in which they were mentioned, and a preliminary reading of a team of researchers, the selection was reduced to around 250 relevant papers. The additional thematic division and organization of a wider team of researchers quickly prototyped the relevant group and the choice remained on those papers mentioned in this paper. If the reader considers that some paper has been unfairly neglected, the authors are open to contact and correction in future papers.
Aware of the fact that the impossibility of repeating the outcome of a single paper does not immediately imply the unacceptability of the observed solution for processing in this paper, we consulted external domain experts. The covered domains are the field of artificial and computational intelligence, distribution network optimization techniques and development of monitoring and control solutions for distribution power networks. Such an interdisciplinary team provided a multi-perspective review of the observed solutions that was in some cases crucial to understanding what was presented.
Although researchers were given the opportunity to independently assess and organize individual development teams, it turned out that regular synchronization meetings could achieve more results in less time. By dynamically adapting the research team according to Agile principles [10,11], a larger amount of methods than originally conceived was processed.
The risk of bias and false applicability estimation was solved by following the next procedure:
- Extraction of the presented mathematical model—In this step, a multi-member team took responsibility for extracting key information from each paper and, if necessary, filling in the gaps in the mathematical model.
- Synthesis of a defined mathematical model—If key parameters are missing in the first step, the paper is marked as incomplete and is temporarily not considered. However, it happened that some other work was based on the same laws as the one that was neglected, so one complements the other. In this step it is crucial to obtain the same or approximately the same starting point as the original authors.
- Development of an identical or similar solution—In this step, it has proved crucial to have a team of specialized experts and profiled researchers who can understand the principles to be set out in development in order to achieve greatest effect. Usually, rapid prototyping does not require more than a few days of work for a well-organized team, and as these are very similar methods based on common principles the testing time decreased exponentially throughout the research phase.
- Analysis of the obtained results—In this phase, the involvement of external domain experts proved to be crucial, who could intuitively, based on many years of experience, suggest measures for improvement if the results did not correspond to expectations. Moreover, they were able to explain some unexpected results and thus immediately conclude where the shortcomings of the basic observed model of some papers are. Analysis was conducted ad-hoc by the whole research team and most of the time heterogeneity of results was discussed.
- Brainstorming session—This is a key part of the whole process; in this step, there was an exchange of ideas, knowledge and solutions, and often with loud commenting a certain hypothesis or assumption was fiercely defended. After this session, the certainty of validity was ensured and the whole process was repeated as many times as necessary to process all the papers selected for processing.
Conclusions after the comprehensive review of papers are that there are scientific databases in which papers are generally published with more detail with traceable results, while at the same time there are scientific databases that nurture papers in a shorter reporting form which makes repeating the outcomes more challenging. For some papers, mathematical experts with deep knowledge of statistics had to be consulted, and for the purposes of mathematical synthesis, several mathematical experts were engaged.
The limitations of this methodology are certainly relying on a group of researchers without using any of the artificial intelligence (AI) methods. However, the authors are of the opinion that, given the specificity of the observed challenge and previous experiences, there is greater reliability if we are guided by the opinions of domain experts and long-term scientists, than by the algorithm. In the case of considering many scientific papers for development purposes, it is more reasonable to rely on natural intelligence.
Of course, it may seem that this is completely contradictory to the topic of this paper, but it should be considered that this paper observes applications of CI, a subset of AI that always relies on exact mathematical calculations and it is in fact specifically modeled by natural intelligence.
Within the space–time possibilities and with the available literature, this paper aims to shorten the cognitive process and provide an overview in one place for all those who are just starting or are currently dealing with the field of distribution network optimization using CI methods. For better understanding, the abbreviation list is provided in the Appendix A at the end of this paper. Of course, given the context in which this research is conducted, all papers are viewed from the point of view that they must be feasible as actual optimization systems or at least as a basis for the development of future management procedures. With this work, science is viewed as a platform for launching innovative engineering solutions that should serve all of humanity.
3. DG and the Distribution Network
DG impact on the power grid is a complex mathematical problem, changing over time and depending on the parameters of each grid. Precisely because of the diversity of the system in which DG is integrated, there is no universal solution that can be magically applied to every case while respecting the laws of calculation such as real power balance equations, Jacobian Matrices and Newton—Raphson Power flow.
Current growing demand for energy in the world accompanied by an increase in energy prices, accelerated the technology development for RES utilization, which introduce additional variability. According to installed capacity, Viral et al. [12] classify RES and non-RES DG, such as micro DG with installed capacity up to 5 kW, small DG with installed capacity up to 5 MW, medium DG with installed capacity up to 50 MW and large DG with installed capacity from 50 to 300 MW. The same authors refer to the utilization of DG for the base and the peak load demand and capability to provide ancillary services to the system, while considering a power plant a DG only when it is connected to the distribution network. Similar findings on different types of DG technology and power can be found in Reference [13] in which the authors also refer to Viral et al. [12]. Sambaiah’s [13] considerations of the method of optimal allocation are given in later sections. Although Reference [13] can be considered similar in its content, this paper is about reconstructed models and tested systems and is not a mere enumeration of what was read, but about presented scientific papers that the development team successfully reconstructed according to the guidelines for software development.
Considering integration location, DG is integrated in two ways: local level and end-point level [12]. Local DG means independent production units in the distribution network, and the end-point DG is a production unit integrated with the consumer. According to power system management, DG based on technologies independent of the energy resource incidence are fundamental generation while solar and wind power plants with volatile production cannot be considered as fundamental generation in power system [14,15]. However, such systems can be enriched with an energy storage and in that case increase the efficiency of the distribution network and enable the balancing of part or all of the system [16].
When modeling and developing a specific CI method for ADN management, there is a big difference depending on which type of DG integration CI needs to be observed. Aggregating end-point production at the local level has proven to be a good entry point for a challenge formulation that CI can solve more successfully.
Technical advantages of DG can relate to a wide range of influences such as the power supply of the system peak load, voltage profile improvement, system losses reduction, power supply continuity, system reliability improvement and elimination of power supply quality issues [17,18,19].
Voltage dips are still a challenge in many distribution grids so Ipinnimo et al. [20] point on mutual coordination of a large number of DG units in order to reduce the voltage dips. Location and power of DG are two key factors in reducing system losses [12]. Voltage dips reduction and transient voltage reductions between 10% and 90% of the nominal effective root-mean square value lasting between half cycle and one minute [9] are recognized as a key issue in distribution network with high DG penetration level, as can be seen in References [20,21]. However, there are specific circumstances in which an optimization algorithm needs to be adapted, such as a Long Distribution environment that includes manufacturing, distribution centers, terminals, geographic units, suppliers and end users [22]. Review paper of Djafar et al. hits a very specific niche and it is important to emphasize it because it can be useful to those who are in a similar environment of complex power distribution systems, without being discouraged that perhaps such a case has not been processed in the scientific literature.
Common challenges of DG integration to distribution grid mentioned by the authors of References [21,23,24,25,26,27] are impossibility of reactive power production of some DG technologies, necessity of power system protection settings change, possible occurrence of DG island operation, high order harmonic generation of some DG technologies, influence on power system stability, possible excessive voltage increase, short-circuit currents increase. While DG strengthens the distribution grid resulting in number of dips decreasing, the transmission network may weaken as described in Reference [28] and enforcement of distribution grid is necessary.
DG units have a significant role in European objectives, as presented in Reference [29], where the possibility of control and connection point is described with centralization and decentralization trends in European area. Moreover, Reference [29] gives The Smart Grid Architecture Model (SGAM) Framework that is to be respected in order to address interoperability in a way described in Reference [30]. Concise description of the SGAM Framework is given by Panda and Das [31], who address the still open questions of the SGAM and provide an insight of the Smart Grid environment in the year 2050.
3.1. SGAM Framework
SGAM Framework introduces six functional zones for specific purposes and functionalities, respecting user requirements and possibilities. First zone, Process, implies equipment that participates in energy conversion and transmission. Field zone, the second one, implies monitoring and protection equipment responsible for data acquisition. Aggregation level is in third zone, Station, in which substation automation supervises the first two layers. ADN management processed by this paper can be part of third zone, or, even better, part of fourth zone, called Operation.
Operation handles multiple Energy management systems (EMS), Distribution Management Systems (DMS), multiple microgrids, aggregation of various type RES into Virtual Power Plants (VPP) and electric vehicles (EV). The fifth zone, Enterprise, includes utilities, service providers, energy traders, customer relationships, asset management and procurement [29]. Market operations are in the sixth zone, Market, where energy trading and mass market occurs.
SGAM Framework also proposes the methodology which was used for this research to examine the validity and applicability of multiple CI methods in real-world power systems. The methodology within this research has seven crucial principles of validation:
- Universality—The proposed solutions must be vendor-agnostic and without preferences in existing architectures and solutions. Neutral and scientifically objective perspective is mandatory when evaluating the possible solutions for future power networks.
- Localization—Given the functional zones, the application of possible solution needs to be clearly stated for which zone it is intended. Systematic view of the whole framework is needed to clearly understand the level in the topology in which any solution can be applied to.
- Consistency—The use case must not violate the existing SGAM framework and in no case must single out one zone as dominant. Interdependence and reliable functioning with other zones must be respected.
- Flexibility—Alternative designs and implementation of use cases, functionalities and services to any SGAM layer or zone need to be covered. Methods and algorithms observed in this paper can be part of any SGAM layer or zone, with the best starting point in the third or fourth zone.
- Scalability—Once the proposed solution is part of one zone or a smaller part of the network, it must be able to successfully scale to other zones or to the whole network. Of course, the limiting factor here may be computational power, but this is not the subject of discussion in this paper and it can be solved by Cloud Computing [32].
- Extensibility—Solutions need to adapt to evolutionary changes in the Smart Grid environment.
- Interoperability—Interaction between multiple actors, applications and systems occurs via information exchange with defined protocols and data models. Chain of entities and connections define interfaces in which the consistency and interoperability become secured.
By combining Station and Operation zones with Communication, Information and Function layers in SGAM, it is possible to reach an enclosure in which there is an exceptional need to apply methods presented in this paper.
As mentioned above, in bullet 4, the good starting point for integration of CI-based methods for ADN management is Station or Operation zone in distribution system, DER and Customer environment. The bounding section for CI applications in ADN is given by Figure 1, where the application zone observed by this paper is shaded in red.
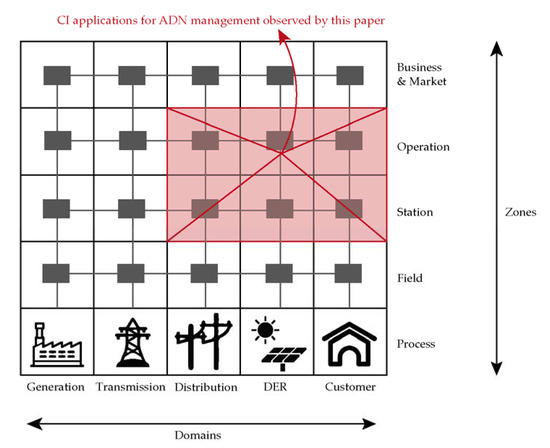
Figure 1.
SGAM reference architecture with emphasis of CI applications observed by this paper.
Process and Field zones are most often oriented to smaller systems that can be explicitly mathematically described and that depend on a finite set of known parameters. Such systems are micro-grids of a local character or even small micro-grids at the end-point [33,34].
Large centralized generation connected to the transmission network is a separate category by itself, regardless of the zone of application. The laws of system management at these levels are completely different from the established methodologies of managing the distribution system, as can be understood from comprehensive overview given in Reference [35]. Interconnected power grids are multi-layered system where CI can be useful as a distributed optimization platform that acts as one part of the overall algorithm. This concept is explained in a little more detail later in this paper when one of the most applicable optimization methods is described.
Enterprise and Market zones can benefit from the solutions defined in the Station and Operation zones because such security of the right solutions will enable a different market presence and even develop new market possibilities, most often consequently with greater RES integration [36].
Considering that this paper is the result of the project that respects the SGAM architecture and according to the basic principles of the described methodology, it is possible to imagine the trend of developing inventive solutions for the Smart Grid environment. Such inventive solutions must by their nature react quickly enough to be taken into account and precisely enough for their application to come to life at all.
3.2. DG Impact in ADN
When considering CI methods for the application in system solutions complied with SGAM Framework, the properties of DG and the background mathematical models of each observed technology should be considered. The mathematical models of DG and the mathematical background of the power system represent a system of complex equations that are not easily solvable by conventional methods. A clear and comprehensive overview of the essential characteristics of different DG allocation methodologies types is given in Table 1.

Table 1.
Comparison of main content of selected papers.
It is necessary to consider the fact that the data from the paper [12] published in 2012 have been changed today in the field of the installation cost. Furthermore, distributed generation allows reactive compensation control voltage level, can contribute to the regulation of frequency and can be used as spinning reserve during faults if the technology of production units permits [12,25,26,27,39,42,48,49].
Beside the technical advantages of the distributed generation, the authors of Reference [12] also provide an additional, indirect economic benefits expressed through the possibility of delaying investment in power system components and reductions of different power system management costs, while papers [12,48] refer reducing investment cost for the network equipment upgrade, reducing the operating costs of transmission and distribution systems, increasing the security of supply at critical loads, reducing the cost of mandatory reserves in the system, etc. The benefits of integrating DG units are reduction of losses, improvement of voltage profile and voltage stability, increased quality of electricity and efficiency of energy use, but direct current flows certainly have a negative impact on the reliability of the system [13].
Distributed generation in a whole with a consumption becomes a micro grid, while more micro grids make an active distribution network [50,51]. It can be concluded that DG change the technical properties of distribution network making this network an active distribution network—a precondition for development of Smart Grid where the distribution network has the ability to supply the consumers from distribution generation and upper voltage level network together while maintaining an optimal operational [50].
Distributed generation is the most useful when placed as close to consumers as possible to ensure the greatest impact on DG benefits. A terminal in the distribution network where DG has the greatest beneficial impact is called an optimal location. Selection of the optimal location is crucial for the planning of the distributed generation.
4. Optimal DG Planning and Scheduling
ADN Management is a real-time and operational planning problem when it is following functional criteria. Solutions for allocation problem described in the technical and scientific literature and papers can be used as scheduling problem if functionality, modeling constraints and performance rules are obliged. That interest requires the identification of papers which present solutions that enable development of a potentially new method for DG operational management planning in Smart Grid. Optimal ADN management with an increased share of RES-based and non-RES-based DG technologies is a modern challenge for the distribution system operators since most of the current distribution grids are not designed for the new, bidirectional operating conditions. ADN operational planning represents the necessary precondition to ensure the most favorable effects of distributed generation in Smart Grid environment [12,48,52]. Proper operations in Smart Grid manage power flows in a most efficient and reliable manner, but require integration of multiple technologies described in Reference [53].
4.1. Optimization Methods
Optimization methods that can be applicable to Smart Grid must comply with the requirements of real-time performance, consideration of technical requirements and actual production situation of various production capacities, while mitigating difficulties of weak convergence and local pinning [12,48]. The observed works in the literature distinguish five optimization-method groups [12,54]:
- Analytical methods;
- Heuristic and meta-heuristic methods;
- Artificial Intelligence–based methods;
- Evolutionary principles and biologically inspired methods;
- Distinct methods for specific purposes.
Analytical methods require the definition of algebraic expressions basis of which can the optimization process be analyzed. Such approach will result with a well-developed mathematical model of the observed system. That model can be used in together with measurement data, but it is very demanding, almost impossible, to use it for more complex systems and challenges [12,26]. The advantage of the analytical approach is manifested through the usage of the model in conjunction with measured values and external input data. The common opinion in the literature is how optimization procedures can be divided into methods that result in precise solutions and methods that result in good-enough optimal Pareto solutions [55,56,57,58]. An overview and grouping of optimization methods is shown in Figure 2.
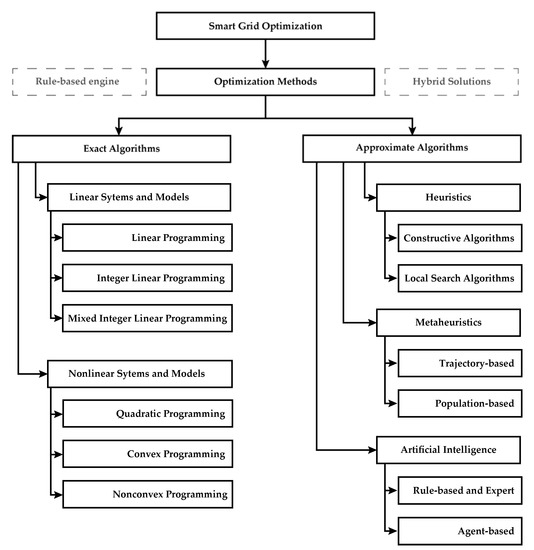
Figure 2.
Optimization methods for Smart Grid applications.
This paper observes best practices and methods that according to the authors can be used for real-world use cases. The usability is tried and proved by modeling and simulation in software engineering environment. This paper deals with the groups from Figure 2 and gives an overview of what has been tried, what has been repeated and what can be applied to real-world systems.
A meta-heuristic approach is an iterative optimization process that can be assigned as a guidance for subordinate heuristics [59]. The heuristic process is beneficial for solving optimization problems in cases where a precise and accurate solution is not unique, when the set of acceptable solutions exist and when the precision of all solutions does not necessarily have to be absolute but good enough to be pragmatic enough [60]. Heuristic algorithms can be specifically developed to solve a particular problem or universally applicable with the common search criteria. In any case, heuristic algorithms can be used in a search for a specific set of possible solutions and finding out the best solution in the set. Meta-heuristic methods represent advanced procedures in which the heuristic process is further enhanced in every iteration of the solution search and most often apply universally applicable heuristic procedures [61]. The way of refining heuristic process with each iteration can be defined as a separate heuristic process and therefore such complex methods are called meta-heuristics. If the meta-heuristic optimization is complemented with the precise calculation results of individual solutions, it becomes possible to state that general strategies are specifically applicable, and the results are accurate and precise, thus using best of both worlds. For most meta-heuristic methods, it is necessary to properly represent the problem, procedures and operators within the legitimacy of performing the heuristics and to partially limit the scope of the solution. Metaheuristic methods that are significantly proven and applicable in solving various problems are local search, tabu search, simulated annealing, genetic algorithm (GA) and ant-colony algorithm [54,60,61,62].
Computational intelligence approach includes dedicated tools and intelligent procedures for solving certain types of problems that do not necessarily need to be optimization problems. Recognized examples of the methods based on the computational intelligence are fuzzy logic, artificial neural networks, rough sets theory, expert systems and probabilistic agents [63] and application of these methods is often necessary for the purpose of making decisions about individual values, sorting and numeric marking according to certain rules. The wider conception of computational intelligence comprises all heuristic and meta-heuristic optimization procedures and the boundary of the specific category where particular approach belongs to is often unclear.
Methods based on evolutionary principles are powerful optimization procedures most often used in optimization problems where is necessary to consider the fulfillment of two or more objectives. A common feature of optimization methods based on evolutionary principles is the existence of one or more decision-making procedures, the so-called evaluation according to fitness function [56]. Using iterative optimization process based on these methods it is possible to direct the search for solutions in each subsequent iteration to the area where the previous iteration achieved the best solution. Considering the above principle, it is possible to conclude that these methods are like meta-heuristic procedures, which additionally confirms the ambiguous boundary and complexity of the categorization of certain methods.
Hybrid methods combine two or more processes to a single optimization process. The most common hybrid methods are synthesis of the optimization process and computer intelligence decision-making procedures [60]. All optimization methods may encounter certain performance problems in finding the best global solution, low convergence, and long calculation time if they are not properly adapted to the observed problem [9].
4.2. Analytical Methods
Analytical methods are briefly addressed with the emphasis that their capabilities are limited and that advanced computer intelligence methods are better used in multi-objective optimization problems. In Reference [37], the authors show the possibility of analytical calculation of voltage drops and power losses instead of iterative load-flow calculation used to determine the node in radial or doubly fed feeder where DG will provide the lowest power losses. The analytical approach described in the mentioned paper observes two objectives; the location of the distributed generation to obtain the lowest power losses and to fulfil the target voltage values along the observed feeder. If the second objective is not satisfied, the location is changed near the original solution until both objectives are met. Power dispatched from DG authors limit with the injected current value that cannot exceed the power consumption from the DG location. The proposed method can be performed with the following load-distribution constraints: uniform load distribution in the feeder, centralized load distribution in the feeder load where the largest power consumers are in the middle of the feeder and loads are increasing towards the feeder. When solving the allocation problem in ring and interconnected distribution networks, authors use the admittance matrix and minimize the objective function (1) [37].
For the location of distributed generation in the node j, the aim is to find the lowest value of losses which is in the function of the equivalent resistance between the first and the i-th node. Additionally, the authors have investigated the possibility of renewable energy production volatility representation through a series of different data. Since the authors did not use iterative procedures there is no problem of convergence of the proposed method.
Achary et al. [25] are considering the GA usage in order to optimize the location of distributed generation but are abandoning the idea due to many iterative load-flow calculations which significantly affected the calculation time consumption needed for optimization. In their work, they use the theorem of the complex power that represents the basis for determination of the most sensitive node where distributed generation achieve the least loss in the system. The proposed solution according to the expression (2) will result in the optimal distributed generation dispatch for each node, while the contribution of each distributed generation to total system losses will be determine using theorem of the complex power. The node “I” with the least losses represents the optimal location of the distributed generation considering the consumed power “PDi” at that node.
Gözel et al. [26] developed a similar method to the one developed by the authors of Reference [14], with significant changes in the representation of the results in relation to the authors of Reference [25]. A significant contribution to their work stems from the definition of mutual influence of distributed generation node to other nodes in the distribution network. The results of their calculations are also based on power losses calculation as decisive and clear indication of distributed generation influence. In addition, the authors compare their results with the authors of Reference [25] and concluded that their method consumes less computing time.
Aman et al. [38] presented the Power Stability Index (PSI) method in order to find nodes in network which have the most favorable impact on voltage profile and grid losses when distributed generation is connected to them. The authors tested their method on a 69-bus test system and a significant contribution is shown defining the new voltage stability indicator for valuation of the nodes. PSI method is compared to Golden Section Search Algorithm (GSSA) and results are compared with strong similarities, but GSSA used more computation time when compared to PSI-based method given by expression (3), in which represents active power of distributed generation, stands for real part of line impedance and Vi is the real voltage of the i-th bus with the voltage angle,.
4.3. Computational Intelligence–Based Methods
Significant development of CI and numerous papers have pointed the applicability of selected metaheuristic methods used as higher order procedures to determine sufficiently good solutions without the necessary knowledge of the entire mathematical model or the values of all variables. Solutions derived from metaheuristic approaches are result of search for global best solutions in the predesignated and finite search space [64,65]. If the search space consists of many possible solutions and solution variants, metaheuristic methods often repeat some of the properties and re-evaluate already visited space. That feature often results in more precise and refined solution. Classification of metaheuristic methods is given by Figure 3 which presents most viable algorithms, grouped by type, governance rules, modeling rules and the way they determine the best solution.
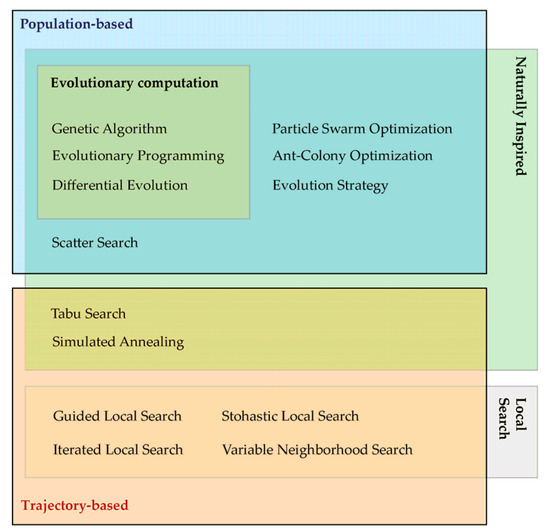
Figure 3.
Metaheuristic methods classification.
Computational intelligence implies hybrid approaches created by combining several optimization methods and is characterized by successful application for continuous values, the ability to self-evaluate and change the way of execution, stochastic approach, parallelism in execution and the ability to generate approximate or Pareto solutions [66]. Procedures and methods contained in computer intelligence often base their principles of operation on biological principles or natural processes [67] and are applied in solving problems for which there are no effective or specialized procedures [68]. The lack of specific procedures for specific problems may be caused by complexity that does not allow effective modeling or the inability to explain or model certain problems and all observed factors [69]. In power engineering, computer intelligence can be used to solve many optimization challenges, calculate optimal power flows [70,71,72], system modeling and monitoring of ADNs using fuzzy logic systems with evolutionary algorithms and artificial neural networks, while some procedures and algorithms can be used in data and event analysis and diagnostics of ADNs using qualitative reasoning, planning methods and hybrid procedures [73]. In addition, computer intelligence is successfully used to solve problems of designing electromechanical oscillation stabilizers, determining the causes and sorting of faults in the transmission network, reliability assessment, consumption forecasting, power system protection coordination, electricity quality assessment, economic supply of electricity, reactive power optimization and determination of optimal power flows—basically everywhere where iterative processes need faster convergence [74].
An extensive review of optimization procedures used in mathematical modeling in 360 scientific papers was provided by Theo et al. [7] outlining the advantages and disadvantages of each approach. For a GA, the authors outline suitability for solving problems that may have more favorable solutions, it is generally easy to integrate into an existing simulation framework, it is tolerant to the objective functions with chaotic attributes, and it is suitable for topological and categorical variable optimizations. However, as a lack of a GA authors outline the convergence to the local best solution instead of the global best solution, long-term convergence and complex approach of determining the criteria for the optimization process termination. When reviewing the Particle Swarm intelligence algorithm, the authors outline the advantages of fast execution, flexibility and openness to the other soft computing procedures but warn that the algorithm requires definition of coordinate motion system and a proper number of particles otherwise can result in local best solutions.
A comprehensive overview of optimization methods that can contribute to the more efficient integration of DG into the power system are given by Colmenar-Santos et al. [75] in their paper from 2016. The authors of Reference [75] state that the problem of the multi-objective optimization of various technology DG integration into a fully developed active network has not yet been completely solved and outline the idea of the development of a robust distribution management system called AMN (Active Management Network) whose role is a real-time operational management of DG and other control devices in distribution networks. Analyzing the optimization methods and grouping seen in the literature, the authors of this paper represent the division of optimization approaches into three groups:
- Conventional approaches.
- Approaches based on the artificial intelligence.
- Hybrid approaches based on multiple methods of artificial intelligence.
According to Reference [75], conventional approaches are analytical methods, power flow calculations, non-linear programming method and rule 2/3; approaches based on artificial or computer intelligence consider evolutionary algorithms, algorithm of simulated annealing, differential evolution algorithm, Particle Swarm algorithm, fuzzy logic systems, ant-colony algorithm, tabu search algorithm, artificial bee colony algorithm, firefly algorithm while hybrid approaches include methods of unification of the GA and fuzzy logic systems, GA and tabu search algorithm, GA and Particle Swarm Optimization (PSO) algorithm, GA and power flow calculation, PSO algorithm and power flow calculation, tabu search algorithm and fuzzy logic systems.
After reviewing all of the methods, the authors [75] state that solutions based on the swarm intelligence algorithm are complex in development if reliable global solutions are sought while fuzzy logic systems and hybrid systems are not sufficiently represented in the literature. The authors outline that premature convergence is extremely emphasized for the methods based on the evolutionary principles if solution approach is not detail enough, while other significant methods, such as the simulated annealing algorithm and ant-colony algorithm, have long execution time which excludes them for possible application in short-term planning.
The largest number of scientific papers where meta-heuristic optimization methods are applied for allocation of distributed generation use the GA method or the PSO method, and there are also papers that use a hybrid method as a compound of these two procedures as well. Singh and Goswami [39] use GA determined by the objective function (4) for solving specially designed multi-objective optimization problem, where the impact of the distributed generation integration on active power market price λ is considered beside the power losses reduction and voltage conditions improvement. The authors used the knowledge presented in Reference [76] when assuming distributed generation influence on the electricity price Ci(DG), depending on consumer active power PDi and distributed generation active power PDGi.
The presented considerations of the authors of Reference [39] successfully confirm the simulations on the radial distribution network model, where they prove the usefulness of the proposed method for the allocation of one or more distributed generation in radial distribution networks.
4.3.1. GA-Based Methods
GA is a space search heuristic that is inspired by biological process of natural selection in which the most potent individuals of one generation give birth to individuals of the new, improved, generation. Genetic sequences determine the possibilities of the individuals within the population. The individuals are rated based on fitness function and the most fit ones reproduce to design a novel individual with better set of genes. If modeled correctly, GA can bring real adaptive computer programs. Main genetic operators are crossover and mutation, with all its advantages and disadvantages and difficulties in coding physical and mathematical models from the power industry domain as genes [77]. Binary encoding can be used in discrete search areas, while for continuous values a real-value encoding or tree encoding scheme needs to be used [77,78]. The process by which binary GA operates, as described in Reference [79] is presented by Figure 4. The process starts with objective function formulation, as with any method, but after the initial population the GA operators take place. In this example, each individual is encoded with n number of genes and each gene consist of m number of bits, as given by Figure 4. The fitness evaluation is usually in power engineering done my means of co-simulation and calculations. GA operators are mandatory as they ensure that the algorithm observes the whole search space.
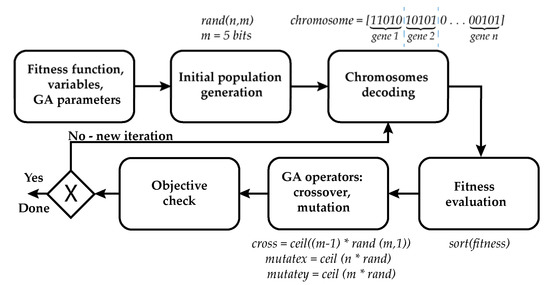
Figure 4.
Binary GA general process diagram.
A fundamental feature of GA is competition among individuals and the principle of elitism. Elitism implies the survival of only those individuals who have a high fitness score, and all other individuals are rejected. When observing multiple objectives simultaneously, it is necessary to pair individuals that have an elitist grade according to one of the criteria, in order to obtain an offspring that can have elitist grades according to all criteria. In some cases, most often when multiple solutions have equal value, not numerically, but value to the observer, selection methods such as Tournament Selection and Rank Selection are used in which individuals compete among each other in random manner to prove the unquestionability of the best individual.
Injeti et al. [27] used simulated annealing method for optimization and compared results with results obtained with GA and PSO method. In Reference [27], the authors clearly stated constraints that should be considered when using advanced optimization methods of computational intelligence such as simulation limitations. Successful implementation of one method of computer intelligence and review of other methods used for allocation of distributed generation are clear indicators of the future research, as shown in the more recent paper of the same authors [80].
In Equations (5) and (6) stands for total feeder losses and represents line losses, the main minimization objectives considered in Reference [27].
Abou El-Ela et al. [40] used a method based on the GA for DG allocation and examined the proposed method by linear programming. The same authors concluded that there is no significant deviation in the obtained results, thus confirming the usefulness of computational intelligence–based methods. The authors of Reference [40] define clear indicators with or without DG for voltage profile improvement—VPI according to (7); spinning reserve increasing—SRI according to (8); power flow reduction—PFR according to (9); and total line loss reduction—LLR according to (10) [40]. The developed-algorithm authors successfully tested on a model of a real distribution network in Egypt.
The benefits of DG are present with index MBDG—maximal composite benefits of DG—according to the authors of Reference [40]. For the limitations of the computer intelligence optimization process, the authors state the limitations are the maximum number of distributed generation units so in their paper authors analyze the distribution of one distributed generation in the distribution network and conclude that the nominal power of the power plant significantly affects the indicators determined by expressions (7)–(10) unlike the location—node—of the power plant. The authors present the energy balance of the observed system as a limitation of the optimization procedure and determine the condition according to which the power of total production in the observed network must be equal to the sum of all time-constant consumers and power losses. Similar authors use GA to allocate the remote measurement and monitoring units in the Smart Grid environment Reference [81], where they deeply explain the parameters of GA-based optimization process.
Biswas et al. [41] used genetic algorithm for the optimal DG allocation in order to reduce voltage sags in a real complex distribution network. Presented problems are perceived by the authors through the real power losses (RPL) reduction objective function (11) that takes into account quotient of product of voltage angle difference cosine and line resistance with voltage level , and quotient of product of voltage angle difference sinus and line resistance with voltage level ; objective function for decrease of customers that can be affected by the voltage sags in observed time period (NF) (12) with the total load distributed, SDIST, and the load distributed for the i-th fault, ; the objective function of DG integration costs reduction (13), which is determined by financial units per kilowatt of installed DG power (KC) and observed as the objective of determining the least power of DG which will meet the previous two objectives [41]. The constraints of the proposed algorithm that the authors have defined, similarly to previous authors, are load-flow constraints through the specific branches, voltage constraints and limitations of the number of DG units.
The specifics of the proposed method based on the genetic algorithm is emphasized in the integrated use of power flow calculations when evaluating the benefit of the best solutions in each iteration. After evaluating the benefit of individual solutions based on the power flow calculation, an additional algorithm of voltage failure analysis is performed, which evaluates the impact of the proposed solutions on the number of time-constant consumers covered by voltage failures. This approach is innovative because it considers multiple objectives taking place as several separate optimization procedures. The way in which the authors graphically present the results of several iterations with a three-dimensional surface is seen later, in other works.
The limitations of methods based on a genetic algorithm for solving more complex optimization problems are explained in the paper by Yang et al. [18] in which a hybrid method of two genetic algorithms is used with the aim of determining the maximum power of distributed generation, taking into account the voltage and technical limitations of the elements of the distribution network. The first genetic algorithm, determined by the objective function (14), determines the minimum power of distributed generation limited by the short-circuit power on the primary side of the competent transformer, voltage level and technical characteristics of the equipment in the system. The second genetic algorithm, according to the function of the goal (15), determines the power of distributed production that will meet the requirements of consumers of the observed derivative, while respecting the solutions of the first genetic algorithm.
Using this hybrid approach and using two genetic algorithms, the authors determined the possible power intervals of distributed generation depending on the short-circuit power on the busbars of the parent network. Moreover, same authors showed that in some specific cases the usual meta-heuristic methods may give false solutions.
Methods based on genetic algorithms that solve optimization problems of reactive energy generation with the objective of reducing losses in the observed systems are particularly presented in papers [82,83] and the paper of the author López-Lezama [84] where the optimal distribution of the DG is determined according to the electricity price criterion. In Reference [84], the advantage DG is presented through the possibility of achieving a higher generated power price from the market price due to the fact that DG is near to consumers and that feature results in fewer power losses. The same authors emphasize that repeated optimization procedures with the random initial settings resulted in almost identical solutions, thus confirming the usefulness of the proposed method.
4.3.2. PSO-Based Approaches
PSO is a population-based, biologically inspired method with a limited search space, that can repeatedly result in usable optimization results. The intrinsic feature of the method is the re-evaluation of an already past search space. Each possible solution in PSO is called particle and it is described by position, mass and velocity. Particle has its own memory of personal best solution and communicates with the group of particles to examine group’s best solutions. PSO initialization implies random particles at random places and with random parameters that are updated with each iteration. Particles follow their own fitness criteria, called personal best or pbest, but comply with the group’s fitness goals, called group best or gbest. Depending on the fitness value, the particle follows the group, or vice versa, as described by Figure 5.
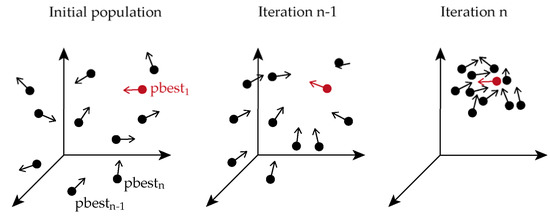
Figure 5.
Particle following in PSO.
There are cases where particles take the entire population in the wrong direction or where a population converges toward a solution that is not globally best. This most often occurs when the number of particles and parameterization in the population does not correspond to the observed problem. When observing a challenge in a Smart Grid environment, it is possible to easily solve wrong convergence by determining the number and parameters of particles according to the observed electric power system. This means that the number of particles in each generation should at least correspond to the number of observed cases, and their random parameters should be limited to the uniqueness of the search space.
Figure 6 gives a general overview of the PSO method process. At first it seems that the PSO has more steps than GA, but given that PSO evolves around single swarm representation, it shows better performance in most cases. Random swarm generation should in most cases consist of at least same number of particles as there are discrete possible solutions—in case of ADN and DG that number represents number of buses. Each particle has its own velocity, which is encoded as power generation. When a swarm identifies a spot, or a bus in distribution network, in which the DG is most necessary, that becomes a new swarm orientation. Similarly, when a particle finds a most appropriate power is more that becomes the global information. Particles are then updated with the new information and the search space gets explored by the complete swarm.
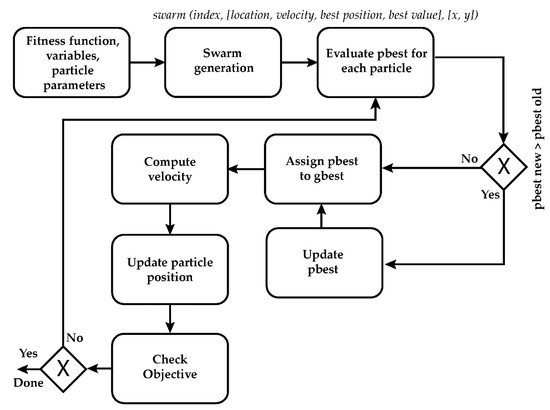
Figure 6.
General PSO process diagram.
In Section 3.1 of this paper, the possibility of distributed optimization platform was mentioned for large power systems. Each CI-based solution in an interconnected multi-layer power grid can be represented as a single particle of an overall PSO-based power system management solution. Of course, at the time of writing this paper, this idea is only a far theoretical consideration, but such were once the ideas and concepts discussed in this paper, and today they are the basis for the development of advanced software solutions. It will certainly be interesting to witness the development of modern power engineering and the growing representation of CI methods in modern solutions.
A novel approach for solving problem of multiple DG units distribution suggest the authors Alrashidi et al. [42] with the PSO algorithm as a basis of their method. The proposed method is confirmed on the model of the distribution network with several feeders and ten nodes where the optimal distribution of DG units have been determined through the multiple scenarios with the power losses reduction objective according to (16).
The constraints of the algorithm of the authors of Reference [42] define through the voltage constraints, load-flow limitations, size of the transformers and maximum permitted number of DG units. The authors especially emphasize that their method requires consideration of only one DG per node and only time-invariant production and invariant consumers can be. This paper, together with Reference [85], represents a framework of the development of a new method based on the Particle Swarm intelligence algorithm that will solve the problem of multiple DG multiple per node by considering the time-varying feature of loads and RES-based DG units. El-Zonkoly [85] defines the algebraic indicators for the objective function used for multi-objective optimization problem solution. Such indicators in the observed system are the influence of DG on active (ILP) and reactive (ILQ) power, the influence of DG on the voltage conditions, the possibility of DG dispatch in dependence of DG location and consumer location (IC), the influence of DG on short-circuit currents (ISC). For each defined indicator, the author assigns the weight factor σ whose variation opens the possibility to orientate the set of solutions to system management solutions or to system development adapted solutions [86,87,88]. Multi-objective function (MOF) thus becomes the sum of the indicator’s multiplications and the corresponding weight factors according to expression (17).
Such an approach is common in the scientific literature and represents the combination of several individual functions into one objective function. In that way, a modeled optimization problem can be considered both single-objective and multi-objective optimization. Actual multi-objective optimization implies a vector of functions and the existence of opposing solutions.
In the second paper of the same author [88], the problem of the system load peak following is solved by the optimal DG allocation using the method based on the artificial bee colony algorithm, a subset of PSO algorithm. The proposed algorithm addresses the DG distribution by considering the criterion that the most demanding consumers are designated as primary for the DG integration. In this paper, the author considers three DG units in a system with 45 nodes or three DG units in a 33-node system while the installed DG capacity does not exceed 30% of total system load. A significant advantage of this paper is the consideration of two types of DG technology, one time-varying and unmanageable and other manageable DG. Moreover, the author anticipates the use of electricity storage system to reduce the required commitment of manageable DG.
Authors Gomez-Gonzalez et al. [43] represents an integration of load-flow calculation with an algorithm based on Particle Swarm intelligence to determine the optimal distribution of DG units, as presented by Figure 7. The authors of Reference [43] used the frog-jumping algorithm (18), which belongs to the group of PSO algorithms. Because of its specificities during particle coding, the algorithm is better adapted for the optimization of discrete values.
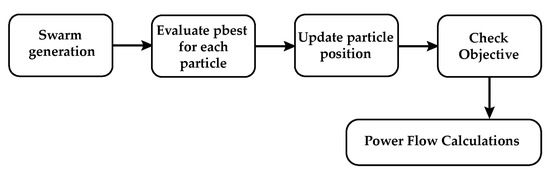
Figure 7.
Simplified illustration of PSO and Power Flow co-simulation by Gomez-Gonzalez et al.
Significant contribution of this paper is a determination of an optimal number of DG units which must result in the ability of the observed system self-sufficiency. This emphasizes the value of this paper compared to previous papers in which the location and the capacity of only one DG unit were considered.
Moradi and Abedini [44] produced a new method based on a synergy of GA and PSO. The authors propose the genetic algorithm for optimal DG location determination and Particle Swarm Optimization technique for adequate DG capacity. This paper wisely used GA’s possibility to perform better for integer-based, binary encoded, problems and continuous orientation towards the best solutions specific for the PSO algorithm.
Interestingly, the authors examined three separate cases, one with PSO only, one with GA only, and one with the proposed GA/PSO combination. According to the results presented in their work, the highest value of the objective function was achieved by a separate GA, while PSO and GA/PSO gave equal values of the objective function. However, the variance of the solution in PSO is many times less than in GA, while in the combination of GA/PSO variances in the objective function are negligible compared to any other algorithm.
Simplified flowchart of the presented hybrid method is given by Figure 8 by which the statement how the discrete values of the buses in the power system is a mitigatory circumstance is confirmed. The authors Moradi and Abedini used GA for DG location observations; since the DG location can be only on a system bus, it cannot be somewhere in between, and PSO is used for continuous optimization of DG power once the bus is identified.
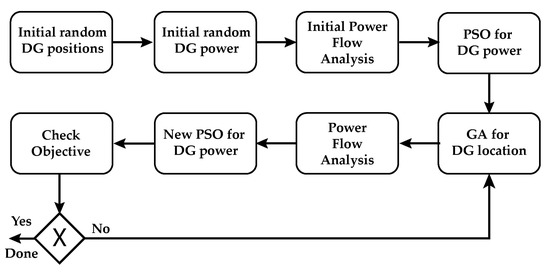
Figure 8.
Simplified illustration of PSO and GA hybrid method by Moradi and Abedini.
The fulfillment of the technical conditions is defined by the algorithm constraints that are integrated into a common function according to (19). The function f1 represents the objective of real power losses reduction, the function f2 represents the objective of the voltage profile improvement while the function f3 is the radial feeder voltage stability index taken from the literature. Coefficients k1, k2, β1 and β2 represent the penalizing coefficients of the corresponding expressions. The presented objective function considers the values of the voltage (Vni) and the apparent power (Sni) on the observed radial feeder busbars.
According to the authors, the proposed method shows a significant increase in the accuracy and repeatability of the results, but the authors conclude that more time is needed for the method implementation compared with using one of the methods separately.
An innovative approach to optimization is offered by Saif et al. [46] defining a simulation-optimization process where the technical validity of the optimization is evaluated by a simulation check instead of the optimization process limited by equality or inequality. The developed method, which authors call dual layer simulation optimization because of its simultaneous performance in the MATLAB and the GAMS programming tool, uses the load-flow calculation for all simulation cases and Particle Swarm method to determine the distribution of different types of unmanageable DG with objective to increase the reliability of the system supply and to reduce operating and investment costs. The developed method is successfully implemented on the part of the real power system. Surprisingly, among the optimal DG distribution solutions solar power plants and electricity storage systems are not included, but only a wind power plants which authors attribute to the availability of primary energy in the observed area. The conclusion of their work is to meet the energy needs of the observed network with multiple radial feeders using unmanageable DG thus creating the precondition for the island operation of a future Smart Grid.
Two papers by Aman et al. [49,89] describe the use of the PSO algorithm with the objective of scheduling multiple DG units. The authors introduce new criteria for describing the impact of a DG unit on the observed network—the criteria of possible increase of load and index of feeder stability. By additional checks and comparisons of the proposed method with the analytical method and the search algorithm, the authors confirm the correctness of the use of the PSO algorithm to solve the DG scheduling problem with losses reduction objective thus achieving the most useful impact of DG on the observed network.
Comparison of optimization methods developed on the basis of the PSO algorithm and the analytical approach were presented in the paper of Kansal et al. [47] which addresses the problem of distribution of different DG technologies with objective of reducing losses according to (20).
Authors define four DG types, considering the possibility of generating active and reactive power and suggest integration of one of them with respect to the results of the simulation. The results obtained with different optimization approaches are identical in the analysis of the optimal DG location and vary up to 5% for the optimal DG power dispatch.
In the leading scientific bases exist several scientific papers that use biologically inspired optimization algorithms. Niknam et al. [90,91,92] published several papers where honey-bee mating algorithm is used to solve the multi-objective problem of DG distribution in the distribution network [90] or to solve the problem of change of distribution network topology [91,92]. Equations from Reference [90] are given by (21)–(24):
In the papers authored by Niknam, according to the principle of selection of the queen bee among the bees, the best candidate for the survival of a population in the power engineering represents the DG or network topology.
The usefulness and efficacy of the PSO algorithm is further clarified in References [70,93,94,95,96,97,98,99], where this algorithm has been used to solve optimization problems or prediction problems and algorithms of evolution strategy have been compared with this algorithm.
Authors Kumari et al. [70] compared the GA, the improved GA and PSO algorithm for optimizing static VAR compensators in the network with the objective of reducing losses and achieving optimum load flows in the network. The improved GA suggested by authors is highlighted by the implementation of five additional gene crossing operators, in addition to the three commonly used ones, and according to their results, it provides the best optimization results.
Authors Yin et al. [93] used the PSO algorithm to optimize the allocation of computer processes to distributed processors, and this work, although in the field of computer science, thoroughly clarifies the application of the used algorithm. With the hybrid method which arose from the combining of the PSO algorithm and fuzzy logic systems authors Zhang et al. [94] solve the problem optimal reactive power flows to maintain voltage in transmission networks. The best solutions of each iteration of the Particle Swarm intelligence algorithm in this paper have been used as a measure of the feature parameters for the next iteration.
The adjusted PSO algorithm that addresses the problem of optimal DG allocation with the objective of losses reduction in the observed system is presented by Ashari et al. [95] while the usual Particle Swarm intelligence algorithm approach to solve the same problem is used by Bhumkittipich et al. [96] for the similar problem. A complete review of all derivatives of the PSO algorithm that have been known to authors Zhang et al. [97] and which can result in a number of best solutions, points to the usefulness of the PSO algorithm to solve many optimization problems. The apparent similarity of the algorithms in the papers of various authors [44,98] suggests that it is possible to achieve somewhat different approach and custom algorithm with exceptionally small variations in the principles of performance. That is also warned by authors [59] who advocate for a different development process of meta-heuristic methods and more significant changes.
A hybrid approach for addressing the DG distribution with the objective of total losses reduction and maintenance of a complex distribution network voltage profile, based on a unified GA and artificial neural networks, along with the GA and power flow calculation, is presented in Reference [100]. In this paper, the genetic algorithm determines the optimal location of one DG in a distribution network while the DG impact on the total losses is determined by the artificial neural network integrated into the GA. Described approach has not resulted in valid solutions when addressing the DG distribution problem in ring topology of distribution networks and a new hybrid approach has been developed by combining the genetic algorithm and the power flow calculation. In the same paper is presented a hybrid algorithm developed on the unification of two artificial neural networks with operating principles based on the search algorithms, but the authors point to the disadvantages of such an approach.
The need for active distribution network management is mentioned for the first time in the scientific paper of authors Soares et al. [45], who recognized the need for answering to consumer demands and the periodicity of some energy resources. The authors presented a special form of signaled PSO algorithm that enabled particles to change the speed parameter during the optimization process to gain the most feasible combination of wind, photovoltaic, fuel cell and energy storage. Change of speed was defined by given rules and observed with demand response and optimal storage charge/discharge. The proposed method was successfully tested on a model of Portugal’s power system. Use of such precisely designed meta-heuristic optimization methods in market environment and real-life conditions was proven, and the direction of future scientific research was given in the form of one-day division in 24 independent simulations, which later became the paradigm of all future research. Although the proposed method did not provide the most economical result, but the second of six different methods, the most efficient method mixed-integer nonlinear programming (MINLP) is not suitable for larger systems and is not fully usable in production [45]. The authors presented with great quality a mathematical model of contemporary challenges in the power system, given by expression (25).
Expression (21) lacks the observability of power losses in power equipment, such as cables and transformers, that can be described as and added to the right side of the equation for the part of the Smart Grid to be self-sufficient. Observed units PV,,, and present appropriate technologies used in period .
Presented scientific papers are clear indicator of the possibility for the development of robust intelligent solutions that can solve a certain set of complex problems in the power engineering, but without needed criticism, approaches based on soft computing methods should not be accepted as general solutions for absolutely all cases [101]. The authors also gave a mathematical model of technical limitations of the power system as inequalities that consider the specifics of individual technologies.
Reliability of distributed generation supply was introduced by Saif et el. [46] who presented double-layer simulation optimization, using load flow for all simulations and Particle Swarm Optimization in order to increase reliability of observed system. The authors optimized the given problem by aiming for operating and investment cost reduction. Developed method was successfully tested on a British power system model and the results were compared to other optimization methods. The authors of Reference [46] identified conditions for isolated distribution network operation. Aman et al. [38,49] used standard Particle Swarm Optimization algorithm, but introduced new criteria for describing the impact of distributed generation such as increasing the load capacity of observed system and the stability of network feeder.
The presented papers clearly point to the logical conclusion that, the once advanced and sometimes obscure methods known only to the scientific community, with today’s computing power, can be used effectively in real production and be integrated into tools to optimize the distribution network in real time. Detailed mathematical models with metaheuristic methods supported by iterative calculations with thoroughly examined features and shortcomings of individual methods promise a new advanced Smart Grid in the future.
4.3.3. GA and PSO Comparison
GA and PSO share many common features, such as random start, fitness values, population update based on randomness and necessity for fine-tuning in order to find global optimum [57]. However, PSO does not have crossover and mutation operators and particles have memory and velocity. Main difference between two methods is that GA comes with new solutions with struggle among individuals, while PSO nurtures social interaction between particles.
Social interaction in PSO defines natural leaders that spread information to others, while in GA chromosomes share information with each other and guide the whole group towards distinct area, leaving only elite individuals in each iteration. Moreover, population in GA gets smaller with each iteration since some of the individuals become removed, while in PSO population is constant and particles always have purpose in fine tuning the possible solution.
PSO is derivative-free, robust and flexible method, but prone to premature convergence if tuning parameters are not correct. However, particle parameters can be enhanced with solid mathematical equations that improve analysis and provide realistic convergence conditions. Self-organization of PSO with bottom-up approach integrated in the method prove wide applicability in many scientific areas.
Global perspective of each particle in PSO improves clustering efficiency and enables PSO algorithm to test multiple areas of the search space at the same time. Instead of competition-based GA, PSO values the cooperation of particles and the exchange of values according to objective criteria.
For greater overview and comparison Table 1 gives a perspective on solved challenges in ADN and SG environments. In accordance with the Chapter I—Introduction of this paper, Table 1 clearly gives a standpoint how the Distribution Network Optimization includes many topics and issues identified in the modern distribution networks, such as feeder reconfiguration, island operation, pricing and energy market, voltage profile improvements, etc.
5. Optimal Smart Grid Management
Intuitive thinking about the purposefulness of presented papers and research is confirmed by studying features in the field of research in current European and world research activities. Since 2009, the Working Group for Advanced Power Grids of the European Commission Smart Grids Task Force has been continuously issuing guidelines for the development of modern power systems [102].
Advanced power systems imply a change in paradigm by enabling DG, but also the application of technologies for monitoring, operational management, regulation of production and consumption using information technologies that are not the subject of this scientific research. The Joint Research Center for Smart Electricity Systems and Interoperability leads regulatory, technical and economic research at the level of the European Union. According to the relationship matrix [103] of the Joint Research Center, the countries most involved in research into advanced power systems are Spain, France, Italy, Germany, the United Kingdom, Belgium and the Netherlands. Looking at the overview of the identified trends of the Joint Research Center [104] and the reviews of European distribution system operators [105], it is easy to conclude that innovative scientific research should provide answers to the challenges observed in the literature.
The issue of active distribution network management is observed in recent scientific papers, mostly continuously for the past two years, and factors that can contribute to significant DG integration are identified and structured as multi-objective planning and active management [50,106,107,108,109,110,111,112,113,114]. Modern grids imply multiple technologies such as advanced metering infrastructure, EMS, DMS, Big Data solutions and data management, pricing mechanisms on a day ahead market and inner day markets, various paradigms such as demand response, fault classification and DG scheduling, and horizontal and/or vertical control possibilities [53,115,116,117]. Colmenar-Santos et al. [75] detailed the challenges raised from increased DG integration in distribution network identifying advantages and technology characteristics of active management network with DG operational optimization. In the fourth section of their paper authors distinguish optimization techniques based on Reference [54] and give comprehensive overview of advantages and disadvantages of different DG optimization techniques focusing on hybrid methods, thus becoming basis of future research by many scientists. Multi-objective planning, controllable loads, dispatched DG, stochastic DG and demand response become more prominent in Reference [75] as the report progresses. The authors touch upon regulatory and policy barriers preventing significant DG integration in the fifth and sixth sections of their paper, identifying the need for policy change according to the example of Germany, Denmark and Spain [75].
Power System of the future will enable justified use of energy, fairness in energy sharing, security of data and data governance, user own control and autonomy of the household while participating in a fair manner in energy community and virtual energy hubs [118]. The transition of the power industry will not go smoothly and synergy of all actors, legal and technical, regulatory and market, is needed for the transition to succeed [119], but when it does, the benefit will be for everyone included. As mentioned in Section 2, shifting the Smart Grid towards Cloud computing enables smoother transition, and the emergence of the Edge Computing paradigm enables the power industry to flourish [120].
Future of distribution networks are discussed by Bayod-Rújula et al. [50] and authors conclude that active distribution network with total control represents the first stage towards more advanced Smart Grid. According to the authors, second stage of distribution network development represents the microgrid system, a fully controlled entity that may provide ancillary services to the main system; third stage are virtual utilities with operational energy management system yielding optimization opportunities; demand-side management and demand response techniques become available once the previous prerequisites are met hence paving the way towards information and communication technology implementation [50].
In the wake of such information is paper by Shi et al. [109] where authors show operational energy management in microgrid system consisting of dispatchable and non-dispatchable DG, interruptible and deferrable loads and energy storages. Simplified overview of the described system is given by Figure 9, and similar models can be used to validate any other control solution intended for production purposes, as it was the case for the validation purposes of this paper.
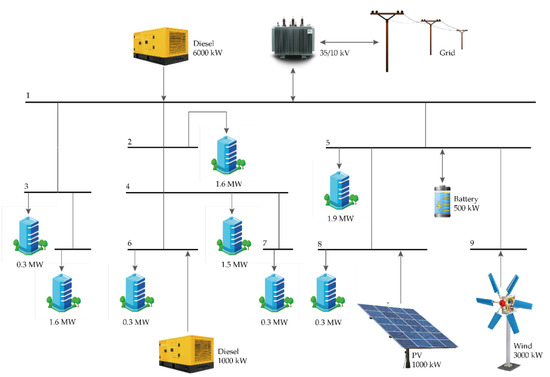
Figure 9.
Simplified model of microgrid used for validation in this paper, inspired by Reference [109].
Authors comply their proposed management solution with IEC 61850, a communication standard for Smart Grids [121] and present output schedules for grid-connected and islanded modes of operation, respecting bus voltages while minimizing network requirements. Operational energy management in distribution network is identified as the central problem of future distribution networks, microgrids and Smart Grids. Importance of this paper is evident in direct application of the scientific method in real-life microgrid environment. The authors present the results on a daily diagram, divided in 24 intervals, and give operating schedules for PV system, Wind power plant, Diesel generator, battery storage and controllable load.
The system is controlled by Micro-Grid Central Controller (MGCC) with Exact, Convex Programming–based algorithm for Nonlinear Systems and Models based on predictor corrector proximal multiplier algorithm and optimal power flow formulation [109].
Operational microgrid energy management based on mixed-integer linear programming solution considering wind power and PV system generation volatile characteristics, aided by storage system and grid connection can be found in the paper by Umeozor and Trifkovic [122]. The authors collected meteorological data to eliminate forecasting errors and schedule DG production accordingly. Different pricing scenarios were considered, and the authors concluded that economic circumstances of observed system greatly affect the output parameters.
The authors of Reference [123] represent the hybrid method emerged by combination of sorting GA without dominant solutions and Rough Set Theory tests. The method is used for solving the problem of optimal energy management in a distribution network that consists of 123 nodes, 7 micro-grid systems and 9 distributed energy sources. The authors suggest a game theory interactive matrix described by 10 mathematical expressions for solving the interaction between different sources observed through the point of common coupling (PCC). Multiple sources are observed during the operative control of one or multiple micro-grid systems inside of distribution network with L number of nodes. Interactive matrix is optimized by the minimization of three objective functions, (26)–(28), using the adapted hierarchically arranged GA, and the proposed method is tested on the IEEE 33 node test network in which the authors integrate three microgrid systems. In expressions (22)–(24), implies voltage at node l within a network consisting of nodes set L; stands for PCC power exchange of microgrid at node l; represents power loss of ADN and is power exchange level of the observed system.
By comparing the results from the soft computing optimization methods with the results from the classical mathematical approach, the authors conclude that proposed approach yields betters results during the optimization of more complex systems with multiple DG units. The authors emphasize the specific achievement of the paper in the efficient methodology for solving complex optimization problems by using the computer intelligence, while the additional procedures and other hybrid solutions must be explored.
Automatic generation control (AGC) of distribution network with high share of DG and electric vehicles based on framework established for transmission systems is presented in the work by Batisetelli et al. [113]. The authors scaled the known AGC hierarchy to control DG, local distribution and load subsystems and logically divided active distribution network to virtual power isles managed by centralized control. Electric vehicles may contain both generation and load characteristics therefore authors deal with both problems simultaneously through linear programming model optimized by CPLEX optimizer that can be implemented in energy management system of active distribution network. The model described in Reference [113] was tested and confirmed on a realistic four-feeder system from which the “smart user grid (SUG)” paradigm is developed by integrating multi-agent system procedures and entities of different functionalities. Extremely revealing contribution of the authors [113] is evident in “criteria for implementation and coordination of automatic generation control”, comprising the communication necessary between observed levels, similar to the one presented in Reference [29]. Discrete 24-segment simulations representing 24-hour schedule is the methodology of most authors, including the one in Reference [113]. Although not the typical computational intelligence approach, paper considered important aspects of ADN management with increased ratio of various types of DG. The absence of advanced optimization techniques is completely justified by an excellent principle demonstration that was clearly the goal of Reference [113], while the practicality and robustness of optimization solution developed on this research basis should consider more complex methods.
Scientific work in the wake of the abovementioned paper can be found in paper by Jun et al. [114] where authors solved the multi-agent optimization problem by means of integer programming dividing the day planning in 24 segments. EMS has a significant role in valid operation, optimization, control and balancing of “hybrid renewable energy generation system”, as stated by the authors, and specific challenges of management scheme are described in this paper. Complex unified modeling language diagram, solved in Java Agent Development Framework, of multi-agent system is presented, showing system classes, attributes and relationships between them. The authors introduce new parameters computed by individual agent that indicate the attention of observed agent as load, or as DG. These parameters suggest the economic and power qualities of each agent integrating the stochastic nature of some RES. Detailed analysis of EMS conclude the structural requirements of future communication, behavior and optimizations objectives.
Significant papers indicate the importance of considering meteorological dependencies of some RES-based DGs along with independencies of other types of non-RES DG units. Gu et al. [124] thoroughly defined factors of the future management service consisting of demand side management, operation objectives, energy pricing, weather forecast, energy management, maintenance scheduling, physical limitations of equipment involved, operation scheduling and interaction with main supply grid via PCC. The authors define the perspective of energy management by achieving higher level of efficiency and lower emission levels while maintaining power quality and providing ancillary services.
From their work, one can get a clear idea of what a future energy management system for the distribution network should look like and what should be taken into account, as illustrated by Figure 10. The authors thus state how to respect consumers, plan according to meteorological indicators, consider equipment limitations and the situation on the energy market, all in order to plan the optimal timetable of DG.
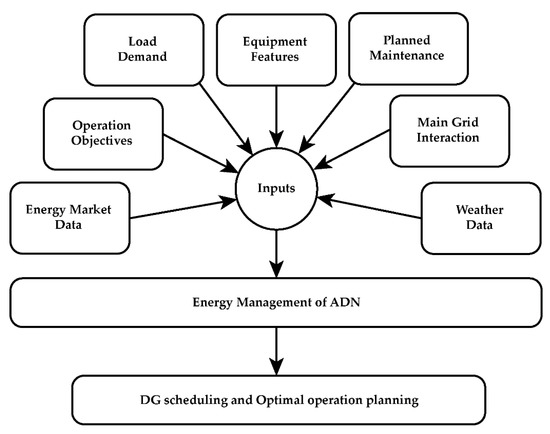
Figure 10.
Energy management system of the future distribution grids, inspired by Gu et al.
Zhang et al. [125] concluded that operational management can reduce line losses and improve voltage profiles which will benefit DG developers as well as distribution network operators. The authors define the traditional distribution network planning and operation as “fit and forget” methodology and conclude that this principle will need to change in order to allow higher penetration levels and development of Smart Grid. Mohamed and Mohammed [126] developed effective mathematical algorithm for distribution grid management in a Smart Grid form by giving priority to renewable energy resources while maintaining least possible cost and satisfying load demand. The authors predicted PV generation by historical data and statistical smoothing techniques, while wind generation and load data were modeled by non-linear regression modeling. The main objective achieved by Reference [126] is minimizing the power obtained from parent grid while retaining additional power for sudden demand changes. A case study of Smart Grid management in Japan is presented in Reference [127] from a policy perspective, and an essential requirement for management services in order to achieve maximal benefits is highlighted in this paper.
Significant achievement towards real-time economic dispatch and operational management of active distribution network is evident in paper by Kellerer et al. [128] in which authors propose new method based on statistical inference method—a probabilistic graphical model method. The authors prove algorithm functionality in global optimal search, irrelevant of network size, and with the assumptions that 70% of consumer nodes have randomly integrated RES-based DG units. The main subject of their observations is in solving the economic dispatch problems without having a full knowledge of all component models, for which they assume is difficult in competitive market environment. The proposed algorithm is successfully tested on a network whose topology is based on real Smart Grid data in Southern Germany.
With the objective of reducing CO2 emissions Lamadrid et al. [129] proposed a novel optimization solution that favors RES in power dispatch and scheduling, if the technology permits planning. From the perspective of system operator and in compliance with network policies, authors present their optimization formulation respecting technical and economic limitations and prove the usefulness of their method by testing it on 279-bus transmission network in Texas, USA. The authors have taken into consideration a stochastic nature of some RES and gave them priority in dispatch schedule. Although modeling is complex, authors managed to perform it correctly by using mathematical correct workaround solutions. By proposed solution authors managed to simulate a future 24-hour period which is adequate for system schedule and operation in market conditions. For wind power modeling, authors used combination of historical and calculated data. This paper is very important due to the complexity of observed problem, and although the authors themselves say that improvements are needed, this paper presents state-of-the-art in operational management and DG scheduling.
A modified self-adaptive PSO algorithm serviceability for multi-objective optimal operation management of a distribution network containing a fuel-cell power plant was proven in paper by Niknam et al. [130], and a computational intelligence principle was described that contained fuzzy-controlled decision-making. The authors developed a practical 24-segment algorithm, providing Pareto solutions. A similar fuzzy controlled approach can be found in paper by Elamine et al. [131] where wind speed is determined by PSO optimized ANN based on small historical set and fuzzy agent for battery storage management.
Previous scientific works have successfully identified key issues and constraints that need to be addressed when creating a widely applicable solution for active distribution network operational management and scheduling. The biggest disadvantage of presented papers is the need for a complex mathematical model of the observed system which is usually not sensitive to structural changes in the same system, hence not applicable to distribution grids. Accordingly, universal applicability of the proposed solutions is not always achieved, and each observed case is at the same time the only case observed and researched by a group of scientists. Issues in Smart Grid application can be compartmentalized into five categories [132]: concept presentation—advantages and limitations of renewable energy distributed generation; technology adoption for hybrid energy system; optimal allocation problems and technical characteristics; forecasting, pricing and policy issues; Smart Grid–integration challenges.
With the development of active distribution networks, which aspire to become Smart Grids, the emphasis of scientists in this area will tend to be on the development of widely applicable and robust solutions for which it will be necessary to consume and respect the knowledge and achievements displayed in all of the so-far listed scientific works.
6. Conclusions
The initial premise of the presented research was to identify scientific breakthroughs and papers that can be delivered as a working solution for future power grids.
The research was conceived in five key steps that begin with the selection of papers and continues with the modeling of the described procedures and testing of the solutions traceability. Finally, the usefulness and applicability were discussed at the research team level, and conclusions are given in this paper.
Papers with precise models and comprehensive descriptions of computational intelligence–based methods proved to be highly usable in the development of real solutions for Smart Grid operational management. Modern systems for monitoring and managing an advanced distribution network according to the assumed European Smart Grid framework will have to integrate scientifically validated and model-tested solutions that consistently provide accurate data.
Within the space–time possibilities and within the available literature, the authors of this paper collected, processed, examined and evaluated as many papers as possible, which with their content promise applicability of computational intelligence in real-world systems. If any work was missed, it was certainly not intentional, and the knowledge and information presented in this article were compiled with the idea of serving anyone involved in optimization and management in the Smart Grid environment. The presented works systematically and precisely present the advantages of the applicability of meta-heuristic methods in the optimization of various challenges in the power industry, with an emphasis on the optimization of operating conditions in the distribution network. Although the emphasis of the paper was placed on metaheuristics—because only with it does it become possible to solve very complex systems—the paper also presents simpler analytical methods that can be used to solve the optimization problems of smaller systems. However, scalability of potential real-world solutions can only be ensured with computational intelligence and advanced custom-made metaheuristics.
This paper illustrates the problem of planning the optimal operation of an advanced distribution network with a significant number of distributed generation units and provides the cognitive process of deciding on the framework for the development of contemporary management solutions. Metaheuristic proves to be a necessity in large and complex systems, such as the modern Smart Grid, and modern control solution that integrate metaheuristic methods will provide good-enough solutions for everyday usage. Operators of the future grid will need to settle with such “good-enough” solutions as the grid becomes more complex and variable in nature.
A detailed overview of more than a hundred key papers with important mathematical indicators provides a unique insight into the application of computer intelligence in power engineering. According to the authors of this paper, population methods in a limited search space can yield the best result in terms of repeatability and usability, and with increasing computing power, such optimization procedures based on computational intelligence can take place within the market conditions of real systems.
Finally, methods, procedures and paradigms that can provide reliable operational management in advanced distribution networks were explained, and features of each of them were discussed with the mark-up of leading algorithms, PSO and GA, which can be, to a greater or lesser extent, applied in real-world applications.
Author Contributions
Conceptualization, M.V. and P.M.; methodology, M.V. and G.H.; validation, Z.B. and S.S.; formal analysis, Z.B.; resources, P.M.; writing—original draft preparation, M.V.; writing—review and editing, M.V. and P.M.; visualization, M.V. and G.H.; revision, M.V. and P.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research was co-funded by project “PEGASOS”, through the grant of Croatian Ministry of Regional Development and EU Funds “Increasing the development of the new products and services arising from research and development activities—phase II/KK.01.2.1.02” of the program “Competitiveness and Cohesion 2014–2020” from the European Regional Development Fund. The information and views set out in this study are those of the author(s) and do not necessarily reflect the official opinion of the European Union and national implementing bodies. Neither the European Union institutions and bodies nor any person acting on their behalf may be held responsible for the use which may be made of the information contained therein.
Acknowledgments
The authors of this paper express their deepest gratitude to the external domain experts from the Faculty of Electrical Engineering, Computer Science and Information Technology Osijek. Special appreciation authors declare to the experts from Končar—Power Plant and Electric Traction Engineering, Inc., who contributed to validity and analysis. Finally, the authors are grateful to the whole team of Base58 for their technical virtuosity in modeling and testing, administrative skills in project preparation and management, and finally, their motivation and support.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A
For better understanding and reproduction of the findings of this paper, and for easier catching-up with the mentioned papers, the authors have prepared an abbreviation list. Since some authors choose similar letters and abbreviations, in the description field of Table A1, we give the paper to which the abbreviation applies.

Table A1.
Nomenclature and abbreviation list.
Table A1.
Nomenclature and abbreviation list.
| Abbreviation | Description | Unit |
|---|---|---|
| Sensitivity factor of real power loss with respect to Real power injection from DG (Acharya et al., 2006) | MW | |
| The transmission coefficient of the real part of the complex power by Kansal et al. (2013) | ||
| Quotient of product of voltage angle difference cosine and line resistance with voltage level (Biswas et al., 2012) | ||
| Sensitivity factor of reactive power loss with respect to reactive power injection from DG (Acharya et al., 2006) | MVAr | |
| The transmission coefficient of the reactive part of the complex power by Kansal et al. (2013) | ||
| Quotient of product of voltage angle difference sinus and line resistance with voltage level (Biswas et al., 2012) | ||
| Penalty coefficient ( (Moradi and Abedini, 2012) | ||
| Penalty coefficient ( (Moradi and Abedini, 2012) | ||
| Active power prices with DG (Singh and Goswami, 2010) | US$/MWh | |
| Reactive power prices with DG (Singh and Goswami, 2010) | US$/MWh | |
| Total cost associated with the DGs (Biswas et al., 2012) | US$ mil. | |
| Cost of power generation from fuel cell (Niknam et al., 2011) | US$ | |
| Cost of power generation from wind power (Niknam et al., 2011) | US$ | |
| Cost of power generation from photovoltaic system (Niknam et al., 2011) | US$ | |
| Cost of substation (Niknam et al., 2011) | US$ | |
| Voltage angle difference between bus i and bus j (Alrashidi and Alhajri, 2011) | rad | |
| Emission of atmospheric pollutants from fuel-cell power generation (Niknam et al., 2011) | kg/h | |
| Emission of atmospheric pollutants from wind power generation (Niknam et al., 2011) | kg/h | |
| Etpv | Emission of atmospheric pollutants from photovoltaic power generation (Niknam et al., 2011) | kg/h |
| Actual current of the i-th branch (Niknam et al., 2011) | A | |
| Real power losses after DG integration by El-Zonkoly (2014.) | % | |
| Reactive power losses after DG integration by El-Zonkoly (2014.) | % | |
| MVA capacity index regarding the power flows through conductors in paper by El-Zonkoly (2014.) | % | |
| Voltage profile index, observed as voltage deviation from the nominal value by El-Zonkoly (2014.) | % | |
| Short circuit level index, observed as DG impact on short circuit current increase in paper by El-Zonkoly (2014.) | % | |
| Penalty coefficient (Moradi and Abedini, 2012) | ||
| Penalty coefficient (Moradi and Abedini, 2012) | ||
| Is the cost of DG per KW (Biswas et al., 2012) | US$ | |
| Electricity price at power supply point (Singh and Goswami, 2010) | US$/MWh | |
| Set of nodes in ADN by Lv and Ai (2016) | ||
| Total line-loss reduction (Abou El-Ela et al., 2010) | % | |
| Line-loss without the DG (Abou El-Ela et al., 2010) | MW | |
| Line-loss with the DG (Abou El-Ela et al., 2010) | MW | |
| Load distributed for the i-th fault (Biswas et al., 2012) | MW | |
| Maximal composite benefits of DG (Abou El-Ela et al., 2010) | ||
| PSO-based multi-objective function by El-Zonkoly (2014.) | ||
| Number of buses in distribution system by Kansal et al. | N | |
| Number of radial distribution system buses (Alrashidi and Alhajri, 2011) | ||
| Number of the branches (Niknam et al., 2011) | ||
| Total number of the buses (Niknam et al., 2011) | ||
| Number of years (Niknam et al., 2011) | ||
| Total number of faults within a specified time duration (Biswas et al., 2012) | ||
| Nfc | Number of fuel-cell units (Niknam et al., 2011) | |
| Number of photovoltaic units (Niknam et al., 2011) | ||
| Number of wind units (Niknam et al., 2011) | ||
| Power exchange level by Lv and Ai (2016) | kW/t | |
| Inertial probability (Gomez-Gonzalez et al., 2012) | ||
| Maximal inertia per population (Gomez-Gonzalez et al., 2012) | ||
| Minimal inertia per population (Gomez-Gonzalez et al., 2012) | ||
| Active power demand at any bus i (Singh and Goswami, 2010) | MW | |
| Real power injection at node i (Acharya et al., 2006) | MW | |
| Active power generated by DG (Singh and Goswami, 2010) | MW | |
| Size of the i-th DG (Biswas et al., 2012) | MW | |
| Load demand at node i (Acharya et al., 2006) | MW | |
| Real power flows at the receiving end of the forward-update procedure by Injeti el al. | MW | |
| The active power injections at bus i and bus j by Kansal et al. | MW | |
| Power generated from fuel cell (Niknam et al., 2011) | kWh | |
| Active power of distributed generation (Aman et al., 2012) | MW | |
| PCC power exchange of MG n by Lv and Ai (2016) | kW | |
| Line losses (Injeti and Prema Kumar, 2013) | MW | |
| Total feeder losses (Injeti and Prema Kumar, 2013) | MW | |
| power loss of ADN in paper by Lv and Ai (2016) | kW | |
| The price of electricity (Singh and Goswami, 2010) | US$/MWh | |
| Power flow reduction in critical lines (Abou El-Ela et al., 2010) | % | |
| Power flow in line k without DG (Abou El-Ela et al., 2010) | MW | |
| Power flow in line k with DG (Abou El-Ela et al., 2010) | MW | |
| Power generated from photovoltaic system (Niknam et al., 2011) | kWh | |
| Power generated from wind power (Niknam et al., 2011) | kWh | |
| Reactive power flows at the receiving end of the forward-update procedure by Injeti el al. | MVAr | |
| Reactive power demand at any bus i (Singh and Goswami, 2010) | MVAr | |
| Reactive power generated by DG (Singh and Goswami, 2010) | MVAr | |
| The reactive power injections at bus i and bus j by Kansal et al. | MVAr | |
| Resistance of the i-th branch (Niknam et al., 2011) | /km | |
| Real part of line impedance (Aman et al., 2012) | /km | |
| Equivalent resistance between bus 1 and bus i when DG is located at bus j (Wang and Nehrir, 2004) | p.u. | |
| Real power loss (Biswas et al., 2012) | MW | |
| Weights for corresponding importance of each DG impact index by El-Zonkoly (2014.) | ||
| Total load distributed (Biswas et al., 2012) | ||
| Apparent power at bus (Moradi and Abedini, 2012) | MVA | |
| Maximum apparent power at bus (Moradi and Abedini, 2012) | MVA | |
| Spinning reserve with DG [23] (Abou El-Ela et al., 2010) | p.u. | |
| Spinning reserve without DG (Abou El-Ela et al., 2010) | p.u. | |
| Spinning reserve increasing (Abou El-Ela et al., 2010) | % | |
| The sum of scheduling period t in paper by Lv and Ai (2016) | ||
| Time step (one year) (Niknam et al., 2011) | ||
| set of types of DGs in Microgrid n; u = 1, 2, 3, 4 and 5 denote fuel cell, microturbine, battery storage, Photovoltaic System and Wind turbine, respectively, by Lv and Ai (2016) | ||
| The bus i voltage (Alrashidi and Alhajri, 2011) | p.u. | |
| Real voltage of the i-th bus (Niknam et al., 2011) | p.u. | |
| Voltage magnitude at the receiving end of the forward-update procedure Injeti el al. | p.u. | |
| The bus j voltage (Alrashidi and Alhajri, 2011) | p.u. | |
| Voltage of bus (Moradi and Abedini, 2012) | p.u. | |
| Maximum voltage at bus (Moradi and Abedini, 2012) | p.u. | |
| Minimum voltage at bus [(Moradi and Abedini, 2012) | p.u. | |
| Nominal voltage of the i-th bus (Niknam et al., 2011) | p.u. | |
| Voltage profile improvement (Abou El-Ela et al., 2010) | % | |
| Voltage profile index of the system with DG (Abou El-Ela et al., 2010) | p.u. | |
| Voltage profile index without DG (Abou El-Ela et al., 2010) | p.u. | |
| Weight factors, (Yang and Chen, 2011) | ||
| Benefit weighting factors (Abou El-Ela et al., 2010) |
References
- Colak, I.; Fulli, G.; Sagiroglu, S.; Yesilbudak, M.; Covrig, C.F. Smart grid projects in Europe: Current status, maturity and future scenarios. Appl. Energy 2015, 152, 58–70. [Google Scholar] [CrossRef]
- Palensky, P.; van der Meer, A.A.; Lopez, C.D.; Joseph, A.; Pan, K. Cosimulation of Intelligent Power Systems: Fundamentals, Software Architecture, Numerics, and Coupling. IEEE Ind. Electron. Mag. 2017, 11, 34–50. [Google Scholar] [CrossRef]
- Pérez-Ortiz, M.; Jiménez-Fernández, S.; Gutiérrez, P.A.; Alexandre, E.; Hervás-Martínez, C.; Salcedo-Sanz, S. A Review of Classification Problems and Algorithms in Renewable Energy Applications. Energies 2016, 9, 607. [Google Scholar] [CrossRef]
- Uslar, M.; Schmedes, T.; Lucks, A.; Luhmann, T.; Winkels, L.; Appelrath, H.J. Interaction of EMS related systems by using the CIM standard. In Proceedings of the ITEE 2005 2nd Internacional ICSC Symposium Information Technologies Environmental Engineering, Magdenburg, Germany, 25–27 September 2005; pp. 596–610. [Google Scholar]
- Molzahn, D.K.; Dorfler, F.; Sandberg, H.; Low, S.H.; Chakrabarti, S.; Baldick, R.; Lavaei, J. A Survey of Distributed Optimization and Control Algorithms for Electric Power Systems. IEEE Trans. Smart Grid 2017, 8, 2941–2962. [Google Scholar] [CrossRef]
- Liao, H. Review on Distribution Network Optimization under Uncertainty. Energies 2019, 12, 3369. [Google Scholar] [CrossRef]
- Theo, W.L.; Lim, J.S.; Ho, W.S.; Hashim, H.; Lee, C.T. Review of distributed generation (DG) system planning and optimisation techniques: Comparison of numerical and mathematical modelling methods. Renew. Sustain. Energy Rev. 2017, 67, 531–573. [Google Scholar] [CrossRef]
- Mahmoud Pesaran, H.A.; Huy, P.D.; Ramachandaramurthy, V.K. A review of the optimal allocation of distributed generation: Objectives, constraints, methods, and algorithms. Renew. Sustain. Energy Rev. 2016, 75, 293–312. [Google Scholar] [CrossRef]
- Ruiz-Romero, S.; Colmenar-Santos, A.; Mur-Pérez, F.; López-Rey, Á. Integration of distributed generation in the power distribution network: The need for smart grid control systems, communication and equipment for a smart city—Use cases. Renew. Sustain. Energy Rev. 2014, 38, 223–234. [Google Scholar] [CrossRef]
- Madsen, D.Ø. The Evolutionary Trajectory of the Agile Concept Viewed from a Management Fashion Perspective. Soc. Sci. 2020, 9, 69. [Google Scholar] [CrossRef]
- Malik, M.; Sarwar, S.; Orr, S. Agile practices and performance: Examining the role of psychological empowerment. Int. J. Proj. Manag. 2021, 39, 10–20. [Google Scholar] [CrossRef]
- Viral, R.; Khatod, D. Optimal planning of distributed generation systems in distribution system: A review. Renew. Sustain. Energy Rev. 2012, 16, 5146–5165. [Google Scholar] [CrossRef]
- Sambaiah, K.S. A review on optimal allocation and sizing techniques for DG in distribution systems. Int. J. Renew. Energy Res. 2018, 8, 1236–1256. [Google Scholar]
- Mazidi, M.; Zakariazadeh, A.; Jadid, S.; Siano, P. Integrated scheduling of renewable generation and demand response programs in a microgrid. Energy Convers. Manag. 2014, 86, 1118–1127. [Google Scholar] [CrossRef]
- Lopes, J.P.; Hatziargyriou, N.; Mutale, J.; Djapic, P.; Jenkins, N. Integrating distributed generation into electric power systems: A review of drivers, challenges and opportunities. Electr. Power Syst. Res. 2007, 77, 1189–1203. [Google Scholar] [CrossRef]
- Kim, H.-S.; Hong, J.; Choi, I.-S. Implementation of Distributed Autonomous Control Based Battery Energy Storage System for Frequency Regulation. Energies 2021, 14, 2672. [Google Scholar] [CrossRef]
- Urbanetz, J.; Braun, P.; Rüther, R. Power quality analysis of grid-connected solar photovoltaic generators in Brazil. Energy Convers. Manag. 2012, 64, 8–14. [Google Scholar] [CrossRef]
- Yang, N.-C.; Chen, T.-H. Evaluation of maximum allowable capacity of distributed generations connected to a distribution grid by dual genetic algorithm. Energy Build. 2011, 43, 3044–3052. [Google Scholar] [CrossRef]
- Vukobratović, M.; Nikolovski, S.; Marić, P. Improving the Conditions in a Radial Distribution Feeder by Implementing Distributed Generation. Int. J. Electr. Comput. Eng. Syst. 2021, 6, 5. [Google Scholar] [CrossRef]
- Ipinnimo, O.; Chowdhury, S.; Mitra, J. A review of voltage dip mitigation techniques with distributed generation in electricity networks. Electr. Power Syst. Res. 2013, 103, 28–36. [Google Scholar] [CrossRef]
- Yadav, A.; Srivastava, L. Optimal placement of distributed generation: An overview and key issues. In Proceedings of the 2014 International Conference on Power Signals Control and Computations (EPSCICON), Atlanta, GA, USA, 3–5 December 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 8–10. [Google Scholar] [CrossRef]
- Djafar, W.; Amer, Y.; Lee, S.-H. Models and Optimisation Techniques on Long Distribution Network: A Review. Procedia Manuf. 2015, 2, 519–526. [Google Scholar] [CrossRef]
- Kotamarty, S.; Khushalani, S.; Schulz, N. Impact of distributed generation on distribution contingency analysis. Electr. Power Syst. Res. 2008, 78, 1537–1545. [Google Scholar] [CrossRef]
- Bignucolo, F.; Cerretti, A.; Coppo, M.; Savio, A.; Turri, R. Impact of Distributed Generation Grid Code Requirements on Islanding Detection in LV Networks. Energies 2017, 10, 156. [Google Scholar] [CrossRef]
- Acharya, N.; Mahat, P.; Mithulananthan, N. An analytical approach for DG allocation in primary distribution network. Int. J. Electr. Power Energy Syst. 2006, 28, 669–678. [Google Scholar] [CrossRef]
- Gözel, T.; Hocaoglu, M.H. An analytical method for the sizing and siting of distributed generators in radial systems. Electr. Power Syst. Res. 2009, 79, 912–918. [Google Scholar] [CrossRef]
- Injeti, S.K.; Kumar, N.P. A novel approach to identify optimal access point and capacity of multiple DGs in a small, medium and large scale radial distribution systems. Int. J. Electr. Power Energy Syst. 2013, 45, 142–151. [Google Scholar] [CrossRef]
- Bollen, M.; Hassan, F. Integration of Distributed Generation in the Power System; Wiley: Hoboken, NJ, USA, 2011; ISBN 978-1-118-02901-5. [Google Scholar]
- Bruinenberg, J.; Colton, L.; Darmois, E.; Dorn, J.; Doyle, J.; Elloumi, O.; Englert, H.; Forbes, R.; Heiles, J.; Hermans, P.; et al. CEN -CENELEC—ETSI: Smart Grid Coordination Group—Smart Grid Reference Architecture Report 2.0.; CEN-CENELEC-ETSI: Brussels, Belgium, 2012. [Google Scholar]
- Shewale, A.; Mokhade, A.; Funde, N.; Bokde, N.D. An Overview of Demand Response in Smart Grid and Optimization Techniques for Efficient Residential Appliance Scheduling Problem. Energies 2020, 13, 4266. [Google Scholar] [CrossRef]
- Panda, D.K.; Das, S. Smart grid architecture model for control, optimization and data analytics of future power networks with more renewable energy. J. Clean. Prod. 2021, 301, 126877. [Google Scholar] [CrossRef]
- Markovic, D.S.; Zivkovic, D.; Branovic, I.; Popovic, R.; Cvetkovic, D. Smart power grid and cloud computing. Renew. Sustain. Energy Rev. 2013, 24, 566–577. [Google Scholar] [CrossRef]
- Machinda, G.T.; Chowdhury, S.; Mbav, W.N. Power management of inverter interfaced solar PV microgrid: A review of the current technological trend. In Proceedings of the 47th International Universities Power Engineering Conference (UPEC), London, UK, 4–7 September 2012; pp. 1–6. [Google Scholar]
- Choudar, A.; Boukhetala, D.; Barkat, S.; Brucker, J.-M. A local energy management of a hybrid PV-storage based distributed generation for microgrids. Energy Convers. Manag. 2015, 90, 21–33. [Google Scholar] [CrossRef]
- Häger, U.; Rehtanz, C.; Editors, N.V. Power Systems Monitoring, Control and Protection of Interconnected Power Systems; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-642-53847-6. [Google Scholar]
- Adefarati, T.; Bansal, R.C. Integration of renewable distributed generators into the distribution system: A review. IET Renew. Power Gener. 2016, 10, 873–884. [Google Scholar] [CrossRef]
- Wang, C.; Nehrir, M.H.H. Analytical Approaches for Optimal Placement of Distributed Generation Sources in Power Systems. IEEE Trans. Power Syst. 2004, 19, 2068–2076. [Google Scholar] [CrossRef]
- Aman, M.M.; Jasmon, G.B.; Mokhlis, H.; Bakar, A.H.A. Optimal placement and sizing of a DG based on a new power stability index and line losses. Int. J. Electr. Power Energy Syst. 2012, 43, 1296–1304. [Google Scholar] [CrossRef]
- Singh, R.K.; Goswami, S.K. Optimum allocation of distributed generations based on nodal pricing for profit, loss reduction, and voltage improvement including voltage rise issue. Int. J. Electr. Power Energy Syst. 2010, 32, 637–644. [Google Scholar] [CrossRef]
- El-Ela, A.A.; Allam, S.M.; Shatla, M.M. Maximal optimal benefits of distributed generation using genetic algorithms. Electr. Power Syst. Res. 2010, 80, 869–877. [Google Scholar] [CrossRef]
- Biswas, S.; Goswami, S.K.; Chatterjee, A. Optimum distributed generation placement with voltage sag effect minimization. Energy Convers. Manag. 2012, 53, 163–174. [Google Scholar] [CrossRef]
- AlRashidi, M.R.; Alhajri, M.F. Optimal planning of multiple distributed generation sources in distribution networks: A new approach. Energy Convers. Manag. 2011, 52, 3301–3308. [Google Scholar] [CrossRef]
- González, M.G.; López, A.; Jurado, F. Optimization of distributed generation systems using a new discrete PSO and OPF. Electr. Power Syst. Res. 2012, 84, 174–180. [Google Scholar] [CrossRef]
- Moradi, M.; Abedini, M. A combination of genetic algorithm and particle swarm optimization for optimal DG location and sizing in distribution systems. Int. J. Electr. Power Energy Syst. 2012, 34, 66–74. [Google Scholar] [CrossRef]
- Soares, J.; Silva, M.; Sousa, T.; Vale, Z.; Morais, H. Distributed energy resource short-term scheduling using Signaled Particle Swarm Optimization. Energy 2012, 42, 466–476. [Google Scholar] [CrossRef]
- Saif, A.; Pandi, V.R.; Zeineldin, H.; Kennedy, S. Optimal allocation of distributed energy resources through simulation-based optimization. Electr. Power Syst. Res. 2013, 104, 1–8. [Google Scholar] [CrossRef]
- Kansal, S.; Kumar, V.; Tyagi, B. Optimal placement of different type of DG sources in distribution networks. Int. J. Electr. Power Energy Syst. 2013, 53, 752–760. [Google Scholar] [CrossRef]
- Hung, D.Q.; Mithulananthan, N.; Lee, K.Y. Optimal placement of dispatchable and nondispatchable renewable DG units in distribution networks for minimizing energy loss. Int. J. Electr. Power Energy Syst. 2014, 55, 179–186. [Google Scholar] [CrossRef]
- Aman, M.; Jasmon, G.B.; Bakar, A.H.A.; Mokhlis, H. A new approach for optimum simultaneous multi-DG distributed generation Units placement and sizing based on maximization of system loadability using HPSO (hybrid particle swarm optimization) algorithm. Energy 2014, 66, 202–215. [Google Scholar] [CrossRef]
- Bayod-Rújula, A.A. Future development of the electricity systems with distributed generation. Energy 2009, 34, 377–383. [Google Scholar] [CrossRef]
- Borges, C.L.T.; Martins, V.F. Multistage expansion planning for active distribution networks under demand and Distributed Generation uncertainties. Int. J. Electr. Power Energy Syst. 2012, 36, 107–116. [Google Scholar] [CrossRef]
- El-Khattam, W.; Salama, M.M.A. Distributed generation technologies, definitions and benefits. Electr. Power Syst. Res. 2004, 71, 119–128. [Google Scholar] [CrossRef]
- Alotaibi, I.; Abido, M.A.; Khalid, M.; Savkin, A.V. A Comprehensive Review of Recent Advances in Smart Grids: A Sustainable Future with Renewable Energy Resources. Energies 2020, 13, 6269. [Google Scholar] [CrossRef]
- Tan, W.-S.; Hassan, M.Y.; Majid, S.; Rahman, H.A. Optimal distributed renewable generation planning: A review of different approaches. Renew. Sustain. Energy Rev. 2013, 18, 626–645. [Google Scholar] [CrossRef]
- Ongsakul, W.; Vo Ngoc, D. Artificial Intelligence in Power System Optimization; CRC Press: Boca Raton, FL, USA, 2013; ISBN 978-1-4665-7342-0. [Google Scholar]
- Ashlock, D. Evolutionary Computation for Modeling and Optimization. In Evolutionary Computation for Modeling and Optimization; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Kordon, A. Applying Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-540-69910-1. [Google Scholar]
- Sumathi, S.; Surekha, P. Computational Intelligence Paradigms: Theory and Applications Using MATLAB; CRC Press: Boca Raton, FL, USA, 2010; ISBN 978-1-4398-0902-0. [Google Scholar]
- Sörensen, K. Metaheuristics-the metaphor exposed. Int. Trans. Oper. Res. 2013, 22, 3–18. [Google Scholar] [CrossRef]
- Tang, K.S. Multiobjective Optimization Methodology: A Jumping Gene Approach; Wilamowski, B.M., Irwin, D.J., Eds.; CRC Press: Boca Raton, FL, USA, 2018; ISBN 978-1-4398-9919-9. [Google Scholar]
- Gopalakrishnan, K.; Khaitan, S.K.; Kalogirou, S. Soft Computing in Green and Renewable Energy Systems; Gopalakrishnan, K., Khaitan, S.K., Kalogirou, S., Eds.; Studies in Fuzziness and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2011; Volume 269, ISBN 978-3-642-22175-0. [Google Scholar]
- Luna-Rubio, R.; Trejo-Perea, M.; Vargas-Vázquez, D.; Ríos-Moreno, G. Optimal sizing of renewable hybrids energy systems: A review of methodologies. Sol. Energy 2012, 86, 1077–1088. [Google Scholar] [CrossRef]
- Rutkowski, L. Computational Intelligence Methods and Techniques; Springer: Warszawa, Poland, 2005; ISBN 978-3-540-76287-4. [Google Scholar]
- Borenstein, Y.; Moraglio, A. Theory and Principled Methods for the Design of Metaheuristics; Borenstein, Y., Moraglio, A., Eds.; Natural Computing Series; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-642-33205-0. [Google Scholar]
- Yang, X.-S.; Chien, S.F.; Ting, T.O. Computational Intelligence and Metaheuristic Algorithms with Applications. Sci. World J. 2014, 2014, 425853. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J. Swarm Intelligence. In Handbook of Nature-Inspired and Innovative Computing; Kluwer Academic Publishers: Boston, UK, 2001; pp. 187–219. ISBN 978-0-387-40532-2. [Google Scholar]
- Kruse, R.; Borgelt, C.; Braune, C.; Mostaghim, S.; Steinbrecher, M. Computational Intelligence; Texts in Computer Science; Springer London: London, UK, 2016; ISBN 978-1-4471-7294-9. [Google Scholar]
- Hopgood, A.A. The State of Artificial Intelligence. In Advances in Organometallic Chemistry; Elsevier BV: Amsterdam, The Netherlands, 2005; Volume 65, pp. 1–75. ISBN 0120121654. [Google Scholar]
- Ibrahim, D. An Overview of Soft Computing. Procedia Comput. Sci. 2016, 102, 34–38. [Google Scholar] [CrossRef]
- Kumari, M.S.; Priyanka, G.; Sydulu, M. Comparison of Genetic Algorithms and Particle Swarm Optimization for Optimal Power Flow Including FACTS devices. In Proceedings of the 2007 IEEE Lausanne Power Technology, Lausanne, Switzerland, 1–5 July 2007; pp. 1105–1110. [Google Scholar]
- Liu, S.; Hou, Z.; Wang, M. A hybrid algorithm for optimal power flow using the chaos optimization and the linear interior point algorithm. In Proceedings of the International Conference Power System Technology, Kunming, China, 13–17 October 2002; Volume 4, pp. 793–797. [Google Scholar]
- AlRashidi, M.; El-Hawary, M. Applications of computational intelligence techniques for solving the revived optimal power flow problem. Electr. Power Syst. Res. 2009, 79, 694–702. [Google Scholar] [CrossRef]
- Santofimia-Romero, M.-J.; Toro-García, X.; López-López, J.-C. Artificial Intelligence Techniques for Smart Grid Applications; CEPIS: Brussels, Belgium, 2011; Volume XII. [Google Scholar]
- Abraham, A.; Das, S. Computational Intelligence in Power Engineering; Panigrahi, B.K., Abraham, A., Das, S., Eds.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2010; Volume 302, ISBN 978-3-642-14012-9. [Google Scholar]
- Colmenar-Santos, A.; Reino-Rio, C.; Borge-Diez, D.; Collado-Fernández, E. Distributed generation: A review of factors that can contribute most to achieve a scenario of DG units embedded in the new distribution networks. Renew. Sustain. Energy Rev. 2016, 59, 1130–1148. [Google Scholar] [CrossRef]
- Sotkiewicz, P.M.; Vignolo, J.M. Nodal Pricing for Distribution Networks: Efficient Pricing for Efficiency Enhancing DG. IEEE Trans. Power Syst. 2006, 21, 1013–1014. [Google Scholar] [CrossRef]
- Mitchell, M. An Introduction to Genetic Algorithms; The MIT Press: Cambridge, MA, USA; London, UK, 1996; ISBN 0262631857. [Google Scholar]
- Poli, R.; Langdon, W.; McPhee, N. A Field Guide to Genetic Programming; Lulu Press, Inc.: Morrisville, NC, USA, 2008; ISBN 9781409200734. [Google Scholar]
- Haupt, R.L.; Haupt, S.E. Practical Genetic Algorithms; Wiley: Hoboken, NJ, USA, 2004; ISBN 0-471-45565-2. [Google Scholar]
- Injeti, S.K. A Pareto optimal approach for allocation of distributed generators in radial distribution systems using improved differential search algorithm. J. Electr. Syst. Inf. Technol. 2018, 5, 908–927. [Google Scholar] [CrossRef]
- Shammah, A.; El-Ela, A.A.; Azmy, A.M. Optimal location of remote terminal units in distribution systems using genetic algorithm. Electr. Power Syst. Res. 2012, 89, 165–170. [Google Scholar] [CrossRef]
- Wu, Q.H.; Cao, Y.J.; Wen, J.Y. Optimal reactive power dispatch using an adaptive genetic algorithm. Int. J. Electr. Power Energy Syst. 1998, 20, 563–569. [Google Scholar] [CrossRef]
- Subbaraj, P.; Rajnarayanan, P.N. Optimal reactive power dispatch using self-adaptive real coded genetic algorithm. Electr. Power Syst. Res. 2009, 79, 374–381. [Google Scholar] [CrossRef]
- López-Lezama, J.M.; Contreras, J.; Padilha-Feltrin, A. Location and contract pricing of distributed generation using a genetic algorithm. Int. J. Electr. Power Energy Syst. 2012, 36, 117–126. [Google Scholar] [CrossRef]
- El-Zonkoly, A.M. Optimal placement of multi-distributed generation units including different load models using particle swarm optimization. Swarm Evol. Comput. 2011, 1, 50–59. [Google Scholar] [CrossRef]
- El-Zonkoly, A. Optimal scheduling of observable controlled islands in presence of energy hubs. Electr. Power Syst. Res. 2017, 142, 141–152. [Google Scholar] [CrossRef]
- El-Zonkoly, A. Intelligent energy management of optimally located renewable energy systems incorporating PHEV. Energy Convers. Manag. 2014, 84, 427–435. [Google Scholar] [CrossRef]
- El-Zonkoly, A. Optimal placement and schedule of multiple grid connected hybrid energy systems. Int. J. Electr. Power Energy Syst. 2014, 61, 239–247. [Google Scholar] [CrossRef]
- Aman, M.M.; Jasmon, G.B.; Bakar, A.H.A.; Mokhlis, H. A new approach for optimum DG placement and sizing based on voltage stability maximization and minimization of power losses. Energy Convers. Manag. 2013, 70, 202–210. [Google Scholar] [CrossRef]
- Niknam, T.; Taheri, S.I.; Aghaei, J.; Tabatabaei, S.; Nayeripour, M. A modified honey bee mating optimization algorithm for multiobjective placement of renewable energy resources. Appl. Energy 2011, 88, 4817–4830. [Google Scholar] [CrossRef]
- Niknam, T. An efficient multi-objective HBMO algorithm for distribution feeder reconfiguration. Expert Syst. Appl. 2011, 38, 2878–2887. [Google Scholar] [CrossRef]
- Niknam, T. An efficient hybrid evolutionary algorithm based on PSO and HBMO algorithms for multi-objective Distribution Feeder Reconfiguration. Energy Convers. Manag. 2009, 50, 2074–2082. [Google Scholar] [CrossRef]
- Yin, P.-Y.; Yu, S.-S.; Wang, P.-P.; Wang, Y.-T. A hybrid particle swarm optimization algorithm for optimal task assignment in distributed systems. Comput. Stand. Interfaces 2006, 28, 441–450. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y. Multi-objective reactive power and voltage control based on fuzzy optimization strategy and fuzzy adaptive particle swarm. Int. J. Electr. Power Energy Syst. 2008, 30, 525–532. [Google Scholar] [CrossRef]
- Ashari, M.; Soeprijanto, A. Optimal Distributed Generation (DG) Allocation for Losses Reduction Using Improved Particle Swarm Optimization (IPSO) Method. J. Basic. Appl. Sci. Res. 2012, 2, 7016–7023. [Google Scholar]
- Bhumkittipich, K.; Phuangpornpitak, W. Optimal Placement and Sizing of Distributed Generation for Power Loss Reduction Using Particle Swarm Optimization. Energy Procedia 2013, 34, 307–317. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, S.; Ji, G. A Comprehensive Survey on Particle Swarm Optimization Algorithm and Its Applications. Math. Probl. Eng. 2015, 2015, 931256. [Google Scholar] [CrossRef]
- Moghaddas-Tafreshi, S.M.; Zamani, H.A.; Hakimi, S.M. Optimal sizing of distributed resources in micro grid with loss of power supply probability technology by using breeding particle swarm optimization. J. Renew. Sustain. Energy 2011, 3, 43105. [Google Scholar] [CrossRef]
- Ganguly, S.; Sahoo, N.; Das, D. Multi-objective particle swarm optimization based on fuzzy-Pareto-dominance for possibilistic planning of electrical distribution systems incorporating distributed generation. Fuzzy Sets Syst. 2013, 213, 47–73. [Google Scholar] [CrossRef]
- Vukobratović, M.; Marić, P.; Hederić, Ž. Voltage and power losses control using distributed generation and computational intelligence. Teh. Vjesn. Tech. Gaz. 2016, 23, 23. [Google Scholar] [CrossRef][Green Version]
- De Tré, G.; Zadrożny, S. Springer Handbook of Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2015; ISBN 9783662435052. [Google Scholar]
- EU Commission European. Task Force for the implementation of Smart Grids into the European Internal Market. In Mission Work Programme; EU Commission European: Geneva, Switzerland, 2012; pp. 1–15. [Google Scholar]
- Joint Research Centre—Smart Electricity Systems and Interoperability European Smart Grid Projects: Relationship Matrix. Available online: http://ses.jrc.ec.europa.eu/european-smart-grid-projects-relationship-matrix (accessed on 12 December 2017).
- Gangale, F.; Vasiljevska, J.; Covrig, C.F.; Mengolini, A.; Fulli, G. Smart Grid Projects Outlook 2017: Facts, Figures and Trends in Europe; Publications Office of the European Union: Luxembourg, 2017. [Google Scholar]
- Prettico, G.; Gangale, F.; Mengolini, A.; Lucas, A.; Fulli, G. DISTRIBUTION SYSTEM OPERATORS OBSERVATORY: From European Electricity Distribution Systems to Representative Distribution Networks; Publications Office of the European Union: Luxembourg, 2016. [Google Scholar]
- Jalali, M.M.; Kazemi, A. Demand side management in a smart grid with multiple electricity suppliers. Energy 2015, 81, 766–776. [Google Scholar] [CrossRef]
- Fahrioglu, M.; Alvarado, F.L.; Lasseter, R.H.; Yong, T. Supplementing demand management programs with distributed generation options. Electr. Power Syst. Res. 2012, 84, 195–200. [Google Scholar] [CrossRef]
- Kinhekar, N.; Padhy, N.P.; Gupta, H.O. Multiobjective demand side management solutions for utilities with peak demand deficit. Int. J. Electr. Power Energy Syst. 2014, 55, 612–619. [Google Scholar] [CrossRef]
- Shi, W.; Xie, X.; Chu, C.-C.; Gadh, R. Distributed Optimal Energy Management in Microgrids. IEEE Trans. Smart Grid 2015, 6, 1137–1146. [Google Scholar] [CrossRef]
- Niknam, T.; Meymand, H.Z.; Nayeripour, M. A practical algorithm for optimal operation management of distribution network including fuel cell power plants. Renew. Energy 2010, 35, 1696–1714. [Google Scholar] [CrossRef]
- Singh, A.; Parida, S. Congestion management with distributed generation and its impact on electricity market. Int. J. Electr. Power Energy Syst. 2013, 48, 39–47. [Google Scholar] [CrossRef]
- Macedo, M.N.Q.; Galo, J.J.M.; de Almeida, L.A.L.; de Lima, A.C. Demand side management using artificial neural networks in a smart grid environment. Renew. Sustain. Energy Rev. 2015, 41, 128–133. [Google Scholar] [CrossRef]
- Battistelli, C.; Conejo, A.J. Optimal management of the automatic generation control service in smart user grids including electric vehicles and distributed resources. Electr. Power Syst. Res. 2014, 111, 22–31. [Google Scholar] [CrossRef]
- Zeng, J.; Liu, J.; Wu, J.; Ngan, H.W. A multi-agent solution to energy management in hybrid renewable energy generation system. Renew. Energy 2011, 36, 1352–1363. [Google Scholar] [CrossRef]
- Dileep, G. A survey on smart grid technologies and applications. Renew. Energy 2020, 146, 2589–2625. [Google Scholar] [CrossRef]
- Rivas, A.E.L.; Abrão, T. Faults in smart grid systems: Monitoring, detection and classification. Electr. Power Syst. Res. 2020, 189, 106602. [Google Scholar] [CrossRef]
- Tan, W.-S.; Shaaban, M. Dual-timescale generation scheduling with nondeterministic flexiramp including demand response and energy storage. Electr. Power Syst. Res. 2020, 189, 106821. [Google Scholar] [CrossRef]
- Milchram, C.; Künneke, R.; Doorn, N.; van de Kaa, G.; Hillerbrand, R. Designing for justice in electricity systems: A comparison of smart grid experiments in the Netherlands. Energy Policy 2020, 147, 111720. [Google Scholar] [CrossRef]
- Rohde, F.; Hielscher, S. Smart grids and institutional change: Emerging contestations between organisations over smart energy transitions. Energy Res. Soc. Sci. 2021, 74, 101974. [Google Scholar] [CrossRef]
- Feng, C.; Wang, Y.; Chen, Q.; Ding, Y.; Strbac, G.; Kang, C. Smart grid encounters edge computing: Opportunities and applications. Adv. Appl. Energy 2021, 1, 100006. [Google Scholar] [CrossRef]
- Pala, D. ICT Standards for Smart Grids: IEC 61850, CIM and Their Tmplementation in the ERIGrid Project; ERIGrid: Vienna, Austria, 2018. [Google Scholar]
- Umeozor, E.C.; Trifkovic, M. Operational scheduling of microgrids via parametric programming. Appl. Energy 2016, 180, 672–681. [Google Scholar] [CrossRef]
- Lv, T.; Ai, Q. Interactive energy management of networked microgrids-based active distribution system considering large-scale integration of renewable energy resources. Appl. Energy 2016, 163, 408–422. [Google Scholar] [CrossRef]
- Gu, W.; Wu, Z.; Bo, R.; Liu, W.; Zhou, G.; Chen, W.; Wu, Z.Z. Modeling, planning and optimal energy management of combined cooling, heating and power microgrid: A review. Int. J. Electr. Power Energy Syst. 2014, 54, 26–37. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, H.; Wang, C. Technical and economic impacts of active management on distribution network. Int. J. Electr. Power Energy Syst. 2009, 31, 130–138. [Google Scholar] [CrossRef]
- Mohamed, A.; Mohammed, O. Real-time energy management scheme for hybrid renewable energy systems in smart grid applications. Electr. Power Syst. Res. 2013, 96, 133–143. [Google Scholar] [CrossRef]
- Mah, D.N.-Y.; Wu, Y.-Y.; Ip, J.C.-M.; Hills, P.R. The role of the state in sustainable energy transitions: A case study of large smart grid demonstration projects in Japan. Energy Policy 2013, 63, 726–737. [Google Scholar] [CrossRef]
- Kellerer, E.; Steinke, F. Scalable Economic Dispatch for Smart Distribution Networks. IEEE Trans. Power Syst. 2015, 30, 1739–1746. [Google Scholar] [CrossRef]
- Lamadrid, A.J.; Shawhan, D.L.; Nchez, C.E.M.-S.Á.; Zimmerman, R.D.; Zhu, Y.; Tylavsky, D.J.; Kindle, A.G.; Dar, Z. Stochastically Optimized, Carbon-Reducing Dispatch of Storage, Generation, and Loads. IEEE Trans. Power Syst. 2015, 30, 1064–1075. [Google Scholar] [CrossRef]
- Niknam, T.; Kavousifard, A.; Tabatabaei, S.; Aghaei, J. Optimal operation management of fuel cell/wind/photovoltaic power sources connected to distribution networks. J. Power Sources 2011, 196, 8881–8896. [Google Scholar] [CrossRef]
- Elamine, D.O.; Nfaoui, E.H.; Jaouad, B. Multi-agent system based on fuzzy control and prediction using NN for smart microgrid energy management. In Proceedings of the 2015 Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 25–26 March 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Phuangpornpitak, N.; Tia, S. Opportunities and Challenges of Integrating Renewable Energy in Smart Grid System. Energy Procedia 2013, 34, 282–290. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).