1. Introduction
Singing constitutes a central component of many musical traditions. Identifying segments of singing activity—often denoted as
singing voice detection (SVD)—therefore provides essential information about the content and structure of music recordings and may also serve as a pre-processing step for tasks such as lyrics alignment [
1,
2] or lyrics transcription [
3]. SVD has historically received a lot of attention within the field of music information retrieval (MIR) [
4,
5]. The majority of SVD systems are designed for and evaluated on popular music [
6,
7,
8,
9,
10]. However, Scholz et al. [
11] showed that data-driven SVD methods usually do not generalize well to other genres not seen during training, implying that the pop-music focus limits the general applicability of SVD systems.
Particular differences exist between popular and classical music, which is due to the distinct singing techniques and instrumentations involved. Within classical music, opera recordings constitute challenging scenarios where singing voices are often embedded in a rich orchestral texture. As a peculiarity of classical music, several recorded performances (
versions) of a musical work are usually available. Such cross-version scenarios provide great opportunities for testing the robustness of MIR algorithms in different tasks [
12,
13] and their capability for generalizing across different versions [
14,
15]. In particular, such cross-version analyses have shown that machine-learning algorithms can overfit to characteristics of certain versions or musical works [
15]. In the light of these observations, we want to investigate whether—and to what extent—SVD algorithms suffer from such overfitting effects. While one obtains good evaluation results with state-of-the-art SVD systems, previous investigations have shown that these systems sometimes over-adapt to confounding factors such as loudness [
16] or singing style [
11]. Therefore, we cannot generally expect these systems to generalize to unseen musical scenarios. Following these lines, our case study yields insights into the generalization behavior of machine-learning systems, the aspects of training data that are relevant for building robust systems, and the benefits of deep learning against traditional machine-learning approaches, which may be relevant beyond the SVD task. With this, our study may serve as an inspiration for similar research on other data-driven approaches to MIR, audio, and speech processing.
In this paper, we aim at gaining a deeper understanding of two state-of-the-art SVD methods, which represent two commonly used strategies: The traditional strategy based on hand-crafted features [
17] and the strategy based on deep learning (DL) [
16], respectively (see
Section 3 for details). To analyze these systems, we make use of a cross-version scenario comprising the full cycle
Der Ring des Nibelungen by Richard Wagner (four operas, 11 acts) in 16 different versions, thus leading to a novel dataset spanning more than 200 h of audio in total. In this scenario, different versions vary with regard to singers’ timbre and singing style, musical interpretation, and acoustic conditions, whereas different operas vary in singing registers and characters, lyrics, and orchestration. We exploit this scenario in a series of systematic experiments in order to analyze the robustness of the two algorithms depending on the musical and acoustic variety, as well as on the size of the training dataset. Our results indicate that both systems perform comparably well and are capable of generalizing across versions and operas—despite the complexity of the scenario and the variety of the data. This result shows that SVD systems based on traditional techniques may perform on par with DL-based approaches while having practical advantages such as lower computational costs and higher stability against random effects. Moreover, we find a small tendency for both systems to overfit to specific musical material, as well as a tendency for the DL-based system to benefit from large dataset sizes. With these general observations, our experimental results may inform the use of SVD algorithms in other musical scenarios beyond the opera context.
The paper is organized as follows. In
Section 2, we discuss related work on singing voice detection in opera settings and SVD algorithms. In
Section 3, we describe our re-implementations of the two SVD systems used for our experiments.
Section 4 provides an overview of our cross-version dataset.
Section 5 contains our experimental results and discusses their implications.
Section 6 concludes our paper.
2. Related Work
In this section, we discuss approaches that have been proposed for the task of singing voice detection, as well as related work on SVD for opera recordings.
From a technical perspective, one may distinguish between two general types of SVD approaches. Traditional systems [
10,
17,
18] usually consist of two stages—the extraction of hand-crafted audio features and the supervised training of classifiers such as random forest classifiers (RFC). Often, mel-frequency cepstral coefficients (MFCC) are combined with classifiers, such as support vector machines or decision trees [
18,
19]. Lehner et al. [
20] showed that considering further hand-crafted features together with RFCs can surpass the results obtained with MFCCs in isolation. In particular, they proposed a so-called
fluctogram representation, which is well-suited for capturing vibrato-like modulations in different frequency bands. They further added features that describe, for each frequency band, the magnitude variance (
spectral flatness) and concentration (
spectral contraction), and a feature responding to gradual spectral changes (
vocal variance). Dittmar et al. [
17] adopted this feature set and classifier setup and tested their system within an opera scenario.
More recently, SVD systems relying on deep neural networks (DNNs) have become popular [
7,
8,
21,
22,
23], with convolutional neural networks (CNN) being among the most effective types of network [
14,
16,
22]. In particular, Schlüter et al. proposed a state-of-the-art deep-learning system for SVD [
16,
22]—a CNN architecture inspired by VGGNet [
24] consisting of stacked convolutional and max-pooling layers applied to mel-spectrogram excerpts (overlapping excerpts of length 1.64 s). More precisely, their network uses five convolutional layers followed by three fully-connected layers, leading to a total of around 1.6 million parameters. Their approach follows the paradigm of automated feature learning—in contrast to the hand-crafted features described above. Further extensions of this are possible, such as a recently proposed approach by Zhang et al. [
25] combining recurrent and convolutional layers.
While most of the mentioned approaches were developed and tested on popular music datasets, there is some previous work focussing on SVD for opera recordings. For example, Dittmar et al. [
17] performed SVD experiments within an opera scenario comprising recordings of C. M. von Weber’s opera
Der Freischütz. Using hand-crafted features and RFCs, they showed that bootstrap training [
9] helps to overcome genre dependencies. In particular, they report frame-wise F-measures up to 0.95, which still constitutes the state of the art for SVD in opera recordings. They further showed that the existence of different versions can be exploited for improving SVD results by performing late fusion of the individual versions’ results. Mimilakis et al. [
14] used a cross-version scenario comprising three versions of Richard Wagner’s opera
Die Walküre (first act) for evaluating three SVD models based on deep learning. As one contribution of our paper, we perform experiments using both a traditional and a DL-based system and in both cases outperform the results reported in [
14]. Furthermore, we substantially extend the scenario of [
14] to the full work cycle
Der Ring des Nibelungen by adding the other acts and operas of the
Ring cycle, as well as 13 further versions (see
Section 4). We use this extended dataset to perform a series of systematic experiments, analyzing our two systems in depth.
3. Singing Voice Detection Methods
In this paper, we consider two approaches to SVD, one based on traditional machine learning [
17] and one based on DL [
16]. In our re-implementations of these methods, we aimed to be as faithful to the original publications as possible. A conceptual overview of both methods is given in
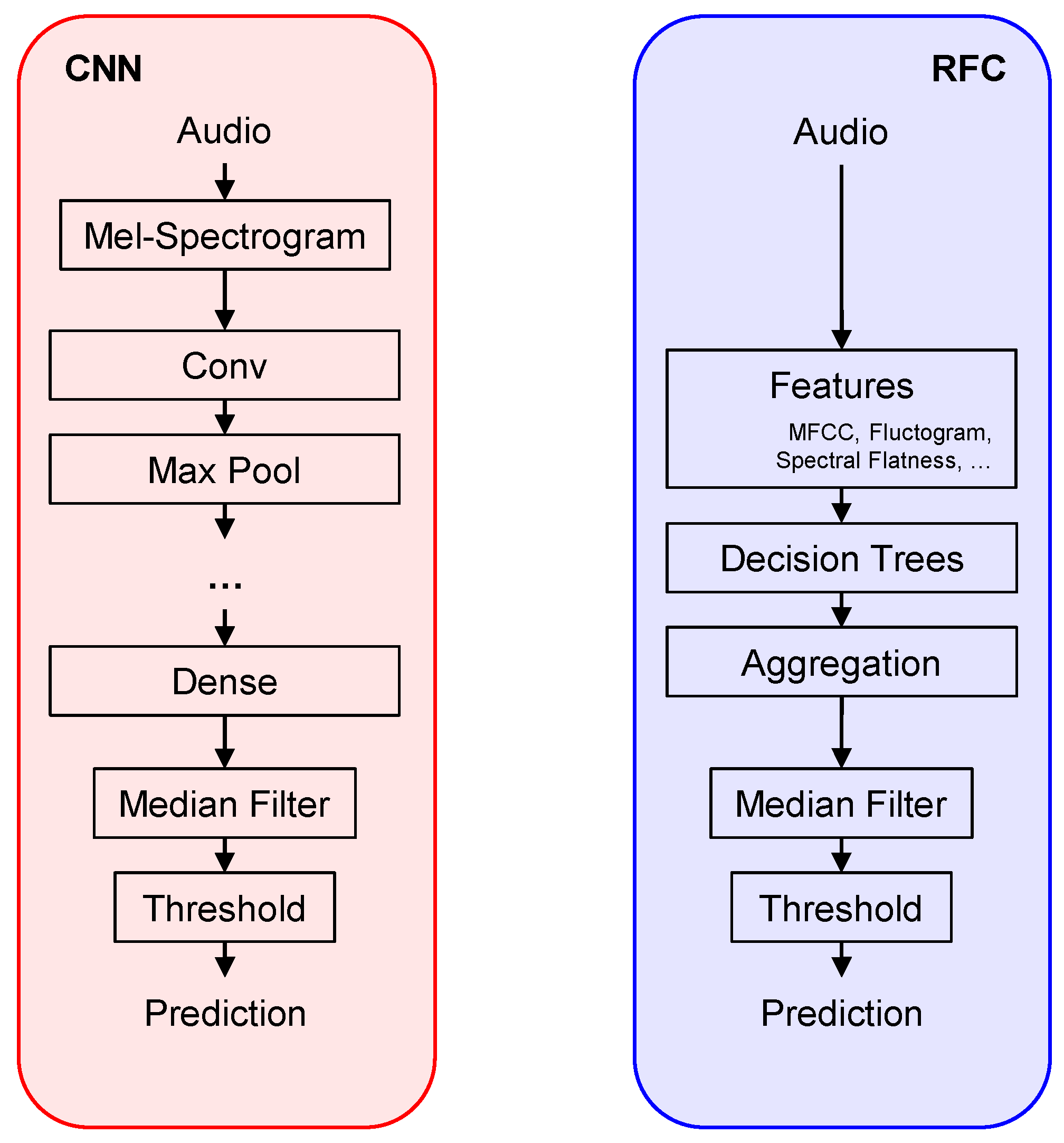
Figure 1.
Closely following [
17], we first realize a traditional SVD system relying on hand-crafted features and an RFC classifier. In our re-implementation, we take special care in reproducing the exact feature set, comprising 110 feature dimensions with a feature rate of 5 Hz. Each feature vector incorporates information from 0.8 s of audio (with the exception of the vocal variance feature covering 2.2 s). For the RFC, we use 128 trees per forest as in [
17] and use standard settings wherever possible [
26,
27] (this leads to minor differences in sampling the training data per decision tree and the feature set per decision node compared to [
17]). In order to test the validity of our re-implementation, we performed an experiment where we train and test on the public
Jamendo corpus (
https://zenodo.org/record/2585988#.YDNvfmhKhaQ, accessed on 1 February 2021), for which results were also reported in [
17].
Jamendo is a dataset of over six hours of popular music recordings (published under creative commons licenses), which has been used for experiments on SVD and other tasks [
28]. In our experiment, we obtain a frame-wise accuracy of 0.887 and a frame-wise F-measure (with singing as the relevant class) of 0.882. This is close to the accuracy of 0.882 and F-measure of 0.887 as reported in [
17] for the same scenario.
For our re-implementation of the DL-based system, we follow the description in [
16]. We take special care in reproducing the input representation, the model architecture and the training scheme (since the convolution-activation-batch normalization order is not explicitly stated in [
16], we use a potentially different order). To resolve ambiguities in [
16], we also consulted a previous publication by the authors [
22] and their public source code. As opposed to [
16], we do not use any input augmentation in order to ensure comparability with the RFC approach where no such augmentations are used. The results in [
16] are reported on an internal dataset. However, for the related method proposed in [
22] the authors report an error rate of 9.4% (i.e., an accuracy of 0.906) when training and testing on the
Jamendo corpus (no data augmentation). Our re-implementation achieves a comparable accuracy of 0.913 for the same scenario.
Both systems output continuous values between 0 and 1 (sigmoid probabilities for the CNN and the fraction of agreeing decision trees for the RFC). Inspired by several SVD approaches [
16,
17,
22], we post-process the results of both the RFC and the CNN using a median filter. As suggested in [
17], we use a filter length of 1.4 s and binarize the output with a fixed decision threshold of 0.5. The CNN system outputs predictions at a rate of 70 Hz. To ensure comparability to the RFC-based approach, we, therefore, downsample the CNN predictions to 5 Hz for comparison.
Since neither [
17] nor [
16] make use of a separate validation set for optimizing hyperparameters, we follow this convention. For the RFC-based system, we try to avoid overfitting by averaging over many trees, each of which is based on a different subsets of the training data. For the CNN-based system, we compute the training loss on mini-epochs of 1000 batches instead of the entire training set. Because of this, we can use early stopping on the training loss to try to prevent overfitting.
Both the traditional and the DL system involve random effects: For the CNN, this includes parameter initialization and random sampling of batches, whereas for the RFC, the choice of features at each split is randomized. Thus, each run of these algorithms produces slightly different results. In our experiments, we compensate for such random effects by averaging all results over multiple runs of the respective algorithm.
The two approaches differ in the computational resources required for training and testing. The computations for individual trees in the RFC can easily be parallelized and run on a standard CPU. The CNN requires a GPU or TPU for efficient training and testing. For example, when training both systems on the same training set of around 200 h of audio (excluding feature computation), the RFC finishes after requiring eight minutes runtime and 3.5 GB of RAM on a desktop computer, while the CNN requires around two hours of training time and 3 GB VRAM on a medium-sized cluster node. These numbers are highly implementation- and hardware-specific, but they demonstrate that the classical system requires less computation time than the deep-learning approach. Inference can be parallelized for both approaches and takes less than a second for the RFC and about one minute for the CNN on roughly 70 min of test audio.
4. Dataset and Training Scenarios
In this section, we present our cross-version opera dataset, which we use for our systematic experiments in different training–test configurations.
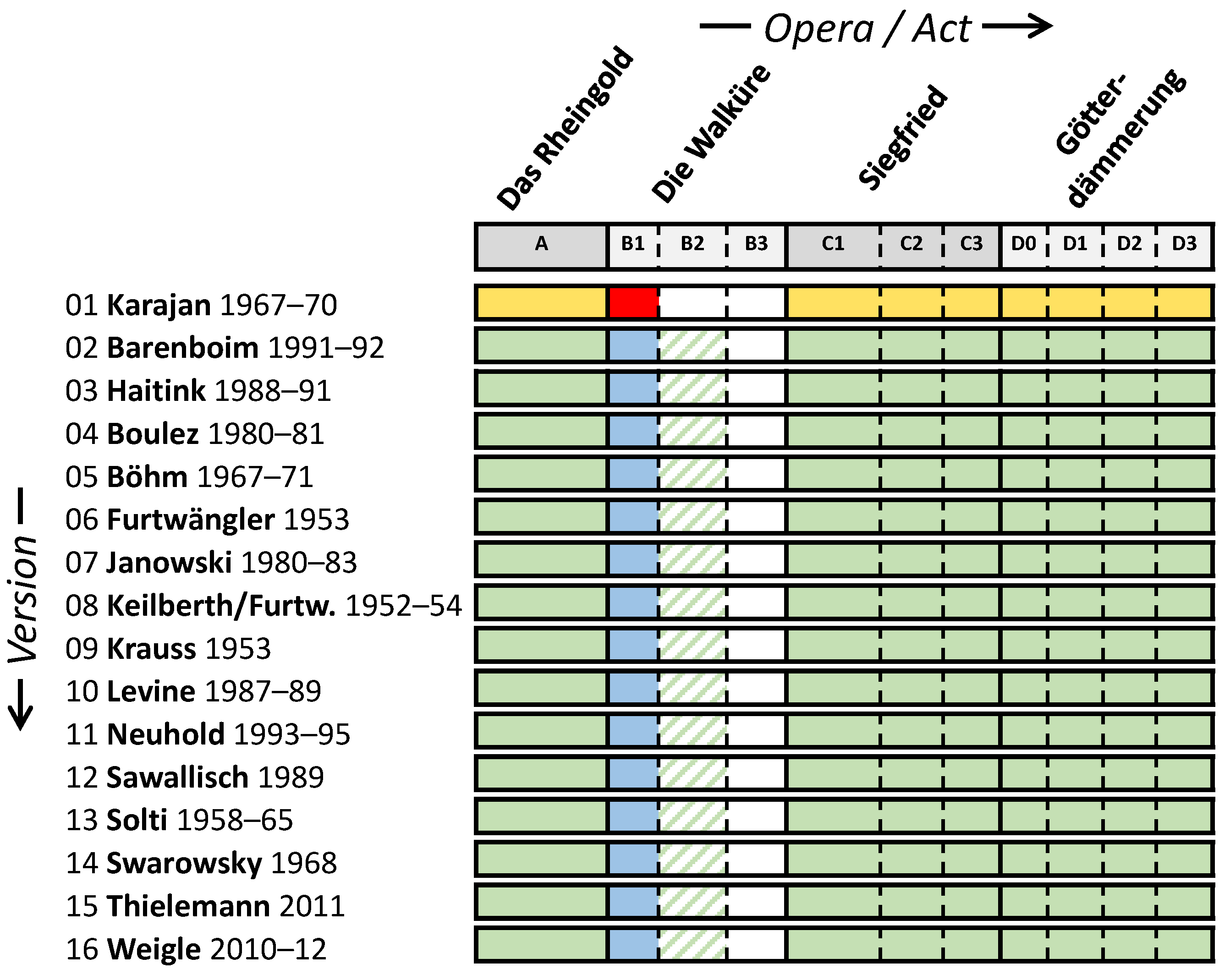
Within Western classical music, Richard Wagner’s tetralogy
Der Ring des Nibelungen WWV 86 constitutes an outstanding work, not least because of its extraordinary length (see
Figure 2). Spanning the four operas
Das Rheingold (WWV 86 A),
Die Walküre (WWV 86 B),
Siegfried (WWV 86 C), and
Götterdämmerung (WWV 86 D), the cycle unfolds an interwoven plot involving many different characters. The characters are represented by different singers with the orchestra adding a rich texture of accompaniment, preludes, and interludes, thus making singing voice detection in recordings of the
Ring a challenging task. For our experiments, we make use of a cross-version dataset comprising 16 recorded performances—denoted as
versions—of the
Ring, each consisting of 13:30 up to 15:30 h of audio data (see
Figure 2 and [
29] for an overview). All versions are structurally identical, i.e., there are no missing or repeated sections.
To enable comparability between versions, we produced manual annotations of musical measure positions for versions 01–03 as listed in
Figure 2 (see [
30] for details). We transferred these measure annotations to versions 04–16 using an automated alignment procedure [
31]. We then used the resulting measure positions to generate audio-based singing voice annotations. To this end, we start from the libretto’s phrase segments and manually annotate the phrase boundaries as given by the score (in musical measures or beats). To transfer the boundaries to the individual versions, we rely on the measure annotations, refined to the beat level using score-to-audio synchronization [
32] within each measure. We use these beat positions to transfer the singing voice segments from the
musical time of the libretto to the
physical time of the performances. The accuracy of the resulting annotations depends, on the one hand, on the accuracy of the measure annotations, which have typical deviations in the order of 100 ms for the manual measure annotations [
30] and 200 ms for the transferred measure annotations [
31]. On the other hand, score-to-audio synchronization within a measure may introduce further inaccuracies. This is an important consideration for putting any experimental results into context, e.g., for a feature rate of 5 Hz (200 ms) and an average length of a singing voice segment of, say, 4 s, an inaccuracy of one frame already results in a frame-wise error rate of 5%.
For the first act of
Die Walküre (WWV 86 B1) in version 01 conducted by Karajan (DG 1998), we manually refined the phrase boundaries, thus accounting for both alignment errors and imprecision of singers. We chose this act (B1) since our manual measure annotations are most reliable here, as described in [
30]. Moreover, its content is roughly balanced between singing characters, with one female (Sieglinde) and two male singers (Siegmund and Hunding), and with singing activity covering about half its duration (37 of 67 min). In our experiments, we always use this recording and its more accurate annotations for testing (red box in
Figure 2).
Inspired by [
15], our novel dataset allows us to systematically test the generalization capabilities of our SVD systems in different training–test configurations. To this end, we split our dataset along different axes (
Figure 2). In the
opera split, we train our methods on other operas in the same version and, thus, need to generalize to different musical works (yellow cells in
Figure 2). In the
version split, we use the same act in other versions for training so that the methods need to generalize to a different musical interpretation, different singers, and different acoustic conditions (blue cells). In the
neither split, neither the test opera nor the test version is seen during training so that the systems have to generalize across both dimensions. In our experiments, we consider different variants of these splits, utilizing, e. g., varying numbers of training versions, operas, or acts. Furthermore, we also exclude in some experiments the second and third act of
Die Walküre (B2 & B3) since the individual singers (characters) from the first act (B1) re-appear in these acts. When considering all versions or all operas (except
Die Walküre B1, B2, & B3) for training, we refer to this as a
full split. Compared to our scenario, Mimilakis et al. [
14] used the same test recording (B1 in version 01), but considered only a
version split with the two versions 02 and 03 (conducted by Barenboim and Haitink, respectively) used for training and validation. We extend this configuration in a systematic fashion in order to study individual aspects of generalization within the opera scenario.
5. Experiments
In the following, we describe our experiments using the systems described in
Section 3, taking advantage of the different split possibilities offered by our dataset as described in
Section 4. We average all results over five runs in order to balance out effects of randomization during training, as discussed in
Section 3. For comparability, we
always use the first act of
Die Walküre (B1) in the version by Karajan (01) as our test set as highlighted in
Figure 2.
5.1. Training on Different Versions
We begin with a variant of the
version split as used in [
14], which only considers the first act of
Die Walküre, WWV 86 B1. Here, the training set consists of version 02 (Barenboim) only. On the test set (version 01, Karajan), Mimilakis et al. [
14] reported a frame-wise F-measure of 0.80 (we only refer to the results of the zero-mean CNN evaluated in [
14], which is most similar to our CNN approach). Using our CNN implementation within the same scenario, we achieve an F-measure of 0.948. The reasons for this substantial improvement remain unclear. With the RFC system, we obtain a comparable result of 0.941, which is similar to the F-measures reported in [
17] for the
Freischütz opera scenario. From this experiment, we conclude that both a traditional and a DL-based system—when properly implemented and fairly compared—can achieve strong results that are roughly on par with each other.
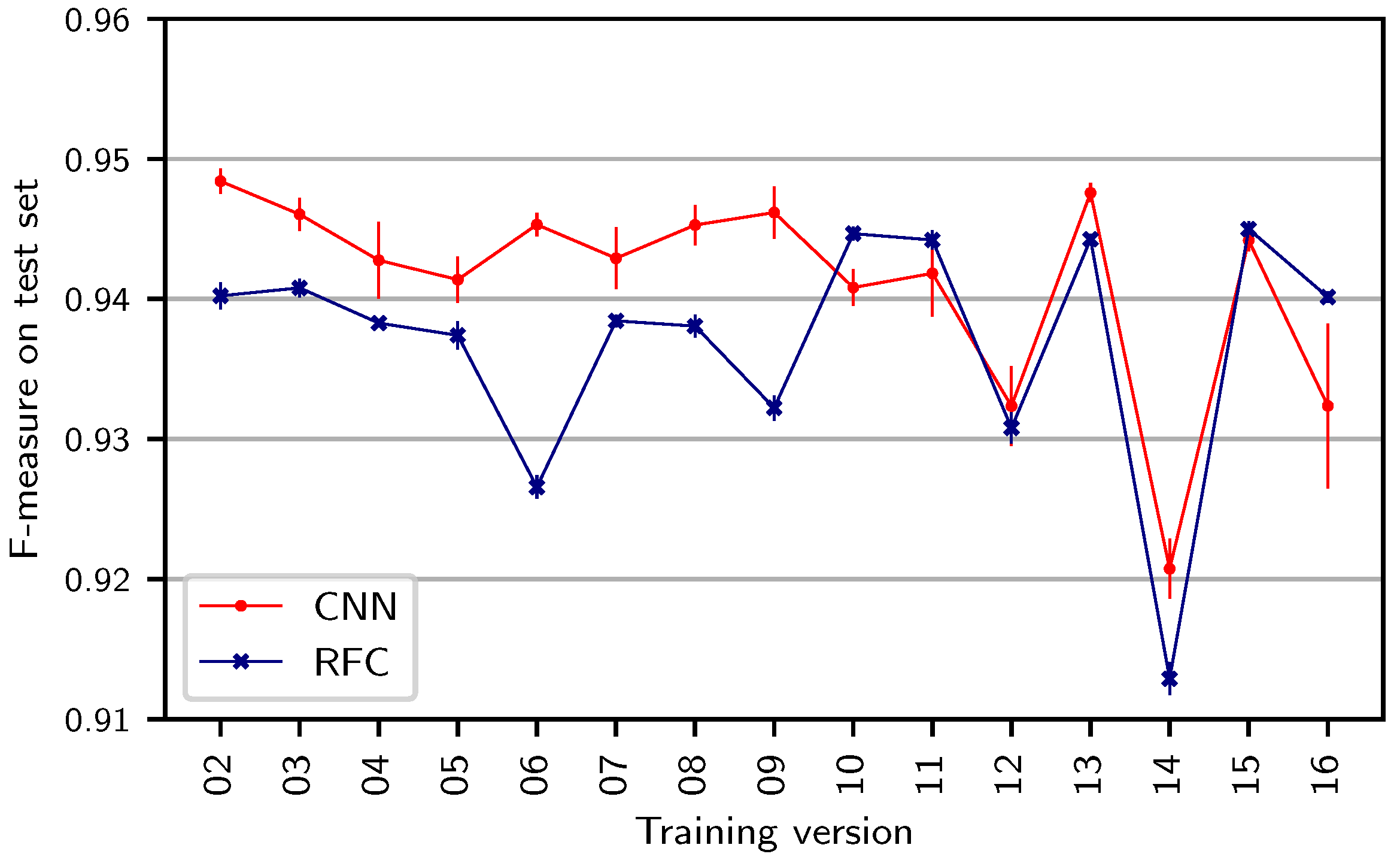
In the previous experiment, we chose version 02 (Barenboim) as the training version. To investigate the impact of this choice, we repeat the same experiment while changing the training version.
Figure 3 shows results for both systems. Dots correspond to mean results averaged over five runs of the same experiment while vertical bars indicate the corresponding standard deviations over those runs. We observe that the choice of training versions has an impact on the test F-measure. The resulting F-measures range from 0.913 for the RFC (version 14) to 0.948 for the CNN (version 02). Furthermore, one can observe that the standard deviations over the runs for individual experiments are higher in the CNN than in the RFC case (see the blue and red vertical bars). In all scenarios, the results are above 0.91 F-measure, which shows that both traditional and deep-learning approaches are capable of generalizing from one version to another version of the same work. Nevertheless, the choice of the training version affects test results, up to around 0.03 F-measure. From a practical point of view, such a difference may seem negligible at first, but when considering a full performance of the
Ring lasting around 15 h, a difference of 0.03 F-measure can affect roughly 27 min of audio.
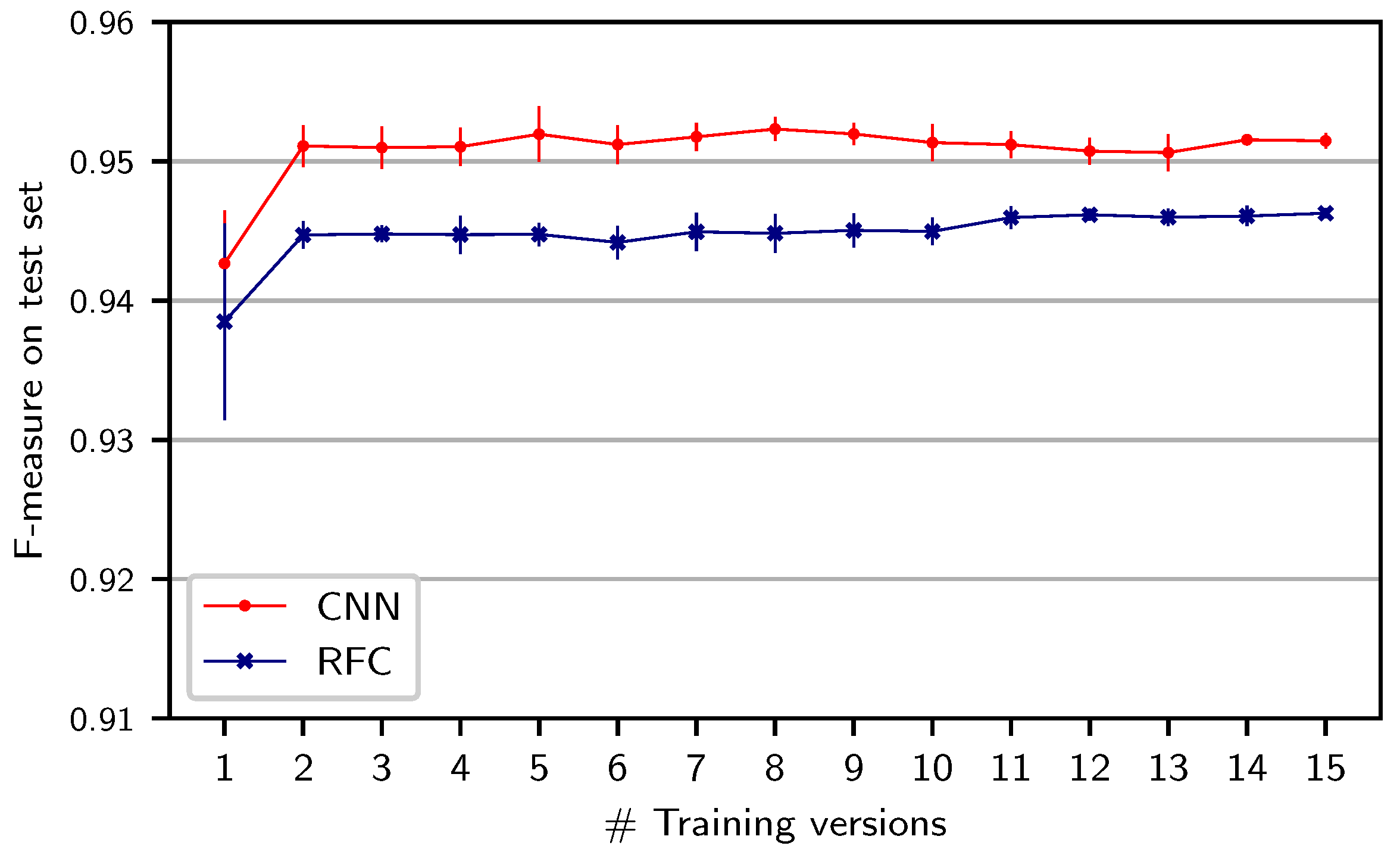
The previous results raise the question whether our systems could benefit from increasing the acoustic and interpretation variety in the training set by training on multiple versions.
Figure 4 shows results when systematically increasing the number of training versions of the same act (B1) used in the
version split. In order to suppress the effect of the particular choice of versions, we repeat each experiment five times and, in each run, randomly sample (without replacement) from all possible versions to create a training set with the specified number of versions. For both classifiers, adding one additional training version leads to improved results. However, adding further training versions does not yield clear improvements. Moreover, these small differences have to be seen in light of the annotation accuracy as discussed in
Section 4. Adding one additional training version seems to sufficiently prevent the systems from adapting to the characteristics of individual versions. Additionally, the RFC seems to be more sensitive to the choice of training version: The standard deviation over runs with only one version is larger for the RFC (0.007 percentage points) than for the CNN (0.001), as indicated by the vertical bars around the left-most dots.
5.2. Training on Different Musical Material
In the experiments reported so far, we made use of the
version split where training and test set consist of the same musical material (B1) in different versions. We now want to test generalization to a different musical content and, to this end, use a different act for training (second act of
Die Walküre, B2) than for testing—a variant of the
neither split (green hatched cells in
Figure 2). As before, we successively increase the number of training versions used. The curves in
Figure 5 indicate the results, which are worse in general compared to
Figure 4. The RFC system now benefits slightly more from additional training versions, while the CNN seems unaffected by this. Although the CNN yields better results than the RFC, neither system reaches its efficacy on the
version split. A possible explanation for this may be that both systems might overfit to the musical material in the training act, adapting, e.g., to the instrumentation or the singing characters (high or low register, male or female voice) as appearing in the training data. The small but consistent gap between the curves of the same color in
Figure 4 and
Figure 5 could be attributed to such work-related overfitting. We understand such small differences to illustrate a trend in the learning behaviors of our methods (though, as mentioned before, these differences may still be of practical relevance when considering an entire performance).
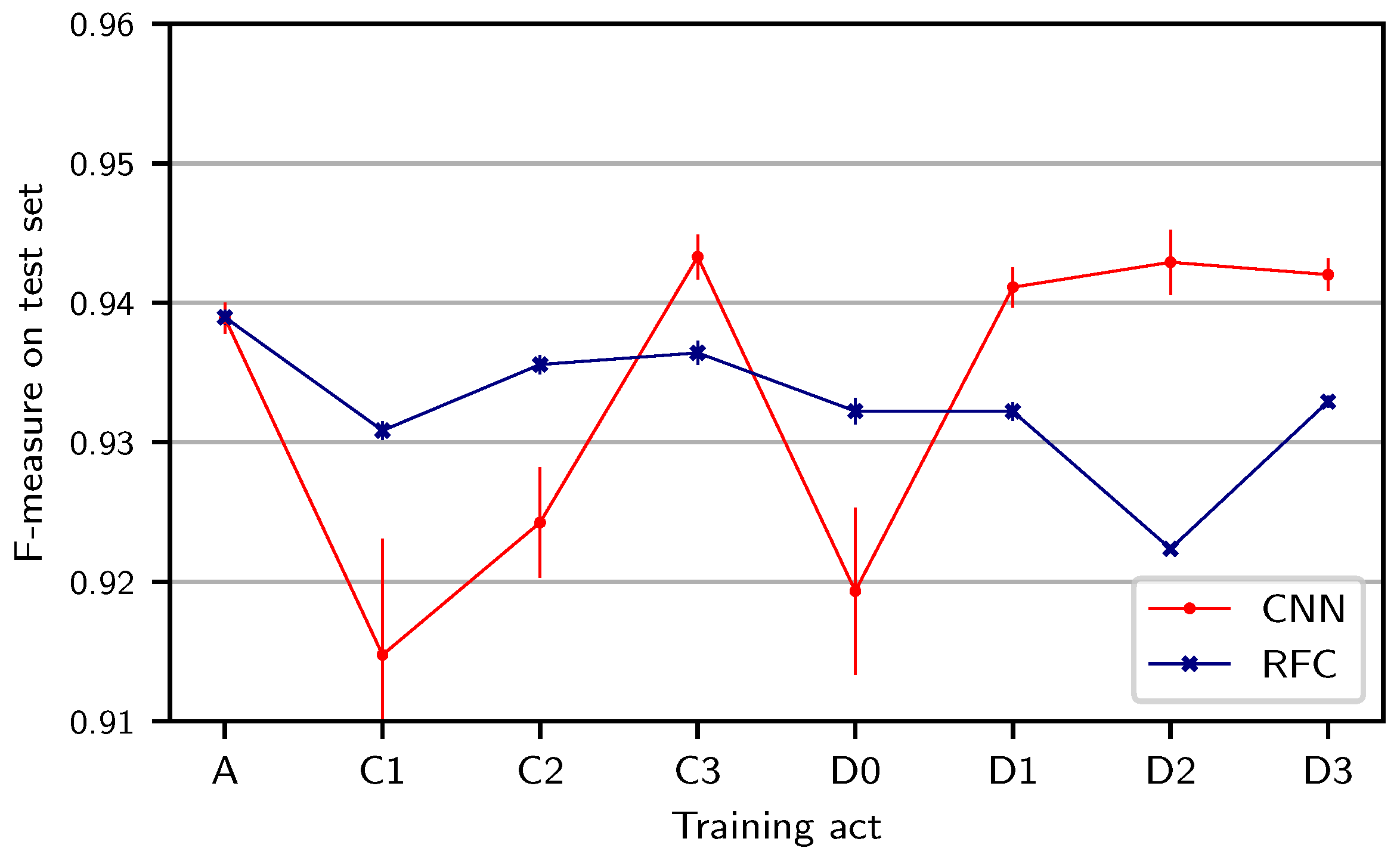
To investigate the impact of such work-related overfitting in more detail, we now examine specific variants of the
opera split where we use the test version (01, Karajan) for training but take one act from another opera (A, C, or D—excluding B) as the training act, respectively. Compared to the previous experiment, the musical generalization is now harder (a different opera, rather than different acts from the same opera) but the acoustic generalization is less hard (same version). The results for this experiment (see
Figure 6) are generally worse than for training on a different act of the same opera (cf.
Figure 5). While the F-measure for the RFC depends only slightly on the particular choice of the training act, this effect is stronger for the CNN. Most prominently, we observe substantial drops when using C1 or C2 (first and second act of
Siegfried) or D0 (Prologue to
Götterdämmerung) for training the CNN. This provides insights into specific challenges of generalization: In C1, only male characters (Siegfried, Mime, Wanderer) are singing. In C2, this is similar, except for several short appearances of the character “Waldvogel” (soprano). In D0, in contrast, mainly female singers are singing. All these cases result in a more challenging generalization to B1, where both female and male characters appear. We also observe a drop for the RFC when training on act D2, which does not occur for the CNN. One reason for this difference could be the prominence of the men’s choir (Mannen) over large parts of D2, which is mostly absent from the rest of the work cycle. Choir singing could negatively affect, e.g., the fluctogram features used as input to the RFC (which are sensitive to vibrato) but could be accounted for by the automated feature extraction of the CNN. In general, the RFC-based system, which relies on hand-crafted features (capturing vibrato and other singing characteristics), seems to be more robust to different singers and registers in training and test data. The CNN, in contrast, seems to generalize better to other musical content with the same characters and registers (as in
Figure 5) and to choir singing.
Furthermore, we can again observe that the standard deviation over CNN runs is higher than for the RFC (see vertical bars). Nevertheless, all results are well above an F-measure of 0.9, meaning that even without training examples for a certain gender of singers, both methods can robustly detect singing in unseen recordings.
5.3. Training on Full Splits
We now extend these experiments to the full splits as shown in
Figure 2 (solid cells).
Table 1 shows the corresponding results. Let us first discuss the full
opera split, where we train the systems on all acts from the three other operas (A, C, D) in the test version 01, Karajan (yellow cells in
Figure 2). We observe F-measures of 0.948 (CNN) and 0.938 (RFC), respectively. Next, we consider the full
version split, where we train on all other versions (02–16) for the test act B1 (blue cells in
Figure 2). Here, we obtain results of 0.951 for the CNN and 0.946 for the RFC, which are slightly better than for the
opera split. This confirms our observation that work-related overfitting effects (e.g., to singers’ register or gender) help to obtain better results in a
version split compared to an
opera split. For the
neither split, we use all acts of A, C, and D in all other versions (02–16) for training (solid green cells in
Figure 2). In this case, we observe F-measures of 0.952 (CNN) and 0.940 (RFC). Here, interestingly, the CNN performs similar as in the
version split, though neither test act nor test version are seen during training. In contrast, the RFC yields an F-measure close to its result on the
opera split. With more versions and operas available, the CNN seems to compensate for the missing test act in the training set. As before, all results are high in general, meaning that both systems work for all considered splits.
To better understand the important aspects of the training set—especially in the case that less versions and works are available—we now present an extension of the
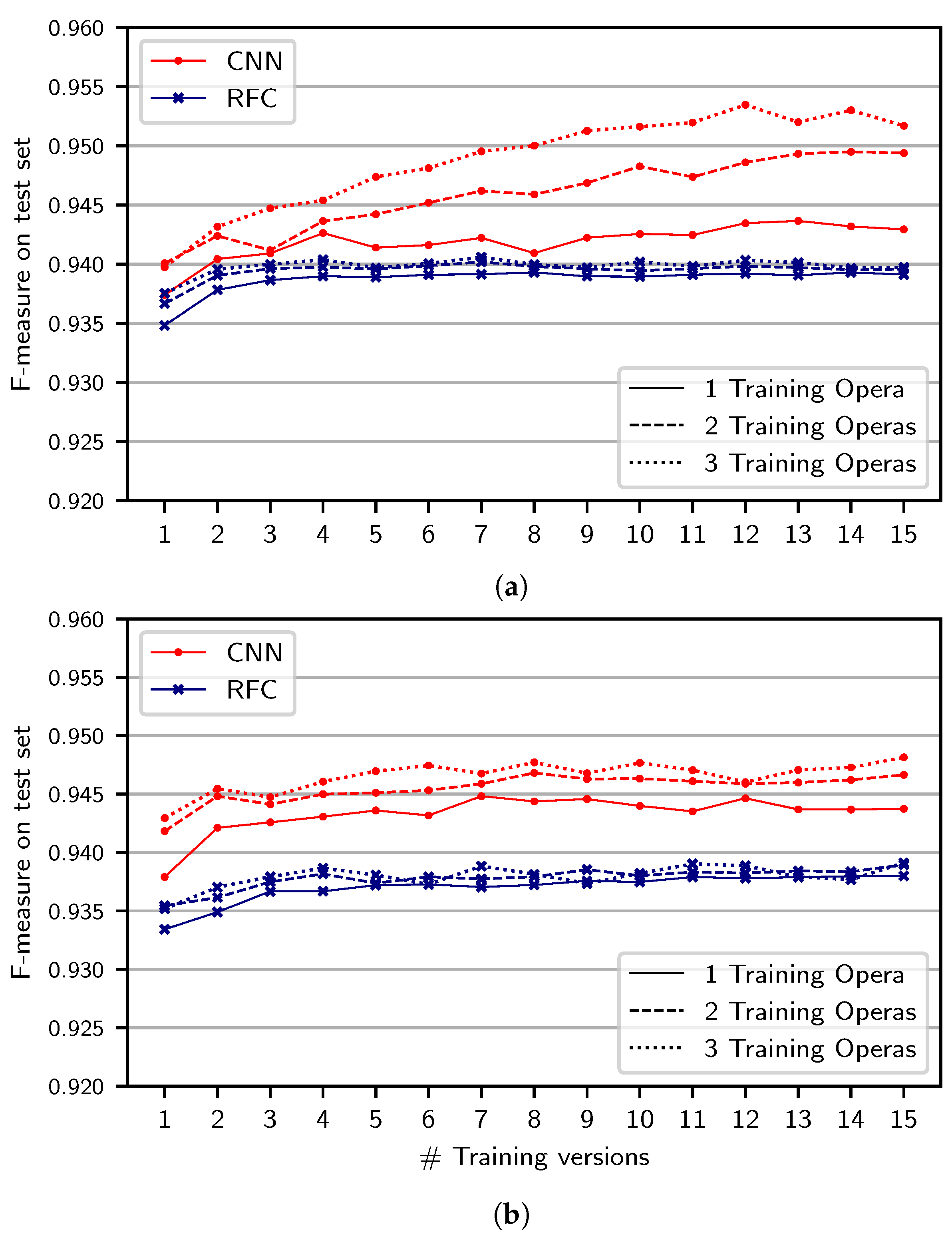
neither split where we successively increase the number of training versions and operas, always using all acts of an opera (
Figure 7a). In each of the five experiment runs, we randomly sample among the versions and operas used for the training set. In this visualization, we omit the vertical bars indicating standard deviations for better visibility. For the RFC (blue curves), we observe that the results are almost identical for different numbers of training operas (solid vs. dashed and dotted curves), but slightly improve for higher numbers of training versions. The CNN, in contrast, benefits from using more operas in the case that more training versions are available as well.
Summarizing these results, we find that the CNN has a slightly stronger tendency than the RFC to overfit to the musical material of the training set. We further see that the RFC-based system primarily exploits acoustic variety present in multiple training versions. In comparison, the CNN seems to also exploit variety in musical material and singing characters stemming from different operas. As a consequence, the CNN trained on the full training data of the neither split can generalize better to other operas and, thus, better compensate for the missing test act during training. We further find that the results for the CNN system vary more across runs, especially in the case that only few training versions and acts are used. As mentioned above, however, the results for all experiment settings are consistently high, meaning that both methods are feasible for singing voice detection in opera, even if only little training data variety is available.
5.4. Impact of Dataset Size
In our previous experiments, we systematically added training versions and operas, which led to an increase not only of the
variety of training data but also of the training dataset’s
size. To separately study the two effects, we repeat the experiment from
Figure 7a while randomly sub-sampling all training datasets to have equal size (of about as many input patches as obtained from a single act of a single version). Results are shown in
Figure 7b. For the RFC (blue), results are almost identical as in
Figure 7a. For the CNN, we observe smaller improvements in
Figure 7b than in
Figure 7a for increasing the number of training versions and operas. Therefore, the improvement seen in
Figure 7a appears to stem mainly from the training dataset’s size rather than from its variety. This suggests a fundamental difference between the two systems: While the CNN benefits from a larger amount of training data, the RFC is widely unaffected by this. For the RFC, a certain variety in training data seems to be sufficient for reaching an optimal efficacy.
5.5. Transfer between Pop and Opera Datasets
We finally compare system results when training on datasets from another genre of music. Specifically, we use the
Jamendo dataset already discussed in
Section 3. We expect generalization between the pop and opera styles to be poor, since SVD methods are known to be heavily genre specific [
11] and, in particular, opera singers employ singing techniques that are distinct from those found in Western pop music. Consequently, when training on the
Jamendo training corpus and evaluating on our own test set, we observe a low F-measure of
for the RFC (not better than random choice) and a medium result of
for the CNN. When using the training set of the full
neither split of our dataset (see
Figure 2) and testing on the
Jamendo test set instead, we obtain
for the RFC and
for the CNN. Thus, generalizing from opera to pop works better for the RFC and worse for the CNN, but genre-specific overfitting is evident in both scenarios.
6. Conclusions
Summarizing our experimental findings, we conclude that machine-learning approaches both relying on traditional techniques and on deep learning are useful for building well-performing SVD systems, which are capable of generalizing to unseen musical works, versions, or both at the same time. Both systems achieve F-measures in the order of 0.94 and their results do not drop below 0.91, even when considering training datasets with little musical or acoustic variety. While these are strong results for a challenging SVD scenario, we find a tendency of both systems to overfit to the specific musical material in the training set. Moreover, we observe that both systems benefit from a certain amount of acoustic variety in the training dataset. Nevertheless, overfitting to musical or acoustic characteristics does not lead to complete degradation of results in our scenario. For practical applications, the traditional approach based on random forest classifiers requires less resources and training time and is more robust to random effects of different training runs. In contrast, the CNN-based method leads to slightly better results in most scenarios, especially when a large training dataset is available.
In a manual analysis, we could trace back most of the remaining errors made by our systems to difficult situations where annotation errors and musical ambiguities play a major role. One source of such ambiguity is the discrepancy between a phrase-based and a note-based consideration of singing voice segments, i.e., the question whether a short musical rest within a singing phrase should be considered as singing. Further ambiguities arise about whether to include breathing as singing, or how to deal with choir passages. In the present study, breathing is mostly excluded from singing since our semi-automatic transfer relies on chroma features. Choir passages are included as singing but only occur in acts D2 and D3. However, as our annotations are based on phrases in the libretto, we could not differentiate, e.g., between silence and singing within sung phrases. Manual annotation could provide more accurate ground truth but is only feasible for smaller datasets. These and other challenges of annotation indicate that both systems are already close to a “glass ceiling” of SVD efficacy, where the definition of the task itself becomes problematic.
Such encouraging results close to the “glass ceiling” cannot generally be expected for other MIR tasks such as, e.g., the recognition of a specific register (soprano, mezzo, alto, tenor, baritone, or bass) or even a specific singer or character (such as Siegfried or Sieglinde). The hand-crafted features used in the RFC-based system have been specifically designed to work well for SVD and may not perform equally well on such more advanced tasks. Thus, deep learning based-approaches may yet outperform classical systems in those contexts. Therefore, it may be promising to extend our studies to such further tasks and to more complex scenarios (including other composers and genres). More generally, the experimental procedures presented in this paper can be applied to various domains of audio and music processing where different data splits are possible. In future work, these procedures may contribute to understanding the benefits of deep learning against traditional machine learning and to identifying the aspects of training data that are relevant for building robust systems.