Estimating Software Development Efforts Using a Random Forest-Based Stacked Ensemble Approach

Abstract

Software Project Estimation is a challenging and important activity in developing software projects. Software Project Estimation includes Software Time Estimation, Software Resource Estimation, Software Cost Estimation, and Software Effort Estimation. Software Effort Estimation focuses on predicting the number of hours of work (effort in terms of person-hours or person-months) required to develop or maintain a software application. It is difficult to forecast effort during the initial stages of software development. Various machine learning and deep learning models have been developed to predict the effort estimation. In this paper, single model approaches and ensemble approaches were considered for estimation. Ensemble techniques are the combination of several single models. Ensemble techniques considered for estimation were averaging, weighted averaging, bagging, boosting, and stacking. Various stacking models considered and evaluated were stacking using a generalized linear model, stacking using decision tree, stacking using a support vector machine, and stacking using random forest. Datasets considered for estimation were Albrecht, China, Desharnais, Kemerer, Kitchenham, Maxwell, and Cocomo81. Evaluation measures used were mean absolute error, root mean squared error, and R-squared. The results proved that the proposed stacking using random forest provides the best results compared with single model approaches using the machine or deep learning algorithms and other ensemble techniques.

1. Introduction

Software engineering follows a systematic and cyclic approach in developing and maintaining the software [1]. Software engineering solves problems related to the software life-cycle. The life cycle of software consists of the following phases:

⮚

Inception phase

⮚

Requirement phase

⮚

Design phase

⮚

Construction phase

⮚

Testing phase

⮚

Deployment phase

⮚

Maintenance phase

Figure 1 shows the schematic diagram of SDLC phases. During the inception phase, the following are the works carried out by the project team: project goal identification, carrying out various project estimations [2], and identification of the scope of the project. During the requirement or planning phase, user needs are analyzed, and functional and technical requirements are identified. During the design phase, the establishment of architecture is carried out by considering the requirements as input.

Figure 1. Software Development Life Cycle (SDLC) phases.

In the construction phase, implementation of the project was carried out. During the starting stage of the Construction Phase, a prototype model was developed. Later, the prototype was implemented as a working model. In the testing phase, identification of bugs, errors, and defects was carried out and, finally, the software was assessed for quality. After successful testing of the software, it moved onto the deployment phase wherein the software was released into the environment for the usage of end-users. During the maintenance phase, the feedback from the end-users was received and software enhancement was carried out by the developers.

Estimation, which is the process of finding the approximation or estimate, was performed during the initial stage with several uncertain and unstable data. Estimations were used as input for planning the project, for iteration planning, investment analysis, budget analysis, and etc. [2]. Estimation identifies the size, as well as the amount of time, effort of human skill, money, [3] and resources [4] required to build a system or product. Though several models have been developed for the past two decades, effort estimation remains a challenging tasks, as there are more uncertain and unstable data during the initial stages of software development. Software effort estimation [5] is performed in terms of person-hours or person-months.

Software effort estimations are carried out using the following techniques [6]: expert judgment, analogy-based estimation, function point analysis, machine-learning techniques comprising of regression techniques, classification approaches and clustering methods, neural network and deep learning models, fuzzy-based approaches, and ensemble methods.

Initially, software effort estimation is performed based on expert judgment [7] rather than using a model approach. It is a simple way to implement estimation, and also produced realistic estimations. Delphi technique and work breakdown structure are the most prevalent expert judgment techniques used for estimation. In the Delphi technique, a meeting is conducted among the project experts and, from the arguments during the meeting, the final decision about the estimation is made. In the work breakdown structure, the entire project is broken down into sub-projects or sub-tasks. The process is continued until the baseline activities are reached.

Analogy-based estimation to predict effort was performed based on similar past projects. It also produced accurate results as it was based on past data. Function point analysis approaches were used for effort estimation, which consider the number of functions required for developing software. Various machine learning techniques like regression, classification, and clustering approaches created a large impact in predicting software effort. Various regression techniques used for effort estimation were linear regression (single and multiple linear regressions), logistic regression, elastic net regression, ridge regression, LASSO regression and stepwise regression [8].

Linear regression is a best-fit straight line that is produced as the relationship between dependent and independent variables. The difference between the estimated value and observed value is called an error. Generally, the error must be minimized.

The estimated value is provided as

$$Y{}^{\prime }=b_0+b_{1}X$$

(1)

In Equation (1), b₀ is the Y-intercept, X is the independent variable and b₁ is the slope of the line, which is provided by Equation (2),

$$b_1=\frac{{\displaystyle \sum _{}^{}}\left(X-\overline{X}\right)\left(Y-\overline{Y}\right)}{\left({\displaystyle \sum _{}^{}{(X-\overline{X})}^2}\right)}$$

(2)

Multiple linear regression is the extension of linear regression. It uses ‘p’ number of independent or predictor variables.

The estimated value denoted as Y′ is provided as follows:

$$Y{}^{\prime }=b_0+b_1{X}_1+\dots +b_p{X}_p+\in$$

(3)

In Equation (3), b₀, b₁…b_p denote the coefficients, X₁, X₂…X_p denote predictor variables and $\in$ denotes the error.

Logistic regression produces solutions only to linear problems. The sigmoid function, which is also said to be a logistic function, is provided as follows:

$$Y=\frac{1}{1+e^{-Y^{\prime }}}$$

(4)

In Equation (4), $Y{}^{\prime }=b_0+b_1{X}_1+\dots +b_p{X}_p+\in$, b₀, b₁,…,b_p denote the coefficients, X₁, X₂,…X_p denote predictor variables and $\in$ denotes the error.

In ridge regression, L2 regularization techniques are used to minimize the error between actual and predicted value. A huge number of input variables can be used, but produce high bias. LASSO (Least Absolute Shrinkage and Selection Operator) regression uses the L1 regularization technique. LASSO avoids overfitting problems. Elastic net type is the combination of the LASSO and ridge regression methods [9].

In forward selection regression, the operation starts with the most important predictor variable; there will be a step-by-step increase in the predictor variables. In backward elimination regression, initially, all the predictor variables are included and, at every step, predictors of least significance are removed.

Various classification approaches used for estimation were the decision tree method, random forest approach, SVM classifier, KNN algorithm, and Naïve Bayes approach. The decision tree is a simple method, and is subjected to overfitting for a smaller training dataset. Random forest is the extension of the decision tree, and is an optimal and accurate algorithm compared with the decision tree approach; it is robust against overfitting. SVM [10] is best for linear, non-linear, structured, semi-structured, and unstructured data. KNN is a statistical approach.

KNN is sensitive to noise. The Naïve Bayes approach is based on Bayes theorem and produces a good result if the input variables are independent from one another. In the clustering-based approach, clusters are points with similar data. Hierarchical clustering, K-means clustering, and subtractive clustering were the approaches used for effort estimation.

Neural network [11] and deep learning models used for Effort Estimation were a multi-layer feed forward neural network, a radial basis neural network, a cascaded neural network [12], and Deepnet. The neural network model used a layered approach and a back propagation algorithm. It is suitable for linear and non-linear data, but an overfitting problem occurs. Fuzzy-based approaches are sensitive to outlier data. Mostly fuzzy logic models [13] are combined with other machine learning models for software effort estimation.

Ensemble Techniques are robust predictive models [14]. It provides better accurate results when compared to an existing individual machine or deep learning models. In the ensemble technique, multiple models (called as base learners) are combined to provide better results. Ensemble techniques considered for estimation [15,16] are Averaging, Weighted Averaging, Bagging, Boosting and Stacking.

• Averaging: It is performed by taking the average of prediction from a single model.
• Weighted Average: It is calculated by applying different weights to different single models, based on their prediction and finally taking the average weighted predictions.
• Bagging: It is otherwise called Bootstrap aggregation, a kind of sampling technique. Multiple samples are considered from the original dataset and similar to random forest techniques.
• Boosting: It uses a sequential method to reduce the bias. Various boosting algorithms used are XGBoost (eXtreme Gradient Boosting), GBM (Gradient Boosting Machine), AdaBoost (Adaptive Boosting).
• Stacking: Stacking does prediction from multiple models and builds a novel model.

2. Related Work

Software effort estimations are mostly carried out using the following techniques: expert judgment, analogy-based estimation, function point analysis, various machine learning techniques, which include regression techniques, classification approaches and clustering methods, neural network and deep learning models [17], fuzzy-based approaches, and ensemble methods. Table 1 describes the survey of software effort estimation using various algorithms, datasets used for estimation, evaluation measures, and findings from each paper.

Table 1. Software Effort Estimation Analysis.

Existing Work	Datasets	Algorithm	Evaluation Measures	Findings
Idri et al. [18]	Desharnais, ISBSG (International Software Benchmarking Standards Group), Albrecht, COCOMO, Kemerer, Maxwell, Abran, and Telecom	Analogy-based software effort estimation (ASEE)	(MMRE)-Mean Magnitude of Relative Error (MdMRE)-Median Magnitude of Relative Error (Pred(25)-Prediction percentage with an MRE less than or equal to 25%	The authors compared analogy-based software effort estimation (ASEE) with eight ML and Non-ML techniques such as the COCOMO model, regression, expert judgment, artificial neural network, function point analysis, support vector regression, decision trees, and radial basis function. From the results, the ASEE technique outperformed eight techniques and provided more accuracy based on the three evaluation measures, namely MMRE, MdMRE, and Pred(25). Several techniques such as fuzzy logic, genetic algorithm, expert judgment, artificial neural network, etc., are combined with ASEE methods. Fuzzy logic and genetic algorithm combined with ASEE provided good results compared with other combined techniques. It was found that estimation accuracy increased when ML and Non-ML techniques were combined with the ASEE technique.
Suresh Kumar et al. [19]	Commonly used datasets: COCOMO, NASA, and ISBSG	Analysis of SEE using artificial neural network algorithms (ANN)	Commonly used metrics:(MMRE)-Mean Magnitude of Relative Error, (MRE)-Mean Relative Error	In this paper, analysis of software effort estimation using various ANN algorithms such as a higher-order neural network, basic NN and a deep learning network was carried out. This paper mainly focused on comparing the quantitative and qualitative analysis of the papers under software effort estimation. They also created a survey on the following aspects: the most frequently used datasets for prediction, most frequent hybrid algorithm considered for prediction, and most-used evaluation measures, namely MMRE, MdMRE, and MRE.
Fedotova et al. [20]	Real time data of a mid-level multinational software development company	Multiple linear regression (MLR)	(MRE)-Mean Relative Error (MMRE)-Mean Magnitude of Relative Error, Pred(x)-Prediction percentage with an MRE less than or equal to x%	The project was carried out using a real-time dataset of a medium-sized multinational organization. This paper compared multiple linear regression (MLR) with the expert judgment method; MLR produced good results compared with expert judgment. Evaluation metrics considered were MRE, MMRE, and Pred(x).
Abdelali et al. [21]	ISBSG R8, Tukutuku, and COCOMO.	random forest	Pred(0.25), MMRE, and MdMRE	In this paper, the random forest algorithm was compared with the regression tree model. Before using the random forest algorithm, they explored the impact of the number of trees and the number of attributes to accuracy and found accuracy was sensitive to these parameters. Finally, the optimized random forest outperformed the regression tree algorithm.
Nassif et al. [22]	ISBSG 10 Desharnais	Decision tree, decision tree forest, andmultiple linear regression	Pred(0.25), MMRE and MdMRE	The decision tree forest model was compared with the traditional decision tree model and multiple linear regression. The evaluation was performed using ISBSG and Desharnais datasets. Decision tree uses a recursive partitioning approach, whereas the decision tree forest model is a collection of decision trees that are grown in parallel. The decision tree forest model outperformed the decision tree model and multiple linear regressionwhen the evaluation measures used were MMRE, MdMRE, and PRED (0.25).
Corazza et al. [23]	TUKUTUKU Dataset	Support Vector Regression	(Pred(25)) (MEMRE)-Mean Magnitude of Relative Error relative to the estimate (MdEMRE)-Median Magnitude of Relative Error relative to the estimate.	The authors compared Support Vector Regression (SVR) with step-wise, case-based reasoning and Bayesian network; SVR outperformed the other compared algorithms. Four kernel methods of SVR were considered for estimation, namely linear, Gaussian, polynomial, and sigmoid. Two preprocessing methods, namely logarithmic and normalization approaches, were carried out over the dataset. Final results showed that SVR with linear kernel and logarithmic transformation provides better results.
Bhaskar [24]	COCOMO81, COCOMO Nasa, and COCOMO Nasa2	Linear regression and K nearest neighbor	Mean squared error (MSE) and Mean magnitude relative error (MMRE)	In this paper, the authors proposed that linear regression and K nearest neighbor (KNN) algorithms forecasted the effort accurately. The advantage of linear regression is it is fast at training the data and it produces good results when the output attribute is linear to the input attribute. KNN algorithms are preferred when there is less past knowledge regarding the data description.
Amjad et al. [25]	NASA Dataset	Naïve Bayes, support vector machine, K nearest neighbor, decision trees	F1, Precision and Recall	Software defect prediction was carried out using Naïve Bayes, support vector machine, K nearest neighbor (KNN), and decision trees. KNN is a simple model, and uses a statistical approach; Naïve Bayes is a probabilistic model that uses the Bayes theorem; and decision trees uses the recursive partitioning approach and SVM used for both structured and unstructured data. In this paper, the NASA dataset was used and the Naïve Bayes algorithm outperformed the support vector, KNN, and decision tree.
Wu et al. [26]	Desharnais, Cocomo81, Maxwell, China, Nasa93, and Kemerer	Hierarchical clustering for analogy-based software effort estimation (ABE)	MMRE-Mean Magnitude Relative Error	The research was carried out using analogy-based software effort estimation (ABE), which uses case-based reasoning that depends on the K value (K-th similar project that is completed over the past). The hierarchical clustering technique was used to identify the optimized set of K values. The proposed hierarchical clustering to the ABE method showed good improvement to ABE.
Sree et al. [27]	NASA 93	Fuzzy model using subtractive clustering	Variance Accounted For(VAF) Mean Absolute Relative Error(MARE) Variance Absolute relative Error(VARE) Mean Balance Relative Error(Mean BRE) Mean Magnitude of Relative Error(MMRE) Prediction	In this paper, the fuzzy model using subtractive clustering used three rules and provided better estimates compared with cascading the fuzzy logic controller. The computational time for fuzzy logic controller was higher because the rule base was quite large. To reduce the rule base, cascading fuzzy logic controllers were used and to find the correct number of cascading, a subtractive clustering method was employed.
Rijwani et al. [28]	COCOMO II	Multi-layered feed forward artificial neural network	Mean-Square-Error (MSE) and Mean Magnitude of Relative Error (MMRE)	Artificial Neural Network (ANN) can handle complex datasets with various dependent and independent variables. Multi-layered Feed Forward ANN with backpropagation method is employed over here. Multi-layered Feed Forward ANN provided better results and accuracy in forecasting effort.
Nassif et al. [29]	International Software Benchmarking Standards Group (ISBSG)	Multilayer perceptron; general regression neural network; radial basis function neural network; cascade correlation neural network	Mean Absolute Residual (MAR)	Models considered for estimation are General Regression Neural Network, Multilayer Perceptron, Radial Basis Function Neural Network and Cascade Correlation Neural Network. In comparison with the four models, 3 models overestimate the accuracy and Cascade Correlation Neural Network outperforms other compared algorithms. ISBSG dataset is used for estimation.
Pospieszny et al. [30]	ISBSG 1192 projects 13 attributes	ensemble averaging of 3 ML models -SVM(support vector machines) MLP(multi- layer perceptron) -GLM(general linear model)	MAE, MSE, and RMSE MMRE PRED MMER- Mean magnitude relative error to estimate MBRE-mean of balanced relative error	The dataset used for estimation was the ISBSG dataset. Ensemble averaging of three machine learning algorithms was used for estimation. Three models considered for ensemble averaging were SVM (support vector machines), MLP (multi-layer perceptron), and GLM (general linear model). In ensemble, multiple base learners’ models were combined for effort estimation. The ensemble model outperformed the single models.
Mensah et al. [31]	Github: Albrecht Telecom PROMISE: China Cocomo Cocomonasa1 Cocomonasa Cosmic Desharnais Kemerer Kitchenham Maxwell Miyazaki Industry:php_projects	Regression-based effort estimation techniques: ordinary least squares regression (OLS), stepwise regression (SWR), ridge regression (RR), LASSO regression, elastic net regression,	Mean Absolute Error(MAE), Balanced Mean Magnitude of Relative Error (BMMRE) and Adjusted R2	Software Effort Estimation models incur a drawback in prediction termed conclusion instability. In this paper, 14 datasets are considered for estimation and based on the effort attribute each dataset are grouped into three classes namely high, low and medium which is considered as the first output and again to the effort classes, six regression models were applied to predict accuracy which is considered as the second output. Elastic net regression outperformed the other compared algorithms.
Prerna et al. [32]	cocomo81 and nasa93	differential evolution (DE) approach	MMRE	The differential evolution (DE) approach was applied over COCOMO and COCOMO II models for the datasets from the PROMISE repository. DE approach produced less computational complexity and less memory utilization. The Proposed DE-based COCOMO and COCOMO II approach provided better effort estimates compared with the original COCOMO and COCOMO II models.

3. Mathematical Modeling

3.1. Software Effort Estimation Evaluation Metrics

3.1.1. Mean Absolute Error (MAE)

It is the average sum of absolute errors.

$$\mathrm{Prediction}\mathrm{error}=y_i-{\widehat{y}}_i$$

(5)

Absolute error = |Prediction error|

MAE = average of all absolute errors.

$$\mathrm{MAE}={\displaystyle \sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|}$$

(6)

In Equation (6), ‘n’ is the total number of data points, $y_i$ is the original value, and ${\widehat{y}}_i$ is the predicted value.

3.1.2. Root Mean Square Error (RMSE)

The root mean square error is the measure of the standard deviation of the predicted deviation.

$$\mathrm{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}}$$

(7)

In Equation (7), ‘n’ is the total number of data points, $y_i$ is the original value, and ${\widehat{y}}_i$ is the predicted value.

3.1.3. R-Squared

R-squared is a statistical measure that finds the proportion of variance in the dependent variable that is predicted from the independent variable. The R-squared is found by dividing the residual sum of squares (RSS) by the total sum of squares (TSS); then, it is subtracted from 1, as provided by Equation (8). RSS is the average squared error between original values y and $\widehat{y}$. TSS is the squared Error between original value ‘y’ and the average of all ‘y’. The R-squared value ranges between 0 and 1. The model is preferable if the R-squared value is nearer or equal to 1. Here, a negative R-value indicates there is no correlation between the data and the model. It is also known as the co-efficient of determination.

$$\mathrm{R}\text{-}\mathrm{Squared}=1-\frac{RSS}{TSS}$$

(8)

where RSS is the residual sum of squares and TSS is the total sum of squares.

3.2. Proposed Stacking Using Random Forest for Estimation

Ensemble techniques were used to create multiple models termed base-level classifiers; they were combined to produce better predictions as compared with single-level models. There are several techniques used under ensembling, namely averaging, weighted averaging, bagging, boosting, and stacking. Proposed stacking using random forest was compared with other stacking techniques such as generalized linear model (S-GLM), stacking using decision tree (S-DT), stacking using support vector machine (S-SVM), and stacking using the random forest (S-RT) in Section 5.1. Various ensemble techniques and single-level models were compared with the proposed stacking using the random forest model in the prediction of software effort in Section 5.2. Algorithm 1 provided below explains the pseudocode of proposed stacking using random forest.

Algorithm 1. Pseudocode of proposed stacking using random forest.

1. Input: Training data, Dtrain =$\left\{a_i,b_i\right\}$ where $a_i$ = Input attributes, $b_i$ = Output attribute, i = 1 to n, n = Number of base classifiers.

2. Output: Ensemble classifier, E

3. Step 1: Learn about base-level classifiers

(Apply first-level classifier)

Base-level classifiers considered were svmRadial, decision tree (rpart), RandomForest(rf), and glmnet

4. for t = 1 to T do

5. learn $e_t$ based on Dtrain

6. end for

7. Step 2: Build a new dataset for predictions based on the output of the base classifier with the new dataset

8. for i = 1 to n do

9. $Dtrai{n}_e=\left\{a_i{}^{\prime },b_i\right\};$

where $a_i{}^{\prime }=\left\{e_1(a_i),\dots \dots ,e_T(a_i)\right\}$

10. end for

11. Step 3: Learn a meta classifier. Apply second-level classifier for the new dataset

Random Forest(rf) applied over the stacked base classifiers svm Radial, rpart, rf and glmnet (Figure 2)

12. Learn E based on $Dtrai{n}_e$

13. Return E (ensemble classifier)

14. Predicted software effort estimation evaluation metrics using the ensemble approach are as follows:

15. Mean absolute error (MAE) = ${\displaystyle \sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|}$

where ‘n’ is the total number of data points, $y_i$ is the original value and ${\widehat{y}}_i$ is the predicted value.

16. Root mean squared error (RMSE) = $\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}}$

where ‘n’ is the total number of data points, $y_i$ is the original value, and ${\widehat{y}}_i$ is the predicted value.

17. R-squared=$1-\frac{RSS}{TSS}$, where RSS is the residual sum of squares and TSS is the total sum of squares.

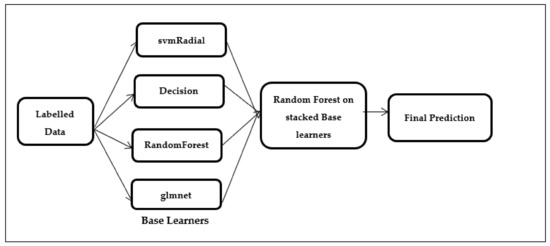
Figure 2. Stacked random forest (SRF).

In Step 1, load the required packages and dataset. Set the seed function to ensure that we acquire the same result when the same seed is used to run the same process. As the numerical attributes have different scaling range and units, the statistical technique is used to normalize the data. The summary() command is used to find the different scaling ranges of the attributes. To normalize the data, a preprocessing method is used with the range as the factor. After normalization, the range of values are within 0 to 1. Method trainControl() is used, which specifies the cross-validation method used and, by setting class probability as True, it generates probability values as a replacement of directly forecasting the class.

The first-level classifiers considered were svmRadial, decision tree (rpart), RandomForest (rf), and glmnet as they had correlation values less than 0.85. Sub-models having less correlation suggested that the model is better and allows for the production of new classifiers. The resamples() method was used to evaluate multiple machine learning models. The dotplot(), which is a graphical representation of the results, was also obtained. In Step 2, a new dataset was obtained based on the evaluation of the first-level classifiers, namely svmRadial, decision tree (rpart), RandomForest (rf), and glmnet.

In Step 3, second-level classifiers were applied. Figure 2 shows that four different stackings of second level classifiers were done, namely the stacking of the generalized linear model over the baseline classifiers, the stacking of decision tree over baseline classifiers, the stacking of support vector machine over the baseline classifiers, and the stacking of random forest over the baseline classifiers.

4. Data Preparation

Software effort estimation was predicted using seven benchmarked datasets. Datasets were checked for missing values, and feature selection was performed based on highly correlated values in each dataset. Single base learner algorithms were compared with ensemble techniques. Proposed stacked ensemble using random forest was relatively effective compared with all other methods. Evaluation measures employed were mean absolute error, root mean square error, and R-squared.

Software Effort Estimation Datasets

Attributes and records of the datasets are elaborated in Table 2. Datasets considered for software effort estimation were Albrecht, China, Desharnais, Kemerer, Kitchenham, Maxwell, and Cocomo81. The Albrecht dataset consisted of 8 attributes and 24 records, the China dataset consisted of 16 attributes and 499 records, the Desharnais dataset consisted of 12 attributes and 81 records, the Kemerer dataset consisted of 7 attributes and 15 records, the Maxwell dataset consisted of 26 attributes and 62 records, the Kitchenham dataset consisted of 9 attributes and 145 records, and the Cocomo81 dataset consisted of 17 attributes and 63 records. The output attributes of the datasets Albrecht, Kemerer, and Cocomo81 were in the units of person-months. The datasets China, Desharnais, Maxwell, and Kitchenham were in the unit of person-hours.

Table 2. Dimensions of the dataset.

Dataset Name	Source Repository	No. of Records	No. of Attributes	Output Attribute-Effort (Unit)
(i) Albrecht	PROMISE	24	8	Person-months
(ii) China	PROMISE	499	16	Person-hours
(iii) Desharnais	GITHUB	81	12	Person-hours
(iv) Kemerer	GITHUB	15	7	Person-months
(v) Maxwell	PROMISE	62	27	Person-hours
(vi) Kitchenham	GITHUB	145	9	Person-hours
(vii) Cocomo81	GITHUB	63	17	Person-months

Table 3 provides the original attributes, description and attributes considered after feature selection for the datasets: Albrecht, China, Desharnais, Kemerer, Maxwell, Kitchenham and Cocomo81. Attributes having a high correlation values are considered after feature selection.

Table 3. Datasets – Original attributes and attributes considered after Feature selection.

Datasets Name	Attributes and Description		Attributes Considered after Feature Selection
Albrecht	InputNumeric	Count of input functions	⮚ OutputNumeric ⮚ InquiryNumeric ⮚ RawFPcounsNumeric ⮚ AdjfpNumeric ⮚ Effort
	OutputNumeric	Count of output functions
	InquiryNumeric	Count of query functions
	FileNumeric	Count of file processing
	FPAdjNumeric	Function point
	RawFPcounsNumeric	Raw function points
	AdjfpNumeric	Adjusted function points
	Effort	Effort in person-months
China	AFP	Adjusted function points	⮚ AFP ⮚ Output ⮚ File ⮚ Interface ⮚ Added ⮚ PDR_AFP ⮚ NPDR_AFP ⮚ NPDU_UFP ⮚ N-Effort ⮚ Effort
	Input	Function points of input
	Output	Function points of external output
	Enquiry	Function points of external output enquiry
	File	Function points of internal logical files
	Interface	Function points of external interface added
	Added	Function points of added functions
	Changed	Function points of changed functions
	PDR_AFP	Productivity delivery rate(adjusted function points)
	PDR_UFP	Productivity delivery rate(Unadjusted function points)
	NPDR_AFP	Normalized productivity delivery rate(adjusted function points)
	NPDU_UFP	Productivity delivery rate(Unadjusted function points)
	Resource	Team type
	Duration	Total elapsed time for the project
	N-Effort	Normalized effort
	Effort	Summary work report
Desharnais	Project	Project number	⮚ Transactions ⮚ PointsNonAdjust ⮚ PointsAjust ⮚ Effort
	TeamExp	Team experience in years
	ManagerExp	Project manager’s experience in years
	YearEnd	Year of completion
	Length	Length of the project
	Transactions	Number of transactions processed
	Entities	Number of entities
	PointsNonAdjust	Unadjusted function points
	Adjustment	Adjustment factor
	PointsAjust	Adjusted function points
	Language	Programming language
	Effort	Measured in person-hours
Kemerer	Language	Programming language	⮚ Duration ⮚ KSLOC ⮚ AdjFP ⮚ RawFP ⮚ Effort
	Hardware	Hardware resources
	Duration	Duration of the project
	KSLOC	Kilo lines of code
	AdjFP	Adjusted function points
	RawFP	Unadjusted function points
	Effort	Measured in person-months
Maxwell	Year	Time	⮚ Year ⮚ Source ⮚ Nlan ⮚ T05 ⮚ T09 ⮚ T15 ⮚ Duration ⮚ Size ⮚ Time ⮚ Effort
	App	Application type
	Har	Hardware platform
	Dba	Database
	Ifc	User interface
	Source	Where developed
	Telonuse	Telon use
	Nlan	Number of development languages
	T01	Customer participation
	T02	Development environment adequacy
	T03	Staff availability
	T04	Standards use
	T05	Methods use
	T06	Tools use
	T07	Software logical complexity
	T08	Requirements volatility
	T09	Quality requirements
	T10	Efficiency requirements
	T11	Installation requirements
	T12	Staff analysis skills
	T13	Staff application knowledge
	T14	Staff tool skills
	T15	Staff team skills
	Duration	Duration (months)
	Size	Application size (FP)
	Time	Time taken
	Effort	Work carried out in person-hours
Kitchenham	Clientcode	Client code {1,2,3,4,5,6}	⮚ Duration ⮚ Adjfp ⮚ Estimate ⮚ Effort
	Projecttype	Project Type {A,C,D,P,Pr,U}
	Startdate	Starting date of the project
	Duration	Duration of the project
	Adjfp	Adjusted function points
	Completiondate	Completion date of the project
	Estimate	Effort estimate
	Estimate method	Estimate method {A,C,CAE,D,EO,W}
	Effort	Work carried out in person-hours
Cocomo81	Rely	Required software reliability	⮚ Rely ⮚ Data ⮚ Time ⮚ Stor ⮚ Acap ⮚ Modp ⮚ Sced ⮚ Loc ⮚ Effort
	Data	Database size
	Cplx	Complexity of product
	Time	Time constraint
	Stor	Storage constraint
	Virt	Virtual machine volatility
	Turn	Computer turnaround time
	Acap	Analyst capability
	Aexp	Application experience
	Pcap	Programmer capability
	Vexp	Virtual machine experience
	Lexp	Programming language experience
	Modp	Modern programming practices
	Tool	Software tools use
	Sced	Development schedule
	Loc	Lines of code
	Effort	Work carried in person-months

5. Results and Discussion

For effort prediction, the datasets considered were Albrecht, China, Desharnais, Kemerer, Maxwell, Kitchenham, and Cocomo81. The evaluation measures considered were mean absolute error (MAE), root mean square error (RMSE), and R-squared value. It was found that the lesser the values of MAE and RMSE, the better the model; additionally, if the R-squared value was closer to 1, it was the better model. Various ensemble techniques available were averaging, weighted averaging, bagging, boosting, and stacking. Single models considered for comparison were random forest, SVM, decision tree, neural net, ridge, LASSO, elastic net and deep net algorithms.

5.1. Stacking Models

Herein, stacking built a novel model from multiple classifiers. The various stacking models considered for evaluation were stacking using generalized linear models (S-GLM), stacking using decision tree (S-DT), stacking using support vector machine (S-SVM), and stacking using random forest (S-RT).

For the stacking model approaches, the first-level classifiers considered were svmRadial, decision tree (rpart), RandomForest(rf), and glmnet. A new dataset was obtained based on the evaluation of the first-level classifiers. Four different stacking models were used as the second-level classifiers individually over the baseline (first-level) classifiers. They were stacking of generalized linear model, stacking of decision tree, stacking of support vector machine, and stacking of random forest; they were are individually applied as the second level-classifiers over the baseline classifiers. MAE, RMSE, and R-squared values were predicted for all the four stacked model approaches. The stacking model was considered a better model if it produced fewer errors (MAE and RMSE) and if the R-squared value was nearer to 1.

Based on the inference from Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9, stacking using random forest produced less errors (MAE & RMSE) compared with other stacking models; the R-squared values were also closer to 1.

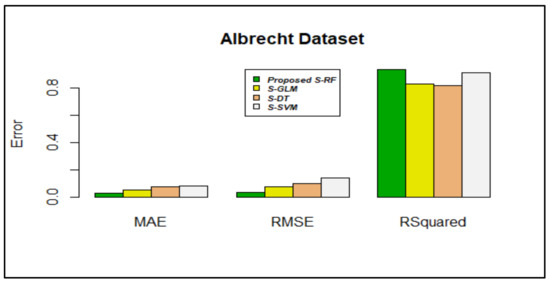
Figure 3. Error rate vs. stacking models in the Albrecht dataset.

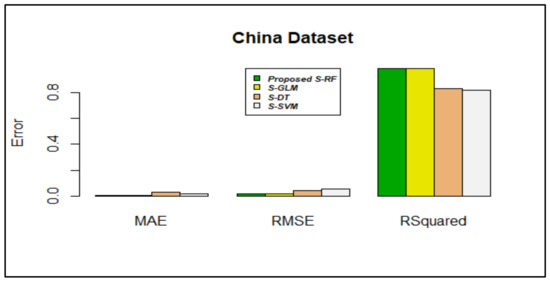
Figure 4. Error rate vs. stacking models in the China dataset.

Figure 5. Error rate vs. stacking models in the Desharnais dataset.

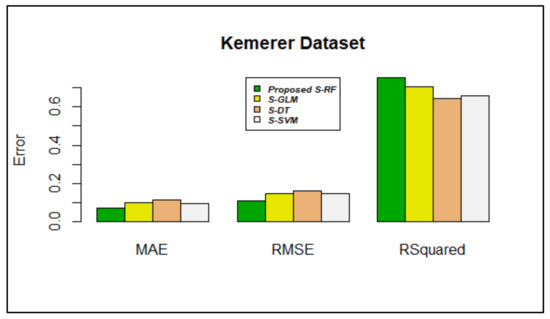
Figure 6. Error rate vs. stacking models in the Kemerer dataset.

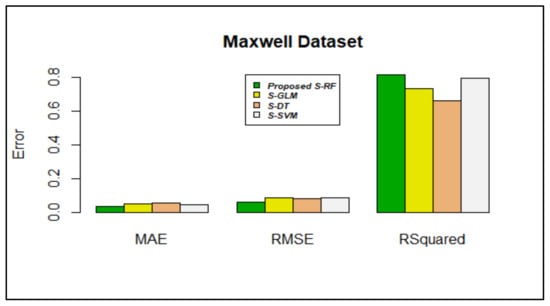
Figure 7. Error rate vs. stacking models in the Maxwell dataset.

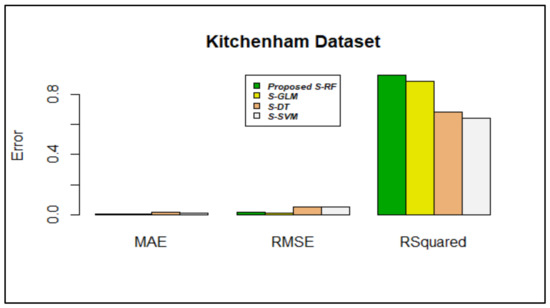
Figure 8. Error rate vs. stacking models in the Kitchenham dataset.

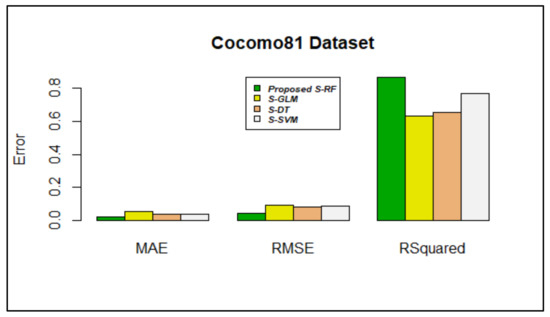
Figure 9. Error rate vs. Stacking models in Cocomo81 dataset.

Figure 3 shows that stacking using RF produces less value in terms of MAE and RMSE, which were 0.0288617 and 0.0370489, respectively. The value of R-squared is preferred to be nearer to 1; compared with other stacking algorithms, the R-squared value was nearer to 1(0.9357274) in the proposed stacking using the RF algorithm.

Figure 4 shows that stacking using RF produced less error, MAE (0.004016189), and RMSE (0.01562433) compared with other algorithms. For a better predictive model, the R-squared value should be closer to 1; in stacking using RF, the R-squared value (0.9839643) was closer to 1.

In the Desharnais dataset, MAE and RMSE values of stacking using RF produced less error values, 0.07027704 and 0.1072363, respectively; the R-squared value is 0.6556170. As shown in Figure 5, compared with other stacking algorithms, the proposed algorithm provided better results.

Figure 6 shows that stacking using random forest produced lower MAE (0.07030604) and RMSE (0.1094053) values. The r-squared value (0.7520435) was also closer to 1.

Figure 7 shows that stacking using RF produced lower MAE (0.03566583) and RMSE (0.06379541) values compared with other algorithms. The R-squared value (0.8120214) was also closer to 1.

In the Kitchenham dataset, MAE and RMSE values of stacking using RF produced less error values, 0.005384577 and 0.01505940, respectively; the R-squared value was 0.9246614. Figure 8 shows that, compared with other algorithms, the proposed algorithm provided better results.

Figure 9 shows that stacking using RF produced lower MAE and RMSE values, as 0.02278088 and 0.04415005, respectively. The value of R-squared was preferred to be nearer to 1; compared with other algorithms, the R-squared value is nearer to 1 (0.8667750) in proposed stacking using the RF algorithm.

5.2. Proposed Stacking Using Random Forest against Single Base Learners and Ensemble Techniques for Estimation

Single base learners considered for estimation were random forest (RF), support vector machine (SVM), decision tree (DT), neural net (NN), ridge regression (Ridge), LASSO regression (LASSO), elastic net regression (EN), and deep net (DN) and ensemble techniques including averaging (AVG), weighted averaging (WAVG), bagging (BA), boosting (BS), and stacking using RF (SRF). The software used for estimation was RStudio. Evaluation measures considered were mean absolute error (MAE), root mean square error (RMSE), and R-squared.

Ensemble approaches considered for comparison were averaging, weighted averaging, bagging, boosting, and stacking using RF. Single models considered for comparison were random forest, SVM, decision tree, neural net, ridge regression, LASSO regression, elastic net, and deep net algorithms.

Table 4 shows the mean absolute error values for the base learners and ensemble approaches against seven datasets. Out of all compared 12 algorithms, the proposed stacking using random forest produced minimal error values (mean absolute error) for all seven datasets. Based on the inference from Table 4, mean absolute error value of the proposed stacking using random forest was lower when compared with all other considered algorithms against seven datasets. The values of the proposed stacking using RF model were 0.0288617, 0.004016189, 0.07027704, 0.07030604, 0.03566583, 0.005384577, and 0.02278088 for the datasets Albrect, China, Desharnais, Kemerer, Maxwell, Kitchenham, and Cocomo81, respectively. The values suggest that the proposed stacking using the RF model produced lower MAE only when compared with other base learner algorithms such as random forest, SVM, decision tree, neural net, ridge regression, LASSO regression, elastic net, and deep net and other ensemble approaches including averaging, weighted averaging, bagging, and boosting.

Table 4. Base learners and ensemble techniques vs. MAE of 7 datasets.

Mean Absolute Error (MAE)
Algorithms	Dataset 1 Albrecht	Dataset 2 China	Dataset 3 Desharnais	Dataset 4 Kemerer	Dataset 5 Maxwell	Dataset 6 Kitchenham	Dataset 7 Cocomo81
Random Forest	0.1940703	0.03832486	0.1161946	0.2076936	0.2330224	0.1047124	0.06047924
SVM	0.271210	0.04872961	0.1052762	0.219517	0.311288	0.1189372	0.07500071
Decision Tree	0.2299442	0.0222997	0.1067227	0.3709271	0.2896955	0.1174008	0.08838886
Neuralnet	0.2208348	0.01775594	0.08394905	0.2179616	0.2245069	0.03921013	0.05387155
Ridge	0.2495593	0.01977087	0.08810373	0.1971335	0.2162983	0.04342892	0.07912894
LASSO	0.2672776	0.01344521	0.08731722	0.183967	0.2106617	0.03876806	0.08097285
ElasticNet	0.2522743	0.01406866	0.08874032	0.1890074	0.211274	0.03961122	0.07980254
Deepnet	0.2702398	0.09730134	0.1913845	0.4011895	0.2901784	0.1400501	0.2548906
Averaging	0.2133583	0.01996002	0.09603559	0.239746	0.09006789	0.01797183	0.06160017
Weighted Averaging	0.1658832	0.05308728	0.1378911	0.1811016	0.1211871	0.02715146	0.06493144
Bagging	0.1784421	0.01207605	0.1195285	0.2042914	0.2356023	0.009002502	0.08604002
Boosting	0.1237017	0.01059957	0.1072595	0.2345743	0.08203951	0.009002502	0.08095949
Proposed Stacking using RF	0.0288617	0.004016189	0.07027704	0.07030604	0.03566583	0.005384577	0.02278088

Table 5 shows the root mean square error values for the base learners and ensemble approaches against seven datasets. Table 5 shows that, out of all compared 12 algorithms, the proposed stacking using random forest produced minimal error values (root mean square error) for all seven datasets. The values of the proposed stacking using the RF model were 0.0370489, 0.01562433, 0.1072363, 0.1094053, 0.06379541, 0.01505940, and 0.04415005 for the datasets Albrecht, China, Desharnais, Kemerer, Maxwell, Kitchenham, and Cocomo81, respectively. When compared with the proposed stacking using the RF model with other base learner algorithms such as random forest, SVM, decision tree, neural net, ridge regression, LASSO regression, elastic net, and deep net and other ensemble approaches including averaging, weighted averaging, bagging, and boosting, the proposed model produced lower RMSE values.

Table 5. Base learners and ensemble techniques vs. RMSE of 7 datasets.

Root Mean Squared Error (RMSE)
Algorithms	Dataset 1 Albrecht	Dataset 2 China	Dataset 3 Desharnais	Dataset 4 Kemerer	Dataset 5 Maxwell	Dataset 6 Kitchenham	Dataset 7 Cocomo81
Random Forest	0.2273109	0.0651549	0.1744573	0.2357751	0.3098055	0.1715596	0.1402015
SVM	0.291869	0.109964	0.1993475	0.2635159	0.4006657	0.2379881	0.1976564
Decision Tree	0.3140069	0.05380968	0.1724028	0.3954624	0.3897197	0.2013018	0.1869692
Neuralnet	0.2676081	0.0439852	0.1508566	0.3219353	0.2914014	0.0739	0.09447618
Ridge	0.274339	0.03703651	0.1482106	0.2810334	0.2901234	0.08774596	0.1592412
LASSO	0.2952834	0.02381411	0.1455049	0.256731	0.2859893	0.07402251	0.1766792
ElasticNet	0.2771694	0.02462756	0.1463786	0.26093	0.2865395	0.07542022	0.1747383
Deepnet	0.3222748	0.1497018	0.2396687	0.4142278	0.3571974	0.2242306	0.285657
Averaging	0.2403676	0.06114447	0.1569477	0.2719905	0.1386882	0.04447122	0.1272475
Weighted Averaging	0.2789538	0.1214186	0.2275768	0.3253842	0.2096006	0.1059557	0.1831177
Bagging	0.2264107	0.04121619	0.1764452	0.2399795	0.3120326	0.02091779	0.176543
Boosting	0.184356	0.03618514	0.162724	0.2626449	0.1215997	0.02091779	0.1693169
Proposed Stacking using RF	0.0370489	0.01562433	0.1072363	0.1094053	0.06379541	0.01505940	0.04415005

Table 6 shows the R-squared values for the base learners and ensemble approaches against seven datasets. The data suggest that, out of all 12 compared algorithms, the proposed stacking using random forest produced values nearer to 1 (R-squared) for all seven datasets. The values of the proposed stacking using the RF model were 0.9357274, 0.9839643, 0.6556170, 0.7520435, 0.8120214, 0.9246614, and 0.8667750 for the datasets Albrecht, China, Desharnais, Kemerer, Maxwell, Kitchenham, and Cocomo81, respectively. The values clearly suggest that the proposed stacking using the RF model produced R-squared values nearer to 1 when compared with other base learner algorithms like Random Forest, SVM, decision tree, neural net, ridge regression, LASSO regression, elastic net, and Deepnet and other ensemble approaches including averaging, weighted averaging, bagging, and boosting. The algorithm that provided R-squared values nearer to 1 indicates a good correlation between the data and the model. Thus, ensemble approaches are preferred over single models for two reasons: better performance in terms of prediction, and robustness, which reduces the spread of predictions.

Table 6. Base learners and ensemble techniques vs. R-squared of seven datasets.

R-Squared
Algorithms	Dataset 1 Albrecht	Dataset 2 China	Dataset 3 Desharnais	Dataset 4 Kemerer	Dataset 5 Maxwell	Dataset 6 Kitchenham	Dataset 7 Cocomo81
Random Forest	0.4732279	0.8028527	0.38059	0.6032962	0.109088	0.3928102	0.6062928
SVM	0.1315232	0.4384377	0.1912367	0.5044536	-0.4901189	-0.1684357	0.2174898
Decision Tree	0.0052189	0.8655325	0.3950932	-0.1160428	-0.4098123	0.1640318	0.2998227
Neuralnet	0.2699029	0.9101517	0.5368423	0.2603814	0.2117937	0.8873365	0.8212226
Ridge	0.232714	0.9362975	0.5529472	0.4363801	0.2186921	0.8411641	0.4920992
LASSO	0.1110852	0.9736631	0.5691211	0.5296434	0.2407999	0.8869626	0.3747712
ElasticNet	0.2168	0.9718331	0.563931	0.5141316	0.2378761	0.8826536	0.3884329
Deepnet	-0.05885081	-0.0407606	-0.169022	-0.2244724	-0.1843314	-0.037252	-0.6343981
Averaging	0.4109746	0.8263755	0.498686	0.4720681	0.5942589	0.9096699	0.6756852
Weighted Averaging	0.2066829	0.3153521	-0.05403761	0.24444970	0.07326536	0.4872298	0.3283723
Bagging	0.4773922	0.9211081	0.3663932	0.5890217	0.09623293	0.9800149	0.3757349
Boosting	0.6855181	0.9478667	0.461106	0.5907376	0.6880857	0.9800149	0.425793
Proposed Stacking using RF	0.9357274	0.9839643	0.6556170	0.7520435	0.8120214	0.9246614	0.8667750

Initially, stacking models considered for evaluation were stacking using the generalized linear model (S-GLM), stacking using decision tree (S-DT), stacking using support vector machine (S-SVM), and stacking using random forest (S-RF). Stacking using random forest was found to be the best model for prediction when compared with seven datasets against evaluation measures MAE, RMSE, and R-squared metrics. The proposed stacking using random forest compared with the single base learners such as random forest (RF), support vector machine (SVM), decision tree (DT), neural net (NN), ridge regression (Ridge), LASSO regression (LASSO), elastic net regression (EN), and deep net (DN) and with ensemble techniques including averaging (AVG), weighted averaging (WAVG), bagging (BA), and boosting (BS). Based on the data from Table 4, Table 5 and Table 6, it was found that the proposed stacking using RF provided better results in terms of the evaluation measures MAE, RMSE, and R-squared when compared with the single model approaches and ensemble approaches that included averaging, weighted averaging, bagging and boosting.

6. Conclusions

This paper presented software effort estimation using ensemble techniques and machine and deep-learning algorithms. Ensemble techniques compared were averaging, weighted averaging, bagging, boosting, and stacking. Various stacking models considered for evaluation were stacking using generalized linear model, stacking using decision tree, stacking using support vector machine, and stacking using random forest. The proposed stacking using random forest provided the best results and was compared with the single models, namely random forest, SVM, decision tree, ridge regression, LASSO regression, elastic net regression, neural net and deep net using Albrecht, China, Desharnais, Kemerer, Maxwell, Kitchenham, and Cocomo81 datasets. The results suggest that the proposed stacking using RF provides better results compared with single models. This estimation is used as input for the pricing process, project planning, iteration planning, budget, and investment analysis. Evaluation metrics considered were mean absolute error (MAE), root mean square error (RMSE), and R-squared. In the future, a hybrid model will be developed for better prediction of software effort estimation.