An Analog Voltage Similarity Circuit with a Bell-Shaped Power Consumption
Abstract
:1. Introduction
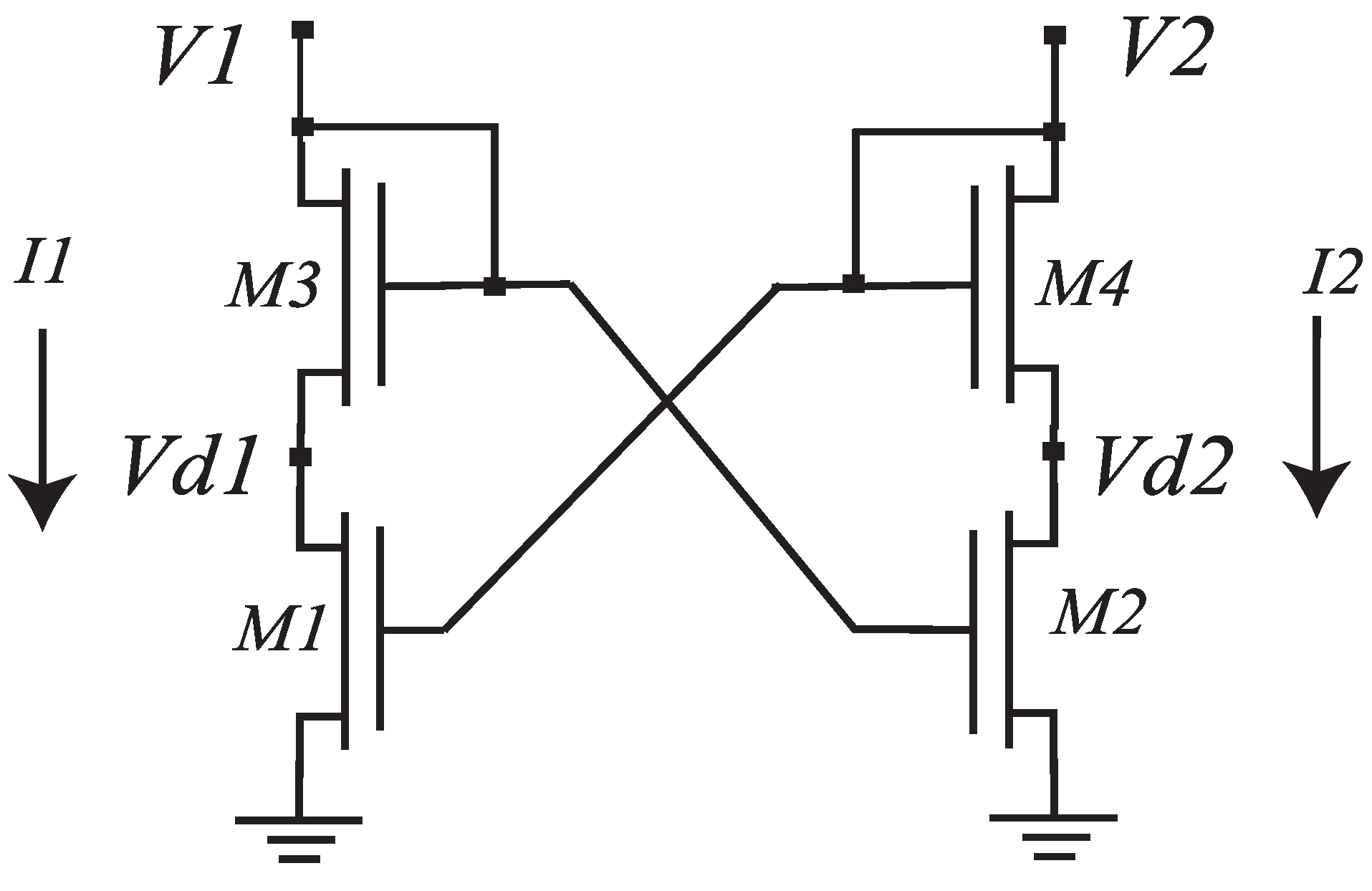
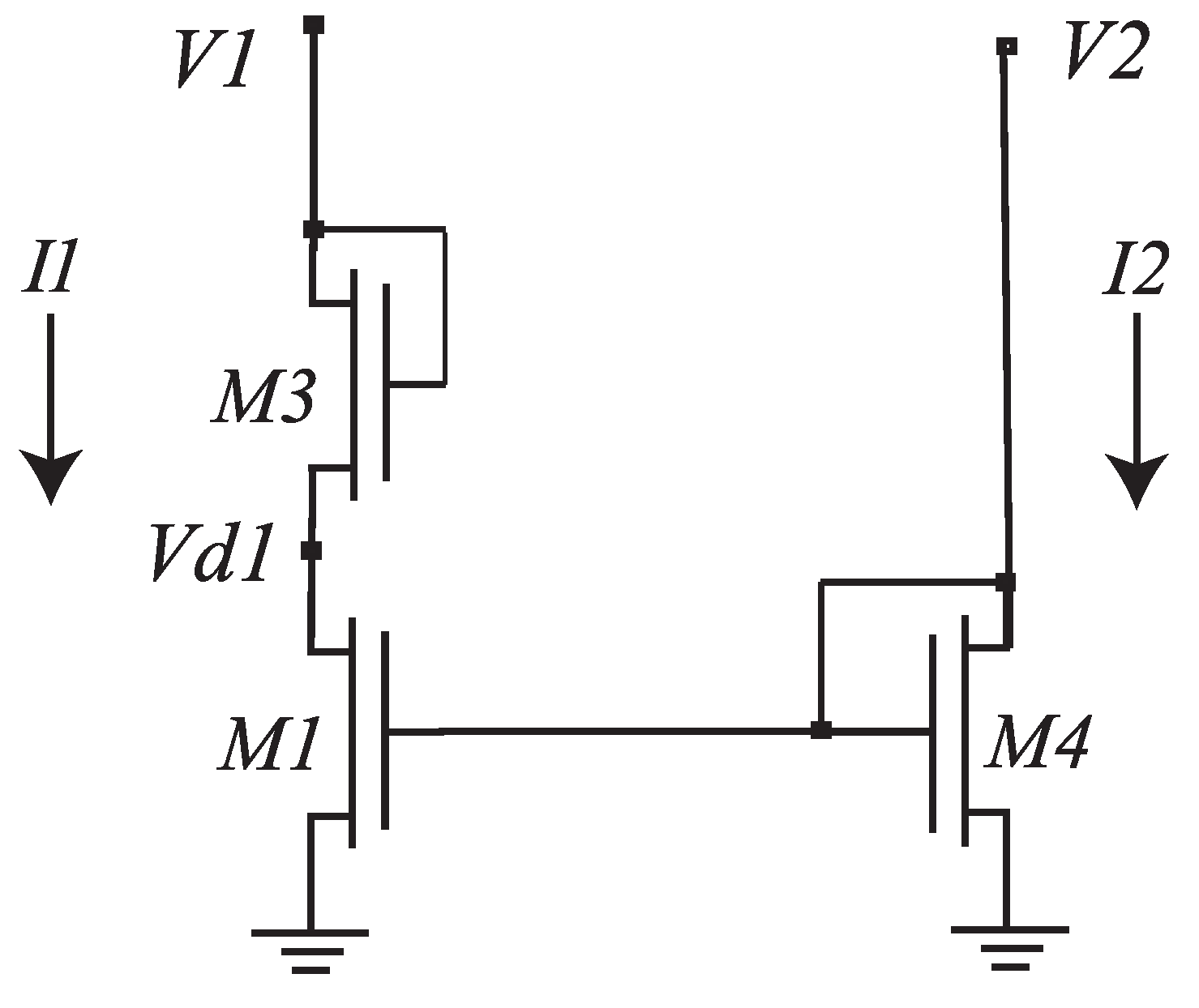
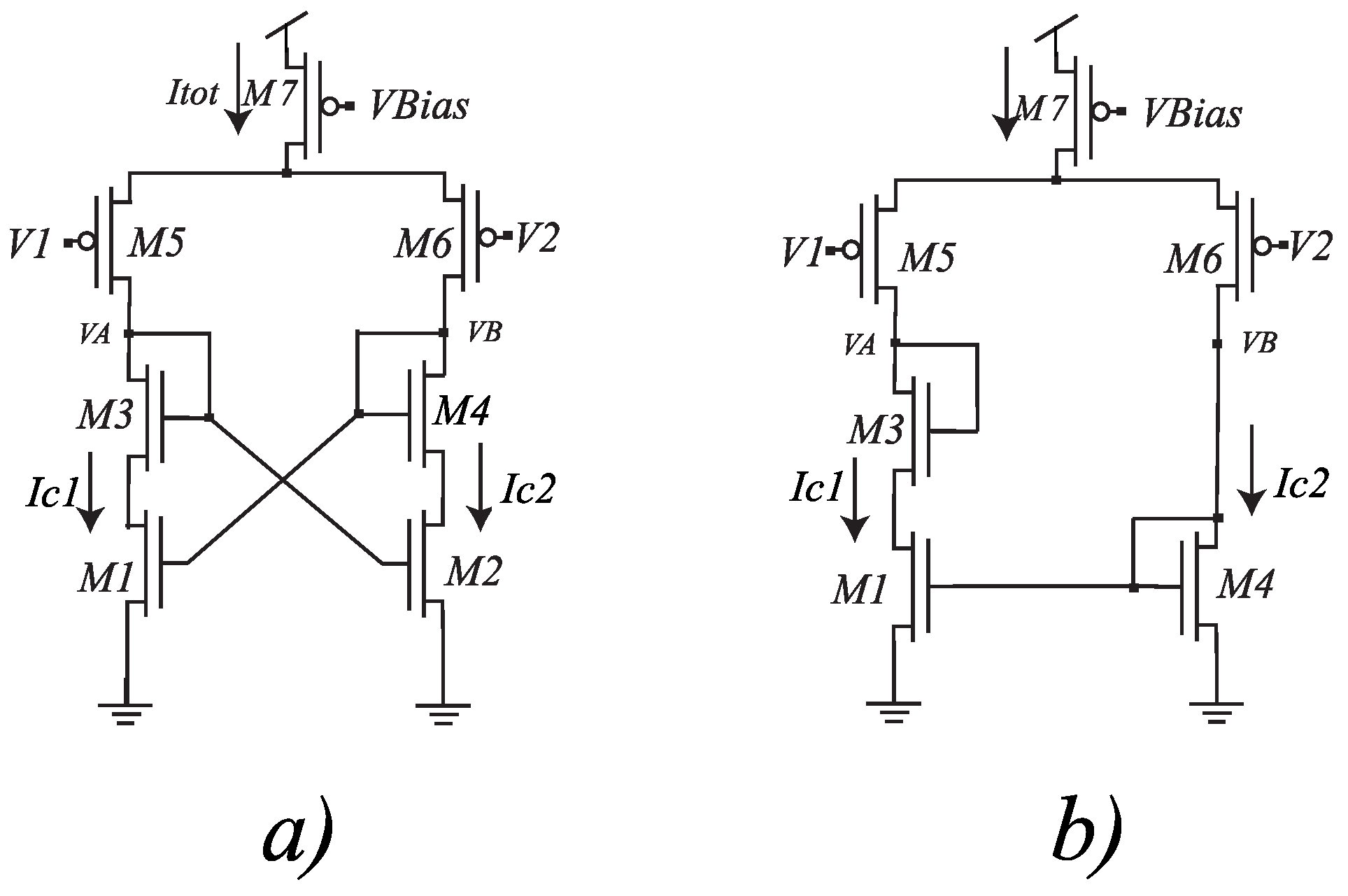
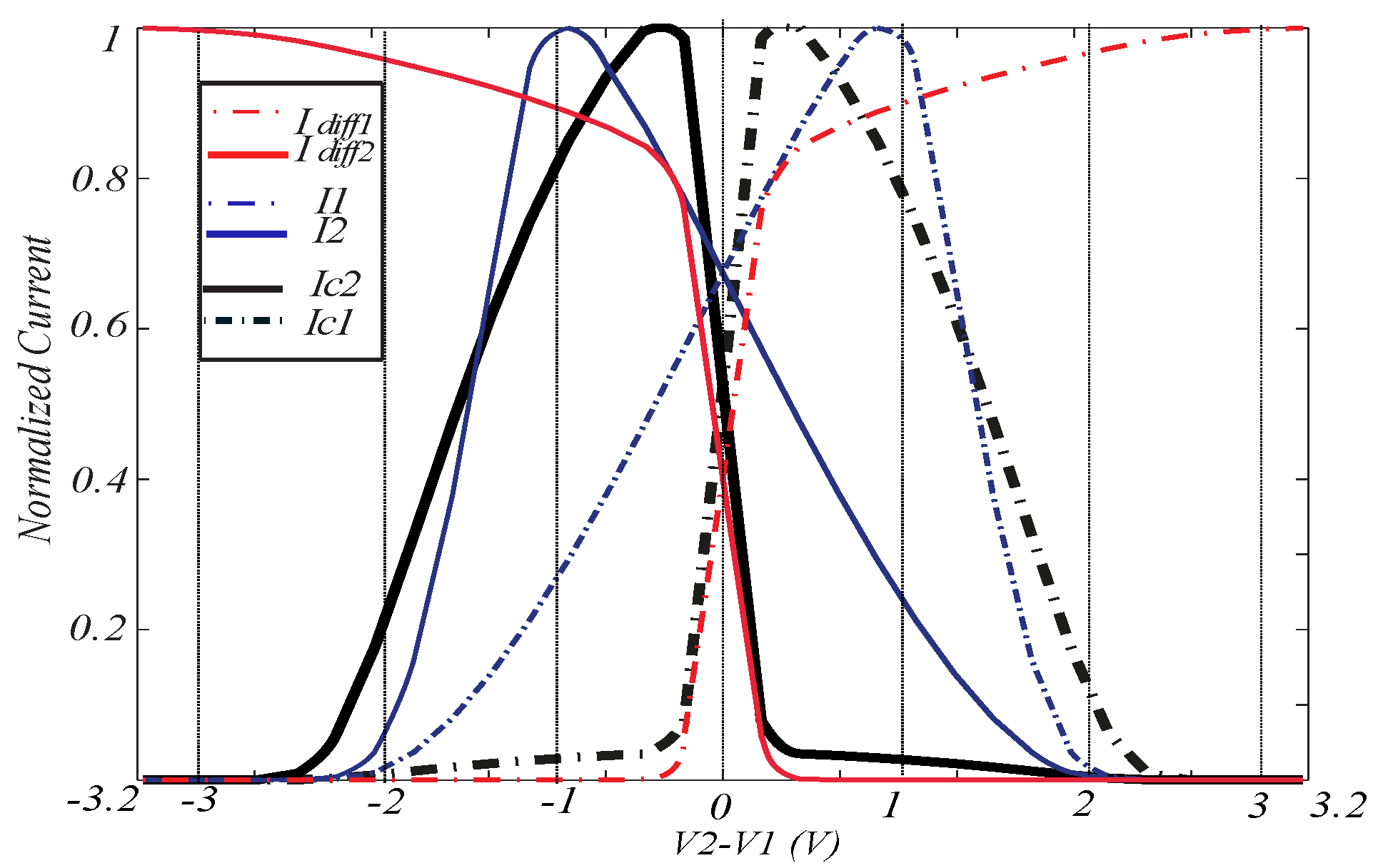
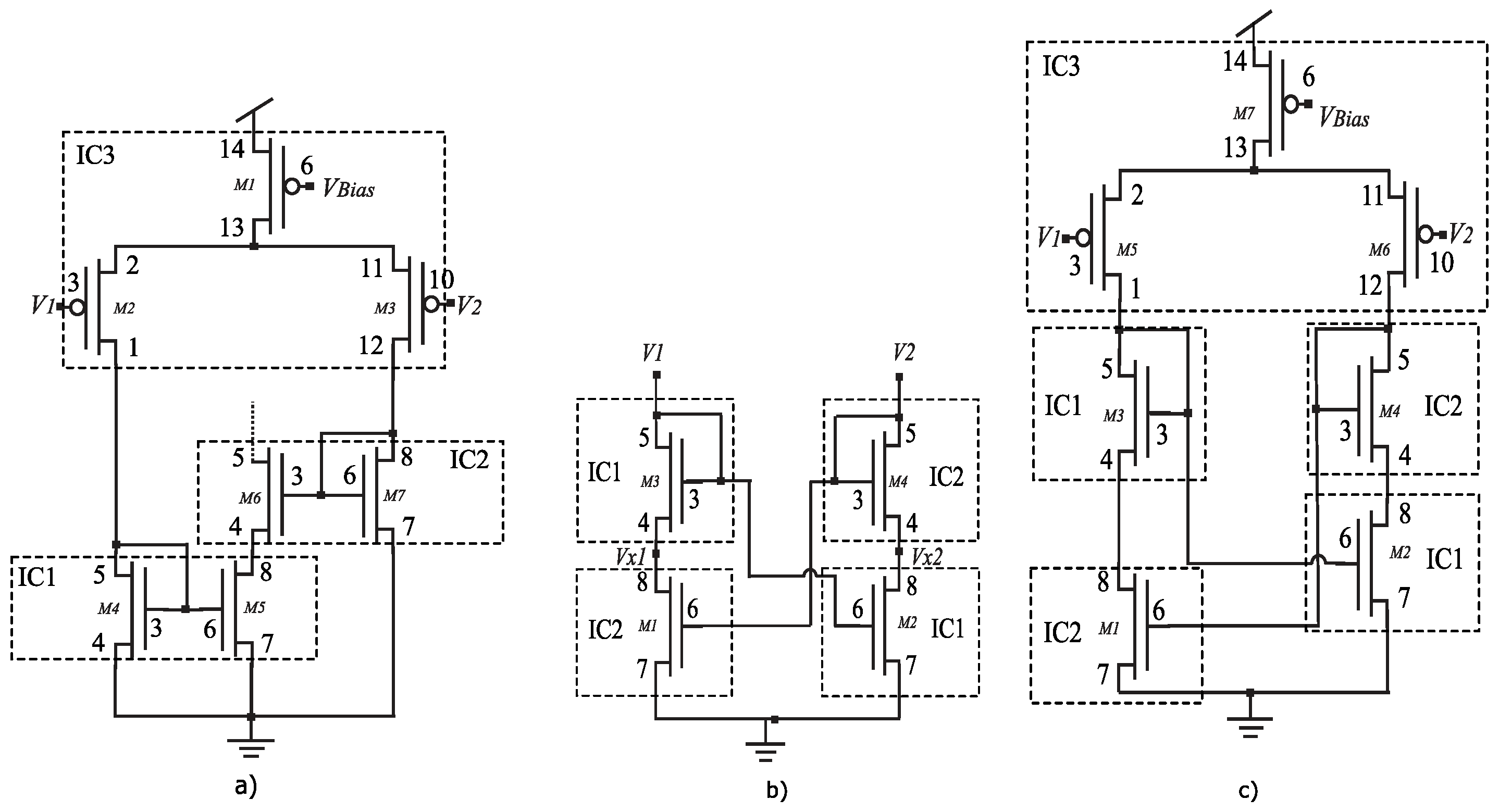
2. New Voltage Correlator Circuit
Voltage Correlator Connected to a Differential Pair
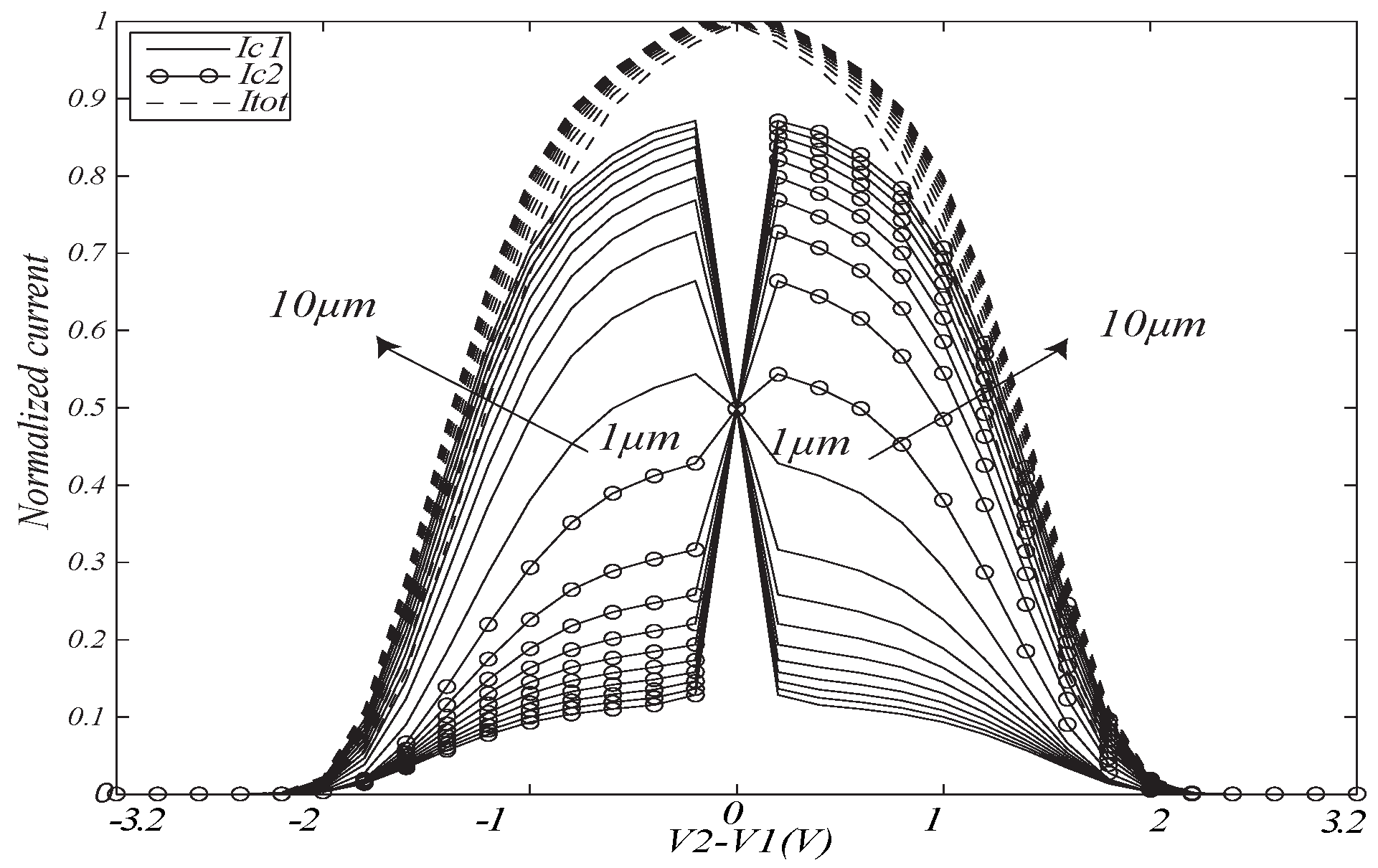
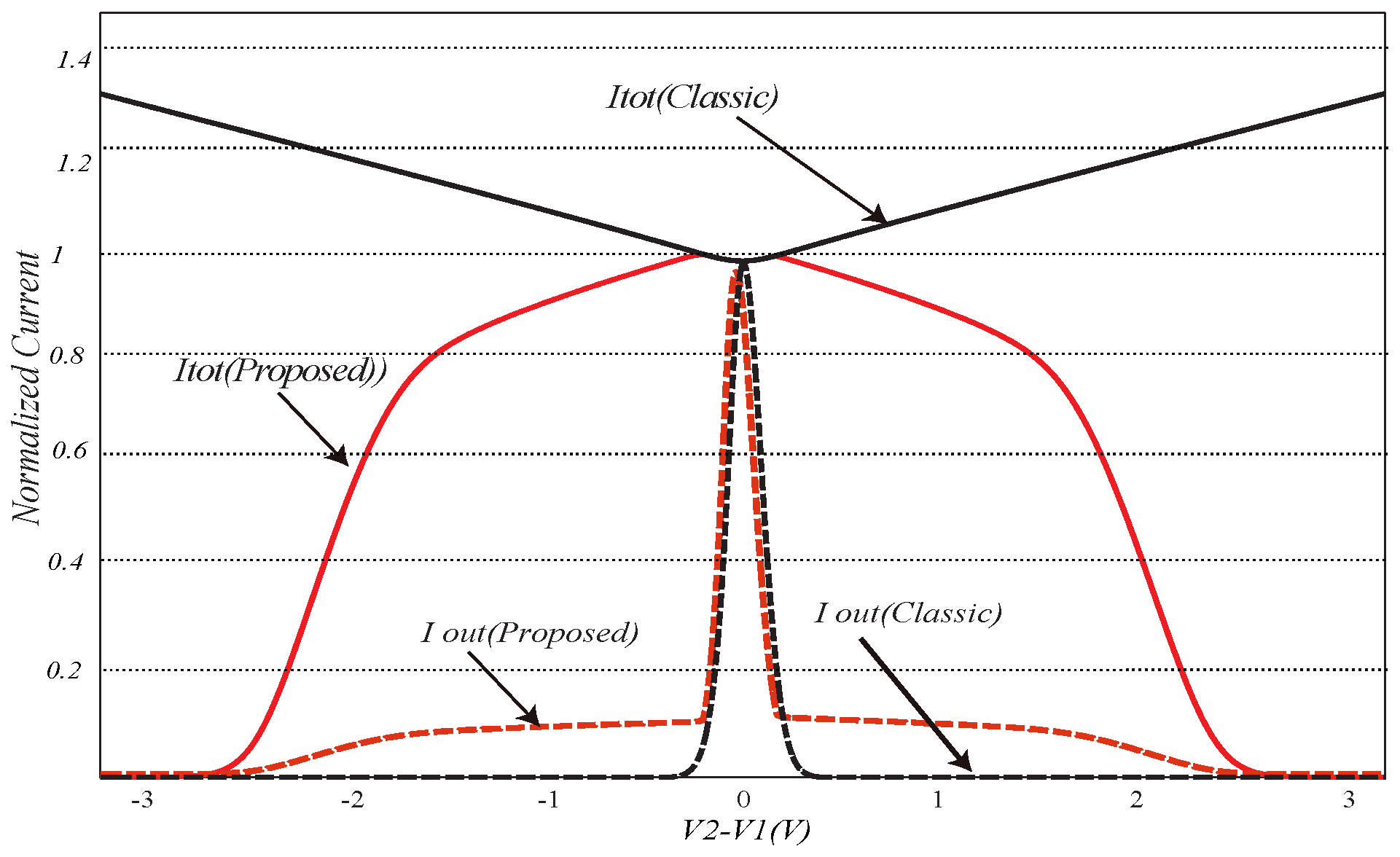
3. The Proposed Bump Circuit
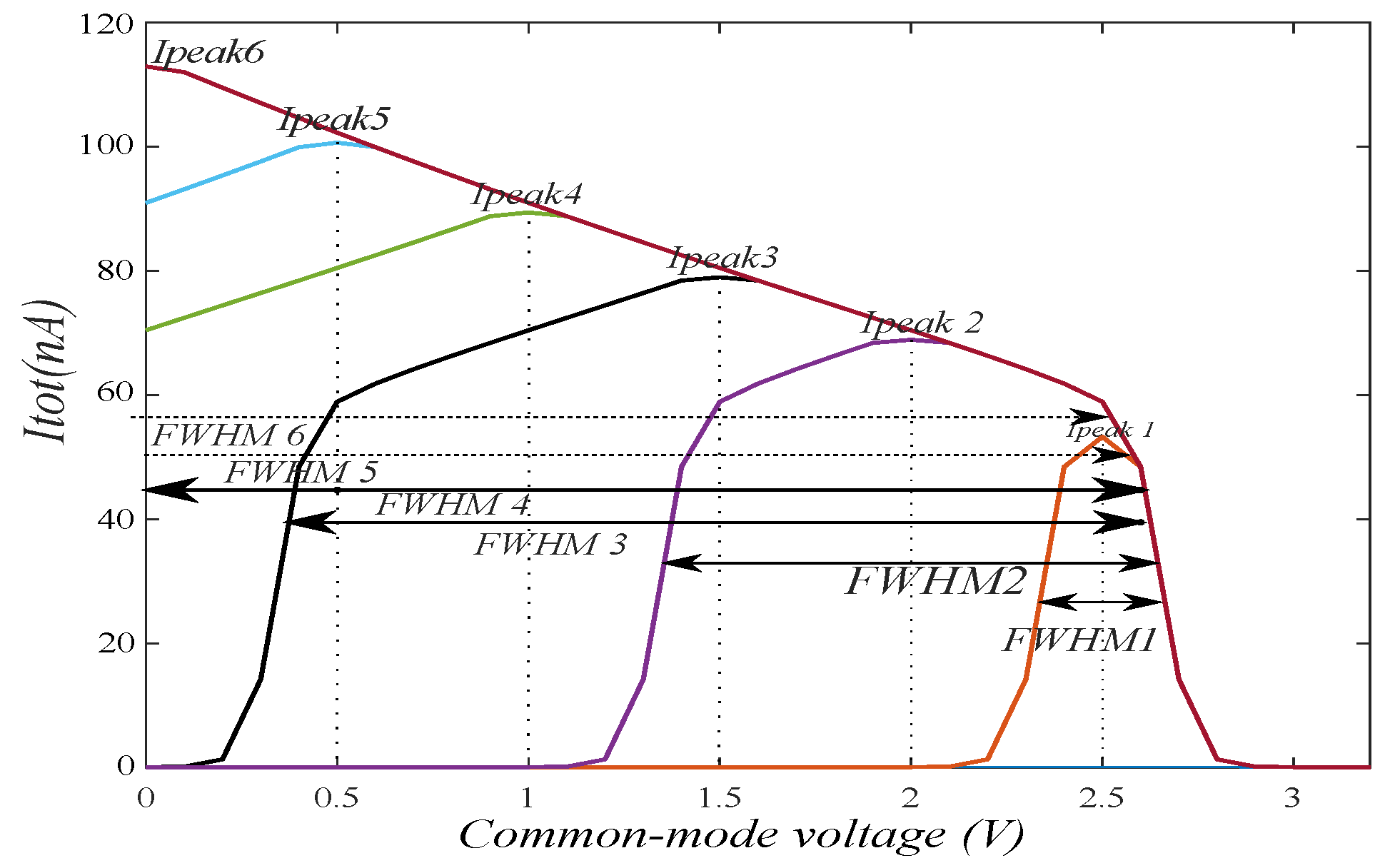
Common-Mode Behavior of Proposed Bump Circuit
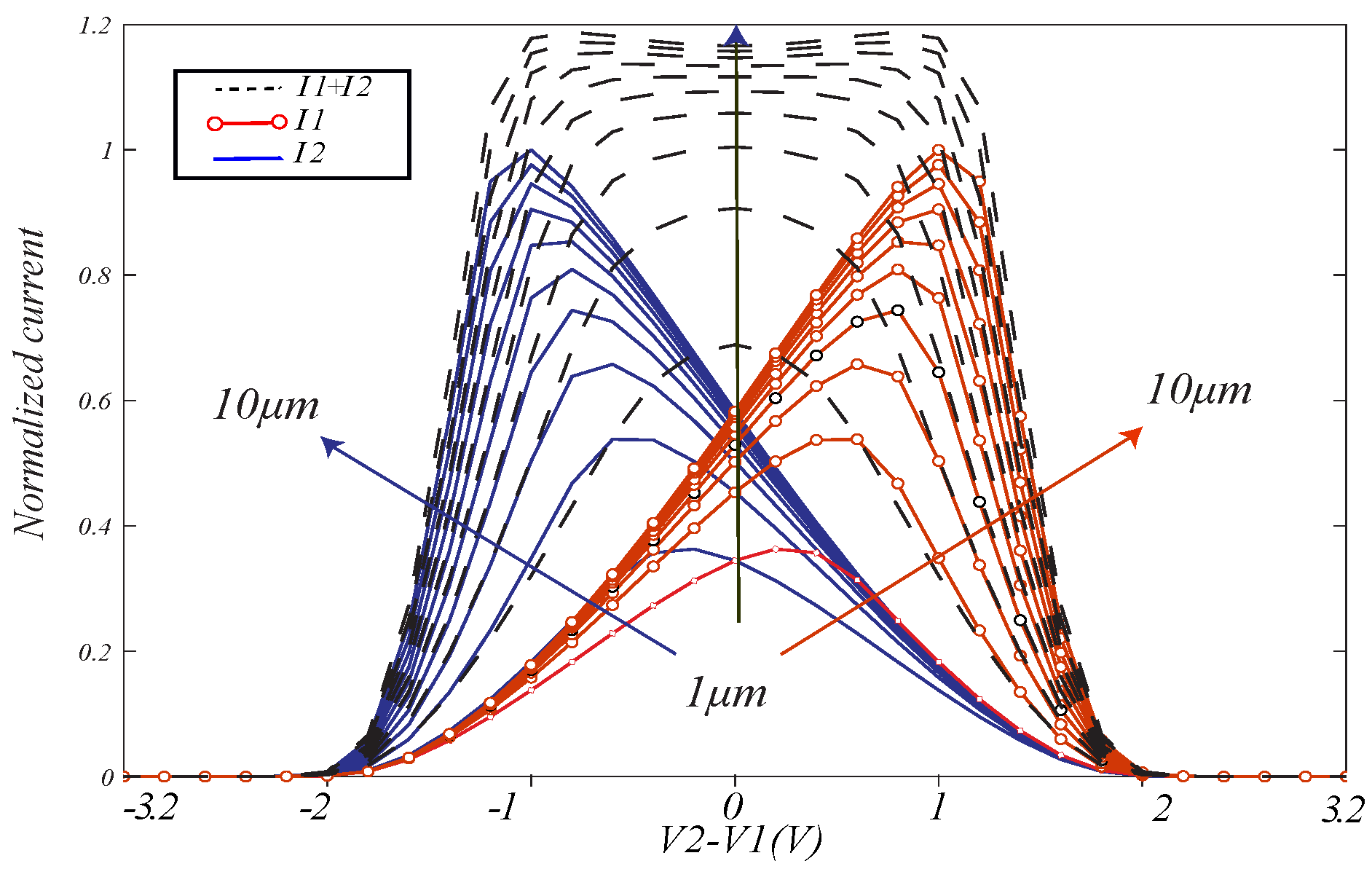
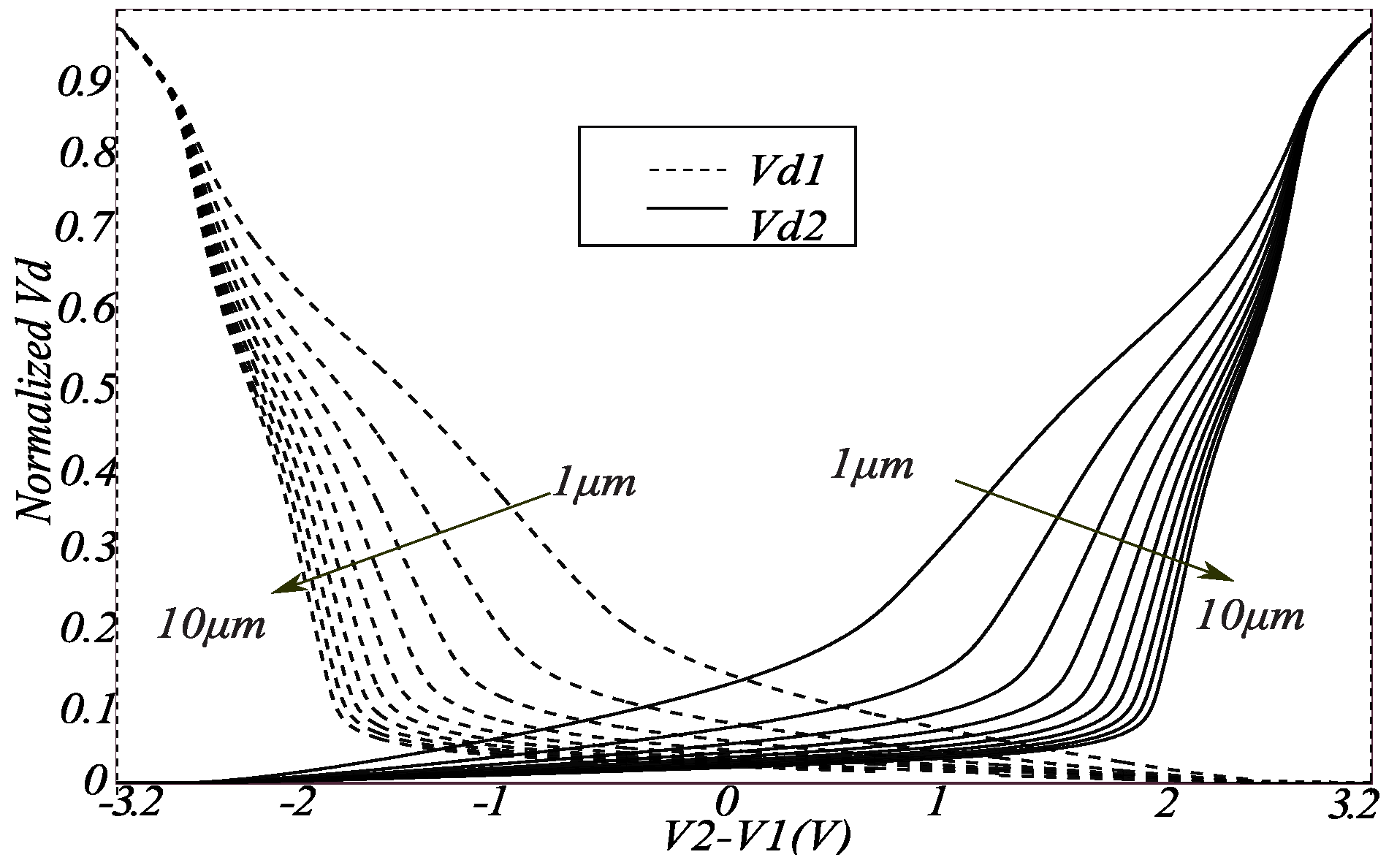
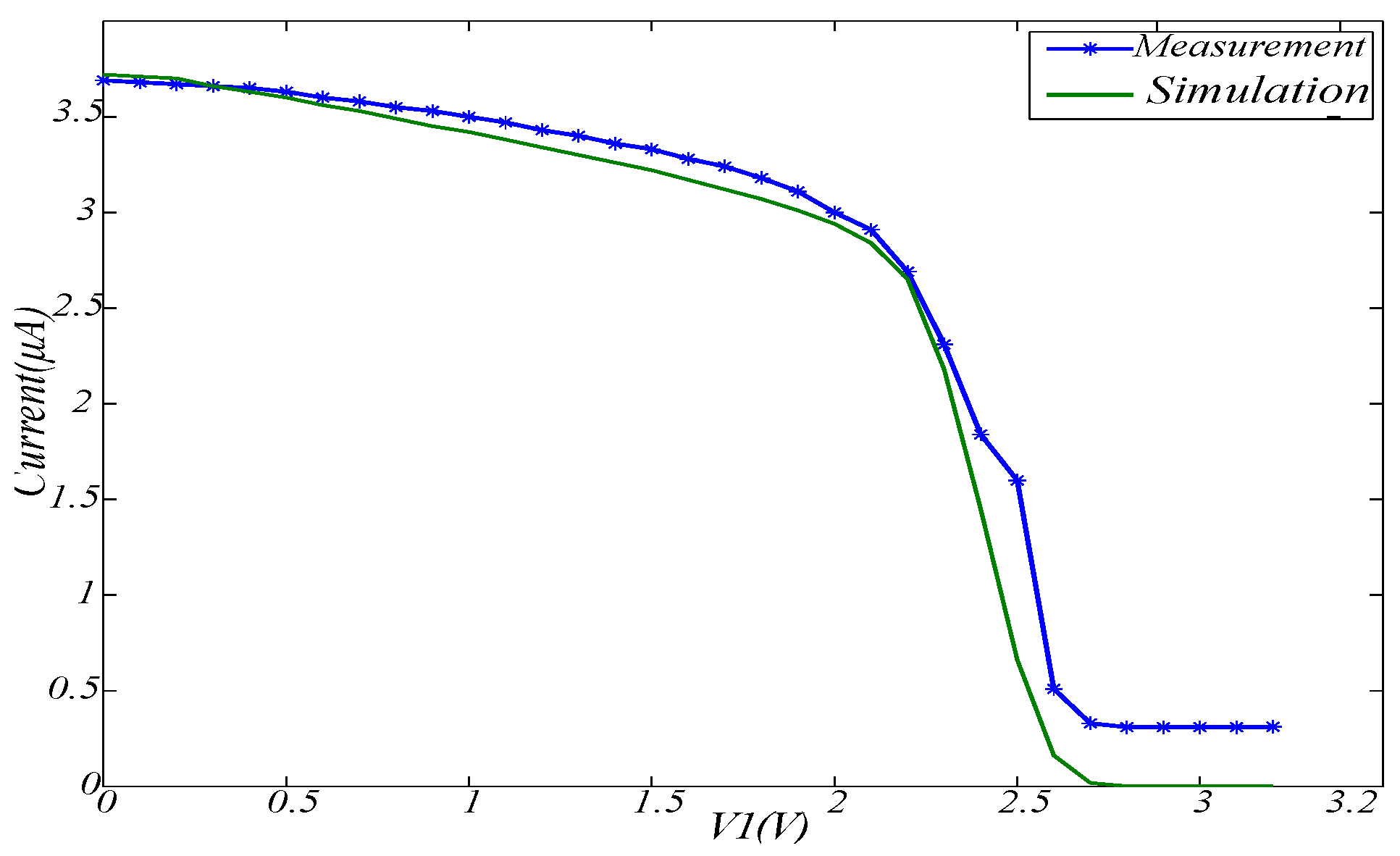
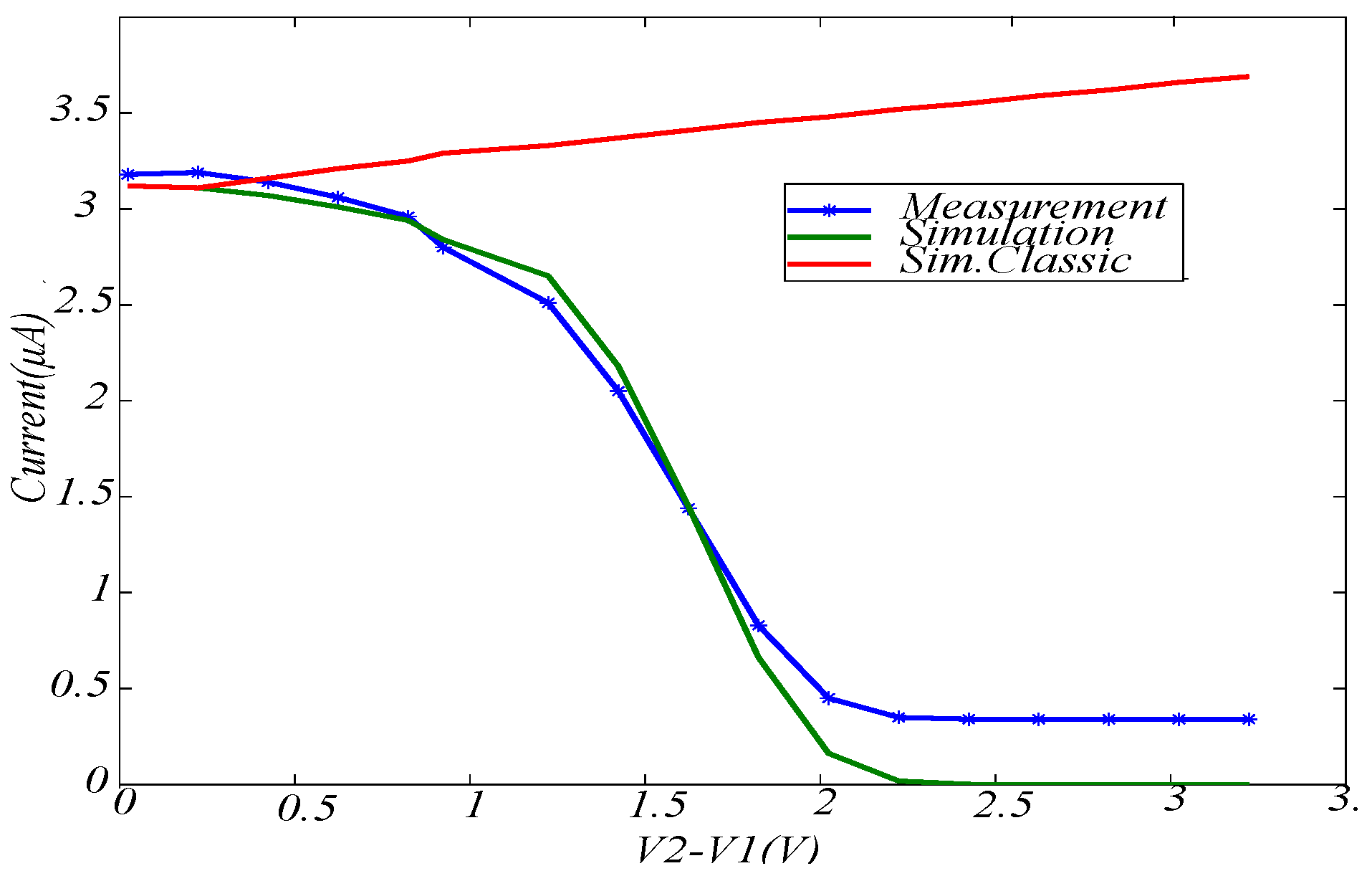
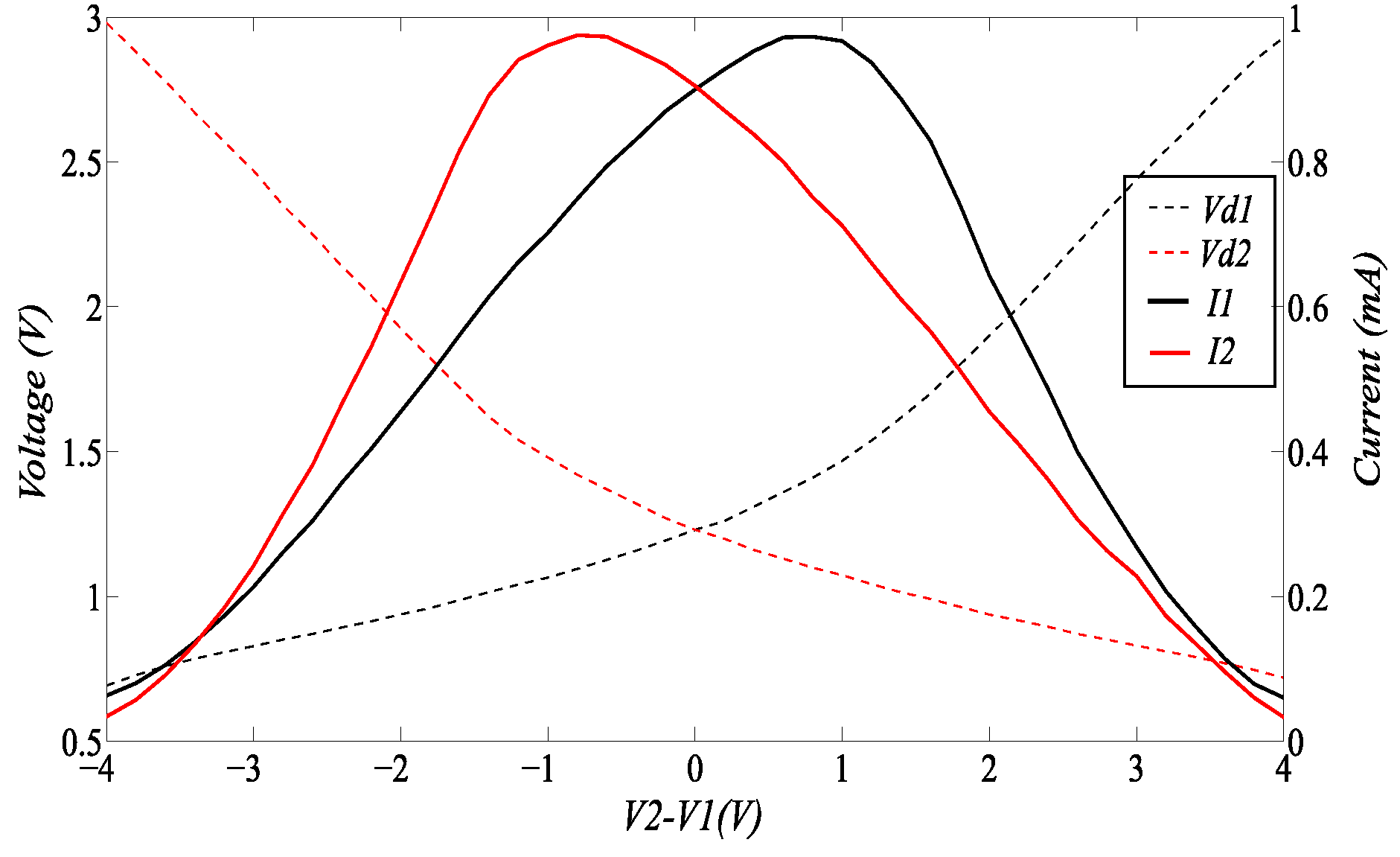
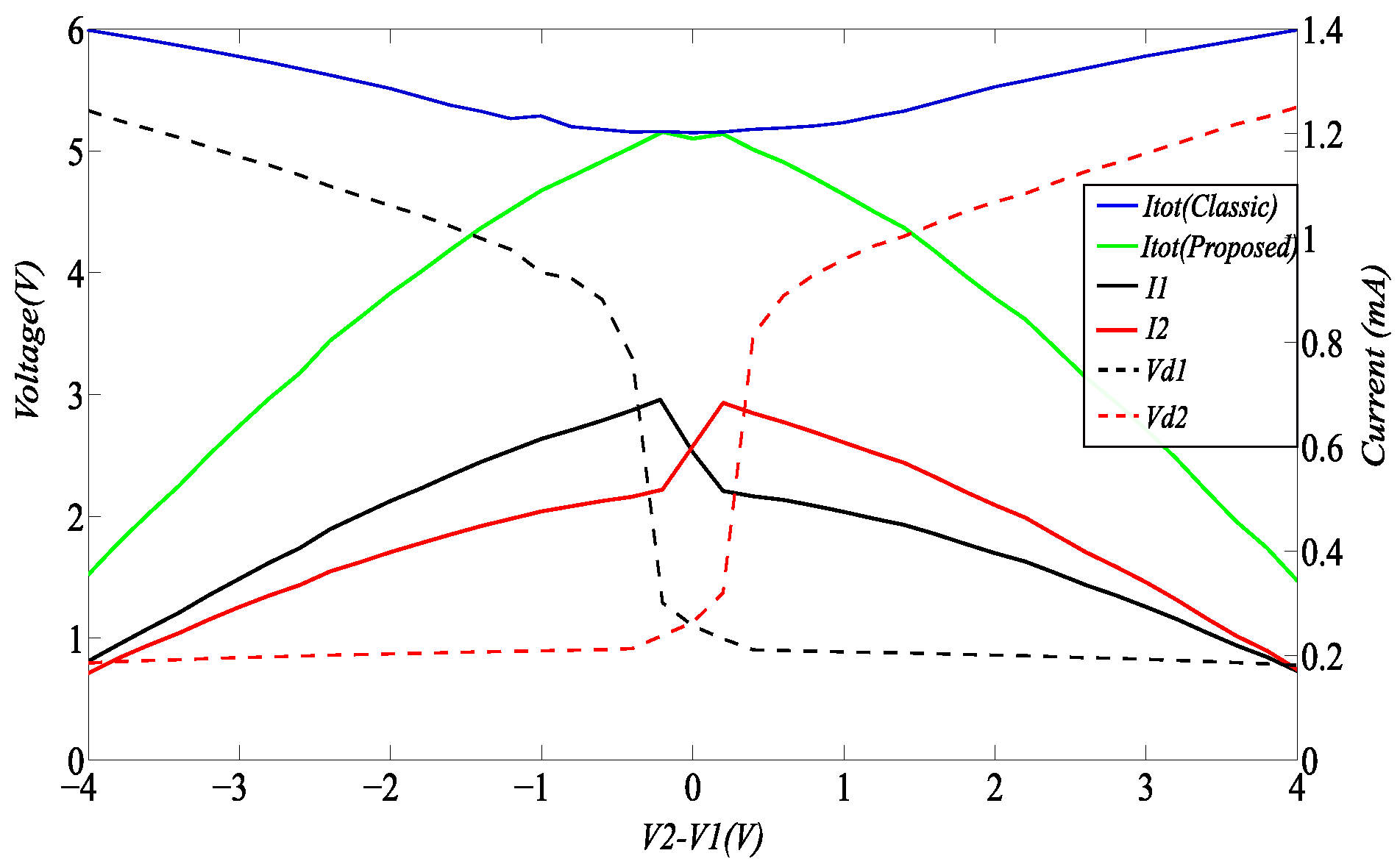
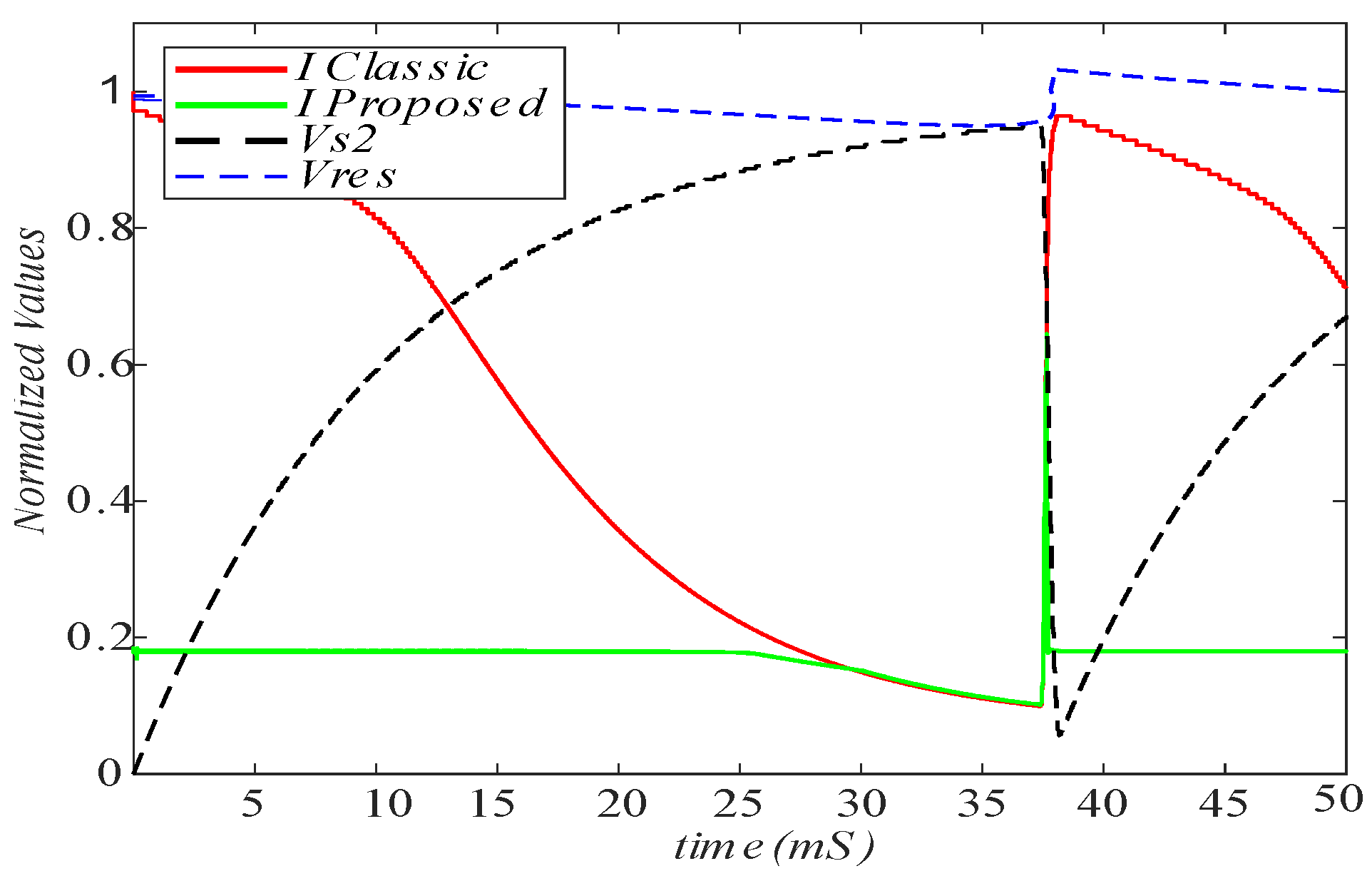
4. Measurement Results
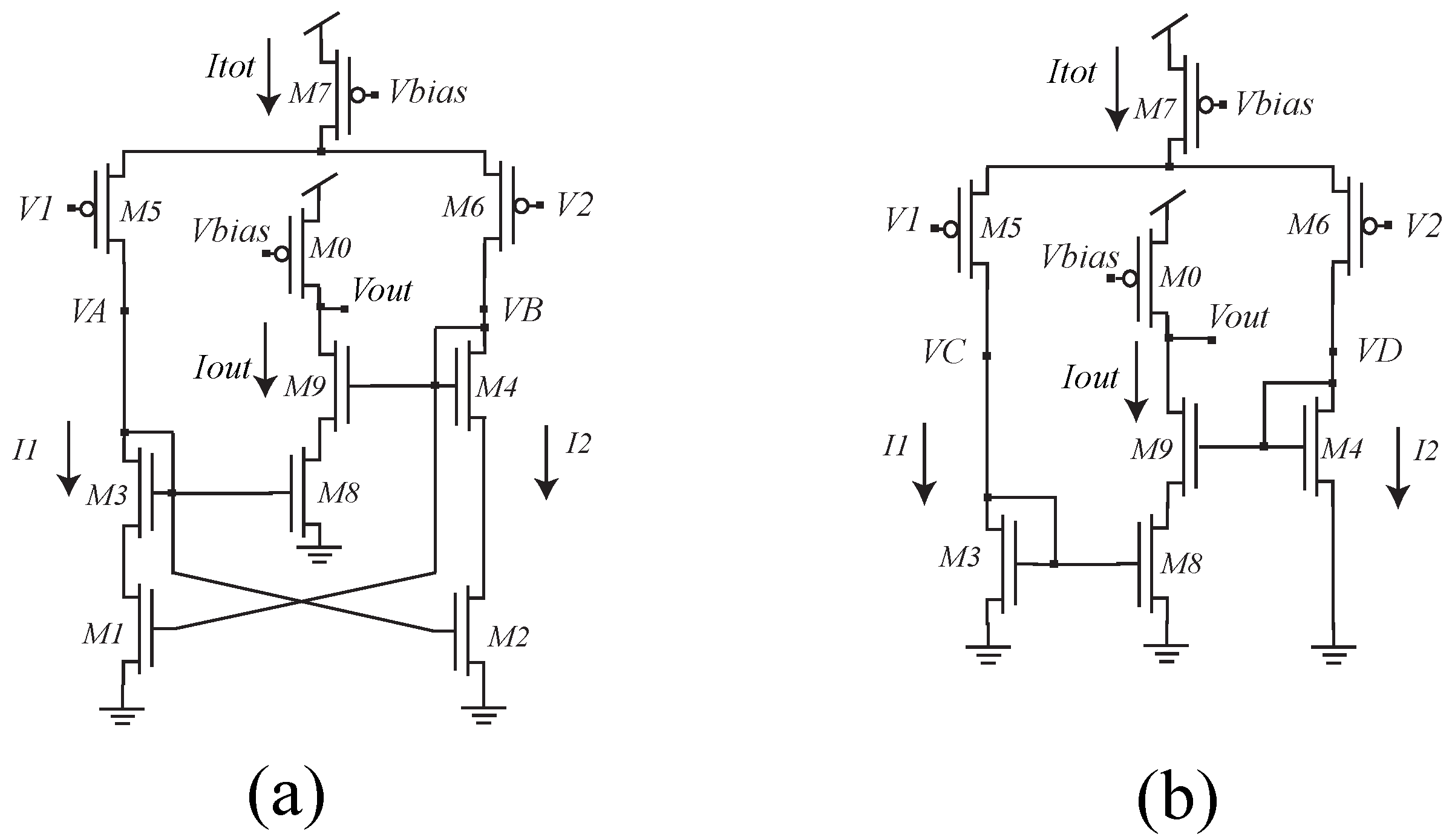
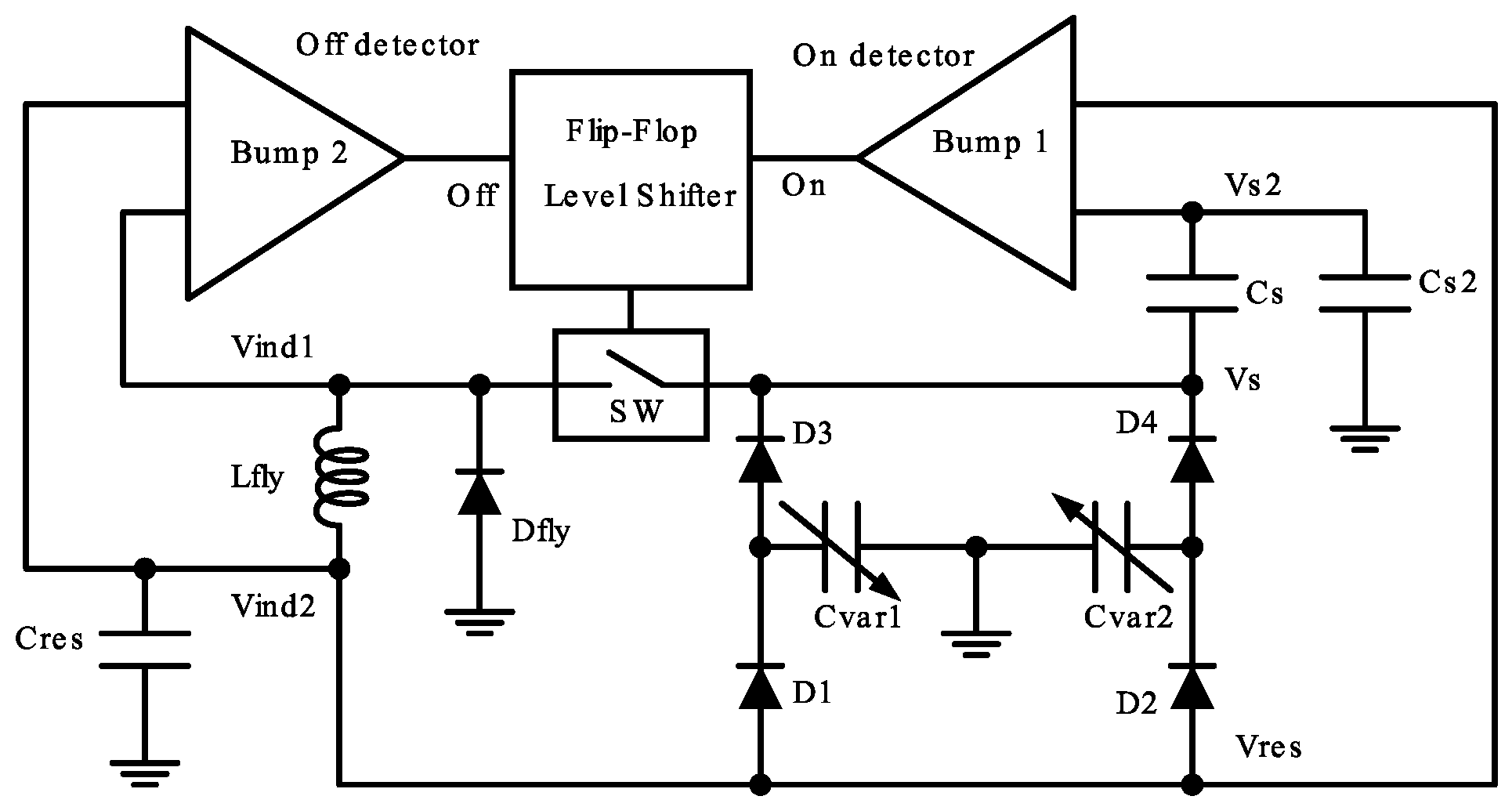
5. Double Charge Pump Interface with Bump Circuits
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bubb, F.W. A Circuit for Generating Polynomials and Finding Their Zeros. Proc. IRE 1951, 39, 1556–1561. [Google Scholar] [CrossRef]
- Jung, W. Op Amp Applications Handbook; Newnes/Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Ragazzini, J.R.; Randall, R.H.; Russell, F.A. Analysis of Problems in Dynamics by Electronic Circuits. Proc. IRE 1947, 35, 444–452. [Google Scholar] [CrossRef]
- Popa, C. Low-power low-voltage CMOS analog signal processing circuits using a functional core. In Proceedings of the 2016 IEEE International Conference on Electronics, Circuits and Systems, Monte Carlo, Monaco, 11–14 December 2016. [Google Scholar]
- Bryant, M.D.; Yan, S.; Tsang, R.; Fernandez, B.; Kumar, K.K. A Mixed Signal (Analog-Digital) Integrator Design. IEEE Trans. Circuits Syst. I Regul. Pap. 2012, 59, 1409–1417. [Google Scholar] [CrossRef]
- Hiratkar, S.; Tijare, A.; Dakhole, P. VLSI design of analog multiplier in weak inversion region. In Proceedings of the 2016 International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, India, 6–8 April 2016. [Google Scholar]
- Liu, S.C. Analog VLSI: Circuits and Principles. In Bradford Book; MIT Press: Cambridge, MA, USA, 2002; Chapter 6; p. 168. [Google Scholar]
- Delbruck, T. Bump circuits for computing similarity and dissimilarity of analog voltages. In Proceedings of the International Joint Conference on Neural Networks, Seattle, WA, USA, 8–12 July 2019; pp. 475–479. [Google Scholar]
- Phan, T.N.; Azadmehr, M.; Le, C.P.; Halvorsen, E. Low power electronic interface for electrostatic energy harvesters. J. Phys. Conf. Ser. 2015, 660, 012087. [Google Scholar] [CrossRef]
- Theogarajan, L.; Akers, L.A. Novel circuits for neural information processing. J. Comput. Electr. Eng. 1999, 25, 409–420. [Google Scholar] [CrossRef]
- Azadmehr, M.; Abrahamsen, J.P.; Hafliger, P. A foveated AER imager chip. In Proceedings of the 2005 IEEE International Symposium on Circuits and Systems (ISCAS), Kobe, Japan, 23–26 May 2005. [Google Scholar]
- Lu, J.; Yang, T.; Jahan, M.S.; Holleman, J. Nano-power tunable bump circuit using wide-input-range pseudo-differential transconductor. Electron. Lett. 2014, 50, 921–923. [Google Scholar] [CrossRef] [Green Version]
- Peng, S.Y.; Minch, B.A.; Hasler, P. A programmable floating-gate bump circuit with variable width. IEEE Int. Symp. Circuits Syst. 2005, 5, 4341–4344. [Google Scholar]
- Bragg, J.A.; Brown, E.A.; Deweerth, S.P. A Tunable Voltage Correlator. Analog. Integr. Circuits Signal Process. 2004, 39, 89–94. [Google Scholar] [CrossRef]
- Lin, S.Y.; Huang, R.J.; Chiueh, T.D. A tunable Gaussian/square function computation circuit for analog neural networks. IEEE Trans. Circuits Syst. II Analog. Digit. Signal Process. 1998, 45, 441–446. [Google Scholar] [CrossRef]
- Minch, B.A. A simple variable-width CMOS bump circuit. In Proceedings of the 2016 IEEE International Symposium on Circuits and Systems (ISCAS), Montreal, QC, Canada, 22–25 May 2016; pp. 1354–1357. [Google Scholar]
- Azadmehr, M.; Marchetti, L.; Berg, Y. A low power analog voltage similarity circuit. In Proceedings of the 2017 IEEE International Symposium of Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017. [Google Scholar]





| Ref. | This Work | [8] | [12] | [13] | [14] | [15] | [16] |
|---|---|---|---|---|---|---|---|
| Vdd (V) | 3.2 | 3.2 | 3 | 2 | 5 | 5 | |
| Power (W) | 256 n | 256 n | 18.9 n | na | na | na | na |
| Technology | 350 | 350 | 500 | 1.2 m | 500 | 3 m | ALD1106/7 |
| Nr of devices | 10 | 8 | 18 | 15 | 11 | 14 | 11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azadmehr, M.; Marchetti, L.; Berg, Y. An Analog Voltage Similarity Circuit with a Bell-Shaped Power Consumption. Electronics 2021, 10, 1141. https://doi.org/10.3390/electronics10101141
Azadmehr M, Marchetti L, Berg Y. An Analog Voltage Similarity Circuit with a Bell-Shaped Power Consumption. Electronics. 2021; 10(10):1141. https://doi.org/10.3390/electronics10101141
Chicago/Turabian StyleAzadmehr, Mehdi, Luca Marchetti, and Yngvar Berg. 2021. "An Analog Voltage Similarity Circuit with a Bell-Shaped Power Consumption" Electronics 10, no. 10: 1141. https://doi.org/10.3390/electronics10101141
APA StyleAzadmehr, M., Marchetti, L., & Berg, Y. (2021). An Analog Voltage Similarity Circuit with a Bell-Shaped Power Consumption. Electronics, 10(10), 1141. https://doi.org/10.3390/electronics10101141







