Routing Algorithm Based on User Adaptive Data Transmission Scheme in Opportunistic Social Networks

Abstract

With the rapid popularization of 5G communication and internet of things technologies, the amount of information has increased significantly in opportunistic social networks, and the types of messages have become more and more complex. More and more mobile devices join the network as nodes, making the network scale increase sharply, and the tremendous amount of datatransmission brings a more significant burden to the network. Traditional opportunistic social network routing algorithms lack effective message copy management and relay node selection methods, which will cause problems such as high network delay and insufficient cache space. Thus, we propose an opportunistic social network routing algorithm based on user-adaptive data transmission. The algorithm will combine the similarity factor, communication factor, and transmission factor of the nodes in the opportunistic social network and use information entropy theory to adaptively assign the weights of decision feature attributes in response to network changes. Also, edge nodes are effectively used, and the nodes are divided into multiple communities to reconstruct the community structure. The simulation results show that the algorithm demonstrates good performance in improving the information transmission’s success rate, reducing network delay, and caching overhead.

1. Introduction

With the rapid development of 5G technology, people’s frequency and scale using mobile devices for communication are increasing. From smart homes to smart cities [1,2], the internet of things(IoT) technology is becoming more and more popular in people’s daily lives. According to the “2019–2020 China Internet of Things Development Annual Report” released by the Xinhua News Agency, the global Internet of Things connections exceeded 11 billion, of which Internet of Things connections in China exceeded 1.2 billion [3]. Besides, in the last few years, classical social networking is turning into a more complex social internet-working and is extending from human users to objects. Indeed, social internet-working and the IoT are becoming more and more contiguous giving rise to several social and/or multiple IoT paradigms [4], and they require the high-speed transmission of large amounts of data. Traditional multi-hop wireless networks, like mobile ad hoc network (MANET) [5], wireless sensor network (WSN) [6], and wireless mesh network (WMN) [7], may appear congestion when the network connection is interrupted. This will slow down the network transmission speed or even directly lead to network collapse [8]. Hence, traditional wireless network technology performs poorly in the internet of things. In order to make up for the disadvantages of traditional wireless networks in this respect, the concept of opportunistic social networks came into being.

Opportunity social network is a new type of network developed from Mobile adhoc network (MANET) and delay tolerant network (DTN) [9,10]. Unlike the traditional multi-hop wireless network, its size and node location are not initialized, and there is no need to have a complete path between the terminals. The encounter between the nodes carries out the communication in the network. It is a unique delay tolerant network [11]. However, due to the popularity of 5G technology and the internet of things, the network’s scale is getting larger and larger. Meanwhile, the number of nodes and information has increased sharply [12,13,14,15]. In an opportunistic social network, each node’s cache resources are limited, each node is not evenly distributed, communication between nodes is opportunistic, and information transmission depends on the encounter between nodes. Consider that the source node carrying the information does not find a suitable forwarding node. In that case, the information will occupy the node’s cache until the forwarding node completes the information transfer task [16,17]. On the one hand, this will lead some destination nodes to fail to receive information in time. On the other hand, the information that can’t be transmitted will occupy many cache resources of the source node, which reduces the available resources of the source node and increases the burden on the node [18,19].

Scholars’ research on opportunistic social networks mainly focuses on routing algorithms and is committed to designing appropriate message forwarding mechanisms to find the best forwarding nodes at present. In practical applications, opportunistic social network nodes are generally composed of mobile devices that can communicate over short distances (one-to-one mapping devices, such as mobile phones, notebooks, smart watches and other human-computer interaction devices [20,21]) carried by humans, and human activities have a large number of decision feature attributes (such as similarity, daily transactions, movement patterns, interests, etc.) [22]. The social relationship is the relationship between people formed in the direct communication between people in social production and life. From the existing form of the social relationship, it includes static relationship and dynamic relationship. The former refers to the constitutional mode of social relationship, also known as social structure, such as family structure, class structure, and occupational structure. The latter refers to the interaction mode of social relationship, also known as social interaction, like assimilation, cooperation, and competition [23,24]. People cannot exist independently from society, and they must have various social relationships with other people in society. The social relationship between nodes can be quantified by discovering the decision feature attributes of nodes. Designing routing algorithms based on social relationships can find reliable forwarding nodes, thereby significantly improving the performance of message transmission. Most of the existing opportunistic social network routing algorithms only analyze the static topological attributes between nodes and quantify the social relationship by using limited characteristics [25,26,27,28], without fully considering the human community clustering and the variability of social relationship. When the social relationship between people becomes close, the amount of information transferred between nodes will increase. When the social relationship between people becomes estranged, the amount of information transferred between nodes will decrease. If the dynamic changes in the relationship between nodes are not considered, it may lead to a shortage or waste of node resources, thereby considerably reducing network performance.

Meanwhile, cache management in opportunistic social networks also needs more in-depth discussion. The “storage-save-forward” mechanism makes the waiting data stay in the node for a long time, but there is no user response. Therefore, there is a shortage of cache resources in the network, and it is challenging to update node data. Considering the sociality and mobility of network users, data forwarding has small data packets and extensive connections. Mass data make the amount of data forwarding in the network extremely high. The data forwarding strategy using flooding technology will cause information congestion, increasing the transmission delay [29,30]. It will significantly limit the performance of the network. Edge computing is a new computing model that pushes computing and storage to the edge of cloud computing [31,32]. Also, in the network information, the edge node cache information is used. These nodes are close to the central information node and cooperate to relieve the pressure on the central node. Simultaneously, it is usually difficult to connect to the Internet in some areas with low Internet penetration. Therefore, under these conditions [33], the network connection is unstable, and the information transfer rate is low. Besides, increasing the global penetration of the internet is costly, but its effectiveness is low [34].

Users hope to obtain information in a short time and realize stable and timely communication. The edge collaboration mechanism can effectively increase the message forwarding rate and reduce forwarding energy consumption and delay. For this reason, we have introduced edge nodes to optimize the information transmission efficiency of the backbone network and alleviate data congestion. Thus, central node storage pressure is relieved, and network performance and user experience are improved [35].

Therefore, in order to solve the above problems, this paper proposes an opportunistic social network routing algorithm based on user-adaptive data transmission (UADT). The algorithm will combine the similarity factor, communication factor, and transmission factor of network nodes and use information entropy and joint entropy theory to assign weights to related feature attributes. Besides, it can adaptively adjust the weight of each attribute according to network changes in different application scenarios, which will help to study the dynamic changes of social relationship between nodes. Moreover, it uses edge nodes and divides nodes into multiple communities to reconstruct the community structure, effectively reducing network delay and cache overhead and improving information transmission’s success rate.

The contributions of this article are as follows:

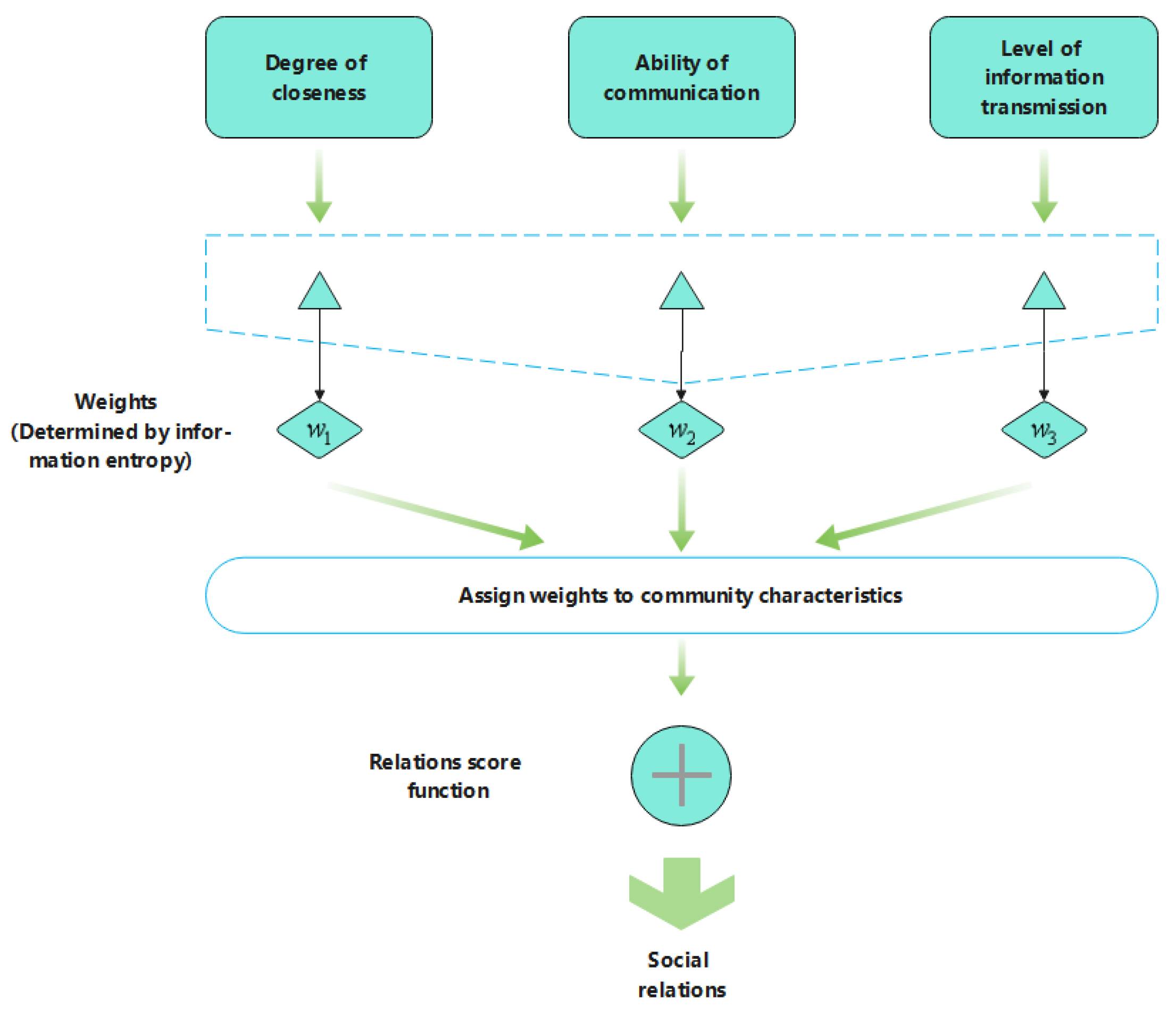
• Propose the concept of edge node based on the characteristics of information transfer, comprehensively consider the three decision feature attributes that affect the node relationship and the method of quantifying the social relationship between nodes so that the social relationship between nodes can be fully and intuitively measured.
• Introduce information entropy and joint entropy theory. The weight assigned to each attribute is adjusted in time according to the dynamic changes of the node relationship, which is convenient to find the best forwarding node. It can improve the efficiency of information transmission and reduce malicious forwarding.
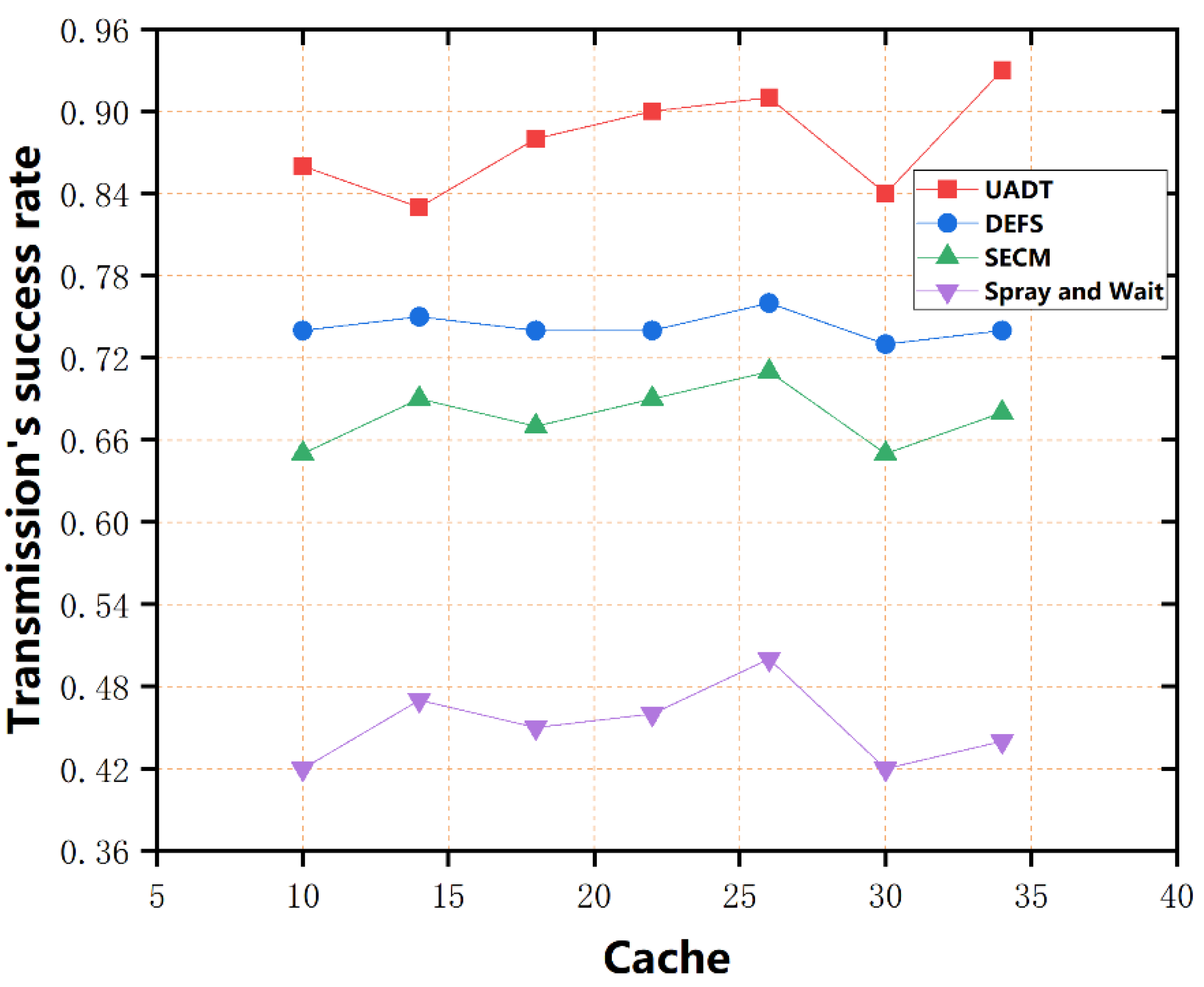
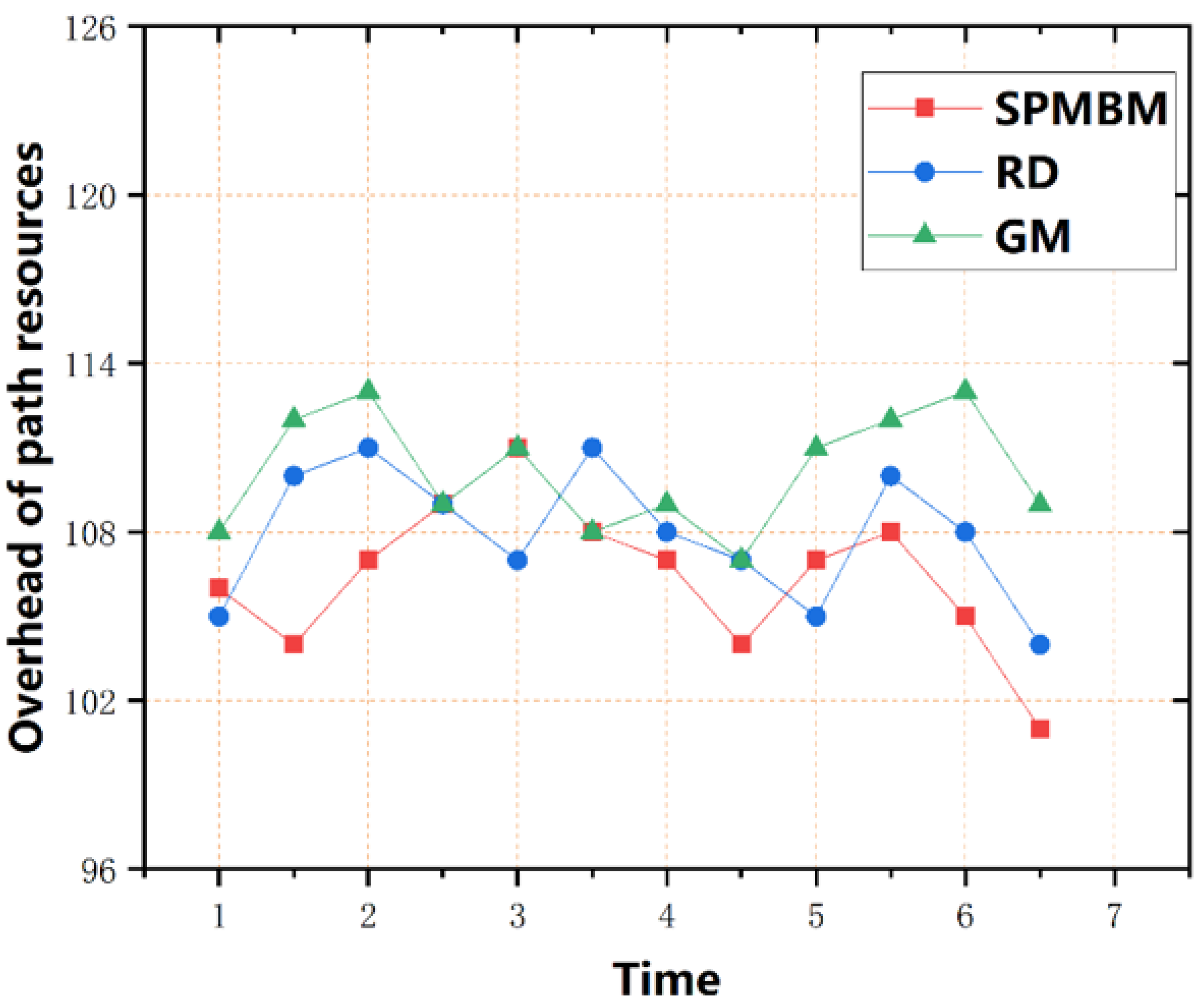
• This paper compares the UADT algorithm with the spray and wait algorithm, the DEFS (direction entropy-based forwarding scheme) [36] algorithm, and the SECM (status estimation and cache management) [37] algorithm to analyze each algorithm’s performance through simulation experiments. The results show that the algorithm proposed in this study has good performance in improving data transmission rate, reducing delay and overhead.

The remaining parts of this paper are composed as follows: The second part introduces the related research of opportunistic social network routing algorithms. Secondly, the third part explains our proposed network model and routing algorithm. Then, the fourth part carries on the simulation comparison experiments for several algorithms. The fifth part is a summary and prospect.

2. Related Work

In opportunistic social networks, nodes use the “storage-carry-forward” routing mechanism to deliver messages, so selecting neighboring forwarding nodes has become a core research topic of routing algorithm research. In the past two decades, scholars have proposed various algorithms to select appropriate relay nodes, thereby significantly improving data transmission efficiency. Some typical research results are listed below.

Epidemic algorithm [38] adopts the idea of flooding. When a node meets a node, it confirms the other party’s information and exchanges information that is missing from each other. As the nodes move, after enough information exchange, all nodes will receive data information. However, this sort of algorithm requires each node to have an ample buffer space, and in actual applications, it cannot guarantee that each node has sufficient network resources, resulting in poor data transmission effects. The spray and wait algorithm [39] is improved based on the epidemic algorithm. In the spray phase, the source node forwards the cached information to neighboring relay nodes. In the Wait phase, the nodes that have not completed the information transfer in the Spray phase use the replication forwarding strategy to directly transfer the information to the destination node. This algorithm reduces the copy of the data and reduces network routing overhead. Wang et al. [40] proposed the spray and wait algorithm based on node-link capabilities. The algorithm can dynamically allocate cached information based on the node-link strength and node-link stability, reasonably select forwarding nodes, and significantly improve network performance.

The PRoPHET algorithm [41] transmits information based on the probability of node encounters. When node and node meet, compare their forwarding probabilities. If the opposite node’s forwarding probability is greater than the forwarding probability of the source node, the information is passed to the opposite node. Otherwise, it continues to wait for other forwarding nodes. Through this kind of routing algorithm, the network can transmit more information with lower network resource overhead. Duan et al. [42] proposed an improved PRoPHET algorithm based on connection time, which added the duration of the encounter as an influencing factor of the predicted value of delivery.

The MaxProp algorithm [43] is developed based on the PRoPHET algorithm. It can calculate each message’s overhead in nodes to destination nodes and sorts the message according to the size of the overhead. When information is forwarded, the most probable information to reach the destination node is first forwarded. This algorithm improves the possibility of successful information transmission and reduces resource overhead and transmission delay. Das et al. [44] improved the MaxProp algorithm and proposed a MaxProp routing algorithm based on time-to-live. The algorithm focuses on the survival time of the information transmitted, ranks the data to be transmitted according to time, and avoids the loss of information with a high TTL value. Compared with the MaxProp algorithm, this algorithm considerably reduces resource usage and network fluctuations and improves resource utilization.

In addition, opportunistic social network routing algorithms based on community characteristics have been paid more and more attention. The DEFS algorithm [36] uses the main direction and direction entropy based on the information collected about the directions of the nodes in the network. Each node sends a message to another node with a different location and less direction entropy, which provides better balance. The SECM algorithm [37] can identify neighbors to calculate the probability of each information in the node and ensure that the node preferentially accesses the high-probability information, which reasonably allocates the cache. Experimental results show that, compared with the spray and wait algorithm, the SECM algorithm has a higher information forwarding rate and fewer hops. The node social features relationship evaluation algorithm (NSFRE) [45] establishes a fuzzy matrix according to the node’s various characteristics. Each node continuously iteratively filters out a part of the feature attributes according to the confidence coefficient and combines them to obtain a multi-dimensional similarity matrix. Moreover, it determines the weight under different characteristic attributes so as to select the appropriate forwarding node, which can effectively improve the message forwarding rate and reduce the network delay.

Based on the above research and problems, this paper proposes an opportunistic social network routing algorithm based on user-adaptive data transmission to solve the problems like low information transmission efficiency and waste of node resources in social networks. Theoretically, it can improve the efficiency of information transmission and the network’s life span and reduce network delays and waste of network resources.

3. Routing Algorithm Design

3.1. Node Community Decision Feature Design

In the opportunistic social network, mobile devices (such as smart phones, pads, etc.) connected to user nodes are often used to identify the community relationship between nodes. At the moment, most methods for calculating the community relationship between nodes measure the community relationship using scales like the number of encounters between nodes, the time of encounters, and the length of information exchange. However, in practical applications, the node relationship is dynamic, and the cost of node resources in some traditional routing algorithms is vast. For example, a community may have multiple nodes, where the source node selects an appropriate relay node for information transmission based on the social relationship between it and its neighbor nodes. The variety of node relationships changes the probability of encountering between nodes, and the phenomenon of information congestion may occur in the network, leading to a substantial increase in node resource overhead and ultimately reducing the efficiency of message forwarding.

To prevent excessive overhead in the network and improve the efficiency of message forwarding, we designed an opportunistic social network routing algorithm based on user-adaptive data transmission to quantify the dynamic relationship between nodes and select appropriate forwarding nodes. Because the nodes under the opportunistic network of mobile devices conform to the attributes of human society, this article uses the multiple feature attributes of nodes (similarity factor, communication factor, transmission factor) to express the social relationship, such as relevance, interactivity, uncertainty, and forwarding ability from multiple aspects, as shown in Figure 1. Then, the information entropy theory is used to assign weights to different attributes to calculate the dynamic community relationship between nodes. Finally, we calculate and compare the community relationship between nodes to select the best forwarding node.

First, we define a topological structure $G_0=(A_0,B_0,W)$ according to the characteristics of the wireless transmission of messages by nodes through encounters. $A_0$ includes all nodes in the network. $B_0$ includes all edges in the network, which can be expressed as $B_0=\{(a,b)|a\in A_0,b\in B_0\}$, where $a$ and $b$ are nodes in the network, and $W$ is the weight between two nodes. Only when the maximum transmission radius is greater than or equal to the distance between two nodes is there an edge between the two points.

Besides, because of the high information transfer rate of the optimal forwarding node, the node’s cache may overflow due to too much information. Traditional cache management solutions release cache resources by directly clearing information. This method can easily reduce the information transfer rate. In this article, we propose a concept of the edge node to avoid invalid cache redundancy. Suppose there are two communities in the community network, community1, community2. User nodes will move and transmit information. When the optimal forwarding node cache is full, the neighbor nodes (edge nodes) cache will empty or schedule the information. When the nodes in the cache of the optimal forwarding node are complete, the edge nodes that have excess cache space should be transmitted.

Then, we design the specific node attributes as follows:

Step 1: Quantify the relationship between nodes

In order to help measure the social relationship between two different nodes, we propose an evaluation index (i.e., the node’s relationship score) to quantify this abstract relationship. In the opportunity social network, the relationship score between nodes a and b can be measured as $S(a,b)$:

$$\begin{array}{l}S(a,b)={\displaystyle \sum {}_{i=1}^n}{w}_i{p}_i(a,b),0\le w_i\le 1,\\ {\displaystyle \sum {}_{i=1}^n}{w}_i=1,a,b\in N\end{array}$$

(1)

where $w_i$ are the weights of different decision feature attributes, $p_i$ are the decision feature attributesbetween different nodes, which describe the relationship between a pair of nodes from a certain perspective. In this paper, decision feature attributes include similarity factor, communication factor, and transmission factor between nodes. $n$ is the sum of decision feature attributes, and $N$ is the total number of nodes in the network. The larger the value of $S(a,b)$, the closer the relationship between the node $a$ and the node $b$; the smaller the value of $S(a,b)$, the more distant the relationship between the node $a$ and the node $b$. If $S(a,b)$ = 0, there is no relationship between nodes $a$ and $b$; if $S(a,b)$ = 1, nodes $a$ and $b$ are the same node.

Step 2: Calculate the similarity factor between nodes

In opportunistic social networks, the interaction model between nodes reflects the similarity factor between nodes, and similarity can evaluate the correlation between nodes. To accurately describe the community relationship between nodes, the similarity factor between nodes must be obtained. The SimBet [46] routing proposed by Elizabeth Daly et al. defines the similarity parameters of nodes. It refers to the degree of similarity of nodes in the law of motion, so two nodes with more similarity have more common neighbors. The closer the similarity factor is to 1, the more similar the two nodes are. The closer the similarity factor is to 0, the more dissimilar the two nodes are. Therefore, we can use the similarity factor to characterize the similarity between nodes. Assuming that the node $a$ in the network is the source node, the node $b$ is the destination node. Node $a$ can transmit information to node $b$, and their neighbor nodes act as transmission media in this process. If the neighbor nodes of nodes $a$ and $b$ are $\eta (a)$ and $\eta (b)$, the similarity factor between $a$ and $b$ can be defined as

$$Sm(a,b)=\frac{\eta (a)\cap \eta (b)}{\eta (a)\cup \eta (b)}$$

(2)

where $\eta (a)\cap \eta (b)$ is the set of neighbor points common to nodes $a$ and $b$, and $\eta (a)\cup \eta (b)$ is the sum of the neighbor nodes of nodes $a$ and $b$.

With the advancement of positioning technology, nodes in the network can obtain location information through the mobile devices they carry. The location information can reveal the movement of the node. The social relationship between nodes with similar moving trajectories is relatively close. The position information of the nodes can be used to infer the state between the nodes regularly appearing in similar paths, and the corresponding decision feature attributes can be obtained.

Step 3: Compute the communication factor between nodes

In the opportunistic social network, the transmission of information requires communication between nodes, and the success of node communication will directly affect the quality of information transmission in the network. Thus, the communication factor of nodes can help measure the dynamic community relationship between nodes. Suppose $C{o}_t(a,b)$ is the evaluation of node $a$ on node $b$ at time $t$, and $l=\{l_1(a,b),l_2(a,b),\dots ,l_e(a,b)\}$ is the preference of $a$ compared to $b$ in the $e$ times that $a$ and $b$ meet, where $l_1(a,b)\in [0,1],t\in [1,e],e\in [0,E]$. The elements in $l$ are arranged from far to near according to the time of encounter. So, the communication factor measurement index of $a$ to $b$ is defined as

$$C{o}_t(a,b)=C{o}_t(a,b)+\alpha \times \frac{{\displaystyle \sum _{i=1}^e{l}_i(a,b)\times \beta (t)}}{E}-Loss(a,b)$$

(3)

where the weight factor is $\alpha$, the maximum number of effective encounters between $a$ and $b$ is $E$, and $\beta (t)$ is used to control the degeneration of communication factor over time, defined as

$$\beta (t)=\{\begin{array}{c}1,\Delta t=0\\ \frac{1}{{(t-t^{\prime })}^{\frac{1}{\epsilon }}}=\frac{1}{\Delta t^{{}^{\frac{1}{\epsilon }}}},\Delta t\ne 0\end{array}$$

(4)

where $t$ is the duration of the communication between nodes $a$ and $b$, $t^{\prime }$ is the duration of the previous communication between nodes $a$ and $b$, $\Delta t$ is the difference between the last node meeting time and the current node meeting time, and $\epsilon$ is the control factor.

$Loss(a,b)$ is the loss function, which is used to quantify the information lost when $a$ communicates $b$:

$$Loss(a,b)=\frac{u}{\kappa \times e}$$

(5)

where $u$ is the number of times that node $a$ fails to deliver complete information, $e$ ≤ $E$ is the number of all encounters of $a$ and $b$, and $\kappa$ is used to control the degree of information loss.

Step 4: Measure the transmission factor between nodes

In the opportunistic social network, information may pass through several relay nodes to transfer information from a source node to a destination node. The information transmission level of these relay nodes indirectly shows the relationship score between the source node and the destination node. Since there may be multiple paths for information from the source node to the destination node, and the number of relay nodes through different paths may be different, this article will use a weighted method to calculate there lay nodes’ transmission factor. Assuming that the set of relay nodes in the information transmission path is $\{r_1,r_2,\dots ,r_i\}$, and the relationship score of the relay node $r_i$ to its immediate successor is denoted as $S(r_i,r_{i+1})$, the transmission factor of node $a$ compared to $b$ is:

$$TL(a,b)=\{\begin{array}{c}0,k=0\\ \frac{{\displaystyle \sum {}_{i=1}^n(\delta (r_{i+1})\times S(r_i,r_{i+1}))}}{{\displaystyle \sum {}_{i=2}^k\delta (r_i)}},k\ge 1\end{array}$$

(6)

where $k$ is the number of relay nodes; $\delta (r_i)$ is the degenerate function of information transmission paths:

$$\delta (r_i)=\{\begin{array}{c}1,K=0\\ {\displaystyle {\displaystyle \prod }_{i=1}^{level}}\lambda (u_i,u_{sub}),K\ge 1\end{array}$$

(7)

where $\lambda (u_i,u_{sub})$ is the relationship score between the relay node $u_i$ and its successor node $u_{sub}$ on the information transmission path; $K$ is the number of hops between the relay node and the destination node.

Step 5: Assign the weight of each attribute of nodes

So as to calculate the community relationship between nodes and find the best forwarding node, in addition to finding the attributes mentioned above of nodes, it is also necessary to analyze the correlation between the attributes. Because the community relationship between nodes is dynamically changing, we use information entropy and joint entropy [47] to measure this uncertainty. The following formula can express information entropy and joint entropy:

$$H(A_u)=-{\displaystyle \sum _{a_u\in A_u}f(a_u){\log }_2}(f(a_u))$$

(8)

$$H(A_u,A_v)=-{\displaystyle \sum _{a_u\in A_u,a_v\in A_v}f(a_u,a_v){\log }_2}(f(a_u,a_v))$$

(9)

where $H(·)$ is the information entropy and $f(a_u)$ is the output probability function. The greater the variable’s uncertainty is, the greater the entropy is, and the greater the amount of information needed to determine the variable is.

In addition, since mutual information and conditional mutual information are obtained through the addition and subtraction of information entropy, they can be used to describe the degree of correlation between two variables. Therefore, this paper introduces mutual information and conditional mutual information to compare the correlation between node attributes, thereby Assign appropriate weights to each attribute. The following formula can express mutual information and conditional mutual information:

$$I(D;A_u)=H(A_u)+H(D)+H(D,A_u)$$

(10)

where $I(D;A_u)$ is mutual information, namely the amount of information that variable $A_u$ has about variable $D$.

$$\begin{array}{l}I(D;A_u|A_{\mathrm{v}})=H(D|A_v)-H(D|A_u,A_v)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=H(A_u,A_{\mathrm{v}})+H(D,A_v)-H(A_v)-H(D,A_u,A_v)\end{array}$$

(11)

where $H(D|A_v)$ is the conditional entropy of information $D$ under the condition of known feature $A_v$; $H(A_u,A_{\mathrm{v}})$ is the joint entropy of feature $A_u$ and feature $A_v$.

The larger the value of $I(D;A_u|A_{\mathrm{v}})$ is, the smaller the number of features carrying information $D$ apart from the feature $A_u$ is, and the better the compatibility of the feature $A_u$ to the information $D$ is. The smaller the value of $I(D;A_u|A_{\mathrm{v}})$ is, the bigger the number of features that carry information $D$ is, or the feature $A_u$ does not carry information $D$, and the worse the compatibility of feature $A_u$ to information $D$ is. According to the above description, we can get the following formula:

$$\rho (1)=\arg \underset{u}{\max }I(D;A_u)$$

(12)

$$\rho (J+1)=\arg \underset{u}{\max }\underset{g(u,j)}{\underbrace{\left\{\underset{q\le j}{\min }I(D;A_u|A_{\rho (q)})\right\}}}$$

(13)

where $\rho (1),\cdot \cdot \cdot ,\rho (J+1)$ is a part of the feature subset that carries as much information as possible to minimize $H(D|A_{\rho (1)},\cdot \cdot \cdot ,A_{\rho (J)})$.

According to the theory proposed above, we can obtain multiple attributes that affect node communities’ characteristics and combine information entropy-related knowledge to assign weights to different attributes, thereby obtaining the community relationship between nodes. By comparing the community relationships of different nodes in the network, nodes with high relationship scores are selected for information transmission. The specific algorithm is explained as Figure 2.

3.2. Node Relationship Analysis

There may be no steady connection path for communication between nodes in opportunistic social networks, so it is necessary to design nodes with a message forwarding mechanism of “accept-carry-forward”. To obtain appropriate forwarding nodes and forwarding timings and to effectively analyze the relationship between nodes, we need to prove that changes in node relationships will lead to changes in the structure of the opportunistic social network. Our proposition and proof are as follows.

According to the characteristics of the weight distribution of the opportunistic social network, we can define the unitization degree of the community M as

$$\psi (m)=\frac{{\tau }_m}{\tau }-\frac{{\mu }_a{}^2}{{(2\tau )}^2}=\frac{4\tau {\tau }_m-{\mu }_a{}^2}{{(2\tau )}^2}.$$

(14)

$\psi (m)$ is the degree of unitization of community $M$. $\tau$ is the total weight of the opportunity social network. ${\tau }_m$ is the total weight of community $M$. ${\mu }_a$ is the total score of source node $a$ in the community. $\Delta \varsigma$ is the difference before and after the weight change. ${\varsigma }_{ab}$ is the weight of the connection path between the source node $a$ and its neighboring node $b$, and ${\mathsf{\Gamma }}_M^a$ is the path weight of the source node $a$ in the community $M$.

Proposition 1.

If the movement of the source node $a$ in the social network meets the condition $(\frac{{\mu }_a{\mu }_b}{2\tau })<{\varsigma }_{ab}<((\frac{{\mu }_a{\mu }_b+{\mu }_a\Delta \varsigma +\Delta {\varsigma }^2}{2(\tau +\Delta \varsigma )})+\Delta \varsigma )$, the node will be separated from the community of node $b$.

We propose a hypothesis that community $M$ is divided into two sub-communities $S{C}_{m1}$ and $S{C}_{m2}$, where node $a$ and node $b$ are in community $M1$ and community $M2$, respectively. The total weight in the network structure declined.

Then,

$$\{\begin{array}{c}{\tau }_{m1}+{\tau }_{m2}<\tau \\ \frac{4\tau {\tau }_{m1}-{\mu }_a{}^2}{{(2\tau )}^2}+\frac{4\tau {\tau }_{m2}-{\mu }_b{}^2}{{(2\tau )}^2}<\frac{4\tau ({\mu }_a+{\mu }_b+{\varsigma }_{ab})-{({\mu }_a+{\mu }_b)}^2}{{(2\tau )}^2}\\ {\varsigma }_{ab}>\frac{{\mu }_a{\mu }_b}{2\tau }\end{array}$$

(15)

Due to the reduction of the total weight, we can simplify the above formula to

$$\{\begin{array}{c}{\tau }_{m1}^{\prime }+{\tau }_{m2}^{\prime }>{\tau }^{\prime }\\ {\varsigma }_{ab}<(\frac{{\mu }_a{\mu }_b+{\mu }_a\Delta \varsigma +\Delta {\varsigma }^2}{2(\tau +\Delta \varsigma )})+\Delta \varsigma \end{array}$$

(16)

According to the above proof, if the two sub-communities $S{C}_{m1}$ and $S{C}_{m2}$ meet the condition $(\frac{{\mu }_a{\mu }_b}{2\tau })<{\varsigma }_{ab}<((\frac{{\mu }_a{\mu }_b+{\mu }_a\Delta \varsigma +\Delta {\varsigma }^2}{2(\tau +\Delta \varsigma )})+\Delta \varsigma )$, we can separate the community $M$ into two parts.

Proposition 2.

If there is a connection path between source node $a$ and node $b$, and this path is the only path of node $b$, the weight of this path is reduced, and node $b$ will not be separated from the community.

If node $b$ is separated from the current community $M$, it needs to meet the following conditions:

$$\{\begin{array}{c}{\tau }_{m1}+{\tau }_{m2}<\tau \\ \frac{4\tau {\tau }_{m1}-{\mu }_a{}^2}{{(2\tau )}^2}+\frac{4\tau {\tau }_{m2}-{\mu }_b{}^2}{{(2\tau )}^2}<\frac{4\tau ({\mu }_a+{\mu }_b+{\varsigma }_{ab})-{({\mu }_a+{\mu }_b)}^2}{{(2\tau )}^2}\\ {\varsigma }_{ab}>\frac{{\mu }_a{\mu }_b}{2\tau }\end{array}$$

(17)

After considering the weight change, we can get the formula as follow:

$$\{\begin{array}{c}{\tau }_{m1}^{\prime }+{\tau }_{m2}^{\prime }>{\tau }^{\prime }\\ {\varsigma }_{ab}<(\frac{{\mu }_a{\mu }_b+{\mu }_a\Delta \varsigma +\Delta {\varsigma }^2}{2(\tau +\Delta \varsigma )})+\Delta \varsigma \end{array}$$

(18)

It can be stated as:

$$\frac{{\mu }_a{\mu }_b}{2\tau }<{\varsigma }_{ab}<\frac{{\mu }_a{\mu }_b+{\mu }_a\Delta \varsigma }{2(\tau +\Delta \varsigma )}$$

(19)

Because

$$\frac{{\mu }_a{\mu }_b+{\mu }_a\Delta \varsigma }{2(\tau +\Delta \varsigma )}-\frac{{\mu }_a{\mu }_b}{\tau }=\frac{{\mu }_a\Delta \varsigma (\tau -{\mu }_b)}{\tau (\tau +\Delta \varsigma )}<0\left(\Delta \varsigma <0\right)$$

(20)

We can deduce

$$\frac{{\mu }_a{\mu }_b+{\mu }_a\Delta \varsigma }{2(\tau +\Delta \varsigma )}<\frac{{\mu }_a{\mu }_b}{\tau }$$

(21)

In the end we can prove that Formula (19) is a false inference.

According to the above proof, we can deduce that if there is a connection path between two nodes, this path is the only path of the node. Then, the weight of this path is reduced, and this node will not be separated from the community.

Proposition 3.

There are two different communities $M$ and $N$, and node $a$ is in community $M$. If the weight of the connection path between the two communities rises, $R_N^{out}$ will rise, $R_M^{in}$ will reduce, and the opportunistic social network will change. If the weight of the connection path between node $a$ and community $M$ rises, the opportunistic social network will also change.

The initial values of $R_M^{in}$ and $R_N^{out}$ are

$$R_M^{in}=r_M^a-\frac{{\mu }_a({\mu }_M-{\mu }_a)}{2\tau }$$

(22)

$$R_N^{out}=r_N^a-\frac{{\mu }_a{\mu }_N}{2\tau }$$

(23)

If the weight increases, then

$$R_M^{out}=r_M^a-\frac{{\mu }_a{\mu }_M+{\mu }_M\Delta \varsigma -({\mu }_a{}^2+{\mu }_a\Delta \varsigma )}{2(\tau +\Delta \varsigma )}$$

(24)

$$R_N^{out}=r_N^a+\Delta \varsigma -\frac{{\mu }_a{\mu }_N+({\mu }_a+{\mu }_N)\Delta \varsigma +\Delta {\varsigma }^2}{2(\tau +\Delta \varsigma )}$$

(25)

$$\begin{array}{l}{R}_N^{out}{}^{\ast }-R_N^{out}=\frac{{\mu }_a{\mu }_N}{2\tau }+\Delta \varsigma -\frac{{\mu }_a{\mu }_N+({\mu }_a+{\mu }_N)\Delta \varsigma +\Delta {\varsigma }^2}{2(\tau +\Delta \varsigma )}\\ \ge \frac{{\mu }_a{\mu }_N+2\tau \Delta \varsigma }{2(\tau +\Delta \varsigma )}-\frac{{\mu }_a{\mu }_N+({\mu }_a+{\mu }_N)\Delta \varsigma +\Delta {\varsigma }^2}{2(\tau +\Delta \varsigma )}\\ =\frac{2\tau -({\mu }_a+{\mu }_N+\Delta \varsigma )}{2(\tau +\Delta \varsigma )}\Delta \varsigma \end{array}$$

(26)

Since $\tau >0$, $\mu >0$, and $2\tau ={\displaystyle \sum {\mu }_i}$, we can get $2\tau >2\tau -({\mu }_a+{\mu }_N+\Delta \varsigma )$ and $R_N^{out}{}^{\ast }-R_N^{out}>0$. Thus, when the weight of the connection path increases, $R_N^{out}$ of node $a$ also increases.

Similarly,

$$R_M^{in}{}^{\ast }-R_M^{in}=\frac{{\mu }_a-\tau }{2\tau (\tau +\Delta \varsigma )}({\mu }_M-{\mu }_a)\Delta \varsigma$$

(27)

Since $\tau >0$, $\Delta \varsigma >0$, ${\mu }_M-{\mu }_a>0$, and ${\displaystyle \sum {\mu }_i}>{\mu }_a$, we can get ${\mu }_a-\tau <0$. In a word, when the weight of the connection path decreases, $R_M^{in}$ of node $a$ will also decrease.

According to the above design and weight distribution of the multiple community attributes of nodes, as well as the analysis of node relationships, we can find the best forwarding nodes and find that changes in node relationships will lead to changes in the structure of the opportunistic social network. In the next section, we will compare our model’s performance with other classic models from many aspects through simulation experiments.

4. Simulation

This article uses Opportunity Network Environment (ONE) as our simulation tool to measure the performance of UADT in practical applications. This tool can obtain the movement trajectory of nodes by controlling the movement of nodes and then record various details of the information transmission process. Also, this research will simulate three classic routing algorithms: spray and wait [39], DEFS (direction entropy-based forwarding scheme) [36], and SECM (status estimation and cache management algorithm) [37] and evaluate the advantages and disadvantages of UADT through comparison. A brief introduction of the algorithm is as follows:

• Spray and wait [39]: In the spray phase, the algorithm forwards the information to neighboring nodes by flooding. If no available node is found, the information is directly copied to the target node in the Wait phase.
• DEFS [36]: The algorithm calculates the node’s primary direction and direction entropy to capture the certainty of the node’s direction. The source node selects a node with a slight direction entropy as a relay node for message forwarding, which balances network traffic and transmission delay well.
• SECM [37]: The algorithm can analyze the relationship between the source node and its neighbor nodes and compare the forwarding probabilities of different neighbor nodes, thereby adjusting the cache information between nodes. The source node selects a neighbor node with a higher probability and uses node coordination to transfer information, which effectively utilizes cache space.

The parameters used to measure the above algorithms’ performance in opportunistic social networks mainly include the following four items: transmission’s success rate, average end-to-end delay, overhead of path resources, and energy consumption [48].

Considering the data source of the algorithm, this paper selects an open street map to edit the city map. There are different parks, streets, and shops on the map. They can show the natural environment. As shown in Figure 3, it uses a real map of Helsinki, which is suitable for node message forwarding activities.

The simulation parameter settings in this study are shown in

Table 1. Experimental parameters setting.

Parameter	Value
Simulation time	1–6.5 h
Simulation area	2500 m × 3200 m
Cache	10–34 M
TTL	6 h
Data packet transmission time	27–40 s
Maximum transmission radius	12 m
Message size	255 KBps
Interval time between message generation	28 s
Node initial energy	100 J
The packet loss threshold	13%
Pedestrian speed	0.8–4.8 m/s
Frequency range	25–35 Hz

. The simulation time is 1–6.5 h, and the simulation area is 2500 m × 3200 m. The cache of each node is 10–34 M, and the survival time is 6 h. All nodes move randomly at a speed of 0.8–4.8 m/s. The node’s transmission model is the social model, the message size is 255 KBps, the maximum transmission radius is 12 m, the data packet transmission time is 27–40 s, the sending interval is 28 s, the loss threshold is 13%, and the frequency range is 25–35 Hz. Simultaneously, the energy of a node is initially 100 J, and the energy consumption of each data packet sent is 1 J.

As the node cache space increases, network performance will also change. Based on the simulation experiment’s data, the relationship between time and four parameters of four algorithms in the SPMBM (shortest path map-based movement) model [49] is shown in Figure 4, Figure 5, Figure 6 and Figure 7.

Figure 4 shows the relationship between buffering and transmission’s success rate among the four algorithms. Among all the algorithms, the transmission’s success rate of UADT is the highest, up to 0.93. Because UADT dynamically scores the relationship between nodes according to the nodes’ multiple attributes, to select the optimal node for information transmission, the cache resource utilization rate is high, so the transmission’s success rate is the highest. The SECM and DEFS algorithms are similar. They use different indicators to measure the probability of information forwarding. By comparing the forwarding probability to select the appropriate node for information transmission, the transmission’s success rate is higher. Nevertheless, when the cache space is large, the cache utilization of the two is reduced, and the information transfer rate is subject to certain constraints, with an average of 0.68 and 0.74. The algorithm with the lowest transmission’s success rate is spray and wait. Because its essence is a kind of flooding algorithm, nodes need to copy a large number of data packets for information transmission. These data packets will occupy many cache resources, resulting in a decrease in the number of available cache resources, information can’t be forwarded in time, and congestion occurs at nodes. According to the experimental results analysis, the transmission’s success rate of the UADT algorithm is 75% higher than that of the traditional algorithm.

Figure 5 shows the relationship between cache and average overhead in the four algorithms. From the data in the figure, we can find that as the cache space increases, the average overhead of the four algorithms is greatly reduced. Compared with the other three algorithms, the overhead of UADT on average is significantly reduced, from 145 to 19. Because UADT selects the relay node with the highest relationship score, the utilization of cache space is improved, and the number of message copies is markedly reduced. The average cost of SECM and DEFS is higher than that of UADT, which respectively drops from 152 and 140 to 31 and 25. Because the two need to calculate the forwarding probability and similarity of the nodes, and the appropriate forwarding node is selected by comparing the probability and the similarity, specific network resources will be consumed. However, UADT measures nodes’ relationships through multiple nodes’ attributes and uses information entropy theory to make dynamic adjustments. The considerations are completer, and the accuracy of selecting the best forwarding node is higher than the SECM and DEFS. The spray and wait algorithm copies a large amount of data and spreads the data to various nodes in the network by flooding, resulting in a large number of cache resources being occupied by these data, reducing the effective cache, so the average overhead is relatively large.

Figure 6 shows the relationship between cache and energy consumption in the four algorithms. From the data shown in Figure 6, we can find that the algorithm with the lowest energy consumption among the four algorithms is UADT. The reason is that UADT dynamically measures the relationship between nodes through feature selection so that more cache space is used for practical information forwarding, reducing the consumption of cache resources by invalid data copies, and reducing network energy consumption. The spray and wait algorithm copies a large number of messages, resulting in low cache resource utilization. A large amount of cache is consumed by invalid data, which causes the valid data is blocked at relay nodes. Thus, the network requires more energy to carry out information transmission to maintain its regular operation. SECM and DEFS adopt the approach of encounter transfer. They obtain the data through a single copy and calculate the encounter probability and matching degree of nodes to determine the suitable transmission scheme. To a certain extent, information transmission speed and success rate are improved, and the energy consumption is reduced. Compared with the spray and wait algorithm, the energy balance performance of SECM and DEFS algorithm is better. It can be seen from the above results that UADT has the best effect in controlling energy consumption. When the cache is larger than 30 M, the energy usage is only 46 J.

Figure 7 shows the relationship between the cache and the average end-to-end delay in the four algorithms. Through the data in the graph, we can get that the average delay of nodes increases with the increase of the cache size. Because as the cache increases, the number of message copies in the network increases, and many cache resources are consumed by these useless data, resulting in a decrease in the success rate and rate of information delivery and increased network delay. The spray and wait algorithm has the most considerable delay among the four algorithms, with an average delay of 480 time-units. The reason is that it uses the flooding algorithm to randomly select neighbor nodes for information transfer so that a large number of unnecessary message copies consume node cache resources, resulting in high network delay and an extensive adjustment range of cache resources. The UADT algorithm’s delay is stable at about 57, and the adjustment range of the cache resources is the smallest. The reason is that we have proposed a better method for selecting relay nodes. By measuring nodes’ various attributes and considering the dynamic changes in the relationship between nodes, the nodes with high relationship scores are given priority to forwarding data so that the information has been transmitted through the best relay node. Thus, the data reachability is higher, and the average end-to-end delay is lower than other algorithms. Compared with the SECM algorithm, the delay of the UADT algorithm is reduced by 70%.

In opportunistic social networks, in addition to the node cache space, the network running time is also a vital reference variable. Also, different mobile modes will also affect the transmission of information on the network. Accordingly, this article will use three mobile models for simulation experiments to verify the stability of UADT in different environments. They are random direction mobility model (RD), Gauss–Markov mobility model (GM), and SPMBM (shortest path map-based movement) [49]. According to the experimental data, the relationship between time and four parameters in the three mobile models is shown in Figure 8, Figure 9, Figure 10 and Figure 11.

The relationship between the transmission success rate and time of the UADT algorithm in different mobile models is shown in Figure 8. The transmission’s success rate of the UADT algorithm in the three mobile models has increased over time. Among them, the transmission success rate of the SPMBM model is the highest, reaching a peak of 0.671 at 5 h. The transmission success rate of the RD model is slightly lower than that of SPMBM, reaching the highest value of 0.63 at 6.5 h. Comparing the three mobile models, the UADT algorithm performs best in the SPMBM model, and the transmission success rate in the GM model is lower than that in the RD model.

The relationship between energy consumption and time in different mobile models of the UADT algorithm is shown in Figure 9. The energy consumption of the UADT algorithm in the three mobile models increases as time rises, and the three are similar. It can be seen that the performance of the UADT algorithm in node forwarding messages is relatively reliable and requires less additional energy when changing the mobility model.

The relationship between the end-to-end delay and time of the UADT algorithm in different mobile models is shown in Figure 10. We can observe from the results that the three mobile models’ delays are between 170 and 215. Among them, the RD model has the highest delay which hits the peak at 213, and the SPMBM model has the lowest delay with a peak value of 201. Experimental results illustrate that the UADT algorithm has the best compatibility with the SPMBM model in terms of message forwarding.

The relationship between path resource overhead and time in different mobility models of the UADT algorithm is shown in Figure 11. The cost of the three mobile models is not remarkably different, all between 105 and 115. As time increases, nodes continue to move in the network, a large amount of data enters the network and is forwarded through node encounters, and the task of message forwarding is shared between nodes.

5. Conclusions

This paper proposes an opportunistic social network routing algorithm (UADT) based on user-adaptive data transmission. The algorithm measures the decision feature attributes of the nodes in the opportunistic social network from many aspects. It uses information entropy and feature selection to dynamically assign weights to the features, thereby selecting the best neighbor nodes to transmit information and ensuring high-speed data transmission in the network. Experimental results show that compared with spray and wait, DEFS, and SECM, UADT performs better in improving the transmission success rate, reducing end-to-end delay and path resource overhead. Additionally, UADT demonstrates excellent performance in three different mobile models, which means that the algorithm has high stability in different environments.

The interaction between IoT devices requires rapid transmission of a large amount of information, resulting in a large quantity of cache space being occupied. Accordingly, the allocation of buffer space in the context of mass message transmission will become the focus of our future work. We will study more efficient data transmission mechanisms, reasonably adjusting node cache resources to optimize the overall network structure.