A Cartesian Genetic Programming Based Parallel Neuroevolutionary Model for Cloud Server’s CPU Usage Prediction

Abstract

Cloud computing use is exponentially increasing with the advent of industrial revolution 4.0 technologies such as the Internet of Things, artificial intelligence, and digital transformations. These technologies require cloud data centers to process massive volumes of workloads. As a result, the data centers consume gigantic amounts of electrical energy, and a large portion of data center electrical energy comes from fossil fuels. It causes greenhouse gas emissions and thus ensuing in global warming. An adaptive resource utilization mechanism of cloud data center resources is vital to get by with this huge problem. The adaptive system will estimate the resource utilization and then adjust the resources accordingly. Cloud resource utilization estimation is a two-fold challenging task. First, the cloud workloads are sundry, and second, clients’ requests are uneven. In the literature, several machine learning models have estimated cloud resources, of which artificial neural networks (ANNs) have shown better performance. Conventional ANNs have a fixed topology and allow only to train their weights either by back-propagation or neuroevolution such as a genetic algorithm. In this paper, we propose Cartesian genetic programming (CGP) neural network (CGPNN). The CGPNN enhances the performance of conventional ANN by allowing training of both its parameters and topology, and it uses a built-in sliding window. We have trained CGPNN with parallel neuroevolution that searches for global optimum through numerous directions. The resource utilization traces of the Bitbrains data center is used for validation of the proposed CGPNN and compared results with machine learning models from the literature on the same data set. The proposed method has outstripped the machine learning models from the literature and resulted in 97% prediction accuracy.

1. Introduction

Demand for cloud computing applications upsurges with the advent of new technologies like the Internet of Things and smart cities. According to Gartner’s survey, the mandate for IaaS services will be sturdy in the future (https://www.gartner.com/doc/3849464/survey-analysis-impact-iaas-paas). The projected per second Internet traffic spawned by the data center in 2021 will be 655,864 Giga Bytes (https://www.cisco.com/c/en/us/solutions/collateral/service-provider/global-cloud). The profoundly loaded data centers will consume colossal volumes of energy. In a data center, the information technology (IT) equipment such as communication links, switching and aggregation elements, servers consume 40% of the total data center energy [1,2], and servers consume 27% of the data center energy [3]. A cloud data center server remains idle from 70% to 80% of the time [4]. For energy saving in an idle time of the server, investigators in [5] and [6,7] have proposed dynamic voltage and frequency scaling (DVFS) and hot plugging of CPU cores. The DVFS and hot plugging mechanisms implement scaling reactively without using any intelligence/knowledge about resource usage or the workload patterns and trends. The energy conservation capability of DVFS and hot plugging mechanisms can be boosted by using CPU usage estimation/prediction beforehand the scaling of frequency or cores [7,8].

Cloud servers execute diverse workloads with diverse CPU (Central Processing Unit) requirements. On the other hand, clients’ requests reach at uneven interludes to cloud servers. Consequently, the diverse nature of workloads and the irregular arrival of clients’ requests make CPU usage prediction a puzzling task [9]. We propose a Cartesian genetic programming (CGP) based parallel neuroevolutionary prediction model to solve the CPU usage prediction problem.

Neuroevolution is a technique used for evolving parameters of a neural network using evolutionary operators such as mutation and crossover. A neural network is encoded into strings called chromosomes, and each substring is called a gene. The encoded genes of the chromosome are evolved with mutation/crossover to form new chromosomes (offspring). These chromosomes are evaluated for fitness, and the best one is selected as the parent for producing next-generation offspring. This process of generation, evaluation, and the selection continues until either producing the desired solution or reaching the maximum number of generations/iterations [10].

In conventional neuroevolution, the topology of the neural network is fixed, and only the weights of the network are evolved. In the proposed technique, we use parallel neuroevolution varying weights, topology, and the number of neurons in the network. It boosts the learnability of the network. Moreover, we use diverse initialized seeds to avoid local optima and to enhance prediction accuracy. The architecture uses a sliding window that averages the predicted outputs. Technical contributions are in resource usage estimation accuracy, improved learnability, and escaping from local optima. We highlight our technical contributions as follows:

• We present the mathematical model of CGP based neural network with parameters and hyperparameters;
• We evolve synaptic weights, topology, and the number of neurons for boosting learnability;
• We conduct multiple search path optimization to avoid local optima;
• We use a sliding window-based parallel architecture that makes several parallel predictions. These predictions are averaged for improving accuracy.

2. Purpose of Resource Prediction and Related Work

CPU usage can be realized as a function of time; hence it belongs to the time-series class. In literature, numerous statistical and machine learning techniques have been proposed for time series (e.g., workload, CPU usage) forecasting. In statistical techniques, linear regression (LR), autoregression (AR), and autoregressive integrated moving average (ARIMA) have been used for forecasting CPU usage time-series. Rodrigo N Calheiros et al. used ARIMA for workload prediction of real traces of requests to web servers [11]. They used a built-in library (i.e., auto.arima) of the forecast package (of the R statistical language) for predicting web servers’ request time-series. Sadeka Islam et al. [12] used ANN and LR for predicting CPU usage. They used third-party packages dynlm [13] and nnet [14] in the R-Project [15] for LR and ANN, respectively. John J. Prevost et al. [16] prophesied clients’ requests on the cloud with both ANN and AR for hot plugging of cloud nodes. They used the back-propagation optimization scheme for the training of ANN weights. Ismaeel et al. [17] used an extreme learning machine (ELM) with control of the training process for fast learning. F. Farahnakian et al. in [18] used k-nearest neighbor (KNN) for forecasting over-utilized and under-utilized cloud servers. A.Y. Nikravesh et al. [19] applied SVR (support vector regression) and ANN to the IaaS cloud resources estimation. Their results indicated that SVR has better forecast accuracy in periodic and developing workloads prediction, while ANN has superiority in forecast accuracy for unpredicted workload configurations over SVR.

Predictive elastic resource scaling (PRESS) in [20] casted-off configuration matching (signal processing techniques) and state-driven (discrete-time Markov chain) methodologies for foretelling workloads. S. Sudevalayam et al. used linear regression models for prophesying CPU usage of a virtual machine (VM) [21]. AR-NN (autoregressive neural network) and ARIMA based adaptive prediction system is used for predicting future CPU usage of an IaaS cloud [22]. AR-NN uses back-propagation for learning its weights, and it can be enriched by training through evolutionary methods, i.e., through crossover and/or mutation [23]. N. B. Rizvandi et al. proposed a polynomial regression model for envisaging total CPU usage (in clock cycles) of jobs in the MapReduce environment before their actual deployment on clusters and/or clouds [24]. Dinda et al. casted-off autoregression (AR), moving average (MA), autoregressive integrated moving average (ARIMA), autoregressive moving average (ARMA), and fractional ARIMA for guesstimating CPU load [25]. They claimed the AR model as the best estimation model due to its low computational penalty. Authors in [26] proposed numerous low overheads and one-step-ahead forecasting models for time-series. Liang et al. proposed a multi-resource prophecy model, which can improve forecast accuracy by correlation among resources [27]. In References [28,29], the authors proposed a parameter-adaptive hybrid model for cloud workload approximation. Their model adaptively fluctuates to variable patterns of the load.

Although time-series forecasting has been deliberated by several researchers, it is still a hot topic due to its integral obscurity and complexity [30]. Besides designing new linear and nonlinear estimation models, the amalgamation of diverse models is also being revealed [31,32]. Cao, Jian et al. [33] suggested a collaborative technique for foretelling the CPU load of the cloud server. They pooled different forecast models for the same training data. Their methodology is ensemble but time-inefficient as online training of several models for the same data may take minutes or hours. M. Verma et al. [34] used an amalgamation of binary classification and linear forecast models for estimation of the core-wise CPU load of a cloud server. Sandeep K. Sood in [35] used linear regression and ANN for forecasting resource usage based on the number of points computed from the users’ requests. Chen, Jianguo et al. proposed a periodicity-based parallel time-series forecast algorithm for large-scale time-series data. They employed their model on the Apache Spark cloud computing environment [36].

Methods like KNN and SVR used in literature for CPU usage time-series forecasting have large computation time complexities than ANNs [7]. The computation time complexity of KNN is around $O\left(nk+nd\right)\approx O\left(n\times \sqrt{n}\right)$ where $d=1$ and $k=\sqrt{n}$, where $n$ denotes the number of training examples in the data set, $k$ symbolizes neighbors in a direction, and $d$ characterizes the dimension/features of the data set [37]. Similarly, the computation time complexity of SVR is $O\left(nS\right)\approx O\left(n^2\right)$, where $n$ denotes the number of training examples, and $S$ symbolizes the number of support vectors. In the worst-case scenario, the number of support vectors almost equals the number of training examples that make SVR’s complexity in the order of quadratic time [38]. Therefore, KNN and SVR based forecast schemes will have enormous forecast overheads that will vitiate the performance of the cloud server. On the other hand, large forecast overheads lead to hindered scaling decisions of the DVFS/hotplugging system in cloud servers [7]. On the other hand, linear techniques like AR, LR, ARMA, MA, and ARIMA will be incompetent to tackle the nonlinear behavior of CPU usage time series. In literature, linear models have shown poor forecast accuracy for CPU usage estimation than ANNs [39,40]. Conventional ANNs have limited learning ability as these learn only synaptic weights [41,42]. In one of our preceding works, we used recurrent CGP-based ANN [7]. As recurrent ANNs require memory for storing prior states of the network, thus we propose a feed-forward form of Cartesian genetic programming (CGP) with boosted learning ability by learning synaptic weights, synaptic connections, and the number of neurons.

Comprehensive analysis and comparison of the proposed technique with techniques from literature are tabulated in Table 1. We investigate cloud resource prediction mechanisms based on the type of machine learning model, the data set, and the optimization procedure used. For each contribution, we provided remarks with a focus on the merits/demerits of the hypothesis and the optimization method. Moreover, we also provided remarks on the learnability of the optimization method (training parameters and hyperparameters) and the mechanism for avoiding local optima. It is clear from the analysis of Table 1 that the proposed CGP-based parallel neuroevolution has a better mechanism for escaping local optima and has enhanced learnability characteristics than the models used in the literature.

Table 1. Analysis and comparison of proposed and related work.

Ref., Year	Contribution	Model (s)	Data Set	Optimization Method	Remarks
[16], 2011	Prediction of the number of cloud resource requests	Multilayer perceptron (MLP)	URL: www.server@NASA and www.server@EPA	Back-propagation	The back-propagation cannot avoid local optimum thus may have less prediction accuracy [43]. Linear hypothesis cannot capture the nonlinear behavior of the CPU usage data set (unseen) [44].
		Autoregression (AR)		Gradient descent
[12], 2012	Cloud resource estimation	Linear regression (LR)	TPC-W benchmark based CPU usage	QR-decomposition	Linear hypothesis cannot capture the nonlinear behavior of the CPU usage data set (unseen) [44]. The back-propagation cannot avoid local optimum thus may have less prediction accuracy [43].
		Artificial neural network (ANN)		Back-propagation
[18], 2013	Hosts CPU usage prediction for deciding about ON/OFF of hosts.	K-nearest neighbor (KNN)	Planet Lab	Euclidean distance with K values 1–10	KNN can have poor run-time performance when the training set is large [45]. Computation cost is quite high because we need to compute the distance of each query instance to all training samples [45].
[46], 2013	CPU load prediction in cloud computing	Recurrent neural network (RNN)	Google Trace data	Genetic algorithm	The genetic algorithm may stick in local optimum [43].
[47], 2014	Load forecasting based cloud resource provisioning	Support vector regression (SVR)	Google Trace data	SVR-type: epsilon-regression kernel: radial basis	Support vector regression has large time complexity [48].
[11], 2015	Cloud workload prediction	Autoregressive integrated moving average (ARIMA)	Traces of requests to the web servers from the Wikimedia Foundation	Hyndman–Khandakar algorithm	Low accuracy for unseen data [49] and model linearity [44] are issues of the autoregressive integrated moving average.
[19], 2015	Machine learning techniques for auto-scaling prediction	Support vector regression (SVR)	TPC-W benchmark based number of user requests per minute	Not given	The authors found that SVR has better prediction accuracy for growing and periodic workload patterns than ANN. However, in the case of un-predicted workload, ANN outperforms SVR.
		Artificial neural network (ANN)		Not given
[17], 2016	Cloud data center workload prediction	Extreme learning machine (ELM)	Google Trace data (VM requests)	The Levenberg–Marquardt algorithm (Trust Region Search)	The performance can be unstable for large-scale, imbalanced, and noisy data sets [50].
[51], 2017	An autonomic prediction suite for cloud resource provisioning	ANN	TPC-W benchmark based number of user requests per minute	Back-Propagation and Back-Propagation with weight decay	Authors used prediction models for predicting periodic, growing, and unpredictable types of workloads. The back-propagation based optimization used for the neural network may be influenced by the local optimum [43]. In contrast, the support vector regression has large time and space complexities [48].
		SVR		SVR type: Epsilon regression, Kernel: Radial Basis
[43], 2018	Cloud host CPU utilization prediction	Recurrent neural network (RNN)	Planet Lab CPU usage	Optimization (PSO) particle swarm	In PSO, the non-oscillatory route can quickly cause a particle to stagnate, and also, it may prematurely converge on suboptimal solutions that are not even guaranteed to be local optimum [52]. Thus, the authors found prediction with PSO based optimization with the mean absolute error of 0.1564. CMA-ES does not work well for large population size and has large time complexity $O\left(n^6\right)$ [53]. The authors found prediction with CMA-ES-based optimization with the mean absolute error of 0.1498.
				Covariance matrix adaptation evolutionary strategy (CMA-ES) algorithm
[54], 2019	Resource prediction for energy efficiency in cloud environment	ARIMA	Planet Lab workload traces	Not given	The authors compared the resource prediction accuracy of the models under study. Their study showed that ANN has the best accuracy of all the models. They used back-propagation for weights optimization of artificial neural networks that may be influenced by local optimum [43].
		ANN		Back-propagation
		Moving average (MA)		Not given
		Random walk (RW)		Not given
[22], 2017	Adaptive resource prediction of cloud server	ARIMA	Bitbrains workload traces	Hyndman–Khandakar’s (auto.arima) algorithm	The adaptive system analyses the distribution of the data set and selects the appropriate prediction model
		AR-NN		Back-propagation
[7], 2020	Predictive scaling of iaas server resources	Recurrent Cartesian genetic programming-based ANN (RCGPANN)	Bitbrains workload traces, Geekbench workloads	Neuro-evolution	The predictive scaling system is tested on a computer with a few CPU cores.
Proposed	Parallel neuro-evolution based cloud resource estimation	Cartesian genetic programming-based Parallel neuroevolutionary neural network (CGPNN)	Bitbrains workload traces	Parallel neuro-evolution	The prediction model trained with parallel neuroevolution enhances the prediction accuracy by avoiding the local optima.

3. CGP-Based Neuroevolutionary Neural Network (CGPNN)

Cartesian genetic programming (CGP) is a genetic programming method in which the genetic code of the program is denoted by integers placed in the form of a directed graph. Programs signified in the form of a graph can be applied to many problems in electronic circuits, scheduling and neural networks [55].

Cartesian genetic programming-based neuroevolutionary neural network (CGPNN) is an ANN that uses the basic principles of CGP. A CGPNN neuron is shown in (1) that has three types of parameters. The first type of parameter is $\Psi$ that triggers/disables a CGPNN neuron (i.e., defines neural plasticity). The second type parameter is $\Phi$, which delineates the plasticity of synaptic connections of a neuron. The 3rd type of parameter is the weight $\theta$ of the synaptic connection of a neuron. In (2), we present a mathematical model of the linear combination of inputs, synaptic connections plasticity and synaptic weights used by sigmoid hypothesis $h$.

$$h_{\Psi \Phi \theta }\left(x\right)=\Psi \left(\frac{1}{1+e^{-{\theta }^T\left(\Phi x\right)}}\right), \Phi =\left[\begin{array}{ccc}{\Phi }_0& 0& 0\\ 0& {\Phi }_1& 0\\ 0& 0& {\Phi }_2\end{array}\right] \in {ℝ}^{3\times 3}$$

$$x=\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\end{array}\right]\in {ℝ}^{3\times 1} , \theta =\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ {\theta }_2\end{array}\right]\in {ℝ}^{3\times 1}$$

(1)

where $\Psi \in \left\{0,1\right\}$ for single neuron it is scalar, $\Phi \in {ℝ}^{3\times 3}$ matrix and $\theta \in {ℝ}^{3\times 1}$ matrix for $x\in {ℝ}^{3\times 1}$.

$$h_{\Psi \Phi \theta }\left(x\right)=\Psi \times h\left({\theta }_0{\Phi }_0{x}_0+{\theta }_1{\Phi }_1{x}_1+{\theta }_2{\Phi }_2{x}_2\right)$$

(2)

where h is the sigmoid hypothesis defined in (1).

In CGP, the processing units (nodes) are placed in the Cartesian plane. The processing units may use any of the microscopic functions like AND, OR, XOR, Multiplexer, etc. Whereas in CGPNN, the processing units are artificial neurons as an alternative to the microscopic functions of CGP. Besides neurons, all doctrines and directions of the CGP are followed by CGPNN.

We present a four-layer ANN in Figure 1 and then renovate this network to CGPNN, as shown in Figure 2. The ANN model, displayed in Figure 2, presents a basic architecture of ANN that has four layers, of which two middle layers are hidden layers, one input and output layer, respectively. The parameters $\left({\theta }^{\prime }\mathrm{s}\right)$ and activation function(s) are not shown here for providing a modest illustration of the ANN. The input layer consists of two system inputs $x_1$ and $x_2$ and a bias input $x_0$ (where input $x_0=1$). Layers 2 and 3 are hidden layers; each has two processing neurons and bias input. In layer 2, $c_0$ is the bias input while $c_1$ and $c_2$ are processing neurons. In layer 3, $d_0$ is the bias input while $d_1$ and $d_2$ are processing neurons. Layer 4 has one processing neuron $o_1$ that outputs the hypothesis $\left(h_{\theta }\left(x\right)\right)$ result. Where $h_{\theta }\left(x\right)$ is a hypothesis $h$ that maps the given inputs $x_0,x_1$ and $x_2$ onto the given output $\mathrm{y}$ by fine-tuning the parameters/weights $\left({\theta }^{\prime }\mathrm{s}\right)$.

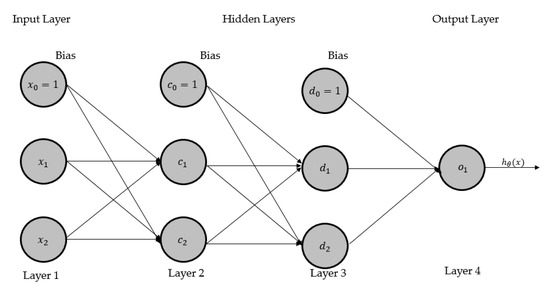
Figure 1. A four-layered artificial neural network: layer 1 consists of bias input $x_0$ and two system inputs $x_1$ and $x_2$. Layer 2 consists of a bias input $c_0$ and two processing neurons $c_1$ and $c_2$. Layer 3 consists of a bias input $d_0$ and two processing neurons $d_1$ and $d_2$. Layer 4 has one processing neuron $o_1$ that generates the output of $h_{\theta }\left(x\right)$.

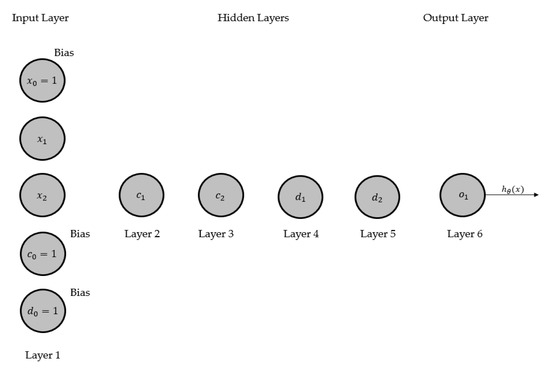
Figure 2. Transformed model of 4 layers ANN of Figure 1, into CGPNN.

A general architecture of CGPNN is shown in Figure 2, which is transmuted from the ANN of Figure 1. The processing neurons (i.e., $c_1, c_2, d_1, d_2, \mathrm{and} o_1$) are placed in the Cartesian plane where the vertical coordinate is one (i.e., one row), and horizontal coordinates are five (i.e., five columns, first four columns have hidden layers neurons and the 5th column has output neuron). The number of neurons in hidden layers’ columns and output layer column may vary. All the bias inputs are placed in the input layer along with inputs according to the CGP convention.

In CGPNN, the number of hidden layers’ neurons contributing to the production of hypothesis estimate is not fixed in contrast to the ANN. In Figure 3, there are four hidden layers of neurons (i.e., $c_1, c_2, d_1$, and $d_2$), the total possible combinations are fifteen, so fifteen different networks may be spawned based on varying the number and location of neurons. The possible networks of neurons may be either $[c_1, c_2, d_1, d_2$] or $\left[c_1, c_2, d_1\right]$ or $[c_1, c_2, d_2$] or $[c_2, d_1, d_2$] or $\left[c_1, d_1, d_2\right]$ or $\left[c_1, c_2\right]$ or $\left[c_1, d_1\right]$ or $\left[c_1, d_2\right]$ or $\left[c_2, d_1\right]$ or $\left[c_2, d_2\right]$ or $\left[d_1, d_2\right]$ or $\left[c_1\right]$ or $\left[c_2\right]$ or or $\left[d_2\right]$. Thus, there are fifteen possible networks to be generated from the network shown in Figure 3.

Figure 3. The genotype of a generic CGPNN neuron.

The matrix $ɴ$ lists the neurons of the hidden layer as given in (3). In (3), we use parameter matrix $\Psi$ that describes neural plasticity of the network by triggering or disabling a neuron or neurons in the hidden layers of the network. Whereas ${\Psi }^{\mathrm{j}}$ is used to trigger/disable a neuron in the $j^{\mathrm{th}}$ layer. Thus, neural plasticity parameters matrix $\Psi$ is multiplied with matrix $ɴ$ to select the neurons for a new configuration of the network.

$$ɴ=\left[\begin{array}{c}\begin{array}{c}{c}_1\\ c_2\\ d_1\end{array}\\ d_2\end{array}\right], \Psi =\left[\begin{array}{c}\begin{array}{c}{\Psi }^2\\ 0\\ 0\end{array}\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ {\Psi }^3\\ 0\end{array}\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ {\Psi }^4\end{array}\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ {\Psi }^5\end{array}\right]$$

(3)

where $\left\{{\Psi }^2, {\Psi }^3, {\Psi }^4, {\Psi }^5\right\}\in \left\{0,1\right\}$.

Similarly, the synaptic inputs for hidden layer neurons and output layer neurons of CGPNN are not fixed in contrast to the ANN. After selecting the neurons, as mentioned earlier, the synaptic inputs for each neuron are then selected by evolution. Layer 2 can get inputs from layer 1 (except $c_0$ and $d_0$). Layer 3 can get inputs from both layer 1 and layer 2 (except $c_0$ and $d_0$). Layer 4 can get inputs (except $x_0$ and $d_0$) from all previous layers (i.e., layers 1, 2, 3). Layer 5 can have inputs from 1st, 2nd, 3rd, and 4th layers (except $x_0$ and $d_0$). Similarly, the output layer can get inputs from 1st, 2nd, 3rd, 4th, and 5th layers (except $x_0$ and $c_0$). The matrices $I^2,I^3, I^4, I^5,$ and $I^6$ given in (4), represent the possible inputs for 2nd, 3rd, 4th, 5th, and 6th layers, respectively. Where $I^{\mathrm{j}}$ represents the input matrix for $j^{\mathrm{th}}$ layer neurons. The parameter ${\alpha }_{\mathrm{i}}^{\mathrm{j}}$ in (4), shows the output of $i^{\mathrm{th}}$ neuron in $j^{\mathrm{th}}$ layer.

In ANN, the number of inputs for each processing neuron is fixed, but in CGPNN, it is not obligatory that a neuron will get all these synaptic inputs simultaneously. As in ANN of Figure 1, each processing neuron gets three inputs, but here in CGPNN, each processing neuron may get any amalgamation of inputs from the given list of inputs. Thus, we define synaptic input parameters in (5). The synaptic inputs plasticity parameters are listed in matrices ${\Phi }^2, {\Phi }^3, {\Phi }^4, {\Phi }^5$ and ${\Phi }^6$ for synaptic inputs matrices $I^2,I^3, I^4, I^5,$ and $I^6,$ respectively. The synaptic inputs plasticity parameters matrices ${\Phi }^2, {\Phi }^3, {\Phi }^4, {\Phi }^5$ and ${\Phi }^6$ defines the plasticity of synaptic inputs listed in matrices $I^2,I^3, I^4, I^5,$ and $I^6,$ respectively. Where ${\Phi }^{\mathrm{j}}$ represents synaptic plasticity matrix for $j^{\mathrm{th}}$ layer neurons inputs. The parameter ${\Phi }_{\mathrm{k}}^{\mathrm{j}}$ defines plasticity of $k^{\mathrm{th}}$ input in $j^{\mathrm{th}}$ layer.

$$I^2=\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\end{array}\right],I^3=\left[\begin{array}{c}\begin{array}{c}{x}_0\\ x_1\\ x_2\end{array}\\ {\alpha }_1^2\end{array}\right],I^4=\left[\begin{array}{c}\begin{array}{c}{x}_1\\ x_2\\ c_0\end{array}\\ {\alpha }_1^2\\ {\alpha }_1^3\end{array}\right],\hspace{1em}{I}^5=\left[\begin{array}{c}\begin{array}{c}{x}_1\\ x_2\\ c_0\end{array}\\ {\alpha }_1^2\\ {\alpha }_1^3\\ {\alpha }_1^4\end{array}\right],I^6=\left[\begin{array}{c}\begin{array}{c}{x}_1\\ x_2\\ {\alpha }_1^2\end{array}\\ {\alpha }_1^3\\ d_0\\ {\alpha }_1^4\\ {\alpha }_1^5\end{array}\right]$$

(4)

$$\begin{gathered} {\Phi }^2=\left[\begin{array}{c}{\Phi }_1^2\\ 0\\ 0\end{array} \begin{array}{c}0\\ {\Phi }_2^2\\ 0\end{array} \begin{array}{c}0\\ 0\\ {\Phi }_3^2\end{array}\right], {\Phi }^3=\left[\begin{array}{c}\begin{array}{c}{\Phi }_1^3\\ 0\\ 0\end{array}\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ {\Phi }_2^3\\ 0\end{array}\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ {\Phi }_3^3\end{array}\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ {\Phi }_4^3\end{array}\right] {\Phi }^4=\left[\begin{array}{c}\begin{array}{c}{\Phi }_1^4\\ 0\\ 0\end{array}\\ 0\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ {\Phi }_2^4\\ 0\end{array}\\ 0\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ {\Phi }_3^4\end{array}\\ 0\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ {\Phi }_4^4\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ 0\\ {\Phi }_5^4\end{array}\right]{\Phi }^5=\left[\begin{array}{c}\begin{array}{c}{\Phi }_1^5\\ 0\\ 0\end{array}\\ 0\\ 0\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ {\Phi }_2^5\\ 0\end{array}\\ 0\\ 0\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ {\Phi }_3^5\end{array}\\ 0\\ 0\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ {\Phi }_4^5\\ 0\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ 0\\ {\Phi }_5^5\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ 0\\ 0\\ {\Phi }_6^5\end{array}\right] \\ {\Phi }^6=\left[\begin{array}{c}\begin{array}{c}{\Phi }_1^6\\ 0\\ 0\end{array}\\ 0\\ 0\\ 0\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ {\Phi }_2^6\\ 0\end{array}\\ 0\\ 0\\ 0\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ {\Phi }_3^6\end{array}\\ 0\\ 0\\ 0\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ {\Phi }_4^6\\ 0\\ 0\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ 0\\ {\Phi }_5^6\\ 0\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ 0\\ 0\\ {\Phi }_6^6\\ 0\end{array} \begin{array}{c}\begin{array}{c}0\\ 0\\ 0\end{array}\\ 0\\ 0\\ 0\\ {\Phi }_7^6\end{array}\right] \end{gathered}$$

(5)

where $\left\{{\Phi }^2, {\Phi }^3, {\Phi }^4, {\Phi }^5, {\Phi }^6\right\}\in \left\{0,1\right\}$.

The parameters $\Psi$ and ${\Phi }^{\mathrm{j}}$ delineate plasticity of CGPNN two-fold, first by triggering/disabling neuron(s), also called neural plasticity, and second by triggering/disabling of synaptic inputs, also called synaptic plasticity. Here we define the third type of parameter that is common to both ANNs and CGPNN, i.e., the weights matrix of neuron inputs. The weight matrix for $j^{\mathrm{th}}$ layer neurons inputs are represented by ${\theta }^{\mathrm{j}}$. Where ${\theta }_{\mathrm{k}}^{\mathrm{j}}$ represents the weight of $k^{\mathrm{th}}$ input in the $j^{\mathrm{th}}$ layer. The weights matrices are given in (6).

$${\theta }^2=\left[\begin{array}{c}{\theta }_1^2\\ {\theta }_2^2\\ {\theta }_3^2\end{array}\right], {\theta }^3=\left[\begin{array}{c}\begin{array}{c}{\theta }_1^3\\ {\theta }_2^3\\ {\theta }_3^3\end{array}\\ {\theta }_4^3\end{array}\right] ,{\theta }^4=\left[\begin{array}{c}\begin{array}{c}{\theta }_1^4\\ {\theta }_2^4\\ {\theta }_3^4\end{array}\\ {\theta }_4^4\\ {\theta }_5^4\end{array}\right] ,{\theta }^5=\left[\begin{array}{c}\begin{array}{c}{\theta }_1^5\\ {\theta }_2^5\\ {\theta }_3^5\end{array}\\ {\theta }_4^5\\ {\theta }_5^5\\ {\theta }_6^5\end{array}\right] ,{\theta }^6=\left[\begin{array}{c}\begin{array}{c}{\theta }_1^6\\ {\theta }_2^6\\ {\theta }_3^6\end{array}\\ {\theta }_4^6\\ {\theta }_5^6\\ {\theta }_6^6\\ {\theta }_7^6\end{array}\right]$$

(6)

After defining all three types of parameters of CGPNN, we now formulate layer-wise outputs. Here $h_{ \mathrm{i}}^{ \mathrm{j}}$ is the sigmoid hypothesis of $i^{\mathrm{th}}$ neuron in $j^{\mathrm{th}}$ layer and ${\alpha }_{\mathrm{i}}^{\mathrm{j}}$ represents output of $i^{\mathrm{th}}$ neuron in $j^{\mathrm{th}}$ layer.

The output of the 2nd layer of CGPNN shown in Figure 2 is represented by ${\mathsf{\alpha }}_1^2$ and is given in (7). The output of the 3rd layer is given in (8) that is characterized by ${\mathsf{\alpha }}_1^3$. Layer 4 output is defined in (9), and the 5th layer’s output is given in (10). The CGPNN output is represented by $h_{\Psi \Phi \theta }\left(x\right)$ as given in (11). As in (11) the neural plasticity operator for output layer neuron, i.e., ${\Psi }^6=1$. The hypothesis that maps the inputs of the output layer (i.e., the 6th layer) with the desired output $\mathrm{y}$ is represented by $h_1^6$. This hypothesis is $h_1^6$ a linear combination of inputs when CGPNN is used for solving a regression problem. In the case of the classification problem, $h_1^6$ is the sigmoid function of its inputs that is defined in (11).

$${\alpha }_1^2={\Psi }^2\times h_{ 1}^{ 2}\left({\theta }_1^2 {\Phi }_1^2 x_0 +{\theta }_2^2 {\Phi }_2^2 x_1+ {\theta }_3^2 {\Phi }_3^2 x_2\right)$$

(7)

$${\alpha }_1^3={\Psi }^3\times h_{ 1}^{ 3}\left({\theta }_1^3 {\Phi }_1^3 x_0 +{\theta }_2^3 {\Phi }_2^3 x_1+ {\theta }_3^3 {\Phi }_3^3 x_2+ {\theta }_4^3 {\Phi }_4^3 {\alpha }_1^2\right)$$

(8)

$${\alpha }_1^4={\Psi }^4\times h_{ 1}^{ 4}\left({\theta }_1^4 {\Phi }_1^4 x_1 +{\theta }_2^4 {\Phi }_2^4 x_2+ {\theta }_3^4 {\Phi }_3^4 c_0+ {\theta }_4^4 {\Phi }_4^4 {\alpha }_1^2+ {\theta }_5^4 {\Phi }_5^4 {\alpha }_1^3\right)$$

(9)

$${\alpha }_1^5={\Psi }^5\times h_{ 1}^{ 5}\left({\theta }_1^5 {\Phi }_1^5 x_1 +{\theta }_2^5 {\Phi }_2^5 x_2+ {\theta }_3^5 {\Phi }_3^5 c_0+ {\theta }_4^5 {\Phi }_4^5 {\alpha }_1^2+ {\theta }_5^5 {\Phi }_5^5 {\alpha }_1^3+ {\theta }_6^5 {\Phi }_6^5 {\alpha }_1^4\right)$$

(10)

$$h_{\Psi \Phi \theta }\left(x\right)={\Psi }^6\times h_{ 1}^{ 6}\left({\theta }_1^6 {\Phi }_1^6 x_1 +{\theta }_2^6 {\Phi }_2^6 x_2+ {\theta }_3^6 {\Phi }_3^6 {\alpha }_1^2+ {\theta }_4^6 {\Phi }_4^6 {\alpha }_1^3+ {\theta }_5^6 {\Phi }_5^6 d_0+ {\theta }_6^6 {\Phi }_6^6 {\alpha }_1^4+ {\theta }_7^6 {\Phi }_7^6 {\alpha }_1^5\right)$$

(11)

where ${\Psi }^6=1 \mathrm{for} \mathrm{output} \mathrm{layer} \mathrm{neuron}$

$$h_1^6\left(z\right)=\{\begin{array}{cc}z& \mathrm{for} \mathrm{regression} \mathrm{problems}\\ \left(\frac{1}{1+e^{-\mathrm{z}}}\right)& \mathrm{for} \mathrm{classification} \mathrm{problems}\end{array}$$

The mathematical model of CGPNN in terms of $\Psi , \Phi ,\theta$ and network inputs $x_0, x_1, x_2, d_0, d_1$ and $d_2$ by substituting for ${\alpha }_1^2, {\alpha }_1^3, {\alpha }_1^4$ and ${\alpha }_1^5$ from (7)–(10) in (11), is given in (12).

$$\begin{array}{cc}\hfill h_{\Psi \Phi \theta }\left(x\right)& ={\Psi }^6\times h_{ 1}^{ 6}[{\theta }_1^6 {\Phi }_1^6 x_1 +{\theta }_2^6 {\Phi }_2^6 x_2+ {\theta }_3^6 {\Phi }_3^6 \left\{{\Psi }^2\times h_{ 1}^{ 2}\left({\theta }_1^2 {\Phi }_1^2 x_0 +{\theta }_2^2 {\Phi }_2^2 x_1+ {\theta }_3^2 {\Phi }_3^2 x_2\right)\right\} \hfill \\ & + {\theta }_4^6 {\Phi }_4^6 \{{\Psi }^3\times h_{ 1}^{ 3}({\theta }_1^3 {\Phi }_1^3 x_0 +{\theta }_2^3 {\Phi }_2^3 x_1+ {\theta }_3^3 {\Phi }_3^3 x_2+ {\theta }_4^3 {\Phi }_4^3 ({\Psi }^2\hfill \\ & \times h_{ 1}^{ 2}\left({\theta }_1^2 {\Phi }_1^2 x_0 +{\theta }_2^2 {\Phi }_2^2 x_1+ {\theta }_3^2 {\Phi }_3^2 x_2\right)))\}+ {\theta }_5^6 {\Phi }_5^6{d}_0\hfill \\ & + {\theta }_6^6 {\Phi }_6^6 \{{\Psi }^4\times h_{ 1}^{ 4}({\theta }_1^4 {\Phi }_1^4 x_1 +{\theta }_2^4 {\Phi }_2^4 x_2+ {\theta }_3^4 {\Phi }_3^4 c_0+ {\theta }_4^4 {\Phi }_4^4 ({\Psi }^2\hfill \\ & \times h_{ 1}^{ 2}\left({\theta }_1^2 {\Phi }_1^2 x_0 +{\theta }_2^2 {\Phi }_2^2 x_1+ {\theta }_3^2 {\Phi }_3^2 x_2\right) )+ {\theta }_5^4 {\Phi }_5^4 ({\Psi }^3\times h_{ 1}^{ 3}({\theta }_1^3 {\Phi }_1^3 x_0+{\theta }_2^3 {\Phi }_2^3 x_1\hfill \\ & + {\theta }_3^3 {\Phi }_3^3 x_2+ {\theta }_4^3 {\Phi }_4^3 \left({\Psi }^2\times h_{ 1}^{ 2}\left({\theta }_1^2 {\Phi }_1^2 x_0 +{\theta }_2^2 {\Phi }_2^2 x_1+ {\theta }_3^2 {\Phi }_3^2 x_2\right)\right)\left)\right)\left)\right\}\hfill \\ & + {\theta }_7^6 {\Phi }_7^6 \{{\Psi }^5\times h_{ 1}^{ 5}({\theta }_1^5 {\Phi }_1^5 x_1 +{\theta }_2^5 {\Phi }_2^5 x_2+ {\theta }_3^5 {\Phi }_3^5 c_0+ {\theta }_4^5 {\Phi }_4^5 ({\Psi }^2\hfill \\ & \times h_{ 1}^{ 2}\left({\theta }_1^2 {\Phi }_1^2 x_0 +{\theta }_2^2 {\Phi }_2^2 x_1+ {\theta }_3^2 {\Phi }_3^2 x_2\right) )+ {\theta }_5^5 {\Phi }_5^5 ({\Psi }^3\times h_{ 1}^{ 3}({\theta }_1^3 {\Phi }_1^3 x_0+{\theta }_2^3 {\Phi }_2^3 x_1\hfill \\ & + {\theta }_3^3 {\Phi }_3^3 x_2+ {\theta }_4^3 {\Phi }_4^3 \left({\Psi }^2\times h_{ 1}^{ 2}\left({\theta }_1^2 {\Phi }_1^2 x_0 +{\theta }_2^2 {\Phi }_2^2 x_1+ {\theta }_3^2 {\Phi }_3^2 x_2\right))\right))+ {\theta }_6^5 {\Phi }_6^5 ({\Psi }^4\hfill \\ & \times h_{ 1}^{ 4}({\theta }_1^4 {\Phi }_1^4 x_1 +{\theta }_2^4 {\Phi }_2^4 x_2+ {\theta }_3^4 {\Phi }_3^4 c_0+{\theta }_4^4 {\Phi }_4^4 ({\Psi }^2\hfill \\ & \times h_{ 1}^{ 2}\left({\theta }_1^2 {\Phi }_1^2 x_0 +{\theta }_2^2 {\Phi }_2^2 x_1+ {\theta }_3^2 {\Phi }_3^2 x_2\right) )+ {\theta }_5^4 {\Phi }_5^4 ({\Psi }^3\times h_{ 1}^{ 3}({\theta }_1^3 {\Phi }_1^3 x_0+{\theta }_2^3 {\Phi }_2^3 x_1\hfill \\ & + {\theta }_3^3 {\Phi }_3^3 x_2+ {\theta }_4^3 {\Phi }_4^3 \left({\Psi }^2\times h_{ 1}^{ 2}\left({\theta }_1^2 {\Phi }_1^2 x_0 +{\theta }_2^2 {\Phi }_2^2 x_1+ {\theta }_3^2 {\Phi }_3^2 x_2\right))\right)\left)\right)\left)\right)\left\}\right]\hfill \end{array}$$

(12)

The parameters $\Psi , \Phi ,$ and $\theta$ in (12) are optimized for minimizing the difference between the estimates made by the hypothesis $h_{\Psi \Phi \theta }\left(x\right)$ and the actual output of a system, i.e., $y$, defined by a loss function $J\left(\Psi , \Phi ,\theta \right)$. The loss function $J\left(\Psi , \Phi ,\theta \right)$ is the mean absolute percentage error (MAPE) as given in (13). We use MAPE because it measures residual errors that give a global idea of the difference between estimates made by hypothesis $h_{\Psi \Phi \theta }\left(x\right)$ and the actual output $y$. In (13), $m$ represents the number of training examples, and $s$ represents an index for each training example that ranges from 1 to $m$. The loss function $J\left(\Psi , \Phi ,\theta \right)$ is minimized by the evolutionary optimization method given in figure.

$$J\left(\Psi ,\Phi ,\theta \right)=\frac{{{\displaystyle \sum }}_{s=1}^m\left|\frac{y^s-h_{\Psi \Phi \theta }\left(x^s\right)}{y^s}\right|}{m}\times 100$$

(13)

4. CGPNN Optimization Method

CGPNN follows the basic principles of CGP for optimization. During optimization, each neuron is denoted by its genotype. In Figure 3, the genotype of a generic CGPNN neuron is shown. Inputs range from ${\mathrm{input}}_0$ to ${\mathrm{input}}_q$, along each input are respective synaptic plasticity parameters $\Phi$ and weight $\theta$.

Now, the genotype CGPNN of Figure 2 is placed in an array. Inputs $x_0, x_1, x_2, c_0$ and $d_0$ are represented by integers 0, 1, 2, 3 and 4, respectively. The hidden layers neurons $c_1, c_2, d_1$ and $d_2$ are represented by integers 5, 6, 7 and 8, respectively. In array first five locations are dedicated to the CGPNN input layer. Each neuron of hidden and output layers is placed in eleven consecutive locations of the array. The layer 2 neuron $c_1$ is placed at indices 5 to 15 of the array,$c_2$ at indices 16 to 26, $d_1$ at indices 27 to 37, ${\mathrm{d}}_2$ at indices 38 to 48 and $o_1$ at indices 49 to 59 of the array. The inputs indices of the array for $c_1$ may have values 0, 1, and 2, for $c_2$ input values maybe 0, 1, 2 and 5, for $d_1$ input locations may have values 1, 2, 3, 5, and 6, for $d_2$ input locations may have values 1, 2, 3, 5, 6, and 7, while for $o_1$ input locations may have values 1, 2, 4, 5, 6, 7, and 8. All locations of the array having $\Psi$ and $\Phi$ will have values 0 or 1. As we are using two types of hypothesis functions, so for a neuron having a logistic sigmoid function, then in genotype its code will be 0, and for linear hypothesis function code will be 1. Thus, in all function’s locations of neurons except for $o_1$, the function genetic code is 0. For $o_1$ function, code maybe 0 for classification problem and 1 for a regression problem. All parameters and bias inputs are initialized, as presented in the algorithm shown in Figure 4. The genes of the initialized array are mutated (e.g., 10% mutation) so as to make λ mutants (e.g., λ = 9, where mutant is offspring generated after mutation operator). The value of loss function $J\left(\Psi , \Phi ,\theta \right)$ for each mutant is calculated according to the definition of (13). The mutant with the lowest $J\left(\Psi , \Phi ,\theta \right)$ value is selected for the next generation. In the next generation, the parent mutant is again mutated to generate λ offspring mutants, again $J\left(\Psi , \Phi ,\theta \right)$ is calculated. The mutant with the lowest $J\left(\Psi , \Phi ,\theta \right)$ is selected for the next generation, and the process continues. Until the lowest limit of $J\left(\Psi , \Phi ,\theta \right)$ is reached or the maximum number of iterations is completed, then the optimization stops. The last mutant is the genotype of the CGPNN that has optimized parameters $\Psi , \Phi ,$ and $\theta .$

Figure 4. A single thread of parallel neuroevolution.

5. Experimental Platform and Methodology

We execute the training and testing experiments on HP Pro Desk 400G3 MT Business PC (HP, Palo Alto, CA, USA) that has Intel^® Core™ i7-6700 CPU 3.40 GHz processor and 8 GB RAM (Intel, Santa Clara, CA, USA). We used real CPU traces of Bitbrains (http://gwa.ewi.tudelft.nl/datasets/gwa-t-12-bitbrains) data center during our experiments. The dataset is composed of records of performance metrics of 1250 VMs from a distributed datacenter Bitbrains. Bitbrains is a service provider that is specialized in managed hosting and business computation for enterprises. Customers include many major banks, credit card operators, and insurers. In this study, we use resource usage traces of 120 VMs running on a single cloud server of the (from the fastStorage data set) Bitbrains data center. For each VM, the data set has monthly usage records for CPU, memory, network, and storage. We have selected CPU as a candidate for estimation due to its excessive usage for CPU intensive workloads. We have divided the CPU data set into two halves for each half for training and testing. We have conducted the experiments according to the methodology pictorially shown in Figure 5. In the experiments, we used six different prediction points/instances, five different seeds, and three different initial chromosome size (number of neurons). Before running an experiment, we select prediction points either 1 or 2 or 3 or 4 or 5 or 6. Then we select the seed number (i.e., either 1, 2, 3, 4 or 5). After the selection of prediction points and the seed number, we then select the chromosome size from three possible options of 50, 100 and 500. After these initial settings, we feed the training data to the neuroevolutionary algorithm for training the CGPNN.

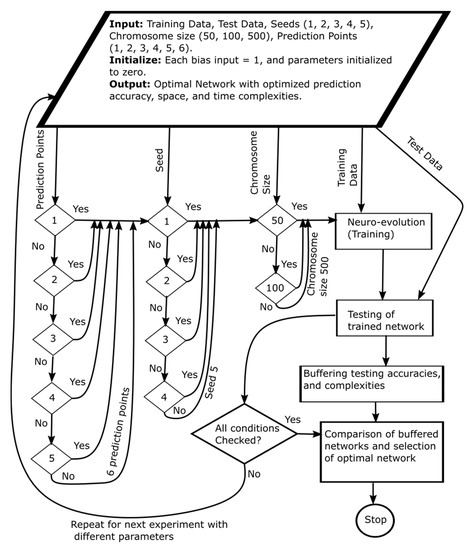
Figure 5. Experimental methodology of parallel neuroevolution.

Then we feed the testing data set to the trained CGPNN for testing. We extract the CGPNN model accuracy on test data and its space and time complexities for storing in a buffer. We repeat the above-mentioned process until all possible initial conditions for prediction points, seed numbers, and chromosome sizes are checked/executed. When all possible conditions/options are checked, we then compare all CGPNNs results stored in the buffer. Moreover, select the CGPNN model with the best prediction accuracy and possibly least space and time complexities.

6. Results and Discussion

Table 2 presents the results of the experiments for each prediction instance. It can be seen that the one instance prediction has the least mean absolute error (MAE). Two instances of prediction have the least space complexity. While one, three, and six instances prediction have smaller time complexities than two, four, and five instances prediction models. To avoid scaling errors/overheads, space complexity can be compromised for MAE. Thus, the one instance prediction can be chosen that has the least MAE and time complexity by compromising on space complexity.

Table 2. Summary of prediction results for different numbers of prediction samples.

Number of Instances	Space Complexity	Time Complexity	MAE	MAPE
1	O(14)	O(14)	0.0463	3%
2	O(9)	O(16)	0.0467	4%
3	O(10)	O(14)	0.0472	5%
4	O(16)	O(22)	0.0493	7%
5	O(14)	O(18)	0.0498	8%
6	O(12)	O(14)	0.0549	11%

Table 3 presents the results for a one-point prediction with five different seeds and three different chromosome sizes. In the table, we have shown time complexity in terms of critical path multipliers and logistic sigmoid functions. It can be seen that seeds one and five have the least number of critical path multipliers and logistic sigmoid functions for optimal networks with initial chromosome sizes of hundred and fifty neurons, respectively. In contrast, the optimal network of seed five with an initial chromosome size of fifty neurons has the least MAE (i.e., 0.046356). The space complexity is represented by the number of active neurons in Table 3. In seeds two, three, and five, the networks with chromosome size fifty and hundred and in seed four, the network with chromosome size of five hundred, have the least number of active neurons. Thus, the network with a chromosome size of fifty in seed five can be chosen as the final optimal network due to its least MAE, least number of active neurons, least number of critical path multipliers, and logistic sigmoid functions.

Table 3. Summary of results of optimal networks for one sample/instance prediction.

Seed	Neurons per Chromosome	No. of Active Neurons	MAE	Critical Path Multipliers	Sigmoid Functions
1	50	16	0.046493	9	9
	100	15	0.046413	7	7
	500	69	0.046591	32	32
2	50	14	0.046629	8	8
	100	14	0.046558	9	9
	500	24	0.046650	16	16
3	50	14	0.046580	8	8
	100	14	0.046502	9	9
	500	16	0.047080	10	10
4	50	17	0.046560	9	9
	100	16	0.046580	8	8
	500	14	0.046567	10	10
5	50	14	0.046356	7	7
	100	14	0.046444	8	8
	500	34	0.046803	22	22

Figure 6 presents the prediction results of the network of seed five with an initial chromosome size of fifty neurons that shows one-day CPU usage prediction results of the Bitbrains data center server. It is clear from the results that our CGP based neuroevolutionary model predicts CPU usage with an accuracy (MAE) of 0.046356. In the next section, we compare our CGP based neuroevolutionary model with models from literature for accuracy and space and time complexities.

Figure 6. Cloud server CPU usage prediction result of proposed model.

Comparison with Related Work

Table 4 presents the model comparison for testing accuracy (MAE), space, and time complexities. For comparison, we trained all models from the literature on training data of Bitbrains CPU data set. The tabulated results are based on test data.

Table 4. Comparison of cloud server prediction models: proposed vs. related work.

Model	Type/Characteristics	Space Complexity	Time Complexity	MAE
AR-NN	Univariate/hybrid, no built-in window	O(1)	O(1)	0.11874602
ARIMA	Univariate/parametric, no built-in window	O(1)	O(1)	0.16476377
MLP	Multivariate/non-parametric, no built-in window	O(1)	O(1)	0.1172989
ANN	Multivariate/non-parametric, no built-in window	O(1)	O(1)	0.1100977
SVR-linear	Epsilon with linear kernel, no built-in window	O(n2)	O(n2)	0.1108303
SVR-sigmoid	Epsilon with the sigmoid kernel, no built-in window	O(n2)	O(n2)	0.1112155
SVR-radial	Epsilon with the radial kernel, no built-in window	O(n2)	O(n2)	0.1158454
SVR-polynomial	Epsilon with the polynomial kernel, no built-in window	O(n2)	O(n2)	0.1127533
ELM	No built-in window	O(1)	O(1)	0.1193865
RNN-Elman	Elman, no built-in window	O(1)	O(1)	0.1133194
RNN-Jordan	Jordan, no built-in window	O(1)	O(1)	0.1139574
LR	No built-in window	O(1)	O(1)	0.1690222
KNN	No built-in window	O$(\mathrm{n}\times \sqrt{\mathrm{n}}$)	O$(\mathrm{n}\times \sqrt{\mathrm{n}}$)	0.1978246
Proposed model	Built-in window	O(1)	O(1)	0.046356

AR-NN has MAE 0.16874602 and constant time Space and time Complexities. ARIMA, MLP, and ANN have constant time Space and time Complexities. MAE of ARIMA is 0.11476377. Whereas MLP and ANN have 0.1172989 and 0.1200977 MAE values, respectively. SVR with linear, sigmoid, radial, and polynomial kernels have Space and time Complexities of order $O\left({\mathrm{n}}^2\right)$, while their MAE values are 0.1208303, 0.1212155, 0.1358454, and 0.1227533, respectively. ELM, RANN (recurrent artificial neural network ) -Elman, RANN-Jordan, and LR have constant time space and time complexities. While their MAE values are 0.1193865, 0.1133194, 0.1239574, and 0.1190222, respectively. Similarly, KNN has Space and time Complexities of order $O\left(\mathrm{n}\times \sqrt{\mathrm{n}}\right)$ and MAE 0.1978246. While the proposed neuroevolutionary model has constant time space and time complexities and MAE 0.046356. The proposed model has the least MAE that makes it the best predictor of all the models under research.

Results show that all trained models except SVR and KNN have constant-time space and computation time complexities. We have used the notation $O\left(1\right)$ for constant time space and time complexities (there are slight differences among space and time complexities of models). Results show that our neuroevolutionary model has lesser space and time complexities than KNN and SVR models. The model has better prediction accuracy than other neural networks like feed-forward ANNs and recurrent ANNs (RNNs) [41,42]. While the proposed model has the best prediction accuracy (MAE) of all models from the literature. To present the proposed model’s difference in performance/accuracy from other models more clearly, we have plotted the MEs of all models in Figure 7. That shows that the proposed model has the least MAE. In other words, Figure 7 shows that the proposed model has the best prediction performance/accuracy of all models under study.

Figure 7. Cloud server CPU usage prediction performance comparison.

7. Conclusions and Future Directions

With the increasing demand for cloud services, the load on cloud data centers increases in an irregular fashion. For executing the irregular workload patterns, cloud servers use predictive scaling mechanisms to conserve energy in idle/low load times [7]. The energy conservation capability of predictive scaling mechanisms can be enhanced by accurately predicting CPU demand before the scaling of resources.

We introduced a CGP-based parallel neuroevolutionary model and evaluated its accuracy for future CPU usage prediction using real CPU usage traces of Bitbrains data center. We also evaluated the model for space and computation time complexities with six different instances of prediction, five different seeds, and three different initial network/chromosome sizes. Our model has achieved the best prediction accuracy of all models (i.e., AR, ARIMA, KNN, ELM, SVR, and ANNs). Experimental results showed that our model achieved 97% prediction accuracy, which will lead to correct scaling decisions in predictive scaling mechanisms of cloud servers.

In the future, we plan to integrate our CGP-based parallel neuroevolutionary model with a predictive scaling mechanism on a multicore cloud server. In addition, our model can be used with hotplugging mechanisms in hand-held devices for conserving battery charge.