Development of Frequency Weighted Model Reduction Algorithm with Error Bound: Application to Doubly Fed Induction Generator Based Wind Turbines for Power System
Abstract
1. Introduction
- Ranges:
- Voltage operating range;
- Frequency operating range.
- Controls:
- Active power control;
- Frequency control;
- Voltage control;
- Reactive power control;
- Communications and external control.
- Rides Through:
- Low voltage ride through (LVRT);
- High voltage ride through (HVRT).
- Power quality;
- Wind farm modeling and verification.
- Frequency weighted Gramians based MOR approach for the wind turbine power system is proposed.
- A priori error bound formula for frequency weighted cases is derived.
- ROMs of DFIG (current, flux) models are obtained based on frequency weighted scenario which ensure the stability.
- Comparison among different existing MOR technique with proposed technique is presented.
2. Grid Connection Configuration of Induction Machines
2.1. Double Fed Induction Generator (DFIG)
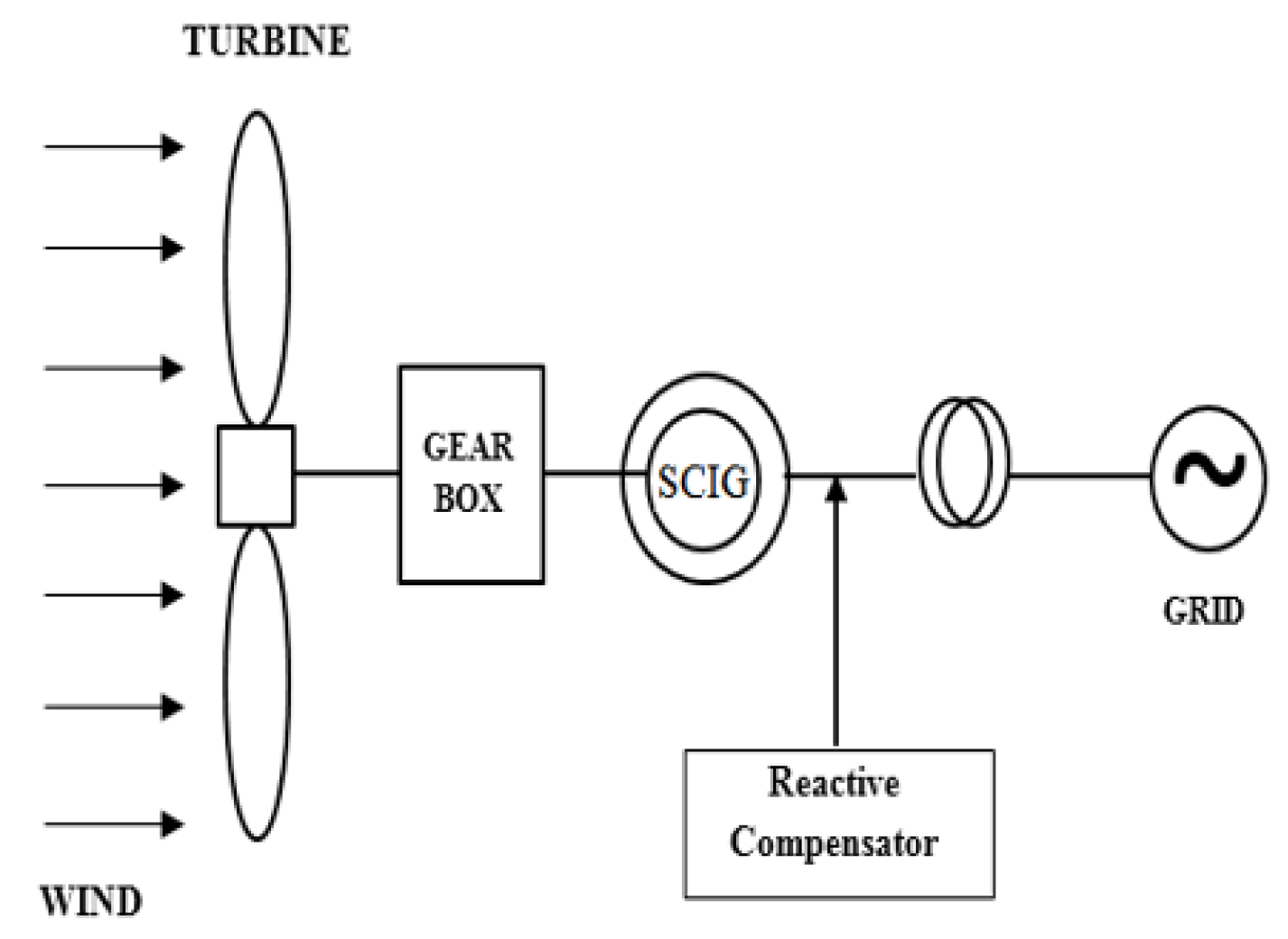
2.2. Squirrel Cage Induction Generator (SCIG)
2.3. Mathematical Model for DFIG and SCIG
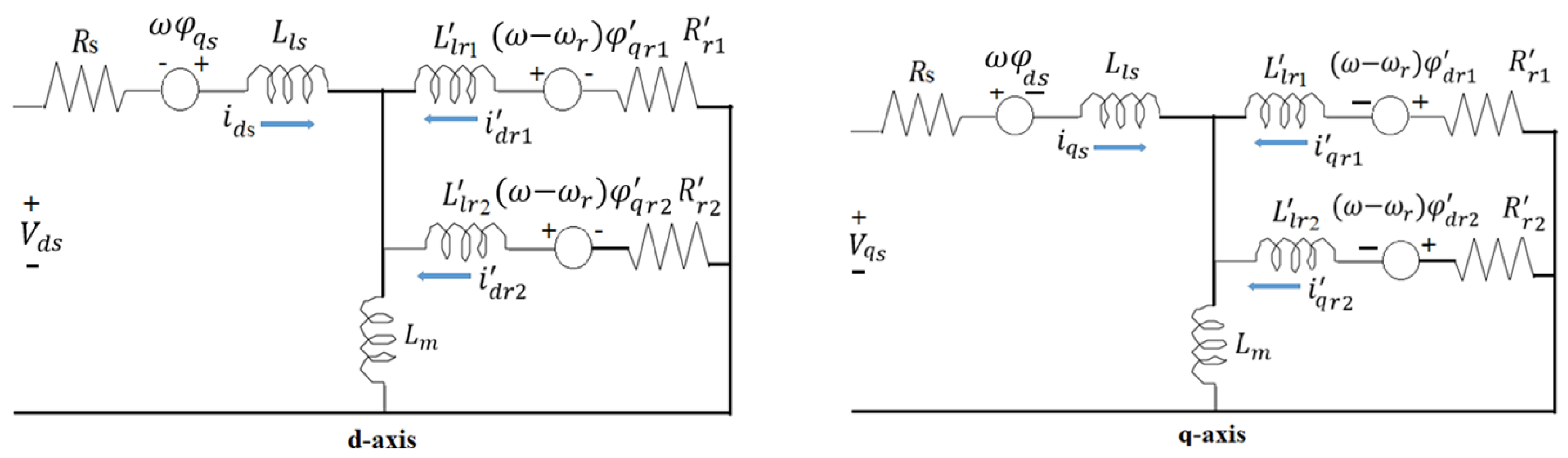
3. Mathematical Model for Double Cage Induction Machines (DCIM)
3.1. Electrical System
- 1.
- Selected core is made up of ferromagnetic material organized in lamination to minimize the core losses
- 2.
- The core losses are negligible when compared to the stator and rotor copper winding losses
3.2. Mechanical System
4. Mathematical Model for DFIG and SCIG Systems
4.1. Wind Energy Conversion
- Performance coefficient of the turbine
- Tip speed ratio of the rotor blade tip speed to wind speed
- Blade pitch angle (deg)
- Density of Air (kg/m)
- Radius of the turbine blades (m)
- Wind speed (m/s)
4.2. Electrical Systems for Wound Rotor (DFIG) and Squirrel Cage (SCIG) Machine
5. Balancing Related Model Order Reduction Schemes
5.1. Balance Truncation Technique (Moore, B. 1981)
5.2. Enns’s Technique (Enns, D.F. 1984)
5.3. Wang and Sreeram’s Technique (Wang, G. 1999)
5.4. Imran and Ghafoor’s Technique (Imran, M. 2014)
6. Main Results
- and .
- and are obtained by subtracting Equations (16)–(28) and (18)–(29) respectively
Computational Aspects
- Proposed Technique: The Cholesky factors and satisfy and , where (26) and (27). Next we establish a relationship between Cholesky factors Gramian matrices of Enns and proposed technique. Equations (26) and (27) can be expressed as:SinceBy using the Hammarling’s technique [60] to calculate the Cholesky factors of the Gramians and from the realization , we can write and . Therefore, and (27) can be expressed as:
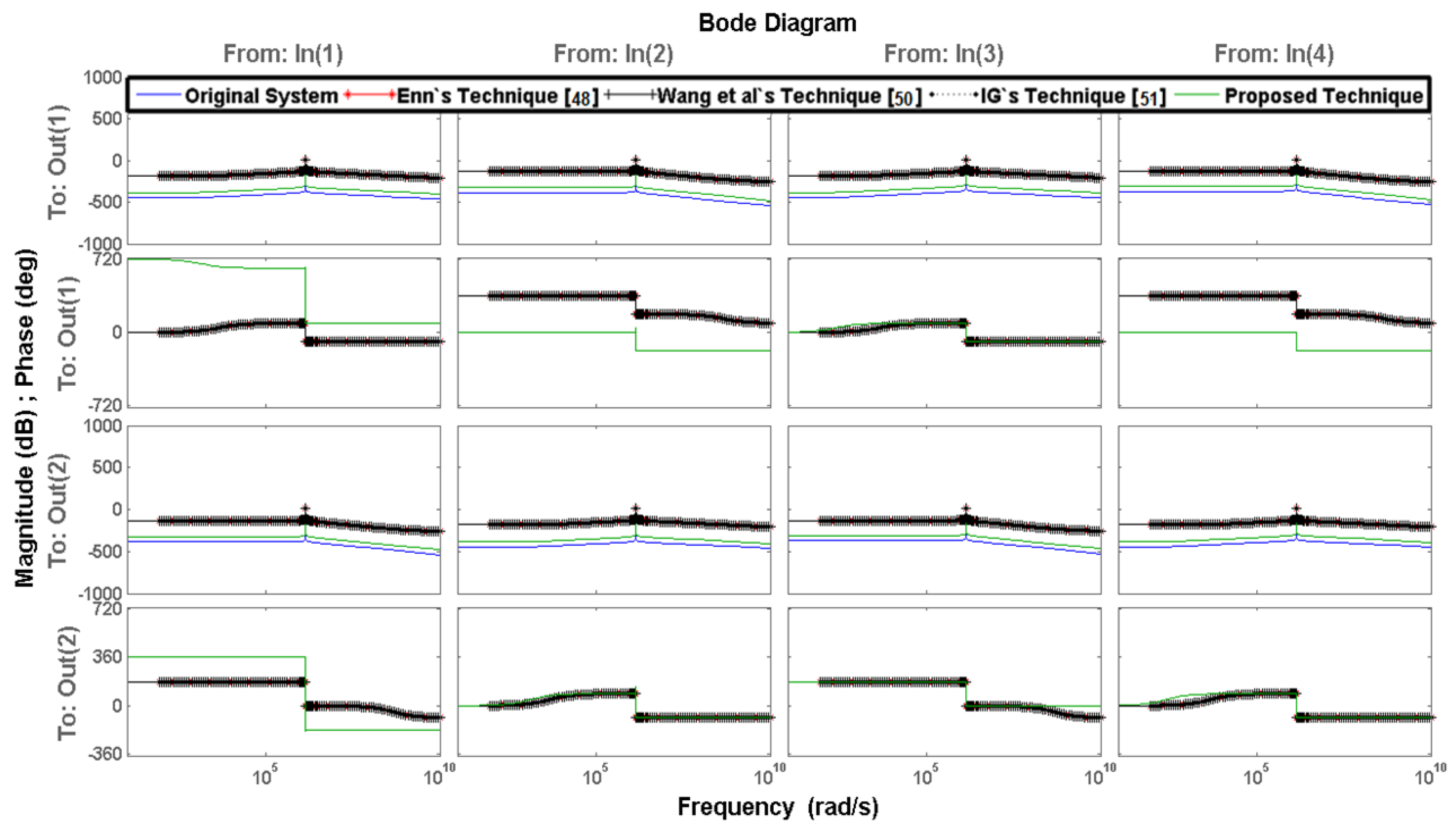
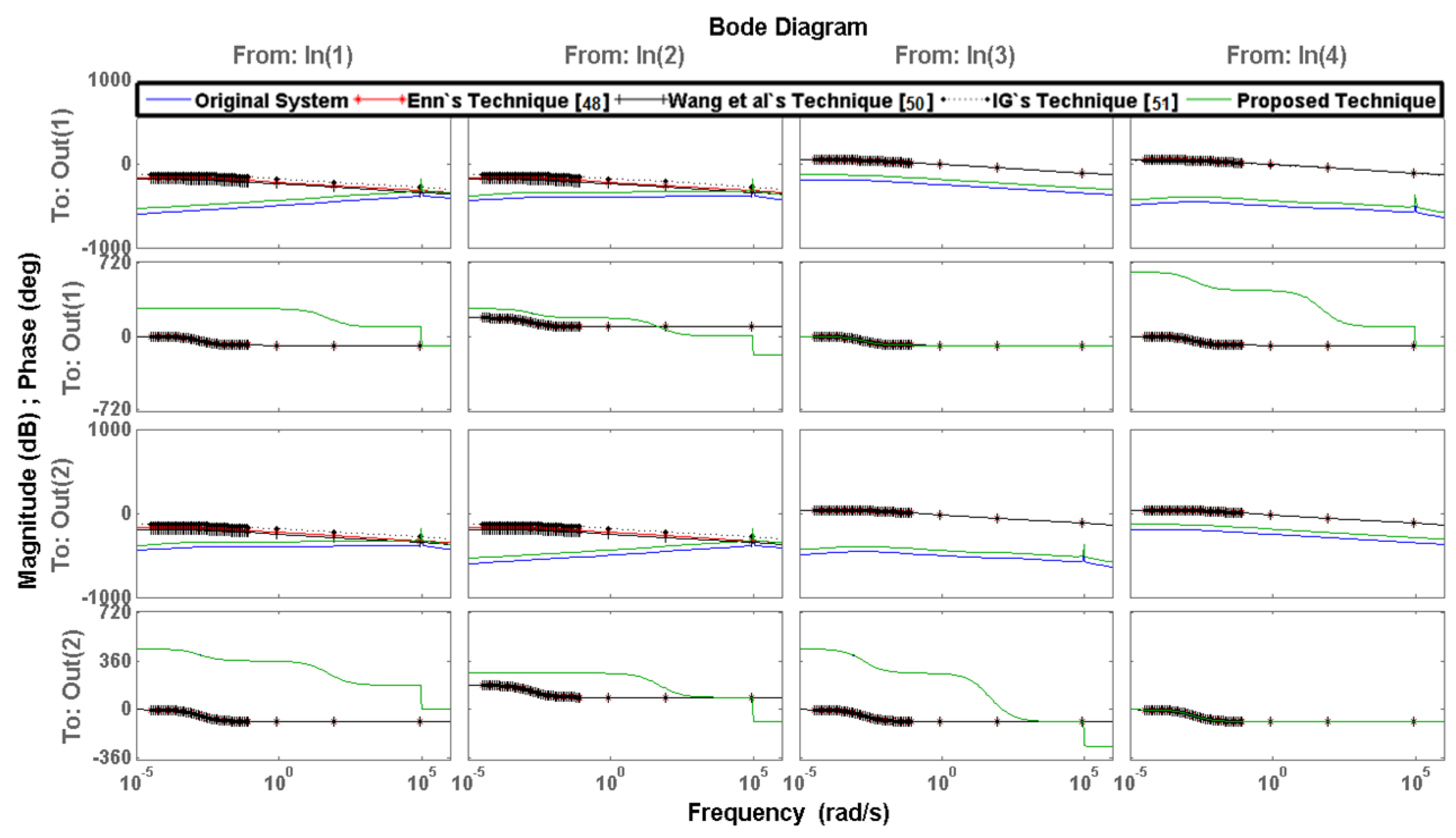
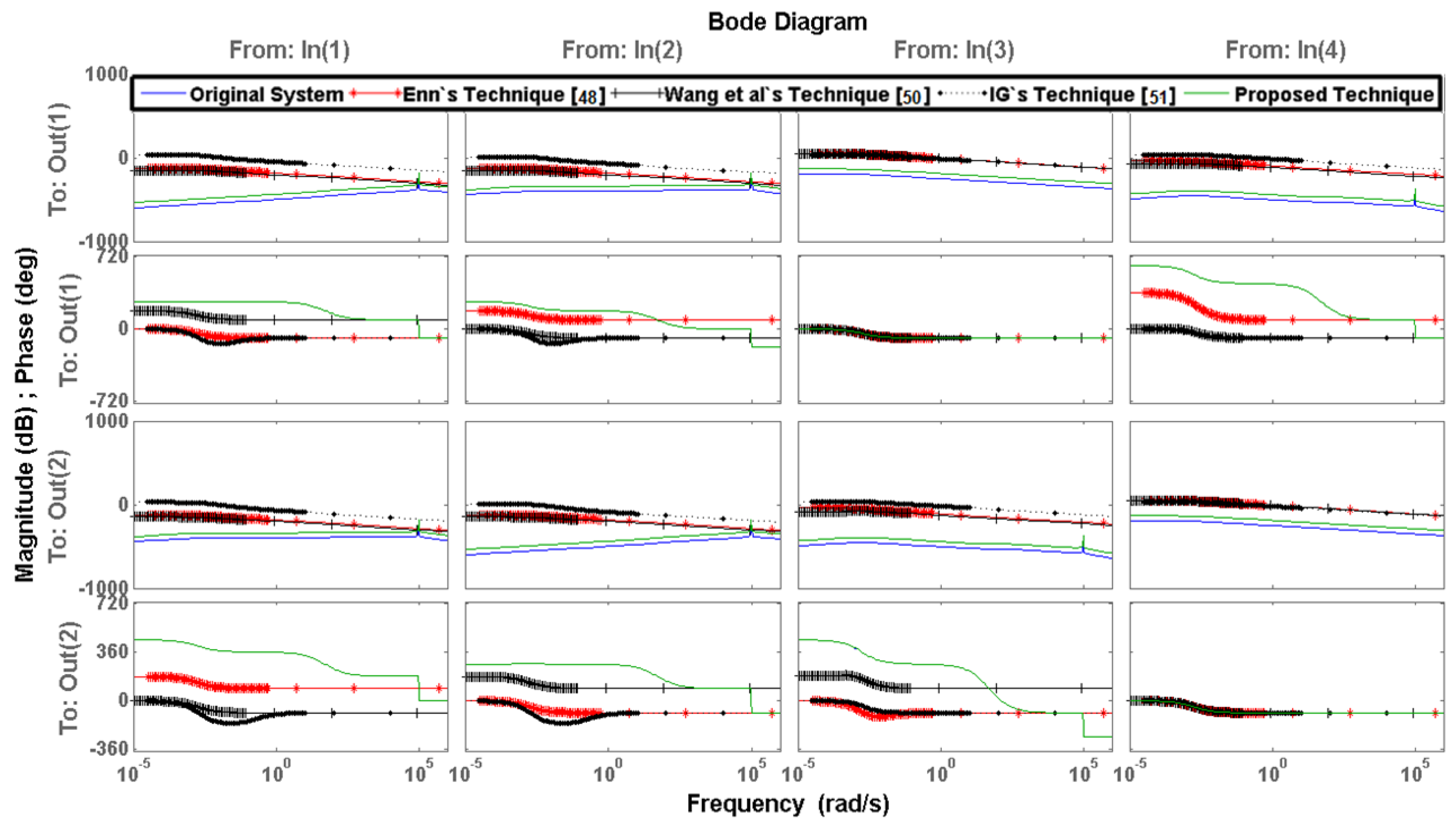
7. Numerical Examples
8. Analysis and Discussion
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LVRT | Low voltage ride through |
| HVRT | High voltage ride through |
| SCIG | Squirrel Cage Induction Generator |
| DFIG | Doubly Fed Induction Generator |
| PMSG | Permanent Magnet Synchronous Generator |
| SCIM | Squirrel Cage Induction Machines |
| MOR | Model order reduction |
| ROM | Reduced order model |
| RSC | Rotor Side Converter |
| GSC | Grid Side Converter |
| DCIM | Double Cage Induction Machine |
References
- Giefer, L.A.; Staar, B.; Freitag, M. FPGA-Based Optical Surface Inspection of Wind Turbine Rotor Blades Using Quantized Neural Networks. Electronics 2020, 9, 1824. [Google Scholar] [CrossRef]
- Villena-Ruiz, R.; Honrubia-Escribano, A.; Jiménez-Buendía, F.; Molina-García, Á.; Gómez-Lázaro, E. Requirements for Validation of Dynamic Wind Turbine Models: An International Grid Code Review. Electronics 2020, 9, 1707. [Google Scholar] [CrossRef]
- Sahragard, A.; Falaghi, H.; Farhadi, M.; Mosavi, A.; Estebsari, A. Generation expansion planning in the presence of wind power plants using a genetic algorithm model. Electronics 2020, 9, 1143. [Google Scholar] [CrossRef]
- Abdollahi, A.; Ghadimi, A.A.; Miveh, M.R.; Mohammadi, F.; Jurado, F. Optimal power flow incorporating FACTS devices and stochastic wind power generation using krill herd algorithm. Electronics 2020, 9, 1043. [Google Scholar] [CrossRef]
- Lee, J.; Zhao, F. Global Wind Report 2019; Global Wind Energy Council: Brussels, Belgium, 2020; Available online: https://gwec.net/global-wind-report-2019/ (accessed on 27 December 2020).
- Ohlenforst, K.; Sawyer, S.; Dutton, A.; Backwell, B.; Fiestas, R.; Lee, J.; Qiao, L.; Zhao, F.; Balachandran, N. Global Wind Report 2018; Global Wind Energy Council: Brussels, Belgium, 2019; Available online: https://gwec.net/global-wind-report-2018/ (accessed on 27 December 2020).
- Mlecnik, E.; Parker, J.; Ma, Z.; Corchero, C.; Knotzer, A.; Pernetti, R. Policy challenges for the development of energy flexibility services. Energy Policy 2020, 137, 111147. [Google Scholar] [CrossRef]
- Lu, Y.; Khan, Z.A.; Alvarez-Alvarado, M.S.; Zhang, Y.; Huang, Z.; Imran, M. A critical review of sustainable energy policies for the promotion of renewable energy sources. Sustainability 2020, 12, 5078. [Google Scholar] [CrossRef]
- Schwarz, M.; Nakhle, C.; Knoeri, C. Innovative designs of building energy codes for building decarbonization and their implementation challenges. J. Clean. Prod. 2020, 248, 119260. [Google Scholar] [CrossRef]
- Nazir, M.S.; Mahdi, A.J.; Bilal, M.; Sohail, H.M.; Ali, N.; Iqbal, H.M. Environmental impact and pollution-related challenges of renewable wind energy paradigm–A review. Sci. Total Environ. 2019, 683, 436–444. [Google Scholar] [CrossRef]
- Andrić, I.; Koc, M.; Al-Ghamdi, S.G. A review of climate change implications for built environment: Impacts, mitigation measures and associated challenges in developed and developing countries. J. Clean. Prod. 2019, 211, 83–102. [Google Scholar] [CrossRef]
- Qiao, W.; Harley, R.G. Grid connection requirements and solutions for DFIG wind turbines. In Proceedings of the 2008 IEEE Energy 2030 Conference, Atlanta, GA, USA, 17–18 November 2008; pp. 1–8. [Google Scholar]
- Hlaing, S. Basic Concepts of Doubly Fed Induction Generator Driven by Wind Energy Conversion System. Int. J. Sci. Eng. Technol. Res. 2014, 3, 3242–3246. [Google Scholar]
- Tiwari, A.R.; Shewale, A.J.; Gagangras, A.; Lokhande, N.M. Comparison of various wind turbine generators. Multidiscplinary J. Res. Eng. Technol. 2014, 1, 129–135. [Google Scholar]
- Yang, B.; Jiang, L.; Wang, L.; Yao, W.; Wu, Q. Nonlinear maximum power point tracking control and modal analysis of DFIG based wind turbine. Int. J. Electr. Power Energy Syst. 2016, 74, 429–436. [Google Scholar] [CrossRef]
- Tande, J.O.; Di Marzio, G.; Uhlen, K. System Requirements for Wind Power Plants; SINTEF: Trondheim, Norway, 2007. [Google Scholar]
- Kazachkov, Y.; Feltes, J.W.; Zavadil, R. Modeling wind farms for power system stability studies. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting (IEEE Cat. No. 03CH37491), Toronto, ON, Canada, 13–17 July 2003; Volume 3, pp. 1526–1533. [Google Scholar]
- Rodríguez, J.M.; Fernández, J.L.; Beato, D.; Iturbe, R.; Usaola, J.; Ledesma, P.; Wilhelmi, J.R. Incidence on power system dynamics of high penetration of fixed speed and doubly fed wind energy systems: Study of the Spanish case. IEEE Trans. Power Syst. 2002, 17, 1089–1095. [Google Scholar] [CrossRef]
- Ullah, N.R.; Larsson, A.; Petersson, A.; Karlsson, D. Detailed modeling for large scale wind power installations-a real project case study. In Proceedings of the 2008 Third International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; pp. 46–56. [Google Scholar]
- Reddy, S.S.; Prathipati, K.; Lho, Y.H. Transient stability improvement of a system connected with wind energy generators. Int. J. Emerg. Electr. Power Syst. 2017, 18. [Google Scholar] [CrossRef]
- Maity, D.; Chowdhury, A.; Reddy, S.S.; Panigrahi, B.K.; Abhyankar, A.R.; Mallick, M.K. Joint energy and spinning reserve dispatch in wind-thermal power system using IDE-SAR technique. In Proceedings of the 2013 IEEE Symposium on Swarm Intelligence (SIS), Singapore, 16–19 April 2013; pp. 284–290. [Google Scholar]
- Ekanayake, J.B.; Holdsworth, L.; Wu, X.; Jenkins, N. Dynamic modeling of doubly fed induction generator wind turbines. IEEE Trans. Power Syst. 2003, 18, 803–809. [Google Scholar] [CrossRef]
- Akhmatov, V.; Nielsen, A.H.; Pedersen, J.K.; Nymann, O. Variable-speed wind turbines with multi-pole synchronous permanent magnet generators. Part I: Modelling in dynamic simulation tools. Wind. Eng. 2003, 27, 531–548. [Google Scholar] [CrossRef]
- Ugalde-Loo, C.E.; Ekanayake, J.B. State-space modelling of variable-speed wind turbines: A systematic approach. In Proceedings of the 2010 IEEE International Conference on Sustainable Energy Technologies (ICSET), Kandy, Sri Lanka, 6–9 December 2010; pp. 1–6. [Google Scholar]
- Ackermann, T. Wind Power in Power Systems; John Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Ramtharan, G.; Jenkins, N.; Anaya-Lara, O. Modelling and control of synchronous generators for wide-range variable-speed wind turbines. Wind. Energy Int. J. Prog. Appl. Wind. Power Convers. Technol. 2007, 10, 231–246. [Google Scholar] [CrossRef]
- Holdsworth, L.; Wu, X.; Ekanayake, J.B.; Jenkins, N. Comparison of fixed speed and doubly-fed induction wind turbines during power system disturbances. IEE Proc. Gener. Transm. Distrib. 2003, 150, 343–352. [Google Scholar] [CrossRef]
- Quang, N.P.; Dittrich, J.A. Vector Control of Three-Phase AC Machines; Springer: Berlin/Heidelberg, Germay, 2008; Volume 2. [Google Scholar]
- Ekanayake, J.B.; Holdsworth, L.; Jenkins, N. Comparison of 5th order and 3rd order machine models for doubly fed induction generator (DFIG) wind turbines. Electr. Power Syst. Res. 2003, 67, 207–215. [Google Scholar] [CrossRef]
- Pulgar-Painemal, H.A.; Sauer, P.W. Reduced-order model of type-c wind turbine generators. Electr. Power Syst. Res. 2011, 81, 840–845. [Google Scholar] [CrossRef]
- Slootweg, J.; Polinder, H.; Kling, W. Reduced-order modelling of wind turbines. Wind. Power Power Syst. 2005, 25. [Google Scholar] [CrossRef]
- Rezaei, M.M.; Behzad, M.; Haddadpour, H.; Moradi, H. Development of a reduced order model for nonlinear analysis of the wind turbine blade dynamics. Renew. Energy 2015, 76, 264–282. [Google Scholar] [CrossRef]
- García Planas, M.I. Input observability analysis of fixed speed wind turbine. In Proceedings of the 3rd International Conference on Energy, Environment, Devices, Systems, Communications, Computers, Rovaniemi, Finland, 18–20 April 2012; WSEAS Press: Athens, Greece, 2012; pp. 13–19. [Google Scholar]
- Zhao, X.; Weiss, G. Well-posedness and controllability of a wind turbine tower model. IMA J. Math. Control. Inf. 2011, 28, 103–119. [Google Scholar] [CrossRef]
- Al-Iedani, I.; Gajic, Z. Order reduction of a wind turbine energy system via the methods of system balancing and singular perturbations. Int. J. Electr. Power Energy Syst. 2020, 117, 105642. [Google Scholar] [CrossRef]
- Lee, K.; Carlberg, K.T. Model reduction of dynamical systems on nonlinear manifolds using deep convolutional autoencoders. J. Comput. Phys. 2020, 404, 108973. [Google Scholar] [CrossRef]
- Lin, K.K.; Lu, F. Data-driven model reduction, Wiener projections, and the Koopman-Mori-Zwanzig formalism. J. Comput. Phys. 2020, 424, 109864. [Google Scholar] [CrossRef]
- Idiart, M.I.; Lahellec, N.; Suquet, P. Model reduction by mean-field homogenization in viscoelastic composites. I. Primal theory. Proc. R. Soc. 2020, 476, 20200407. [Google Scholar] [CrossRef]
- Klus, S.; Nüske, F.; Peitz, S.; Niemann, J.H.; Clementi, C.; Schütte, C. Data-driven approximation of the Koopman generator: Model reduction, system identification, and control. Phys. Nonlinear Phenom. 2020, 406, 132416. [Google Scholar] [CrossRef]
- Parish, E.J.; Wentland, C.R.; Duraisamy, K. The Adjoint Petrov–Galerkin method for non-linear model reduction. Comput. Methods Appl. Mech. Eng. 2020, 365, 112991. [Google Scholar] [CrossRef]
- Campbell, K.; Sreeram, V.; Wang, G. A Frequency-weighted discrete system balanced truncation method and an error bound. In Proceedings of the 2000 American Control Conference. ACC (IEEE Cat. No. 00CH36334), Chicago, IL, USA, 28–30 June 2000; Volume 4, pp. 2403–2404. [Google Scholar]
- Varga, A.; Anderson, B.D. Accuracy enhancing methods for the frequency-weighted balancing related model reduction. In Proceedings of the 40th IEEE Conference on Decision and Control (Cat. No. 01CH37228), Orlando, FL, USA, 4–7 December 2001; Volume 4, pp. 3659–3664. [Google Scholar]
- Imran, M.; Ghafoor, A.; Sreeram, V. Frequency weighted model order reduction technique and error bounds for discrete time systems. Math. Probl. Eng. 2014, 2014, 498453. [Google Scholar] [CrossRef]
- Haider, K.S.; Ghafoor, A.; Imran, M.; Malik, F.M. Model reduction of large scale descriptor systems using time limited gramians. Asian J. Control 2017, 19, 1217–1227. [Google Scholar] [CrossRef]
- Imran, M.; Ghafoor, A. Frequency weighted passivity preserving model reduction technique. IMA J. Math. Control. Inf. 2018, 35, 837–844. [Google Scholar] [CrossRef]
- Haider, S.; Ghafoor, A.; Imran, M.; Malik, F.M. Time-limited Gramians-based model order reduction for second-order form systems. Trans. Inst. Meas. Control 2019, 41, 2310–2318. [Google Scholar] [CrossRef]
- Moore, B. Principal component analysis in linear systems: Controllability, observability, and model reduction. IEEE Trans. Autom. Control 1981, 26, 17–32. [Google Scholar] [CrossRef]
- Enns, D.F. Model reduction with balanced realizations: An error bound and a frequency weighted generalization. In Proceedings of the 23rd IEEE Conference on Decision and Control, Las Vegas, NV, USA, 12–14 December 1984; pp. 127–132. [Google Scholar]
- Sreeram, V.; Anderson, B.; Madievski, A. New results on frequency weighted balanced reduction technique. In Proceedings of the 1995 American Control Conference-ACC’95, Seattle, WA, USA, 21–23 June 1995; Volume 6, pp. 4004–4009. [Google Scholar]
- Wang, G.; Sreeram, V.; Liu, W. A new frequency-weighted balanced truncation method and an error bound. IEEE Trans. Autom. Control 1999, 44, 1734–1737. [Google Scholar] [CrossRef]
- Imran, M.; Ghafoor, A.; Sreeram, V. A frequency weighted model order reduction technique and error bounds. Automatica 2014, 50, 3304–3309. [Google Scholar] [CrossRef]
- Gawronski, W.; Juang, J.N. Model reduction in limited time and frequency intervals. Int. J. Syst. Sci. 1990, 21, 349–376. [Google Scholar] [CrossRef]
- Wang, D.; Zilouchian, A. Model reduction of discrete linear systems via frequency-domain balanced structure. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2000, 47, 830–837. [Google Scholar] [CrossRef]
- Gugercin, S.; Antoulas, A.C. A survey of model reduction by balanced truncation and some new results. Int. J. Control 2004, 77, 748–766. [Google Scholar] [CrossRef]
- Ghafoor, A.; Sreeram, V. A survey/review of frequency-weighted balanced model reduction techniques. J. Dyn. Syst. Meas. Control 2008, 130, 061004. [Google Scholar] [CrossRef]
- Ghafoor, A.; Sreeram, V. Model reduction via limited frequency interval Gramians. IEEE Trans. Circuits Syst. Regul. Pap. 2008, 55, 2806–2812. [Google Scholar] [CrossRef]
- Imran, M.; Ghafoor, A. Stability preserving model reduction technique and error bounds using frequency-limited Gramians for discrete-time systems. IEEE Trans. Circuits Syst. II Express Briefs 2014, 61, 716–720. [Google Scholar] [CrossRef]
- Imran, M.; Ghafoor, A. A frequency limited interval Gramians-based model reduction technique with error bounds. Circuits Syst. Signal Process. 2015, 34, 3505–3519. [Google Scholar] [CrossRef]
- Imran, M.; Ghafoor, A. Frequency limited model reduction techniques with error bounds. IEEE Trans. Circuits Syst. II Express Briefs 2017, 65, 86–90. [Google Scholar] [CrossRef]
- Hammarling, S.J. Numerical solution of the stable, non-negative definite lyapunov equation lyapunov equation. IMA J. Numer. Anal. 1982, 2, 303–323. [Google Scholar] [CrossRef]
- Ghafoor, A. Frequency-Weighted Model Reduction and Error Bounds; University of Western Australia: Crawley, WA, Australia, 2007. [Google Scholar]



| Parameters for Double Cage Induction Machine (DCIM) | |||
|---|---|---|---|
| Stator | Double Cage Rotor | ||
| Stator Resistance and Leakage Inductance | Rotor resistance and leakage inductance of cage 1 | ||
| Total Stator inductance | Rotor resistance andleakage inductance of cage 2 | ||
| q-axis stator voltage and current | Total rotor inductances of cage1 and 2 | ||
| d-axis stator voltage and current | d-axis rotor current of cage 1 and 2 | ||
| Stator d axis flux | q-axis rotor current of cage 1 and 2 | ||
| Stator q axis fluxes | d and q-axis rotor fluxes of cage 1 | ||
| d and q-axis rotor fluxes of cage 2 | |||
| Magnetizing inductance | |||
| H | Combined rotor and load inertia constant. Set to infinite to simulate a locked rotor. | ||
| Angular velocity of rotor | |||
| p | Number of pole pairs | ||
| Electromagnetic torque | |||
| Shaft mechanical torque | |||
| F | Combined rotor and load viscous friction coefficient | ||
| Stator active power | |||
| Stator reactive power | |||
| Rotor active power | |||
| Rotor reactive power | |||
| Mechanical power | |||
| Examples | Weights | Order of ROMs | Frequency Response Error and Error Bound | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Error Value | Error Bound | ||||||||
| Example 1 | Input | Enns [48] | Wang et al. [50] | IG [51] | Proposed | Wang et al [50] | IG [51] | Proposed | |
| 1st | 21041 | 63123 | 63119 | 10521 | 2.5089 | 1.5787 | 6.9691 | ||
| 2nd | 21041 | 28691 | 28691 | 874.95 | 1.0394 | 6.5403 | 9.3939 | ||
| 3rd | 15.192 | 42.536 | 42.53 | 16.682 | 66711 | 41977 | 1.471 | ||
| 4th | 0.00012504 | 0.00036244 | 0.00036553 | 5.3999 | 0.45676 | 0.2874 | 0.012688 | ||
| 5th | 0.00019472 | 0.00058435 | 0.00058452 | 9.7367 | 0.22828 | 0.14364 | 0.0063412 | ||
| Output | 1st | 600.83 | 3605 | 3605 | 600.83 | 7360.1 | 7360.1 | 1226.7 | |
| 2nd | 17.468 | 104.81 | 104.81 | 17.468 | 787.08 | 787.08 | 131.18 | ||
| 3rd | 781.13 | 1292.7 | 1292.7 | 272.56 | 33356 | 20988 | 7.355 | ||
| 4th | 0.00012504 | 0.00013769 | 0.00023402 | 5.8358 | 0.018923 | 0.011907 | 0.097036 | ||
| 5th | 0.00019472 | 0.0011334 | 0.001152 | 3.997 | 0.009441 | 0.0059405 | 0.048396 | ||
| Both | 1st | 21041 | 63123 | 63119 | 10521 | 2.5089 | 1.5787 | 6.9691 | |
| 2nd | 15.192 | 45.574 | 45.569 | 7.5957 | 1.6103 | 1.0132 | 44730 | ||
| 3rd | (Unstable) | 2343.4 | 2343.4 | 390.57 | 8.0515 | 5.0662 | 22365 | ||
| 4th | (Unstable) | 204.75 | 204.75 | 34.125 | 393.54 | 393.54 | 65.59 | ||
| 5th | (Unstable) | 0.0002598 | 0.00035015 | 5.0657 | 0.00013076 | 0.00013076 | 2.1794 | ||
| Example 2 | Input | 1st | 25.423 | 160.96 | 133.56 | 220.41 | 1174.3 | 2534 | 1076.2 |
| 2nd | 4.7919 | 9.4436 | 9.4436 | 1.5739 | 154 | 71.553 | 41.611 | ||
| 3rd | 122.46 | 23.105 | 9.4436 | 11.125 | 76.999 | 35.974 | 20.807 | ||
| 4th | 0.0010232 | 0.0010362 | 0.001036 | 0.00017269 | 0.0025148 | 0.3957 | 0.0022101 | ||
| 5th | 5.0869 | 8.5879 | 0.0001078 | 2.0143 | 0.00014916 | 0.19785 | 0.00026321 | ||
| Output | 1st | 91.661 | 654.98 | 549.97 | 41.26 | 1136.9 | 2992.7 | 1103.5 | |
| 2nd | 3.7281 | 22.369 | 22.369 | 3.52 | 67.124 | 1942.3 | 41.8 | ||
| 3rd | 9.8125 | 22.369 | 67.155 | 7.21 | 33.563 | 971.17 | 20.6 | ||
| 4th | 0.00026695 | 0.00064997 | 0.00071741 | 0.00010833 | 0.0013756 | 0.00098094 | 0.00041012 | ||
| 5th | 5.8325 | 0.0002288 | 0.0002288 | 0.00010653 | 0.00035221 | 0.00025725 | 0.00012167 | ||
| Both | 1st | 25.423 | 100.1 | 149.21 | 15.82 | 8223.2 | 43426 | 1384.5 | |
| 2nd | 4.7919 | 14.376 | 14.376 | 42.759 | 2110.3 | 28221 | 780.36 | ||
| 3rd | (Unstable) | 14.376 | 303.11 | 15.82 | 1055.2 | 14112 | 176.26 | ||
| 4th | (Unstable) | 0.00098241 | 0.0012763 | 0.00021014 | 0.042506 | 3.3415 | 0.00083643 | ||
| 5th | (Unstable) | 5.1359 | 9.0852 | 8.5553 | 0.00090627 | 0.87629 | 1.787 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bashir, S.; Batool, S.; Imran, M.; Imran, M.; Ahmad, M.I.; Malik, F.M.; Ali, U. Development of Frequency Weighted Model Reduction Algorithm with Error Bound: Application to Doubly Fed Induction Generator Based Wind Turbines for Power System. Electronics 2021, 10, 44. https://doi.org/10.3390/electronics10010044
Bashir S, Batool S, Imran M, Imran M, Ahmad MI, Malik FM, Ali U. Development of Frequency Weighted Model Reduction Algorithm with Error Bound: Application to Doubly Fed Induction Generator Based Wind Turbines for Power System. Electronics. 2021; 10(1):44. https://doi.org/10.3390/electronics10010044
Chicago/Turabian StyleBashir, Sajid, Sammana Batool, Muhammad Imran, Muhammad Imran, Mian Ilyas Ahmad, Fahad Mumtaz Malik, and Usman Ali. 2021. "Development of Frequency Weighted Model Reduction Algorithm with Error Bound: Application to Doubly Fed Induction Generator Based Wind Turbines for Power System" Electronics 10, no. 1: 44. https://doi.org/10.3390/electronics10010044
APA StyleBashir, S., Batool, S., Imran, M., Imran, M., Ahmad, M. I., Malik, F. M., & Ali, U. (2021). Development of Frequency Weighted Model Reduction Algorithm with Error Bound: Application to Doubly Fed Induction Generator Based Wind Turbines for Power System. Electronics, 10(1), 44. https://doi.org/10.3390/electronics10010044








