Is There a Relationship between Transepidermal Water Loss and Microbial Biodiversity on the Skin?
Abstract
1. Introduction
2. Methods
Data Analysis—Correlation and Distribution
3. Results
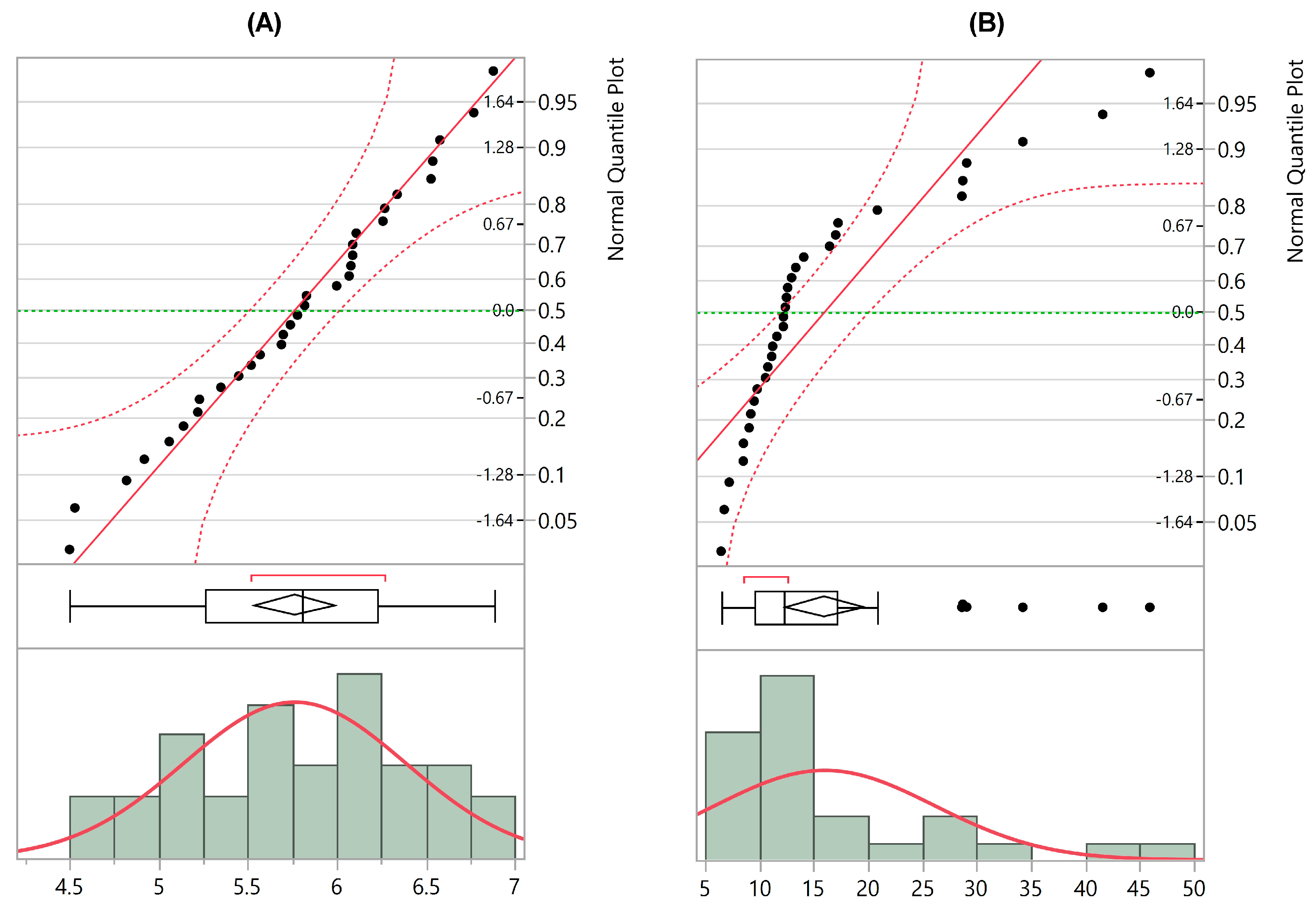
3.1. Sample Characteristics
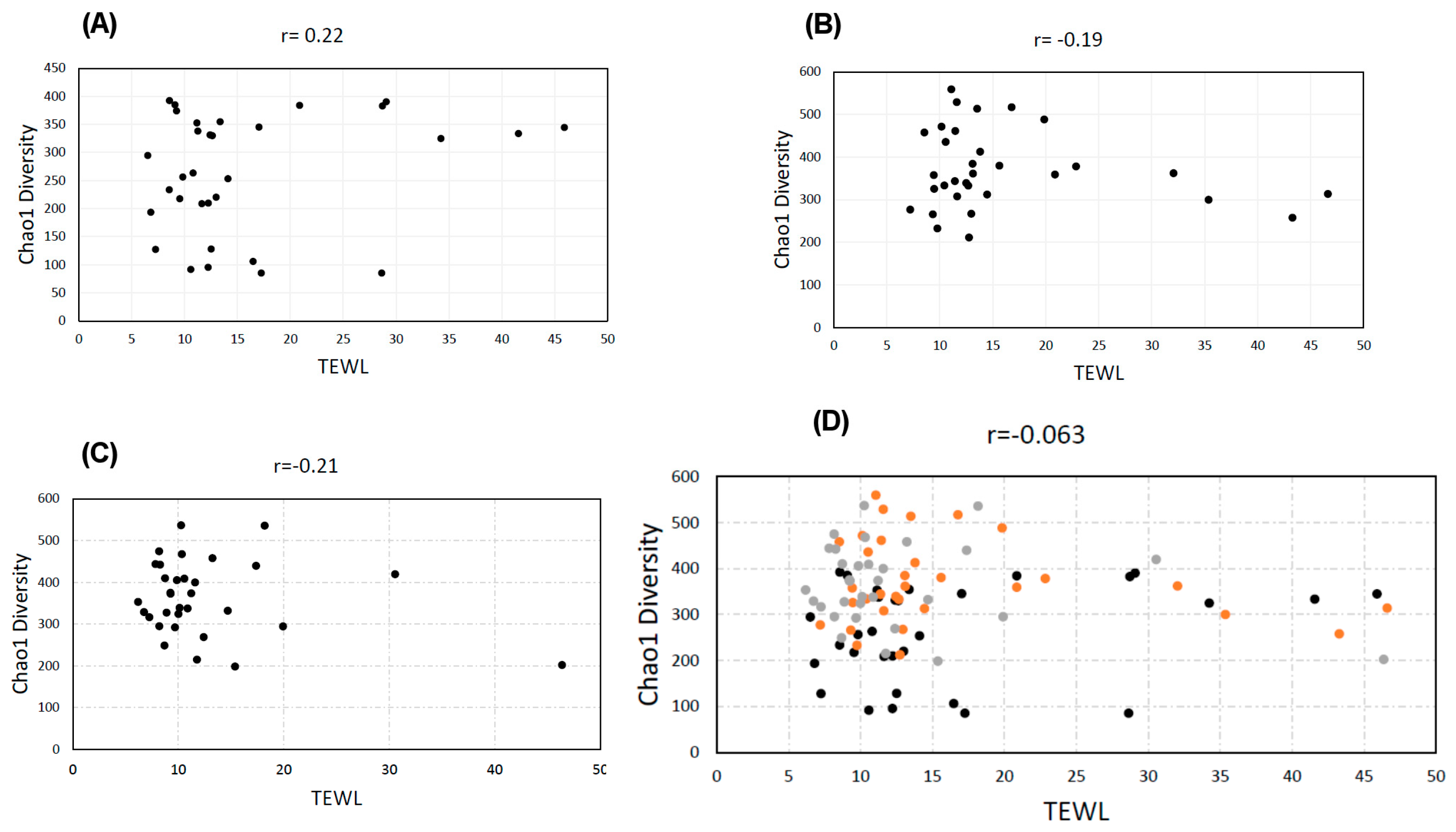
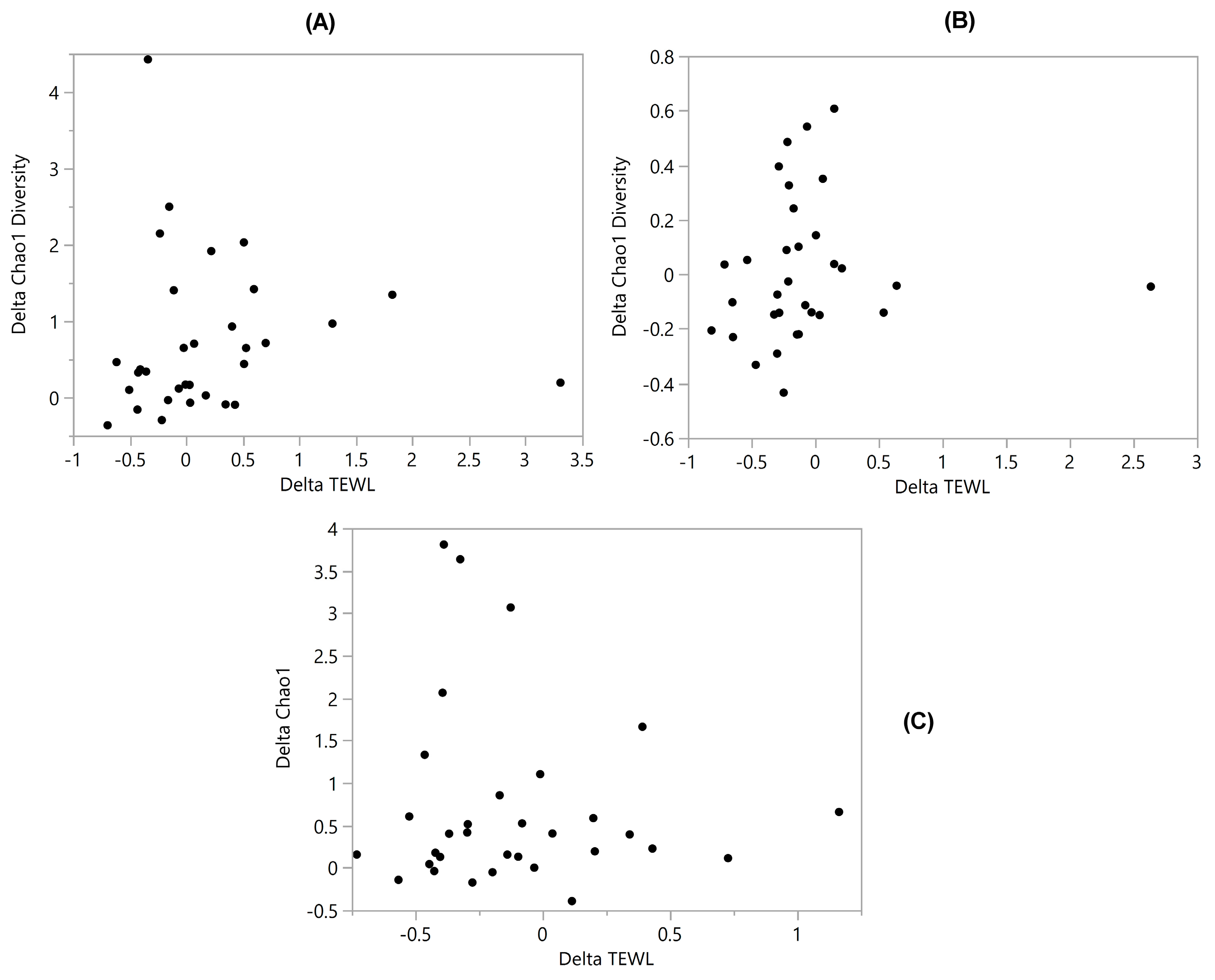
3.2. Diversity vs. TEWL
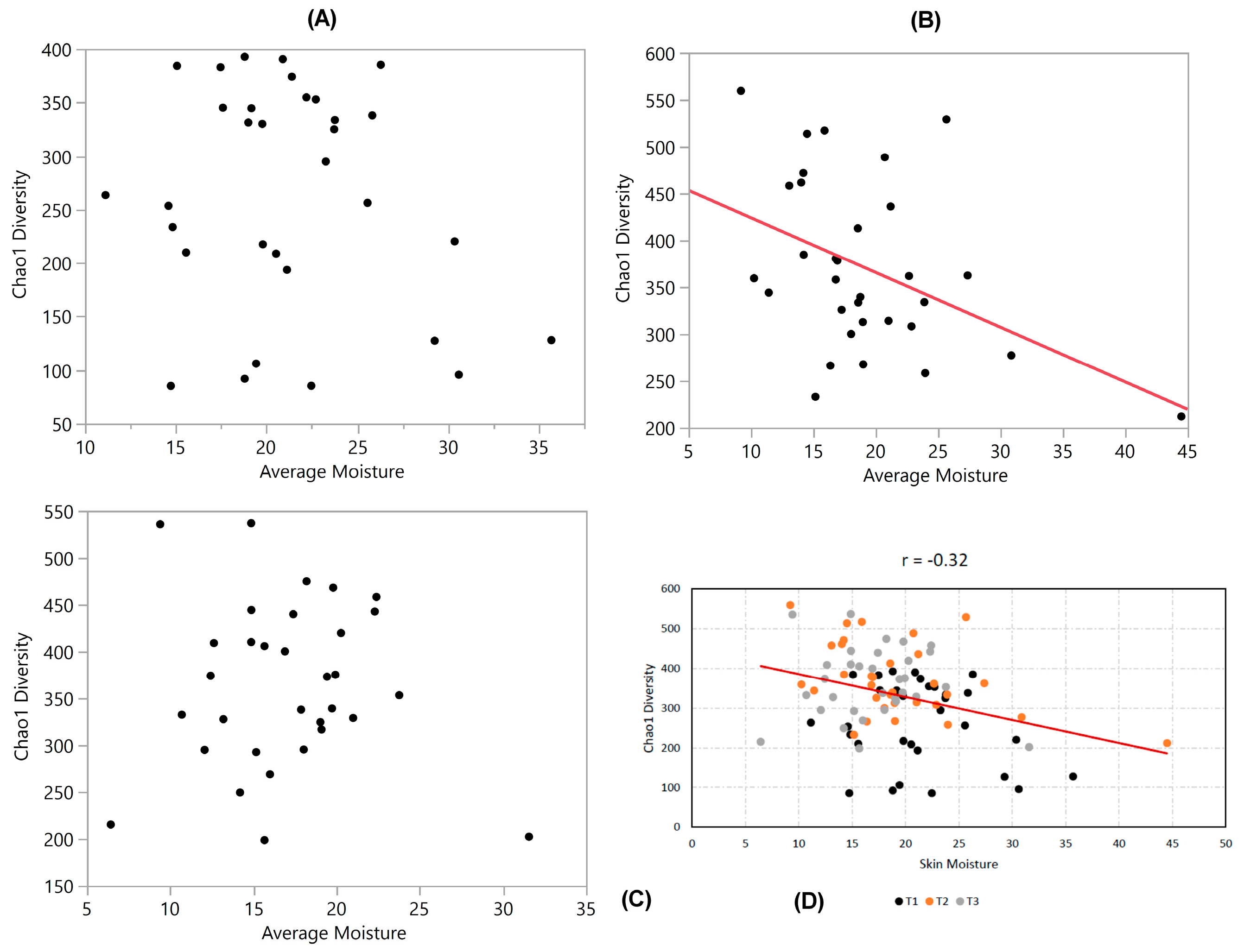
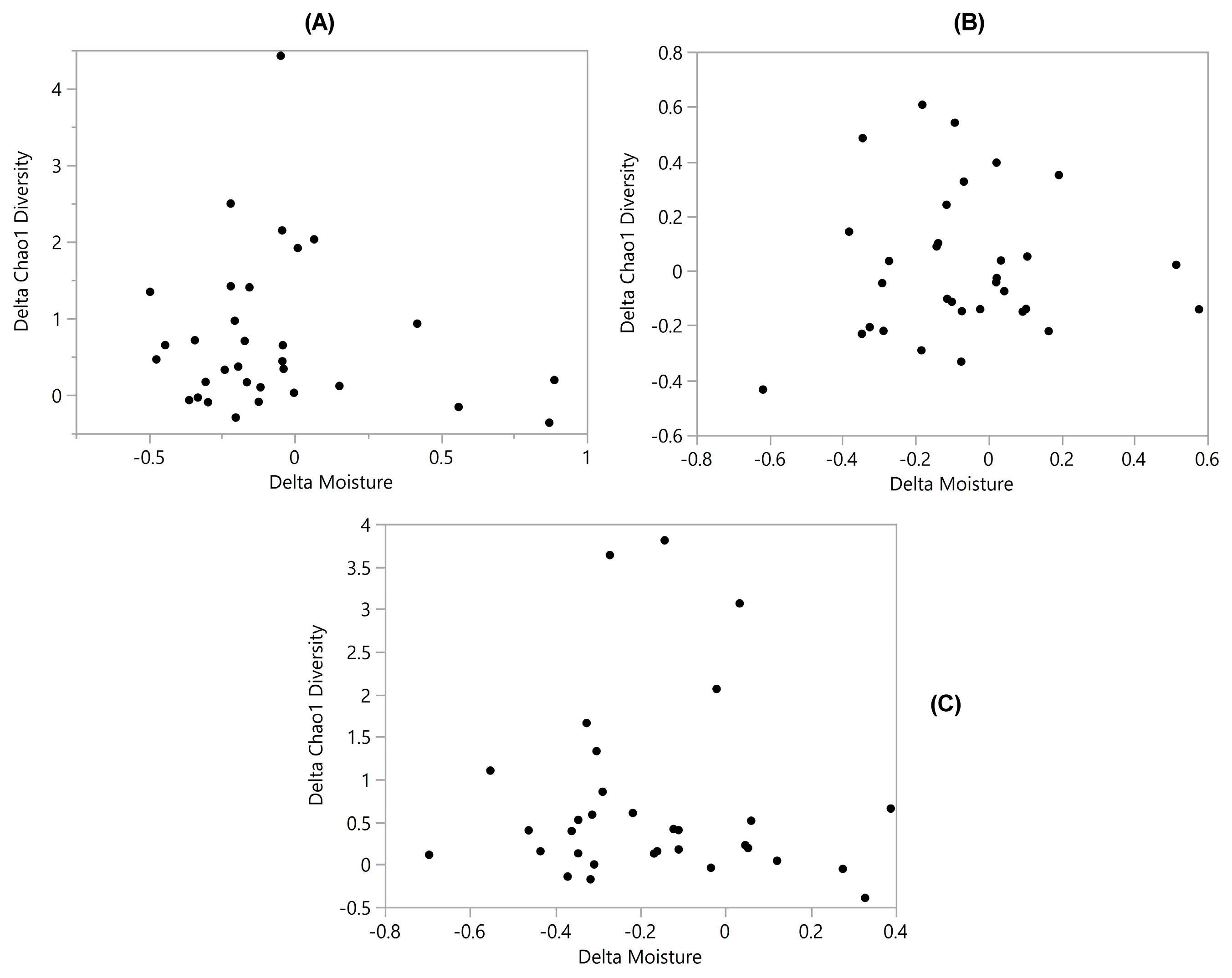
3.3. Diversity vs. Moisture
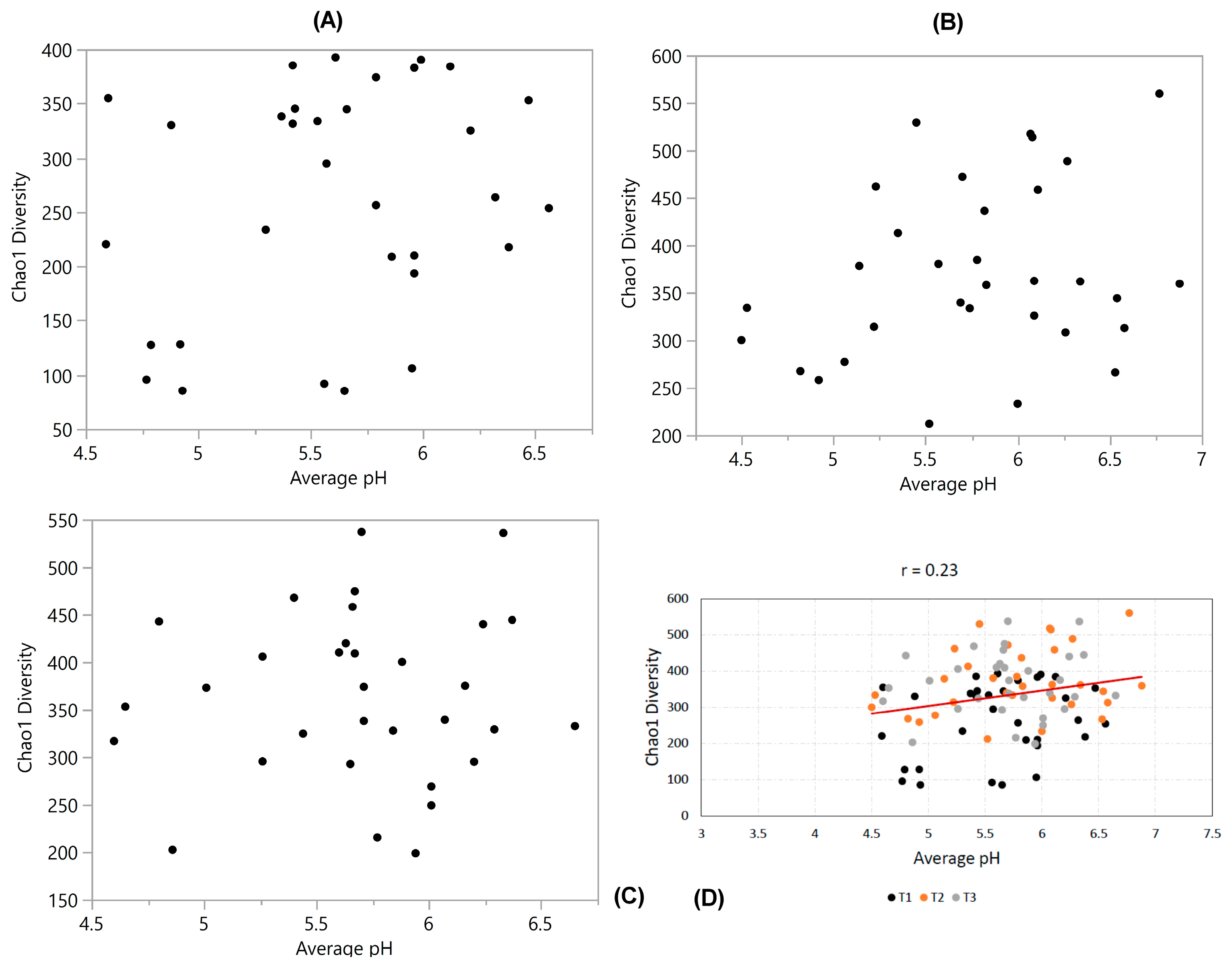
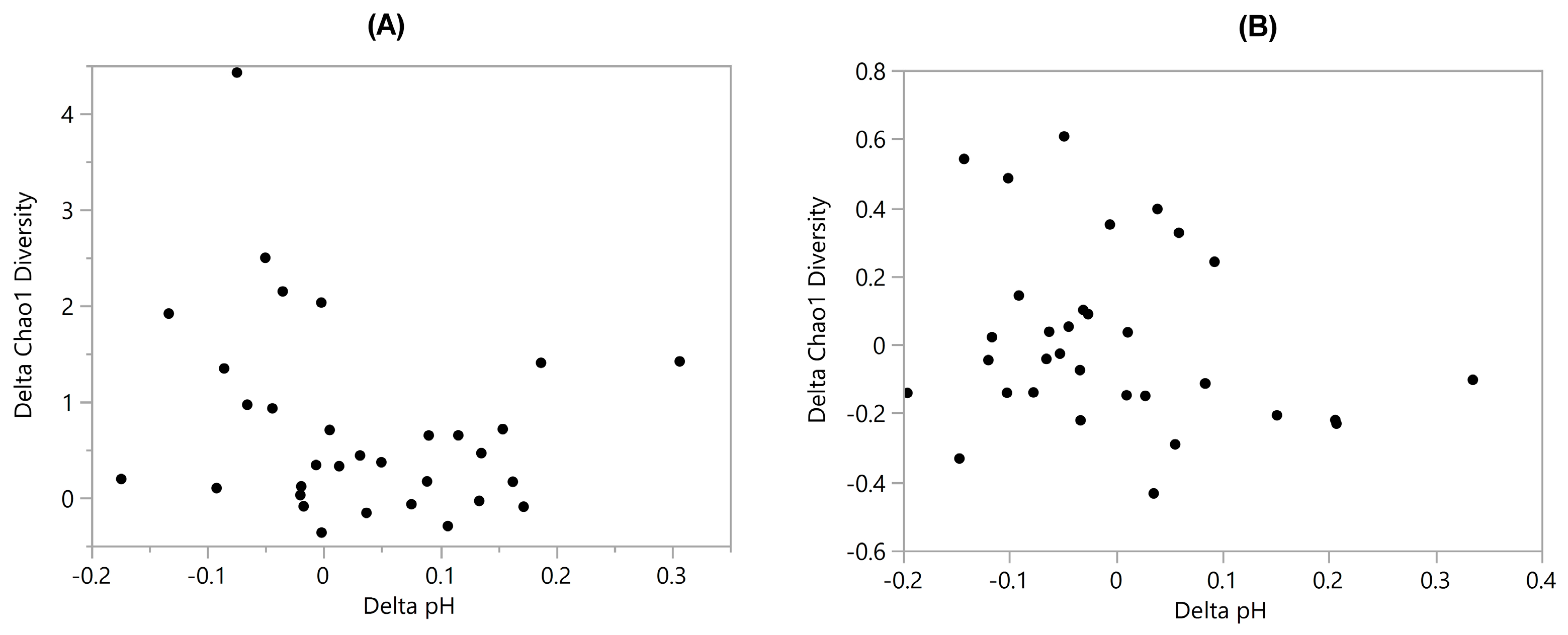
3.4. Diversity vs. pH
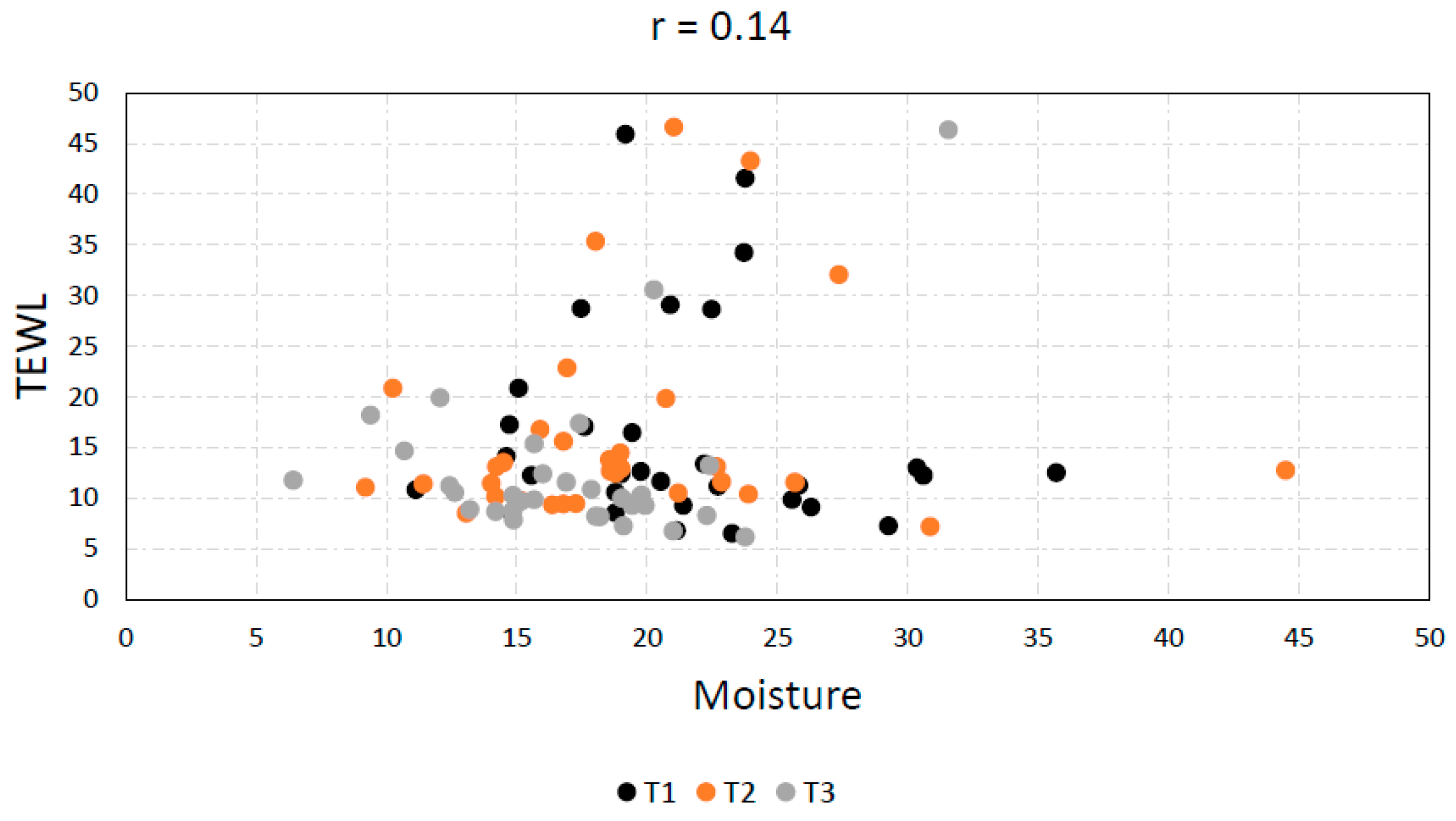
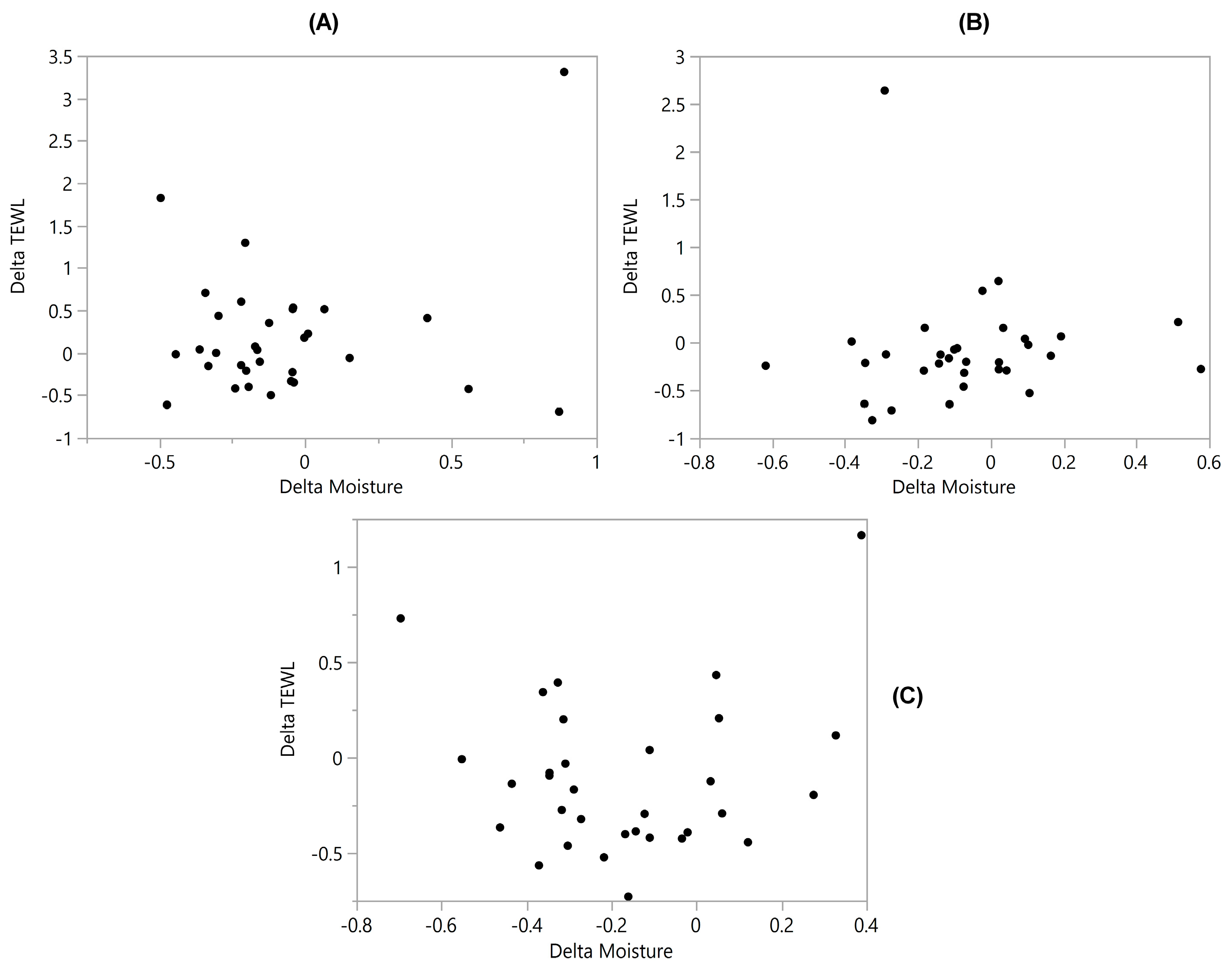
3.5. TEWL vs. Skin Moisture
3.6. Correlation Coefficients (‘r’ Values)
4. Discussion
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Lamke, L.-O.; Nilsson, G.E.; Reithner, H.L. Insensible perspiration from the skin under standardized environmental conditions. Scand. J. Clin. Lab. Investig. 1977, 37, 325–331. [Google Scholar] [CrossRef]
- Nilsson, G.E. Measurement of water exchange through skin. Med. Biol. Eng. Comput. 1977, 15, 209–218. [Google Scholar] [CrossRef] [PubMed]
- Lotte, C.; Rougier, A.; Wilson, D.R.; Maibach, H.I. In vivo relationship between transepidermal water loss and percutaneous penetration of some organic compounds in man: Effect of anatomic site. Arch. Dermatol. Res. 1987, 279, 351–356. [Google Scholar] [CrossRef] [PubMed]
- Freeman, S.; Maibach, H. Study of irritant contact dermatitis produced by repeat patch test with sodium lauryl sulfate and assessed by visual methods, transepidermal water loss, and laser Doppler velocimetry. J. Am. Acad. Dermatol. 1988, 19, 496–502. [Google Scholar] [CrossRef]
- Nicander, I.; Ollmar, S.; Eek, A.; Rozell, B.L. Emtestaml Correlation of impedance response patterns to histological findings in irritant skin reactions induced by various surfactants. Br. J. Dermatol. 1996, 134, 221–228. [Google Scholar] [CrossRef] [PubMed]
- Wallen-Russell, C.; Wallen-Russell, C. The Role of Every-Day Cosmetics in Altering the Skin Microbiome: A Study Using Biodiversity. Cosmetics 2018, 6, 2. [Google Scholar] [CrossRef]
- Lamaude, E.; Schallaw, W. Influence of UV irradiation on penetration of hydrocortisone. In vivo study in hairless rat skin. Br. J. Dermatol. 1984, 111, 152–157. [Google Scholar] [CrossRef]
- Van der Valk, P.G.; Maibach, H.I. A functional study of the skin barrier to evaporative water loss by means of repeated cellophane-tape stripping. Clin. Exp. Dermatol. 1990, 15, 180–182. [Google Scholar] [CrossRef]
- Lévêque, J.L.; de Rigal, J.; Saint-Léger, D.; Billy, D. How Does Sodium Lauryl Sulfate Alter the Skin Barrier Function in Man? A Multiparametric Approach. Skin Pharm. Physiol. 1993, 6, 111–115. [Google Scholar] [CrossRef]
- Boer, M.; Duchnik, E.; Maleszka, R.; Marchlewicz, M. Structural and biophysical characteristics of human skin in maintaining proper epidermal barrier function. Postepy Dermatol. Alergol. 2016, 33, 1–5. [Google Scholar] [CrossRef]
- Tagami, H.; Kobayashi, H.; Zhen, X.-S.; Kikuchi, K. Environmental Effects on the Functions of the Stratum Corneum. J. Investig. Dermatol. Symp. Proc. 2001, 6, 87–94. [Google Scholar] [CrossRef] [PubMed]
- Kligman, A.M. Corneobiology and Corneotherapy—A final chapter. Int. J. Cosmet. Sci. 2011, 33, 197–209. [Google Scholar] [CrossRef] [PubMed]
- Giusti, F.; Martella, A.; Bertoni, L.; Seidenari, S. Skin Barrier, Hydration, and pH of the Skin of Infants Under 2 Years of Age. Pediatr. Dermatol. 2001, 18, 93–96. [Google Scholar] [CrossRef] [PubMed]
- Chamlin, S.L.; Kao, J.; Frieden, I.J.; Sheu, M.Y.; Fowler, A.J.; Fluhr, J.W.; Williams, M.L.; Elias, P.M. Ceramide-dominant barrier repair lipids alleviate childhood atopic dermatitis: Changes in barrier function provide a sensitive indicator of disease activity. J. Am. Acad. Dermatol. 2002, 47, 198–208. [Google Scholar] [CrossRef] [PubMed]
- Horimukai, K.; Morita, K.; Narita, M.; Kondo, M.; Kabashima, S.; Inoue, E.; Sasaki, T.; Niizeki, H.; Saito, H.; Matsumoto, K.; et al. Transepidermal water loss measurement during infancy can predict the subsequent development of atopic dermatitis regardless of filaggrin mutations. Allergol. Int. 2016, 65, 103–108. [Google Scholar] [CrossRef]
- Kelleher, M.; Dunn-Galvin, A.; Hourihane, J.O.; Murray, D.; Campbell, L.E.; McLean, W.H.I.; Irvine, A.D. Skin barrier dysfunction measured by transepidermal water loss at 2 days and 2 months predates and predicts atopic dermatitis at 1 year. J. Allergy Clin. Immunol. 2015, 135, 930–935. [Google Scholar] [CrossRef]
- Pinto, P.; Rosado, C.; Parreirão, C.; Rodrigues, L.M. Is there any barrier impairment in sensitive skin?: A quantitative analysis of sensitive skin by mathematical modeling of transepidermal water loss desorption curves. Skin Res. Technol. 2011, 17, 181–185. [Google Scholar] [CrossRef]
- Angelova-Fischer, I.; Wuthe, D.; Zillikens, D.; Kahle, B. Noninvasive bioengineering assessment of the skin barrier function in patients with chronic venous insufficiency. Br. J. Dermatol. 2010, 162, 1071–1075. [Google Scholar] [CrossRef]
- Plessis, J.; Stefaniak, A.; Eloff, F.; John, S.; Agner, T.; Chou, T.-C.; Nixon, R.; Steiner, M.; Franken, A.; Kudla, I.; et al. International guidelines for the in vivo assessment of skin properties in non-clinical settings: Part 2. transepidermal water loss and skin hydration. Skin Res. Technol. 2013, 19, 265–278. [Google Scholar] [CrossRef]
- Darlenski, R.; Sassning, S.; Tsankov, N.; Fluhr, J.W. Non-invasive in vivo methods for investigation of the skin barrier physical properties. Eur. J. Pharm. Biopharm. 2009, 72, 295–303. [Google Scholar] [CrossRef]
- Rogiers, V.; EEMCO Group. EEMCO guidance for the assessment of transepidermal water loss in cosmetic sciences. Skin Pharm. Appl. Skin Physiol. 2001, 14, 117–128. [Google Scholar] [CrossRef] [PubMed]
- Chilcott, R.P.; Dalton, C.H.; Emmanuel, A.J.; Allen, C.E.; Bradley, S.T. Transepidermal Water Loss Does Not Correlate with Skin Barrier Function In Vitro. J. Investig. Dermatol. 2002, 118, 871–875. [Google Scholar] [CrossRef]
- Darlenski, R.; Fluhr, J.W. Influence of skin type, race, sex, and anatomic location on epidermal barrier function. Clin. Dermatol. 2012, 30, 269–273. [Google Scholar] [CrossRef]
- Muizzuddin, N.; Hellemans, L.; Van Overloop, L.; Corstjens, H.; Declercq, L.; Maes, D. Structural and functional differences in barrier properties of African American, Caucasian and East Asian skin. J. Dermatol. Sci. 2010, 59, 123–128. [Google Scholar] [CrossRef] [PubMed]
- Ramos-e-Silva, M.; da Silva Carneiro, S.C. Elderly skin and its rejuvenation: Products and procedures for the aging skin. J. Cosmet. Dermatol. 2007, 6, 40–50. [Google Scholar] [CrossRef] [PubMed]
- Maibach, H.; Honari, G.; Honari, G.; Maibach, H. Skin Structure and Function. Appl. Derm. 2014, 1–10. [Google Scholar] [CrossRef]
- Akdeniz, M.; Gabriel, S.; Lichterfeld-Kottner, A.; Blume-Peytavi, U.; Kottner, J. Transepidermal water loss in healthy adults: A systematic review and meta-analysis update. Br. J. Dermatol. 2018, 179, 1049–1055. [Google Scholar] [CrossRef] [PubMed]
- Blank, I.H.; Scheuplein, R.J. Transport into and within the skin. Br. J. Dermatol. 1969, 81, 4–10. [Google Scholar] [CrossRef]
- Mathias, C.T.; Wilson, D.M.; Maibach, H.I. Transepidermal Water Loss as a Function of Skin Surface Temperature. J. Investig. Dermatol. 1981, 77, 219–220. [Google Scholar] [CrossRef] [PubMed]
- Grice, K.; Sattar, H.; Sharratt, M.; Baker, H. Skin Temperature and Transepidermal Water Loss. J. Investig. Dermatol. 1971, 57, 108–110. [Google Scholar] [CrossRef]
- Pinnagoda, J.; Tupkek, R.A.; Agner, T.; Serup, J. Guidelines for transepidermal water loss (TEWL) measurement. Contact Dermat. 1990, 22, 164–178. [Google Scholar] [CrossRef]
- Kao, J.; Hall, J.; Shugart, L.R.; Holland, J.M. An in vitro approach to studying cutaneous metabolism and disposition of topically applied xenobiotics. Toxicol. Appl. Pharmacol. 1984, 75, 289–298. [Google Scholar] [CrossRef]
- Chilcott, R.P.; Farrar, R. Biophysical measurements of human forearm skin in vivo: Effects of site, gender, chirality and time. Skin Res. Technol. 2000, 6, 64–69. [Google Scholar] [CrossRef] [PubMed]
- Wallen-Russell, C.; Wallen-Russell, S. Meta Analysis of Skin Microbiome: New Link between Skin Microbiota Diversity and Skin Health with Proposal to Use This as a Future Mechanism to Determine Whether Cosmetic Products Damage the Skin. Cosmetics 2017, 4, 14. [Google Scholar] [CrossRef]
- Mukaka, M.M. Statistics corner: A guide to appropriate use of correlation coefficient in medical research. Malawi Med. J. 2012, 24, 69–71. [Google Scholar]
- Rodgers, J.L.; Nicewander, W. Thirteen Ways to Look at the Correlation Coefficient. Am. Stat. 1987, 42, 59–66. [Google Scholar] [CrossRef]
- Chao, A. Nonparametric Estimation of the Number of Classes in a Population Nonparametric Estimation of the Number of Classes in a Population. Scand. J. 1984, 11, 265–270. [Google Scholar]
- Colwell, R.K.; Coddington, J.A. Estimating terrestrial biodiversity through extrapolation. Philos. Trans. R. Soc. 1994, 345, 101–118. [Google Scholar]
- Sokal, R.R.; Rohlf, F.J. Biometry: The Principles and Practice of Statistics in Biological Research; W.H. Freeman: New York, NY, USA, 1995. [Google Scholar]
- Kim, H.-Y. Statistical notes for clinical researchers: Assessing normal distribution (2) using skewness and kurtosis. Restor. Dent. Endod. 2013, 38, 52–54. [Google Scholar] [CrossRef]
- Mohd Razali, N.; Bee Wah, Y. Power comparisons of Shapiro-Wilk, Kolmogorov-Smirnov, Lilliefors and Anderson-Darling tests. J. Stat. Model. Anal. 2011, 2, 13–14. [Google Scholar]
- Shapiro, S.S.; Wilk, M.B. An Analysis of Variance Test for Normality (Complete Samples). Biometrika 1965, 52, 591. [Google Scholar] [CrossRef]
- Baran, R.; Maibach, H.I. Textbook of Cosmetic Dermatology; CRC Press: Boca Raton, FL, USA, 2017; 594p. [Google Scholar]
- Devlins, J.; Gnanadesikan, R.; Kettenring, J.R. Robust estimation and outlier detection with correlation coefficients. Biometrika 1975, 62, 531–545. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics Hoboken; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1981. [Google Scholar]
- Kim, Y.; Kim, T.-H.; Ergün, T. The instability of the Pearson correlation coefficient in the presence of coincidental outliers. Financ. Res. Lett. 2015, 13, 243–257. [Google Scholar] [CrossRef]
- Glass, G.V.; Hopkins, K.D. Statistical Methods in Education and Psychology, 3rd ed.; Allyn & Bacon: Boston, MA, USA, 1996. [Google Scholar]
- Carroll, J.B. The Nature of the Data, or How to Choose a Correlation Coefficient. Psychometrika 1961, 26, 347–372. [Google Scholar] [CrossRef]
- Nunnally, J.C.; Bernstein, I.H. Psychometric Theory, 3rd ed.; McGraw-Hil: New York, NY, USA, 1994. [Google Scholar]
- Caruso, J.C.; Cliff, N. Empirical Size, Coverage, and Power of Confidence Intervals for Spearman’s Rho. Educ. Psychol. Meas. 1997, 57, 637–654. [Google Scholar] [CrossRef]
- Cramer, D. Fundamental Statistics for Social Research: Step-by-Step Calculations and Computer Techniques Using SPSS for Windows New York; Routledge: New York, NY, USA, 1998. [Google Scholar]
- Cramer, D.; Howitt, D. The Sage Dictionary of Statistics: A Practical Resource for Students in the Social Sciences; SAGE Publications: Thousand Oaks, CA, USA, 2004; 188p. [Google Scholar]
- Doane, D.P.; Seward, L.E. Measuring Skewness: A Forgotten Statistic? J. Stat. Educ. 2011, 19. [Google Scholar] [CrossRef]
| Degrees of Freedom | Probability, p | |
|---|---|---|
| 0.05 | 0.01 | |
| 1 | 0.997 | 1 |
| 5 | 0.755 | 0.875 |
| 10 | 0.576 | 0.708 |
| 15 | 0.482 | 0.606 |
| 20 | 0.423 | 0.457 |
| 25 | 0.381 | 0.487 |
| 30 | 0.349 | 0.449 |
| 90 | 0.205 | 0.267 |
| 100 | 0.195 | 0.254 |
| Measurement | T1 | T2 | T3 | Combined | T1 to T2 | T1 to T3 | T2 to T3 |
|---|---|---|---|---|---|---|---|
| Diversity | 0.0042 | 0.307 | 0.768 | 0.0925 | 0.0001 | <0.0001 | 0.0741 |
| TEWL | <0.0001 | <0.0001 | <0.0001 | <0.0001 | <0.0001 | 0.0096 | <0.0001 |
| Moisture | 0.397 | 0.001 | 0.418 | 0.0002 | 0.0001 | 0.52 | 0.161 |
| pH | 0.302 | 0.741 | 0.261 | 0.109 | 0.817 | - | 0.0577 |
| Graph | T1 | T2 | T3 | Combined | T1 to T2 | T1 to T3 | T2 to T3 |
|---|---|---|---|---|---|---|---|
| Diversity vs. TEWL | 0.22 | −0.19 | −0.21 | −0.063 | 0.025 | −0.089 | 0.084 |
| Diversity vs. Moisture | −0.2 | −0.43 * | −0.04 | −0.32 * | −0.12 | −0.038 | 0.056 |
| Diversity vs. pH | 0.24 | 0.26 | 0.071 | 0.22 | −0.24 | - | −0.23 |
| TEWL vs. Moisture | −0.082 | 0.12 | 0.34 | 0.14 | 0.21 | 0.096 | 0.022 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wallen-Russell, C. Is There a Relationship between Transepidermal Water Loss and Microbial Biodiversity on the Skin? Cosmetics 2019, 6, 18. https://doi.org/10.3390/cosmetics6010018
Wallen-Russell C. Is There a Relationship between Transepidermal Water Loss and Microbial Biodiversity on the Skin? Cosmetics. 2019; 6(1):18. https://doi.org/10.3390/cosmetics6010018
Chicago/Turabian StyleWallen-Russell, Christopher. 2019. "Is There a Relationship between Transepidermal Water Loss and Microbial Biodiversity on the Skin?" Cosmetics 6, no. 1: 18. https://doi.org/10.3390/cosmetics6010018
APA StyleWallen-Russell, C. (2019). Is There a Relationship between Transepidermal Water Loss and Microbial Biodiversity on the Skin? Cosmetics, 6(1), 18. https://doi.org/10.3390/cosmetics6010018





