A Case Study of the Retention Efficiency of a Traditional and Innovative Drainage System

Abstract

To determine the effectiveness of the retention capacity utilization of traditional and innovative drainage systems equipped with damming partitions, the detailed model tests were carried out. The research results allowed indicating what values of the hydraulic parameter of the innovative drainage system should be adopted in order to effectively use the retention capacity of drainage collectors. The adoption of short distances between the LKR damming partitions and a high level of permissible rainfall of stormwater Hper turned out to be the most effective solution. In the most favorable conditions, the peak flow was reduced by up to 60% (717.46 dm³/s) compared to the values established in the traditional drainage system (1807.62 dm³/s). The benefits obtained resulted from the increased retention efficiency of the drainage system after equipping it with the damming partitions. It was found that the innovative system always achieved the maximum retention capacity with longer rainfall compared to the traditional system. In the real catchment area, an increase in the use of the retention capacity of the drainage system, from an initial value of 65% for a traditional system to almost 88% for an innovative system, was also found. Very large variability of the volume of accumulated stormwater in the conduits of the traditional and innovative drainage system was observed during rainfall, which generated the peak rainfall discharge in the innovative system. With rainfall of TRK duration, the innovative system accumulated up to 746.50 m³ more stormwater compared to a traditional system, which was 49.2% of the total retention capacity of the drainage system, with a value of 1515.76 m³. The approach to reduce the growing flood risk in cities provided the right approach to long-term urban drainage system planning, especially since traditional drainage systems are still the leading way to transport stormwater in cities. In addition, the innovative sewage system gives the possibility of favorable cooperation with any objects (LID) and retention tanks with any hydraulic model. The implementation of an innovative system allows achieving significant financial savings and reducing the need to reserve areas designated for infrastructure investments.

1. Introduction

Due to the increasing concentration of greenhouse gases in the atmosphere, climate changes cause significant transformations in the characteristics of extreme weather phenomena [1,2] manifested by an increase in the incidence of short-term torrential rainfall [3,4]. This implies a more frequent incidence of local urban floods, whose range shows great variability due to natural and human impacts, with particularly severe adverse effects in high-density urban catchments and a significant proportion of impervious surfaces [5,6,7]. The proper assessment of future hydrological changes in cities caused by uncertain climates is very important and is required for the proper management of stormwater [8,9,10]. Many studies have determined the potential impact of climate changes on the frequency and patterns of rainfall, especially those of a torrential nature [11,12]. For instance, Ishida et al. [13] studied a growth in maximum rainfall in Northern California and predicted a significant increase in storm intensity by the end of the century. Researchers from Poland also came to similar conclusions [14,15]. Thus, it can be certainly stated that, in the future, during short-term rainfall, larger volumes of stormwater will flow into existing drainage systems. Reducing the risk of natural disasters (e.g., floods and droughts) requires the effective management of water resources [16] and advanced seasonal forecasting [17].

Urban floods, which are caused by high-intensity short-term rainfall, are generally local [18,19,20]. It is worth emphasizing that the collectors located outside the flooded area are often not used effectively in terms of hydraulics and have, in the upper zone, free spaces, sometimes of considerable capacity, which can be successfully included in the retention volume of the entire drainage system [21,22,23].

Traditional drainage systems that operate in a gravitational way are still the leading way of the hydraulic transport of stormwater when draining urbanized areas. For example, in more than 90% of Chinese cities, flood risk management is based on the use of traditional engineering infrastructure in the form of a traditional indoor stormwater drainage system, which, by definition, is intended to outflow urban discharges to the receiver as quickly as possible [24]. However, this way of dealing with excess stormwater is considered inefficient and does not have the characteristics of the facilities that are framed in the standards of sustainable urban development [25,26,27]. In order to reduce the risk of urban floods and the impact of urban growth, it is necessary to take measures aimed at increasing the efficiency of underground infrastructure management in cities [28,29,30,31].

Engineering solutions currently recommended to increase the hydraulic efficiency of traditional drainage systems are cubature objects for intentional retention [32,33,34] and/or devices to infiltrate stormwater into the ground [35,36,37] and devices for their economic use [38,39,40].

Numerous research has shown [41,42,43,44,45,46,47,48] that the low-impact development practices (LID), including a bioretention system, permeable surfaces and retention ponds, were becoming more and more attractive solutions to manage surface runoff at its origin by promoting retention, infiltration and absorption. In the works [49,50,51], the hydrological effect of LID was assessed by means of laboratory and field experiments. The efficiency of the LID devices was also determined based on hydrological models, such as the storm water management model (SWMM) and long-term assessment of the hydrological impact of LID practices with long-term data on daily rainfall, adopting different types of land and drainage basins [52,53,54]. Over the past decade, an interest in LID devices has increased due to their flexibility in use and comprehensive advantages [55]. In addition to relieving the drainage system, these types of devices can increase the resilience of spatial structures [56], restore the natural water balance [57], contribute to the improvement of the urban microclimate [58,59], improve health and well-being [60] and provide social and economic benefits [61].

The use of LID objects and retention tanks, especially in densely built-up areas and the ones with low soil permeability, may be difficult [62]. In addition, the quantity and quality of stormwater flowing from different areas of the drained drainage catchment show great variation [63,64]. Following a universal scheme without a thorough technical and economic analysis of many variants and taking into account local [65,66,67] and environmental conditions [68,69] will result in drawing up inefficient concepts for the development of drainage systems.

As previous studies have shown [21,22,23], taking into account the retention capacity of the drainage systems operated in the first place for practical and economic reasons was rational and even necessary. The use of the retention capacity of gravitational drainage systems is possible by introducing the devices into the wells and sewer chambers that enable the accumulation of transported stormwater in pipes [70]. Such a practice of stormwater management allows reducing significantly the risk of urban floods, while limiting the expenditure on investments and the required area for building cubature objects of the drainage systems. Therefore, the use of the retention capacity of drainage systems is a good alternative for LID devices and classic retention tanks, especially in the areas with dense buildings and low soil filtration rates. In addition, the research [71] proved that an innovative drainage system could interact with LID devices and retention reservoirs, maximizing the effectiveness of the drainage system in global terms. Thus, the use of the retention capacity of the drainage system is undoubtedly part of the policy of sustainable stormwater management, bringing many benefits to the environment, operators of drainage systems and people living in drained areas. This method of stormwater management allows to minimize social losses, which can manifest in the forms of damage to the infrastructure, damage to human health and even loss of life. Unfortunately, these types of drainage systems will not increase the overall area of urban greenery and more recreational space for society.

This paper aims to present the possibilities of controlling the process of stormwater retention in conduits of the drainage system. This approach makes an increased hydraulic and retention efficiency of the drainage system by introducing special partitions. This concept allows determining the exact value of the peak stormwater discharge and their volumes retained in the drainage system, depending on the geometry and the number of damming partitions used and the height of the stormwater damming.

2. Materials and Methods

2.1. Case Study

The studies on the effectiveness of the drainage of urbanized areas were carried out for the real urban catchment area, which is located in Southeastern Poland (Figure 1).

Parameters characterizing the catchment are presented in

Table 1. Land-use characteristics of the urban catchment.

Land Use	Area		Mannings n	Depth of Depression Storage on Area
	(ha)	(%)	(s/m1/3)	(mm)
Rooftop	4.78	10.30	0.011–0.012	0.3–0.5
Road, pavement and other impervious	9.60	20.70	0.011–0.013	0.8–1.4
Green area	32.00	69.00	0.15	3.4
Total areas	46.38	100.00	-	-

and

Table 2. Characteristic parameters for the Horton infiltration method.

Parameter	Value	Units
Maximum infiltration rate	122.0	(mm/h)
Minimum infiltration rate	17.5	(mm/h)
Infiltration rate decay constant	3.5	(1/h)
Drying Time	6	(days)

. The values of the parameters were assumed based on the author’s own research and the literature [72].

The parameters characterizing the designed traditional drainage system are presented in

Table 3. Hydraulic parameters of the traditional drainage system.

Parameter	Value
	Minimum	Maximum
Length of links	19.36 m	97.40 m
Total length of links	3769.70 m
Slope of links Diameter of links	1.1‰ 0.3 m	3.1‰ 1.0 m
Drainage system capacity	1515.76 m3

.

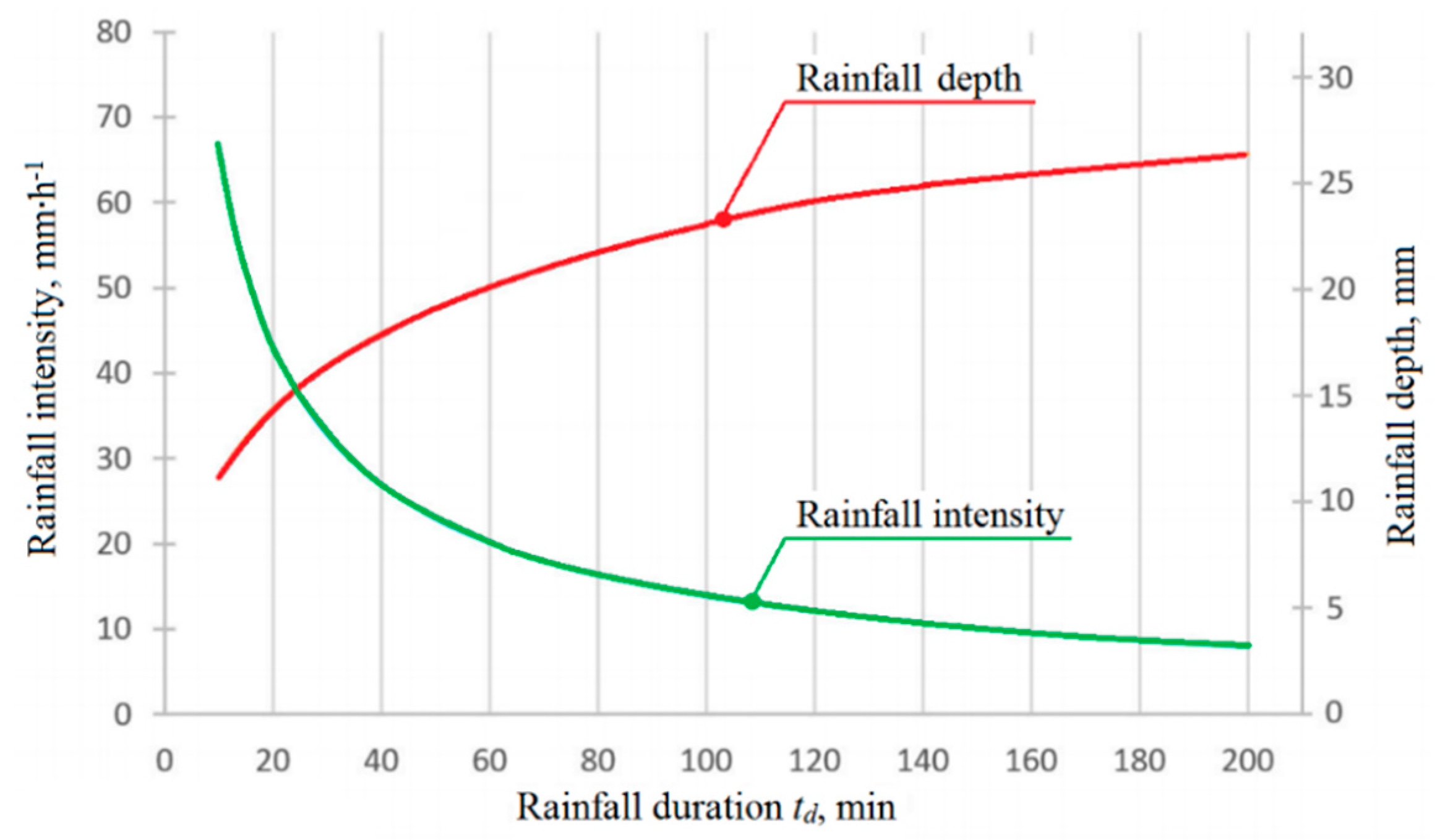
2.2. Precipitation Model

The precipitation model of Bogdanowicz and Stachy (recommended in Poland) was used to calculate the unit precipitation intensity [73]. It determines the correlations between the intensity of precipitation and its duration (1):

h_max = 1.42t_d^0.33 + α(t_d) (−lnp)^0.584

(1)

where h_max is the maximum total amount of precipitation with a duration t_d and a probability of occurrence p (mm); α is a parameter (scale) adopted depending on the region of Poland and the duration of precipitation t_d, p is the probability of rainfall: p ∈ (0, 1] and R is a region of Poland.

All simulations were carried out assuming the probability of rainfall of p = 0.5. Precipitation intensity estimated according to the Bogdanowicz and Stache formula concerned block precipitation with uniform intensity throughout their duration. Figure 2 shows the IDF curve determined on the basis of Formula (1).

2.3. Hydrodynamic Simulation—Storm Water Management Model

The simulation of hydrological and hydraulic phenomena occurring in the “rainfall–drainage, basin–drainage and system–receiver” system was mapped using the Storm Water Management Model (SWMM) version 5.1 program.

Hydrodynamic models of the drainage system, made in the SWMM program, allow determining hydraulic values that describe its operation in variable conditions (static and dynamic), including flow rate and liquid stream velocity, hydrostatic pressure and stormwater-filling heights in canals [72].

2.4. Innovative Drainage Systems (Retention Sewage Canal)

A significant improvement in the hydraulic efficiency of traditional drainage systems was obtained as a result of the use of an innovative solution [70], whose idea resulted in the intentional installation of damming partitions across the direction of stormwater flow in gravity conduits of existing or planned drainage systems (Figure 3).

According to the features of the invention [70], the damming partition has an outflow orifice (4) in the bottom part, and the upper edge of the partition is a typical frontal overflow (2). For the analysis of the research on the hydraulic processes, an outflow orifice (4) with a circular cross-section was adopted, which was mapped in the SWMM program using the Orifice link function. The emergency overflow (2) was designed using the Weir link function.

The hydraulic parameters of nine models of the innovative drainage system variants are presented in

Table 4. Hydraulic characteristics of an innovative drainage system.

Variant	Average Distance between the Damming Partitions, LKR	Parameter Ratio Hper/dk
Variant 0	-	-
Variant I	75 m	0.99
Variant II	148 m	0.99
Variant III	235 m	0.99
Variant IV	75 m	0.90
Variant V	148 m	0.90
Variant VI	235 m	0.90
Variant VII	75 m	0.80
Variant VIII	148 m	0.80
Variant IX	235 m	0.80

.

Variant 0 is a traditionally functioning drainage system. The study also analyzed in detail nine different variants of the hydraulic operation of the innovative drainage system (drainage system with damming partitions). In Variants 1–9 adopted, they differ in the distances between the L_RK damming partitions and the permissible level of stormwater accumulation H_per in canals. In all the adopted variants, the drainage system has the same canal geometry presented in Table 1.

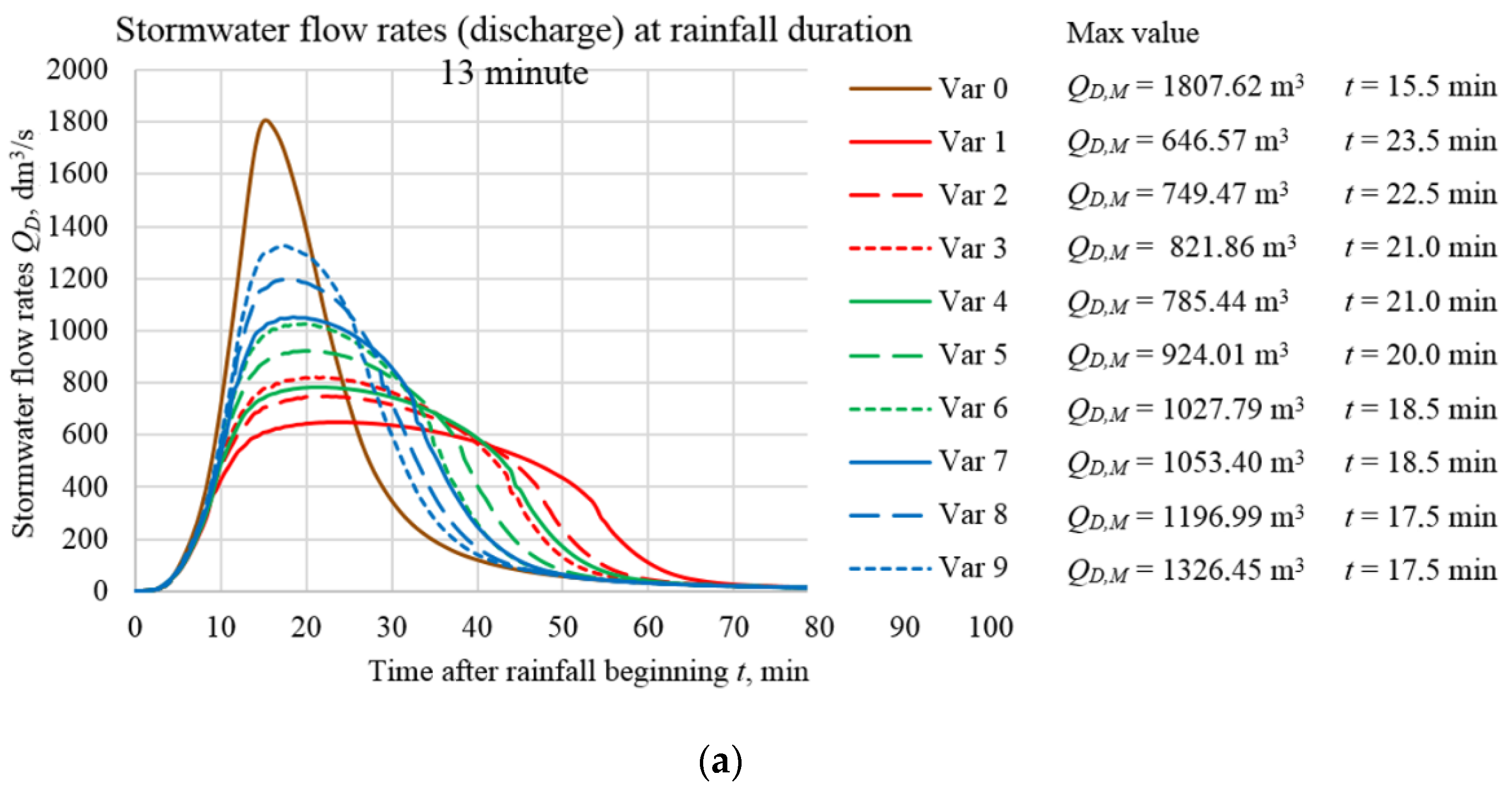
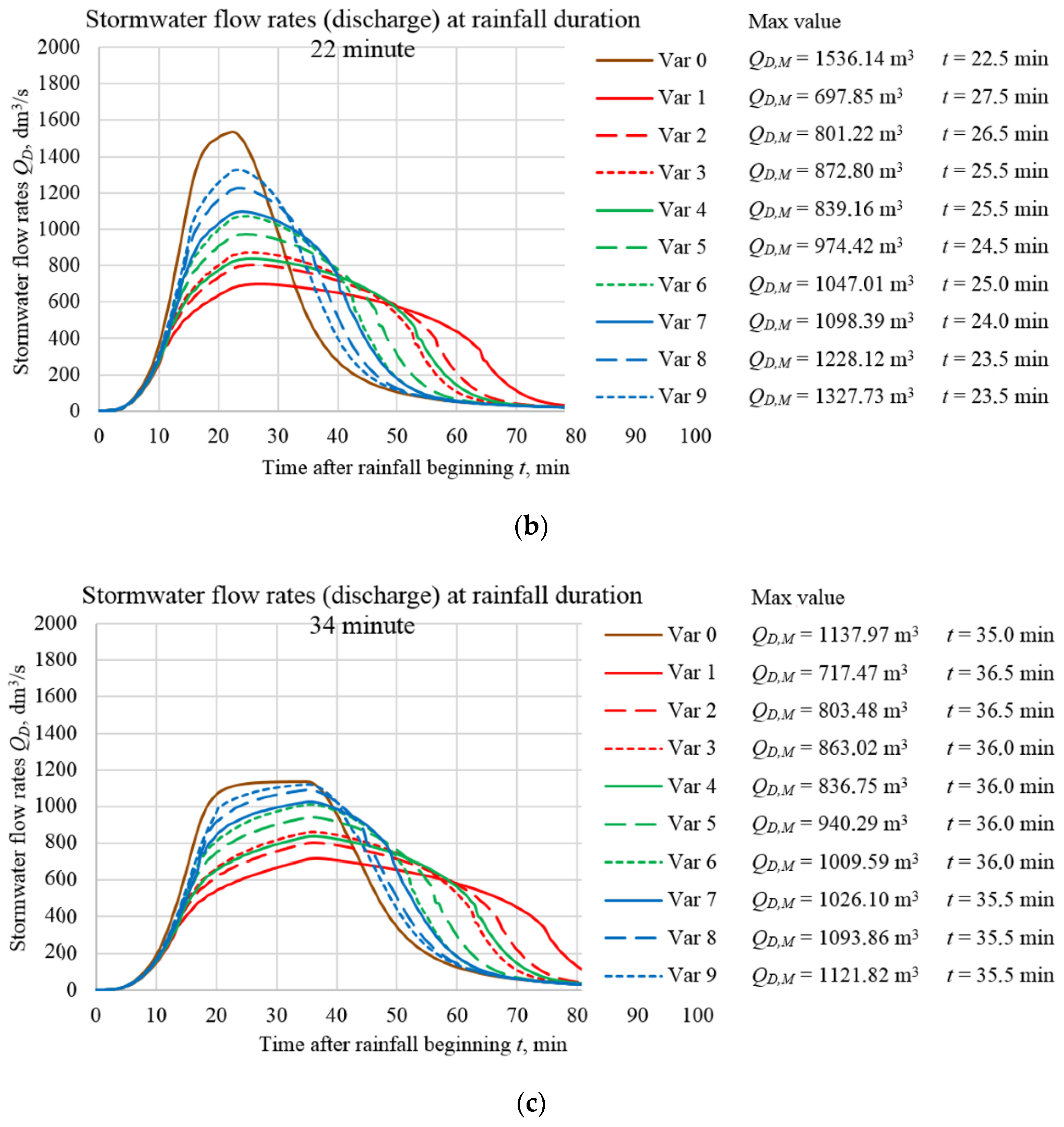
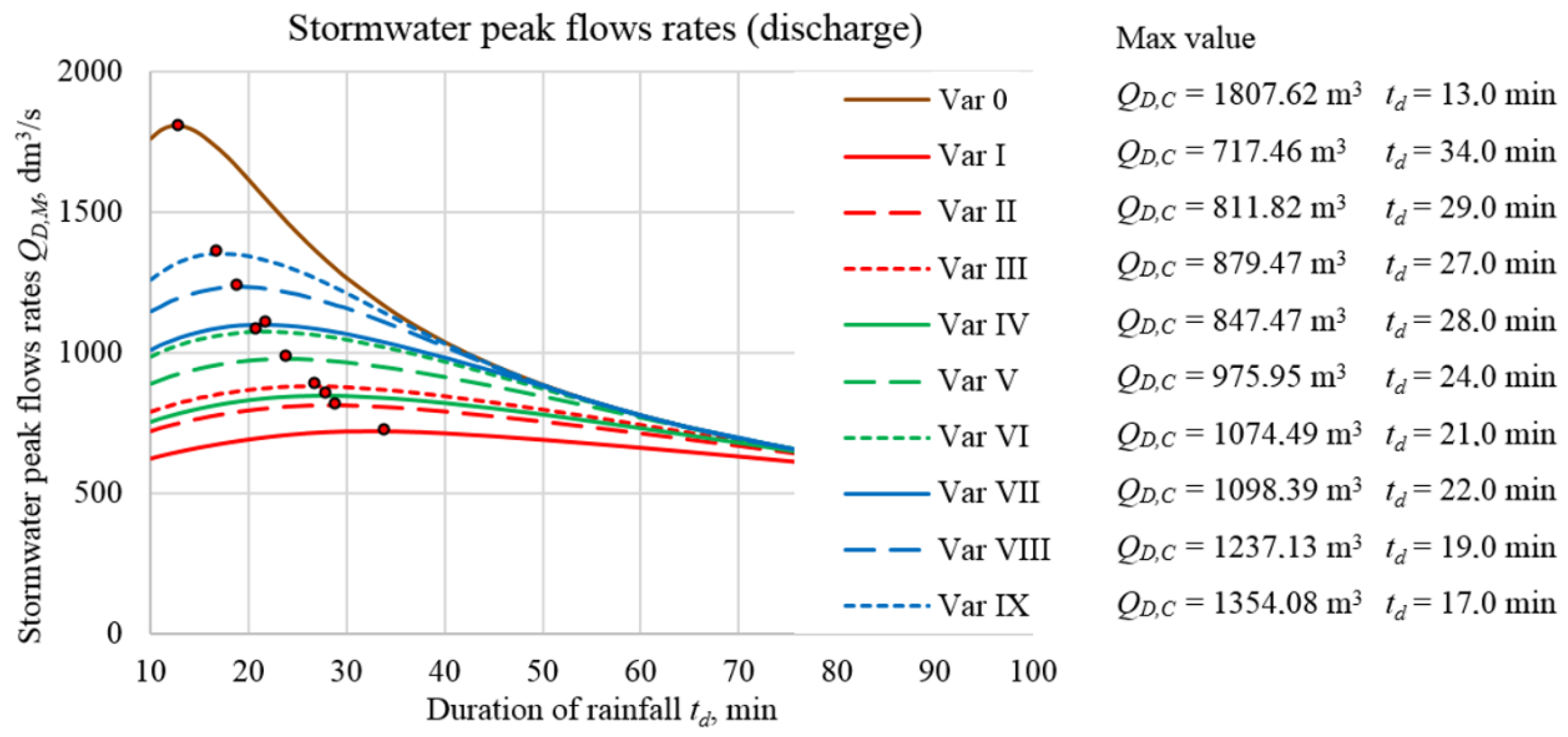
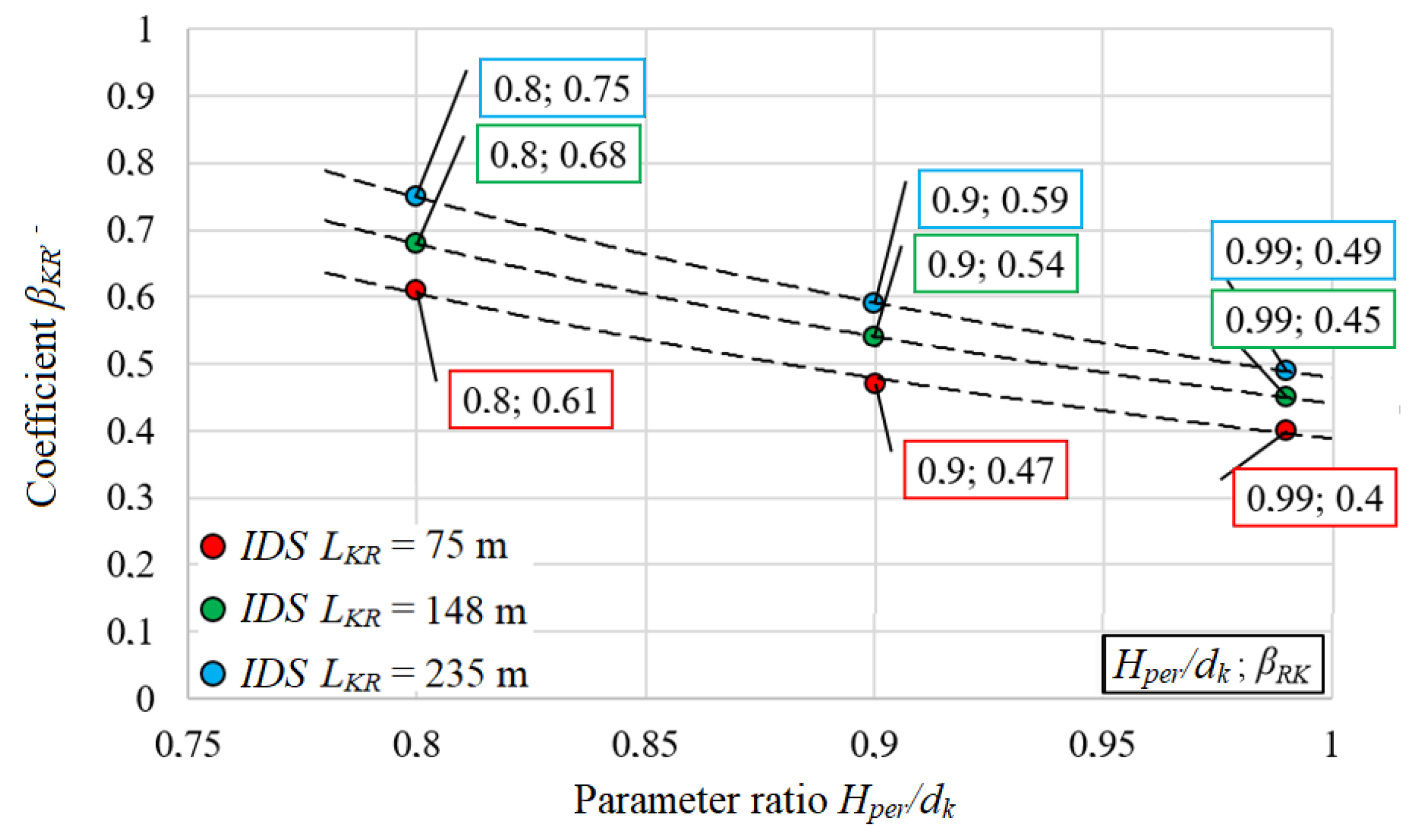
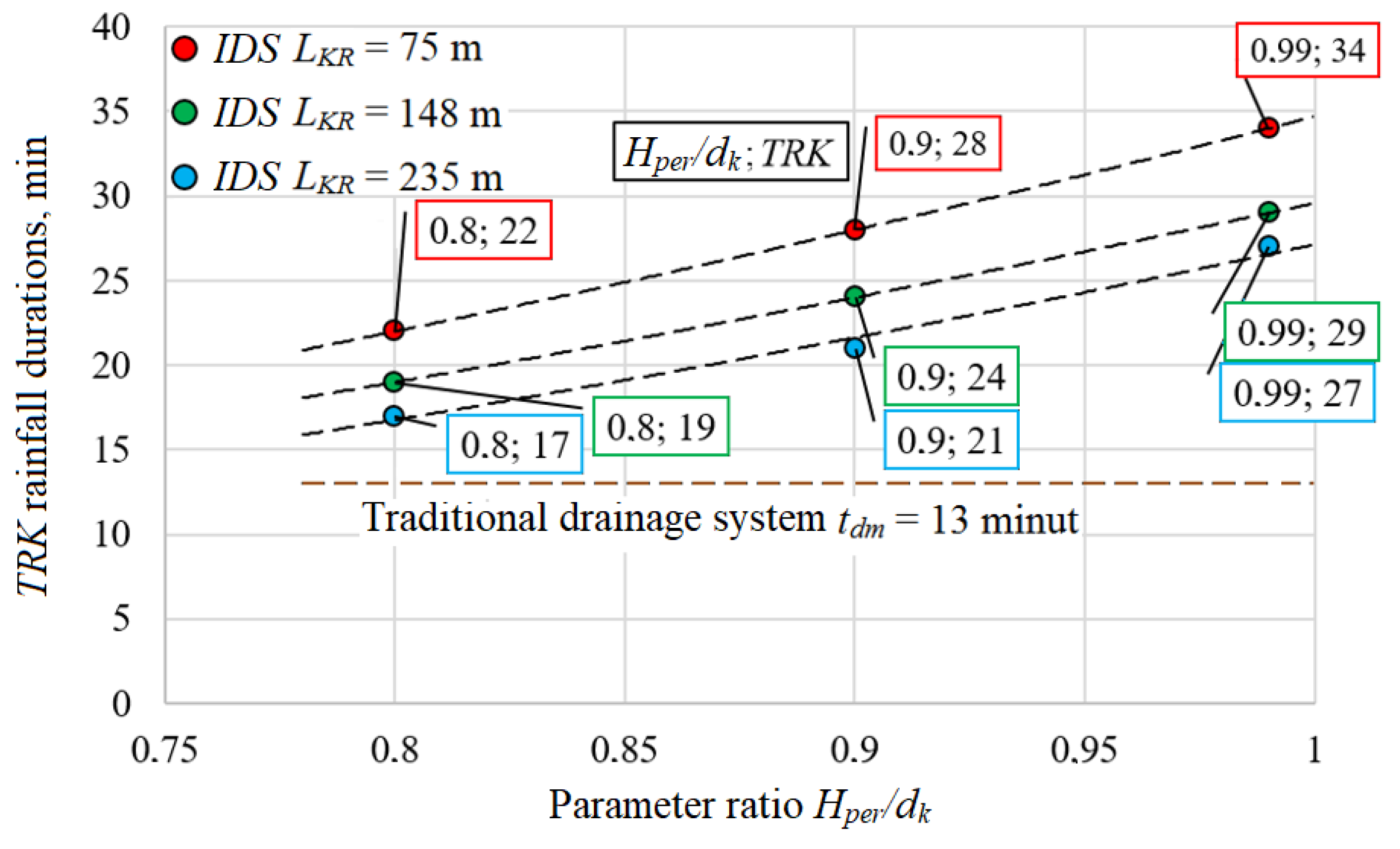
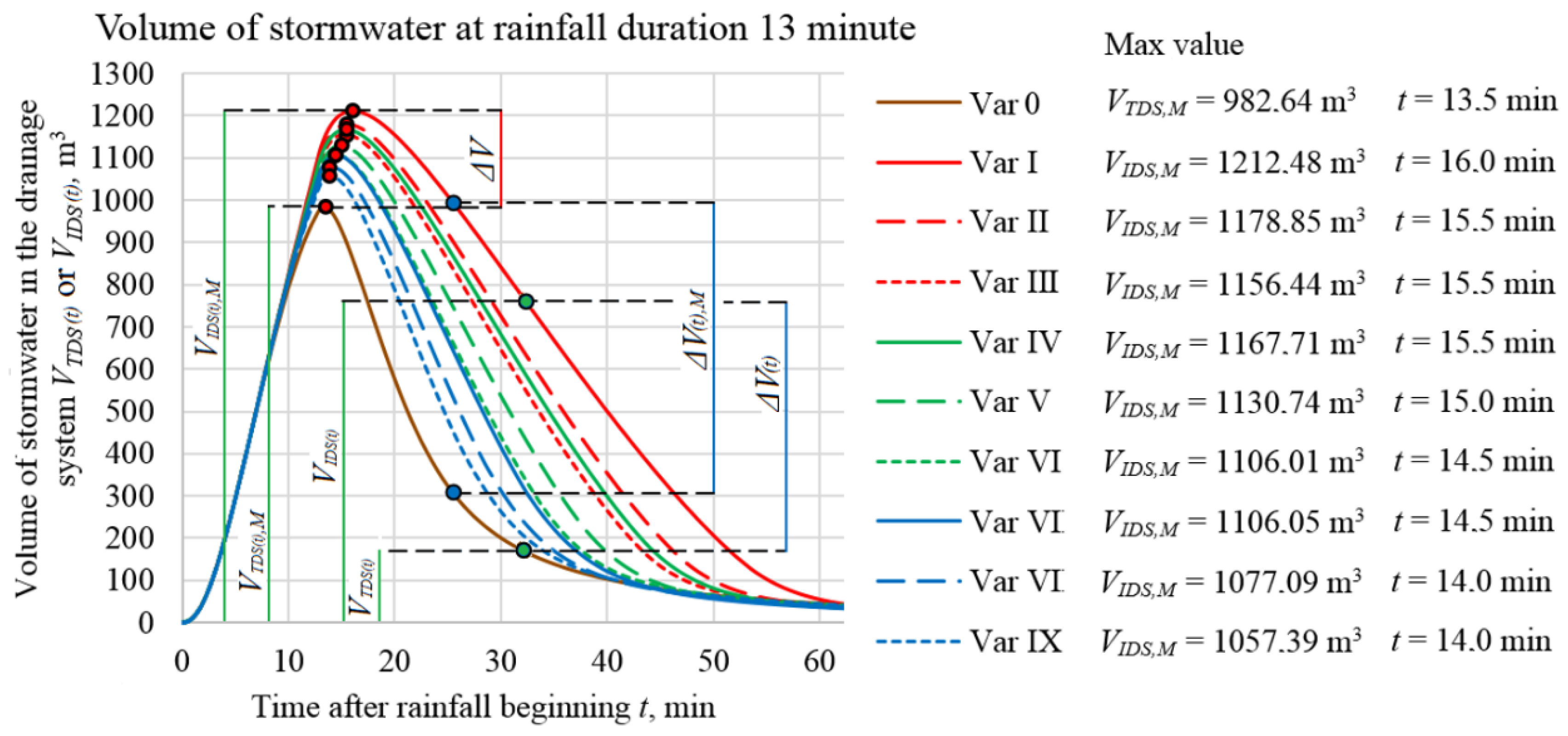
3. Results

In order to assess the possibility of controlling the transport, the volume of the accumulated and the amount of stormwater discharge from the drained catchment and the functioning of the adopted drainage system was examined by separating the ten designed variants, simultaneously creating their hydrodynamic models.

First, the impact of the damming partitions was determined on the volume of Q_D stormwater discharges during rainfall with different durations (Figure 4). It was done by turning the traditional drainage system into a retention canal system that creates an innovative drainage system.

The results of the tests confirmed the close dependence of the degree of reduction of the stormwater outflow from the drained catchment due to the assumed distances between the damming partition (L_KR) and the admissible stormwater damming heights before the damming partitions H_per, regardless of the considered duration of the rainfall t_d. It was established that, with the simultaneous reduction of the distance between the damming partitions L_KR and increasing the stormwater damming heights before the damming partitions H_per, the value of the parameter Q_D is gradually reduced. Therefore, regardless of the rainfall duration t_d, the most favorable variant in terms of reducing the risk of urban flooding is Var1.

A significant hydraulic effect results from the favorable flattening of the hydrograph and the simultaneous slowdown of the stormwater discharge from the drainage system equipped with a retention canal system. A practical benefit of stormwater damming in the innovative drainage system is the hydraulic relief of the traditional system located below the retention canal system—in particular, the negative effects of rapid short-term rainfall discharges into the receiver. The transformation of time-varying flows as a result of the use of a retention canal system is particularly important in a situation where the drainage system cooperates with retention facilities or when the construction of such facilities will be planned in the future. The flattened hydrograph of stormwater outflow from the innovative drainage system allows a significant reduction in the required usable capacity of retention tanks and selected LID devices (objects for retention and the temporary retention of stormwater, e.g., stormwater retention pound) cooperating with it. In special cases, and in the event of favorable local conditions, a properly designed system of retention canals allows taking over part or all of the tasks set for retention tanks and/or other unloading facilities. Thus, it even enables to abandon the construction of such facilities. This situation will occur when the determined maximum allowable stormwater flow rate Q_D,DT from the planned retention tank exceeds the critical storm fall flow rate Q_D,IDS,M from the drainage catchment with a drainage system equipped with a retention canal system at the intended location of the tank.

The inclusion of a sufficiently wide range of rainfall times t_d in the study allowed confirming the interesting relationship. Each rainfall corresponds to a precisely defined value of the maximum stormwater outflow Q_D,M from the drainage system. When analyzing the functioning of the traditional drainage system and retention canal system with the changing duration of the rainfall t_d, the critical value of stormwater outflow from the system examined was determined (Figure 5).

Using the simulation by means of hydrodynamic modeling, the lowest critical value of stormwater outflow from the retention canal system was determined with Q_D,IDS,C = 717.46 dm³/s. This outflow will occur in the Var1 variant, where the system is equipped with 42 damming partitions with an average distance of every L_KR = 75 m and with the permissible momentary level of stormwater accumulation just before the damming partitions H_per/d_k = 0.99 but ensuring the drainage system of all canals.

It is obvious that the adoption of a higher level of stormwater accumulation in front of damming partitions H_per/d_k directly affects the beneficial decrease in the value of the peak critical stormwater outflow rate Q_D,IDS,C from the innovative drainage system, since a larger volume of stormwater remains in the system. Additionally, the reduction of the distance between the L_KR damming partitions affects the successive decrease of the Q_D,IDS,C parameter values for all permissible system fillings specified by the H_per/d_k parameter. The scenarios of the functioning of the designed drainage system equipped with a retention canal system confirmed the validity of each variant of the concept of hydraulic transport and stormwater accumulation in an innovative drainage system in order to determine the optimal solution in the given design conditions.

Formulated theoretical foundations and models describing the process and the impact of the H_per/d_k and L_KR parameters of the drainage system with the retention canal system on the conditions of its hydraulic functioning each time give a possibility to determine clearly the amount of stormwater outflow intensity reduction from the innovative drainage system. Therefore, through the assumptions made at the design stage, it is possible to control the degree of stormwater flow reduction in a wide range, which was proposed to be determined by the β_KR factor. The value of this coefficient is closely related to the capacity of the drainage system and decreases as this capacity grows [21]. When designing an innovative drainage system, its value is determined using the relationship (2):

$${\beta }_{KR}=\frac{Q_{D,IDS,C}}{Q_{D,TDS,C}}$$

(2)

where β_KR is stormwater flow reduction factor in an innovative drainage system (-), Q_D,IDS,C is the value of the determined critical intensity of stormwater outflow from the drainage system equipped with damming partitions (d m³/s) and Q_D,TDS,C is the determined value of the critical intensity of stormwater outflow from the traditional drainage system (d m³/s).

The value of the β_RK flow reduction factor shows the scale of the advisability of implementing damming partitions in an operated stormwater drainage system. The lower the value β_RK is, the more justified the implementation of the retention canal system. The results of the research in this area that were carried out in the real catchment area analyzed are presented in Figure 6.

Based on the adopted for the design values of the H_per/d_k parameters from 0.80 to 0.99 and L_KR from 75 m to 235 m, the values of the stormwater flow reduction coefficient β_KR were determined separately for each of the nine variants, which ranged from 0.40 to 0.75. Thus, in the study case, it was proven that, in each design variant, the distances at which subsequent L_KR partitions were placed had significant impact on the determined value of the β_KR coefficient. This was regardless of the assumed value of the permissible instantaneous level of stormwater accumulation H_per just before the partitions.

The simulation tests carried out on the catchment area allowed the dependence of the reliable rainfall time to dimension the innovative drainage system (TRK) to be determined on the basis of the accepted values of variable parameters that characterize the object (Figure 7) in nine assumed variants. TRK values for this time range from 17 min to 34 min. On the other hand, in the variant allowing the highest filling, i.e., at H_per/d_k = 0.99, and, at the same time, minimizing the L_KR distance between damming partitions, the set TRK valid rainfall time for dimensioning the innovative drainage system was almost three times longer than the reliable time t_dm, which was determined when dimensioning the designed, traditional drainage system.

The basic effect of implementing the idea of an innovative drainage system is, in addition to the hydraulic transport of stormwater in the network, the occurrence of the phenomenon of their effective accumulation in drainage system pipes. The volume of stormwater that is accumulated in the classic V_TDS(t) and innovative V_IDS(t) drainage pipes is constantly changing during rainfall (Figure 8).

Considering any rainfall of a specific duration t_d and adopting a specific way of hydraulic functioning of the drainage system, one can determine:

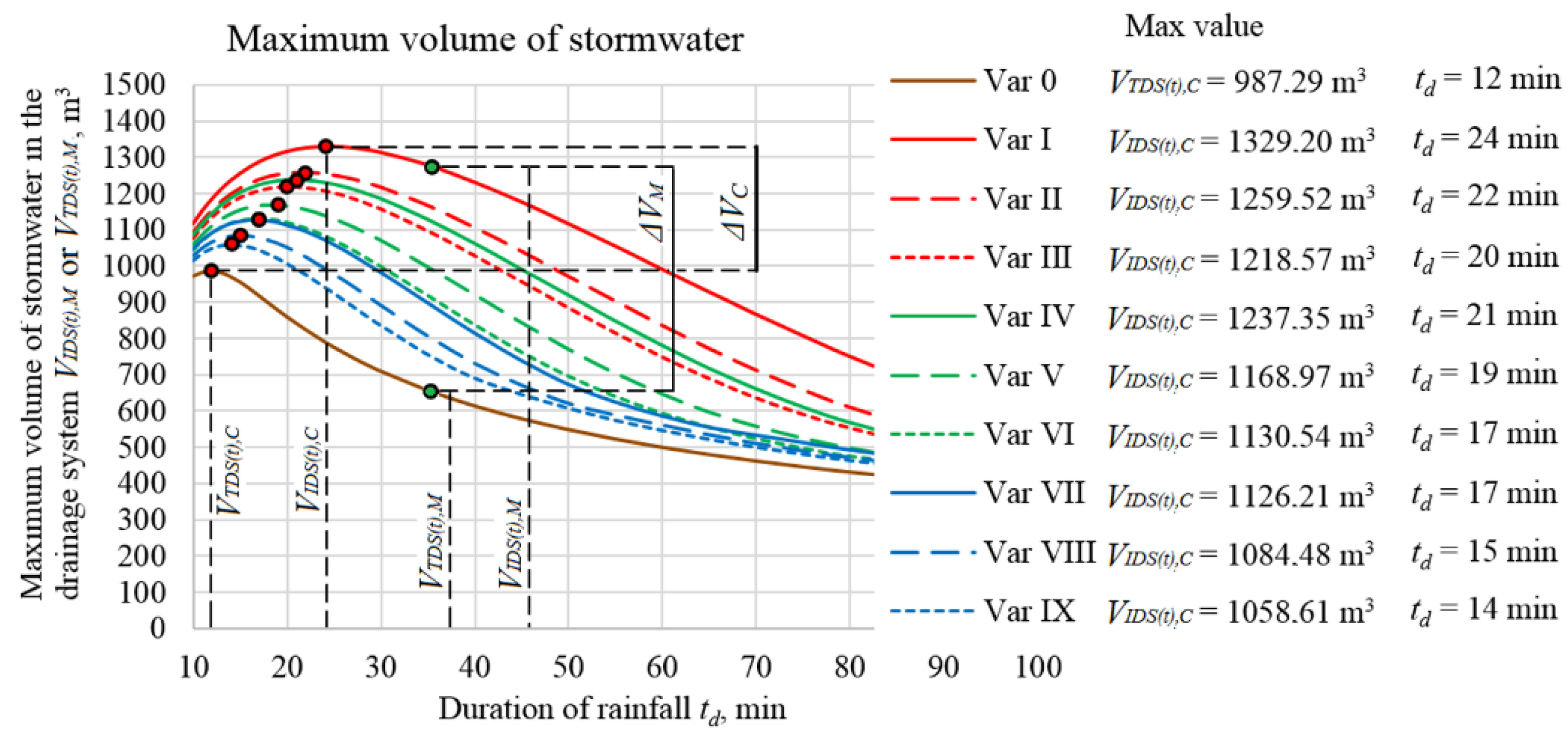
• the maximum value of the instantaneous variable volume of accumulated stormwater V_TDS(t),M in the drainage system:

  V_TDS(t),M = max(V_TDS(t)) − a system that works traditionally

  (3)

  V_IDS(t),M = max(V_IDS(t)) − an innovative system

  (4)
• the value of the instantaneous difference in the variable volume of accumulated stormwater ΔV_(t) in a drainage system that works traditionally and innovatively:

  ΔV_(t) = V_IDS(t) − V_TDS(t)

  (5)
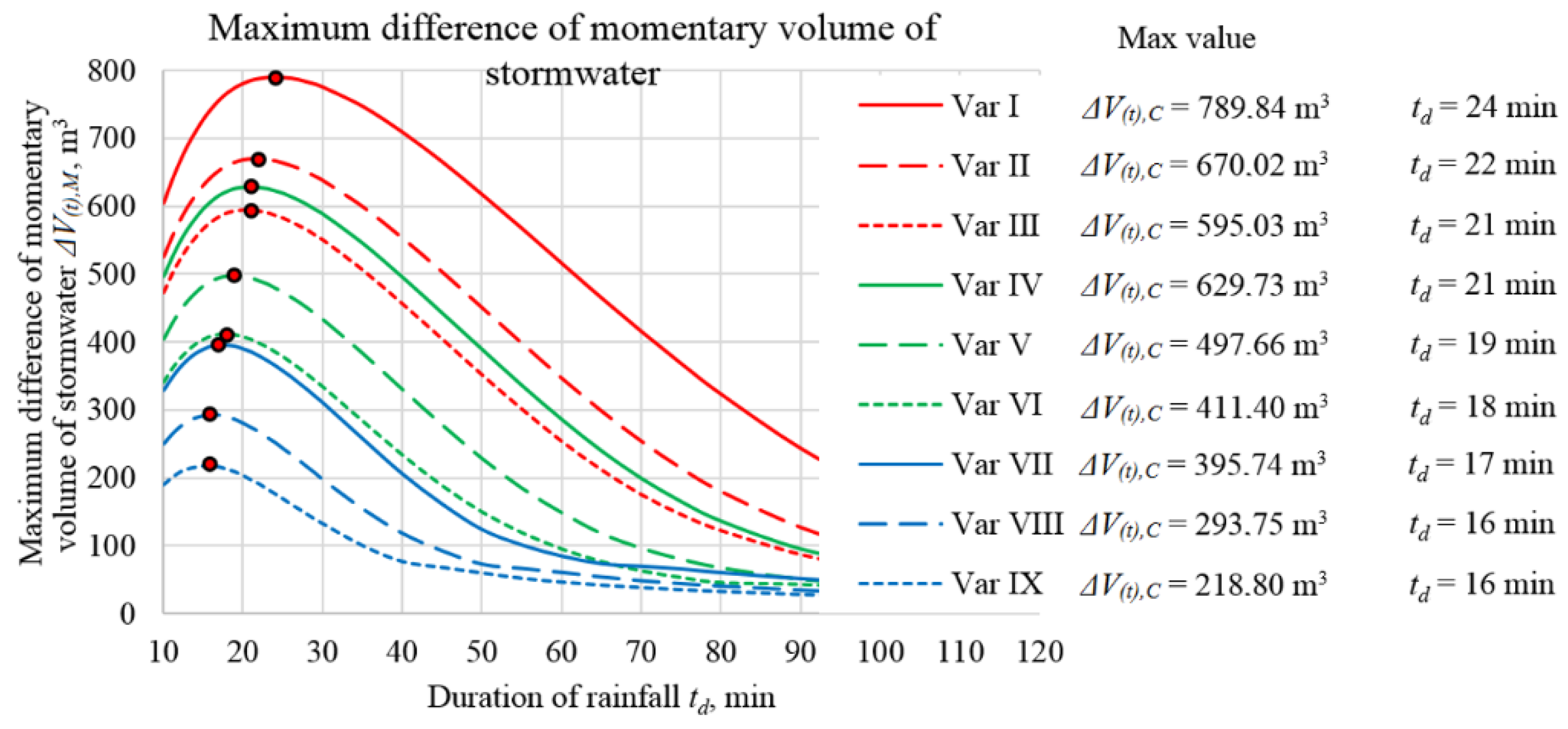
• the value of the maximum instantaneous difference in the variable volume of accumulated stormwater ΔV_(t),M in the traditional and innovative drainage system:

  ΔV_(t),M = max(ΔV_(t))

  (6)
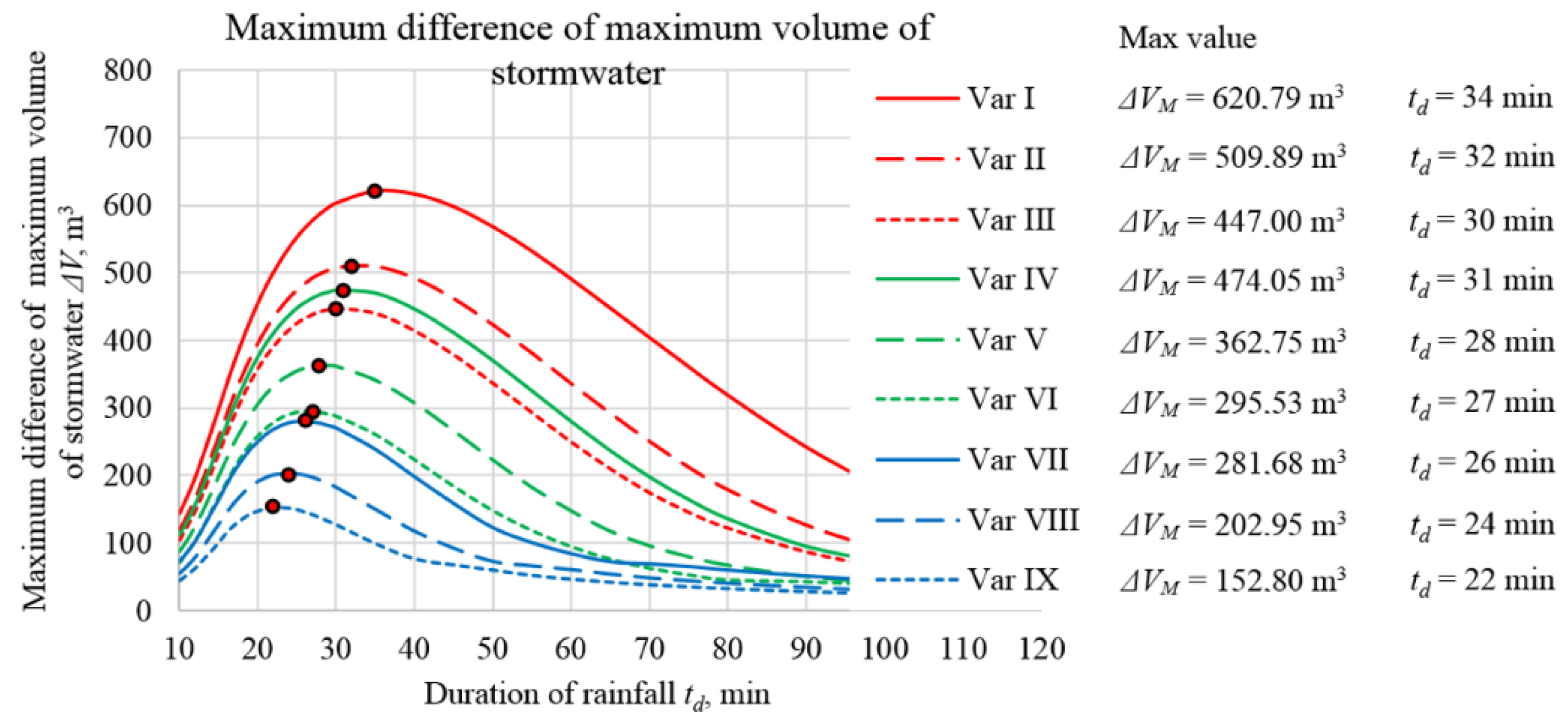
• the difference in the maximum stormwater volume ΔV accumulated in the drainage system functioning in a traditional and innovative way:

  ΔV = V_IDS(t),M − V_TDS(t),M

  (7)

When conducting an in-depth analysis of the functioning of many formulated variants of the drainage system, it was found that the use of damming partitions changed the process described so far related to the hydraulic transport of stormwater into a more complex one. It also covers the transport and accumulation of stormwater in the drainage system during and after rainfall. It turns out that the most favorable results were obtained in the variant VarI, where the largest volume of stormwater with V_IDS(t),M = 1212.48 m³ was retained in the drainage system at the same time with the longest retention time in the pipes of the system. In a situation where the drainage system operated traditionally, the maximum value of the instantaneous variable volume of accumulated stormwater was V_TDS(t),M = 982.64 m³. Adoption of a greater distance between the L_KR damming partitions or/and reducing the permissible level of stormwater damming H_per/d_k will reduce the retention efficiency of the innovative drainage system, as well as the value of the V_IDS(t),M parameter.

Performing many hydrodynamic simulations in various models of the hydraulic functioning of the drainage system, taking into account the wide range of variable rainfall times t_d, allowed determining four important parameters that characterize the innovative drainage system.

• Critical value of the instantaneous variable volume of accumulated stormwater in the drainage system:

  V_TDS(t),C = max(V_TDS(t),M) − traditionally functioning system

  (8)

  V_IDS(t),C = max(V_IDS(t),M) − an innovative system

  (9)
• Maximum difference in the maximum volume of stormwater accumulated in a drainage system that operates in a traditional and innovative way:

  ΔV_M = max(ΔV) = V_IDS(t),M − V_TDS(t),M

  (10)
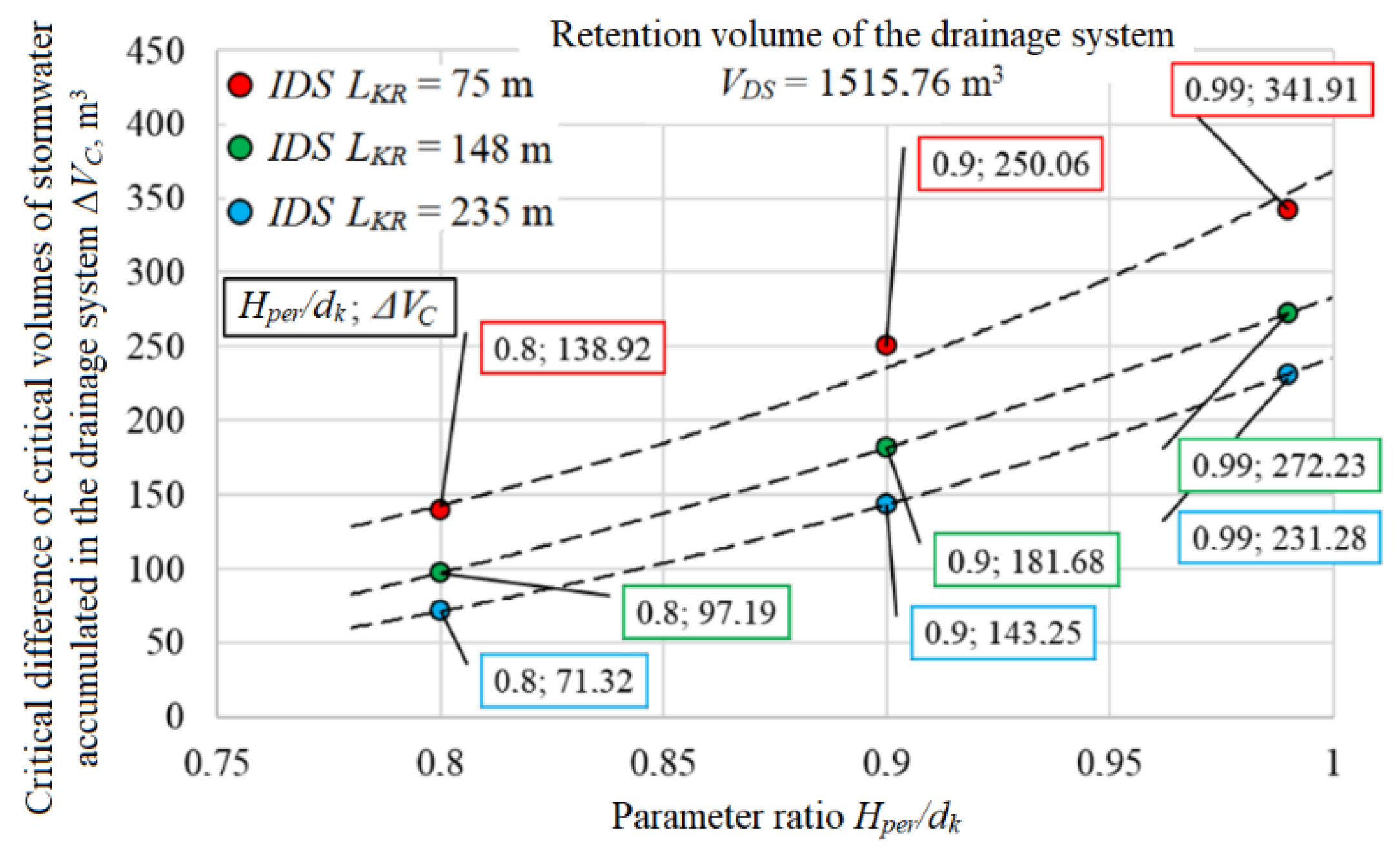
• Critical difference of critical volumes of stormwater accumulated in the drainage system functioning traditionally and innovatively:

  ΔV_C = V_IDS(t),C − V_TDS(t),C

  (11)
• Critical value of the maximum instantaneous difference in the variable volume of accumulated stormwater in a drainage system that operates in a traditional and innovative way:

  ΔV_(t),C = max(ΔV_(t),M)

  (12)

In the tested, real drainage system, including ten design variants, the maximum volumes of accumulated stormwater V_IDS(t),M and V_TDS(t),M were determined, assuming different rainfall durations t_d, which are presented in Figure 9.

It was agreed that the determined values of the V_IDS(t),M and V_TDS(t),M parameters depended strictly on the duration of rainfall t_d. For instance, the highest value of the parameter V_TDS(t),C = 987.29 m³ in the variant Var0 was determined during the rainfall with a duration of t_d = 12 min. However, in the variant VarI, the maximum value of the parameter is equal, V_IDS(t),C = 1329.20 m³, with the rainfall duration t_d = 24 min, i.e., twice as long. The curves illustrated in Figure 9 allow determining the difference in critical volumes of accumulated wastewater ΔV_C. On the other hand, the results of simulation tests carried out in this area for nine variants of the hydraulic functioning of the innovative drainage system are shown in Figure 10.

Comparing the hydraulic functioning of the drainage system in the Var0 and Var1 variants, it was found that the parameter ΔV_C reached the highest value of 341.91 m³ and constituted 23% of the total retention capacity V_DS of the designed drainage system. The determined value is also extreme for this parameter in the analyzed model catchment variants.

Ensuring the largest accumulation of stormwater with a volume of 341.91 m³ in the variant Var1 of the innovative drainage system at H_per/d_k = 0.99 and L_KR = 75 m in relation to the value in the Var0 variant with the traditional drainage system allowed reducing the peak outflow of stormwater from the catchment 1807.62 d m³ s to just 717.45 d m³/s (Figure 5).

However, the peak flows of Q_D,IDS,C, as well as the critical volumes of stormwater V_IDS(t),C accumulated in the drainage system in the Var0 and VarI variants, are achieved at other times of the rainfall duration t_d. Therefore, the determined critical value of the ΔV_C parameter does not directly translate into the determined reduction of the peak outflow Q_D. With this in mind, in-depth simulation studies were conducted to determine the course of variation in the volume of accumulated stormwater in the innovative drainage system IDS during rainfall with different t_d duration times.

The use of damming partitions in drainage systems turns a typical stormwater transport system into a complex one where it is also possible to control the process of the accumulation of a significant part of the transported stormwater, which is shown in detail in Figure 11. Along with the change in the duration of the rainfall, the maximum difference also changes the stormwater volume ΔV, as well as the value of the maximum instantaneous difference in the variable stormwater volume ΔV_(t),M accumulated in the traditional and innovative drainage systems.

The variability of the determined values of the parameters ΔV and ΔV_(t),M, depending on the assumed duration of the rainfall, is shown in Figure 11 and Figure 12.

It turns out that the differences in the volume of accumulated stormwater in the innovative and traditional drainage system reach values much higher than results from the set value of the ΔV_C parameter. It was shown that traditional and innovative drainage systems achieved maximum retention capacity at different durations of rainfall t_d (Figure 11 and Figure 12). By analyzing the hydraulic functioning of both systems during the rainfall of any duration t_d, each retention capacity of the innovative drainage system was confirmed. However, the differences in the maximum volumes of accumulated stormwater ΔV during a strictly determined duration of rainfall significantly exceed those determined by assigning the value of the ΔV_C parameter. For instance, in the Var1 variant, the ΔV parameter reaches the maximum value of 620.79 m³ with the rainfall duration of t_d = 34 min. At the same time, the td value is equal to the TRK rainfall value, which generates the critical stormwater runoff Q_D,IDS,C. However, in the case of the eight other analyzed variants of the functioning of the innovative sewage network (from Var2 to Var9), the t_d times proved to be longer than the TRK times.

To sum up, one should state that the duration of the rainfall, at which the greatest differences in the maximum fillings of the conduits in a traditional and innovative drainage system with stormwater is achieved, is equal to or slightly longer than the time of TRK, determined for the design of the retention canal systems.

When analyzing the curves illustrating the change in the volume of accumulated stormwater during the rainfall t_d = 13 min (Figure 8), the momentary maximum difference in their volume was determined, ΔV_(t),M = 689.03 m³. On the other hand, the performance of a full analysis, taking into account the full range of rainfall times, enabled the determination of the highest value of the parameter, ΔV_(t),C = 789.84 m³, in the Var1 variant (Figure 12). This value is achieved at the rainfall with a duration of t_d = 24 min, and it is much shorter than the time set for dimensioning the innovative drainage system, which, in the Var1 variant, is TRK = 34 min. During the rainfall with a duration of t_d = TRK = 34 min, the maximum instantaneous volume of accumulated stormwater is ΔV_(t),M = 746.50 m³ and is only slightly lower than the critical value of this parameter by ΔV_(t),C = 789.84 m³.

Thus, the use of damming partitions allows increasing significantly the retention capacity of gravity drainage systems, especially in relation to the rainfall, which generates a peak rainfall discharge from the drained catchment. For example, in the Var1 variant, the determined temporary increase in volume is as much as 52.1% (789.84/1515.76) of the volume of the drainage system analyzed. During the rainfall of TRK, which causes the occurrence of peak outflow Q_D,IDS,C, this volume accounts for 49.2% (746.50/1515.76) of the retention capacity of the IDS drainage system.

The high degree of reduction of the reliable stormwater flow rate at the outflow (node K) from the real catchment is, in practical terms, the effect of the full use of the retention capacity of the drainage system after it is equipped with an innovative retention canal system. However, the measure of its effectiveness is determined by the hydrodynamic modeling values of the coefficients λ_TDS and λ_IDS, which show the degree of utilization of the retention possibilities of the traditional and innovative drainage system. The values of the coefficients λ_TDS and λ_IDS are described by the following Equations (13) and (14):

$${\lambda }_{TDS}=\frac{V_{TDS(t),C}}{V_{DS}}$$

(13)

$${\lambda }_{IDS}=\frac{V_{IDS(t),C}}{V_{DS}}$$

(14)

where λ_TDS is the coefficient of percentage capacity utilization of the traditional drainage system (-), λ_IDS is the coefficient of percentage capacity utilization of the innovative drainage system (-), V_TDS(t),C—the critical value of stormwater volume stored in a traditional drainage system (m³), V_IDS(t),C is the critical value of stormwater volume stored in the innovative drainage system (m³) and V_DS—total retention volume of the drainage system (m³).

The values of the coefficients λ_TDS and λ_IDS are shown in Figure 13.

With the most favorable scenario marked as Var1 variant, an increase in the use of the network retention capacity from 65% in the traditional system to 88% using an innovative drainage system with damming partitions was determined. Thus, the use of an appropriate number of damming partitions and the adoption of a high level of stormwater accumulation in the conduits allows incorporating virtually all the free space of the drainage system conduits into the retention volume.

4. Conclusions

The analysis of the hydraulic functioning of the traditional and innovative drainage system allowed drawing the following conclusions:

(1)

Reducing the distance between damming partitions L_KR (implementation of a greater number of damming partitions) reduces the peak runoff of stormwater from the drained catchment.

(2)

The level of stormwater accumulation H_per in canals affects the hydraulic functioning of the drainage system. Increasing the level of stormwater accumulation H_per reduces the peak flows in the drainage system.

(3)

A modern approach to the design of innovative drainage systems is a competitive alternative in terms of usability and economy in relation to fairly commonly used retention tanks or other cubature facilities.

(4)

The transformation of the traditional drainage system into an innovative drainage system requires only the implementation of damming partitions in the existing manholes.

A multi-variant analysis of the functioning of the hydraulic drainage system, equipped with damming partitions, confirmed the practical need to transform known, traditional gravity drainage systems into innovative systems that are equipped with damming facilities. The results of the application of the concept in the drainage system are highly satisfactory, as the costs associated with the implementation and operation of an innovative drainage system are disproportionately small to the benefits obtained.

As with any solution, the concept of an innovative drainage system also has some negative aspects. Determining the required geometry of the damming barriers requires the use of hydrodynamic modeling and spending more time designing a solution in relation to the traditional drainage system. Additionally, these types of drainage systems will not increase the overall areas of urban greenery and more recreational spaces for society. However, it should be mentioned that an innovative drainage system can interact with LID devices, maximizing the effectiveness of the drainage system in global terms.

All things considered, the application of the concept of an innovative drainage system is part of a modern approach to the design of systems for the drainage and management of stormwater. Traditional drainage systems that operate in a gravitational way are still the leading way of draining and managing stormwater both in Poland and internationally. For this reason, there is a large area of practical applications of the results of the tests conducted whose measurable effects will be an increase in the degree of hydraulic safety of drained and designed drainage systems, while achieving significant financial savings and reducing the area allocated for infrastructure investments.