A Spatially Resolved Thermodynamic Assessment of Geothermal Powered Multi-Effect Brackish Water Distillation in Texas
Abstract
1. Introduction
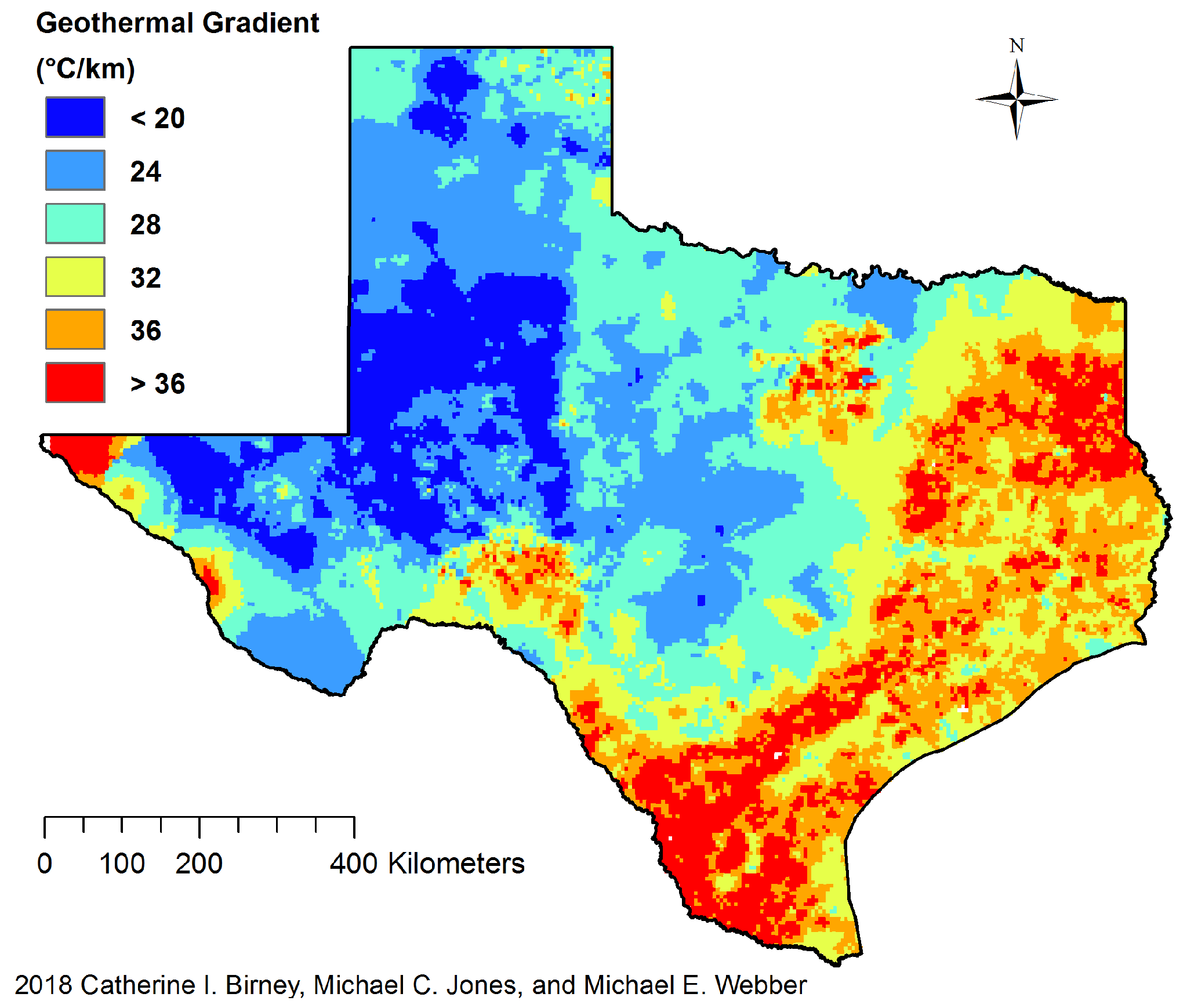
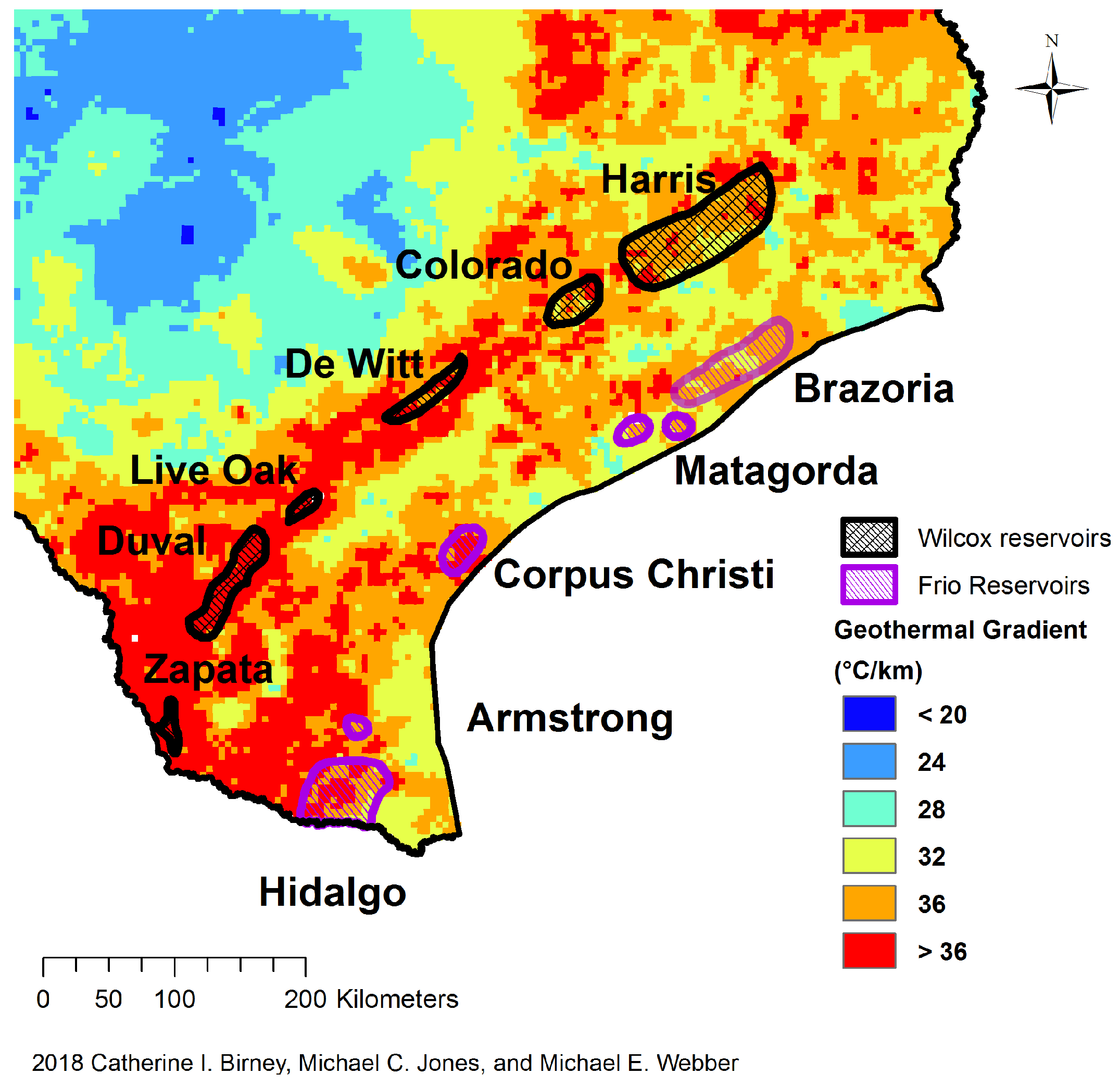
1.1. Texas as a Case Study
1.2. Desalination Design
1.3. Implementation of a Geothermal MED Plant
2. Materials and Methods
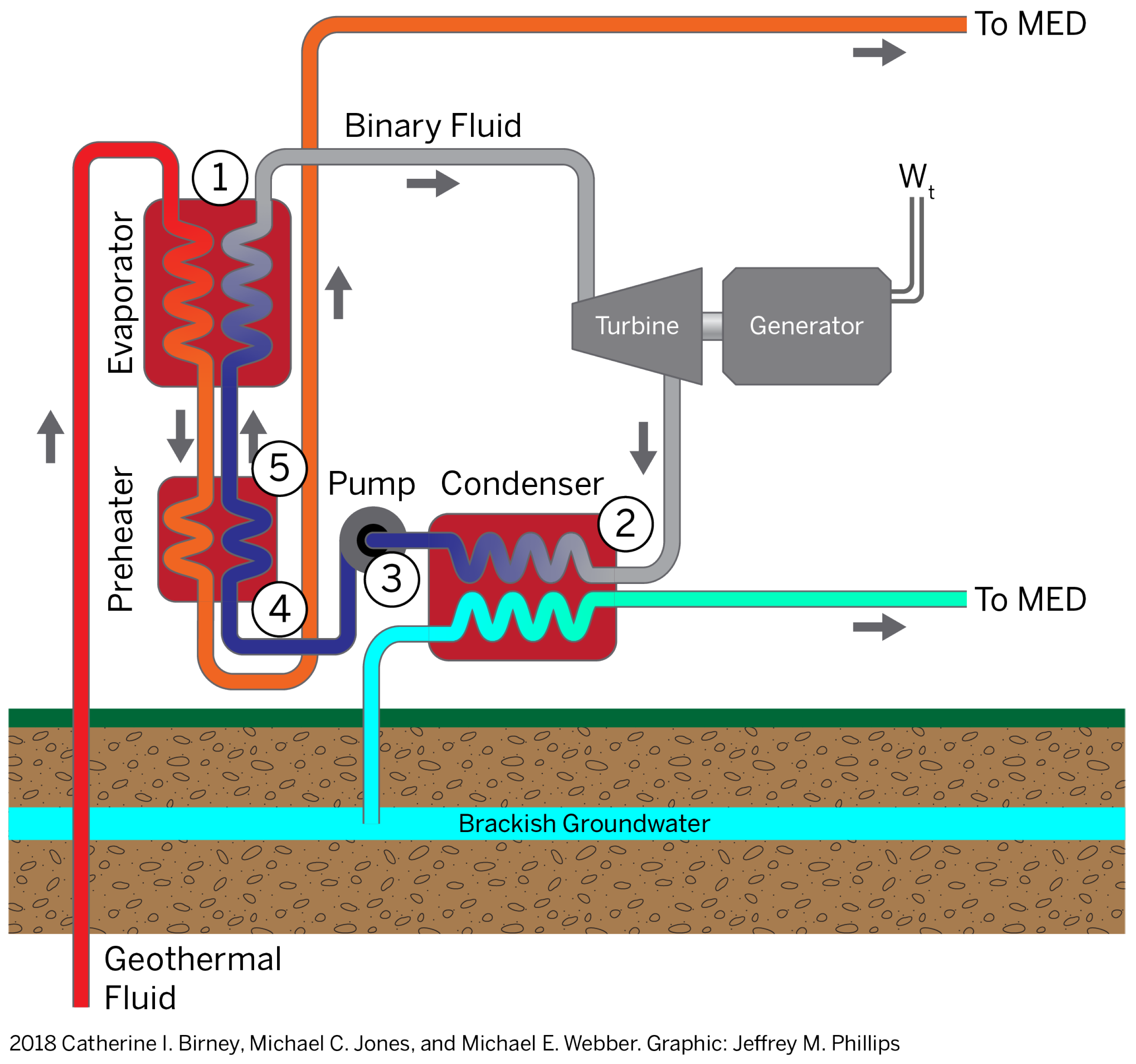
2.1. Principle of the Binary Cycle
- = Rate of work output from turbine [kW].
- = Turbine efficiency [%].
- = Generator efficiency [%].
- = Isentropic enthalpy of working fluid at point i in Figure 3 [kJ/kg].
- = Mass flow rate of feed water (brackish groundwater) [kg/s].
- = Specific heat capacity of feed water [kJ/kg-K].
- = Temperature of feed water at point i in Figure 3 [K].
- = Rate of work required by binary cycle pump [kW].
- = Pump efficiency [%].
- = water density (kg/m3).
- g = acceleration due to gravity (m/s2).
- = volumetric flow rate of water (m3/s).
- = pump efficiency (%).
- = desalination capacity factor.
- = depth to water (m).
- d = pipe diameter (m).
- f = friction factor.
- l = pipe length (m).
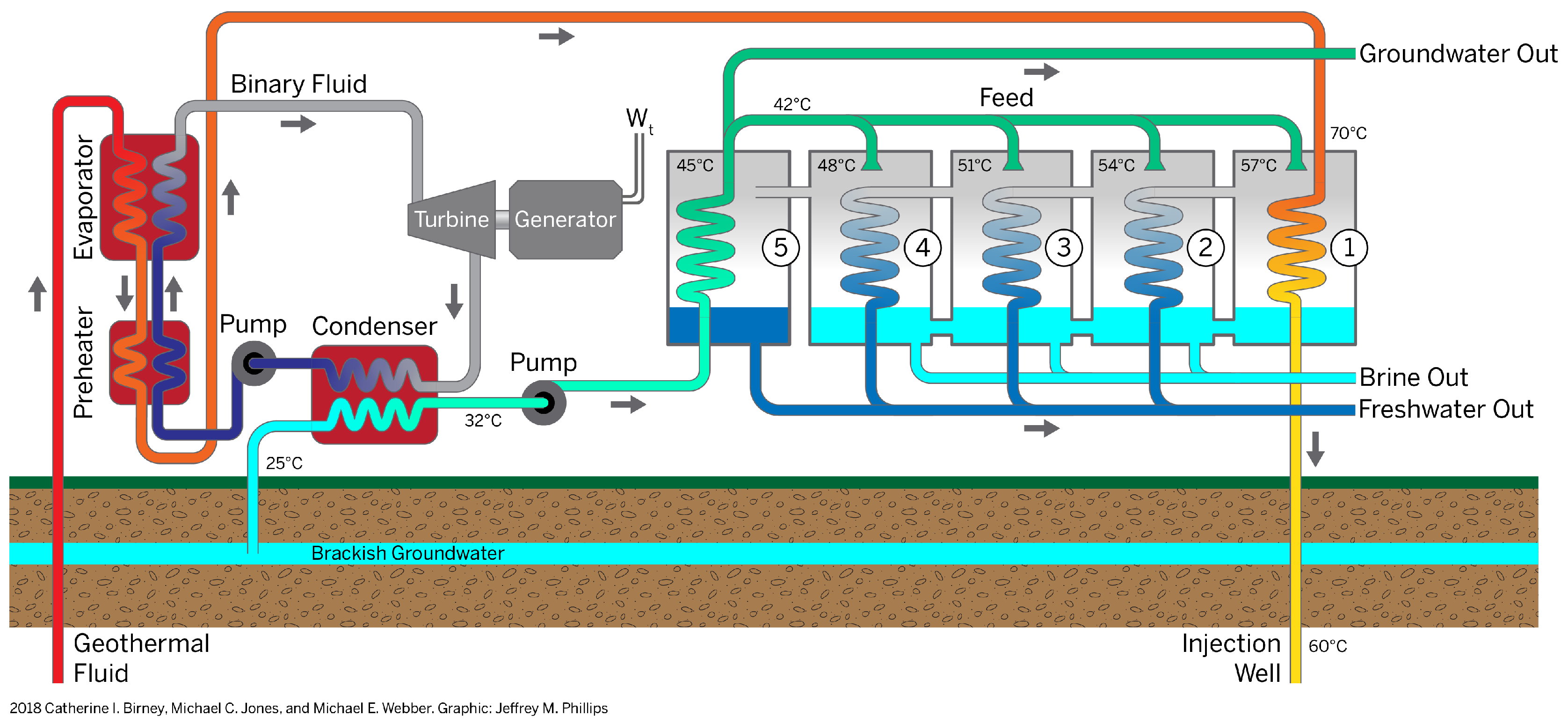
2.2. Principle of the Multi-Effect Distillation System
- = Geothermal temperature entering 1st effect in Figure 1 (K).
- = Geothermal temperature exiting 1st effect in Figure 1 (K).
- = Mass flow rate of feed water entering effect n in Figure 1 (kg/s).
- = Temperature of brine exiting effect n in Figure 1 (K).
- = Temperature of feed water entering effect n in Figure 1 (K).
- = Mass flow rate of vapor in effect n (kg/s).
- = Latent heat of evaporation in effect n (kJ/kg).
- = Specific heat of water vapor (kJ/kg).
- = Vapor saturation temperature, effect n (K).
- = Temperature difference between liquids in the heat exchanger in the first effect [K].
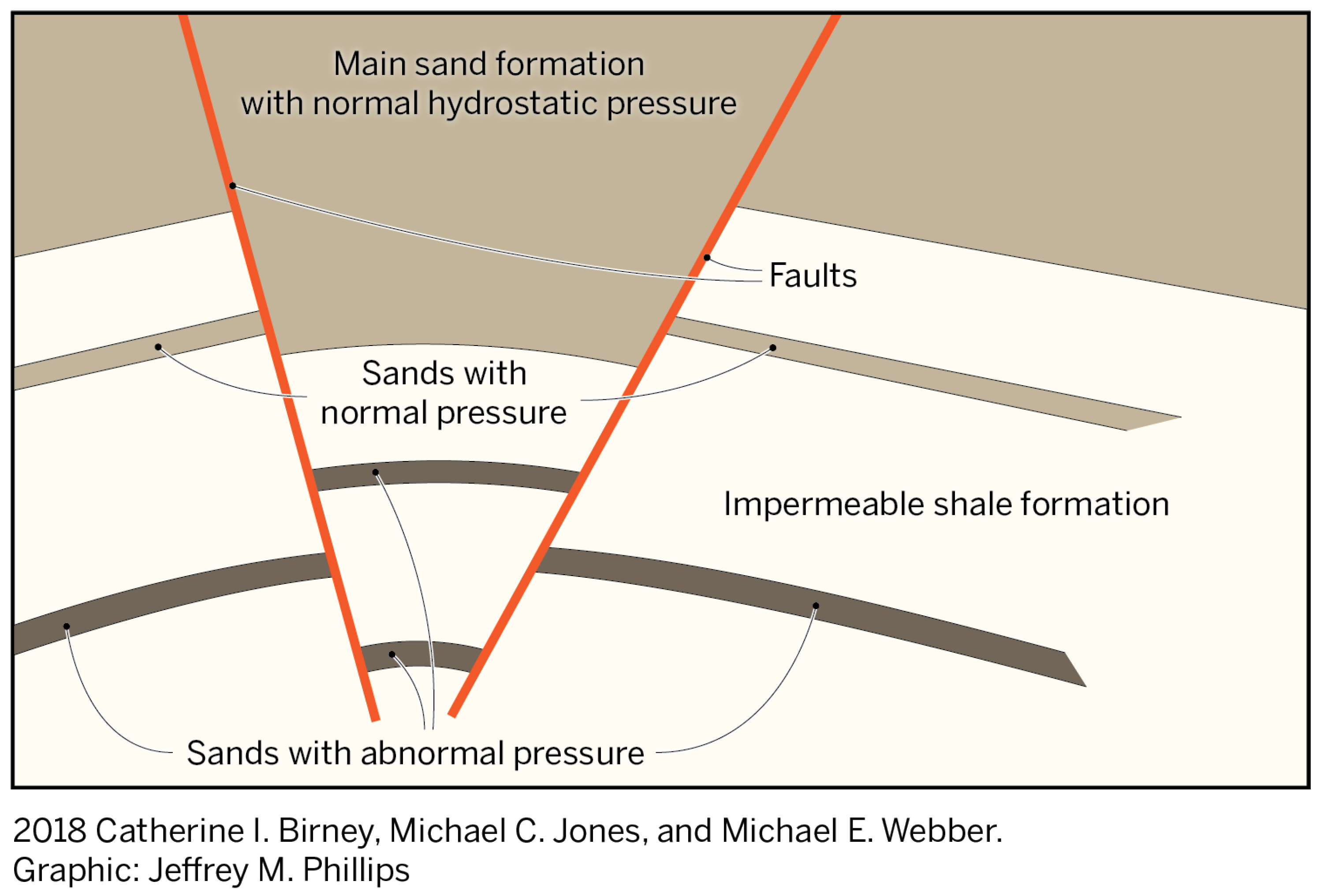
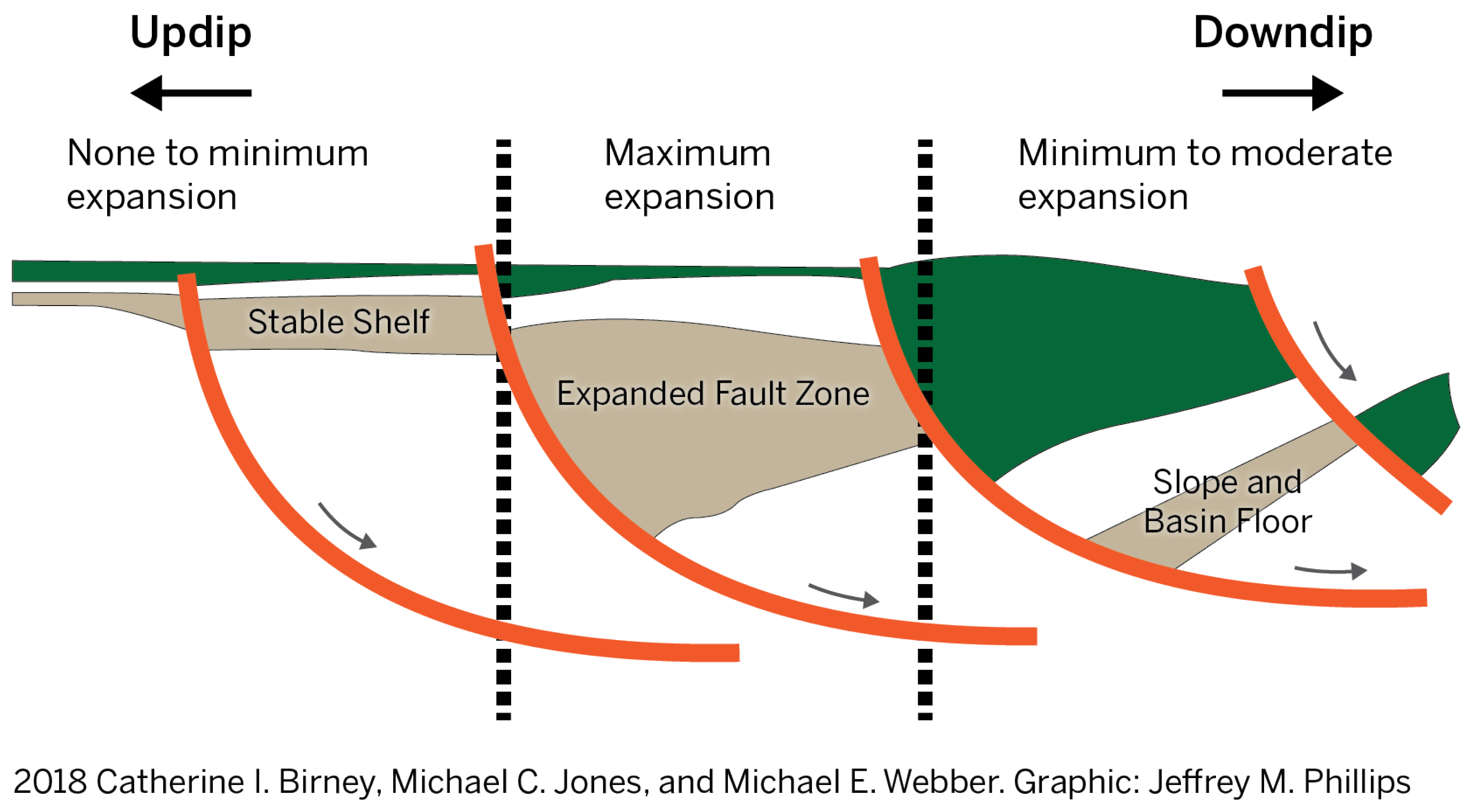
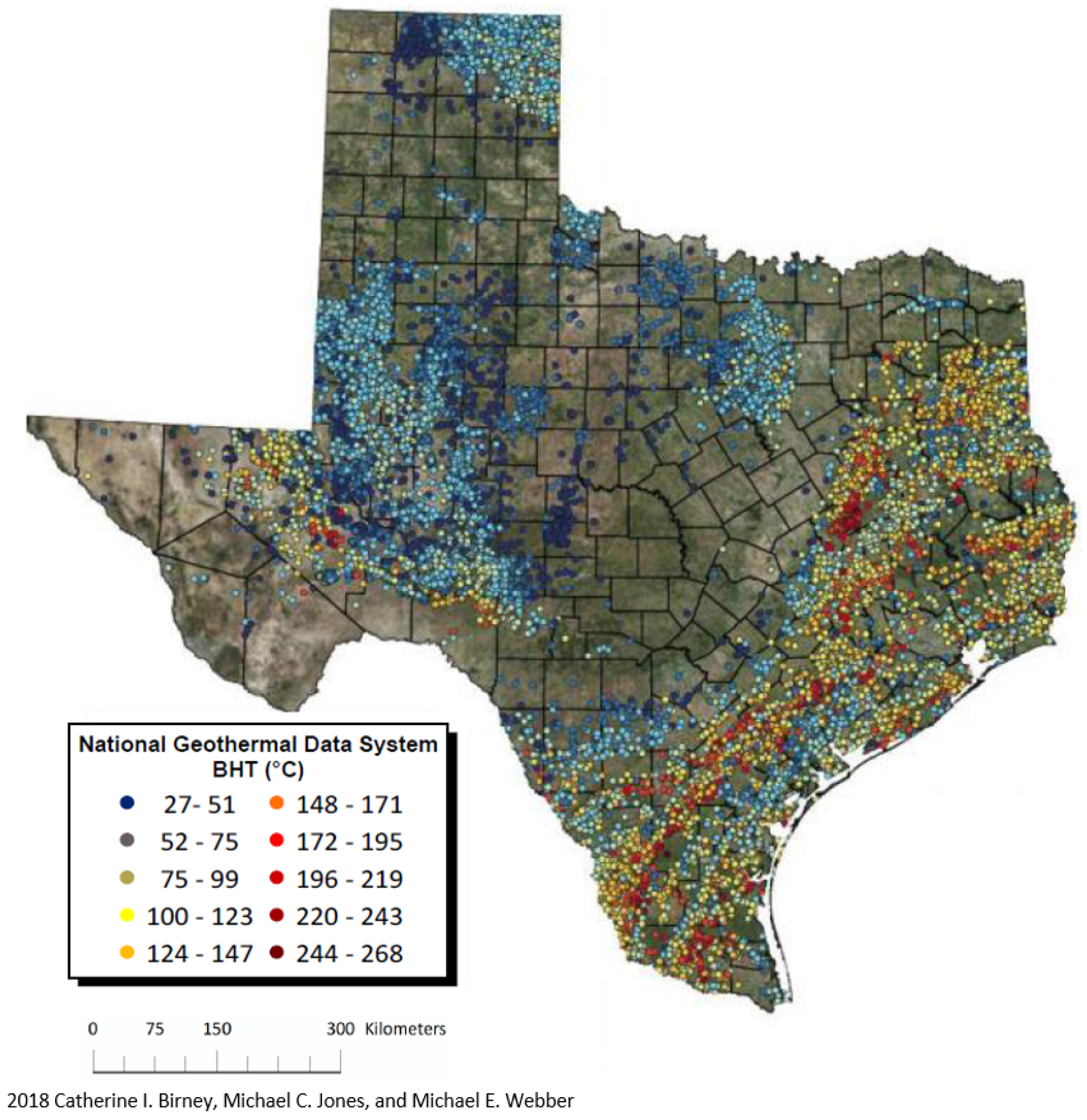
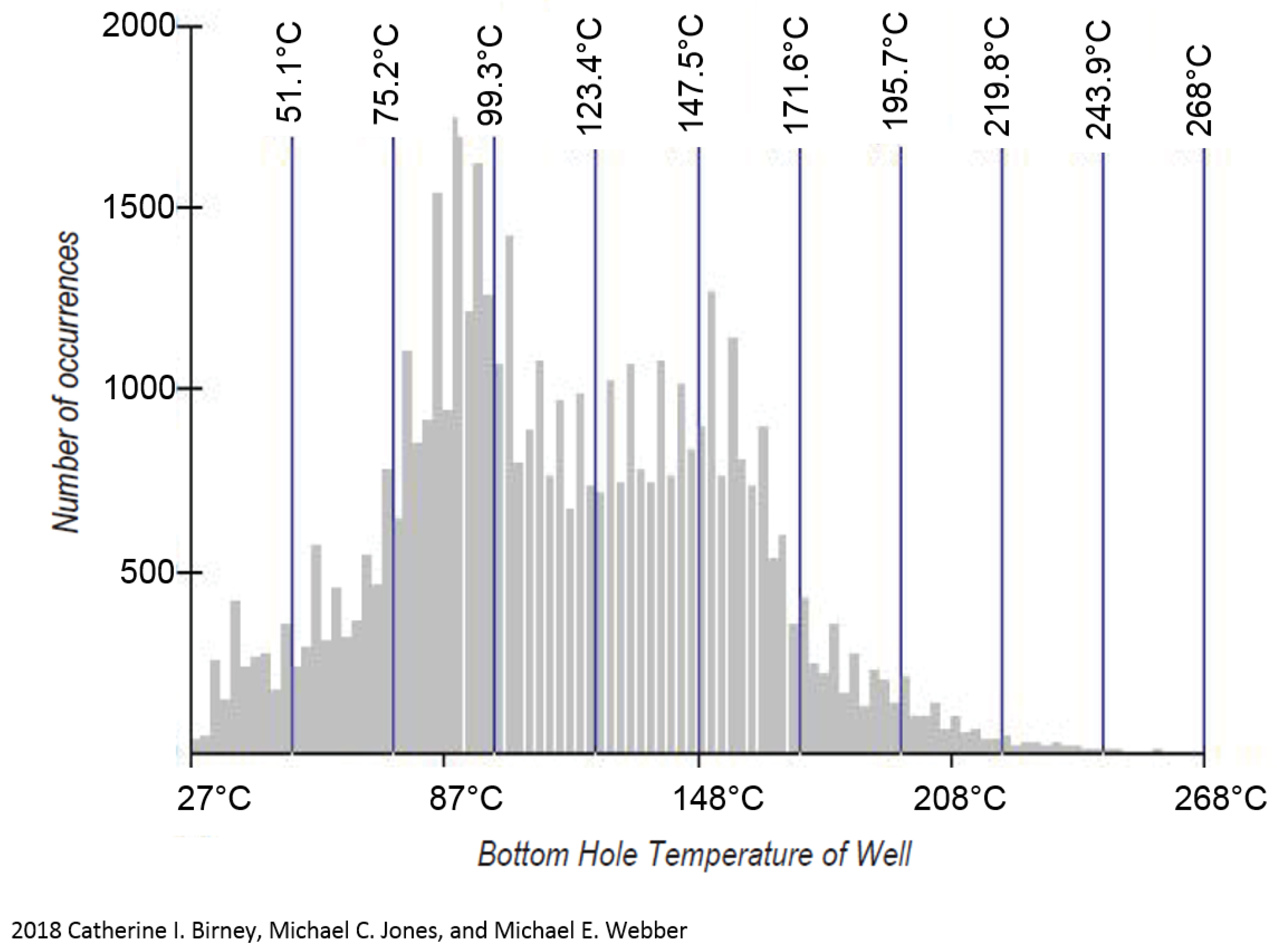
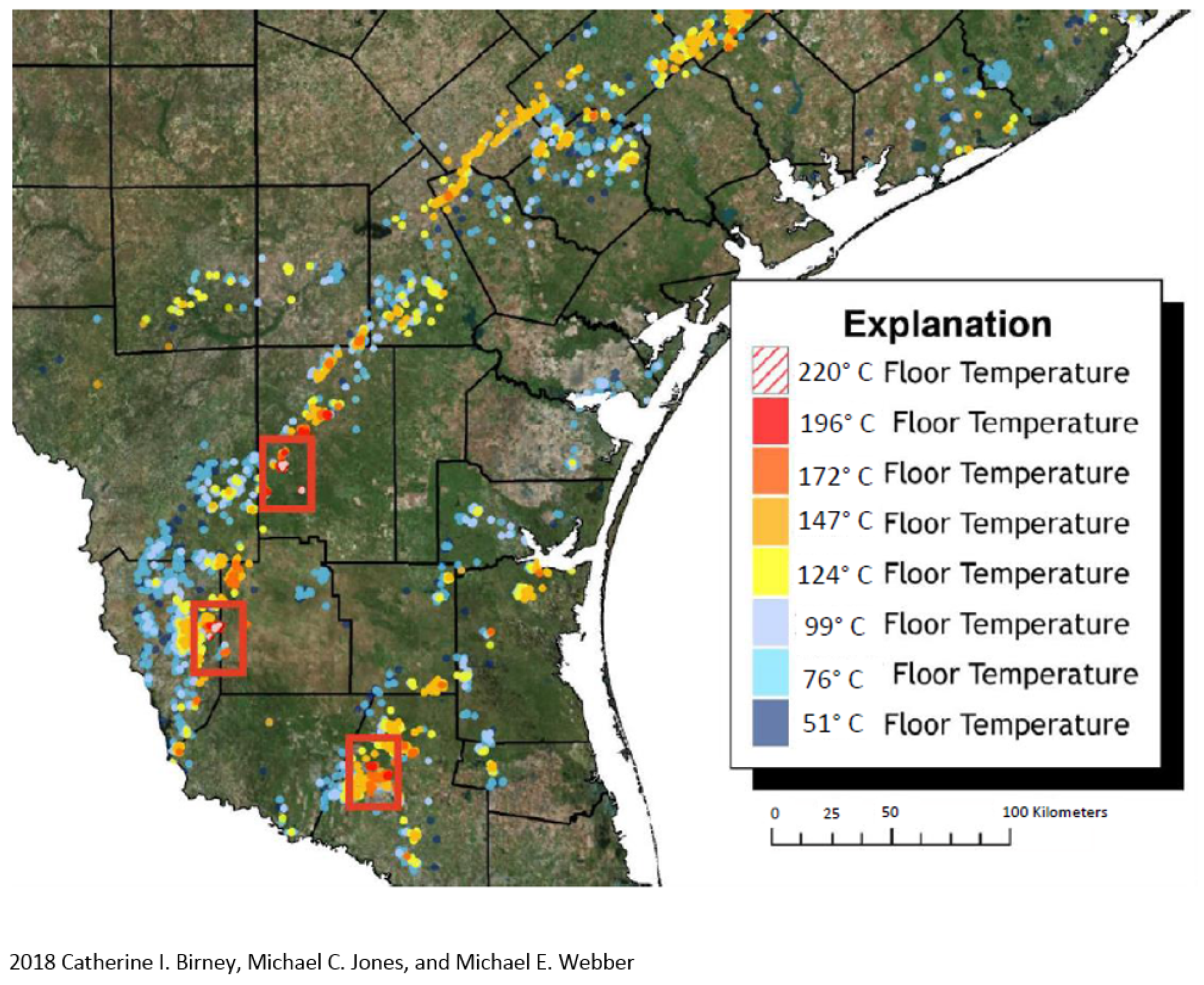
2.3. Resource Feasibility in Texas for Binary-MED System
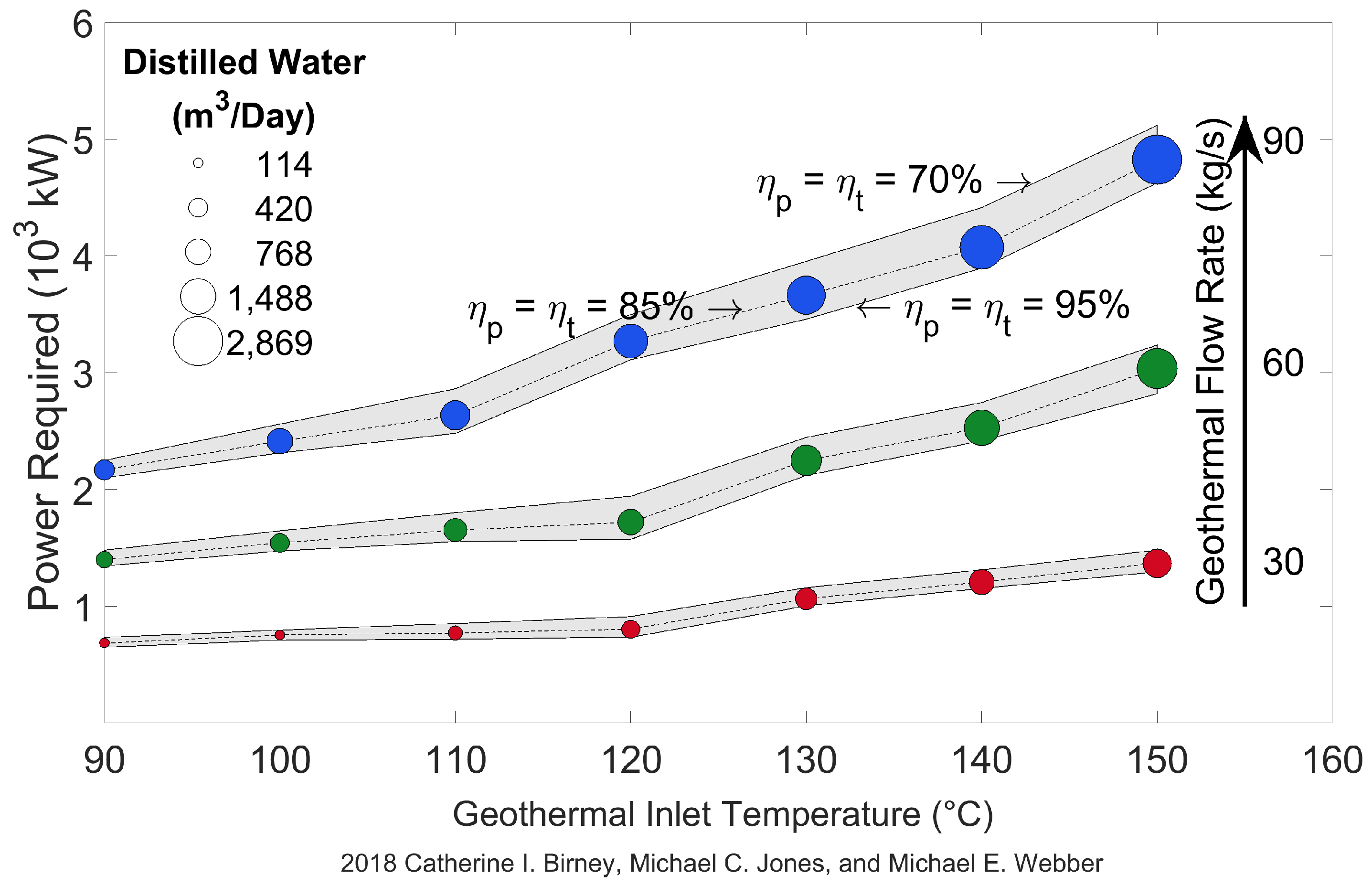
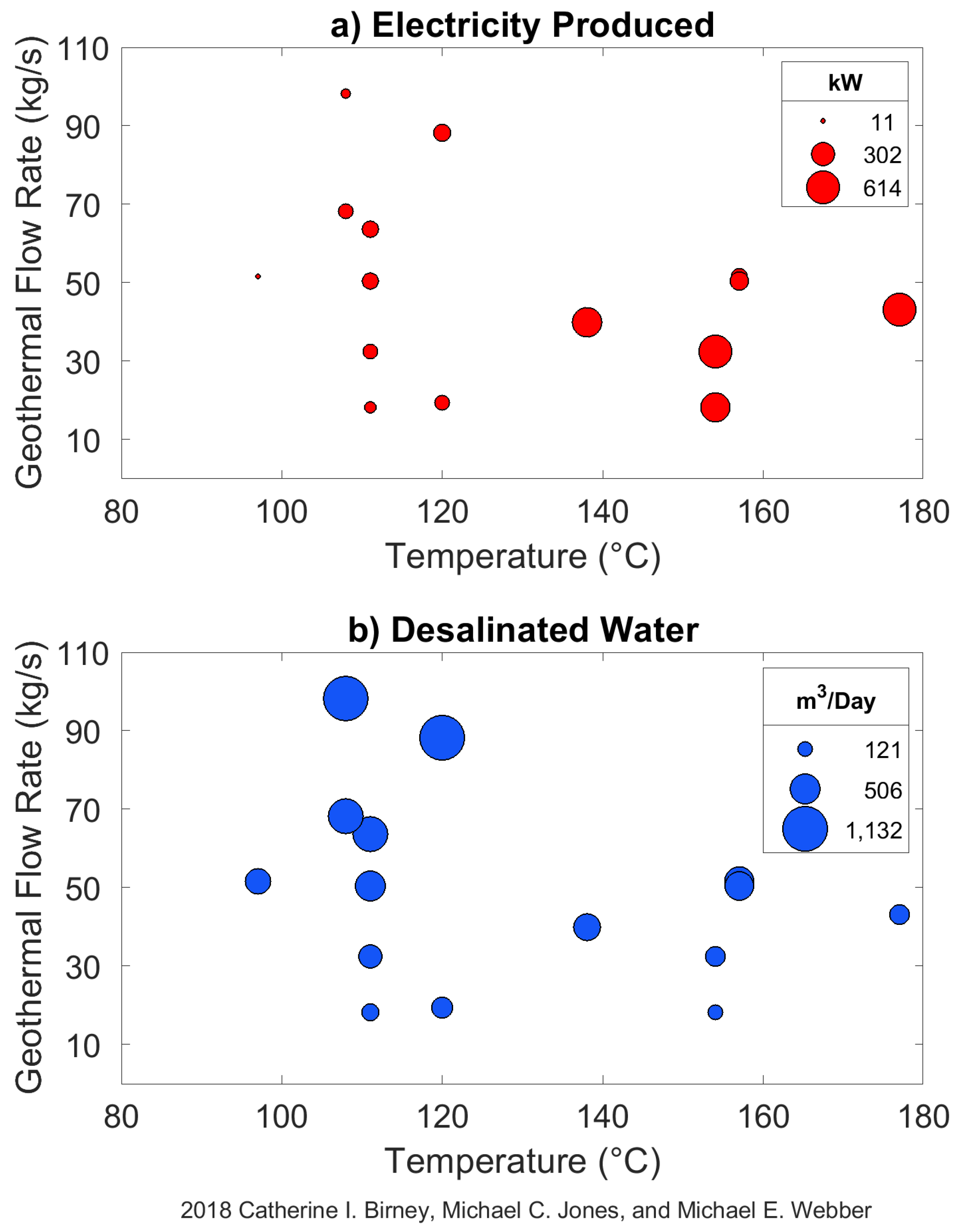
3. Results
4. Discussion
Limitations and Future Work
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Parameter | Definition | Unit |
| Specific heat capacity of feed water | (kJ/kg-K) | |
| Specific heat capacity of geothermal water | (kJ/kg-K) | |
| Specific heat of water vapor | (kJ/kg) | |
| Desalination capacity factor | (%) | |
| d | Pipe diameter | (m) |
| Energy intensity | (kwh/m3) | |
| f | Friction factor | |
| g | Acceleration due to gravity | (m/s2) |
| Enthalpy of working fluid at point i in Figure 3 | (kJ/kg) | |
| Isentropic enthalpy of working fluid at point i in Figure 3 | (kJ/kg) | |
| Latent heat of evaporation in effect n | (kJ/kg) | |
| l | Pipe length | (m) |
| Mass flow rate of feed water (brackish groundwater) | (kg/s) | |
| Mass flow rate of geothermal water | (kg/s) | |
| Mass flow rate of feed water entering effect n in Figure 1 | (kg/s) | |
| Mass flow rate of vapor in effect n | (kg/s) | |
| Mass flow rate of working fluid in binary cycle | (kg/s) | |
| Generator efficiency | (%) | |
| Pump efficiency | (%) | |
| Turbine efficiency | (%) | |
| Binary cycle efficiency | (%) | |
| P | Power to run binary-MED plant | (kW) |
| Power requirement for the desalination process | (kW) | |
| Power requirements for pumping the geothermal fluid | (kW) | |
| Power requirements for pumping the brackish groundwater | (kW) | |
| Water density | (kg/m3) | |
| Volumetric flow rate of water | (m3/s) | |
| Rate of heat transfer in heat exchanger | (kW) | |
| Pinch Point Temperature | (K) | |
| Geothermal temperature entering 1st effect in Figure 1 | (K) | |
| Geothermal temperature exiting 1st effect in Figure 1 | (K) | |
| Temperature of feed water at point i in Figure 3 | (K) | |
| Temperature of geothermal water at point i in Figure 3 | (K) | |
| Temperature difference between liquids in the heat exchanger in the first effect | (K) | |
| Temperature of brine exiting effect n in Figure 1 | (K) | |
| Temperature of feed water entering effect n in Figure 1 | (K) | |
| Vapor saturation temperature, effect n | (K) | |
| Rate of work generated by turbine | (kW) | |
| Rate of work required by binary cycle pump | (kW) | |
| Rate of work output from turbine | (kW) | |
| Depth to water | (m) |
References
- UNEP. Vital Water Graphics-An Overview of the State of the World’s Fresh and Marine Waters; Technical Report; United Nations Environment Programme: Nairobi, Kenya, 2002. [Google Scholar]
- Varis, O.; Vakkilainen, P. China’s 8 challenges to water resources management in the first quarter of the 21st century. Geomorphology 2001, 41, 93–104. [Google Scholar] [CrossRef]
- Roudi-Fahimi, F.; Creel, L.; De Souza, R.M. Finding the Balance: Population and Water Scarcity in the Middle East and North Africa. Popul. Ref. Bureau 2002, 1, 1–8. [Google Scholar]
- UN-Water. Coping with Water Scarcity; Technical Report; FAO Water Reports: Chhattisgarh, India, 2006. [Google Scholar]
- Voutchkov, N. Desalination Engineering Planning and Design; McGraw-Hill Publishing: New York, NY, USA, 2013. [Google Scholar]
- Karagiannis, I.C.; Soldatos, P.G. Water desalination cost literature: Review and assessment. Desalination 2008, 223, 448–456. [Google Scholar] [CrossRef]
- Kjellsson, J.; Webber, M. The Energy-Water Nexus: Spatially-Resolved Analysis of the Potential for Desalinating Brackish Groundwater by Use of Solar Energy. Resources 2015, 4, 476–489. [Google Scholar] [CrossRef]
- Gold, G.; Webber, M. The Energy-Water Nexus: An Analysis and Comparison of Various Configurations Integrating Desalination with Renewable Power. Resources 2015, 4, 227–276. [Google Scholar] [CrossRef]
- Gude, V.G. Desalination and sustainability–An appraisal and current perspective. Water Resour. 2016, 89, 87–106. [Google Scholar] [CrossRef] [PubMed]
- McMorrow, D. Enhanced Geothermal Systems; Technical Report; The MITRE Corporation: McLean, VA, USA, 2013. [Google Scholar]
- Zafar, S.D.; Cutright, B.L. Texas’ geothermal resource base: A raster-integration method for estimating in-place geothermal-energy resources using ArcGIS. Geothermics 2014, 50, 148–154. [Google Scholar] [CrossRef]
- Tester, J.W.; Anderson, B.J.; Batchelor, A.S.; Blackwell, D.D.; DiPippo, R.; Drake, E.M.; Garnish, J.; Livesay, B.; Moore, M.C.; Nichols, K.; et al. The Future of Geothermal Energy-Impact of Enhanced Geothermal Systems (EGS) on the United States in the 21st Century; Technical Report; Massachusetts Institute of Technology: Boston, MA, USA, 2006. [Google Scholar]
- Loutatidou, S.; Arafat, H.A. Techno-economic analysis of MED and RO desalination powered by low-enthalpy geothermal energy. Desalination 2015, 365, 277–292. [Google Scholar] [CrossRef]
- Davies, P.A.; Orfi, J. Self-powered desalination of geothermal saline groundwater: Technical feasibility. Water 2014, 6, 3409–3432. [Google Scholar] [CrossRef]
- Spang, E. The Potential for Wind-Powered Desalination in Water-Scarce Countries. Ph.D. Thesis, Tufts University, Medford, MA, USA, 2006. [Google Scholar] [CrossRef]
- Grubert, E.A.; Stillwell, A.S.; Webber, M.E. Where does solar-aided seawater desalination make sense? A method for identifying sustainable sites. Desalination 2014, 339, 10–17. [Google Scholar] [CrossRef]
- Texas Water Development Board. 2017 State Water Plan; Technical Report; Texas Water Development Board: Austin, TX, USA, 19 May 2016.
- Raluy, G.; Serra, L.; Uche, J. Life cycle assessment of MSF, MED and RO desalination technologies. Energy 2006, 31, 2025–2036. [Google Scholar] [CrossRef]
- Shatat, M.; Riffat, S.B. Water desalination technologies utilizing conventional and renewable energy sources. Int. J. Low Carbon Technol. 2014, 9, 1–19. [Google Scholar] [CrossRef]
- Ophir, A.; Lokiec, F. Advanced MED process for most economical sea water desalination. Desalination 2005, 182, 187–198. [Google Scholar] [CrossRef]
- Rahimi, B.; Christ, A.; Regenauer-Lieb, K.; Chua, H.T. A novel process for low grade heat driven desalination. Desalination 2014, 351, 202–212. [Google Scholar] [CrossRef]
- Christ, A. A Novel Sensible Heat Driven Desalination Technology. Ph.D. Thesis, The University of Western Australia, Perth, Australia, 2015. [Google Scholar]
- Franco, A.; Villani, M. Optimal design of binary cycle power plants for water-dominated, medium-temperature geothermal fields. Geothermics 2009, 38, 379–391. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory (NREL). Geothermal Electricity Production Basics. Available online: https://www.nrel.gov/research/re-geo-elec-production.html (accessed on 12 October 2015).
- Lund, J.W. Development and Utilization of Geothermal Resources; Technical Report; Oregon Institute of Technology: Klamath Falls, OR, USA, 2007. [Google Scholar] [CrossRef]
- Karytsas, K.; Alexandrou, V.; Boukis, I. The Kimolos Geothermal Desalination Project. In Proceedings of the International Workshop on Possibilities of Geothermal Energy Development in the Aegean Islands Region, Milos, Greece, 5–8 September 2002; pp. 206–219. [Google Scholar]
- Southern Methodist University. SMU Geothermal Lab-Data and Maps. Available online: https://www.smu.edu/Dedman/Academics/Programs/GeothermalLab/DataMaps (accessed on 7 October 2015).
- Texas Water Development Board. Geographic Information System (GIS) Data. Available online: http://www.twdb.texas.gov/mapping/gisdata.asp (accessed on 7 October 2015).
- John, C.J.; Maciasz, G.; Harder, B.J. Gulf Coast Geopressured-Geothermal Program Summary Report Compilation; Technical Report; Basin Research Institute: Baton Rouge, LA, USA, 1998. [Google Scholar]
- Esposito, A.; Augustine, C. Geopressured Geothermal Resource and Recoverable Energy Estimate for the Wilcox and Frio Formations, Texas. Trans. Geotherm. Res. Counc. 2011, 35, 1563–1571. [Google Scholar]
- DiPippo, R. Geothermal Power Plants: Principles, Applications, Case Studies and Environmental Impact Third Edition; Elsevier: Amsterdam, The Netherlands, 2012; p. 624. [Google Scholar]
- Abisa, M.T. Geothermal Binary Plant Operation and Maintenance System with Svartsengi Power Plant as a Case Study; Technical Report 15; The United Nations University: Reykjavik, Iceland, 2002. [Google Scholar]
- El-Dessouky, H.T.; Ettouney, H.M.; Mandani, F. Performance of parallel feed multiple effect evaporation system for seawater desalination. Appl. Therm. Eng. 2000, 20, 1679–1706. [Google Scholar] [CrossRef]
- Xue, J.; Cui, Q.; Ming, J.; Bai, Y.; Li, L. Analysis of Thermal Properties on Backward Feed Multieffect Distillation Dealing with High-Salinity Wastewater. J. Nanotechnol. 2015, 1–3, 1–7. [Google Scholar] [CrossRef]
- Zhao, D.; Xue, J.; Li, S.; Sun, H.; dong Zhang, Q. Theoretical analyses of thermal and economical aspects of multi-effect distillation desalination dealing with high-salinity wastewater. Desalination 2011, 273, 292–298. [Google Scholar] [CrossRef]
- Roll, R.W. Wards of the State: Abandoned Oil and Gas Wells in Texas. 2017. Available online: https://dallasbar.org/book-page/wards-state-abandoned-oil-and-gas-wells-texas (accessed on 15 November 2017).
- Deming, D. Introduction to Hydrogeology, 2nd ed.; McGraw-Hill Publishing: Boston, MA, USA, 2002; pp. 219–239. [Google Scholar]
- Bebout, D.; Loucks, R.; Gregory, A. Frio Sandstone Reservoirs in the Deep Subsurface Along the Texas Gulf Coast Thier Potential for Pordocution of Geopressured Geothermal Energy; Technical Report 91; Bureau of Economic Geology: Austin, TX, USA, 1978. [Google Scholar]
- Swanson, S.M.; Karlsen, A.W.; Valentine, B.J. Geologic Assessment of Undiscovered Oil and Gas Resources—Oligocene Frio and Anahuac Formations, United States Gulf of Mexico Coastal Plain and State Waters; Technical Report; U.S. Geological Survey: Reson, VA, USA, 2013.
- Jones, M.C. Implications of Geothermal Energy Production via Geopressured Gas Wells in Texas: Merging Conceptual Understanding Of Hydrocarbon Production and Geothermal Systems. Master’s Thesis, University of Texas at Austin, Austin, TX, USA, 2016. [Google Scholar]
- Goosen, M.; Mahmoudi, H.; Ghaffour, N. Water Desalination using geothermal energy. Energies 2010, 3, 1423–1442. [Google Scholar] [CrossRef]
- Bundschuh, J.; Ghaffour, N.; Mahmoudi, H.; Goosen, M.; Mushtaq, S.; Hoinkis, J. Low-cost low-enthalpy geothermal heat for freshwater production: Innovative applications using thermal desalination processes. Renew. Sustain. Energy Rev. 2015, 43, 196–206. [Google Scholar] [CrossRef]
- Rao, P.; Aghajanzadeh, A.; Sheaffer, P.; Morrow, W.R.; Brueske, S.; Dollinger, C.; Price, K.; Sarker, P.; Cresko, J. Survey of Available Information in Support of the Energy-Water Bandwidth Study of Desalination Systems. Technical Report; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2016.
- Verlag, F. Roadmap for the Development of Desalination Powered by Renewable Energy; Technical Report; ProDes: Freiburg, Germany, 2010. [Google Scholar]
- Starling, K.E.; West, H.; Iqbal, K.Z.; Hsu, C.; Malik, Z.; Fish, L.; Lee, C. Resource Utilization Efficiency Improvement of Geothermal Binary Cycles-Phase II; Technical Report; University of Oklahoma: Norman, OK, USA, 15 June 1976–31 December 1977.
| Parameter | Value |
|---|---|
| Geothermal Gradient | 36 C/km |
| Depth to brackish groundwater | 1800–3500 m |
| Geothermal Temperature | 90–150 C |
| Geothermal flow rate | 30/60/90 kg/s |
| Turbine efficiency | 70/85/95% |
| Pump efficiency | 70/85/95% |
| Generator efficiency | 99% |
| Binary cycle efficiency | 5–15% |
| Capacity factor | 95 |
| Top brine temperature (TBT) | 70 C |
| Pinch point temperature | 5 C |
| Recovery factor | 1.8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Birney, C.I.; Jones, M.C.; Webber, M.E. A Spatially Resolved Thermodynamic Assessment of Geothermal Powered Multi-Effect Brackish Water Distillation in Texas. Resources 2019, 8, 65. https://doi.org/10.3390/resources8020065
Birney CI, Jones MC, Webber ME. A Spatially Resolved Thermodynamic Assessment of Geothermal Powered Multi-Effect Brackish Water Distillation in Texas. Resources. 2019; 8(2):65. https://doi.org/10.3390/resources8020065
Chicago/Turabian StyleBirney, Catherine I., Michael C. Jones, and Michael E. Webber. 2019. "A Spatially Resolved Thermodynamic Assessment of Geothermal Powered Multi-Effect Brackish Water Distillation in Texas" Resources 8, no. 2: 65. https://doi.org/10.3390/resources8020065
APA StyleBirney, C. I., Jones, M. C., & Webber, M. E. (2019). A Spatially Resolved Thermodynamic Assessment of Geothermal Powered Multi-Effect Brackish Water Distillation in Texas. Resources, 8(2), 65. https://doi.org/10.3390/resources8020065




