A Mathematical Model of Regional Socio-Economic Development of the Russian Arctic Zone
Abstract
:1. Introduction
2. The Deterministic Model of Management of Socio-Economic Development of the Region
- is the demographic activity coefficient;
- is the coefficient of people’s anti-motivation to childbearing;
- is the energy supply coefficient;
- is the coefficient of people’s interest in economic development;
- is the coefficient of the real sector economic development;
- is the coefficient of energy supply per workplace;
- is the energy supply coefficient of the region;
- is the conformity ratio of the population with the energy supply;
- is the conformity ratio of the economic development with the energy supply.
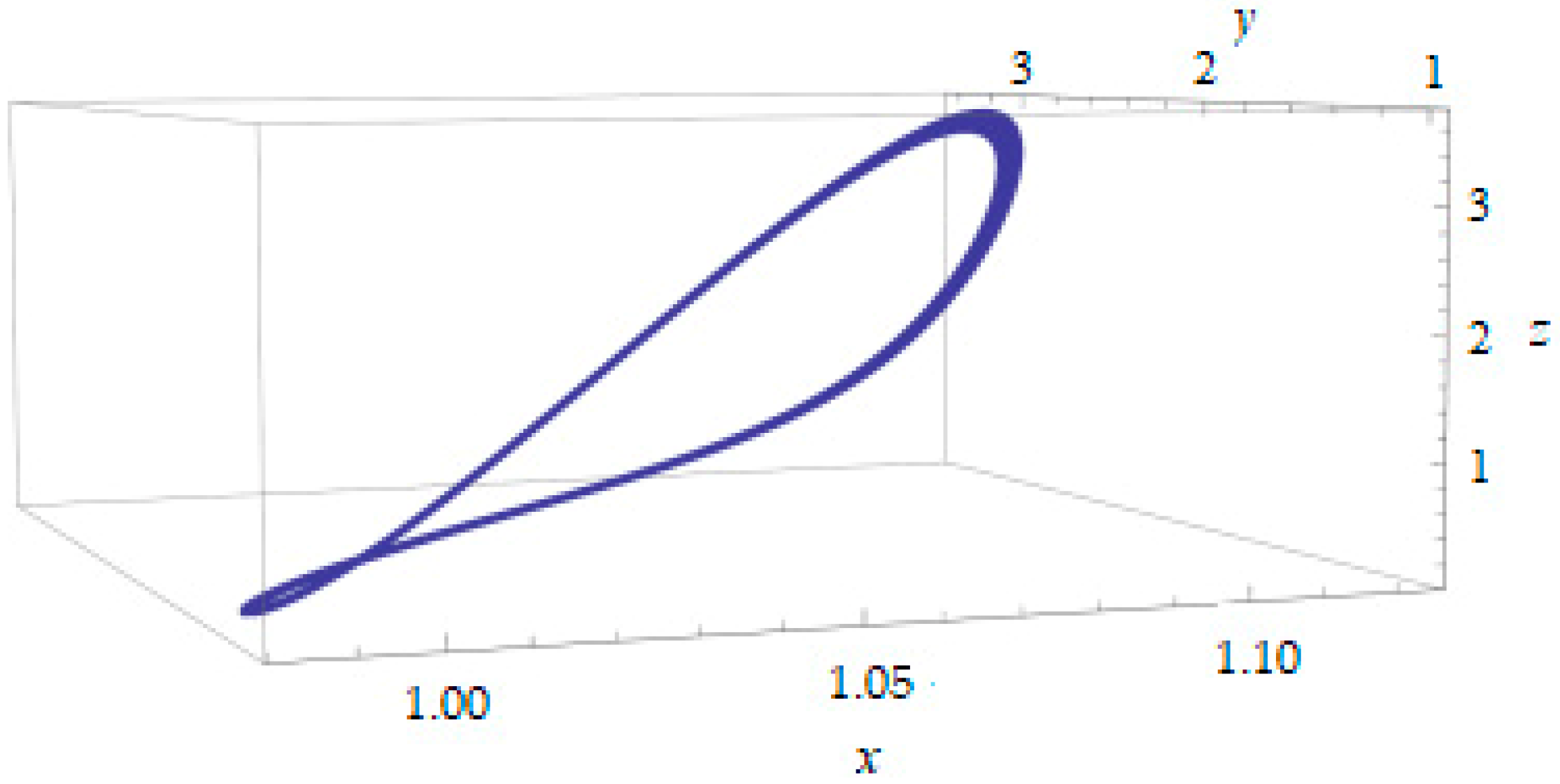
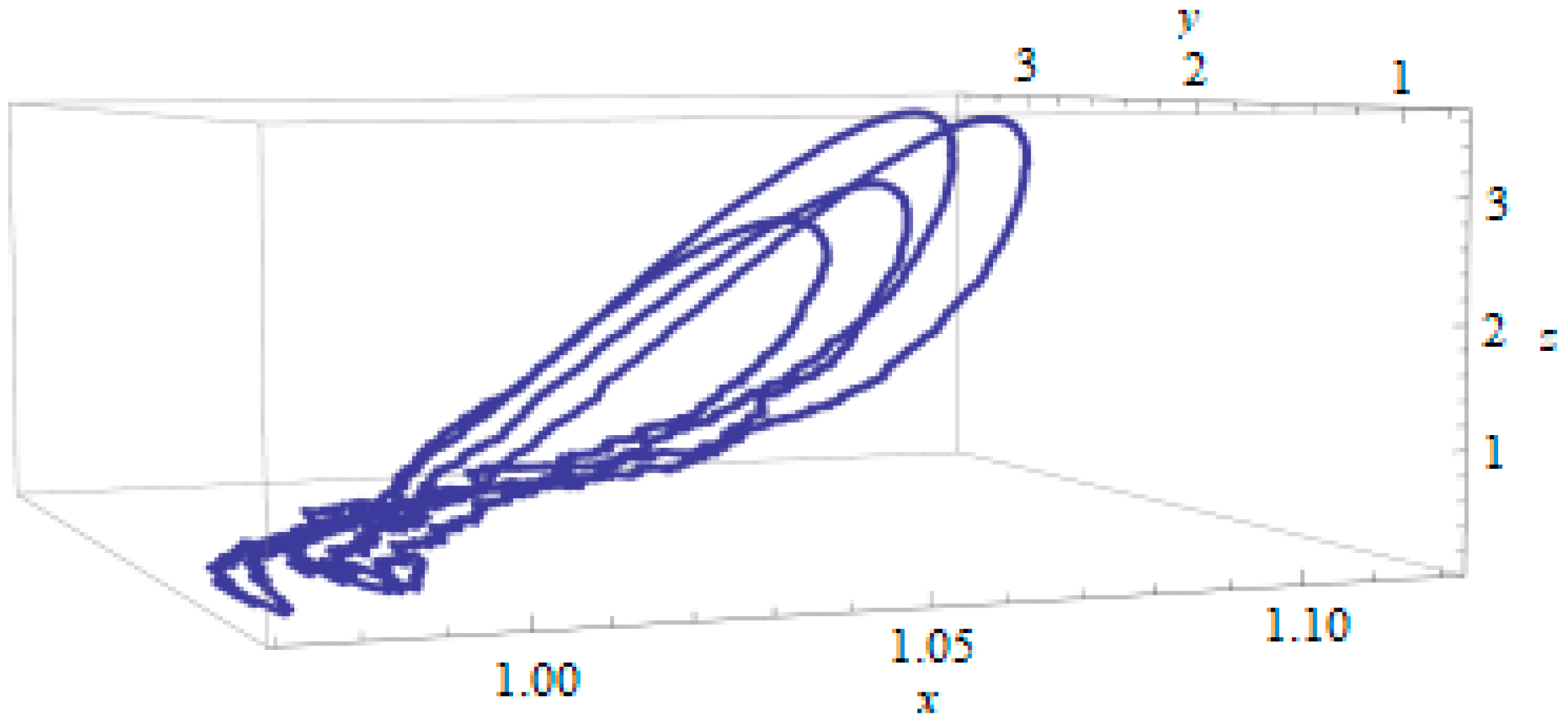
3. The Stochastic Model of Managing the Socio-Economic Development of the Region
- is the population of the region, which is not defined (the indicator is free);
- is fixed (one gives the fixed number of jobs in the real sector of the economy);
- the minimum of the variable is given:
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Williams, G. Economic impacts from development of the coastal town in queensland on tourism and regional economy. Resources 2016, 5, 48. [Google Scholar] [CrossRef]
- Rudneva, L.; Pchelintseva, I.; Gureva, M. Scenario modelling of the “green” economy in an economic space. Resources 2018, 7, 29. [Google Scholar] [CrossRef]
- Cherepovitsyn, A.; Metkin, D.; Gladilin, A. An algorithm of management decision-making regarding the feasibility of investing in geological studies of forecasted hydrocarbon resources. Resources 2018, 7, 47. [Google Scholar] [CrossRef]
- Samarskii, A.A.; Mikhaylov, A.P. Mathematical Modelling: Ideas. Methods. Examples, 2nd ed.; Physical and Mathematical Literature Publishing Company, Russian Academy of Sciences: Moscow, Russia, 2002; p. 320. [Google Scholar]
- Boldyrev, Y. Supercomputer Technology as the Modern Realization of Multidisciplinary Approach in Education and Scientific Activity. Available online: https://infocom.spbstu.ru/en/article/2010.15.16/ (accessed on 29 April 2010).
- Boldyrev, Y.; Petukhov, E. Supercomputer Technologies and Their Applications; Publishing house of Polytechnic University: Saint Petersburg, Russia, 2011. [Google Scholar]
- Arnol’d, V. Hard and Soft Mathematical Models. Available online: http://files.school-collection.edu.ru/dlrstore/d62a30c8-a780-11dc-945c-d34917fee0be/09_arnold-models.pdf (accessed on 23 March 2011).
- Klochkov, Y.; Gazizulina, A.; Golovin, N.; Glushkova, A.; Zh, S. Information model-based forecasting of technological process state. In Proceedings of the 2017 International Conference on Infocom Technologies and Unmanned Systems (Trends and Future Directions) (ICTUS), Dubai, United Arab Emirates, 18–20 December 2017; pp. 709–712. [Google Scholar]
- Petrov, L.F. Methods of Nonlinear Dynamics as a Management Tool of Economic Efficiency. Available online: http://info.e-c-m.ru/UER_23_03_2011.pdf (accessed on 23 March 2011).
- Burlov, V.; Chernogorskiy, S.; Shvetsov, K. An Inverse Solution-Based Conception of Guaranteed Control of the RF Arctic Zone’s Sustainable Development. Available online: https://elibrary.ru/download/elibrary_27552991_69787270.htm (accessed on 23 March 2011).
- Watanabe, S.; Ikeda, N. Stochastic Differential Equations and Diffusion Processes, 2nd ed.; Elsevier: Tokyo, Japan, 2014; p. 448. [Google Scholar]
- Gardiner, K.V. Stochastic Methods in the Natural Sciences; MIR: Moscow, Russia, 1986. [Google Scholar]
- Arnol’d, V. Mathematics of Chaos. Mosc. Math. J. 2010, 10, 273–283. [Google Scholar] [CrossRef]
- Arrowsmith, D.K.; Place, C.M. Dynamical Systems: Differential Equations Maps and Chaotic Behavior; Chapman & Hall: London, OH, USA, 1992. [Google Scholar]
- Chernogorskiy, S.; Shvetsov, K.; Zherelo, A. Mathematical Model of the Controlled Sustainable Development of the Region. Nonlin. Phenom. Complex Syst. 2016, 19, 297–302. [Google Scholar]
- Gianni, D.; D’Ambrogio, A.; Tolk, A. Modeling and Simulation-Based Systems Engineering Handbook; CRC Press: London, OH, USA, 2014. [Google Scholar]
- Goode, H.; Machol, R. System Engineering: An Introduction to the Design of Large-scale Systems; McGraw-Hill: New York, NY, USA, 1957. [Google Scholar]
- Ivanter, V.; Leksin, V.; Porfiriev, B. Basic Conceptual and Methodological Issues of the Special-Purpose Program Management of the Development of the Russian Arctic’s. Available online: https://elibrary.ru/download/elibrary_23111096_84037911.pdf (accessed on 23 March 2011).
- Kloeden, P.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Didenko, N.I.; Klochkov, Y.S.; Skripnuk, D.F. Ecological criteria for comparing linear and circular economies. Resources 2018, 7, 48. [Google Scholar] [CrossRef]
- Didenko, N.I.; Skripnuk, D.F.; Kikkas, K.N.; Sevashkin, V.; Romashkin, G.; Kulik, S.V. Innovative and technological potential of the region and its impact on the social sector development. In Proceedings of the 2018 International Conference on Information Networking (ICOIN), Chiang Mai, Thailand, 10–12 January 2018; pp. 611–615. [Google Scholar]
- Didenko, N.I.; Skripnuk, D.F.; Mirolyubova, O.V. Big data and the global economy. In Proceedings of the 2017 Tenth International Conference Management of Large-Scale System Development (MLSD), Moscow, Russia, 2–4 October 2017; pp. 1–5. [Google Scholar]
- Pogodaeva, T.V.; Zhaparova, D.V.; Rudenko, D.Y.; Skripnuk, D.F. Innovations and socio-economic development: Problems of the natural resources intensive use regions. Mediterr. J. Soc Sci. 2015, 6, 129–135. [Google Scholar] [CrossRef]
- Rudenko, D.; Skripnuk, D. Environmental Kuznets Curve: The Case of Arctic Russian Regions. Available online: https://search.proquest.com/openview/1e39d5eb710e8cfbd65e855944df1c7a/1?pq-origsite=gscholar&cbl=1536338 (accessed on 23 March 2011).
- Antipov, D.V.; Akhmetzhanova, G.V.; Antipova, O.I.; Gazizulina, A.U.; Sharov, R. Organizational models of teal organizations. In Proceedings of the Reliability, Infocom Technologies and Optimization (Trends and Future Directions), Noida, India, 20–22 September 2017; pp. 222–230. [Google Scholar]
- Gazizulina, A.Y.; Mirolyubova, O.V.; Konakhina, N.A.; Kikkas, K.N.; Grigorieva, A.A.; Danilova, S.Y. Problems of forming requirements to training of specialists for industrial and economic complex. In Proceedings of the 2017 IEEE VI Forum Strategic Partnership of Universities and Enterprises of Hi-Tech Branches (Science. Education. Innovations) (SPUE), St. Petersburg, Russia, 15–17 November 2017; pp. 196–198. [Google Scholar]
- Gazizulina, A.; Eskina, E.; Vasilieva, I.; Valeeva, O. The reasons for the increase in self-organization in companies. Int. J. Reliab. Qual. Saf. Eng. 2017, 24, 1740002. [Google Scholar] [CrossRef]
- Romashkina, G.F.; Didenko, N.I.; Skripnuk, D.F. Socioeconomic modernization of Russia and its arctic regions. Stud. Russ. Econ. Develop. 2017, 28, 22–30. [Google Scholar] [CrossRef]
- Bogach, N.; Dyachkov, V.; Lamtev, A.; Lezhenin, Y. Agent-based modeling software for natural and rural ecosystems. Eng. Rural Develop. 2017, 16, 742–747. [Google Scholar] [CrossRef]
- Ziniakov, V.Y.; Gorodetskiy, A.E.; Tarasova, I.L. Control of vitality and reliability analysis. Stud. Syst. Decis. Contr. 2016, 49, 193–204. [Google Scholar] [CrossRef]
- Bolshev, A.S.; Frolov, S.A. Mathematical modelling of level ice with continental shelf structures interaction. IOP Conf. Ser. Earth Environ. Sci. 2018, 193, 012006. [Google Scholar] [CrossRef]
- Kotlov, A.A.; Maksimenko, I.A. Mathematical modelling the seasonal load of opposite compressors. AIP Conf. Proc. 2018, 2007, 030053. [Google Scholar] [CrossRef]
- Polosin, A.N.; Chistyakova, T.B. Mathematical modeling for resource and energy saving control of extruders in multi-assortment productions of polymeric films. J. Phys. Conf. Ser. 2018, 1015, 032104. [Google Scholar] [CrossRef]
- Borremans, A.D.; Zaychenko, I.M.; Iliashenko, O.Y. Digital economy. IT strategy of the company development. MATEC Web Conf. 2018, 170, 01034. [Google Scholar] [CrossRef]
- Rytova, E.V.; Kozlov, A.V.; Gutman, S.S.; Zaychenko, I.M. Analysis of the regulatory and legal framework of the socio-economic development in the far north regions of Russia. J. Adv. Res. Law Econ. 2016, 7, 1828–1836. [Google Scholar] [CrossRef]
- Nikolova, L.V.; Rodionov, D.G.; Litvinenko, А.N. Sustainability of the business in the conditions of globalization. In Proceedings of the 30th International Business Information Management Association Conference, Madrid, Spain, 8–9 November 2017; pp. 417–421. [Google Scholar]
- Didenko, N.I.; Romashkina, E.S. Assessment of the influence of the extraction of energy resources on the environment. IOP Conf. Ser. Earth Environ. Sci. 2018, 180, 012014. [Google Scholar] [CrossRef]
- Didenko, N.I.; Skripnuk, D.F.; Kikkas, K.N.; Merkulov, V.; Romashkin, G.; Kulik, S.V. The analysis of convergence—divergence in the development of innovative and technological processes in the countries of the arctic council. In Proceedings of the 2018 International Conference on Information Networking (ICOIN), Chiang Mai, Thailand, 10–12 January 2018; pp. 626–631. [Google Scholar] [CrossRef]
- Khludova, M. Evaluation model for the stochastic flowshop cyclic scheduling problem. In Proceedings of the 2017 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), St. Petersburg, Russia, 16–19 May 2017; pp. 1–4. [Google Scholar]
- Baranov, A.O.; Muzyko, E.I.; Maslov, M.P.; Pavlov, V.N. Research methodology of fuzzy characteristics of real options in innovative projects. In Proceedings of the 2016 13th International Scientific-Technical Conference on Actual Problems of Electronics Instrument Engineering (APEIE), Novosibirsk, Russia, 3–6 October 2016; pp. 207–213. [Google Scholar]
| Model Complexity Degree | System Complexity Degree | |||
|---|---|---|---|---|
| Small-Dimensional Natural Scientific or Technical System | Complex System (Meteorology) | Economics | Socio-Economic System | |
| Simple linear models | Resonance | Extremely narrow applicability | Exponentially growing values (do not correspond the reality) | Exponentially growing values (do not correspond the reality) |
| Quasi-linear models | Loss of sustainability. Bifurcation. Synchronization | Some non-linear effects | Some non-linear effects | Some non-linear effects |
| Essentially non-linear small-dimensional models | Various non-linear effects. Determinate chaos | Strange attractor. The butterfly effect | Oscillations of values around the trend line. Loss of trend sustainability as an economic crisis | The crowd-effect as the crisis manifestation of synchronization |
| Synergy. Catastrophic theory. | Self-organization theory | Tornado as a loss of sustainability of laminar current | Econophysics. Synergy economics | Sequenced development, degree of freedom as a measure of system dissipation, chaos and order |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boldyrev, Y.; Chernogorskiy, S.; Shvetsov, K.; Zherelo, A.; Kostin, K. A Mathematical Model of Regional Socio-Economic Development of the Russian Arctic Zone. Resources 2019, 8, 45. https://doi.org/10.3390/resources8010045
Boldyrev Y, Chernogorskiy S, Shvetsov K, Zherelo A, Kostin K. A Mathematical Model of Regional Socio-Economic Development of the Russian Arctic Zone. Resources. 2019; 8(1):45. https://doi.org/10.3390/resources8010045
Chicago/Turabian StyleBoldyrev, Yury, Sergey Chernogorskiy, Konstantin Shvetsov, Anatoly Zherelo, and Konstantin Kostin. 2019. "A Mathematical Model of Regional Socio-Economic Development of the Russian Arctic Zone" Resources 8, no. 1: 45. https://doi.org/10.3390/resources8010045
APA StyleBoldyrev, Y., Chernogorskiy, S., Shvetsov, K., Zherelo, A., & Kostin, K. (2019). A Mathematical Model of Regional Socio-Economic Development of the Russian Arctic Zone. Resources, 8(1), 45. https://doi.org/10.3390/resources8010045






