Abstract
This work touches upon the tasks of describing regional socio-economic development. The nature of the considered problem indicates the fact that the only relevant tool here is mathematical modeling. In this paper, the application of mathematical modeling is considered for the problem of managing regional development. The results of calculations based on the regional dynamic model that passes through the hierarchy of instabilities (the correspondence of the same stationary points of the model to different parameters) are presented. These instabilities lead to increasingly complex structures.
1. Introduction
This paper deals with the tasks of describing the socio-economic development of regions on the basis of constructed descriptions. For the development of the regional economy and tourism, the interested reader can refer to the input–output analysis with the resource of the tourism industry described in [1]. Another example of the development of a region is the modeling of a “green” economy: a dynamic model of the “green” economy, a general extended map, and a reduced-parametric cognitive map of the development of the “green” economy in the economic space of the region [2]. The nature of the analyzed problem indicates the fact that the only applicable tool here is mathematical modeling. Indeed, while studying various kinds of natural-science problems and developing technical systems, machines and technologies, one can rely both on the physical experiment and on the centuries-old experience of constructing models in physics, mechanics, and other branches of natural science. The same approach is barely applicable in the sphere of economic problems, not to mention the problems of effective management in tasks of that sort, where this “experimental” approach is impossible. The conceptual view of applications of mathematical modeling in the considered class of problems [3] is very instructive, since such modeling incorporates all mathematical modeling technologies mentioned by A.A. Samarskii almost 40 years ago. To calculate the parameters of investment attractiveness of the Arctic region, it is also possible to use the mathematical modeling considered by the authors in [4] for poorly researched hydrocarbon objects. Moreover, studying the problem on the level of modern advanced approaches shows that, in the class of considered problems, the implementation of mathematical modeling should be based on computer technologies for the simple reason that the object, or the problem itself, is a unique subject for research, not only as systems of “big data” but also as multi-scale systems containing elements of uncertainties [5,6,7,8].
The application of mathematical modeling approaches is considered with the example of a model problem of regional development management. The core of the model is the state function describing regional development and represented by the vector function with the components , where is the population of the region, is the number of jobs in the real sector of the regional economy, and is the indicator of energy supply in the region. The vector u(t) is the controlling vector that determines the required values for the state vector. The controlling vector has m-components [, , …, ], each of which characterize one or another controlling factor. For example, is the coefficient of demographic activity, is the coefficient of people’s anti-motivation to childbearing, is the energy-supply coefficient of the region, etc.
2. The Deterministic Model of Management of Socio-Economic Development of the Region
The models of nonlinear dynamics represent a mathematical toolset that enables one to describe and analyze the development of various dynamic systems of different complexity levels—from mechanical systems up to social ones—based on objective laws [6,9,10,11,12]. In [6], the classification of the considered systems and models according to the complexity degree and to the possible expected results of modeling is presented (see Table 1).

Table 1.
Systems and models according to the complexity degree.
The concept of managing the socio-economic development of the region is based on a synthesized model of the management process (the inverse problem of the management process). The model introduces three main indicators of the region: is the regional population, is number of jobs in the real sector of the regional economy, and is the indicator of the regional energy supply [13,14,15,16,17].
The system-forming mathematical base of the dynamic model is a system of differential equations describing the changes of the three key indicators introduced. Through the coefficients (there are nine of them all in all), the mechanisms for implementing regional policies directed to achieve the goal of public administration are formed [18].
The development of the system of differential equations can be built on the natural-scientific and the socio-economic interpretation of the meaning of regional performance indicators (i = 1, 2, 3).
We will present the construction of the regional development model in a concise form. We will start with the fact that the derivative of the population of the region is the rate of change in the population and it is naturally connected both with the population and with the number of jobs the real economy of the region (the indicator of economic development) and with the indicator of energy supply in the region . The rate of change for is proportional to the regional population itself, i.e. the higher the population is, the greater the growth rate is:
where is the demographic activity coefficient.
We will determine the influence of indicators and on the population growth rate. The number of jobs in the real sector of the regional economy is determined with the minimum number of workers in the production sector required to produce a certain assortment of goods and services [19,20,21,22,23,24,25,26,27,28].
For a given value of the number of jobs the real economy will reduce the population growth rate by , where is the coefficient of people’s anti-motivation to childbearing. Additionally, for a given value of , the energy supply will increase the regional population growth rate by the amount , where is the ratio of energy supply of the region. In other words, the more energy that enters the region there is, the higher the regional population growth rate is [29,30].
Thus, the first differential equation can be written in the following form:
Turning now to the change in the number of jobs in the real sector of the region , we note that the derivative is the rate of change of the economic development indicator. At the same time, the rate of change of the economic development indicator is inversely proportional to the number of jobs in the real sector; that is, the more jobs created in the real sector there are, the more difficult it is to increase the number of job opportunities:
where is the coefficient of people’s interest in economic development. For a given value of , if people are interested in the economic development, an increase in the regional population will increase the growth rate of economic development in the real sector by the amount , where is the coefficient of people’s interest in economic development. The manifestation of such a property is natural, since it makes up the basis of the society’s self-preservation. The reverse manifestation of this property will lead to the self-destruction of the society. For a given value of , the energy supply of the region will increase the economic growth rate by amount , where is the coefficient of energy supply of the workplaces. That is, the more energy there is for the development of the real sector of the economy, the higher the economic growth is [29]. Thus, the differential equation for the indicator takes the following form:
Turning to the indicator of energy supply of the region , we point out that its derivative is the rate of change in the region’s energy supply. It is quite obvious that the rate of change in energy consumption is proportional to the amount of energy consumed; that is, the more energy consumed in the society there is, the higher the growth rate of the energy supply is:
where is the development factor of the regional energy supply.
For a given value of , the growth of regional population will reduce the rate of change in the energy consumption by amount , where is the conformity ratio of the population with the energy supply. As the population increases, the rate of change in energy supply decreases. For a given value , an increase in the number of jobs in the real sector will reduce the rate of change in energy supply by amount , where is the conformity ratio of the economic development and the energy supply. In other words, the higher the growth rate of the real sector of the regional economy is, the lower the energy supply per workplace is [29].
Hence, the differential equation for the indicator can be written in the following form:
Thus, the management model of sustainable socio-economic development of the region has the following form (all the indicators are presented in the form of relative, dimensionless values):
where the demographic indicator is the value , where is the population at time t, and is the population at the initial time point . The economic development indicator is , where is the number of jobs of the real sector of economy at time t, and is the number of jobs of the real sector of economy at time . Eventually, the energy supply indicator is , where is the current energy supply indicator at time t, and is the current energy supply indicator at time . The coefficients (i = 1, 2, …, 9) in the system of Equation (7) are the following factors:
- is the demographic activity coefficient;
- is the coefficient of people’s anti-motivation to childbearing;
- is the energy supply coefficient;
- is the coefficient of people’s interest in economic development;
- is the coefficient of the real sector economic development;
- is the coefficient of energy supply per workplace;
- is the energy supply coefficient of the region;
- is the conformity ratio of the population with the energy supply;
- is the conformity ratio of the economic development with the energy supply.
3. The Stochastic Model of Managing the Socio-Economic Development of the Region
The nine coefficients involved in the system of differential equations are the components of the vector of public administration: [.
The state of the region vector for the model is
Such an approach to describing the regional management makes it possible to base the management concept on the formulation of the following optimal management problem [30,31,32].
Let us formulate the management problem under the assumption that the controlling vector u is sought on the number set of its components. In this case we are dealing with the problem of parametric optimization. Thus, it is required to determine the vector of the control parameters u, under which the state of the region vector can be described by the system of Equation (7) under the following conditions:
- is the population of the region, which is not defined (the indicator is free);
- is fixed (one gives the fixed number of jobs in the real sector of the economy);
- the minimum of the variable is given:
The system of Equation (7) [33,34,35,36,37] can only partially describe the development dynamics of the region, because is deterministic and therefore does not take into account fluctuations that are constantly arising in the system. These fluctuations are formed by different types of markets (goods, capital, and labor) against the background of competition and limited resources. For these reasons, at the next stage of the research, one moves on to implementation of statistical methods, which also enables more accurate forecasting and the creation of possible future scenarios. However, statistical methods generally require a significant amount of statistical data and some additional studies to identify a set of influencing factors, with a subsequent search for dependencies [38]. From our point of view, the main problem is the determination of the fullest possible number of factors that are used for the further analysis. This will lead to a significant change in the type of model used and will increase the number of parameters used. In addition, the problem of the availability of statistical data on all the possible parameters still remains [39].
Another important point is the evaluation of the values of integral economic indicators, for example, the generalized index of industrial growth. These indicators are especially nonlinearly dependent on the solution of the system of Equation (7). Determining the values of such indicators requires a large-scale simulation of the trajectories space, whereas the modeling scape depends on the desired accuracy.
In order to simplify the analysis, we propose limiting the number of parameters and ignoring the entire set of parameter space. The model will be constructed only on the basis of the factors selected by the experts. It is proposed that a factor of the stochastic nature of the described processes is introduced into the system of Equation (7) for the purpose of taking the stochastic effect into consideration. In this case, due to the transition to a system of stochastic differential equations with a small number of parameters, it is possible to model the behavior of the system not only for a certain set of statistically distinguished values of the parameters. This will also allow us to calculate the integral parameters mentioned above. For solving the problem, the so-called weak methods are used for short time periods, and strong methods (for example, Monte Carlo method) are used for larger time periods. The latter require considerable computational resources, since, in spite of the relative simplicity of the computations performed for calculating of a separate trajectory, a considerable number of independent experiments must be carried out. The required number of simulated trajectories depends not only on the time frame that serves the basis for the simulation but also on the desired accuracy and the type of functionality, in the case of calculating the integrated indicators.
The authors proposed a modified system of Equation (7), which takes into account possible random fluctuations in the calculated parameters.
where in the second equation an additional term is introduced. The term shows that the higher the population is, the higher the competition on the labor market will be; moreover, the more incentives to stick to the job there are, the lower the personnel turnover will be. In the system of Equation (9), a, b, c, d, e, f are calibration coefficients that can be obtained from statistical data processing. The traditional approach to solving the system of Equation (9) is the use of powerful computational resources to determine a certain sample from the entire space of trajectories.
It is necessary to emphasize that the solution of the above-stated problems at the current level involves a high amount of computational experiments. Preliminary evaluation of the needed amount of calculation clearly shows that the capabilities of even powerful workstations are not sufficient.
In contrast to the behavior of the previously introduced deterministic model, the stochastic character of real systems plays an important role in practice. As it is one of the factors leading the system to non-deterministic behavior, one can consider, for example, an economic crisis that leads to the loss of stability, bifurcation, and the emergence of new stable states of the system.
The presence of fluctuations, as a rule, leads to errors in estimating the real parameters of the system and, eventually, to forecasting errors for the observed phenomena. In order to demonstrate the behavioral difference of deterministic and stochastic systems, we added only one stochastic term to the second equation of the original system (Equation (9)). Having introduced the term, we tried to relate the magnitude of fluctuations in the number of jobs to the available working-age population. It was also assumed that the stochastic differential is an Ito differential [7,8,40].
The state vector of the region was defined as the solution of Equations (7) and (9) under the controlling vector ], where , and the boundary conditions are as follows:
is not fixed (free);
is fixed at time t (a fixed number of jobs in the real sector of the economy at time t is given).
In this case, as was stated above, one looks for the minimum of the s3 parameter: .
We present here the results of calculations for the deterministic and the stochastic models. The solution of the deterministic model is shown in Figure 1.
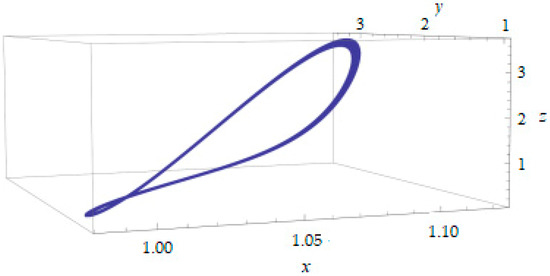
Figure 1.
Solution for the deterministic model.
The solution of the stochastic model is shown in Figure 2.
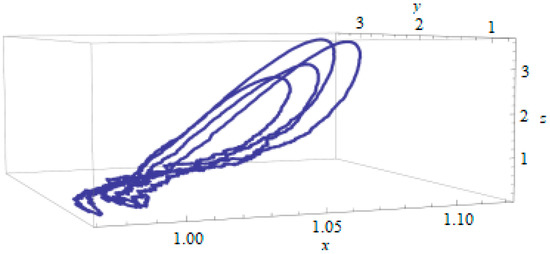
Figure 2.
Solution for the stochastic model.
It should be noted that, due to the properties of the Ito stochastic integral [7,8,40], the averaged trajectory of the solution for the system of Equation (9) will coincide with the trajectory of the deterministic system (see Figure 1). However, it is necessary to pay attention to Figure 2, where the behavior of one fixed trajectory of the solution of the proposed stochastic system is shown. The comparison of the trajectories in Figure 1 and Figure 2 clearly shows that, during significant time intervals, the trajectories differ substantially. Thus, there is a need to evaluate additional parameters of the system in order to describe its possible behavior more accurately. For example, it would be useful to evaluate decision parameters such as the evolution of variance, confidence intervals, and the spatial distribution of the trajectories.
4. Conclusions
Summing up results of the work, we can indicate directions of further research. One priority is the improvement in the mathematical models considered here. This concerns both the model described by the deterministic system of Equation (7) and the stochastic model expressed in Equation (9). Such work would clarify the structure of the right-hand sides of Equations (7) and (9), essentially bringing about more accurate procedures for describing relations for the parameters—the components of the controlling vector u. A second direction is the investigation of the connection between Equation (7) and Equation (9).
Author Contributions
Conceptualization, S.C.; data curation, Y.B.; formal analysis, K.S.; methodology, K.K.; Software, A.Z.
Funding
The paper is based on research carried out with the financial support of the grant of the Russian Scientific Foundation (Project No. 14-38-00009, The program-targeted management of the Russian Arctic zone development), Peter the Great St. Petersburg Polytechnic University.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Williams, G. Economic impacts from development of the coastal town in queensland on tourism and regional economy. Resources 2016, 5, 48. [Google Scholar] [CrossRef]
- Rudneva, L.; Pchelintseva, I.; Gureva, M. Scenario modelling of the “green” economy in an economic space. Resources 2018, 7, 29. [Google Scholar] [CrossRef]
- Cherepovitsyn, A.; Metkin, D.; Gladilin, A. An algorithm of management decision-making regarding the feasibility of investing in geological studies of forecasted hydrocarbon resources. Resources 2018, 7, 47. [Google Scholar] [CrossRef]
- Samarskii, A.A.; Mikhaylov, A.P. Mathematical Modelling: Ideas. Methods. Examples, 2nd ed.; Physical and Mathematical Literature Publishing Company, Russian Academy of Sciences: Moscow, Russia, 2002; p. 320. [Google Scholar]
- Boldyrev, Y. Supercomputer Technology as the Modern Realization of Multidisciplinary Approach in Education and Scientific Activity. Available online: https://infocom.spbstu.ru/en/article/2010.15.16/ (accessed on 29 April 2010).
- Boldyrev, Y.; Petukhov, E. Supercomputer Technologies and Their Applications; Publishing house of Polytechnic University: Saint Petersburg, Russia, 2011. [Google Scholar]
- Arnol’d, V. Hard and Soft Mathematical Models. Available online: http://files.school-collection.edu.ru/dlrstore/d62a30c8-a780-11dc-945c-d34917fee0be/09_arnold-models.pdf (accessed on 23 March 2011).
- Klochkov, Y.; Gazizulina, A.; Golovin, N.; Glushkova, A.; Zh, S. Information model-based forecasting of technological process state. In Proceedings of the 2017 International Conference on Infocom Technologies and Unmanned Systems (Trends and Future Directions) (ICTUS), Dubai, United Arab Emirates, 18–20 December 2017; pp. 709–712. [Google Scholar]
- Petrov, L.F. Methods of Nonlinear Dynamics as a Management Tool of Economic Efficiency. Available online: http://info.e-c-m.ru/UER_23_03_2011.pdf (accessed on 23 March 2011).
- Burlov, V.; Chernogorskiy, S.; Shvetsov, K. An Inverse Solution-Based Conception of Guaranteed Control of the RF Arctic Zone’s Sustainable Development. Available online: https://elibrary.ru/download/elibrary_27552991_69787270.htm (accessed on 23 March 2011).
- Watanabe, S.; Ikeda, N. Stochastic Differential Equations and Diffusion Processes, 2nd ed.; Elsevier: Tokyo, Japan, 2014; p. 448. [Google Scholar]
- Gardiner, K.V. Stochastic Methods in the Natural Sciences; MIR: Moscow, Russia, 1986. [Google Scholar]
- Arnol’d, V. Mathematics of Chaos. Mosc. Math. J. 2010, 10, 273–283. [Google Scholar] [CrossRef]
- Arrowsmith, D.K.; Place, C.M. Dynamical Systems: Differential Equations Maps and Chaotic Behavior; Chapman & Hall: London, OH, USA, 1992. [Google Scholar]
- Chernogorskiy, S.; Shvetsov, K.; Zherelo, A. Mathematical Model of the Controlled Sustainable Development of the Region. Nonlin. Phenom. Complex Syst. 2016, 19, 297–302. [Google Scholar]
- Gianni, D.; D’Ambrogio, A.; Tolk, A. Modeling and Simulation-Based Systems Engineering Handbook; CRC Press: London, OH, USA, 2014. [Google Scholar]
- Goode, H.; Machol, R. System Engineering: An Introduction to the Design of Large-scale Systems; McGraw-Hill: New York, NY, USA, 1957. [Google Scholar]
- Ivanter, V.; Leksin, V.; Porfiriev, B. Basic Conceptual and Methodological Issues of the Special-Purpose Program Management of the Development of the Russian Arctic’s. Available online: https://elibrary.ru/download/elibrary_23111096_84037911.pdf (accessed on 23 March 2011).
- Kloeden, P.; Platen, E. Numerical Solution of Stochastic Differential Equations; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Didenko, N.I.; Klochkov, Y.S.; Skripnuk, D.F. Ecological criteria for comparing linear and circular economies. Resources 2018, 7, 48. [Google Scholar] [CrossRef]
- Didenko, N.I.; Skripnuk, D.F.; Kikkas, K.N.; Sevashkin, V.; Romashkin, G.; Kulik, S.V. Innovative and technological potential of the region and its impact on the social sector development. In Proceedings of the 2018 International Conference on Information Networking (ICOIN), Chiang Mai, Thailand, 10–12 January 2018; pp. 611–615. [Google Scholar]
- Didenko, N.I.; Skripnuk, D.F.; Mirolyubova, O.V. Big data and the global economy. In Proceedings of the 2017 Tenth International Conference Management of Large-Scale System Development (MLSD), Moscow, Russia, 2–4 October 2017; pp. 1–5. [Google Scholar]
- Pogodaeva, T.V.; Zhaparova, D.V.; Rudenko, D.Y.; Skripnuk, D.F. Innovations and socio-economic development: Problems of the natural resources intensive use regions. Mediterr. J. Soc Sci. 2015, 6, 129–135. [Google Scholar] [CrossRef]
- Rudenko, D.; Skripnuk, D. Environmental Kuznets Curve: The Case of Arctic Russian Regions. Available online: https://search.proquest.com/openview/1e39d5eb710e8cfbd65e855944df1c7a/1?pq-origsite=gscholar&cbl=1536338 (accessed on 23 March 2011).
- Antipov, D.V.; Akhmetzhanova, G.V.; Antipova, O.I.; Gazizulina, A.U.; Sharov, R. Organizational models of teal organizations. In Proceedings of the Reliability, Infocom Technologies and Optimization (Trends and Future Directions), Noida, India, 20–22 September 2017; pp. 222–230. [Google Scholar]
- Gazizulina, A.Y.; Mirolyubova, O.V.; Konakhina, N.A.; Kikkas, K.N.; Grigorieva, A.A.; Danilova, S.Y. Problems of forming requirements to training of specialists for industrial and economic complex. In Proceedings of the 2017 IEEE VI Forum Strategic Partnership of Universities and Enterprises of Hi-Tech Branches (Science. Education. Innovations) (SPUE), St. Petersburg, Russia, 15–17 November 2017; pp. 196–198. [Google Scholar]
- Gazizulina, A.; Eskina, E.; Vasilieva, I.; Valeeva, O. The reasons for the increase in self-organization in companies. Int. J. Reliab. Qual. Saf. Eng. 2017, 24, 1740002. [Google Scholar] [CrossRef]
- Romashkina, G.F.; Didenko, N.I.; Skripnuk, D.F. Socioeconomic modernization of Russia and its arctic regions. Stud. Russ. Econ. Develop. 2017, 28, 22–30. [Google Scholar] [CrossRef]
- Bogach, N.; Dyachkov, V.; Lamtev, A.; Lezhenin, Y. Agent-based modeling software for natural and rural ecosystems. Eng. Rural Develop. 2017, 16, 742–747. [Google Scholar] [CrossRef]
- Ziniakov, V.Y.; Gorodetskiy, A.E.; Tarasova, I.L. Control of vitality and reliability analysis. Stud. Syst. Decis. Contr. 2016, 49, 193–204. [Google Scholar] [CrossRef]
- Bolshev, A.S.; Frolov, S.A. Mathematical modelling of level ice with continental shelf structures interaction. IOP Conf. Ser. Earth Environ. Sci. 2018, 193, 012006. [Google Scholar] [CrossRef]
- Kotlov, A.A.; Maksimenko, I.A. Mathematical modelling the seasonal load of opposite compressors. AIP Conf. Proc. 2018, 2007, 030053. [Google Scholar] [CrossRef]
- Polosin, A.N.; Chistyakova, T.B. Mathematical modeling for resource and energy saving control of extruders in multi-assortment productions of polymeric films. J. Phys. Conf. Ser. 2018, 1015, 032104. [Google Scholar] [CrossRef]
- Borremans, A.D.; Zaychenko, I.M.; Iliashenko, O.Y. Digital economy. IT strategy of the company development. MATEC Web Conf. 2018, 170, 01034. [Google Scholar] [CrossRef]
- Rytova, E.V.; Kozlov, A.V.; Gutman, S.S.; Zaychenko, I.M. Analysis of the regulatory and legal framework of the socio-economic development in the far north regions of Russia. J. Adv. Res. Law Econ. 2016, 7, 1828–1836. [Google Scholar] [CrossRef]
- Nikolova, L.V.; Rodionov, D.G.; Litvinenko, А.N. Sustainability of the business in the conditions of globalization. In Proceedings of the 30th International Business Information Management Association Conference, Madrid, Spain, 8–9 November 2017; pp. 417–421. [Google Scholar]
- Didenko, N.I.; Romashkina, E.S. Assessment of the influence of the extraction of energy resources on the environment. IOP Conf. Ser. Earth Environ. Sci. 2018, 180, 012014. [Google Scholar] [CrossRef]
- Didenko, N.I.; Skripnuk, D.F.; Kikkas, K.N.; Merkulov, V.; Romashkin, G.; Kulik, S.V. The analysis of convergence—divergence in the development of innovative and technological processes in the countries of the arctic council. In Proceedings of the 2018 International Conference on Information Networking (ICOIN), Chiang Mai, Thailand, 10–12 January 2018; pp. 626–631. [Google Scholar] [CrossRef]
- Khludova, M. Evaluation model for the stochastic flowshop cyclic scheduling problem. In Proceedings of the 2017 International Conference on Industrial Engineering, Applications and Manufacturing (ICIEAM), St. Petersburg, Russia, 16–19 May 2017; pp. 1–4. [Google Scholar]
- Baranov, A.O.; Muzyko, E.I.; Maslov, M.P.; Pavlov, V.N. Research methodology of fuzzy characteristics of real options in innovative projects. In Proceedings of the 2016 13th International Scientific-Technical Conference on Actual Problems of Electronics Instrument Engineering (APEIE), Novosibirsk, Russia, 3–6 October 2016; pp. 207–213. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).